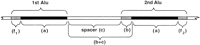Biased Distribution of Inverted and Direct Alus in the Human Genome: Implications for Insertion, Exclusion, and Genome Stability
Abstract
Alu sequences, the most abundant class of large dispersed DNA repeats in human chromosomes, contribute to human genome dynamics. Recently we reported that long inverted repeats, including humanAlus, can be strong initiators of genetic change in yeast. We proposed that the potential for interactions between adjacent, closely related Alus would influence their stability and this would be reflected in their distribution. We have undertaken an extensive computational analysis of all Alus (the database is athttp://dir.niehs.nih.gov/ALU) to better understand their distribution and circumstances under which Alu sequences might affect genome stability. Alus separated by <650 bp were categorized according to orientation, length of regions sharing high sequence identity, distance between highly identical regions, and extent of sequence identity. Nearly 50% of all Alu pairs have long alignable regions (>275 bp), corresponding to nearly full-length Alus, regardless of orientation. There are dramatic differences in the distributions and character of Alupairs with closely spaced, nearly identical regions. For Alupairs that are directly repetitive, ∼30% have highly identical regions separated by <20 bp, but only when the alignments correspond to near full-size or half-size Alus. The opposite is found for the distribution of inverted repeats: Alu pairs with aligned regions separated by <20 bp are rare. Furthermore, closely spaced direct and inverted Alus differ in their truncation patterns, suggesting differences in the mechanisms of insertion. At larger distances, the direct and inverted Alu pairs have similar distributions. We propose that sequence identity, orientation, and distance are important factors determining insertion of adjacentAlus, the frequency and spectrum of Alu-associated changes in the genome, and the contribution of Alu pairs to genome instability. Based on results in model systems and the present analysis, closely spaced inverted Alu pairs with long regions of alignment are likely at-risk motifs (ARMs) for genome instability.
The genomes of many complex organisms contain short, interspersed, intermediate repetitive elements that are nonviral, nonautonomous transposons. The Alu sequence elements, which are derived from 7sRNAs, are the most numerous in primates (for review, see Novick et al. 1996), with the human genome containing over 1,000,000 Alu sequences, or ∼10% of the total DNA (Jurka 1998).
The dissemination of diverged Alu repeats over the last 65 million years have contributed to the structure, function, evolution, and diversity of the human genome. Alus have been regarded as “junk” DNA because of their high frequency and inert nature. Retroposed Alu insertions, however, can coevolve in the context of their target DNA and hence take on diverse functions (Szmulewicz et al. 1998). Besides becoming a structural genetic component by integrating into an exon (Mullersman and Pfeffer 1995), Alu elements can serve in a regulatory capacity through diverse mechanisms. They also can behave as a modulator of DNA replication (Tsuchiya et al. 1998), a positive ( Norris et al. 1995; Gu et al. 1997) or negative enhancer, a regulator of an enhancer, a mediator of alternative splicing, or have a role in genetic imprinting. Recently, Alus also have been proposed to downregulate translation in response to cellular stress and viral infection by antagonizing double-stranded RNA-activated kinase PKR activation (Chu et al. 1998) and they are the subject of p53 transcriptional control (Chesnokov et al. 1996). These many Alu functions help to explain the retention of Alu sequences in the genome.
Alus also may have negative consequences and impact on human health. Besides their ability to retropose to inappropriate regions or to facilitate unequal homologous recombination events (Deininger and Batzer 1999), Alu sequences consist of highly methylated CpG islands that potentiate a risk for point mutations through deamination of 5′ methyl-deoxycytidine. Alu insertions have been found in the vicinity of several diverse human disease-associated genes and Alu-mediated mutagenesis has been estimated to contribute to 0.4% of new human genetic diseases (Deininger and Batzer 1999). Examples include breast cancer (Miki et al. 1996), acute myeloid leukemia (Strout et al. 1998), neurofibromatosis (Wallace et al. 1991), hemophilia B (Vidaud et al. 1993), hypertension (Muratani et al. 1993; Kitamura et al. 1996;Anderson et al. 1998), Ehlers-Danlos syndrome type VI (Pousi et al. 1994, 1998; Toriello et al. 1996; Heikkinen et al. 1997),alphazero-thalassemia (Harteveld et al. 1997), and Tay-Sachs disease (Myerowitz and Hogikyan 1987).
Based on their abundance and an average of approximately 85% identity (Shen et al. 1991), they are considered as potential sites of recombination and, therefore, threats to genome stability. Although several diseases have been associated with rearrangements involvingAlu interactions including cancer (Miki et al. 1996; Slebos et al. 1998; Strout et al. 1998), Tay-Sachs disease (Myerowitz and Hogikyan 1987), and hypercholesterolemia (Chae et al. 1997),Alus generally appear to be relatively stable. However, they have the potential for instability. For example, high levels of recombination between artificial direct identical repeats have been observed in p53-defective human cells (Gebow et al. 2000).
What determines whether Alu elements will be benign or pose a threat to human health? Aside from their appearance within important regions of critical genes, we have pursued features of Aluelements and their arrangement in the human genome that would identify potential destabilizing effects as well as suggest their mode(s) of integration and/or stability. One approach is to examine the pairwise distribution of Alus with the idea that adjacent Alus might interact with higher frequency than Alus that are farther apart. A priori, the appearance and characteristics of an Alu could be independent of other Alus or, alternatively, might be influenced by adjacent Alus. For example, a nonrandom, high frequency of closely spaced Alus might indicate preferential insertion. Therefore, a study ofAlu pairs may reveal mechanisms of insertion and/or subsequent preferred changes. Findings from previous computational analysis ofAlu distributions suggest a strong bias towards pairs in which the Alus are in a direct orientation and closely spaced (Jurka 1995). They appear to integrate preferentially into AT-rich regions, for example, at the poly(A) tails of preexisting Alus. There also is a nonrandom differential distribution of Alu repeats, with clustering in some regions and a paucity of sequences in others.
Driven in part by questions of homologous interactions, we have developed approaches to analyzing Alu pairs based on regions of alignments and degree of sequence identity. Observations with yeast and mouse cells suggest that long closely related inverted repeats are unstable and can cause deletions in eukaryotes (Gordenin et al. 1993;Ruskin and Fink 1993; Lewis 1999; Lewis et al. 1999). Moreover, they are initiators of recombination in yeast (Gordenin et al. 1993; Nag and Kurst 1997; Lobachev et al. 1998). This has led us to propose that long inverted repeats can be at-risk motifs (ARMs) in the genome (Gordenin and Resnick 1998).
Recently, we demonstrated with a yeast-based model system that invertedAlu pairs are hotspots for recombination, even if diverged (Lobachev et al. 2000), suggesting that they could be sites of genomic instability in the human genome. A preliminary analysis of adjacent full-length Alus revealed that there were relatively few closely spaced inverted Alus as expected based on the results in yeast (Lobachev et al. 2000). This has led to the present extensive analysis of the distribution of Alu pairs in the human genome in order to identify motifs that are excluded and to describe motifs that might be at risk. Having established several factors that could influence the ability of inverted Alu pairs to initiate genetic change in yeast, we examined computationally the distribution of Alu pairs in the human genome according to the orientation of Alus within a pair, length of aligned regions, identity of aligned regions, distance between aligned regions, and age. While full-length Alus are ∼300 bp, they frequently are truncated. We found that the Alus in nearly half of all pairs share long regions (>275 bp) of alignment regardless of orientation and that there is a bias for young Alus in pairs whoseAlus are separated by <40 bp. There are several differences in the distribution of direct and inverted Alu pairs. The aligned regions of direct Alu pairs are frequently separated by <20 bp when the alignments correspond to full-size or half-sizeAlus. Alu pairs with long regions of alignment (>275 bp) also tended to be more closely related than shorterAlu pairs. Unlike direct Alu repeats, inverted repeats with closely spaced (<20 bp) aligned regions are rare, suggesting they are excluded from formation and/or are unstable once formed. The inverted and direct Alu pairs also exhibit very different patterns of truncation that likely reflect mechanisms of integration. Based on results in yeast and the observed distributions of adjacent Alu repeats, we suggest that there are invertedAlu motifs that are potentially unstable and may be sources of chromosome instability in somatic tissue.
RESULTS
Approaches to Analyzing Alu Pair Distribution
Our analysis of Alu pairs was guided by observations in model systems that investigated stability of large repeats and their potential for interaction. In particular, results with humanAlus and other long repeats in yeast (Nag and Kurst 1997;Lobachev et al. 1998, 2000) and other organisms ( for review, seeErlich 1989; Leach 1994) suggested that orientation, distance between regions of identity, degree of identity, and length of highly related regions could influence the likelihood that adjacent Alusequences might impact on genome stability. Biases in various classes of Alu repeats were expected to indicate differences in targeting and/or stability of Alu pairs.
First, we identified Alu sequences by comparing them to a well-defined consensus sequence (see Methods). Alu pairs were identified in which the separation was <650 bp and the orientations, direct and inverted, were identified (see Methods). Briefly,Alus were assigned an orientation D or C according to their direction in the human genome sequence database: direct with the poly(A) tail at the 3′ end or complementary with the complement of the tail at the 5′ end. There are four possible orientations for the Alu pairs corresponding two combinations of direct repeats (DD and CC) and two combinations of inverted repeats (CD with the double-strand AT-rich tails pointed outward and DC with AT tails pointed inward). In addition to orientation, the pairs were analyzed according to degree of homology (defined by the identity score; see Methods) and length of identical regions across the aligned Alu region (“a” in Fig.1). Both the distance between Alusequences (c) and more importantly the distance between aligned regions in Alu pairs were determined (see Fig. 1 and Methods). Based on the results of Lobachev et al. (2000), the latter would be an important parameter in determining the potential for instability. The distance between aligned regions was equal to the uniquespacer sequence “c” between two Alus plus anyAlu sequence “b” between them that was not common to bothAlus (i.e., there was a truncation or possibly a highly diverged region). Thus, the actual distance between aligned regions within Alu pairs (b + c) could be much longer than the apparent distance between Alus; however, this was atypical.
Diagram of an adjacent pair of Alus with aligned regions. TwoAlu sequences are presented that can be in inverted or direct-repeat orientation. The Alu sequences are identified by virtue of sharing homology with an Alu consensus sequence (see Methods). The alignment length (a) corresponds to a common (although nonidentical) region shared by both. External flanking sequences (f1) and (f2), if present, correspond to Alu regions of no (i.e., a truncation) or low similarity between the members of an Alupair. The spacer (c) consists of non-Alu sequence between the aligned regions and represents the minimal estimated distance between the two Alus. An internal flanking region is referred to as (b) so that the actual distance between aligned regions is the spacer (c) plus the internal flanking region (b) of an Alu. Therefore, the distance (b + c) is the actual distance between aligned regions of an adjacent pair of Alus.
The information about Alu distributions is available at the Web site, and the extensive Alu pair tables (CC.html, CD.html, DC.html, DD.html) are interfaced to our database. The analysis utilized human sequence information available up to September 9, 1999. (Our system provides for the efficient incorporation of new data as they are added to the human genome database.) Included in the Web site is a description of the associated chromosome region or gene to aid in identifying regions that may be “at-risk” for possible Alu-associated changes (an example is presented in Fig. 2).
An example of an on-line summary of an adjacent pair of Alus. This table corresponds to a “cell” in the CD data table found athttp://dir.niehs.nih.gov/ALU/CD.html. It shows the only twoAlu pairs identified that meet the following criteria: the shared alignment length is between 200 and 276 bp, the pairedAlus are in the CD orientation, the separation distance b + c is between 21 and 40 bp, and there is between 86% and 90% identity. The Locus ID no., fragment coordinates, and family are extracted from the original map file. The number of matches, mismatches, similarity score, and the number of gaps are extracted from the alignment output. The locus description is extracted from the original GenBank sequence data file, as is the information necessary to determine the aligned sequence coordinates for the two fragments. Other features are described in greater detail in Methods.
Preference in the Alignment Length Distribution of Paired Alus
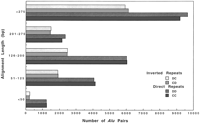
The adjacent Alus first were classified according to relative orientation. Two-thirds of the Alu pairs (46,087 / 70,324) had both Alus pointing in the same direction (Fig.3). As expected, the direct repeats were equally distributed between the DD and CC orientations (23,318 and 22,769, respectively).
Length of alignment between adjacent Alu pairs. Pairs ofAlus were analyzed according to orientation and length of alignment. As noted in the figure, the Alu pairs were grouped into five groups of alignment lengths. Pairs separated by more than 650 bp were excluded from the analysis.
The pairs of Alus then were analyzed according to their alignment lengths, which would correspond to the length of adjacentAlus over which interactions might be possible. These distributions were expected to reflect rules about insertion and stability of Alus. Pairs of Alus were divided into five categories according to the alignment length ‘a’ (in bp): >276, 201–275, 126–200, 51–125, and <50. As shown in Figure 3, nearly 75% of the Alu pairs contained aligned regions corresponding to nearly full-length (>276 bp) or half-lengthAlus regardless of orientation.
Among all the Alu pairs, 41% of direct and 50% of invertedAlu pairs had alignment lengths >276 bps. The second most-frequent category of Alu pairs, containing 24% (17,007) of the total, was that for which the alignment lengths were approximately one half the length of an Alu consensus sequence (126–200 bp). This category may reflect the dimeric nature of the ancestral full-length Alu that is 282 bps long (excluding the poly(A) tails). The upstream half of an Alu sequence, which is derived from the free left Alu monomer (FLAM for review, see Jurka 1995), is 31 nucleotides shorter than the downstream region, which is derived from the free right Alu monomer (FRAM) that contains the polyA tail. In the ancestral Alu, the FLAM and FRAM, are joined by a poly(A) stretch, with the FLAMAlu monomer containing the split RNA polymerase III promoter.
Bias and Exclusion of Adjacent Alus in Relation to Separation of Repeats
Previously, it was shown that distance was a major component in the distribution of Alu pairs, where the distance betweenAlus was simply identified as non-Alu sequence between the pair of Alus (Jurka 1995). Our analyses, based on the separation of aligned regions, are consistent with these findings. Furthermore, as discussed below, they suggest that alignment is an important component in the distribution of pairs.
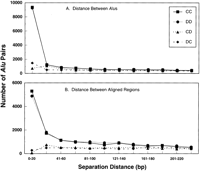
As shown in Figure 4A, nearly 30% of all the direct Alu repeat pairs are separated by <20 bp, similar to the previous report where much less of the genome had been analyzed (Jurka 1995). There was little, if any, bias in the distances separating inverted repeats when only the distance between Alusequences was considered, although the “tails-in” Alu pair category (DC) was greater for “c” <20 bp. For separations <20 bp, the total direct repeat pairs were ∼10-fold more frequent than the total inverted repeats.
Distance between adjacent Alus versus distance between aligned regions of adjacent Alus. (A) Analysis of separation distance according to distance between Alu sequences. Nearly 30% of all direct adjacent Alus are separated by only ≤20 bp. Beyond this distance, and also for all the invertedAlus, there appears to be a random distribution of separation distances (that is, there is no preference in the distance separating adjacent Alus.).(B) Analysis of separation distance according to nucleotides separating aligned regions. Inverted repeats, especially the “tails-out” (CD) category, were uncommon. Beyond 40 bp, there appears to be a random distribution of separation distances for both the inverted and direct Alu pairs. To determine the number of occurrences of Alu pairs separated by the unique spacer distance “c”, we used the Perl program Bins C. For each of the four different orientation data sets, we ranBins using 12 different window settings between 0 and 240 bp, divided into 20-bp bins. A similar program, Bins 2, was used to subdivide the data into groups depending on the “b + c” distance, representing the distance between aligned sequences (see Methods).
Analysis of Alu pair distribution on the basis of distance between aligned regions (b + c), rather than distance betweenAlu sequences revealed a much greater difference in frequencies between direct and inverted Alu repeats. Unlike for direct repeats, only a relatively small number of all the invertedAlu repeats were identified that had aligned regions separated by distances <20 bp (Fig. 4B). This may suggest that invertedAlu repeats are excluded during insertion and/or they are an unstable configuration. The total number of direct repeats separated by <20 bp was ∼12- and 25-fold, more than the DC or CD classes of inverted repeats, respectively. For separations >20 bp, the total number of inverted and direct repeats was nearly constant for different size classes and within a factor of two of each other, suggesting more random insertion. It is interesting that while the most frequent group of inverted Alus are those separated by <20 bp (Fig. 4A), the actual distance between aligned regions often is 20 to 40 bp (compare Fig. 4A to 4B), suggesting that one member of the Alupair is truncated (discussed below).
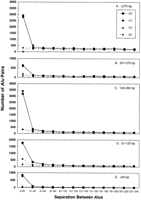
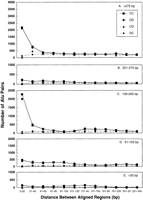
Given the importance of alignment in Alu pair distribution, the Alu pairs were analyzed according to the length of aligned region and either distance between Alu sequences (Fig.5A-E) or distance between aligned regions (Fig. 6A-E). As shown in Figure 5A-E, large differences in the relative number of direct versus inverted repeats were found when the size of aligned regions was considered. ForAlu pairs with approximately full-length alignments (>275 bp, the upper limit was arbitrarily chosen to be 500 bp, although fewAlus exceeded 300 bp) and half-length alignments (125–200 bp), there is a vast excess of direct versus inverted Alupairs for short spacer distances (<20 bp). Surprisingly, there are many fewer direct repeats in the 200–275 bp and the <125 bp alignment categories. Possibly this pattern is a reflection of the dimeric nature of Alus.
Distance between adjacent Alu sequences for Alu pairs having different alignment lengths. The adjacent Alus were analyzed as described in Figure 3A, and the pairs were grouped into five alignment length ranges (bp): (A) >275 ; (B) 201–275; (C) 126–200; (D) 51–125; (E) <50.
The distance between homologous regions for Alu pairs of different alignment lengths. The adjacent Alus were analyzed as described in Figure 3B, where the separation distance “b + c” (see Fig. 1) and the pairs were grouped info five alignment length ranges (bp): (A) >275; (B) 201–275; (C) 126–200; (D) 51–125; (E) <50.
Regardless of the size of the aligned regions, there is clearly a reduction in inverted Alu pairs with short spacer distances (<20 bp) between the aligned regions (Fig. 6A-E), although the exclusion seemed somewhat less for the DC category of the approximately full-length Alus. This is consistent with our previous results, where we found that for full-length Alus, there was a strong bias against inverted repeats that are closely-spaced (Lobachev et al. 2000). There were more than twice as many CD-oriented pairs spaced between 21–40 bp apart as there were of DC pairs (459 versus 220, respectively). Interestingly, this difference applies only to theAlu pairs in the full-length alignment category (>275 bp)(discussed below).
Sequence Identity between Paired Alu Elements
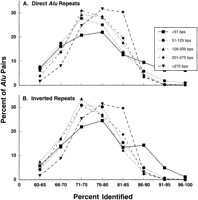
An analysis of Alu pair distribution based on identity between the Alus may reflect a role for homologous interactions in their appearance and stability. Most Alu pairs share between 65% and 85% sequence identity for both direct (Fig.7A) and inverted (Fig. 7B) repeats. There were no apparent differences between distributions for the CC vs DD orientations or the CD vs DC inverted repeat orientations (data not shown). The distributions were similar for alignment lengths up to 275 bp. The exception was for Alu pairs that had a short alignment length (<50 bp) where identities greater than 90% range were observed frequently. For the other categories (>50 bp), there were few Alu pairs that shared >90% identity. The degree of identity distribution for the approximately full-length direct and inverted Alu pairs were somewhat narrower and shifted towards greater identity, possibly suggesting interactions or conservation of some features of the Alus. It will be interesting to determine if there are regions within the full-length Alus that are more conserved.
The frequency of Alu pairs with different levels of homology in their aligned regions. Presented is the distribution of direct (A) and inverted (B) Alu pairs sharing different lengths of alignment in relation to the extent of homology. The data are derived from all the Alu pairs shown in Figure 1.
Because the distributions of direct and inverted full-lengthAlu pairs differed dramatically for short separation distances between aligned regions (Fig. 6A), we examined further their distribution in order to evaluate the relationship between separation of aligned regions and level of homology. Presented in Table1 are the frequency distributions forAlu pairs with long alignment regions (>275 bp) classified by levels of identity and separation distance between the aligned regions. Ninety percent of these Alu pairs exhibit 70%–90% sequence identity, with the number of pairs in the 70%–80% identity group about 1.7-fold greater than in the 80%–90% group, regardless of orientation within the pair (see Table 1). The aligned regions in one third of the direct Alu pairs are separated by 40 bp or less (Fig. 6 and Table 1).
Distribution of Alu Pairs with Long Alignment Regions (>275 bp) According to Orientation, Separation Distance, and Sequence Identity
While closely spaced, inverted Alu pairs generally are less frequent than direct pairs, our analysis revealed features in the distribution of full-length inverted Alu pairs that correlate with the degree of identity and orientation (i.e., tails-out or tails-in). As shown in Table 1, the proportion of inverted Alupairs separated by (<20 bp with 80%–90% identity was considerably lower than for direct repeats, regardless of orientation of the inverted Alus: ∼250- and ∼20-fold lower for theAlu pairs with tails external (CD) and tails internal (DC), respectively. Unlike the direct Alu pairs, the frequency appeared to increase somewhat with decreasing degree of homology. (Although the total number of events is small, these results are consistent with the observation of only one pair of invertedAlus in the 90%–100% identity category up to 40 bp separation as compared to 14 among 34 direct Alu pairs.) The frequencies of CD and DC pairs were comparable at longer separation distances (41 to >80 bp) and were independent of homology; the frequencies also were more comparable to those of direct repeats. There was a difference between the frequencies of CD and DC repeats among theAlus separated by 21–40 bp, with the CD pairs being about twice the frequency of the DC pairs and exhibiting frequencies in the range of the direct repeats. As presented in the Discussion, the rarity of inverted Alu pairs that have closely spaced, highly related regions (e.g., <20 bp), regardless of heads-in or heads-out orientation, is likely because of a destabilizing effect resulting from an interaction between the homologous regions.
Truncations of Large Alus
The similar frequencies for inverted pairs (especially CD) and direct repeat pairs at distances >20 bp may indicate that targeting mechanisms exist for inverted repeats (or at least for the CD category) as well as direct repeats (Jurka 1997). However, at short distances, the high insertion rate may be counteracted by the instability of inverted repeats. The differences in distribution between the direct repeats and inverted repeats that are CD or DC led us to analyzeAlus that are truncated relative to each other within a pair with a view to understanding how they may have originated. For example, the spacer length between aligned regions appears to reflect the insertion and/or stability of repeats. The spacer between aligned regions of adjacent Alus could be formed by non-Alusequence or derived, in part, from asymmetric truncations of adjacentAlus. We, therefore, examined whether adjacent Alupairs were truncated by more than 5 bp relative to each other at the 5′ ends (heads). (The poly(A) 3′ tails were not analyzed because they arise through expansion and their lack of uniformity made such an analysis technically unfeasable.) The truncations were identified among the pairs of Alus with >275 bp alignment each and these were categorized according to whether the 5′ truncated ends were internal (CD category) or external (DC category) (Table 2).
Truncation of “Heads” in Alu Pairs According to Orientation and Distance
For the heads-out repeats, approximately one half (44%–55%) of theAlu pairs have a truncated Alu, regardless of the distance between the Alus. This contrasts with the heads-in inverted repeats and the direct repeat categories, which also were markedly different from each other. For the direct repeats, 45% of the pairs have a truncation when the Alus are closely spaced (<20 bp). However, the truncations are not evenly distributed: there is a strong bias (10:1) for truncations of the 5′ ends ofAlus that are internal to the closely spaced pairs. At greater distances, the frequency of truncations increases and the bias disappears, with the ratio of internal truncations becoming somewhat less than external. For the heads-in category (CD), there is a strong bias towards equal alignment lengths (no truncation) when the spacer is short (20–60 bp). At longer distances, the frequency of truncations is comparable to that for the direct and the heads-out inverted repeat categories. Among the few heads-in Alu repeats that are found at very short distances (<20 bp), they are nearly equally distributed between truncated and equal sizes. We suggest that these differences in truncation patterns reflect differences in mechanisms of insertion and/or stability (see Discussion).
Age of Alus in Pairs Differs with Distance
Recently retroposed Alu sequences usually are not fixed in the population (Batzer et al. 1996) and are, therefore, presumed to be a source of ongoing genomic diversity. Amplification and mobilization is limited to the young Alu subfamily sequences (i.e.,Alu-Y, Alu-Ya1, Alu-Yb8, Alu-Ya5, and Alu-Ya8) that have been inserted in the last 1.5 million years (Arcot et al. 1995). We therefore analyzed the distribution ofAlu pairs in order to explore the relationship between age, orientation, and distance between aligned sequences. The analysis, which was limited to approximately full-length sequences that were at least 80% identical, compared the incidence of closely spacedAlu pairs (b + c <40bp) and more distantly spacedAlus (b + c >41 bp) containing at least one member of the young Alu subfamily (Table 3). Young Alus were nearly 30% more frequent among the closely spaced pairs (<40 bp), regardless of orientation. While the reasons for this preference are not apparent, it is possible that the modest bias for young Alus reflects a more recently evolved targeting mechanism or a slow mechanism for separating them.
Influence of Orientation and Separation Distance on AluPairs Containing a Young Subfamily Member
DISCUSSION
General Approach to Investigating Alu Distribution
Understanding the organization of Alus in the human genome is expected to shed light on Alu integration, Aluchanges, and the potential for Alus to affect genome stability. Our approach incorporated newly developed computational tools along with previously developed programs to analyze Alupairs in terms of the potential for homologous interactions.
The pairwise approach to analyzing Alus was motivated in part by observations from several model systems. Pairs of large inverted DNA repeats can be unstable, lead to deletions, and stimulate recombination between DNAs surrounding the inverted repeats in yeast (Gordenin et al. 1993; Ruskin and Fink 1993; Nag and Kurst 1997; Tran et al. 1997;Lobachev et al. 1998, 2000; ) and mammalian cells (Akgun et al. 1997;Lewis 1999; Lewis et al. 1999). Sequence identity was suggested as a likely factor in the stability of Alu repeats based on results in yeast. Lobachev et al. (1998) demonstrated that large palindromes could stimulate recombination nearly 10,000-fold in yeast. Recently, we established that the shorter inverted human Alu repeats, but not direct Alus, also could stimulate recombination nearly 2000-fold in yeast between surrounding DNA and an ectopic allele when the Alus were separated by <20 bp (Lobachev et al. 2000). The recombination rates decreased exponentially as the distance was increased to 100 bp. The recombination also was reduced as sequence identity decreased, with 80% appearing to be the lower limit for stimulation of recombination by inverted Alu repeats. Mutants were identified in which diverged and distantly separated (100 bp) inverted Alu pairs also were capable of stimulating recombination, suggesting that these inverted repeats are potential ARMs. These observations along with previous computational studies on the distribution of Alu pairs (Jurka 1995), strongly supported new approaches to an investigation into the pairwise distribution ofAlus and provided insight into what parameters should be considered.
Our study focused on four attributes of Alu pairs that might be important in the integration and stability of Alu sequence pairs in genomes of humans: (1) Orientation of each member of the pair, (2) size of the inverted repeat, (3) distance between the aligned regions of the pair, and (4) sequence identity. In addition, we examined the age of Alus. The present study considerably extends our recent report demonstrating a reduction in closely spaced inverted Alus as compared to direct Alu repeats (Lobachev et al. 2000). Based on results from model systems, other factors also are likely to be important in the stability ofAlu sites including genetic background (Gordenin et al. 1993;Ruskin and Fink 1993; Tran et al. 1997; Lobachev et al. 1998, 2000; ). For example, recombination in mammalian cell constructs containing direct identical Alu repeats is high in p53 defective as compared to p53 wild-type cells (Gebow et al. 2000). We suggest that nucleotide sequence, mutagenic agents, and DNA metabolic processes, as well as variation in levels of relevant proteins, may contribute to the ability of inverted Alus to stimulate genomic change.
Direct Alu Repeats and Preferences
It is clear that orientation and distance between aligned regions are important factors in Alu distribution. For long separations (i.e., >80 bp) between aligned regions, there do not appear to be any preferences or exclusions of direct or invertedAlu pairs.
In this study, we confirm that there is a vast excess of closely spacedAlus in the direct as compared to the inverted orientation (Jurka 1995). This excess has been proposed to result from targetedAlu integration to an approximate 15 bp sequence (Jurka 1997). The sequence was identified by the high degree of conservation at the ends of the target represented by 5′ AAAA and TYTN 3′ consensus sequences. In addition, the target is preceded by a 5′ TT, producing the strong 5′ TT/AAAA consensus sequence where “/” indicates the position of a proposed nucleolytic cleavage (nicking) that would occur on the opposite strand (Fig. 4 in Jurka 1997). A second nicking site has been proposed to occur immediately after the 5′ TYTN/consensus sequence and marks the integration position of the incoming Alu. The final arrangement appears as follows: 5′-TTAAAAnnnnnnnnnnTYTN(Alu) where “n” stands for any base; the number of the “n” nucleotides in the middle of the target can vary. (The conserved consensus sequences are indicated by upper-case letters, including the 5′ TT immediately preceding the integration target.) Hexamers derived from the TTAAAA consensus such as TTAAGA, TTAGAA, CTAAAA, TCAAAA etc., also are associated with targets for Alu integration (Table 3; Jurka 1997). Therefore, the likelihood of integration is expected to increase with abundance of the target hexamer sequences. Because Alu sequences frequently contain TTAAAA-like signals at the 3′ ends, the tails ofAlus are good targets for subsequent Aluintegrations. This leads to the prediction that new Alus will integrate about 15 bp from the nicking site “/” within the TTAAAA-like hexamer, and in the same orientation as the preexisting Alu.
It should be noted that complementary AATTTT-like signals within preexisting Alus would determine integration of the incomingAlus in the opposite orientation. However, in directly oriented Alus, the complementary AATTTT-like target signals are about 10 times less frequent than the TTAAAA-like signals (Jurka, unpubl.). Therefore, closely spaced Alu integrations in direct orientation (i.e., CC or DD) would be expected to be around 10 times more frequent than inverted sequences (CD or DC). (Furthermore, the AATTTT-like signals are scattered randomly in Alus so that no systematic pattern of CD or DC pairs would be expected.) Regardless of targeting preferences, this would not explain the rarity of closely spaced inverted Alus (<20 bp) as compared toAlus that are more distant.
The present study differs from previous approaches in that we have classified Alu pairs according to the distance between aligned regions rather than just the distance between Alu sequences. Because the actual distance between aligned regions (b + c) is greater than or equal to the distance between Alu sequences (c), it appears that many of the closely spaced pairs may contain truncatedAlus. Our extensive analysis of approximately full-lengthAlus (Table 2) has demonstrated that most of the truncations are in the internal head of the direct repeats. It is interesting that the strong preference for closely spaced aligned regions ofAlus only applied to the largest categories of direct repeat pairs, >275 bp and 125–200 bp. Possibly this is a result of an integration preference for full-length and half-length Alus (i.e., one member of the dimer within an Alu).
Both the direct and the inverted Alu pairs that have full-length alignments tend to be more closely related than when the alignments are shorter. Among the reasons are that some regions diverge less readily than others, the full-length Alus have long polyA tails that would contribute to overall sequence identity, and possibly there are greater opportunities for homologous interactions. Also, longAlus tend to be younger and less diverged (Arcot et al. 1995;Batzer et al. 1996).
Inverted Alu Pairs and Exclusion
We found that, unlike for direct repeats, inverted Alupairs with closely spaced (<20 bp) aligned regions were uncommon regardless of size of alignment or orientation (Fig. 4B) and especially rare among the Alu pairs with nearly full-length alignments. As the distance between aligned regions increased beyond 20 bp, the frequency of direct and inverted Alu pairs became more uniform, suggesting random integration. Interestingly, forAlus whose alignment regions are separated by <20 bp nucleotides, the CD pairs (tails out) are even more excluded than the DC pairs. Possibly, this is a result of more heterogeneity of tails versus the unique sequence of Alu heads.
The exclusion of closely spaced inverted repeats is consistent with the observation that inverted repeats at close distances are unstable in yeast and, for the case of Alus, the instability is highly dependent on distance (Lobachev et al. 1998; Lobachev et al. 2000). We propose that the observed absence in the human genome of closely spaced inverted Alus that are highly related is a result of this motif adopting a noncanonical DNA form, including intrastrand pairing, that has a high potential for stimulating chromosomal changes. Based on results in yeast, closely spaced Alus may be sites of genetic instability in normal cells or in cells that are defective in repair or some aspect of DNA metabolism (Lobachev et al. 2000). Several human diseases have been found to be associated with changes in regions of inverted Alus (Deininger and Batzer 1999). We also suggest that genetic factors similar to those affecting stability in yeast may extend to humans. While mutations in mismatch repair did not affect the instability of diverged Alus in yeast (Lobachev et al. 2000), it remains to be determined if systems responsible for mismatch recognition may help to prevent Alu associated instability in human cells.
Thus, we conclude that sequence identity and distance are important factors that contribute to the distribution of Alu pairs and the potential for Alu pairs to cause genome stability. These observations with inverted as well as direct repeats may be useful in understanding the frequent clustering of Alus.
Truncations of Closely Spaced Alu Pairs and Mechanisms of Integration and/or Instability
We found that for heads-out repeats (DC) and distantly spaced heads-in (CD) and direct repeats, about one half of the pairs had a truncation in one of the Alus. Departures from this frequency may indicate factors that affect Alu insertion and/or stability of Alu pairs. For closely spaced directAlus, the internal Alu head frequently is truncated relative to the external head. The results with the invertedAlus clearly are different. The closely spaced (20–60 bp) heads-in inverted Alu pairs have a strong bias towardsAlus with no 5′ truncations, while there is no such bias for the heads-out category. (The higher frequency of truncated pairs among the very few with aligned regions that are <20 bp apart may simply reflect the instability of inverted Alus in close proximity.)
The differences between the two categories of inverted repeats and the markedly different observations with the direct repeats have interesting implications both for the origin of Alu repeats and their potential instability. Models based on a simple retroposition at the site of integration do not account for the various truncation patterns we observe: Fifty-percent truncation of one of theAlus in distantly separated pairs of Alus, preferred truncation of the internal head of direct repeats, and no truncation of heads-in inverted repeats. As discussed above, there is a strong preference for insertion of an Alu in a direct orientation immediately next to the tail of an existing Alu. The present results suggest that along with targeting, there is an associated removal of some of the 5′ end of the incoming Alu and as targeting next to an Alu become less likely (i.e., for more distantly spaced repeats), the truncations are less frequent.
The reasons for the lack of truncation in the heads of the closely spaced heads-in Alus but not heads-out inverted Alupairs are not clear. However, they may indicate a directional complementary pairing mechanism prior to integration that starts from the apex of the inverted pair (i.e., the closest sequences in anAlu pair). This would result in a preference for full-length pairing at the apex that could be detected in the heads-in category but not the tails-in category (variability in size of poly AT tails would preclude such analysis of the tails-in pairs). Opportunities for complementary interactions might arise if Alu RNA had been reverse transcribed to cDNA prior to integration. Although there are few direct examples, genetic evidence from yeast are consistent with cDNAs being an intermediate in recombination (Derr and Strathern 1993). More directly, RNA injected into mouse (Giordano et al. 2000) has been shown to yield cDNA. If the cDNA interacted with complementary displaced single-strand flaps that arise during normal DNA replication, this would result in stabilized double-stranded flaps that would be resistant to cleavage by the Fen1 flap-processing enzyme and a stabilized inverted repeat in the lagging strand (Gordenin et al. 1997).
Another possible explanation has to do with the transcription by RNA polymerase III. In the DC class of inverted repeats, 5′ to 3′ transcription from both ends converges toward the center of the repeat. The transcription diverges outward from the center in the CD class. DC repeats therefore can be opened by transcription for recombination because transcription initiating in D's promoter could proceed through the center and into the internal middle run of Ts between the FLAM and the FRAM in the second Alu in the pair. This would be precluded if the C in the DC pair presents a “poly T” tail so that transcription is halted before the second Alu creating the possibility of ATA triplexes from the interaction between single stranded transcribed poly A and the AT duplex in the DC pair.
Genes and Regions with Alu ARMs in the Human Genome
This study was motivated in part by the association of numerous human disorders with Alu-mediated sequence rearrangements. However, given the high frequency of Alu sequences in the human genome, the number of Alu-associated diseases would appear low. The majority of the Alu sequences are stable, having remained in their present position in the human genome for millions of years and may pose relatively little threat to human health. However, we reasoned that a study of the characteristics ofAlu pairs might reveal situations that potentially are unstable. These could include closely spaced, inverted Alupairs of pairs that might be unstable in some backgrounds [as found for yeast (Lobachev et al. 2000)] or in response to environmental challenges.
Because we found that both distance and sequence identity were important factors in defining the distribution of Alu pair repeats and that they influenced the stability of inverted repeats in model systems, these factors may be useful in predicting regions or genes in the human genome that may be at-risk for instability as a result of inverted Alu pairs, based on information available from yeast and the similarity between systems in yeast and humans that deal with genetic stability (Resnick and and Cox 2000). Genes were, therefore, identified that might be at-risk for instability using criteria developed in yeast where 80% identity was the apparent minimum level of detectable recombinational impact of invertedAlus in wild-type strains and inverted highly relatedAlus separated by 40 bp could induce a nearly 10-fold increase in recombination (see Lobachev et al. 2000). We consider these as conservative parameters for identifying at-risk regions because changes in genetic background can turn genetically stable, invertedAlu repeats into stimulators of recombination (Lobachev et al. 2000). Presented in Table 4 are loci that were found to contain inverted Alu pairs in which the separations between aligned regions were <40 bp and there was at least 80% identity between the aligned regions. Many Alu pairs (268) also were identified whose loci have not been ascribed a function and many of which share >86% sequence identity (data not shown).
Closely-Spaced (≥40 bp) and Related (>80% Homology) InvertedAlu Repeats Associated with Known Genes
Loss of heterozygosity (LOH) of several genes on the list have been linked to various genetic illnesses. These include TNX, encoding tenascin-x (associated with an undesignated Ehlers-Danlos syndrome type, clinically similar to type II, but with distinct ultrastructural characteristics) (Burch et al. 1997), MeCP2, encoding x-linked methyl-CpG-binding protein (Rett syndrome) (Amir et al. 1999) and GPC3, associated with Simpson-Golabi-Behmel syndrome, among others. Four of the gene-associated regions contained more than one set of theAlu inverted repeats: the T-cell receptor α δ locus, the LIM kinase1 (LIMK1) gene, the GART- andAML-related genomic DNA, and the basic TFII p44 subunit gene. Because LOH can occur through recombination, it is possible that LOH might be the result of recombination that is stimulated by inverted repeats.
A deletion of the LIMK1 gene coding for the neuregulin-interacting serine, threonine, tyrosine kinase, is associated with the less-severe phenotype of Williams-Beuren syndrome (Robinson et al. 1996), characterized by diminished visuospatial construction cognition and low IQ (Frangiskakis et al. 1996). The more severe phenotype that also includes vascular disease is linked to a more extensive deletion on 7q11.23 that results in a mutated elastin gene (Frangiskakis et al. 1996). This gene may be prone to Alu-facilitated rearrangements. It is striking that theGART- and AML-related regions contain four closely related, large Alu pairs that are separated by less than 40 bp. Also noteworthy is the Huntington's disease region that, in addition to containing one Alu pair that met the above criterion, also had more Alu pairs that had similar features. This region also contains a multiple trinucleotide repeat at-risk DNA motif (Aronin et al. 1995), however, this does not exclude the possibility of another risk factor.
It is interesting that λ DNA immunoglobulin light chain DNA has many inverted Alu pairs, one of which satisfies the criteria of Table 4. Possibly, they provide another means for generating antibody diversity. Of particular interest is the breakpoint cluster region gene BCR, whereAlus within this region have been implicated in chromosomal translocation leading to Ph1 + bcr- acute leukemias (Chen et al. 1989). The identification of this gene in our analysis supports our approach to identifying potential Alu ARMs.
We also have identified many genetically uncharacterized regions that contain Alu pairs with closely spaced, aligned regions (data not shown but available in web site database). Even if these regions are not associated with genes, they might be at-risk if theAlu pairs could initiate genomic changes such as LOH, chromosome loss [as found for yeast (Lobachev, unpubl.)] and translocations. They may correspond to highly polymorphic sites between individuals. It would be interesting to follow the stability of the various closely spaced inverted Alu pairs under different growth and exposure conditions. Based on results with yeast, mutants defective in DNA metabolism or expressing altered DNA metabolic proteins also may reveal situations under which closely spaced, inverted Alus would be unstable.
METHODS
Computational Approaches and Alu Identification
The computational methods used in this study are listed in Table5. They are available at the website http://dir.niehs.nih.gov/ALU/methods.html, where they are described at length. Computations were performed on either a SUN Sparc station running SunOS 5.5 (SUN Microsystems) or a Silicon Graphics O2 workstation running IRIX 6.3.
Program Command Procedures to Interface with GenBank Data Base and Generate Alu Distribution Data Set
Sequences that were related to a consensus Alu sequence were identified. A map file of all human Alu sequences as of September 1999 was developed by comparing human genomic sequences in the GenBank database (release112.0, National Center for Biotechnology Information, National Library of Medicine, National Institutes of Health, Bethesda, Maryland) with a well-defined Alu consensus sequence (Jurka 1993). The map file contains the following information for the 153,645 Alu sequence elements identifed (estimated to be between 14% and 30% of the total Alu sequences present in the human genome) in columnar form: locus, beginning and ending sequence coordinates, family of Alu sequence, the orientation of the sequence (D, denoting direct and C, denoting complementary), the percentage identity to the Alu consensus sequence, the ratio of mismatches to matches, and the alignment score.
The annotated sequence files were extracted from the GenBank database to create a GenBank sublibrary of Alu sequences. This sublibrary was needed to generate alignments between the Alu pairs.
Categorization of Pairs According to Relative Orientation of Alus
The revised map file was used as input to derive a list of loci and their corresponding coordinates for each pair of adjacent Alusequence. The program PFOLLOWS3 (Klonowski and Jurka 1997), which locates adjacent pairs, handled this task by taking the input file, minimum acceptable distance (0 bp), and maximum acceptable distance (650 bp) as parameters. These initial distances represented the “c” distance, or the minimum distance between one Aluconsensus sequence and the next (see Fig. 3). ThePFOLLOWS3 output contained four lines, one for each of the four possible orientation permutations for a pair and each with several thousand characters. Direct repeats could be in the complementary-complementary (CC) orientation (3′ <−5′ 3′ <−5′) or the direct-direct (DD) orientation (5′−> 3′ 5′ −< 3′). The inverted repeats could be CD-oriented inverted repeats, which are oriented such that the 5′ ends, as related to the direction of transcription of activeAlus, are towards each other (3′ <− 5′ 5′−> 3′), or DC oriented inverted repeats (5′−> 3′ 3′ <− 5′ ). All pairs in the CC (complementary-complementary) orientations are listed on the first line of the output, followed by all the pairs in the CD (complementary-direct) orientation, the DC orientation and the DD orientation.
Four simple programs, written in Perl, were run by an executable script to extract the coordinates for each of the four types of pairs (CC, CD, DC, DD) from the PFOLLOWS3 output file. The four subfiles were reformatted to place the pair coordinates side-by-side in list format for subsequent reference and analysis. These coordinate list files were then used to extract the sequences from the GenBank-derived sublibrary by the program VEXT (Klonowski and Jurka 1997).
Extraction and Alignment of Paired Alu Sequence Fragments
Sequences from the sublibrary were extracted for both Aluelements in each pair. For the inverted repeats (the CD and DCAlu pairs), the reverse complementary sequence of the secondAlu in each pair was generated for alignment. The Alupairs that were direct repeats (CC and DD) were aligned with each other; for the inverted repeats, the first Alu in each of the pairs was aligned with the complement of the second Aluelement. These pairwise alignments yielded various alignment characteristics [such as mismatches and matches (Waterman 1984;Faulkner and Jurka 1988)] for subsequent analyses of the various pairs of adjacent Alus.
Retrieval of Coordinates
Once the sequences were aligned, the actual aligned coordinate numbers (the alignment program renumbered the coordinates to start with one) were regenerated using the short program PRENUM02(Klonowski 1998). Summary data were extracted through execution of the UNIX grep command twice, first to get the recovered alignment coordinates, and then to retrieve the alignment statistics that were on separate lines. These files were pasted so that all the pertinent information was on one line.
Alignment Length and Percent Identity within Pairs of Alus
The data were reformatted and files containing chromosome location,Alu sequence, and pairwise alignment characteristics were merged (the loci names were matched to establish correct merging of files). This enabled the alignment length “a”, percentage identity, and other parameters to be determined for pairs of Alus. An example of the parameters associated with each Alu pair in the website is provided in Figure 2. The alignment length “a” (“align len.” in Fig. 2) is obtained as follows: if the aligned sequence ofAlu1 (a1) > the aligned sequence of Alu2 (a2), then a = a1, otherwise a = a2. (The actual length a1 = (“Alu1 aligned finish”) − (“Alu1 aligned start”) + 1, and a similar procedure is used for a2.) The alignment length “a” also is equivalent to the “num(ber) of matches” + the “num(ber) of mismatches” + the total (“ttl. ”) gap length. Individual gap lengths correspond to the deletion needed to bring two sequences into alignment. The similarity score = (total matches) / (total matches + total mismatches + total “num(ber) of gaps”); “percent identity” = (matches) / (alignment length) (note that the similarity score and identity are approximately equal because most gaps are one or a few bases).
The “spacer len(gth) (c) “ = (Alu2 fragment start) − (Alu1 fragment finish). Flanking sequences were identified that corresponded to sequences at either end of an Alu (or fragment) that were not found in the other member of the pair (note that the Alus were initially identified in terms of a consensus Alu). These most likely were the result of oneAlu being truncated relative to the other. An internal flank is referred to as “b” so that the distance between aligned regions is actually b + c.
We next recovered the sequence description headings and the original unaligned sequence fragment coordinates from the sequence files that were used in generating the data. Once the files containing the coordinates for first and second Alus in a pair and the description were generated, they were pasted side-by-side with the “grepped” alignment statistics.
A Perl script called Bins 3 was used to subdivide the summary output from the alignment into different groupings dependent on the percentage identity between the two Alus in the pairs. In the process, the Bins program verified that the loci names in the pasted coordinate data matched the alignment data. TheBins program also recalculated the “c” size by subtracting the end of the first original Alu fragment coordinate from the end of the second original Alu fragment coordinate as an internal check.
Another Perl program, Bins, was written to subdivide the files according to the range in which the “a” length fell to group the data based on length. The data also were grouped according to the percentage identity between the two Alu sequences in a pair. Finally, two more Perl programs were used to subdivide the data according to distances between the Alus (Bins C) and distances between aligned regions (Bins 2).
The data were summarized in four hypertext mark-up language (HTML) tables (cc.html, dd.html, etc.) These tables include the raw data supporting the present results. Links from each of the cells in the tables contain all Alu sequence information available as of September 1999. Each cell has a hypertext link to the characteristics describing each pair. An example of the linked information is provided in Figure 2.
Determination of Internal Truncations
It was necessary to use four different algorithms, one for each of the four possible orientations to determine the length of internal orientations. In the case of CC, p is equal to the fragment finish coordinate minus the alignment finish coordinate of the firstAlu in the pair, while q equals the fragment finish coordinate minus the alignment finish coordinate of the secondAlu in the pair. If q − p >1, then the firstAlu head (internal in the pair) is truncated relative to the second. Otherwise, if they are not equal, the second head (external) is truncated.
For DD, the algorithm is as follows: p is equal to the aligned start coordinate minus the fragment start coordinate of the firstAlu in the pair, while q equals the aligned start coordinate minus the fragment start coordinate of the secondAlu in the pair. If q − p >1, then the firstAlu head (external in the pair) is truncated relative to the second. Otherwise, if p − q >1, then the secondAlu head (internal head in the pair) is truncated relative to the first.
Inverted repeats were more complicated. For CD, where both heads are internal, p is equal to the fragment finish coordinate minus the aligned finish coordinate of the first Alu in the pair, while q equals the aligned start coordinate minus the fragment start coordinate of the second Alu in the pair. Ifq − p >1, then the first Alu head is truncated relative to the second. Otherwise, if p − q>1, then the second Alu head is truncated relative to the first.
Finally, for DC, where both heads are external, p is equal to the aligned start coordinate minus the fragment start coordinate of the first Alu in the pair, while q equals the fragment finish coordinate minus the alignment finish coordinate of the secondAlu in the pair. If q − p >1, then the firstAlu head is truncated relative to the second. Otherwise, ifp − q >1, then the second Alu head is truncated relative to the first.
Acknowledgments
We are grateful to Paul Klonowski for writing PRENUM02and for automating the tabulation of the data in HTML. We greatly appreciate the comments of Rob Slebbos and Jim Mason on the manuscript.
The publication costs of this article were defrayed in part by payment of page charges. This article must therefore be hereby marked “advertisement” in accordance with 18 USC section 1734 solely to indicate this fact.
Footnotes
-
↵4 Present address: Duke Center for Human Genetics, Duke University Medical Center, Box 3445, Durham, NC 27710, USA.
-
↵5 Corresponding author.
-
E-MAIL resnick{at}niehs.nih.gov; FAX (919) 541-7593.
-
Article and publication are at www.genome.org/cgi/doi/10.1101/gr.158801.
-
- Received August 10, 2000.
- Accepted November 6, 2000.
- Cold Spring Harbor Laboratory Press