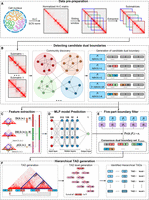
BINDER achieves accurate identification of hierarchical TADs by comprehensively characterizing consensus TAD boundaries
Abstract
As crucial chromatin structures, hierarchical TADs play important roles in epigenetic organization, transcriptional activity, gene regulation, and cell differentiation. Currently, it remains a highly challenging task to accurately identify hierarchical TADs in a computational manner. The key bottleneck for existing TAD callers lies in the difficulty in the prediction of precise TAD boundaries. We solve this problem by introducing a novel algorithm, called BINDER, which conducts a boundary consensus approach, and then precisely locate hierarchical TAD boundaries by developing a multifaceted boundary characterization strategy. In comparison with other leading TAD callers, BINDER shows significant improvement in identifying hierarchical TADs and exhibits the strongest robustness with ultrasparse data, which supports the importance of boundary identification in calling hierarchical TADs. Applying BINDER to experimental data and mouse hematopoietic cases, we find that the hierarchical TADs identified by BINDER show strong biological relevance in their epigenetic organization, transcriptional activity, DNA motifs, and coregulation during cellular differentiation. BINDER discovers differences in the enrichment of two specific transcription factors, CHD1 and CHD2, at TAD boundaries with different hierarchies. It also observes variations in the gene expression of TADs with different hierarchies during cellular differentiation.
The highly organized three-dimensional (3D) structure of the eukaryotic genome within the nucleus is essential throughout the cellular life cycle, intricately intertwined with epigenetics, gene expression, and various cellular activities (Lanctôt et al. 2007; Sexton et al. 2007, 2012; Cavalli and Misteli 2013; Dixon et al. 2015). In the past two decades, chromatin conformational capture methods, particularly the high-throughput technique known as Hi-C, have greatly advanced the development of 3D genomics (Dekker et al. 2002; Dostie et al. 2006; Lieberman-Aiden et al. 2009). For instance, studies by Dixon et al. (2012) demonstrated that chromosomes encompass numerous chromatin domains spanning tens to hundreds of kilobases. Within these domains, which are commonly referred to as topologically associating domains (TADs), DNA sequences exhibit significantly increased interaction compared with sequences outside of the domains in the genome-wide chromatin-folding map. Notably, TADs are widespread across various species, displaying high conservation. Therefore, they are recognized as a crucial secondary structure in chromosome organization, following the chromosome territory model (Lanctôt et al. 2007; Sexton et al. 2007, 2012; Dixon et al. 2012; Dekker and Heard 2015; Sexton and Cavalli 2015).
Empowered by high-resolution Hi-C technology, hierarchically nested TADs, generally termed hierarchical TADs, have been discerned in mammalian genome-wide Hi-C maps. Analogous to domain-like TAD structures, hierarchical TADs are also demarcated by boundaries (Phillips-Cremins et al. 2013; Rao et al. 2014). Notably, hierarchical TADs are able to unveil dynamic cellular folding properties, distinguishing them from nonhierarchical TADs. For instance, Llères et al. (2019) showed the involvement of hierarchical TADs in activating genomic imprinting during mouse development. Meanwhile, Hanssen et al. (2017) uncovered that hierarchical TAD boundaries, particularly in mice housing the α-globin gene cluster, delineate the chromatin region where enhancers gain access and interact with responsive promoters, which underscored the association of hierarchical TADs with gene-specific regulation. Moreover, several studies have documented a category of partially overlapping TADs organized within hierarchical TADs (Norton et al. 2018; Liu et al. 2022). Although they are believed to be linked to a subtle boundary or a transition zone between two adjacent TADs, the mechanism governing their formation and function still remains unclear (Rao et al. 2014; Weinreb and Raphael 2016; Norton et al. 2018; Chang et al. 2020). Taken together, precise and robust identification of TADs, hierarchical TADs, and partially overlapping TADs using Hi-C data are essential for a deeper understanding of 3D-folding mechanisms and their epigenetic and gene regulatory functions.
In recent years, multiple computational methods have emerged for identifying TADs in Hi-C data. Some focus on nonnested TADs, including directionality index (DI) (Dixon et al. 2012), insulation score (IS) (Crane et al. 2015), TopDom (Shin et al. 2016), SBTD (Long et al. 2021), MSTD (Ye et al. 2019), and CATAD (Peng et al. 2023). Additionally, there are methods specially designed to recognize hierarchical TADs, including OnTAD (An et al. 2019), SpectralTAD (Cresswell et al. 2020), and TADfit (Liu et al. 2022). OnTAD first identifies candidate TAD boundaries by a series of size-fixed sliding windows on the diagonal of Hi-C contact matrix and then assembles these boundaries into hierarchical optimized TADs using a recursive dynamic programming algorithm based on scoring functions. SpectralTAD leverages an improved multiclass spectral clustering algorithm and an automated method for determining the number of clusters to identify TADs within a sliding window on the diagonal of the Hi-C contact matrix. TADfit relies on a multiple linear regression model that seeks to fit the interaction frequencies in the Hi-C matrix using all possible combinations of hierarchical TADs. Then, the significance of TADs is evaluated based on the regression coefficients.
Although these methods successfully identified nonhierarchical TADs or hierarchical TADs in many cases, several key issues still need to be improved. First, existing methods cannot comprehensively capture the characteristics of TAD boundaries, potentially leading to a low-refined identification of TADs generated from boundaries. Second, as mentioned in the study (Zufferey et al. 2018), it has become a growing trend for the requirement of low sequencing depth during the expanding applications of Hi-C technology, particularly in the single-cell context. Although current methods have made great improvements with low-quality Hi-C data, more efforts are needed to achieve better performance.
To address the above limitations, we present BINDER for accurately and robustly identifying hierarchical TADs from Hi-C data. Based on the hypothesis that the anchoring of TAD boundaries is a key feature of TADs, BINDER is able to comprehensively characterize consensus TAD boundaries and robustly yield more accurate hierarchical TADs. Powered by the Infomap algorithm (Rosvall and Bergstrom 2008), BINDER first identifies candidate boundaries and records their occurrences from many submatrices extracted by a size-fixed sliding window along the diagonal of the Hi-C contact matrix. The Infomap algorithm is designed based on information flow compression and focuses on the time of information flow of the entire network structure, which satisfies the features of Hi-C data. Then, a neural network model is designed to comprehensively learn the characteristics of TAD and non-TAD boundaries according to three types of boundary features we defined and to predict a reliability score for each boundary. Then, according to the occurrence counts of boundaries and their corresponding reliability scores, the set of consensus boundaries is generated. Finally, a left-neighbor extension method is developed to search for hierarchical TADs, and a hierarchy generation strategy is designed to generate their hierarchies.
In our benchmarking, we compared the performance of BINDER and the other eight TAD callers on four cell lines. After an extensive evaluation, BINDER exhibits higher accuracy and stronger robustness than the other TAD callers. Meanwhile, the hierarchical TADs identified by BINDER demonstrate strong biological relevance through our analyses of epigenetic features, transcription factor (TF) enrichment, and motif enrichment. Additionally, the application of BINDER to the mouse hematopoietic differentiation system provides novel insights into the relationship between hierarchical TADs and cell differentiation. In summary, our comprehensive benchmarking tests and analyses demonstrate that BINDER is an effective hierarchical TAD caller with the potential to contribute to downstream analysis in 3D genomics.
Results
Overview of BINDER
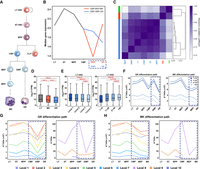
We present BINDER, an effective approach aimed at enhancing the accuracy of hierarchical TAD identification by combining a community discovery algorithm in graph theory and a neural network model to comprehensively characterize consensus TAD boundaries and yield hierarchical TADs (see Fig. 1). BINDER begins by extracting diagonal submatrices through a fixed-sized sliding window in a sequential component normalization (SCN-normalized) Hi-C contact matrix (Fig. 1A). Then, by applying the Infomap algorithm on them, candidate TAD boundaries and their occurrence counts are derived from these submatrices (Fig. 1B). Meanwhile, to maintain bin-continuity within communities identified by Infomap, BINDER performs the following operations. First, if there are two neighboring bins in a community identified by Infomap whose difference in numbering is equal to two, it adds the middle missing bin to ensure its bin-continuity. Second, if there are two neighboring bins whose difference in numbering is greater than two, it breaks this community from this “gap” and divides the community into two communities. Next, three kinds of features are extracted for each candidate boundary (Fig. 1C) and served as inputs to a trained neural network model which is able to predict a reliability score for each boundary (Fig. 1D). Subsequently, through the five-part filter, consensus boundaries are generated based on their occurrence counts and reliability scores (Fig. 1E). Finally, hierarchical TADs are yielded through the left-neighbor extension and hierarchy generation methods (Fig. 1F).
Workflow of BINDER pipeline. (A) BINDER uses a fixed-size sliding window to extract submatrices along the diagonal of a SCN-normalized Hi-C contact matrix. (B) The set of candidate dual boundaries Sdual is generated by applying Infomap to these submatrices (for the description of dual boundary, see Methods). (C) Three features are extracted for each dual boundary in Sdual, including the local interaction density, DI, and P-value of Wilcoxon rank-sum test, and then, they are concatenated to a 220-dimensional feature vector. (D) A trained neural network model with one input layer (containing 220 neurons), four hidden layers (containing 512, 128, 32, and four neurons, respectively), and one output layer (outputting predicted reliability score for each boundary). (E) The set of consensus dual boundary Sreliable is generated by both the reliability scores predicted by the MLP model and the occurrence counts during the community discovery part by Infomap reaching a consensus on boundaries from Sdual. (F) Hierarchical TADs and their hierarchies are finally obtained by the left-neighbor extension and hierarchy generation methods.
BINDER exhibits more accurate TAD identification
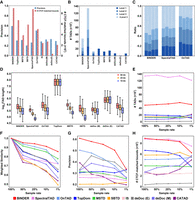
In this study, we compared BINDER with the other eight state-of-the-art TAD callers including TopDom (Shin et al. 2016), MSTD (Ye et al. 2019), SBTD (Long et al. 2021), SpectralTAD, OnTAD, InsulationScore (IS) (Crane et al. 2015), deDoc (deDoc [M] and deDoc [E]) (Li et al. 2018), and CATAD (Peng et al. 2023). Among them, SpectralTAD and OnTAD can identify hierarchical TADs. The running command for each tool is shown in the Parameters for TAD Callers section of the Supplemental Materials. To quantitatively evaluate the identification ability of different TAD callers, we compared the performance of BINDER and these TAD callers in terms of precision (ratio of TAD boundaries overlapping at least one CTCF biding site from ChIP-seq data) and the number of CTCF-matched hierarchical TAD boundaries (for details, see Supplemental Methods) on four cell lines GM12878, K562, NHEK, and HMEC at resolutions of 50 kb, 25 kb, and 10 kb (Fig. 2A; Supplemental Figs. S1–S3; Supplemental Tables S2–S4). After comparison, the results demonstrated that BINDER consistently performed the best among all compared methods across all resolutions and cell lines. Notably, at 10 kb resolution, BINDER exhibited an average improvement of 17.05% in precision (15.39% and 6.43% at 25 kb and 50 kb resolution, respectively) over the second-best TAD caller across four cell lines. Meanwhile, BINDER identified the most TAD boundaries matched by CTCF, which were on average 13.07% higher than the second-best method across the four cell lines at 10 kb (29.24% and 37.56% at 25 kb and 50 kb resolution, respectively). This comprehensive evaluation clearly shows the overall superiority of BINDER in identifying TAD boundaries.
Performance comparison between BINDER and other TAD callers. (A) Precision and the number of CTCF-matched boundaries on 10 kb GM12878 data. (B) Numbers of nested or nonnested TADs identified by BINDER and the other TAD callers. (C) Proportion of TADs of different levels identified by BINDER, SpectralTAD, and OnTAD (four bars of each TAD caller from left to right, representing the results on 10 kb GM12878, K562, NHEK, and HMEC data, respectively). (D) Lengths of TADs identified by BINDER and the others compared TAD callers on GM12878 data at resolutions of 50 kb, 25 kb, and 10 kb. (E–H) Number of TADs (E), weighted similarity (F), precision (G), and number of CTCF-matched TAD boundaries (H) on the whole-chromosome 10 kb GM12878 data at four downsampling rates.
We also showed the number and proportion of TADs of different levels across four cell lines at resolutions of 50 kb, 25 kb, and 10 kb (Fig. 2B,C; Supplemental Figs. S1–S4) for each TAD caller; the length distributions of TADs and hierarchical TADs identified by each TAD caller (Fig. 2D; Supplemental Figs. S5C–E, S6); weighted similarity between hierarchical TADs identified by BINDER, SpectralTAD, and OnTAD (Supplemental Fig. S7); and the proportions of gaps and partially overlapping TADs (Supplemental Tables S6–S8). Moreover, we compared the performance of BINDER and the other TAD callers in terms of TAD convergence to evaluate the accuracy of TAD identification (Rao et al. 2014), and BINDER showed the best performance among all the compared TAD callers (Supplemental Fig. S10; for details, see “Convergence Comparison” section in the Supplemental Materials). The above comparisons were all performed based on the GRCh37 (hg19) genome assembly. To make a comprehensive evaluation, we repeated the above experiments on the latest GRCh38 (hg38) genome assembly by using the GM12878 cell line at resolutions of 50 kb, 25 kb, and 10 kb, and results showed that BINDER consistently performs better than the others compared in terms of precision and the number of CTCF-matched TAD boundaries (see Supplemental Fig. S8A–C; Supplemental Table S5). In terms of the other TAD properties (e.g., the number of TADs, the lengths of TADs, etc.), BINDER demonstrates similar performance with those based on hg19 genome assembly (see Supplemental Figs. S8D–H, S9; Supplemental Table S9).
BINDER demonstrates stronger robustness on downsampled Hi-C data
To test the robustness of BINDER and the other compared TAD callers, we downsampled 50%, 20%, 10%, and 1% of the whole chromosome of 10 kb GM12878 data by utilizing the downsampling method of SpectralTAD (Cresswell et al. 2020). For each sample rate, we randomly performed 10 times and calculated the average performance for each TAD caller. Results showed that BINDER displayed superior stability and robustness. First, BINDER is able to consistently identify a stable number of TADs and TAD boundaries (Fig. 2E; Supplemental Fig. S5A), and the set of TADs it identified in terms of weighted similarity and Jaccard index (for details, see Supplemental Methods) consistently achieves the highest at four sampling rates (Fig. 2F; Supplemental Fig. S5B). In addition, BINDER is also able to yield more accurate TAD boundaries in terms of precision and the number of CTCF-matched TAD boundaries (Fig. 2G,H). Although the number of CTCF-matched boundaries of BINDER is slightly lower than that of SpectralTAD, the precision of BINDER is much higher. Furthermore, we also tested the performance of BINDER and the other eight TAD callers on Dip-C data of 16 GM12878 single cells, and BINDER still demonstrates an excellent overall performance (Supplemental Figs. S11–S13; for details, see “Performance of BINDER on Dip-C Data” section in Supplemental Materials). Taken together, these observations clearly demonstrate the strong robustness of BINDER in predicting hierarchical TADs in ultrasparse Hi-C data.
BINDER reveals explicit epigenetic features near hierarchical TAD boundaries
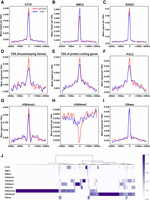
Epigenetic features near TAD boundaries are a critical part of 3D genomics. A recent study suggested that chromatin would be extruded by an engaged cohesin complex, which is a ring-shaped protein complex consisting of SMC1, SMC3, and RAD21, until it encounters two convergent and bound CTCF sites at TAD borders (Watrin et al. 2016; Fudenberg et al. 2017; Vian et al. 2018). This model is also consistent with the TAD boundaries identified by BINDER, as evidenced by the enrichment of CTCF, SMC3, and RAD21 on GM12878 and K562 data (Fig. 3A–C). Additionally, the creation of insulating forces at TAD boundaries has been proposed to be associated with a common property of CTCF binding sites and transcription start sites (TSSs) of highly active housekeeping genes (Fu et al. 2008; Valouev et al. 2011; Gaffney et al. 2012; Dixon et al. 2016). It also coincides with our observation that TSSs of housekeeping genes were highly enriched at TAD boundaries (Fig. 3D). Moreover, TSSs of protein-coding genes were also enriched near TAD boundaries (Fig. 3E).
Hierarchical TAD boundaries are highly correlated with epigenetic factors. Enrichment of epigenetic factors near TAD boundaries identified by BINDER on GM12878 and K562 data, namely, CTCF (A), SMC3 (B), RAD21 (C), TSS of housekeeping genes (D), TSS of protein-coding genes (E), POL2 (F), H3K4me3 (G), H3K9me3 (H), and DNase (I), where the red line indicates GM12878, and the blue line indicates K562. (J) Hierarchical clustering of hierarchical TAD boundaries based on nine biological features and DNase-seq, where each value of a factor for each boundary is normalized to zero to one (for details, see the “Hierarchical Clustering for the Enrichment of Epigenetic Factors near TAD Boundaries” section in Supplemental Methods).
Then, we investigated the enrichment pattern of histone modifications near TAD boundaries identified by BINDER and found that promoter-related POL2 and H3K4me3 were highly enriched near TAD boundaries in GM12878 and K562 cell lines, whereas H3K9me3, a marker of heterochromatin, was not enriched (Fig. 3F–H). Notably, a recent study suggested that H3K4me3 is a crucial post-translational modification that plays a key role in regulating RNA polymerase II pause release (Wang et al. 2023). Additionally, we also found that DNase I hypersensitive sites (DHSs), markers of regulatory DNA and the basis for the discovery of various types of cis-regulatory elements (Thurman et al. 2012), were significantly enriched near TAD boundaries, revealing the role of TADs in restricting cis-regulatory sequences to their target genes (Fig. 3I; Dixon et al. 2016). The results on hg38 GM12878 data remained consistent with the descriptions above, which are shown in Supplemental Figure S14, A through I.
Furthermore, we investigated whether different combinations of epigenetic factors contribute to the construction of TAD boundaries by clustering TAD boundaries identified by BINDER on the whole-chromosome GM12878 data (Fig. 3J). We observed that half of the hierarchical TAD boundaries were marked only by H3K27me3 or H3K36me3, and the DNase-labeled boundaries were largely enriched by other factors, suggesting the potential impact of different epigenetic factor compositions on the organization and function of TAD boundaries. The same clustering results on hg38 GM12878 data are also shown in Supplemental Figure S14J.
Finally, a motif enrichment analysis was conducted on all TAD boundaries identified by BINDER on 25 kb GM12878 data by utilizing the HOMER pipeline (Heinz et al. 2010). The de novo motif results obtained from HOMER revealed a significant correspondence between TAD boundaries and known motifs associated with chromatin organizations and regulations (Table 1). For instance, Xiao et al. (2021) showed the collaborative role of MAZ and CTCF in controlling cohesin positioning and genome organization, and Clouaire et al. (2005) suggested that cellular THAP proteins may serve as zinc-dependent sequence-specific DNA-binding factors, playing crucial roles in chromosome segregation, chromatin modification, and transcriptional regulation. These findings revealed potential mechanisms or regulatory elements involved in TAD boundaries.
De novo motifs related to chromatin organization and regulation
Hierarchical TAD boundaries reveal distinct TF features
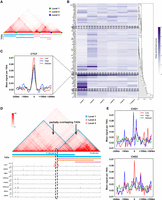
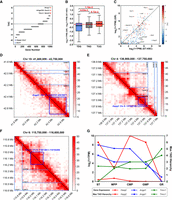
Many studies have emphasized the important role of transcription and 3D genomic interactions in influencing cell fate (Stadhouders et al. 2019). In fact, in addition to common chromatin-associated factors such as CTCF and SMC3, recent investigations demonstrated the significance of TFs, including LIM domain-binding protein 1 (LDB1), paired box 5 (PAX5), and YY1, among others, in mediating or steering promoter-enhancer interactions, which contributed to unraveling how TFs shape the fine-grained organization within TADs (Deng et al. 2012; Andrey and Mundlos 2017; Weintraub et al. 2017). To explore the relationship between hierarchical TAD boundaries and TFs, we first defined the level of a TAD boundary bi as L(bi) = max{NL, NR}, where NL (NR) denotes the number of TADs with their left (right) boundaries being bi (Fig. 4A). Then, ChIP-seq data for 77 TFs in the GM12878 cell line were collected and clustered based on their peak enrichment scores near TAD boundaries of different hierarchies (Fig. 4B; for details, see Supplemental Methods).
Hierarchical TAD boundaries reveal distinct transcription factor (TF) features. (A) An illustration of hierarchical TAD boundaries. Green, blue, and yellow dots indicate TAD boundaries of levels 1, 2, and 3, respectively. (B) Hierarchical clustering of 77 TFs by their peak enrichment scores near hierarchical TAD boundaries, with darker colors indicating higher scores. (C) Enrichment of CTCF near TAD boundaries is represented by red, green, and blue lines for low, medium, and high levels, respectively: low, level < 4; medium, 3 < level < 6; and high, level > 5. (D) Example of a partially overlapping TAD (Chr 1: 76,130,000–78,150,000, 10 kb GM12878), generated by 3D Genome Browser (Wang et al. 2018b) and UCSC Genome Browser (Nassar et al. 2023). (E) Enrichment of CHD1 and CHD2 near hierarchical TAD boundaries of low, median, and high levels.
We also found differences in the enrichment of CTCF near TAD boundaries at different levels: weaker enrichment near higher-level boundaries, as well as SMC3 and RAD21, proteins related to the loop extrusion model (Fig. 4B,C). Notably, the same phenomenon was also observed on hg38 GM12878 data (Supplemental Fig. S15). Subsequently, we investigated the relationship between the enrichment of TFs and the distance between TAD boundaries or length of TADs, and the results showed that even TFs with higher enrichment near TAD boundaries in the same level may still have different preferences for the length of TADs surrounding them (Supplemental Fig. S16). For example, POU2F2 and CEBPB, which were highly enriched at level 2 TAD boundaries, tend to be enriched at the boundaries of larger-size (more than 50 bins) and smaller-size (fewer than 10 bins) TADs, respectively. PML, on the other hand, showed almost no significant TAD size preference. This is an interesting observation, and the specific mechanism involved may deserve to be studied in depth.
Moreover, we observed an absence of CTCF peak near the boundary of a partially overlapping TAD (Fig. 4D), which coincided with the findings of a recent study (Wang et al. 2018a). It may suggest a potential non-CTCF-dependent mechanism in the formation of hierarchical TADs or partially overlapping TADs. We also observed a dual-peak enrichment of CHD1 near high-level boundaries, whereas CHD2 exhibited a single-peak enrichment near low-level boundaries (Fig. 4E), suggesting their distinct binding tendencies near TAD boundaries. Notably, a recent study demonstrated the transcriptional coupling of CHD1 and CHD2 recruitment in chromatin active regions, indicating their differential binding characteristics in active TSS regions (Siggens et al. 2015).
Hierarchical TADs illuminate a brand new landscape of mouse hematopoiesis
To investigate the dynamics of hierarchical TADs during cell differentiation, we chose the mouse hematopoietic system, a well-established model (Fig. 5A; for details, see “Mouse Hematopoietic Differentiation Tree” section in the Supplemental Materials). Here, we used tagHi-C maps of 10 mouse hematopoietic cells, generated by tagHi-C technique (Zhang et al. 2020). First, we observed different gene expression patterns in two differentiation paths: MK path, LT-ST-MPP-CMP-MEP-MK; GR path, LT-ST-MPP-CMP-GMP-GR (Fig. 5B). Then, hierarchical clustering of eight cell types (except CLP and MKP) was performed based on the active gene expression vector of each cell type (for details, see Supplemental Methods), and we found that the clustering pattern fully aligned with the hematopoietic differentiation tree, indicating that cells at different differentiation stages exhibit distinct gene expression patterns (Fig. 5C).
Hierarchical TADs illuminate a brand-new landscape of mouse hematopoiesis. (A) The well-studied differentiation tree of 10 mouse hematopoietic cell types. (B) Median gene expression of each cell type in both GR and MK path. (C) Hierarchical clustering of eight cell types in terms of active gene expression vector of each cell type, in which the three clusters are marked with different colors. The values of the heatmap represent the Pearson's correlation coefficients of active gene expression vector between two cell types. (D) Gene expression in TADs of greater than level 2 identified by BINDER in LT, MK, and GR (P-values, Wilcoxon rank-sum test). (E) Boxplots of gene expression (log2(1 + TPM)) within TADs of different levels and lengths (bin length) of LT-HSC, in which the expression value of a TAD is defined as the average nonzero expression value of all genes within it (P-values, Wilcoxon rank-sum test). (F) Number of TADs of different sizes of six cell types in GR (left) and MK (right) path. Number of TADs of different levels in GR (G) and MK path (H).
Additionally, we calculated the average gene expression within TADs of level greater than 2 in LT, MK, and GR, and the results showed significant differences among them, suggesting dynamic hierarchical TADs during cell differentiation (Fig. 5D). Then, we focused on one cell type to explore gene activities within hierarchical TADs and found that the average gene expression was higher within TADs of lower level (Fig. 5E; Supplemental Fig. S17). Moreover, we also observed higher average gene expression within TADs of larger length (Fig. 5E; Supplemental Fig. S18), which is consistent with the general experience that the higher the TAD level the smaller the length.
Subsequently, we investigated the number of TADs of different lengths and levels in both the MK path and GR path, respectively (Fig. 5F–H), and observed that the number of TADs of different lengths and levels changed dynamically during differentiation as well as the difference in the number of changes between the MK path and GR path. In the GR path, the number of TADs in GMP decreased significantly across all levels and returned to previous levels after differentiation into GR (Fig. 5G). In contrast, the TAD numbers from CMP to MK showed a more gradual and sustained decline (Fig. 5H). All these observations may unveil a dynamic organization mechanism of hierarchical TADs during hematopoiesis and suggest a potential role of chromatin structural remodeling in determining cellular fate.
THC unveils genomic dynamics during cellular differentiation
To explore the relationship between hierarchical TADs and gene activities during hematopoietic differentiation, we first sorted 1013 eligible genes (see Supplemental Methods) based on their TAD hierarchy changes (THCs) (Fig. 6A; for details, see Supplemental Methods). Then, genes are defined as THC-up (-down) genes if their THCs are higher (lower) than the median of all the THCs above (below) zero, denoted as TUGs (TDGs), and genes are defined as THC-normal genes (TNGs) if their THC is zero. We observed distinct gene expression variations among TUGs, TNGs, and TDGs from ST to GR, suggesting a potential impact of THCs on gene transcriptional activity (Fig. 6B,C).
THC unveils genomic dynamics during cellular differentiation. (A) Distribution of THCs of 1013 eligible genes. Genes are sorted in ascending order according to their THCs, for genes with the same THC, we sorted them by string order of their gene names. (B) Boxplot illustrating gene expression variations for TDGs, TNGs, and TNGs between ST and GR (P-values: Wilcoxon rank-sum test). (C) Scatter plot showing gene expression of TUGs and TDGs in GR and ST, with color representing THCs (from low to high, ranging from blue to red). Some representative genes are labeled with their gene symbols. Hi-C submatrices near Angpt1 (D), Hspg2 (E), and Tmcc1 (F), with GR displayed below the diagonal and ST above. Dark blue boxes indicate the locations of genes, and light blue triangles represent hierarchical TADs. (G) Expression of Angpt1, Hspg2, and Tmcc1, along with their corresponding max TAD hierarchies in each cell type (max TAD hierarchy of a gene is defined as the largest level of all TADs containing that gene, and we say that max TAD hierarchy of a gene is zero if there is no TAD containing it) in the GR path.
Specifically, chromosomes near the Angpt1 and Hspg2 genes (TDGs with THCs of −6 and −4, respectively) exhibited a loss of TAD structures and a reduction in gene expression from ST to GR (Fig. 6D,E,G). Notably, Ikushima et al. (2013) suggested that Angpt1-Tie2 signaling has been implicated in influencing the differentiation capacity of hematopoietic lineages and increasing the stem cell activity of HSCs, whereas the Hspg2 gene has been shown to play a crucial role in hematopoietic cell differentiation (Zhou et al. 2020). Besides, the chromosome near the Tmcc1 gene (TUG with THC of four) showed the formation of hierarchical TADs, accompanied by an increase in gene expression (Fig. 6F,G).
Finally, Gene Ontology (GO) enrichment analysis using the DAVID tool (Huang da et al. 2009) for TUGs and TDGs revealed significant enrichment in seven terms related to cellular activity, gene expression, and chromatin organization (Table 2). Taken together, these results may suggest a close relationship between hierarchical TADs and gene activities within them during cell differentiation.
Seven GO terms enriched by TUGs and TDGs
Contribution of hierarchical TADs in transcriptional coregulation
Hierarchical TADs are relatively segregated units in chromatin organization, reflecting functional isolation. Recent studies have highlighted the coregulating activities of genes within hierarchical TADs, referred to as transcriptional coregulation (Nora et al. 2012; Dixon et al. 2016; Zhan et al. 2017; Ramírez et al. 2018).
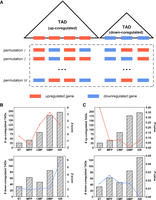
First, a TAD is defined as an up(down)-coregulated TAD if the number of upregulated (downregulated) genes within it is >80% of the total number of genes within it (Fig. 7A; for the definition of upregulated and downregulated genes, see Supplemental Methods). To explore up- and down-coregulation during cell differentiation, we permuted the original genome by 200 times (Fig. 7A; for details, see the “Random Permutation of Genome” section of Supplemental Methods) and calculated Z-scores and P-values (for details, see the “Z-Score and P-Values of Up(Down)-Coregulated TADs” section of Supplemental Methods) for each cell type in GR and MK paths (Fig. 7B,C; Supplemental Fig. S19). We found that both the number of up- and down-coregulated TADs generally increased in the GR path, and the P-value reached its lowest point for up-coregulation in GMP and for down-coregulation in GR, respectively. These observations may suggest a dynamic organizational mechanism for coregulation of TADs during differentiation (for an example of how breaking a down-coregulated TAD relates to a cell-type transition, see Supplemental Fig. S24; see the Supplemental Materials).
Contribution of hierarchical TADs in transcriptional coregulation. (A) Schematic of random genome permutation (for details, see Supplemental Methods) and up(down)-coregulated TADs. Barplot of the number of up(down)-coregulated TADs and lineplot of the corresponding Z-scores (B) and P-values (C) for each cell type in GR path.
Furthermore, we investigated gene activities within TADs identified by BINDER based on our definition of coactive (coinactive) TADs (Supplemental Fig. S20; for details, see the “Coactive (Coinactive) TADs” section of the Supplemental Materials). Taken together, both coregulation and coactivity (coinactivity) within TADs suggest the potential of TADs to function as gene regulatory units, and they appear to be organized in different manner during hematopoietic differentiation.
Discussion
Despite the rapid advancements in 3D genomics facilitated by Hi-C technology, many questions about hierarchical TADs remain unsolved. Computational methods for identifying hierarchical TADs are important for unraveling these complexities and enabling downstream studies. Here, we present BINDER, which comprehensively characterizes consensus TAD boundaries and robustly identifies hierarchical TADs by combining a graph theory–based algorithm and a neural network model. Our ablation experiment results not only present the impact of different normalization methods on the performance of BINDER but also validate the effectiveness of integrating the community discovery method with the neural network model (Supplemental Table S10). These results highlight the robustness of the consensus boundary strategy of BINDER across various feature combinations and normalization strategies. Our extensive evaluation and analysis also demonstrated the strong performance of BINDER, enhancing the understanding of how hierarchical TADs correlate with cellular functions.
When applied to GM12878 and K562 cell lines, BINDER points to significant biological relevance based on the enrichment of various epigenetic features near TAD boundaries. We found that the organization of TAD boundaries appears to involve a combination of diverse epigenetic features. Subsequently, we investigated the relationship between hierarchical TADs and TFs and found that the factors related to the loop extrusion model, CTCF, SMC3, and RAD21, exhibited lower enrichment near higher-level boundaries. Notably, the absence of CTCF at the boundary of partially overlapping TADs suggested a potential non-CTCF-dependent organization mechanism of hierarchical TADs. In addition, we also observed a different enrichment tendency of CHD1 and CHD2 near the TAD boundaries of different levels, and TFs with a higher enrichment score near the same level boundaries still have different preferences for the size of TADs surrounding them. Furthermore, our motif enrichment analysis revealed that TAD boundaries coincide with motifs associated with chromosome organization and gene regulation.
The application of BINDER to the hematopoietic model provides new insights into mouse hematopoietic differentiation. We explored the changes of hierarchical TADs in cell differentiation and gene expression within TADs of different levels and of different lengths. In our THC analysis, we investigated the dynamics of genes within TADs during cell differentiation and observed that TDGs and TUGs were enriched in several GO terms associated with gene regulation and chromosome organization. Then, our analysis of coregulation and coactivity of TADs suggested a potential dynamic organization mechanism and gene regulation functions of TADs during hematopoietic differentiation.
In addition, our benchmarking tests of running time and memory usage demonstrated that although BINDER is not the fastest tool, its running time is acceptable, and its memory usage is among the lowest (Supplemental Fig. S21). In conclusion, the accuracy and robustness of BINDER make it a valuable tool for unraveling the intricate connections between hierarchical TADs and gene regulation, as well as epigenetics, contributing to a better understanding of 3D genomics.
Methods
Data and materials
The resources used in this study and their corresponding websites or accession numbers are all shown in Supplemental Table S1.
Normalization of Hi-C data and extraction of submatrices
To reduce Hi-C data biases, we perform a global normalization on a raw Hi-C contact matrix using the SCN approach (Cournac et al. 2012). This normalization method is protocol independent and applicable to various genomic contact maps (for details, see Supplemental Methods). We also tested other normalization methods such as iterative correction and eigenvector decomposition (ICE) (Imakaev et al. 2012), Knight–Ruiz (KR) (Knight and Ruiz 2013; Rao et al. 2014), and square root vanilla coverage (sqrtVC) (Rao et al. 2014), and the comparison results are shown in Supplemental Table S10. Recognizing that the intra-interactions of TADs are more frequent than the inter-interactions with other TADs, we equate the task of TAD identification to the community discovery problem in a network in which the Infomap algorithm is utilized (for details, see Selection of Community Discovery Algorithms of the Supplemental Materials). Instead of running Infomap on the entire Hi-C contact matrix, we first extract submatrices by a fixed-size sliding window along the diagonal of a SCN-normed contact matrix. Previous studies indicated that the size of the TAD is generally <2 Mb (Nora et al. 2012; Crane et al. 2015), so the size of the sliding window of BINDER is set to 2 Mb/r, where r is the resolution of the input Hi-C matrix; for example, the window size of a Hi-C matrix at resolution of 10 kb is 200 bin length. Then, the Infomap algorithm is applied to these submatrices.
Detection of candidate dual boundaries
For each submatrix, Infomap divides it into nonoverlapping communities C1, C2, …, Cm, represented as monotonically increasing sequences of bin numbers Ci = (B1, B2, …, Bn). For any j = 2, …, n −1, we call Bj in Ci balanced if Bj = Bj−1 + 1 = Bj+1 − 1, right-balanced if Bj = Bj+1 − 1 and Bj > Bj−1 + 1, and left-balanced if Bj = Bj−1 + 1 and Bj < Bj+1 − 1. Ci is considered balanced if any Bj (j = 2, …, n − 1) in Cj is balanced, and is considered partially balanced otherwise. If Cj is balanced, then only two dual boundaries, (B1 − 1, B1) and (Bn, Bn + 1), are derived from Ci. If Ci is partially balanced and contains right-balanced bins 
and left-balanced bins 
, then from Ci we can derive the dual boundary set:
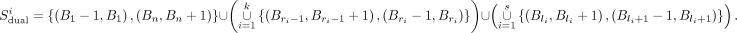
As a result, we denote the set consisting of dual boundaries derived from all submatrices as Sdual. Meanwhile, we record the occurrence count for each dual boundary bi = (i, i + 1), namely, the total number of occurrences of bi in all submatrices, denoted as info(bi). The purpose of introducing the dual boundary in BINDER is to show that we consider the middle of the two nucleotides adjacent to bin i and bin i + 1 to be the boundary of a TAD, which is intended to make the boundary of a TAD more precise.
Extraction of dual boundary features
Here, we extract three kinds of features for each dual boundary bi ∈ Sdual, consisting of local interaction density D(bi), directionality index DI(bi), and P-value of the Wilcoxon rank-sum test P(bi).
Local interaction density
The difference between internal and external interaction frequencies is a discriminative feature of TAD structures in two-dimentional
Hi-C data, based on which we define the “local interaction density” feature for each dual boundary to measure its local interaction
frequency in a Hi-C contact matrix. Given a dual boundary bi = (i, i + 1), a total of 11 dual boundaries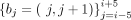 
around bi are first generated. Then, given a window size w1, the local interaction density is defined as for any bj (j = i − 5, i − 4, …, i + 5):
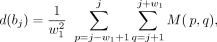where M(p, q) denotes the value of the pth row and qth column of the normalized Hi-C matrix.
Therefore, the local interaction density of a dual boundary bi under a window size w1 can be represented as a 11-dimensional vector D(bi|w1) = [d(bi−5), …, d(bi+5)]. Finally, the local interaction density feature vector of the dual boundary bi is represented as a concatenation of D(bi|w1) under 10 different window sizes, W1 = {5, 10, 20, 30, 50, 60, 70, 80, 90, 100}, which is a 110-dimensional vector, denoted as D(bi).
Directionality index
Dixon et al. (2012) noted that regions at the periphery of the topological domain are highly biased in terms of interaction frequency and then
developed DI to quantify the degree of upstream or downstream deviation for a given bin, which is defined as follows:
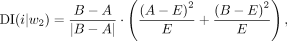where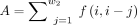 
is the sum of interaction frequencies from a given bin i to the upstream w2 bins length, 
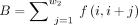is the sum of interaction frequencies from a given bin i to the downstream w2 bins length, and 
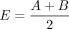denotes the expected interaction frequencies.
Now given a dual boundary bi = (i, i + 1) and a step length w2, DI values of the 10 bins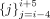 
around bi are calculated, and the 10-dimensional DI vector of bi under step length w2 is defined as DI(bi|w2) = [DI(i − 4|w2), …, DI(i + 5|w2)]. Finally, the DI feature vector of the dual boundary bi is represented as a concatenation of DI(bi|w2) under 10 different step lengths, W2 = {5, 10, 20, 30, 50, 60, 70, 80, 90, 100}, which is a 100-dimensional vector, denoted as DI(bi).
P-value of Wilcoxon rank-sum test
Here, we used the P-value of the Wilcoxon rank-sum test, which is generally used to detect whether two data sets are from the same distributed population, to capture the difference between the inter- and intra-interactions surrounding a given bin; the smaller the P-value, the more likely the bin is to be a TAD boundary.
Now, given a dual boundary bi = (i, i + 1) and a window size w3, the inter- and intra-regions of bi under window size w3, which are two sets, are defined as follows:
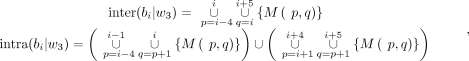where M (p, q) denotes the value of the pth row and qth column of the normalized Hi-C matrix.
Thus, the P-value of the Wilcoxon rank-sum test between inter(bi|w3) and intra(bi|w3) of dual boundary bi under window size w3 is denoted as p(bi|w2), and then, the P-value feature of bi, denoted as P(bi), is defined as a concatenation of p(bi|w2) under different window sizes, W3 = {5, 10, 20, 30, 50, 60, 70, 80, 90, 100}, which is a 10-dimensional vector.
Finally, we can extract a 220-dimensional feature vector, [D(bi), DI(bi), P(bi)], for each dual boundary bi.
Prediction of reliability scores for dual boundaries by a neural network
To quantify the reliability of all candidate dual boundaries in Sdual, a MLP neural network model is designed to learn the characteristics of true and false TAD dual boundaries based on the above extracted 220-dimensional feature vector. The MLP model is composed of six layers (each layer is activated by the ReLU function), in which the first layer comprises 220 neurons for accepting the 220 dimensional feature vectors; the four hidden layers, respectively, contain 512, 128, 32, and four neurons; and the last layer consists of a single neuron whose value Pr(bi) indicates the reliability of the dual boundary bi. The reliability score Rs(bi) of the dual boundary bi is defined as Pr(bi). Therefore, the reliability score belongs to [0, 1], and the closer the value is to one, the more the boundary is considered as a reliable boundary.
In this study, Hi-C maps normalized by SCN, KR, ICE, and sqrtVC methods at four resolutions (100 kb/50 kb/25 kb/10 kb) spanning the entire genome (22 autosomes and an X sex chromosome) of the IMR-90 cell line were employed to train a corresponding neural network model for each normalization method, respectively. To balance positive and negative samples in the training set, a portion of the more negative samples was randomly removed, ensuring an equal number of positive and negative samples. After balancing, taking the SCN-model for example, the data set contains a total of 147,982 samples, which were then randomly divided into a training set containing 118,386 (80%) samples and a validation set containing 29,596 (20%) samples. The test set was generated from the GM12878 cell line and consisted of 29,590 samples (for details, see Supplemental Methods). The results of accuracy of the four trained models on corresponding test sets are shown in Supplemental Figure S23. Additionally, we introduced an early stopping method to avoid overfitting during the model training, and it worked well (Supplemental Fig. S22; Supplemental Table S10; for details, see Supplemental Methods). Finally, the trained neural network is used to predict the reliability score for each dual boundary in Sdual.
Generation of consensus TAD boundaries
To obtain consensus TAD boundaries, we first divided all community-generated dual boundaries in Sdual into five sets based on the number of occurrences of each dual boundary: P1(info(bi) = 0), P2(info(bi) = 1), P3(info(bi) = 2), P4(2 < info(bi) ≤ 8), and P5(info(bi) > 8). Then, we set five thresholds α1, α2, α3, α4, and α5 for each of the five sets for boundary filtering, and a dual boundary bi in Pk (k = 1, 2, 3, 4, 5) that satisfies Rs(bi|Pk) > αk is defined as a consensus dual boundary. We follow the basic hypothesis that a dual boundary is more reliable if it repeats more times in the community discovery part. Therefore, for boundaries with more occurrence counts, the filtering conditions are more relaxed. The fact that a boundary becomes a consensus boundary shows that it has passed not only the previous filtering of the community identification part but also the neural network part; namely, both parts have reached a consensus on whether or not to support this boundary. Here, α1 and α5 are set to 0.77 and zero by default. α2, α3, α4 are set to the 85, 80, and 30 percentiles of the reliability scores for all dual boundaries in the corresponding sets, respectively. Then, the set of all the consensus dual boundaries generated above is denoted as Sreliable.
Generation of hierarchical TADs
In this part, we designed left-neighbor extension and hierarchy generation methods for generating hierarchical TADs and their corresponding hierarchies from Sreliable. In detail, for each dual boundary bi = (i, i + 1) in Sreliable, we search for its left-neighbor dual boundary, termed bj = (j, j + 1), at the genome scale; extract a submatrix corresponding to [j + 1, i] from the Hi-C contact map; and then apply the Infomap algorithm to this submatrix. If it is reported as a complete community by Infomap, we say that [j + 1, i] forms a TAD, which is then output as a TAD. Then we continue searching for the left neighbor of bj, termed bk = (k, k + 1), and check whether [k + 1, i] forms a TAD. We keep searching for left neighbors until we encounter a dual boundary, bn = (n, n + 1), that makes [n + 1, i] fail to form a TAD. After processing the entire dual boundaries in the same manner, TADs are identified that can then be hierarchicalized as follows.
For the generation of their hierarchies, first, it is claimed that TAD T1 = [i1, j1] contains TAD T2 = [i2, j2], if i2 ≥ i1 and j2 ≤ j1, denoted by T2 ⊂ T1. Then, a directed acyclic graph G is constructed with nodes representing all the identified TADs, and two nodes ni and nj are connected by a directed edge ni → nj if the two corresponding TADs satisfy Ti ⊂ Tj. For convenience, a sink node t is added to the graph, and each node nk is connected to t by a directed edge nk → t if the out degree of nk is zero. Based on the graph G, the hierarchy of each TAD Ti is defined as
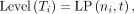where LP(ni, t) is the length of the longest directed path in G from ni to t.
Software availability
The source code of the BINDER-manuscript associated with this study is available at GitHub (https://github.com/LiuYangyangSDU/BINDER) and as Supplemental Code.
Competing interest statement
The authors declare no competing interests.
Acknowledgments
This work was supported by the National Key R&D Program of China with code 2020YFA0712400 and the National Natural Science Foundation of China with code 62272268. The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
Author contributions: J.L. and B.L. conceived and designed the experiments. Y.L. performed the experiments. Y.L. and J.L. analyzed the data. Y.L. and B.L. contributed reagents/materials/analysis tools. Y.L., J.L., and B.L. wrote the paper. Y.L. designed the software used in analysis. J.L. and B.L. oversaw the project.
Footnotes
-
[Supplemental material is available for this article.]
-
Article published online before print. Article, supplemental material, and publication date are at https://www.genome.org/cgi/doi/10.1101/gr.279647.124.
- Received May 30, 2024.
- Accepted February 20, 2025.
This article is distributed exclusively by Cold Spring Harbor Laboratory Press for the first six months after the full-issue publication date (see https://genome.cshlp.org/site/misc/terms.xhtml). After six months, it is available under a Creative Commons License (Attribution-NonCommercial 4.0 International), as described at http://creativecommons.org/licenses/by-nc/4.0/.
