Genome-wide oscillations in G + C density and sequence conservation

  1. Welcome Bender1
  1. 1Department of Biological Chemistry and Molecular Pharmacology, Blavatnik Institute, Harvard Medical School, Boston, Massachusetts 02115, USA;
  2. 2Department of Biology, Kansas State University, Manhattan, Kansas 66506, USA
  • Corresponding author: Welcome Bender +1 (617) 432-1906
    •  
    Next Section

    Abstract

    Eukaryotic genomes typically show a uniform G + C content among chromosomes, but on smaller scales, many species have a G + C density that fluctuates with a characteristic wavelength. This oscillation is evident in many insect species, with wavelengths ranging between 700 bp and 4 kb. Measures of evolutionary conservation oscillate in phase with G + C content, with conserved regions having higher G + C. Loci with large regulatory regions show more regular oscillations; coding sequences and heterochromatic regions show little or no oscillation. There is little oscillation in vertebrate genomes in regions with densely distributed mobile repetitive elements. However, species with few repeats show oscillation in both G + C density and sequence conservation. These oscillations may reflect optimal spacing of cis-regulatory elements.

    The G + C density varies widely among species (Sueoka 1962, 1988). Many vertebrates have large genomic regions (>200 kb) with disparate G + C percentages (GC%), which are often called isochores (Macaya et al. 1976; Elhaik et al. 2010). Germline genomes of ciliates also show large-scale shifts in GC% (Maurer-Alcalá et al. 2018). At higher spatial resolution, there are several reasons for atypical GC%. A:T base pairs are easier to melt, which explains high A + T content at replication origins in fungal genomes (Newlon and Theis 1993; Dai et al. 2005) and at promoters in many eukaryotes (Barrière et al. 2011). Codon use preferences and binding sites for transcription factors will constrain GC% at specific positions.

    There have been several reports of periodic variations in GC%. Large-scale fluctuations (hundreds of kilobases) have been reported for some human chromosomes (Nicolay et al. 2004; Li and Miramontes 2006). A few observations of local oscillations in human DNA with wavelengths in the 400–600 bp range have also been observed (Nicolay et al. 2004; Liu et al. 2007). Shorter fluctuations, with wavelengths between 150 and 250 bp, have been documented in various eukaryotic genomes (Fukushima et al. 2002; Audit et al. 2004; Liu et al. 2007). These latter variations were suggested to reflect nucleosome positioning.

    In our prior work on the Drosophila bithorax complex (Bowman et al. 2014), we noticed a periodicity in the amplitudes of ChIP-seq profiles for H3K27me3. Peaks in the ChIP-seq signal closely correlated with peaks in GC%, perhaps because of the preferential cleavage in A + T rich regions by micrococcal nuclease used for chromatin fragmentation. We were intrigued by this underlying oscillation in GC%, and we began to explore its generality in Drosophila and in other organisms.

    Previous SectionNext Section

    Results

    Oscillations in G + C content

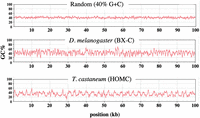
    The GC% oscillations were seen in our studies of the bithorax complex (BX-C) of the fruit fly, Drosophila melanogaster. The BX-C encompasses a ∼310 kb DNA segment that includes only ∼6 kb of protein-coding sequence. The oscillation in GC% for this region is visually obvious when one plots the average G + C content within a sliding window of 200 bp. The plot in Figure 1 compares BX-C DNA to a randomly shuffled sequence of the same overall GC%. Figure 1 also shows a homologous region from the homeotic complex (HOMC) of the red flour beetle, Tribolium castaneum (Shippy et al. 2008). The beetle sequence shows an even more obvious oscillation, but with a longer wavelength. In this study, we use the term “oscillation” loosely; formally, the plots in Figure 1 show periodic fluctuations in GC% that vary over a limited range of wavelengths.

    Figure 1.
    View larger version:
    Figure 1.

    Oscillations in base composition. GC% is plotted for a 200-base sliding window across 100-kb DNA segments, as implemented with the MacVector DNA analysis software. The DNA segments are centered on the abd-A genes (D. melanogaster 3R 16.77–16.87 Mb; T. castaneum LG2 8.021–8.121 Mb).

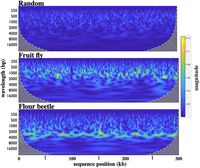
    We used the continuous wavelet transform (CWT) tool to quantify such oscillations (Grossmann and Morlet 1984). This provides a formal representation of signal strength as a function of frequency and typically displays how the oscillation magnitude varies with time. Often, the input for CWT analysis is a recording of sound or of an electromagnetic signal. It is used, for example, to give a two-dimensional graphical representation of a birdsong, with time on the x-axis, frequency on the y-axis, and volume indicated by color. For our analysis, the input signal is GC% as a function of sequence coordinates. Sequence position is indicated on the x-axis, frequency (or wavelength) on the y-axis, and color (blue to yellow) represents the magnitude of the oscillation. The magnitude (technically, the magnitude of the wavelet coefficient for a given wavelength) is a function of both the height of the fluctuations and the spectral purity of the oscillation signal. The magnitude is a weighted function of wavelength; 10 cycles of 1 kb would yield the same magnitude as five cycles of 2 kb. The heatmap in Figure 2 shows the output of the CWT for the three GC% traces shown in Figure 1, each now extended to 300 kb. The yellow highlights (highest magnitude) cluster along a predominant oscillation wavelength of ∼1 kb for the Drosophila sequence and of ∼2.5 kb for the Tribolium sequence.

    Figure 2.
    View larger version:
    Figure 2.

    Heatmaps from continuous wavelet transforms for 300-kb segments of randomly shuffled sequence (40% G + C), of the Drosophila bithorax complex (D. melanogaster 3R 16.66–16.96 Mb), and of the Tribolium homeotic complex (T. castaneum LG2 7.971–8.271 Mb). The magnitude bar on the right shows the linearity of the color scale. The yellow highlights in the heatmaps indicate a predominant oscillation wavelength of ∼1 kb for the fruit fly and ∼2.5 kb for the flour beetle.

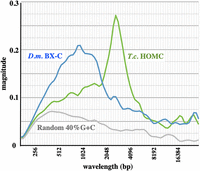
    For any sequence segment, we can generate an average spectral magnitude graph (or simply “magnitude graph”) representing the average oscillation intensity across the sequence as a function of wavelength, as shown in Figure 3. The magnitude graph is similar to a power spectrum in signal analysis; the difference is explained in Methods. Here, magnitude is normalized to the signal strength of a pure sine wave, simulating an oscillation from 20% to 60% G + C, with a 1-kb wavelength. The width of a peak in the magnitude graph indicates the dispersion of wavelengths around the predominant value; the Tribolium oscillation is more uniform than that of Drosophila. Lai et al. (2018) used a different sort of analysis and noted a more subtle indication of a ∼2.5 kb GC% oscillation in the flour beetle, but they did not detect any such oscillation in the fruit fly.

    Figure 3.
    View larger version:
    Figure 3.

    Average magnitude graphs of the continuous wavelet transforms shown in Figure 2. The magnitude metric on the y-axis shows the signal strength relative to that of a perfect sine wave.

    The randomly shuffled DNA sequence gives some spectral magnitude at high frequencies (short wavelengths); this sort of “background noise” might be expected as a baseline for all DNA sequences. Specific sequences may have patterns unrelated to G + C content that generate oscillation power. An appropriate comparison for the G + C oscillations might be a magnitude graph for G + A or G + T; these show somewhat higher spectral magnitudes than our random sequence, but lack the distinctive peaks seen for G + C (Supplemental Fig. S1). We repeated our analyses with a sliding window of 50 bp to detect potential nucleosome-length oscillations. No discernible peaks were in the 250-bp range (Supplemental Fig. S1). We also looked at protein-coding sequence. As one might expect from the base usage of the genetic code, the magnitude graph for Drosophila coding sequence more closely matches that for the randomly shuffled sequence (Supplemental Fig. S2).

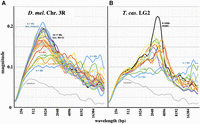
    The GC% oscillations seen in the homeotic complexes are not unique to these developmental regulatory regions. Figure 4A shows superimposed magnitude graphs for 32 successive 1-Mb segments of the right arm of D. melanogaster Chromosome 3. All these graphs are quite similar, with the exception of the first 5 Mb, which encompass centric heterochromatin. For these regions (and for the heterochromatic fourth chromosome) the magnitudes are reduced, and oscillations are spread across a wide range of wavelengths. The 1-Mb segment of Chromosome 3R with the strongest signal includes the Antennapedia complex, the Drosophila homeotic complex regulating the anterior body segments of the fly. Figure 4B includes magnitude graphs for 15 successive 1-Mb segments of T. castaneum linkage group 2 (LG2). Again, the graphs are consistent, with the exception of those for the first 2 Mb, which are largely composed of repetitive sequences. As with Drosophila, such heterochromatic regions display weak oscillations over a wide range of wavelengths. The LG2 segment with the strongest signal includes most of the Tribolium homeotic complex (HOMC).

    Figure 4.
    View larger version:
    Figure 4.

    Chromosome-wide distribution of oscillations. (A) Average magnitude as a function of wavelength for 32 successive 1-Mb segments along Chromosome 3R of D. melanogaster. The first five 1-Mb segments encompass centric heterochromatin, with a high density of repetitive sequences; this region shows weak oscillation. The remaining 27 1-Mb segments all show peak wavelengths of ∼1 kb. The strongest signal comes from the 6–7 Mb segment, which includes the ∼390 kb Antennapedia complex. The 16–17 Mb segment, which includes the ∼315 kb bithorax complex, is also prominent. (B) Average magnitude for 15 successive 1-Mb segments of T. castaneum LG2. Again, the 0–1 and 1–2 Mb segments are highly repetitive and show weak oscillation, and the other 13 segments show stronger signals at wavelengths of ∼2.5 kb. The 8–9 Mb segment, which includes the HOMC, shows the strongest signal.

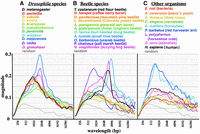
    We have analyzed DNA segments from many other species, usually focusing on the regions homologous to the homeotic loci of flies and beetles. Drosophila species most closely related to D. melanogaster share an oscillation wavelength of ∼1 kb, but three more distantly related species (D. mojavensis, D. virilis, and D. grimshawi) have predominant wavelengths of ∼1.65 kb (Fig. 5A). The higher magnitude in D. mojavensis is a result of larger fluctuations in GC%. Figure 5B shows multiple beetle species, and Figure 5C shows a variety of other species. The oscillation is quite apparent in many insects, with wavelengths that vary from ∼700 to 4000 bp. DNA sequences from bacteria, yeast, nematodes, plants, and vertebrates show relatively little GC% oscillation, although oscillation can sometimes be revealed by another metric (see below).

    Figure 5.
    View larger version:
    Figure 5.

    Magnitude graphs for various species. (A) Eleven Drosophila species (in order of evolutionary distance from D. melanogaster, red to purple). (B) Eleven beetle species. (C) Nine diverse organisms, from bacteria to mammals. Sequences analyzed were centered on homologs of D. melanogaster Ultrabithorax (where available) and covered 1 Mb (where contiguous sequences extended that far). Clear GC% oscillations are apparent in many insects, but not in the non-insect species shown here.

    Oscillations in evolutionary conservation

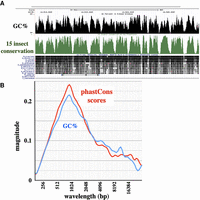
    Cis-regulatory elements in DNA are difficult to identify except by sequence conservation. The genomes of multiple Drosophila species are available to facilitate such an analysis. Figure 6A shows a UCSC Genome Browser (https://genome.ucsc.edu) screen capture of a noncoding region of D. melanogaster (within the large intron of the Ultrabithorax transcription unit). There is a clear correlation between GC% and the phastCons evolutionary conservation score (Siepel et al. 2005). We subjected the phastCons scores as a function of sequence position to the CWT signal analysis and compared the resulting magnitude graph to that for GC% (Fig. 6B). The magnitude scales are not easily correlated, because the phastCons scores depend on the selection of species used for the comparison. We did adjust for the relative magnitudes of the two signals. For Drosophila, the 5th–95th percentile range in GC% content covers a 30.5% difference in GC%, and 5th–95th percentile in phastCons scores spans a 92% difference. Thus, the phastCons magnitude graph was scaled by a factor of 0.33 (30.5/92), resulting in GC% and phastCons magnitude graphs that are very similar. In short, there is a bias toward higher AT% in the nonconserved sequences. Such an AT% bias might arise from spontaneous cytosine deamination (Discussion).

    Figure 6.
    View larger version:
    Figure 6.

    Oscillation in conservation. (A) UCSC Genome Browser screen capture of a 20-kb segment in an intronic region of the D. melanogaster bithorax complex, showing the alignment between GC% and phastCons scores of sequence conservation. (B) Magnitude graph of phastCons scores across D. melanogaster Chromosome 3R: 6–7 Mb. Individual base conservation scores were averaged across a 200 base sliding window and analyzed with the continuous wavelet transform. The GC% magnitude graph for the same interval is plotted in blue, as in Figure 4. An alternative method for plotting CWT magnitudes shows a similar correspondence between GC% and phastCons scores (Supplemental Fig. S6B).

    Transposon insertions dampen the coherence of GC% oscillations

    D. melanogaster and T. castaneum have compact genomes with relatively few mobile element insertions. Transposon insertions might be expected to disrupt any oscillation signal. The effect is illustrated in a comparison between T. castaneum and another flour beetle, T. confusum. Figure 7A shows a Pustell dot matrix sequence comparison (Pustell and Kafatos 1982) for these two species across a long transcription unit (LOC662726) and flanking regions. The diagonal indicates clear homology, but the T. confusum genomic region is 2.7-fold longer than its T. castaneum counterpart. The inset shows GC% magnitude graphs; T. confusum shows a much-reduced peak. Figure 7B is an enlargement of the red boxed part of the dot matrix in Figure 7A. The conserved elements are easily discerned, but they are displaced from one another along the x-axis (T. confusum sequence). These displacements seemed likely to reflect mobile element insertions. Because mobile elements have not been cataloged in the T. confusum genome, we simply assessed genomic copy number for sequences in this region. We scanned across this region in each species with 18-base windows (displaced every nine bases) and counted the exact sequence matches in the organism's entire available genome sequence. Histograms showing these sequence copy numbers are aligned with both sequence axes (Fig. 7B). T. confusum clearly has many more repeats, and these fall predominantly between the conserved elements. The high sequence identity of the conserved sequence blocks implies that the two species are closely related but that T. confusum has suffered a massive invasion of transposons (or, conceivably, that T. castaneum has deleted most of its transposons).

    Figure 7.
    View larger version:
    Figure 7.

    T. castaneum/T. confusum comparison. (A) Pustell DNA dot matrix comparison of the two genomes across a segment of T. castaneum LG2 (11.872–12.222 Mb). Dots indicate identity of ≥18 of 20 bases. The two genomic segments are largely collinear, except that the T. confusum segment is approximately threefold longer. The upper right inset shows the GC% magnitude graphs for these two species across 1-Mb segments in this region. The blue box encloses the LOC662726 transcription unit. The inner red box encloses a ∼30 kb region of T. castaneum, all of which is intronic except for the 600-bp protein-coding third exon. The beetle photos are by Merrilee S. Haas, used with permission. (B) Expansion of the red boxed region in A. The homologous segments are successively offset in the T. confusum genome. Above and to the right of the dot matrix are bar graphs showing the DNA copy number across this region (18 base segments incremented by nine bases) in the T. confusum and T. castaneum genomes, respectively. The single red asterisk marks a T. castaneum TTA triplet repeat, and the double red asterisk marks a T. castaneum repetitive element with homologies with R97, R163, and R287 of the list in Wang et al. (2008).

    As expected, conserved segments are GC-rich and spacers GC-poor. A survey across 52 conserved sequences within the Tribolium HOMC complex showed the G + C content of conserved sequences to be 39% (T. castaneum) and 35% (T. confusum), whereas that of spacer sequences was just 29% (T. castaneum) and 27% (T. confusum). Thus, the coherence of the GC% oscillation signal in T. confusum is dampened by the variability in the length of nonconserved spacers.

    We have examined 12 long T. castaneum/T. confusum homologous regions mapping to five T. castaneum chromosomes. The overall “stretch” of the T. confusum sequence (slope of the castaneum/confusum dot matrix diagonal) is typically uniform over hundreds of kilobases, but it varies among different homologous regions, from 1.2-fold to fourfold. It is not clear why transposon gain or loss in beetles should favor one chromosomal region over another.

    Lacking phastCons data for the beetles, we directly measured the lengths of individual conserved sequence blocks in T. castaneum. These measurements are easily derived from the comparison of T. castaneum with T. confusum (Fig. 7B), because conserved blocks are widely separated by repetitive DNA in the latter genome. We manually curated 200 conserved segments from four different genomic regions of T. castaneum. The median length of a conserved element plus adjacent spacer is ∼1.95 kb. In a CWT magnitude graph, five cycles of 2 kb have the same magnitude as 10 cycles of 1 kb, and so we weighted the number of conserved elements at a given wavelength by the value of that wavelength. The wavelength corresponding to the median of those weighted values is 2.65 kb, which matches the measured peak in the GC% CWT magnitude graph of ∼2.5 kb for these four genomic segments. Thus, sequence conservation in beetles oscillates in phase with GC%, as it does in flies.

    Vertebrate genomes

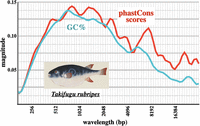
    Because such oscillations correlate tightly with sequence conservation, one can examine signals of conservation in vertebrate genomes that do not show much GC% variation, as long as transposons are rare. Figure 8 shows an analysis for the pufferfish, Takifugu rubripes. Fugu was chosen as a model organism because its genome is unusually compact for a vertebrate and is depleted of transposons (Neafsey and Palumbi 2003). Its genome shows a broad peak in GC% oscillation around 1 kb, but the magnitude is low, in part because the GC% fluctuations are modest (5th percentile to 95th percentile covers only 24% in GC%) and in part because the oscillations occur over a wide range of wavelengths. The magnitude graph for sequence conservation (using phastCons scores) shows a broad peak in the same range. The phastCons fluctuation amplitude (5th–95th percentile = 0.70) is scaled to that of the GC% fluctuation amplitude (scaling factor = 0.34). The scaled phastCons plot closely matches the GC% plot. Overall, the pufferfish genome shows a modest but significant genome oscillation not unlike that seen in insects.

    Figure 8.
    View larger version:
    Figure 8.

    Pufferfish oscillation in GC% and in conservation. Six exon-poor segments of the Takifugu rubripes Chromosome 1, combined with the HOX Aa, Ba, and C loci (∼1.27 Mb in total) were analyzed as in Figure 6. The fish shows broad peaks of oscillation magnitude in GC% and conservation. The pufferfish picture (courtesy of Naturalis Biodiversity Center/Wikimedia Commons) is an early 1800s work by Kawahara Keiga.

    Mammalian genomes are more problematic; they are much larger and contain numerous repetitive elements. However, there are some regions with fewer mobile elements and higher sequence conservation. These include genes or gene clusters with extensive cis-regulatory regions, such as the human HOX loci. The CWT heatmaps for such regions show 1–2 kb oscillation signals (Supplemental Fig. S3), but the magnitudes are low and spread across a broad range of wavelengths. The pattern is less apparent than that of the pufferfish, perhaps owing to residual repetitive sequence interspersion.

    Previous SectionNext Section

    Discussion

    The initial observation of these GC% oscillations was fortuitous, and the analysis was not motivated by a prior hypothesis. Speculation about their origin and biological importance can be organized around two questions: (1) What are the functions of conserved GC-rich regions? and (2) Why are there AT-rich spacers of rather uniform length?

    Potential functions

    Possible functions of oscillating GC% periodicity include a structural role, a function in replication, and/or a cis-regulatory function. We will consider each of these in turn.

    Structure

    The GC-rich regions could reflect a repeating structure in the chromatin fiber, with AT-rich segments serving as linkers. The AT and TA dinucleotides promote DNA bending, and poly(dA:dT) favors nucleosome depletion (Struhl and Segal 2013). A 1-kb oscillation wavelength would span approximately four nucleosomes. However, there is yet no evidence for a prevalent multinucleosome structure of this size. Moreover, individual GC-rich, AT-rich periods (conserved and nonconserved segments) vary in length, so that any such supra-nucleosomal structures would need to accommodate several different compositions. AT-rich regions depleted of nucleosomes could provide entry points for transcription factors or chromatin modifiers, although the lack of conservation precludes sequence specificity. A related possibility is that higher GC% affects a chromatin modification. The Polycomb Repressive Complex 2 (PRC2) binds to G-rich RNA, and so G-rich nascent transcripts might oppose Polycomb repression by competing for PRC2 (Wang et al. 2017; Beltran et al. 2019). However, this specific mechanism would only apply to the fraction of the genome subject to such regulation.

    Replication

    Replication origins are widely separated (∼25 kb apart) in cultured Drosophila and mammalian cell lines (Cayrou et al. 2011), a spacing much larger than the oscillation wavelengths described here. However, in pre-blastoderm Drosophila embryos, when the nuclei divide every few minutes, replication origins are more closely spaced. Blumenthal et al. (1974) observed origins in such cleavage stage nuclei spaced ∼8 kb apart, but they estimated that not all origins are used in each cell cycle, and that potential origins occur on average ∼3.4 kb apart. More recent studies have suggested that potential origins outnumber actual origins in any given cell cycle, with the origin choice influenced by tissue-specific chromatin structure (Eaton et al. 2011; Comoglio et al. 2015). Drosophila origins have no discernible sequence specificity, although they tend to be GC-rich (Cayrou et al. 2011). Thus it is possible that some or all of the GC-rich conserved segments are potential origins, with their abundance (and hence spacing) related to the probability of origin firing.

    Regulation

    The majority of conserved elements in Drosophila are not exons; many are likely to be regulatory sequences, such as enhancers, domain boundaries, Polycomb response elements, or MSL recognition elements. Identified “cis-regulatory modules” show sequence conservation and elevated G + C content (Li et al. 2007). Enhancers identified by STARR-seq (Arnold et al. 2013) also show elevated G + C content (our analysis of their listed 500-bp Drosophila S2 cell enhancers). Active enhancers are thought to be marked by open chromatin, as assayed by DNase I hypersensitivity, shearing after formaldehyde cross-linking (FAIRE), or cutting by TN5 transposase (ATAC-seq). FAIRE analysis of Tribolium chromatin showed high G + C content at fragmentation sites and an enhanced FAIRE peak-to-peak distance of ∼3 kb (Lai et al. 2018). These correlations, and the lack of strong evidence for the structure or replication origin models, support the correspondence of the conserved GC-rich sequence blocks with cis-regulatory elements.

    AT-rich spacer length

    D. melanogaster has a particularly small genome, even among insects (Hanrahan and Johnston 2011). Deletions predominate over insertions in sequences not under selective pressure (Petrov and Hartl 1998; Petrov 2002a). There are very few transposon insertions except in the heterochromatic regions near centromeres and telomeres, and on the fourth and the Y Chromosomes (https://www.flybase.org). In euchromatic regions, the short sequences between conserved elements appear to be AT-rich (Fig. 6). This may reflect spontaneous deamination of cytosine, which converts it to uracil. If this uracil is not removed by uracil-DNA glycosylase, subsequent replications will yield an A:T base pair. Likewise, deamination of 5-methylcytosine (absent in flies but present in present many other insects) (Bewick et al. 2017) yields thymine, which, without repair, also produces an A:T base pair after replication. Indeed, among spontaneous mutations in D. melanogaster, G:C to A:T transitions are sevenfold more common than A:T to G:C (Assaf et al. 2017). Thus, sequences not bound by selective pressure should be relatively AT-rich.

    Given the apparent compaction pressure (Petrov 2002a), why are there any AT-rich spacers between conserved sequence blocks? A likely possibility is that enhancers interfere with each other when they are too closely spaced. This has been shown for a pair of enhancers from the Drosophila even skipped locus combined in reporter constructs (Small et al. 1993; Kim et al. 2013). It is also conceivable that AT-rich sequences are needed adjacent to enhancers, perhaps to facilitate polymerase entry for enhancer transcription (Henriques et al. 2018). The importance of enhancer spacing has not often been tested in vivo, in part because there are few examples of immediately adjacent enhancers whose individual expression patterns have been well documented. We attempted to show some function for the AT-rich sequences on either side of the PBX enhancer of the Drosophila bithorax complex (defined by Pirrotta et al. 1995). Upon deleting these segments, we failed to see any segmental transformation indicative of loss or gain of function (Supplemental Fig. S4). This negative result is not persuasive, because subtle phenotypes would have been missed.

    Wavelength differences among species

    A remaining question is why the GC% oscillation wavelength varies among species. The magnitude graphs for GC% oscillation in D. melanogaster and its close relatives show a peak of approximately 1 kb (Fig. 5A). D. grimshawi, D. virilis, and D. mojavensis (the “virilis group”) are relatively diverged from D. melanogaster. The magnitude graphs for GC% oscillation in these three species peak at ∼1.65 kb, although there is substantial overlap with the spectrum of D. melanogaster (Fig. 5A). These three diverged species show long (>100 kb) collinear regions of intermittent homology with D. melanogaster, but with length expansions of 10%–30% across several regions analyzed. Because the GC-rich homologies between D. melanogaster and the D. virilis group are equal in length, it must be that the AT-rich spacers are expanded in the virilis group.

    The balance between spontaneous insertions and deletions can vary between species (Petrov 2002b). If that balance in D. virilis is shifted more toward insertions, we expect that the extra sequences would be found predominantly in the nonconserved spacer regions, because disruption of conserved coding or regulatory elements would be lost by selection. Over generations, new insertions would drift toward a high AT%, owing to the deamination pressure mentioned above.

    We have modeled this process by randomly inserting bases into AT-rich segments of the 1-Mb D. melanogaster sequence analyzed in Figure 5A (which includes the ∼310 kb bithorax complex), using a ratio of seven A insertions to three G insertions. The D. virilis sequences homologous with this 1-Mb melanogaster sequence are expanded by ∼24%, and so we continued randomly adding bases until the modified sequence measured ∼1.24 Mb (Supplemental Fig. S5A; for details, see Methods). The modified sequence has a G + C content of 40.5%, approximating the ∼40% G + C of the virilis, mojavensis, and grimshawi sequences used in Figure 5A. The magnitude graph of the modified sequence resembles the actual magnitude graph of D. grimshawi, and matches the wavelengths of D. virilis and D. mojavensis, although with lower magnitude.

    There is a greater divergence in GC% wavelength in a fly/beetle comparison, with a ∼2.5 kb peak wavelength in T. castaneum (Fig. 4B). D. melanogaster is sufficiently diverged from T. castaneum that collinear alignments are not possible. The T. castaneum homeotic complex is not significantly expanded in length from the homologous regions in D. melanogaster (combined Antennapedia and bithorax complexes). However, the combined length of a typical conserved block plus spacer (the wavelength) is clearly enlarged in T. castaneum, relative to D. melanogaster (suggesting that the beetle has fewer conserved elements in its homeotic gene cluster than the fly). We added additional insertions to our model sequence up to a 100% expansion; this generated a broadened peak at ∼2.4 kb (Supplemental Fig. S5B), similar to some of the peak wavelengths seen in T. castaneum plots (Fig. 4B). The magnitude graph peak for the 1 Mb T. castaneum DNA segment that includes ∼600 kb of the beetle homeotic complex (8-9 Mb in Fig. 4B) is sharper and taller than the model expansion; large regulatory regions of homeotic gene complexes show more consistent GC% oscillations. Although our simple model does not exactly reproduce the observed magnitude graphs of other insects, it suggests that a slight shift in the insertion/deletion balance among insect species may explain the differences in oscillation wavelength.

    Among the species we have examined, the oscillations in G + C content and sequence conservation are highest in insects, with some species having a very strong oscillation over a narrow wavelength range (Fig. 5). Vertebrates can show such oscillations as well (Fig. 8), although with broader wavelength distributions and, thus, less magnitude at any one wavelength. Because protein-coding sequence shows little oscillation (Supplemental Fig. S2), the oscillations in GC% and sequence conservation must reflect a constraint of the noncoding fraction of the genome. In Drosophila, the average GC-rich conserved block is ∼750 bp (Fig. 6). The typical AT-rich nonconserved block is ∼250 bp (Fig. 6); this may represent the minimal spacing between cis-regulatory elements needed to avoid interference.

    Previous SectionNext Section

    Methods

    Sequences

    D. melanogaster sequences are from release 6.09 (https://www.flybase.org). T. castaneum sequences are from the Tcas5.2 assembly (NCBI). T. confusum sequences are from BeetleBase (https://www.beetlebase.org; or ftp://ftp.bioinformatics.ksu.edu/Tribolium_confusum/Tconfusum-NEB-F100-J100.final.assembly.fasta). Fugu sequences are from the FUGU5/fr5 assembly (NCBI). Human sequences are from the GRCh38/hg38 assembly (NCBI). Homologous sequences from other Drosophila species and other organisms were recovered from FlyBase. phastCons scores were retrieved from the UCSC Genome Browser for the relevant species.

    Computations

    The plots of GC% (Fig. 1) were produced with the MacVector sequence analysis package (version 15.5.4, MacVector Inc.), with the sliding window adjusted to 200 bases. The continuous wavelet transforms were implemented in MATLAB (R2017b, The MathWorks, Inc.), using the default Morse wavelet. G + C base counts or phastCons scores were averaged over a 200-base sliding window (except where noted otherwise).

    The average spectral magnitude graphs (magnitude graphs) are histograms plotting the average CWT magnitude at a given wavelength, summing across all the sequence positions. The magnitude graphs are subtly different from power spectra often used in analysis of electrical signals. Power spectra compute root mean square values as a function of frequency (electrical power is proportional to the square of the voltage). The difference between the simple average and the root mean square plots are illustrated in Supplemental Figure S6A. A time-averaged wavelet spectrum can also be implemented in MATLAB (Supplemental Fig. S6B). This timeSpectrum method shows the fraction of the oscillations occurring at each wavelength, but it does not capture the amplitude values of the oscillations. The simple average calculation is more conservative and more appropriate for GC% or phastCons analysis. MATLAB scripts for both GC% and phastCons are given in the Supplemental Code.

    The magnitude graphs were typically computed from 21 to 215 bp in wavelength (at the maximum 14 octaves in the default MATLAB CWT package, with 10 steps per octave), and were plotted in Numbers (version 3.2, Apple Inc.). Wavelengths less than 200 bases are not presented in Figures 2⇑⇑⇑⇑⇑–8, because all scores were averaged across 200-base windows. For the “random” sequence in Figures 2⇑⇑–5, we started with a 300-kb sequence with 40% G + C content, which we then shuffled using the random module of Python 3.

    In MATLAB, the continuous wavelet transform heatmaps are automatically scaled so that the maximal signal is represented as bright yellow, regardless of its magnitude metric. For the heatmaps in Figure 2, a short artificial sawtooth wave was added to each sequence file. This gave a maximal signal that was the same for all three sequences, so that the color representation of signal strength can be compared among the three panels. The artificial waves were not added to the sequence files for the magnitude graphs in subsequent figures.

    The numerical values of the magnitude graphs are given as a fraction of the maximal magnitude of a pure sine wave, which gives a sharp peak in a magnitude graph, with half maximal values of ± ∼20%. Specifically, our test sine wave oscillated from −0.4 to +0.4, with 1000 measurements per cycle, for 1000 cycles, although the maximal magnitude was independent of wavelength or number of cycles.

    Sequence expansion modeling

    We modeled the possible genome expansion by adding nucleotides to relatively AT-rich areas of a D. melanogaster starting sequence (Chromosome 3R, 16–17 Mb). We scanned across the sequence in 100-bp windows (sliding 7 bp), considering a window AT-rich, and therefore eligible for random sequence addition, if it had no more than 31.2% G + C (one standard deviation below the average G + C content of 100-bp windows of the starting sequence). At every iteration over the sequence, we added a randomized 10-mer consisting of seven A and three G bases to the midpoint of a randomly chosen 1% of eligible AT-rich windows. Successive iterations continued until the sequence length approximated that of the equivalent region in the comparison species.

    Previous SectionNext Section

    Competing interest statement

    The authors declare no competing interests.

    Previous SectionNext Section

    Acknowledgments

    We are indebted to Adam Tanner for help with MATLAB implementation and to Munib Wober for education in signal analysis. Merrilee S. Haas provided beetle pictures. Joe Geisberg assisted in a search for structural oscillation. Heber Domingues assisted in the Drosophila enhancer deletion experiments. This work was funded by the following grants from the National Institutes of Health (NIH): NIH R01GM30186 (Z.M.; to K. Struhl); NIH P20 GM103418 (S.B.); and NIH R01GM028630 (W.B.).

    Previous SectionNext Section

    Footnotes

    • Received November 13, 2020.
    • Accepted September 1, 2021.

    This article is distributed exclusively by Cold Spring Harbor Laboratory Press for the first six months after the full-issue publication date (see https://genome.cshlp.org/site/misc/terms.xhtml). After six months, it is available under a Creative Commons License (Attribution-NonCommercial 4.0 International), as described at http://creativecommons.org/licenses/by-nc/4.0/.

    Previous Section
     

    References

    1. ↵
      Arnold CD, Gerlach D, Stelzer C, Boryń ŁM, Rath M, Stark A. 2013. Genome-wide quantitative enhancer activity maps identified by STARR-seq. Science 339: 1074–1077. doi:10.1126/science.1232542
      Abstract/FREE Full Text
    2. ↵
      Assaf ZJ, Tilk S, Park J, Siegal ML, Petrov DA. 2017. Deep sequencing of natural and experimental populations of Drosophila melanogaster reveals biases in the spectrum of new mutations. Genome Res 27: 1988–2000. doi:10.1101/gr.219956.116
      Abstract/FREE Full Text
    3. ↵
      Audit B, Vaillant C, Arnéodo A, d'Aubenton-Carafa Y, Thermes C. 2004. Wavelet analysis of DNA bending profiles reveals structural constraints on the evolution of genomic sequences. J Biol Phys 30: 33–81. doi:10.1023/B:JOBP.0000016438.86794.8e
      CrossRefGoogle Scholar
    4. ↵
      Barrière A, Gordon KL, Ruvinsky I. 2011. Distinct functional constraints partition sequence conservation in a cis-regulatory element. PLoS Genet 7: e1002095. doi:10.1371/journal.pgen.1002095
      CrossRefMedlineGoogle Scholar
    5. ↵
      Beltran M, Tavares M, Justin N, Khandelwal G, Ambrose J, Foster BM, Worlock KB, Tvardovskiy A, Kunzelmann S, Herrero J, et al. 2019. G-tract RNA removes Polycomb repressive complex 2 from genes. Nat Struct Mol Biol 26: 899–909. doi:10.1038/s41594-019-0293-z
      CrossRefGoogle Scholar
    6. ↵
      Bewick AJ, Vogel KJ, Moore AJ, Schmitz RJ. 2017. Evolution of DNA methylation across insects. Mol Biol Evol 34: 654–665. doi:10.1093/molbev/msw264
      CrossRefMedlineGoogle Scholar
    7. ↵
      Blumenthal AB, Kriegstein HJ, Hogness DS. 1974. The units of DNA replication in Drosophila melanogaster chromosomes. Cold Spring Harb Symp Quant Biol 38: 205–223. doi:10.1101/sqb.1974.038.01.024
      Abstract/FREE Full Text
    8. ↵
      Bowman SK, Deaton AM, Domingues H, Wang PI, Sadreyev RI, Kingston RE, Bender W. 2014. H3K27 modifications define segmental regulatory domains in the Drosophila bithorax complex. eLife 3: e02833. doi:10.7554/eLife.02833
      CrossRefMedlineGoogle Scholar
    9. ↵
      Cayrou C, Coulombe P, Vigneron A, Stanojcic S., Ganier O., Peiffer I, Rivals E, Puy A, Laurent-Chabalier S, Desprat R, et al. 2011. Genome-scale analysis of metazoan replication origins reveals their organization in specific but flexible sites defined by conserved features. Genome Res 21: 1438–1449. doi:10.1101/gr.121830.111
      Abstract/FREE Full Text
    10. ↵
      Comoglio F, Schlumpf T, Schmid V, Rohs R, Beisel C, Paro R. 2015. High-resolution profiling of Drosophila replication start sites reveals a DNA shape and chromatin signature of metazoan origins. Cell Rep 11: 821–834. doi:10.1016/j.celrep.2015.03.070
      CrossRefMedlineGoogle Scholar
    11. ↵
      Dai J, Chuang RY, Kelly TJ. 2005. DNA replication origins in the Schizosaccharomyces pombe genome. Proc Natl Acad Sci 102: 337–342. doi:10.1073/pnas.0408811102
      Abstract/FREE Full Text
    12. ↵
      Eaton ML, Prinz JA, MacAlpine HK, Tretyakov G, Kharchenko PV, MacAlpine DM. 2011. Chromatin signatures of the Drosophila replication program. Genome Res 21: 164–174. doi:10.1101/gr.116038.110
      CrossRefMedlineGoogle Scholar
    13. ↵
      Elhaik E, Graur D, Josić K, Landan G. 2010. Identifying compositionally homogeneous and nonhomogeneous domains within the human genome using a novel segmentation algorithm. Nucleic Acids Res 38: e158–e158. doi:10.1093/nar/gkq532
      CrossRefMedlineGoogle Scholar
    14. ↵
      Fukushima A, Ikemura T, Kinouchi M, Oshima T, Kudo Y, Mori H, Kanaya S. 2002. Periodicity in prokaryotic and eukaryotic genomes identified by power spectrum analysis. Gene 300: 203–211. doi:10.1016/s0378-1119(02)00850-8
      CrossRefMedlineGoogle Scholar
    15. ↵
      Grossmann A, Morlet J. 1984. Decomposition of hardy functions into square integrable wavelets of constant shape. SIAM J Math Anal 15: 723–736. doi:10.1137/0515056
      CrossRefGoogle Scholar
    16. ↵
      Hanrahan SJ, Johnston JS. 2011. New genome size estimates of 134 species of arthropods. Chromosome Res 19: 809–823. doi:10.1007/s10577-011-9231-6
      CrossRefMedlineGoogle Scholar
    17. ↵
      Henriques T, Scruggs BS, Inouye MO, Muse GW, Williams LH, Burkholder AB, Lavender CA, Fargo DC, Adelman K. 2018. Widespread transcriptional pausing and elongation control at enhancers. Genes Dev 32: 26–41. doi:10.1101/gad.309351.117
      Abstract/FREE Full Text
    18. ↵
      Kim A-R, Martinez C, Ionides J, Ramos AF, Ludwig MZ, Ogawa N, Sharp DH, Reinitz J. 2013. Rearrangements of 2.5 kilobases of noncoding DNA from the Drosophila even-skipped locus define predictive rules of genomic cis-regulatory logic. PLoS Genet 9: e1003243. doi:10.1371/journal.pgen.1003243
      CrossRefMedlineGoogle Scholar
    19. ↵
      Lai Y-T, Deem KD, Borràs-Castells F, Sambrani N, Rudolf H, Suryamohan K, El-Sherif E, Halfon MS, McKay DJ, Tomoyasu Y. 2018. Enhancer identification and activity evaluation in the red flour beetle, Tribolium castaneum. Development 145: dev160663. doi:10.1242/dev.160663
      Abstract/FREE Full Text
    20. ↵
      Li W, Miramontes P. 2006. Large-scale oscillation of structure-related DNA sequence features in human chromosome 21. Phys Rev E Stat Nonlin Soft Matter Phys 74: 021912. doi:10.1103/PhysRevE.74.021912
      CrossRefMedlineGoogle Scholar
    21. ↵
      Li L, Zhu Q, He X, Sinha S, Halfon MS. 2007. Large-scale analysis of transcriptional cis-regulatory modules reveals both common features and distinct subclasses. Genome Biol 8: R101. doi:10.1186/gb-2007-8-6-r101
      CrossRefMedlineGoogle Scholar
    22. ↵
      Liu F, Tøstesen E, Sundet JK, Jenssen TK, Bock C, Jerstad GI, Thilly WG, Hovig E. 2007. The human genomic melting map. PLoS Comput Biol 3: e93. doi:10.1371/journal.pcbi.0030093
      CrossRefMedlineGoogle Scholar
    23. ↵
      Macaya G, Thiery JP, Bernardi G. 1976. An approach to the organization of eukaryotic genomes at a macromolecular level. J Mol Biol 108: 237–254. doi:10.1016/s0022-2836(76)80105-2
      CrossRefMedlineGoogle Scholar
    24. ↵
      Maurer-Alcalá XX, Knight R, Katz LA. 2018. Exploration of the germline genome of the ciliate Chilodonella uncinata through single-cell omics (transcriptomics and genomics). mBio 9: e01836–17. doi:10.1128/mBio.01836-17
      CrossRefGoogle Scholar
    25. ↵
      Neafsey DE, Palumbi SR. 2003. Genome size evolution in pufferfish: a comparative analysis of diodontid and tetraodontid pufferfish genomes. Genome Res 13: 821–830. doi:10.1101/gr.841703
      Abstract/FREE Full Text
    26. ↵
      Newlon CS, Theis JF. 1993. The structure and function of yeast ARS elements. Curr Opin Genet Dev 3: 752–758. doi:10.1016/S0959-437X(05)80094-2
      CrossRefMedlineGoogle Scholar
    27. ↵
      Nicolay S, Argoul F, Touchon M, d'Aubenton-Carafa Y, Thermes C, Arneodo A. 2004. Low frequency rhythms in human DNA sequences: a key to the organization of gene location and orientation? Phys Rev Lett 93: 108101. doi:10.1103/PhysRevLett.93.108101
      CrossRefMedlineGoogle Scholar
    28. ↵
      Petrov DA. 2002a. DNA loss and evolution of genome size in Drosophila. Genetica 115: 81–91. doi:10.1023/A:1016076215168
      CrossRefMedlineGoogle Scholar
    29. ↵
      Petrov DA. 2002b. Mutational equilibrium model of genome size evolution. Theor Popul Biol 61: 531–544. doi:10.1006/tpbi.2002.1605
      CrossRefMedlineGoogle Scholar
    30. ↵
      Petrov DA, Hartl DL. 1998. High rate of DNA loss in the Drosophila melanogaster and Drosophila virilis species groups. Mol Biol Evol 15: 293–302. doi:10.1093/oxfordjournals.molbev.a025926
      CrossRefMedlineGoogle Scholar
    31. ↵
      Pirrotta V, Chan CS, McCabe D, Qian S. 1995. Distinct parasegmental and imaginal enhancers and the establishment of the expression pattern of the Ubx gene. Genetics 141: 1439–1450. doi:10.1093/genetics/141.4.1439
      Abstract/FREE Full Text
    32. ↵
      Pustell J, Kafatos FC. 1982. A high speed, high capacity homology matrix: zooming through SV40 and polyoma. Nucleic Acids Res 10: 4765–4782. doi:10.1093/nar/10.15.4765
      CrossRefMedlineGoogle Scholar
    33. ↵
      Shippy TD, Ronshaugen M, Cande J, He JP, Beeman RW, Levine M, Brown SJ, Denell RE. 2008. Analysis of the Tribolium homeotic complex: insights into mechanisms constraining insect Hox clusters. Dev Genes Evol 218: 127–139. doi:10.1007/s00427-008-0213-4
      CrossRefMedlineGoogle Scholar
    34. ↵
      Siepel A, Bejerano G, Pedersen JS, Hinrichs AS, Hou M, Rosenbloom K, Clawson H, Spieth J, Hillier LW, Richards S, et al. 2005. Evolutionarily conserved elements in vertebrate, insect, worm, and yeast genomes. Genome Res 15: 1034–1050. doi:10.1101/gr.3715005
      Abstract/FREE Full Text
    35. ↵
      Small S, Arnosti DN, Levine M. 1993. Spacing ensures autonomous expression of different stripe enhancers in the even-skipped promoter. Development 119: 762–772. doi:10.1242/dev.119.3.767
      CrossRefMedlineGoogle Scholar
    36. ↵
      Struhl K, Segal E. 2013. Determinants of nucleosome positioning. Nat Struct Mol Biol 20: 267–273. doi:10.1038/nsmb.2506
      CrossRefMedlineGoogle Scholar
    37. ↵
      Sueoka N. 1962. On the genetic basis of variation and heterogeneity of DNA base composition. Proc Natl Acad Sci 48: 582–592. doi:10.1073/pnas.48.4.582
      FREE Full Text
    38. ↵
      Sueoka N. 1988. Directional mutation pressure and neutral molecular evolution. Proc Natl Acad Sci 85: 2653–2657. doi:10.1073/pnas.85.8.2653
      Abstract/FREE Full Text
    39. ↵
      Wang S, Lorenzen MD, Beeman RW, Brown SJ. 2008. Analysis of repetitive DNA distribution patterns in the Tribolium castaneum genome. Genome Biol 9: R61. doi:10.1186/gb-2008-9-3-r61
      CrossRefMedlineGoogle Scholar
    40. ↵
      Wang X, Goodrich KJ, Gooding AR, Naeem H, Archer S, Paucek RD, Youmans DT, Cech TR, Davidovich C. 2017. Targeting of Polycomb repressive complex 2 to RNA by short repeats of consecutive guanines. Mol Cell 65: 1056–1067.e5. doi:10.1016/j.molcel.2017.02.003
      CrossRefGoogle Scholar
    | Table of Contents

    This Article

    1. Published in Advance October 14, 2021, doi: 10.1101/gr.274332.120 Genome Res. 31: 2050-2057 © 2021 Moqtaderi et al.; Published by Cold Spring Harbor Laboratory Press

    Article Category

    ORCID

    1. Profile for Moqtaderi, Z.http://orcid.org/0000-0002-2785-7034

    Share

    Preprint Server



    Navigate This Article

    Current Issue

    1. January 2026, 36 (1)
    1. Current Issue
    1. Alert me to new issues of Genome Research