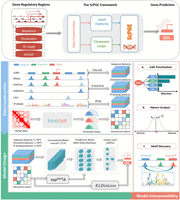
A scalable computational framework for predicting gene expression from candidate cis-regulatory elements

  1. De-Shuang Huang1,5
  1. 1Ningbo Institute of Digital Twin, Eastern Institute of Technology, Ningbo 315201, China;
  2. 2Big Data and Intelligent Computing Research Center, Guangxi Academy of Science, Nanning, 530007, China;
  3. 3School of Information Engineering, Xuzhou University of Technology, Xuzhou 221018, China;
  4. 4Faculty of Data Science, City University of Macau, Macau 999078, China;
  5. 5Institute for Regenerative Medicine, Shanghai East Hospital, Tongji University, Shanghai 200092, China
  • Corresponding author: dshuang{at}eitech.edu.cn
    •  
    Next Section

    Abstract

    Deciphering the relationships between cis-regulatory elements (CREs) and target gene expression has been a long-standing unsolved problem in molecular biology, and the dynamics of CREs in different cell types make this problem more challenging. To address this challenge, we propose a scalable computational framework for predicting gene expression (ScPGE) from discrete candidate CREs (cCREs). ScPGE assembles DNA sequences, transcription factor (TF) binding scores, and epigenomic tracks from discrete cCREs into three-dimensional tensors, and then models the relationships between cCREs and genes by combining convolutional neural networks with transformers. Compared with current state-of-the-art models, ScPGE exhibits superior performance in predicting gene expression and yields higher accuracy in identifying active enhancer–gene interactions through attention mechanisms. By comprehensively analyzing ScPGE's predictions, we find a pattern in true positives (TPs) that the regulatory effect of cCREs on genes decreases with distance. Inspired by the pattern, we design two methods to enhance the ability to capture distal cCRE–gene interactions by incorporating chromatin loops into the ScPGE model. Furthermore, ScPGE accurately discovers some crucial TF motifs within prioritized cCREs and reveals the different regulatory types of these cCREs.

    Cell type–specific gene expression patterns are primarily determined through complex interactions between cis-regulatory elements (CREs) and transcriptional factors, playing a crucial role in differentiation and development (Furlong and Levine 2018). Mutations in CREs contribute to various diseases by disrupting the regular expression of their target genes (Nasser et al. 2021). Decoding how CREs regulate gene expression may reveal the mechanisms of gene regulation and provide insights into the origins of human diseases. However, epigenomic data, such as chromatin accessibility and histone modifications, enhance the dynamic characteristics of CREs to gene regulation, making it more challenging to decipher the relationships between CREs and gene expression.

    High-throughput experimental techniques, such as Hi-C (Rao et al. 2014), ChIA-PET (Tang et al. 2015), and HiChIP (Mumbach et al. 2016), have been developed for identifying physical CRE-gene interactions in a genome-wide fashion, but they just measure physical proximity between CREs and genes instead of direct regulatory impact. Recently, systematic evaluation of the impact of CREs on gene expression has become possible with CRISPR perturbations (Fulco et al. 2019), but only a small subset of CREs can be evaluated in the genome. Meanwhile, the evaluation is restricted to a small number of cell types. Due to its high cost, it is difficult to apply on a large scale.

    Quantitative models have been proposed recently for modeling the relationships between candidate CREs (cCREs) and gene expression. Early models mainly focus on forming binary classification tasks to predict physical cCRE–gene interactions (Li et al. 2019; Tang et al. 2020; Cao et al. 2021) rather than directly predicting gene expression regulated by cCREs. Meanwhile, their performance and generalization ability are always subject to the number of real cCRE–gene interactions, the varying number of cCREs for target genes, and the complex nature of cCRE–gene regulation (Schoenfelder and Fraser 2019). Recent studies on predicting gene expression from DNA sequences have shown that transformer-based algorithms implicitly incorporate modeling cCRE–gene interactions and significantly improve the performance of gene expression prediction (Avsec et al. 2021; Li et al. 2023; Lin et al. 2024). Their special attention mechanisms can effectively capture long-range cCRE–gene interactions, offering a significant advantage over convolutional neural networks (CNNs), which focus on local interactions. Enformer (Avsec et al. 2021), a representative transformer-based model, excels in predicting gene expression, chromatin states, and variant effects. However, because this method only uses sequences, it cannot recognize cell type–specific cCREs, signifying that its adaptability to unseen data from new cell types is limited (Sasse et al. 2023). Moreover, training a new model from scratch using this method requires a substantial amount of computing resources, posing a significant challenge for researchers with limited computing capabilities. To address these challenges, several models of modest size have been proposed to improve the performance of gene expression prediction by utilizing extra data. For example, GraphReg (Karbalayghareh et al. 2022) introduced a graph attention network that integrates chromatin contact data (Hi-C) to predict gene expression. CREaTor (Li et al. 2023) presented a hierarchical deep learning model based on the self-attention mechanism, which utilizes cCREs in open chromatin regions together with ChIP-seqs of transcription factors and histone modifications to predict the expression level of target genes. EPInformer (Lin et al. 2024) introduced an efficient deep-learning framework based on the transformer architecture to predict gene expression by integrating DNA sequences, epigenomic signals, and chromatin contact data in stages. Although these models achieve remarkable predictive performance, their effectiveness is constrained by the scarce availability of extra data across different cell types or by the requirement of elaborately preparing data.

    In this study, we introduce a scalable computational framework for predicting gene expression (ScPGE) from discrete cCREs identified by the Encyclopedia of DNA Elements (ENCODE). ScPGE first assembles DNA sequences, TF binding scores, and epigenomic tracks from discrete cCREs into three 3D tensors, respectively, and then combines CNN with transformer to predict gene expression levels.

    Previous SectionNext Section

    Results

    Overview of ScPGE

    ScPGE is a deep learning framework, composed of a feature-learning module, an interaction-learning module, and a prediction module, which predicts cell type–specific gene expression levels by integrating DNA sequences, TF binding scores, and epigenomic signals from discrete cCREs. In the ScPGE's architecture, CNN serves as a feature extractor to learn the local sequence or chromatin features, whereas transformer serves as a relationship extractor to learn the relationships between genes and cCREs, as well as between cCREs and cCREs. As shown in Figure 1, ScPGE first converts DNA sequences, TF binding scores, and epigenomic signals into three 3D tensors, respectively. Secondly, ScPGE takes the three tensors as input and utilizes multiple 2D convolutional blocks to learn multimodal features of cCREs in parallel, as well as transformer-based blocks to model the relationships between genes and cCREs. Finally, ScPGE extracts the features of cCRE–gene pairs and predicts gene expression levels through the prediction module. Importantly, given that chromatin loops could provide useful information for guiding ScPGE to capture the relationships between genes and cCREs, two approaches are developed to incorporate chromatin loops into the ScPGE model by either increasing the attention weights of chromatin interactions directly or introducing a KL Divergence loss indirectly (Methods). Besides, ScPGE demonstrates its flexible scalability from three aspects: (i) scalability of epigenomic tracks, enabling the use of any number of epigenomic tracks if available; (ii) scalability of cCREs, allowing for the incorporation of any number of cCREs if reasonable; and (iii) scalability of model structure, adjusting the layers of CNN and transformer according to the sequence length.

    Figure 1.
    View larger version:
    Figure 1.

    The framework of ScPGE. The framework predicts gene expression by integrating sequence features, chromatin features, TF motif features, and HiChIP interactions of discrete candidate cCREs on both sides of genes. During the stage of data construction, we transformed sequence features, chromatin features, and TF motif features into three-dimensional tensors and converted chromatin loops identified by FitHiChIP into interaction matrices. During the stage of model design, we combined CNN and transformer to predict gene expression, where CNN is used to learn sequence and chromatin features and transformer is used to learn the relationships between genes and cCREs. Meanwhile, we designed two ways to improve the performance of ScPGE by incorporating chromatin loops. In the stage of model interpretability, we performed cCRE prioritization, pattern analysis, and motif discovery.

    Experimental results confirm the superiority of ScPGE over existing models, showing that ScPGE can predict RNA-seq or CAGE-seq gene expression accurately by modeling the relationships between cCREs and target genes effectively. Moreover, ScPGE greatly reduces computational demands for modeling by using discrete cCREs instead of the entire genomic region flanking target genes, facilitating rapid training and deployment for new cell types. To quantify its computational demand, we systematically evaluated the model complexity of ScPGE from four perspectives, including the training/inference time, number of flops, and number of parameters. As shown in Supplemental Table S1, the model complexity of ScPGE is generally the lowest. We hope that the concept of ScPGE can provide valuable insights for studying gene regulation under resource-limited conditions.

    ScPGE accurately predicts gene expression across multiple cell types

    In this section, we used three state-of-the-art models such as Enformer (Avsec et al. 2021), CREaTor (Li et al. 2023), and EPInformer (Lin et al. 2024) to compare with ScPGE and quantified their performance by the Pearson's correlation coefficient (PCC) and mean absolute error (MAE) between predicted and observed gene expression levels in a variety of cell types.

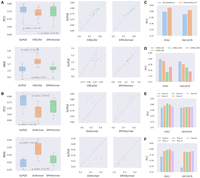
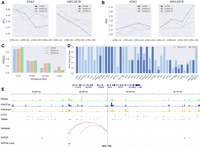
    To assess the performance of ScPGE in predicting RNA-seq gene expression levels, we trained ScPGE, CREaTor, and EPInformer by utilizing RNA-seq data sets from 19 human cell types. As shown in Figure 2A, ScPGE consistently outperforms both CREaTor and EPInformer, achieving significant performance improvements. Specifically, ScPGE surpasses CREaTor's performance by 2.5% and 27% in PCC and MAE, respectively, and exceeds EPInformer's performance by 1.3% and 1% in PCC and MAE, respectively.

    Figure 2.
    View larger version:
    Figure 2.

    Overall performance of ScPGE. (A) The performance of ScPGE in predicting RNA-seq gene expression levels, which was measured by PCC and MAE. (B) The performance of ScPGE in predicting CAGE-seq gene expression levels, which was measured by PCC and MAE. The P-value is calculated using Student's t-test. (C–F) The performance (PCC) of ScPGE's scalability by modifying the number of epigenomic tracks, the number of cCREs, and the structure of ScPGE.

    To evaluate the performance of ScPGE in predicting CAGE-seq gene expression levels, we trained ScPGE and EPInformer by utilizing CAGE-seq data sets from 10 human cell types available in Enformer and compared them with Enformer's pretrained models. As illustrated in Figure 2B, ScPGE significantly outperforms both Enformer and EPInformer across all data sets. ScPGE shows improvements of 10% in PCC and 9.6% in MAE compared to Enformer and improvements of 4.2% in PCC and 2.7% in MAE compared to EPInformer.

    To further evaluate the classification performance of ScPGE, we constructed a binary classification task based on the GM12878 and K562 cell lines to predict whether genes are expressed. Genes with expression levels > 4 were viewed as positive samples (label = 1), and genes with expression levels < 1 were viewed as negative samples (label = 0). In addition, negative samples include genes whose surrounding cCREs were randomly shuffled or their DNA sequences were randomly shuffled while preserving their nucleotide composition. As shown in Supplemental Figure S3, we find that ScPGE achieves very high performance (almost approaching 1), demonstrating that ScPGE is efficient in the gene classification task. This observation also indicates that the task of gene classification is easier than the task of gene expression prediction.

    In summary, the above results obtained from RNA-seq and CAGE-seq data sets indicate that ScPGE can accurately predict gene expression across various cell types, highlighting its effectiveness in predicting gene expression.

    To demonstrate the flexible scalability of ScPGE, we performed a series of experiments by modifying the number of epigenomic tracks, the number of cCREs, and the structure of ScPGE: (i) scalability of epigenomic tracks (Fig. 2C)—we find that ScPGE using 13 epigenomic tracks performs better than ScPGE using four default tracks, suggesting that a greater number of epigenomic tracks provides more valuable information; (ii) scalability of cCREs (Fig. 2D)—we observe a decrease in ScPGE's performance as the number of cCREs increases, implying that more cCREs may introduce noise rather than useful information; and (iii) scalability of model structure (Fig. 2E,F)—we notice that the lack of transformer (Tran-0) significantly reduces the predictive performance of ScPGE, whereas other cases had little impact on its performance, highlighting the crucial role of transformer in modeling the relationships between genes and cCREs. Consequently, ScPGE exhibits flexible scalability by accommodating any number of epigenomic tracks and cCREs, as well as allowing for easy adjustment of the model architecture, which makes it particularly well-suited for gene expression prediction in varying contexts, including situations where data availability is uncertain.

    ScPGE successfully prioritizes cell type–specific cCREs

    Linking candidate enhancers to their target genes through high-throughput experiments remains a critical challenge in terms of time and cost. In this scenario, accurate prioritization of candidate enhancer–gene interactions by computational methods becomes increasingly important. To evaluate ScPGE's accuracy in capturing true enhancer–gene interactions, we focus on genes with experimentally validated enhancers. These enhancer–gene interactions were collected from three public literatures, consisting of positive (677) and negative (2239) interactions, and categorized into four groups based on distance.

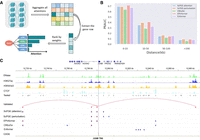
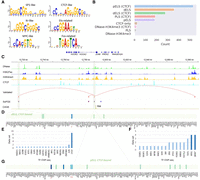
    After the K562-specific ScPGE model was trained, the attention scores from self-attention layers were used to prioritize all candidate enhancer–gene interactions (Fig. 3A). Additionally, in silico perturbation based on ScPGE was performed to prioritize all candidate enhancer–gene interactions by their relative changes. As measured by the PRAUC metric (Fig. 3B), the performance of ScPGE is comparable to EPInformer and superior to Enformer and CREaTor at various distances, demonstrating the effectiveness of ScPGE. Furthermore, the performance of all methods decreases with increasing distance, suggesting that they perform poorly in predicting distal enhancer–gene interactions.

    Figure 3.
    View larger version:
    Figure 3.

    ScPGE prioritizes cell type–specific cCREs. (A) Schematic overview of prioritizing active cCREs by ScPGE's attentions. (B) The performance (PRAUC) of relevant methods in classifying cCRE–gene pairs at different distance groups. (C) Visualization of active cCREs of the JUNB gene prioritized by ScPGE (attention), ScPGE (perturbation), EPIformer, CREaTor, and Enformer, where validated cCREs are represented by red rectangles and correctly identified cCREs are represented by blue rectangles with red outlines.

    To illustrate ScPGE's capability in detecting active enhancers for a given locus, we focused on two important genes (JUNB [Chen et al. 2022] and KLF1 [Myers et al. 2025]) in the human hematopoietic system. We selected all candidate enhancers surrounding the two genes within 100 kb as test targets. These enhancers (gray rectangles) were evaluated via CRISPRi-FlowFISH experiments, and only a few were found to have a significant effect on gene expression. To classify candidate enhancers as active or inactive, we prioritized all enhancers and selected the top k enhancers, where k is the number of validated enhancers, to calculate the true positive rate (TPR). As shown in Figure 3C, there are four validated enhancers (red rectangles) surrounding the JUNB gene, including two proximal enhancers and two distal enhancers. We find that both ScPGE (attention) and EPInformer discover three validated enhancers, achieving the highest TPR of 75%, and outperform other methods. Additionally, we find that ScPGE (attention) tends to capture distal enhancers, whereas ScPGE (perturbation) tends to capture proximal enhancers. Therefore, they complement each other and can be combined to capture active enhancers. As shown in Supplemental Figure S4, there are six validated enhancers (red rectangles) surrounding the KLF1 gene, including three proximal enhancers and three distal enhancers. We can observe that ScPGE (attention + perturbation) discovers all validated enhancers, outperforming other methods in capturing active enhancers.

    Categorization of ScPGE's predictions shows distinct patterns

    Although several computational methods for predicting gene expression have been proposed, there is little in-depth analysis of their predictions. Such analysis is essential for identifying distinct patterns from predictions and providing feedback for optimizing models. To achieve this, we categorized ScPGE's predictions into true positives (TPs), false positives (FPs), true negatives (TNs), and false negatives (FNs) (Methods).

    Through ablation experiments (Supplemental Fig. S5), we observed that chromatin signals were the most significant factor affecting the prediction performance. To uncover distinct patterns from the four types of predictions, we performed a visual analysis of the chromatin signal distributions of cCREs surrounding the transcription start sites (TSSs) of genes. For TPs (Fig. 4A), we discovered a pattern where the distribution of four chromatin signals follows a normal distribution; that is, the intensity of the chromatin signals decreases with distance. In contrast, FPs exhibit a similar normal distribution (Supplemental Fig. S6A), which explains why negative genes were mistakenly predicted as positive genes. For TNs (Supplemental Fig. S6B), we observe a linear distribution of the four chromatin signals, with DNase and H3K27ac signals close to zero. Similarly, FNs also show a linear distribution of the chromatin signals (Supplemental Fig. S6C), particularly with DNase signals close to zero, suggesting that DNase plays a key role in mispredicting positive genes as negative genes. Notably, these patterns indicate that most of the coding genes are primarily regulated by their nearby cCREs.

    Figure 4.
    View larger version:
    Figure 4.

    ScPGE discovers different patterns by analyzing predictions. (A) A pattern found in true positives (TPs) that the regulatory effect of cCREs on target genes decreases with distance. (B) The cross-cell-type predictive performance of ScPGE, where K562→GM12878 indicates using a model trained on K562 data to predict GM12878 data. (C) The cross-species predictive performance of ScPGE, where K562→MEL indicates using a model trained on K562 data (Human) to predict MEL data (Mouse).

    Due to the generalization of the patterns across cells or species (Supplemental Fig. S7), we applied ScPGE to perform cross-cell or cross-species gene expression prediction. In the cross-cell setting, we utilized the ScPGE model trained on the GM12878 cell line to predict gene expression levels in the K562 cell line and then vice versa. As shown in Figure 4B and Supplemental Figure S8A, the performance of the intercellular prediction is very close to the intracellular prediction, with only a slight decrease, demonstrating that ScPGE can effectively generalize the patterns to perform cross-cell gene expression prediction accurately. In the cross-species setting, we utilized the ScPGE models trained on the GM12878 and K562 cell lines to predict gene expression levels in the CH12.LX and MEL cell lines, respectively. As illustrated in Figure 4C and Supplemental Figure S8B, although the PCC of the interspecies prediction is comparable to the intraspecies prediction, the MAE of the interspecies prediction is significantly higher than that of the intraspecies prediction. This suggests that, although ScPGE can capture the general distribution of gene expression, it struggles to accurately predict absolute expression levels due to the strong heterogeneity between different species.

    To further check whether the prediction of cell type–specific genes remains accurate, we selected cell type–specific genes from the K562 and GM12878 cells in this way: (i) we calculated each gene's log2FC using the equation log2(1 + TPMK562) − log2(1 + TPMGM12878); (ii) the genes with log2FC > 2 were regarded as K562-specific genes, and the genes with log2FC < −2 were regarded as GM12878-specific genes; (iii) we performed cross-cell-type prediction using trained models. As shown in Supplemental Figure S9A, not all cell type–specific genes can be accurately predicted; a few genes with high expression level are underestimated. However, the performance of cross-cell-type prediction is worse than that of within-cell-type prediction in terms of MAE, implying that cross-cell heterogeneity may affect the prediction performance. To explain this phenomenon, we visualized the epigenomic signal distributions of two mispredicted genes: BNC2 and DMRT2. From the two examples (Supplemental Fig. S9B), we can find that their DNase signals are approaching 0, significantly affecting the prediction accuracy. The possible reasons for this observation are that: (1) there are noisy data that confuse the model; or (2) the range of four epigenomic signals is not consistent.

    Chromatin loops facilitate the capture of cCRE–gene interactions

    In this study, we have shown an issue that the performance of ScPGE decreases as the number of cCREs increases. To alleviate this issue, we designed two methods to incorporate chromatin loops derived from HiChIP into the ScPGE model (Methods), enhancing its ability to capture distal cCRE–gene interactions. In the direct method, we directly put chromatin loops into the self-attention layer of ScPGE, aiming to increase the attention weights of validated cCRE–gene interactions. For simplicity, we refer to it as ScPGE-LP. Inspired by the pattern found in TPs that the regulatory effect of cCREs on target genes would decrease with distance, we first introduced an exponential decay function exp−|x|/2 into chromatin loops, aiming to alleviate the sparsity of chromatin loops. Then, we added a KL Divergence loss between chromatin loops and attention weights to the training loss, with the goal of aligning their distributions. For simplicity, we refer to this method as ScPGE-KL.

    To evaluate the effectiveness of ScPGE-LP and ScPGE-KL, we trained both models from scratch using 5-kb resolution chromatin loops from the K562 and GM12878 cell lines, which represent physical interactions between cCREs and genes. As shown in Figure 5, A and B, the performance of ScPGE-LP and ScPGE-KL is superior to that of ScPGE, particularly when utilizing a higher number of cCREs (e.g., cCRE-100, cCRE-200), demonstrating that incorporation of cCRE–gene interactions can improve the performance of predicting gene expression. In addition, ScPGE-KL outperformed ScPGE-LP when a smaller number of cCREs were used (e.g., cCRE-20), suggesting that the regulatory pattern of exponential decay enhances the model's ability to identify proximal cCRE–gene interactions. In contrast, ScPGE-LP excelled over ScPGE- KL when a higher number of cCREs were employed (e.g., cCRE-200), indicating that increasing the attention weights through chromatin loops enhances the model's capacity to recognize distal cCRE–gene interactions.

    Figure 5.
    View larger version:
    Figure 5.

    Chromatin loops facilitate ScPGE to capture cCRE–gene interactions. (A,B) Comparison of the performance of ScPGE, ScPGE-KL, and ScPGE-LP as the number of cCREs increases. (C) The performance (PRAUC) of ScPGE, ScPGE-KL, and ScPGE-LP in classifying cCRE–gene pairs at different distance groups. (D) The true positive rates of ScPGE and ScPGE-Loop on validated ccREs. (E) Visualization of active cCREs of the BAX gene missed by ScPGE but identified by ScPGE-Loop, where validated cCREs are represented by red rectangles and correctly identified cCREs are represented by blue rectangles with red outlines.

    Furthermore, we applied ScPGE-LP and ScPGE-KL to distinguish active enhancers from inactive enhancers in the K562-specific gene–enhancer interactions. As shown in Figure 5C, we found that both ScPGE-LP and ScPGE-KL outperformed ScPGE (attention) at different distances. Moreover, ScPGE-LP performed better than ScPGE-KL at a longer distance (>100 kb). These results further demonstrate the effectiveness of the two methods in identifying distal gene–enhancer interactions. Given that ScPGE-LP is proficient in recognizing distal interactions and ScPGE-KL is proficient in recognizing proximal interactions, we combined the two methods to identify validated enhancers of target genes. To be specific, ScPGE-KL was used to identify active enhancers within 100 kb, and ScPGE-LP was used to identify active enhancers beyond 100 kb. For simplicity, we refer to it as ScPGE-Loop. As before, we prioritized all enhancers and selected the top k enhancers, where k is the number of validated enhancers, to calculate the true positive rate. As shown in Figure 5D, ScPGE-Loop performed better than ScPGE on 30 out of 42 genes according to the TRP metric. For example, there are three validated enhancers (red rectangles) surrounding the BAX gene. As a result, ScPGE (attention) failed to identify any validated enhancers, but ScPGE-Loop successfully identified two of the three validated enhancers (Fig. 5E). Taking the MYC gene as another example, ScPGE (attention) failed to identify any validated enhancers, but ScPGE-Loop successfully identified one of the two validated enhancers (Supplemental Fig. S10).

    To explore whether combining the direct and indirect methods is effective for training ScPGE, we integrated Equations 3 and 4 after removing Mg from Equation 4 and tried different α values {0.01, 0.1, 1}. As shown in Supplemental Figure S11, the performance of the combined method does not surpass that of ScPGE-KL and ScPGE-LP, demonstrating that the two mechanisms are not compatible. The essential difference lies in the fact that ScPGE-LP directly incorporates distal chromatin loops into attention calculations, enabling it to focus on cCREs involved in distal regulation. In contrast, ScPGE-KL uses KL divergence to fit a regulatory pattern where regulatory effects diminish with increasing distance, allowing it to concentrate on cCREs involved in proximal regulation. Therefore, ScPGE-LP demonstrates superior performance in detecting distant cCREs, whereas ScPGE-KL excels at identifying proximal cCREs.

    ScPGE captures important TF motifs

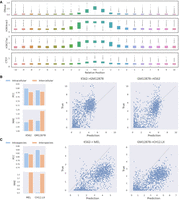
    To capture cell type–specific TF motifs, we first selected all true positives from the test set, and then ran the MEME-ChIP program (Machanick and Bailey 2011), which integrates multiple tools to perform comprehensive motif analysis on DNA sequences, to discover TF motifs from these TPs. The most relevant discovered motifs were matched against HOCOMOCO V11 (Kulakovskiy et al. 2018) using TOMTOM (Gupta et al. 2007). As shown in Figure 6A, we identified a series of important TF motifs that are grouped by TF family and are often enriched in proximal or distal regulatory regions. For instance, SP1-like TFs activate or repress basal transcription by usually binding to the GC box (GGGCGG) or GT/CACC box in the promoter region of many genes. CTCF-like TFs not only function as transcriptional activators or repressors by binding to proximal or distal cCREs but also block communication between enhancers and upstream promoters by binding to a transcriptional insulator element, thereby mediating the formation of three-dimensional structures of chromatin. Kr-like TFs, hematopoietic-specific transcription factors, could induce high-level expression of adult beta-globin and other erythroid genes by binding to the DNA sequence CCACACCCT in the beta hemoglobin promoter.

    Figure 6.
    View larger version:
    Figure 6.

    ScPGE discovers important motifs in specific types of cCREs. (A) Some important TF motifs found in true positives categorized by ScPGE, which are labeled by TF family names. (B) The distribution of types of cCREs, sourced from the SCREEN Registry V3, where pELS means proximal enhancer-like signatures, dELS means distal enhancer-like signatures, and PLS means promoter-like signatures. (C) Visualization of active cCREs of the JUNB gene identified by ScPGE, where validated cCREs are represented by red rectangles and correctly identified cCREs are represented by blue rectangles with red outlines. (D,E) The contributions of TF motifs in a type-specific cCRE (dELS, CTCF-bound), where significant TFs are supported by TF ChIP-seq data sets. (F,G) The contributions of TF motifs in a type-specific cCRE (pELS, CTCF-bound), where significant TFs are supported by TF ChIP-seq data sets.

    To further analyze the different functions of cCREs, we counted the distribution of types of active cCREs. Specifically, (1) we selected all TPs from the test set and computed the attention weights of all TPs using the ScPGE model; (i2) we extracted the middle row of the averaged attention matrix corresponding to the gene index and normalized these weights to a range of 0 to 1. 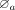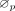Then, we sorted the weights and selected the top k (k = 5) cCREs as the candidate set, denoted by Formula; (3) we performed in silico perturbation using the ScPGE model and calculated the perturbation scores of all TPs. Then, we sorted these scores and selected the top k (k = 5) cCREs as another candidate set, denoted by Formula; (4) we took the intersection of these two sets as the final active cCREs by 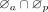Formula; and (5) we counted the distribution of types of the final active cCREs. As shown in Figure 6B, we found that the most frequently regulated types of cCREs are proximal elements (e.g., pELS, PLS), followed by distal elements (e.g., dELS), and that most of these elements involve CTCF binding. This implies that CTCF is an important multifunctional transcription factor that is extensively involved in gene transcriptional regulatory activities.

    For the JUNB gene (Fig. 6C), we picked two cCREs that were correctly recognized by ScPGE from the four validated cCREs, one with the type dELS, CTCF-bound and another with the type pELS, CTCF-bound. For the distal cCRE, we calculated the contributions of TF binding scores by DeepLIFT (Shrikumar et al. 2017) and highlighted a few top TFs by ranking their contributions. As shown in Figure 6, D and E, we observed that CTCF is a primary contributor, just matching the function of the cCRE labeled as dELS, CTCF-bound. Moreover, we searched all K562-specific ChIP-seq binding data sets in CistromeDB (Zheng et al. 2019) and found that the vast majority of CTCF ChIP-seq data had peaks falling in distal cCREs. For the proximal cCRE, the highlighted TFs are a group of proximal regulators, such as ZBTB4, VENTX, FEV (ETS family), CEBPA, POU2F3, which are partly supported by relevant ChIP-seq binding data sets (Fig. 6F,G). It has been reported in the literature that ZBTB4 is involved in the negative regulation of transcription by binding to RNA polymerase II, and VENTX may function as a transcriptional repressor, potentially playing a role in the maintenance of hemopoietic stem cells. Notably, although K562-specific CTCF ChIP-seq peaks are not enriched in the proximal cCRE, CTCF is still recognized as one of the important contributors, just matching the function of the cCRE labeled as pELS, CTCF-bound.

    Previous SectionNext Section

    Discussion

    Deciphering the relationships between cis-regulatory elements and target gene expression has been a long-standing unsolved problem in molecular biology. To address this problem, some quantitative models have been proposed recently for modeling the relationships between cCREs and gene expression. For example, Enformer proposed a large transformer-based model to predict gene expression by taking in long-range genomic regions containing a sufficient number of cCREs. However, training such a large model with long-range sequences requires significant computing resources, posing a substantial challenge for researchers with limited computing resources. To mitigate this challenge, we proposed a scalable computational framework to predict gene expression by integrating DNA sequences, TF binding scores, and epigenomic tracks from discrete cCREs. A series of comparative experiments demonstrates the superiority and scalability of ScPGE. By comprehensively analyzing ScPGE's predictions, we identified distinct regulatory patterns in TPs, FPs, TNs, and FNs, particularly a pattern in TPs where the regulatory effect of cCREs on genes decreases with distance. With this pattern, ScPGE can perform cross-cell or cross-species gene expression prediction with high accuracy, suggesting its potential application to previously unseen cell types or species. Additionally, motivated by this pattern, we developed two methods to improve the performance of identifying distal cCRE–gene interactions by incorporating chromatin loops into the ScPGE model.

    In fact, several key hyperparameters—such as DNA sequence length, nonredundant TF motifs, and cell-specific cCREs—have yet to be systematically explored. Based on the GM12878 and K562 cell lines, therefore, we conducted preliminary investigations into the performance of ScPGE for these hyperparameters, respectively. As shown in Supplemental Figure S12, (i) ScPGE using 1000-bp DNA sequences performs better than that using 600-bp DNA sequences, indicating that longer sequences provide more valuable information for predicting gene expression; (ii) ScPGE using a nonredundant set of all motifs performs better than that using a part of TF motifs; (iii) the performance of ScPGE utilizing cell-specific cCREs is comparable to that utilizing genome-wide cCREs. Compact and representative TF motifs through motif clustering analysis, therefore, may help further improve the performance of ScPGE. In the future, we will explore the performance of ScPGE when utilizing a bigger nonredundant motif collection. For example, the SCENIC+ motif collection includes 34,524 unique motifs gathered from 29 motif collections, which were clustered with a two-step strategy (Bravo González-Blas et al. 2023). The collection spans a total of 1553 TFs, 1357 TFs, and 467 TFs, respectively, in human, mouse, and fly, providing comprehensive, compact, and representative TF motifs for different species. In addition, through analysis of predictions, the patterns found in FPs and FNs were similar to those in TPs and TNs, which may lead to incorrect predictions. Therefore, by utilizing these patterns, it is possible to exclude these noisy samples in advance, thereby further improving the performance of ScPGE. For example, if some samples in TNs satisfy the pattern found in TPs, these samples are considered noise samples and excluded; conversely, if some samples in TPs satisfy the pattern found in TNs, these samples are considered noise samples and excluded.

    ScPGE stands out from gene expression prediction methods due to its lightweight design and flexible scalability. However, we found that the predictive performance of ScPGE decreases as the number of cCREs increases, implying that ScPGE struggles to capture the interactions between genes and distal cCREs effectively. Although chromatin loops were used to enhance the ability of ScPGE to capture the interactions between genes and distal cCREs, the predictive performance of ScPGE using distal cCREs remains relatively low. Given the powerful representational capabilities of large models (Dalla-Torre et al. 2025), we will leverage pretrained DNA models and optimize a student model through knowledge distillation, which not only yields a lightweight model but also preserves the feature learning capabilities of large models. By doing so, we can mitigate to some extent the shortcoming that the model cannot effectively capture distal cCRE–gene interactions.

    Previous SectionNext Section

    Methods

    Data preparation

    Candidate cis-regulatory elements

    cCREs for Human were downloaded from the SCREEN Registry Version 3 (https://screen.encodeproject.org/). The Registry contains 1,063,878 human cCREs in GRCh38, which are derived from ENCODE data using four types of data including DNase, H3K4me3, H3K27ac, and CTCF signals. cCREs with DNase-only and low-DNase marks were removed. Given that CREs usually cluster together to form cis-regulatory modules (CRMs) (Hardison and Taylor 2012), adjacent cCREs were merged within a window of size 600 bp, reducing the number of cCREs to 726,796. All cCREs were expanded to 600 bp for the convenience of modeling.

    Gene expression data

    For RNA-seq, total RNA-seq and poly(A) plus RNA-seq data in 19 human cell types were downloaded from ENCODE. Released transcript quantifications mapped to GRCh38 and annotated to GENCODE V29 were retained. RNA-seq gene expression was calculated as the sum of all transcripts’ TPM, and scaled by the log10(1+x) function.

    For CAGE-seq, 10 in 19 human cell types, signals of all reads mapped to GRCh38 and annotated to GENCODE V24 were downloaded from ENCODE. CAGE-seq gene expression was determined by aggregating read signals within a 384-bp window centered on each gene’s unique TSS, following Enformer’s protocol, and scaled by the log10(1+x) function.

    For each cell type, all coding genes from Chromosome 16 were used for validation, all coding genes from Chromosomes 8 and 9 were used for testing, and all coding genes from the remaining Chromosomes, except Chromosome Y, were used for training.

    DNase-seq and ChIP-seq data

    For each cell type, DNase-seq and ChIP-seq files mapped to GRCh38, including DNase, H3K4me3, H3K27ac, and CTCF types, were downloaded from ENCODE. Multiple read-depth normalized signal files for DNase-seq and fold change over control files for ChIP-seq were retained. Then, the signal files for the same type were merged using the bigWigMerge software from UCSC.

    Active TF motifs

    A full list of 769 TF motifs, represented by position frequency matrix (PFM), was downloaded from the HOCOMOCO V11 (Kulakovskiy et al. 2018). Active TFs were defined as those with higher expression levels in a specific cell type. Therefore, all TFs were first sorted by their expression levels, and the top 600 TFs in the full list were then selected as active TFs for a specific cell type. Finally, the active TF motifs were used to calculate cell type–specific TF binding scores.

    Model design

    Data construction

    To incorporate more cCREs, Enformer took long-range continuous DNA sequences as input and dealt with them using Conv1D operations. However, cCREs are discretely distributed on both sides of genes and therefore cannot be directly handled by Conv1D operations. Inspired by our previous works (Zhang et al. 2019, 2020), we assembled cCREs together with sequence features, TF binding scores, and epigenomic signals into three-dimensional tensors. As shown in Supplemental Figure S1, the details of data construction are as follows:

    Sequence features. DNA sequences of a gene and its surrounding cCREs were expanded to 600 bp and transformed into one-hot matrices of shape (4 × 600) following the protocol {A: [1, 0, 0, 0]; C: [0, 1, 0, 0]; G: [0, 0, 1, 0]; T: [0, 0, 0, T]}. Then, one-hot matrices were separately reshaped into 4 × 1 × 600 and assembled together along the second axis, forming a 3D tensor of shape 4 × (m+1) × 600, where m represents the number of cCREs and is a hyperparameter with a default value of 20. After this processing, we can easily apply Conv2D operations to deal with these discrete cCREs simultaneously.

    Epigenomic signals. According to the coordinates of cCREs on the genome, epigenomic signals (DNase, H3K4me3, H3K27ac, and CTCF) were extracted from their corresponding epigenomic files using the pyBigWig software and scaled by the log10(1+x) function. Following the same idea, the epigenomic signals of cCREs were reshaped and organized into a 3D tensor of shape 4 × (m+1) × 600, where “4” denotes four types of data, and this parameter can be dynamically adjusted according to the availability of epigenomic data.

    TF binding scores. A set of 600 active TF motifs was utilized to calculate the TF binding scores for cCREs. Specifically, for each cCRE, a motif represented by a position frequency matrix was multiplied and summed with one-hot matrix of the cCRE, producing a vector. Then, the maximum value of the vector was taken as the TF binding score for this motif. As a result, this process generated a vector of 600 TF binding scores, which were subsequently normalized to a range of 0 to 1. Following the same idea, the TF binding scores of cCREs were reshaped and organized into a 3D tensor of shape 1 × (m+1) × 600.

    Chromatin loops. Cell type–specific chromatin loops at 5-kb resolution were downloaded from Loop Catalog (Reyna et al. 2025), such as K562 or GM12878, which were derived from H3K27ac HiChIP data by using the FitHiChIP utility (Bhattacharyya et al. 2019). If there exist interactions between cCREs and cCREs, as well as between genes and cCREs in chromatin loops, the normalized counts of chromatin loops were calculated and scaled by the log10(1+x) function, otherwise 0. As a result, for each gene and its surrounding cCREs, an interaction matrix of shape (m+1) × (m+1) was constructed.

    Model architecture

    As shown in Supplemental Figure S2, the backbone of ScPGE is composed of three key modules: (i) a feature-learning module to learn features of cCREs; (ii) an interaction-learning module to model the relationships between genes and cCREs, as well as between cCREs and cCREs; and (iii) a prediction module for predicting gene expression.

    The feature-learning module is composed of three stem blocks for taking sequence features, TF binding scores, and epigenomic signals as input, respectively, and four residual convolutional blocks for learning and integrating the three inputs. In the computational blocks, Conv2D and MaxPool2D are applied to deal with genes and discrete cCREs in parallel by setting kernel size to 1 along the height axis. At last, the feature-learning module uses a projection block to produce a feature embedding of fixed shape, for example, (m+1) × 256.

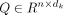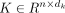    The interaction-learning module is composed of four transformer-based blocks for modeling the relationships between genes and cCREs. Each transformer block consists of a multihead self-attention layer and a position-wise feed-forward network. 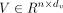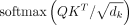In the self-attention layer, scaled dot-product attentions are performed as follows: the query Formula, key Formula, and value Formula are calculated through a linear projection where n denotes the number of embeddings and dk, dv the number of channels; the attention weights are calculated by Formula representing the attention pairwise; the value representing the semantics of all embeddings is aggregated according to the attention weights. For position embedding, we follow T5 (Raffel et al. 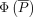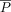2020) to apply a relative positional embedding Formula onto the attention weights, where Formula is the relative position between a gene and its cCREs. Additionally, we mask the attention weights between genes to encourage the model to concentrate on capturing the relationships between genes and cCREs. The feed-forward network integrates the outputs from multihead attention layers and introduces nonlinearity. 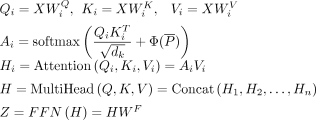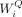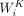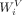The calculation process can be described as the following equation: Formula (1) where Formula, Formula, Formula represent the weights of three linear layers, respectively, Hi denotes the outputs from the i-th self-attention layer, and WF denotes the weights of the feed-forward network.

    The prediction module is composed of a fully connected feed-forward network and a soft plus activation to predict the gene expression. Through the last transformer block, a matrix Z of shape (m+1) × d is generated where d denotes the output dimension of the last transformer block, for example, 256. To encourage the model to concentrate on gene expression prediction, the middle row of Z corresponding to the gene index is extracted, representing the relationships between a gene and its cCREs. Then, the prediction module takes the middle row as input and predicts the expression level of the gene.

    Model training

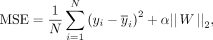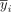    Because gene expression prediction is a regression task, the mean squared error (MSE) was employed to calculate the differences between true and predicted expression levels (Eq. 2). Formula (2) where N is the number of samples, yi and Formula are the true and predicted expression levels, respectively, α is a regularization parameter to leverage the trade-off between the fitting and generalizability of ScPGE, and || ||2 indicates the L2 norm.

    Given that deep learning-based models are sensitive to parameter initialization, we adopted a “warm-up” strategy to reduce the impact of parameter initialization. Specifically, we first warmed up ScPGE by running a few randomly initialized models and selecting the best-performing model in terms of validation performance. Then, we resumed to train the best-performing model with a batch size of 64 using the MSE loss and AdamW with default hyperparameters, except that the initial learning rate was gradually increased from 1 × 10−6 to 1 × 10−3 during the first stage (5000 steps) and decreased from 1 × 10−3 to 1 × 10−6 during the second stage (3000 steps). The model was validated every 1000 steps and the best-performing model is stored. All ScPGE models were implemented in PyTorch and trained on one A100 GPU.

    Incorporation of chromatin loops

    With the advent of technologies such as Hi-C and HiChIP for genome-wide chromatin interaction measurements, a large amount of chromatin interactions has been generated in a variety of cellular environments. Apparently, these interactions can provide highly useful information for guiding ScPGE to capture the relationships between genes and cCREs, but this information has been less utilized by current state-of-the-art models. To incorporate chromatin loops into the ScPGE model, we developed two methods: a direct method and an indirect method.

    In the direct method, we directly put the interaction matrix M, representing cell type–specific chromatin loops, into the self-attention layer with the purpose of increasing the attention weights of physical chromatin interactions. Through this method, the ScPGE model was guided to pay more attention to physical CRE-gene interactions. Correspondingly, the equation for computing Ai is modified as follows: 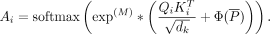Formula (3)

    In the indirect method, we added a new loss to the MSE loss, which is defined as a KL Divergence loss between the interaction matrix and attention weights, with the goal of aligning their distributions by training a joint loss (Eq. 4). 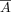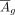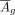Specifically, (i) the multihead attention weights were extracted from transformer blocks and subsequently averaged element by element across all heads and layers, denoted by Formula; (ii) the middle rows of Formula and M corresponding to the gene index were extracted, represented by Formula and Mg, respectively; (iii) given that Mg is extremely sparse, even with all values being 0, and inspired by the pattern found in this study that the regulatory effect of cCREs on target genes would decrease with distance, we added a general regulatory effector Rg to Mg, which can be simulated with a function exp−|x|/2; and (iv) after that, Mg and Formula were normalized to a range of 0 to 1. 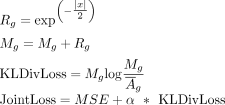Formula (4) where x denotes the distances between a gene and its surrounding cCREs, and α is a hyperparameter that specifies the contribution of the two losses to the prediction. We set it to 1 in this study.

    Model interpretability

    Attention weights

    The multihead attention weights were extracted from all transformer blocks and subsequently averaged element-wise across all heads and layers. Because we focused on the attentions from gene to cCREs, the middle row of the averaged attention matrix corresponding to the gene index was extracted and then normalized to a range of 0 to 1, reflecting the relationships between the target gene and its surrounding cCREs. Therefore, we can directly investigate the importance of each cCRE to the target gene by matching the query index at cCREs.

    In silico perturbation

    ScPGE predicts gene expression levels by utilizing the multimodal information of cCREs. Therefore, we can investigate the effect of cCREs on gene expression prediction by perturbing each cCRE. In silico perturbation was performed by calculating the gene expression changes before and after masking each cCRE, |Go − Gp|/Go.

    Contribution

    DeepLIFT (Shrikumar et al. 2017), a feature attribution method for computing the contribution of each feature in an input to a scalar prediction from a neural network model, was utilized to calculate the contributions of TF binding scores. Specifically, (i) the contributions of TF binding scores were computed by DeepLIFT, generating a matrix with a shape of 1 × (m+1) × 600; (ii) after selecting the target cCRE, a vector with a shape of 1 × 600 was generated, where “600” represents the number of TF motifs, and then TF motifs were ranked by their corresponding contributions; and (iii) top k (e.g., k = 10) TF motifs were selected as the highlighted ones. This process was implemented via Captum (v0.6.0) (Kokhlikyan et al. 2020), which is a PyTorch platform for model interpretability.

    Categorization of predictions

    To discover different patterns of false positives, true positives, false negatives, and true negatives, the predictions from the test set were categorized into FPs, TPs, FNs, and TNs by following the two steps: (1) the predicted and true gene expression levels were converted to a range of 0 to 1 by the equation: (x − xmin)/(xmax − xmin); and (2) we defined them as FPs by the rule: the prediction (P) is above 0.7 and the true (T) is below 0.2, as TPs by the rule: both P and T are above 0.7, as FNs by the rule: P is above 0.2 and T is below 0.7, and as TNs by the rule: both P and T are below 0.2.

    Cross-species gene expression prediction

    For the GM12878 and K562 cell lines from human, we selected the CH12.LX and MEL cell lines from mouse as targets for cross-species prediction, respectively. For CH12.LX and MEL, we downloaded cCREs for mouse from the SCREEN Registry V3, total RNA-seq and poly(A) plus RNA-seq data annotated to GENCODE vM21, DNase-seq, and ChIP-seq files mapped to GRCm38, as well as active TF motifs for mouse from the HOCOMOCO V11, and followed the process of data preparation described above to prepare all relevant data. For each cell type, all coding genes on Chromosome 16 were used for validation, all coding genes on Chromosomes 8 and 9 were used for testing, and all coding genes on the remaining Chromosomes, except Chromosome Y, were used for training. After that, we trained the ScPGE models for CH12.LX and MEL using the corresponding training data.

    Baseline methods

    Three state-of-the-art models, including Enformer (Avsec et al. 2021), CREaTor (Li et al. 2023), and EPInformer (Lin et al. 2024), serve as the baseline methods for gene expression prediction. Enformer, a deep neural network that integrates CNN and transformer, takes long-range DNA sequences of length 196 kbp as input to predict multiple genomic tracks of human and mouse genomes simultaneously. CREaTor, a hierarchical attention-based deep neural network, utilizes cCREs in open chromatin regions together with ChIP-seq of transcription factors and histone modifications to predict the expression level of target genes. CREaTor can model cell type–specific cis-regulatory patterns in new cell types without prior knowledge or additional training. EPInformer introduces a transformer-based framework to improve gene expression prediction by integrating promoter-enhancer interactions with their sequences, epigenomic signals, and chromatin contacts.

    For comparing with Enformer, pretrained Enformer models were downloaded from GitHub (https://github.com/google-deepmind/deepmind-research/tree/master/enformer), and genomic sequences flanking genes of interest were prepared following the original study's instructions. For a specific cell type, all predictions matching that cell type were extracted and aggregated, and then the gene expression level was determined by aggregating the predicted signals within a 384-bp window centered on each gene’s TSS. To ensure a fair comparison, the ScPGE models were trained using the multimodal information of cCREs to predict CAGE-seq gene expression.

    Following the instructions for running CREaTor, we retrained the CREaTor models using DNA sequences and four types of epigenomic signals across 19 human cell types with default hyperparameter settings. Similarly, following the guidelines for training EPInformer from scratch, we retrained the EPInformer models using the original inputs, except for chromatin contacts, across 19 human cell types with default hyperparameter settings, because chromatin contacts are not available for most cell types.

    cCRE–gene interactions

    Three K562-specific enhancer–gene interaction data sets were collected from Fulco et al. (2019), Gasperini et al. (2019), and Schraivogel et al. (2020), in which enhancer–gene pairs were categorized into four groups based on distance, including “<10 kb”, “10–50 kb”, “50–100 kb”, and “>100 kb” groups. For all three data sets, the genomic coordinates of all candidate enhancers were first converted from hg19 to hg38 using UCSC's liftOver software and then integrated together by genes.

    Data sets

    RNA expression, DNase-seq, ChIP-seq, and CAGE files were downloaded from https://www.encodeproject.org/ (Supplemental Tables S2–S4). TF motifs (PFM) were downloaded from the HOCOMOCO V11 (https://hocomoco11.autosome.org/). Cell type–specific chromatin loops at 5-kb resolution were obtained from https://loopcatalog.lji.org/ (Supplemental Tables S5, S6). cCREs for Human were downloaded from the SCREEN Registry Version 3 (https://screen.encodeproject.org/). CRISPR perturbation experiments of cCRE–gene interactions were collected from CREaTor (Supplemental Table S7).

    Code availability

    The ScPGE algorithm was implemented in PyTorch. The source code is available at GitHub (https://github.com/turningpoint1988/ScPGE) and as Supplemental Code.

    Previous SectionNext Section

    Competing interest statement

    The authors declare no competing interests.

    Previous SectionNext Section

    Acknowledgments

    This work was supported in part by the National Natural Science Foundation of China (Nos. 62372255, 62333018, W2412087, 62402250, 62432013, 62433001, U22A2039, 62472301, 62372318), the Natural Science Foundation of Guangxi Province (No. 2021JJA170204), partly supported by the Natural Science Foundation of Zhejiang Province (No. LMS25F020001), and supported by the Key Research and Development Program of Ningbo City (Nos. 2024Z112, 2023Z219, 2023Z226), the Yongjiang Talent Project of Ningbo (Yongrencaifa No. 2024-4), the Natural Science Foundation of Guizhou Province (No. ZK[2024]ZD035), the Youth Innovation Team of Colleges and Universities in Shandong Province (No. 2023KJ329), and the IDT High Performance Computing Platform for providing computational resources for this project.

    Author contributions: D.H. and Q.Z. conceived the basic idea; Q.Z. designed experiments, developed algorithms, and wrote the manuscript; S.W. and Z.L. carried out the data analysis and model interpretation; W.B. and W.L. provided some suggestions for writing the manuscript and designing the experiments.

    Previous SectionNext Section

    Footnotes

    • [Supplemental material is available for this article.]

    • Article published online before print. Article, supplemental material, and publication date are at https://www.genome.org/cgi/doi/10.1101/gr.281219.125.

    • Freely available online through the Genome Research Open Access option.

    • Received July 21, 2025.
    • Accepted November 26, 2025.

    This article, published in Genome Research, is available under a Creative Commons License (Attribution-NonCommercial 4.0 International), as described at http://creativecommons.org/licenses/by-nc/4.0/.

    Previous Section
     

    References

    1. ↵
      Avsec Ž, Agarwal V, Visentin D, Ledsam JR, Grabska-Barwinska A, Taylor KR, Assael Y, Jumper J, Kohli P, Kelley DR. 2021. Effective gene expression prediction from sequence by integrating long-range interactions. Nat Methods 18: 1196–1203. doi:10.1038/s41592-021-01252-x
      CrossRefMedlineGoogle Scholar
    2. ↵
      Bhattacharyya S, Chandra V, Vijayanand P, Ay F. 2019. Identification of significant chromatin contacts from HiChIP data by FitHiChIP. Nat Commun 10: 4221. doi:10.1038/s41467-019-11950-y
      CrossRefMedlineGoogle Scholar
    3. ↵
      Bravo González-Blas C, De Winter S, Hulselmans G, Hecker N, Matetovici I, Christiaens V, Poovathingal S, Wouters J, Aibar S, Aerts S. 2023. SCENIC+: single-cell multiomic inference of enhancers and gene regulatory networks. Nat Methods 20: 1355–1367. doi:10.1038/s41592-023-01938-4
      CrossRefMedlineGoogle Scholar
    4. ↵
      Cao F, Zhang Y, Cai Y, Animesh S, Zhang Y, Akincilar SC, Loh YP, Li X, Chng WJ, Tergaonkar V, et al. 2021. Chromatin interaction neural network (ChINN): a machine learning-based method for predicting chromatin interactions from DNA sequences. Genome Biol 22: 226. doi:10.1186/s13059-021-02453-5
      CrossRefMedlineGoogle Scholar
    5. ↵
      Chen X, Wang P, Qiu H, Zhu Y, Zhang X, Zhang Y, Duan F, Ding S, Guo J, Huang Y, et al. 2022. Integrative epigenomic and transcriptomic analysis reveals the requirement of JUNB for hematopoietic fate induction. Nat Commun 13: 3131. doi:10.1038/s41467-022-30789-4
      CrossRefMedlineGoogle Scholar
    6. ↵
      Dalla-Torre H, Gonzalez L, Mendoza-Revilla J, Lopez Carranza N, Grzywaczewski AH, Oteri F, Dallago C, Trop E, de Almeida BP, Sirelkhatim H, et al. 2025. Nucleotide Transformer: building and evaluating robust foundation models for human genomics. Nat Methods 22: 287–297. doi:10.1038/s41592-024-02523-z
      CrossRefGoogle Scholar
    7. ↵
      Fulco CP, Nasser J, Jones TR, Munson G, Bergman DT, Subramanian V, Grossman SR, Anyoha R, Doughty BR, Patwardhan TA, et al. 2019. Activity-by-contact model of enhancer–promoter regulation from thousands of CRISPR perturbations. Nat Genet 51: 1664–1669. doi:10.1038/s41588-019-0538-0
      CrossRefMedlineGoogle Scholar
    8. ↵
      Furlong EE, Levine M. 2018. Developmental enhancers and chromosome topology. Science 361: 1341–1345. doi:10.1126/science.aau0320
      Abstract/FREE Full Text
    9. ↵
      Gasperini M, Hill AJ, McFaline-Figueroa JL, Martin B, Kim S, Zhang MD, Jackson D, Leith A, Schreiber J, Noble WS, et al. 2019. A genome-wide framework for mapping gene regulation via cellular genetic screens. Cell 176: 377–390.e19. doi:10.1016/j.cell.2018.11.029
      CrossRefMedlineGoogle Scholar
    10. ↵
      Gupta S, Stamatoyannopoulos JA, Bailey TL, Noble WS. 2007. Quantifying similarity between motifs. Genome Biol 8: R24. doi:10.1186/gb-2007-8-2-r24
      CrossRefMedlineGoogle Scholar
    11. ↵
      Hardison RC, Taylor J. 2012. Genomic approaches towards finding cis-regulatory modules in animals. Nat Rev Genet 13: 469–483. doi:10.1038/nrg3242
      CrossRefMedlineGoogle Scholar
    12. ↵
      Karbalayghareh A, Sahin M, Leslie CS. 2022. Chromatin interaction–aware gene regulatory modeling with graph attention networks. Genome Res 32: 930–944. doi:10.1101/gr.275870.121
      Abstract/FREE Full Text
    13. ↵
      Kokhlikyan N, Miglani V, Martin M, Wang E, Alsallakh B, Reynolds J, Melnikov A, Kliushkina N, Araya C, Yan S, et al. 2020. Captum: a unified and generic model interpretability library for PyTorch. arXiv:2009.07896 [cs.LG]. doi:10.48550/arXiv.2009.07896
      CrossRefGoogle Scholar
    14. ↵
      Kulakovskiy IV, Vorontsov IE, Yevshin IS, Sharipov RN, Fedorova AD, Rumynskiy EI, Medvedeva YA, Magana-Mora A, Bajic VB, Papatsenko DA, et al. 2018. HOCOMOCO: towards a complete collection of transcription factor binding models for human and mouse via large-scale ChIP-seq analysis. Nucleic Acids Res 46: D252–D259. doi:10.1093/nar/gkx1106
      CrossRefMedlineGoogle Scholar
    15. ↵
      Li W, Wong WH, Jiang R. 2019. DeepTACT: predicting 3D chromatin contacts via bootstrapping deep learning. Nucleic Acids Res 47: e60. doi:10.1093/nar/gkz167
      CrossRefMedlineGoogle Scholar
    16. ↵
      Li Y, Ju F, Chen Z, Qu Y, Xia H, He L, Wu L, Zhu J, Shao B, Deng P. 2023. CREaTor: zero-shot cis-regulatory pattern modeling with attention mechanisms. Genome Biol 24: 266. doi:10.1186/s13059-023-03103-8
      CrossRefMedlineGoogle Scholar
    17. ↵
      Lin J, Luo R, Pinello L. 2024. EPInformer: a scalable deep learning framework for gene expression prediction by integrating promoter-enhancer sequences with multimodal epigenomic data. bioRxiv doi:10.1101/2024.08.01.606099
      Abstract/FREE Full Text
    18. ↵
      Machanick P, Bailey TL. 2011. MEME-ChIP: motif analysis of large DNA datasets. Bioinformatics 27: 1696–1697. doi:10.1093/bioinformatics/btr189
      CrossRefMedlineGoogle Scholar
    19. ↵
      Mumbach MR, Rubin AJ, Flynn RA, Dai C, Khavari PA, Greenleaf WJ, Chang HY. 2016. HiChIP: efficient and sensitive analysis of protein-directed genome architecture. Nat Methods 13: 919–922. doi:10.1038/nmeth.3999
      CrossRefMedlineGoogle Scholar
    20. ↵
      Myers G, Friedman A, Yu L, Pourmandi N, Kerpet C, Ito MA, Saba R, Tang V, Ozel AB, Bergin IL, et al. 2025. A genome-wide screen identifies genes required for erythroid differentiation. Nat Commun 16: 3488. doi:10.1038/s41467-025-58739-w
      CrossRefGoogle Scholar
    21. ↵
      Nasser J, Bergman DT, Fulco CP, Guckelberger P, Doughty BR, Patwardhan TA, Jones TR, Nguyen TH, Ulirsch JC, Lekschas F, et al. 2021. Genome-wide enhancer maps link risk variants to disease genes. Nature 593: 238–243. doi:10.1038/s41586-021-03446-x
      CrossRefGoogle Scholar
    22. ↵
      Raffel C, Shazeer N, Roberts A, Lee K, Narang S, Matena M, Zhou Y, Li W, Liu PJ. 2020. Exploring the limits of transfer learning with a unified text-to-text transformer. J Mach Learn Res 21: 1–67.
      MedlineGoogle Scholar
    23. ↵
      Rao SS, Huntley MH, Durand NC, Stamenova EK, Bochkov ID, Robinson JT, Sanborn AL, Machol I, Omer AD, Lander ES, et al. 2014. A 3D map of the human genome at kilobase resolution reveals principles of chromatin looping. Cell 159: 1665–1680. doi:10.1016/j.cell.2014.11.021
      CrossRefMedlineGoogle Scholar
    24. ↵
      Reyna J, Fetter K, Ignacio R, Marandi CCA, Ma A, Rao N, Jiang Z, Figueroa DS, Bhattacharyya S, Ay F. 2025. Loop Catalog: a comprehensive HiChIP database of human and mouse samples. Genome Biol 26: 175. doi:10.1186/s13059-025-03615-5
      CrossRefMedlineGoogle Scholar
    25. ↵
      Sasse A, Ng B, Spiro AE, Tasaki S, Bennett DA, Gaiteri C, De Jager PL, Chikina M, Mostafavi S. 2023. Benchmarking of deep neural networks for predicting personal gene expression from DNA sequence highlights shortcomings. Nat Genet 55: 2060–2064. doi:10.1038/s41588-023-01524-6
      CrossRefMedlineGoogle Scholar
    26. ↵
      Schoenfelder S, Fraser P. 2019. Long-range enhancer–promoter contacts in gene expression control. Nat Rev Genet 20: 437–455. doi:10.1038/s41576-019-0128-0
      CrossRefMedlineGoogle Scholar
    27. ↵
      Schraivogel D, Gschwind AR, Milbank JH, Leonce DR, Jakob P, Mathur L, Korbel JO, Merten CA, Velten L, Steinmetz LM. 2020. Targeted Perturb-seq enables genome-scale genetic screens in single cells. Nat Methods 17: 629–635. doi:10.1038/s41592-020-0837-5
      CrossRefMedlineGoogle Scholar
    28. ↵
      Shrikumar A, Greenside P, Kundaje A. 2017. Learning important features through propagating activation differences. In Proceedings of the 34th International Conference on Machine Learning, Sydney, NSW, Australia. PMLR 70: 3145–3153. https://proceedings.mlr.press/v70/shrikumar17a.html
      Google Scholar
    29. ↵
      Tang Z, Luo OJ, Li X, Zheng M, Zhu JJ, Szalaj P, Trzaskoma P, Magalska A, Wlodarczyk J, Ruszczycki B, et al. 2015. CTCF-mediated human 3D genome architecture reveals chromatin topology for transcription. Cell 163: 1611–1627. doi:10.1016/j.cell.2015.11.024
      CrossRefMedlineGoogle Scholar
    30. ↵
      Tang L, Hill MC, Wang J, Wang J, Martin JF, Li M. 2020. Predicting unrecognized enhancer-mediated genome topology by an ensemble machine learning model. Genome Res 30: 1835–1845. doi:10.1101/gr.264606.120
      Abstract/FREE Full Text
    31. ↵
      Zhang Q, Shen Z, Huang D-S. 2019. Modeling in-vivo protein-DNA binding by combining multiple-instance learning with a hybrid deep neural network. Sci Rep 9: 8484. doi:10.1038/s41598-019-44966-x
      CrossRefMedlineGoogle Scholar
    32. ↵
      Zhang Q, Zhu L, Bao W, Huang D-S. 2020. Weakly-supervised convolutional neural network architecture for predicting protein-DNA binding. IEEE/ACM Trans Comput Biol Bioinform 17: 679–689. doi:10.1109/TCBB.2018.2864203
      CrossRefGoogle Scholar
    33. ↵
      Zheng R, Wan C, Mei S, Qin Q, Wu Q, Sun H, Chen C-H, Brown M, Zhang X, Meyer CA, et al. 2019. Cistrome Data Browser: expanded datasets and new tools for gene regulatory analysis. Nucleic Acids Res 47: D729–D735. doi:10.1093/nar/gky1094
      CrossRefMedlineGoogle Scholar
    | Table of Contents
    OPEN ACCESS ARTICLE

    This Article

    1. Published in Advance January 16, 2026, doi: 10.1101/gr.281219.125 Genome Res. 36: 361-374 © 2026 Zhang et al.; Published by Cold Spring Harbor Laboratory Press

    Article Category

    ORCID

    1. Profile for Zhang, Q.http://orcid.org/0000-0002-4232-7736

    Share

    Preprint Server



    Navigate This Article

    Current Issue

    1. February 2026, 36 (2)
    1. Current Issue
    1. Alert me to new issues of Genome Research