Variation in the fitness impact of translationally optimal codons among animals

  1. Laurent Duret1
  1. 1Laboratoire de Biométrie et Biologie Évolutive, Université Lyon 1, UMR CNRS 5558, Villeurbanne, France;
  2. 2Université Claude Bernard Lyon 1, LEHNA UMR 5023, CNRS, ENTPE, F-69622, Villeurbanne, France
  • Corresponding author: laurent.duret{at}univ-lyon1.fr
    •  
    Next Section

    Abstract

    Early studies in invertebrate model organisms (fruit flies, nematodes) showed that their synonymous codon usage is under selective pressure to optimize translation efficiency in highly expressed genes (a process called translational selection). In contrast, mammals show little evidence of selection for translationally optimal codons. To understand this difference, we examined the use of synonymous codons in 223 metazoan species, covering a wide range of animal clades. For each species, we predicted the set of optimal codons based on the pool of tRNA genes present in its genome, and we analyzed how the frequency of optimal codons correlates with gene expression to quantify the intensity of translational selection (S). We observed that few metazoans show clear signs of translational selection. As predicted by the nearly neutral theory, the highest values of S are observed in species with large effective population sizes (Ne). Overall, however, Ne appears to be a poor predictor of the intensity of translational selection, suggesting important differences in the fitness effect of synonymous codon usage across taxa. We propose that the few animal taxa that are clearly affected by translational selection correspond to organisms with strong constraints for a very rapid growth rate.

    Since the early days of DNA sequencing, it has been noticed that the usage of synonymous codons is not random: Some synonymous codons are more frequently used than others, and the patterns of synonymous codon usage (SCU) can vary both across species and among genes within a genome (Grantham et al. 1980). Two types of processes, adaptive or nonadaptive, can contribute to genome-wide patterns of SCU (Sharp et al. 1993). First, neutral substitution patterns (NSPs) vary across taxa and, in some species, can also vary along chromosomes. NSPs are primarily driven by the underlying pattern of mutation, which accounts for 60% of the variance in genome base composition across the tree of life (Long et al. 2018). In addition, in some taxa, NSPs are also strongly affected by GC-biased gene conversion (gBGC), a process associated to meiotic recombination that favors the transmission of G:C alleles over A:T alleles (Duret and Galtier 2009). NSPs affect all genomic compartments (coding or noncoding) and, notably, have a strong impact on SCU (e.g., Pouyet et al. 2017; Long et al. 2018). Besides NSPs, SCU can also be affected by selection. Indeed, it has been observed that, in some species, SCU varies according to gene expression level (Gouy and Gautier 1982; Sharp et al. 1986; Duret and Mouchiroud 1999) and that the synonymous codons that are more frequently used in highly expressed genes correspond to the most abundant tRNAs (Ikemura 1985; Dong et al. 1996; Moriyama and Powell 1997; Kanaya et al. 1999; Duret 2000). This indicates that SCU and tRNA content have coevolved in a way that optimizes translation. This coevolution implies two types of selective pressure (Bulmer 1987): (1) selection on the pool of tRNAs to match the relative abundance of different codons in the transcriptome (i.e., the codon demand) and (2) selection on the SCU of genes to match the pool of tRNAs, referred to as translational selection (TS).

    It is generally considered that there are two main benefits of using translationally optimal codons. First, this leads to faster translation and, hence, to reduction of the time spent by ribosomes on each mRNA, thereby increasing the pool of free ribosomes available in the cell, which ultimately allows a higher cellular growth rate (Bulmer 1991). Second, the usage of synonymous codons decoded by the most abundant tRNAs increases the accuracy of translation and thus reduces the number of mistranslated proteins that cause an important burden on the cell (Akashi 1994; Drummond et al. 2006). It is important to note that for both aspects (speed and accuracy of translation), the benefit of using optimal codons is expected to be proportional to the gene expression level. First, the higher the expression level of a given gene, the stronger the impact of its translation speed on the pool of free ribosomes. Second, for a given mistranslation rate, the cost of erroneous protein production (in terms of waste of resources and of direct toxic effect of misfolded proteins) increases directly with expression level. In bacteria, the intensity of TS is correlated to the minimal cell division time, which suggests that the selective force for the optimization of SCU is the maximization of cellular growth (Rocha 2004; Sharp et al. 2005).

    It should be noted that besides TS, synonymous sites can be subject to additional levels of selective constraints. For instance, the presence of splice enhancers located within exons skews codon usage near exon–intron boundaries in mammalian genes (Parmley and Hurst 2007). However, this type of selective pressure is site specific (i.e., a particular codon is preferred at a specific site in a given gene) and, hence, is not expected to affect the genome-wide pattern of SCU. Similarly, there is evidence that the use of translationally suboptimal codons can be advantageous at some specific sites to slow down translation and favor the proper folding of proteins (Buhr et al. 2016; Walsh et al. 2020). But again, this is expected to be a local effect, with limited genome-wide impact on SCU.

    The intensity of TS varies widely across species, not only in unicellular organisms but also in multicellular eukaryotes (Sharp et al. 2005; Subramanian 2008; dos Reis and Wernisch 2009; Galtier et al. 2018). For instance, among animals, early studies on the two main invertebrate model organisms (the fruit fly Drosophila melanogaster and the nematode Caenorhabditis elegans) showed clear signatures of TS (Shields et al. 1988; Duret and Mouchiroud 1999), whereas there is no sign of TS in humans (Sémon et al. 2006; Pouyet et al. 2017). It should be emphasized that there is clear evidence for an effect of SCU on gene expression in mammals (Kudla et al. 2006; Courel et al. 2019; Wu et al. 2019; Mordstein et al. 2020; Medina-Muñoz et al. 2021), and in practice, codon optimization is essential for the design of heterologous gene expression systems, notably for human mRNA vaccines (Leppek et al. 2022). So, if SCU affects gene expression in humans, why is this trait not under selective pressure? To address this point, and more generally to understand variation in the intensity in TS across animals, it is important to refer to population genetic principles (Ohta 1996). Indeed, the SCU in a given genome reflects a balance between selection favoring translationally optimal codons and the effects of mutation and drift, allowing the fixation of nonoptimal codons (Bulmer 1991). Thus, the frequency of optimal codons is expected to depend on the mutational pattern and on the population-scaled selection coefficient (S = 4Nes), where Ne is the effective population size, and s is the selection coefficient in favor of translationally optimal codons (Bulmer 1991; Sharp et al. 2005). Hence, the lack of TS in some animal taxa might stem from a small Ne (hereafter referred to as the drift-barrier hypothesis) or from a smaller fitness effect of using translationally optimal codons (i.e., lower s).

    To explore these hypotheses, several previous studies analyzed variation in the intensity of TS across eukaryotes (Subramanian 2008; dos Reis and Wernisch 2009; Kessler and Dean 2014; Galtier et al. 2018). Kessler and Dean (2014) did not detect any correlation between Ne and codon usage across mammals, but this might simply reflect the relatively weak efficiency of selection in that clade. The three other studies, covering a wider range of taxa, reported positive correlations between signatures of TS and proxies of Ne. Although this pattern is qualitatively consistent with the predictions of the drift barrier hypothesis, quantitatively, the observations do not fit with this model. For instance, dos Reis and Wernisch (2009) estimated S in 10 eukaryotic species, and they reported only a twofold difference in S between humans and D. melanogaster (respectively, S = 0.5 and S = 1.0), despite an approximately 30-fold difference in Ne between the two species (20,000 vs. 600,000) (Lynch et al. 2023). According to the authors, this poor fit to the drift barrier model might be because their analysis was sensitive to variation in NSP across genes, which might have led to overestimates of S in humans (dos Reis and Wernisch 2009). But, it has also been argued that besides differences in Ne, s is also likely to vary across species, as long-lived organisms, with relatively slow development, are likely to be less constrained to optimize cell growth than species with a very rapid development (Subramanian 2008).

    These three studies were based on relatively limited sample sizes (10 to 30 species), and in the end, the causes of the variation in the intensity of TS across species remained unclear. To try to go further, we decided here to investigate variation in TS intensity across a large data set of 223 metazoan species, covering a wide range of animal clades. For each species, we predicted the set of optimal codons based on the pool of tRNA genes present in its genome, and we analyzed how the frequency of optimal codons varies with gene expression, to quantify S and to investigate the factors that may explain variation in S across taxa.

    Previous SectionNext Section

    Results

    Nonadaptive processes are the primary drivers of codon usage variation among metazoans

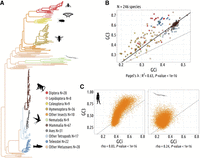
    To investigate the factors driving the intensity of TS in metazoans, we used the GTDrift database, which compiles genomic and transcriptomic data along with life history traits and proxies of Ne for various eukaryotic species (Bénitière et al. 2024). We initially selected 257 metazoan species available in GTDrift, but we excluded 11 species for which there were not enough transcriptomic data to quantify the distribution of expression level (fewer than 5000 genes detected as being expressed). We analyzed patterns of SCU and genomic base composition in the 246 remaining species, covering a wide range of clades (129 vertebrates, 82 insects, and 35 other metazoan species) (Fig. 1A).

    Figure 1.
    View larger version:
    Figure 1.

    Codon usage variations are driven by nonadaptive processes. (A) Phylogenetic tree of the 257 studied species. (B) Gene average GC content at the third position of codons (GC3) and the gene average GC in introns (GCi) for each species. Pagel's lambda model is used to take into account the phylogenetic structure of the data in a regression model (black line). (C) Correlation between GC3 and GCi in Homo sapiens (left) and in Caenorhabditis elegans (right); each point corresponds to one gene. Spearman's rho and corresponding P-values are displayed under the graph. The dotted lines correspond to x = y.

    Patterns of SCU can be affected both by TS and by NSPs (Sharp et al. 1993). It is possible to distinguish the contribution of NSPs because they affect the base composition of both coding and noncoding regions, whereas TS operates only on codons. Thus, if differences in SCU across species are driven by NSPs, then it is expected that they should be correlated with variation in the base composition of noncoding regions. Similarly, if intra-genomic variation of SCU in a given species is driven by the heterogeneity of NSPs along its chromosomes, then this should result in a covariation between the codon usage of genes and the base composition of their introns. Owing to the symmetry of the DNA molecule, NSPs generally affect similarly both strands, resulting in an equal proportion of cytosine (C) and guanine (G), as well as an equal proportion of thymine (T) and adenine (A) (Lobry 1995). Hence, the G + C content provides good summary statistics of the impact of NSPs on the genomic base composition. To examine the potential contribution of nonadaptive processes to the observed variations in SCU across the 246 species, we measured their G + C content in introns (GCi) and at the third position of codons (GC3), averaged over all genes. We observed a strong correlation between the average GC3 and the average GCi (Fig. 1B). This indicates that nonadaptive processes are the primary factor driving the observed variation in codon usage across species.

    NSPs can vary within the genome of a given species and impact codon usage accordingly. In Homo sapiens, the per gene GC3 and GCi are highly correlated (Spearman's correlation coefficient, rho = 0.83, P < 10−16), whereas this correlation is less pronounced in C. elegans (rho = 0.24, P < 10−16) (Fig. 1C). Species showing the strongest intra-genomic variance in codon usage (as assessed by GC3) are the ones with the strongest variance in GCi (Supplemental Fig. 1A). These correlations between GC3 and GCi are particularly strong in tetrapods (107/108 species with rho > 0.7) and in Hymenoptera (25/35 species with rho > 0.7) (Supplemental Fig. 1B). The other clades generally show less variance in GCi and weaker correlations between GC3 and GCi. But overall, 246/246 species (100%) showed a significant positive correlation (P < 0.05), which indicates that in most species, intra-genomic variation in NSPs somehow contributes to the variance in SCU among genes. Hence, it is important to take this source of variance into account to be able to detect signatures of TS within genomes.

    tRNA abundance matches proteome requirements

    To quantify the intensity of TS, we used an approach similar to that of Sharp et al. (2005) and dos Reis and Wernisch (2009). This approach is based on the comparison of the frequency of optimal codons between highly and weakly expressed genes and therefore requires the prior identification of optimal codons. For this, dos Reis and Wernisch focused on the nine amino acids that are encoded by two codons (duet codons) and predicted the optimal codon of each amino acid as being the one that is more frequently used in highly expressed genes. One caveat is that if the NSP varies among genes according to their expression level, this may lead to erroneous prediction of codon optimality. Furthermore, this approach does not capture the signal of TS from the nine other amino acids that are encoded by triplet, quartet, or sextet codons. To avoid these limitations, we sought here to predict optimal codons based on the tRNA pool. Owing to technical difficulties, there are currently few species for which tRNA abundance has been quantified directly. Behrens et al. (2021) recently developed a technique (mim-tRNAseq) that allowed them to measure tRNA abundance in four eukaryotes (Behrens et al. 2021). This study revealed a robust correlation between tRNA abundance and their respective gene copy number, with an adjusted R2 > 0.91 for yeasts (Saccharomyces cerevisiae and Schizosaccharomyces pombe), 0.79 for D. melanogaster, and 0.62 for H. sapiens (Behrens et al. 2021). These results suggest that tRNA gene copy number is a good predictor of tRNA abundance.

    To investigate whether the number of tRNA genes could be used as an indirect measure of tRNA abundance across metazoans, we analyzed the covariation of their tRNA gene repertoires with the amino acid composition of their proteome. The total number of tRNA gene copies varies widely among clades and species (ranging from an average of 201 tRNA gene copies per genome in Hymenoptera to 1539 copies in teleost fish) (Supplemental Fig. 2). However, the relative copy number of distinct isoacceptor tRNA genes is quite conserved among metazoans (Supplemental Fig. 3). There are some rare cases in which the gene copy number of a given tRNA has exploded in a given species compared with other genomes (Supplemental Fig. 2). This might reflect the propensity of tRNA genes to become transposable elements (e.g., the genome of Blattella germanica contains 711 copies of the AGA Ser-tRNA vs. one to 128 copies for the other tRNAs). Indeed, many SINE retrotransposon families derive from tRNA genes (Sun et al. 2007), and it is therefore possible that some recently evolved SINEs are erroneously annotated as bona fide tRNA genes.

    In both D. melanogaster and H. sapiens, we observed a strong correlation between amino acid usage (i.e., the frequency of amino acids, weighted by the gene expression level) and direct measures of tRNA abundance (rho = 0.79) (Supplemental Fig. 4A,B; Behrens et al. 2021). These results indicate that tRNA abundance matches the amino acid demand. As expected, the amino acid usage of these two species also strongly correlates with their tRNA gene copy numbers (rho = 0.78 and 0.68, respectively) (Supplemental Fig. 4C,D). To assess the generality of this relationship, we computed the correlation between tRNA gene copy number and the amino acid demand across 246 animal species. We observed a significantly positive Spearman's coefficient (P-value < 0.05) in 93% of species (Fig. 2). This indicates that in most of metazoans, the tRNA gene copy number is under constraints to match the amino acid demand. This implies that tRNA abundance is primarily regulated by modulating the copy number of tRNA genes rather than their transcription level. We suspect that the few cases in which the number of tRNA genes does not correlate with amino acid usage might be owing to annotation errors: Some tRNA genes may have been missed (e.g., because of gaps in the genome assembly), or conversely, some SINEs or tRNA pseudogenes may have been incorrectly annotated as functional tRNA genes. To ensure that the tRNA gene copy number is a good proxy of the tRNA abundance, we kept in our study only the species for which tRNA gene copy number correlates significantly with amino acid usage (N = 230 species). We also excluded seven species for which the repertoire of annotated tRNA appeared to be incomplete (i.e., the cognate tRNAs of certain codons were not found in the genome assembly).

    Figure 2.
    View larger version:
    Figure 2.

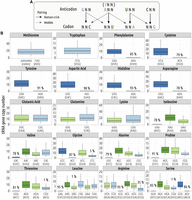
    The tRNA gene copy number is a good predictor of the codon demand. (A) Representative example of the relationship between the number of isoacceptor tRNA gene copy per amino acid and the frequency of amino acid weighted by gene expression in C. elegans. Spearman's rho and corresponding P-value are displayed under the graph. (B) Boxplot showing the distribution of Spearman's correlation coefficients (ρ) from A for each species (N = 246 species). The red line indicates the threshold above which the P-value is lower than 0.05.

    Definition of putative-optimal codons based on tRNA abundance and wobble-pairing rules

    To predict which synonymous codons are optimal for translation, it is first necessary to associate each of the 61 codons to their cognate tRNA. The number of distinct isodecoder tRNAs (i.e., distinct anticodons) ranges from 43 to 60 per species (average = 47). This implies that one to 18 codons cannot be translated through Watson–Crick pairing (WCp) and hence have to be translated via wobble pairing (WBp). We used the rules established by Percudani (2001) to assign each of these codons to their cognate tRNA, allowing for nonstandard base pairing with the first nucleotide of the anticodon (Fig. 3A). For example, deamination of adenine in inosine (I) in anticodon ANN makes them permissive to WBp I:C, I:U, or I:A. Another common WBp is the G:U/U:G pairing (Percudani 2001). As an illustration, in humans, asparagine is translated by a single tRNA (anticodon GTT) that decodes both AAC (by WCp) and AAT (by G:U WBp). AAT accounts for 48% of asparagine codons, highlighting the significance of WBp.

    Figure 3.
    View larger version:
    Figure 3.

    Codon–anticodon assignment. In each genome, we used the rules proposed by Percudani (2001) to assign codons to their cognate tRNA: First, isodecoder tRNAs present in a given genome are assigned to their complementary (Watson–Crick) codons, and then, the remaining codons (for which the genome does not contain any tRNA carrying the complementary anticodon) are inferred to be decoded by wobble pairing. (A) Illustration of the various possible pairings: Watson–Crick and wobble pairing. (B) Distribution of tRNA gene copy number across 223 species. The boxplot represents the median, interquartile range (box edges at 25th and 75th percentiles), and whiskers extending to the largest value no further than 1.5 times the interquartile range. For tRNA isodecoders that are absent from some genomes, the percentage of species in which they are missing is also indicated.

    There are 18 amino acids that are encoded by multiple synonymous codons. These amino acids can be classified in two groups: (1) those whose synonymous codons are translated by at least two distinct isodecoder tRNAs and (2) those for which all synonymous codons are translated by a single isodecoder tRNA. There is some variation in the set of amino acids present in each group, depending on the isodecoder tRNA repertoire of each species. The first group generally corresponds to amino acids encoded by sextet codons (Leu, Arg, Ser), quartets (Val, Gly, Ala, Pro, Thr), triplet (Ile), and NNG/NNA duets (Glu, Gln, Lys). The second group corresponds essentially to the six amino acids encoded by NNC/NNT duets (Phe, Cys, Tyr, Asp, His, Asn) (Fig. 3B).

    In the following analyses, for each amino acid of the first set, synonymous codons were predicted to be optimal if they were decoded by the isodecoder tRNA with the highest gene copy number (i.e., predicted to be the most abundant). In case of ex æquo (i.e., if all synonymous codons are decoded by isodecoders having the same gene copy number), then the optimal codons of this amino acid were considered as unknown (76 ex æquo among 785 cases in total, in 62 species). In the cases in which the most abundant tRNA decodes more than one synonymous codon, we considered all of them as potentially optimal (i.e., at this stage, we do not make any assumption regarding which of the WCp or WBp is the most efficient). This first set of putative-optimal codons will hereafter be referred as POC1. The second set of amino acids corresponds to cases in which the two synonymous codons (NNC/NNT) are decoded by a single isodecoder (anticodon GNN). There is evidence, based on studies in various eukaryotes, that the WBp GNN:NNU is less efficient than the WCp GNN:NNC (Stadler and Fire 2011; Chan et al. 2017; Wang et al. 2017). Consequently, for these amino acids, we defined codons NNC (decoded through WCp) as being the putative-optimal codons POC2.

    For the human genome, POC1 can be defined for 13 amino acids and POC2 for five amino acids. For C. elegans, POC1 and POC2 are defined for 12 and six amino acids, respectively. On average among the 223 species, POC1 is defined for 12.5 amino acids per species (ranging from eight to 17) and POC2 for 5.2 amino acids (ranging from zero to six, except Tyto alba with seven POC2, including Ile).

    Highly expressed genes are enriched in optimal codons

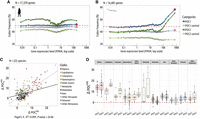
    The intensity of TS depends directly on gene expression levels. Given the very wide range of variation of gene expression levels (more than 1000-fold), the fitness impact of SCU is expected to vary strongly among genes. Hence, a typical feature of genomes subject to TS is that the frequency of optimal codons is particularly high in the most highly expressed genes. Thus, to identify which species are subject to TS, we examined the variations in POC frequency according to gene expression level. To control for possible variations in NSPs, we also analyzed the corresponding triplet usage in introns, referred to as POC-control. It is important to note that even in absence of TS, the frequency of POC-control is not necessarily expected to be equivalent to that of the overall POC frequency, notably because the base composition of noncoding regions is affected by indels and transposable elements, which are counter-selected in coding regions.

    For H. sapiens, POC frequencies show some slight fluctuations with gene expression (Fig. 4A). However, the same weak fluctuations are observed for POC-controls in introns, which implies that the same process, independent of translation efficiency, affects the base composition, both in introns and at synonymous codon positions (Fig. 4A). Indeed, there exists a strong correlation between the GC content of introns and the GC3 content in H. sapiens, along with pronounced variations in GC3 content (Fig. 1C). In contrast, in C. elegans, we observed a strong rise in POC frequencies in highly expressed genes, both for POC1 (from 47% to 76%) and for POC2 (from 38% to 70%). These changes in codon usage are not caused by shift in local substitution patterns as we see no similar variation in POC-control (Fig. 4B).

    Figure 4.
    View larger version:
    Figure 4.

    Relationship between the frequency of putative-optimal codons and gene expression level. (A,B) Variation in the proportion of POC within coding sequences (POC1, dark blue; POC2, dark green) according to gene expression level. To control for variations in neutral substitution patterns, we analyzed the frequency of corresponding triplets within introns (POC1 control, light blue; POC2 control, light green). Each point represents a 2% bin of genes, with the red point at the end of each POC1 curve denoting the 2% most highly expressed genes. The red lines indicate the average POC1 frequency observed in the 50% least-expressed genes (FPKM). The difference in POC frequency between the top 2% most highly expressed genes and the 50% least-expressed genes is noted ΔPOCexp. A represents H. sapiens, and B represents C. elegans. (C) Correlation between Formula and Formula. (D) ΔPOCexp distributions per species and by clades for the POC1 and POC2 (N = 223 species).

    It is important to notice that the nonlinear relationship observed between gene expression level and POC frequency is perfectly consistent with the TS model, which assumes that the selection coefficient on SCU (s) should increase linearly with gene expression level. Indeed, this model predicts that for lowly expressed genes (such that 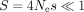Formula), the frequency of optimal codons should evolve neutrally and hence should be independent of expression level. But above the “nearly neutral” point (i.e., the expression level for which S ≈ 1), the frequency of optimal codons should strongly increase with expression level. The shape of the POC1 and POC2 curves in Figure 4B indicates that in C. elegans, this “nearly neutral” point is reached for a gene expression level of about 50 FPKM. This implies that genes with a lower expression level (which represent 83% of genes in C. elegans) are not affected by TS. Of note, all else being equal, the fraction of genes affected by TS is expected to be even more reduced in species with a lower effective population size.

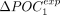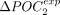    To assess the impact of TS on SCU, we measured the difference between the frequency of POCs in the most-expressed genes (top 2%) and the frequency of POCs in the 50% lowest expressed genes, controlling for POCs-control variations (see Methods). This shift in codon usage (denoted ΔPOCexp) was computed for both POC1 and POC2 codons in each of the studied species (N = 223 species). Formula and Formula are strongly correlated (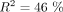Formula, P-value < 10−16), which indicates that the signature of TS is effectively captured by both sets of codons (Fig. 4C). For 211 species (95%), the frequency of POC1 is higher in highly expressed genes (Fig. 4D). Similarly, 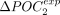Formula is positive for 191 species (86%) (Fig. 4D). The higher ΔPOCexp were observed in C. elegans (+30% for both POC1 and POC2). 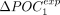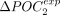There are substantial variations across clades: Average Formula and Formula values are around +14% in Diptera compared with +3% in vertebrates. We obtained very similar results when measuring ΔPOCexp without accounting for POC-control variations (Supplemental Fig. 5). Given that the two sets of codons gave very consistent results, we hereafter considered the whole set of POCs regrouping both POC1 and POC2.

    Weak relationship between the strength of TS and the effective population size

    According to standard population genetic models of TS (Bulmer 1991; Sharp et al. 2005; dos Reis and Wernisch 2009), the difference in codon usage between highly and weakly expressed genes is expected to be directly linked to the population-scaled selection coefficient in favor of optimal synonymous codons (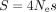Formula). Indeed, considering that SCU evolves neutrally in lowly expressed genes, then S in highly expressed genes can be expressed as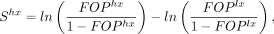Formula (1) where FOPhx and FOPlx are the observed frequencies of optimal codons in highly and lowly expressed genes, respectively (Sharp et al. 2005; dos Reis and Wernisch 2009). It should be noted, however, that this equation holds true only if underlying mutation patterns (and possibly gBGC) do not vary with gene expression level (Sharp et al. 2005; dos Reis and Wernisch 2009). We used the above equation to estimate Shx in each species, based on the observed POC frequencies in the top 2% most highly expressed genes compared with the 50% least expressed. The choice of this latter threshold is based on the observation that in species with clear signatures of TS, POC frequencies show little variation in genes below the median expression level (Fig. 4B; Supplemental Fig. 6).

    If constraints on SCU are similar across species (i.e., if shx is constant), then Shx is expected to vary linearly with the effective population size (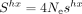Formula). To test this prediction, we sought to estimate Ne for each species. Lynch and colleagues (2023) recently compiled a list of species for which the germline mutation rate (μ) and the level of neutral diversity (πs) have been measured and, hence, for which it is possible to infer the effective population size (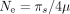Formula). This list included 24 species of our data set. We expanded this data set by including Ne estimates for 17 additional congeneric species. To explore the relationship between Shx and Ne in more species, we also used three indirect proxies (longevity, body length, and the dN/dS ratio) that correlate with the effective population size (Supplemental Fig. 7).

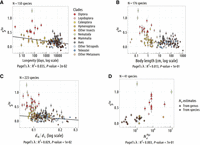
    Among the 223 species analyzed, the strongest intensity of selection is observed in the nematodes C. elegans (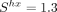Formula) and Caenorhabditis nigoni (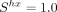Formula) (Fig. 5). Diptera also show relatively strong values of Shx (mean = 0.63 ± 0.16 SD), followed by Lepidoptera (mean Shx = 0.41 ± 0.15 SD). In vertebrates, signals of TS are weak (mean Shx = 0.15 ± 0.12 SD), but nevertheless, Shx is on average significantly nonnull (Student's t-test, P-value < 10−16). As predicted by the drift barrier model, the species with the strongest signs of TS all show a relatively short lifespan, low body mass, and low dN/dS (Fig. 5A–C), that is, traits associated to organisms with large Ne. Conversely species with traits associated to low Ne all show low Shx. However, the correlations between Shx and Ne proxies are weak and are significant for only two of them (longevity and dN/dS) (Fig. 5A,C). The weakness of these correlations might be because these traits are only indirect proxies of Ne. However, even for the few species for which it is possible to get more direct estimates of Ne (based on πs and μ), the correlation between Shx and Ne remains weak (Fig. 5D).

    Figure 5.
    View larger version:
    Figure 5.

    Relationship between Ne and translational selection (TS) intensity. Relationship between the population-scaled selection coefficient (S) and longevity (A), body length (B), dN/dS (C), and 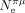Formula (D; N = 223 species). The TS intensity S is measured on the top 2% most highly expressed genes (Shx). Pagel's lambda model is used to take into account the phylogenetic structure of the data in a regression model (the regression line is displayed in black when the correlation is significant). Error bars represent the 2.5th and 97.5th percentiles of Shx values obtained by bootstraping (1000 draws with replacement among the top 2% most highly expressed genes, and the 50% least expressed).

    In species subject to TS, the tRNA pool evolves in response to changes in NSPs

    The above analyses show that for most metazoan species, TS is very weak and, hence, that their SCU is essentially shaped by NSPs. Even in species with a clear signal of TS, codon usage appears to be influenced by variations in NSP. Notably, Diptera and Lepidoptera span a wide range of GC content in noncoding regions (genome-wide average GCi ranging from 0.25 to 0.43) that strongly correlate with their average GC3 (from 0.32 to 0.71) (Fig. 1B). This raises the question of how the tRNA pool evolved in these species in response to NSP changes. To investigate this point, we focused our analyses on the 26 Diptera and Lepidoptera species with a strong signal of TS.

    In this data set, we observed that the decoding of 11 NNA/NNG synonymous codon pairs (Glu, Gln, Lys, Val, Ala, Pro, Thr, Ser, both CTA/CTG and TTA/TTG pairs of Leu, and the AGA/AGG “duet” of Arg) never involves WBp: The two complementary isodecoder tRNAs (anticodons UNN and CNN, respectively) are systematically present altogether (Supplemental Fig. 8). Thus, for each of these 11 pairs, we were able to identify the “preferred” isodecoder tRNA (i.e., the one with the highest gene copy number) in each species. We observed that the proportion of CNN anticodons among the 11 preferred tRNAs correlates positively with the average GCi (Fig. 6A). This implies that in species showing evidence of TS, tRNA gene copy number coevolved in response to changes in NSP, consistent with the hypothesis that tRNA abundance is under selective pressure to match the demand in SCU.

    Figure 6.
    View larger version:
    Figure 6.

    Genomic substitution patterns shape the tRNA pool. (A) Relationship between the per species CNN fraction of preferred isodecoder tRNAs (corresponding to the most abundant tRNAs) among 11 NNA/NNG synonymous codon pairs and the gene average GC in introns (GCi), for Diptera (dark red), and Lepidoptera (light red). (B) Relationship between the per species proportion of NNC preferred codons (the most overused codons in highly expressed genes compare to lowly expressed genes) among NNT/NNC synonymous codon pairs decoded by a single tRNA, along with the GCi. (A,B) Pagel's lambda model is used to take into account the phylogenetic structure of the data in a regression model (black line if significant). (C) Hypothetical schemes explaining how synonymous codon usage can be shaped conjointly by TS and by neutral substitution patterns.

    Variation in optimality between WBp and WCp

    NNT/NNC synonymous codon pairs (N = 16) are generally decoded by a single isodecoder tRNA (Fig. 3B, Supplemental Fig. 2). Among Diptera and Lepidoptera, this is the case for 94% of the 416 NNT/NNC synonymous codons pairs analyzed (16 pairs × 26 species) (Supplemental Fig. 8). In such cases, shifts in NSP cannot be compensated for by a change in the relative abundance of isodecoder tRNAs. Nevertheless, the affinity of tRNAs for their cognate codons can be changed by post-transcriptional modifications and, hence, might evolve in response to the demand. To investigate whether such changes occur, it is necessary to identify which of the two codons is best decoded by this unique isodecoder tRNA. For this, we relied on the fact that in species that are subject to TS, codons that are more efficiently decoded show a higher prevalence in highly expressed genes compared with lowly expressed ones (these codons will hereafter be referred to as preferred codons). Two sets of NNT/NNC synonymous codons pairs can be distinguished: the seven pairs corresponding to the amino acids with duet codons (Phe, Cys, Tyr, Asp, His, Asn, and the AGT/AGC “duet” of Ser) and the nine pairs from amino acids with triplet (Ile) or quartet codons (Val, Gly, Ala, Pro, Thr, Leu, Arg, Ser). For NNT/NNC duets, when a single tRNA is present (95% of cases), it is always the GNN-tRNA, and in 99% of cases, it is the NNC codon, decoded through WCp, that is preferred. For eight of the nine other pairs, when a single tRNA is present (94% of cases), it is always the ANN-tRNA, the only exception being Gly (GNN-tRNA). For Gly, the GGT codon, decoded via WBp, is preferred to the GGC codon in 84% of species. For the other pairs (decoded by ANN-tRNA) there is more variability: The NNC codon (WBp) is preferred in 79% of species, whereas the NNT codon (WCp) is preferred in the others. These observations indicate that when a single tRNA is present for two codons, it is not systematically the one with WCp that is the most efficiently translated. Furthermore, although the NNC codon tends to be preferred to the NNT codon (except for Gly), there is some variation across species, notably for those decoded by an ANN-tRNA (Supplemental Fig. 9). We computed in each species the proportion of NNC preferred codons among NNT/NNC synonymous codon pairs decoded by a single tRNA. We observed that the species showing the highest proportion of NNT preferred codons are the ones with the lowest genomic GC content (Fig. 6B). Thus, it appears that the relative affinity of ANN-tRNAs for the NNT or NNC codon can evolve in response to the demand. This evolution most probably results from variation in the extent of adenosine-to-inosine modification at the first position of ANN anticodons, which affects the extent to which the WCp codon is preferred to the wobble one (Lim and Curran 2001).

    These observations suggest a straightforward model to explain variation in the set of optimal synonymous codons across species (Fig. 6C). First, variation in mutational patterns or in the intensity of gBGC can lead to changes in the base composition of genomes, thereby directly shifting the codon usage of genes. Given that TS is a weak force, most genes are affected by this shift. This results in a change in the codon demand and, hence, induces a selective pressure to change the pool of tRNA (in terms both of abundance and of affinity for their cognate codons). In turn, TS will modify the codon usage of highly expressed genes to match the new set of tRNAs, thereby reinforcing the selection on the tRNA pool to match the codon demand and resulting in the coadaptation of tRNA-pool and codon usage. Of course, this coadaptation is possible only if the optimality of codons can be modulated, either by changes in tRNA abundance (in the cases in which there are multiple isodocoder tRNAs) or by differential level of tRNA modification. NNT/NNC duet codons are decoded by a single GNN-tRNA. Indeed, for these duet codons, tRNAs carrying an ANN anticodon are prohibited because they would lead to misdecoding through WBp with NNA codons (Ou et al. 2019). The pairing affinity of these GNN-tRNAs can be modulated by queuosine modification at the wobble position (Tuorto and Lyko 2016). However, given that eukaryotes are nonautotrophic for queuosine biosynthesis, their capacity to modulate GNN-tRNA affinity depends on the availability of queuosine in their diet (Zaborske et al. 2014). Hence, shifts in NSPs cannot always be followed by a change in codon optimality.

    Weak TS in species with large intra-genomic variability in NSPs

    An implicit assumption of the above coadaptation model is that all genes of a given genome are affected by similar NSPs. There is evidence, however, that some genomes are subject to heterogeneous NSPs. Notably, in mammals and birds, variation in recombination rates along chromosomes induces a strong heterogeneity in GC content, driven by gBGC (Duret and Galtier 2009). This process accounts for 70% of the variance in SCU among human genes (Pouyet et al. 2017). Thus, in these species, the SCU of a given gene essentially depends on the base composition of the genomic region where it resides, as shown by the strong correlation observed between GC3 and GCi across human genes (Fig. 1C). It is important to notice that these regional variations in GC content affect all genes, even those that are widely expressed. To illustrate this point, we analyzed the codon usage of 2249 human housekeeping genes (defined as genes that are in the top 20% most highly expressed genes in at least 75% of the tissues). The distribution of GC3 in housekeeping genes shows a very strong heterogeneity (GC3 ranging from 25% to 95%) (Fig. 7A), as strong as in the entire gene set (Fig. 7B). Housekeeping genes are involved in basal function and have to be expressed at a high level in most cell types. This implies that in any given cell, there is a strong heterogeneity of the codon demand. Such a situation is predicted to hinder the coadaptation between the tRNA pool and codon usage: Any increase in the abundance of a given tRNA (say decoding a GC-ending codon) is expected to be beneficial for the translation of GC-rich genes but detrimental for the translation of the GC-poor ones (and vice versa for a tRNA decoding an AU-ending codon). Hence, the selective pressure imposed by the heterogeneous codon demand is expected to maintain a balanced tRNA pool, able to decode GC-rich genes as well as GC-poor genes. In turn, the presence of a balanced tRNA pool should reduce the difference in translational efficiency between synonymous codons and, hence, is expected to decrease the intensity of TS. Thus, genomes that are subject to heterogeneous NSPs are expected to be less subject to TS.

    Figure 7.
    View larger version:
    Figure 7.

    Impact of intra-genomic variability in neutral substitution patterns on TS. (A) Distribution of GC3 across human housekeeping genes (identified based on gene expression data from 27 healthy tissues, extracted from Pouyet et al. 2017). (B) Distribution of GC content at the third position of codons (GC3) across all human genes. (C,D) Relation between TS intensity Shx and the gene GCi variance. (D) Species are colored with a longevity gradient (log scale). (E,F) Relation between TS intensity Shx and longevity (days). (F) Species are colored with a GC intron variance gradient (log scale; N = 223 species).

    To test this prediction, we analyzed the relationship between the intensity of TS (Shx) and the intra-genomic heterogeneity in base composition (assessed by the variance in GCi across genes). We observed that all species with a strong signal of TS show a very small variance in GCi, whereas species with a high variance in GCi show relatively low Shx (Fig. 7C). This is consistent with the hypothesis that intra-genomic heterogeneity in base composition precludes TS. However, species with a high variance in GCi mainly correspond to three clades (Mammal, Aves, Hymenoptera) that also have relatively small Ne, and hence, it is difficult to disentangle the impact of intra-genomic heterogeneity in base composition from that of drift (Fig. 7D). In any case, even though intra-genomic heterogeneity in base composition might explain the weakness of TS in some species, there must be some other factors that affect the intensity of TS. Indeed, among insect species predicted to have a Ne similar to that of Diptera, many show a low Shx despite a small variance in GCi (Fig. 7E,F).

    Previous SectionNext Section

    Discussion

    Impact of NSPs on SCU

    Patterns of SCU vary widely across metazoan species and are strongly correlated to the base composition of their noncoding regions (Fig. 1A). This implies that variation in codon usage across species is primarily shaped by differences in genome-wide NSPs (driven by the underlying mutation pattern, by gBGC, or by both). NSPs vary not only across species but also along chromosomes, and in some clades, such as tetrapods or Hymenoptera, this intra-genomic heterogeneity of NSPs is a major determinant of the variance in SCU among genes (Supplemental Fig. 1B). The fact that genome-wide patterns of SCU are strongly affected by NSPs does not exclude that it can also be shaped by a selective pressure favoring the use of translationally optimal codons. Indeed, in Diptera and Lepidoptera, which both show clear evidence of TS, we observed that the tRNA pool evolves in response to changes in genome-wide NSPs (Fig. 6). Thus, variation in NSPs can lead to shifts in the translation apparatus and thereby drive the evolution of SCU, not only in weakly expressed genes in which codon usage is effectively neutral but also in genes under strong TS. In other words, selective and nonadaptive models are not mutually exclusive, and as illustrated by previous studies (de Oliveira et al. 2021; Cope and Shah 2022), it is essential to take NSPs into account to be able to quantify TS within genomes.

    Predicting translationally optimal codons

    To quantify the intensity of TS in metazoans, we used a method based on standard population genetic equations, which infers the population-scaled selection coefficient (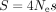Formula) from the difference in optimal codon frequency between highly expressed genes and weakly expressed genes (Sharp et al. 2005; dos Reis and Wernisch 2009). This method first requires identifying the set of optimal codons in each species. To predict optimal codons, previous studies generally searched for codons whose frequency increases with gene expression level (e.g., Duret and Mouchiroud 1999; dos Reis and Wernisch 2009; Shah and Gilchrist 2011). This methodological framework proved to be very efficient to quantify TS in yeasts (Shah and Gilchrist 2011; Wallace et al. 2013; Cope and Shah 2022). One caveat, however, is that in some species, NSP varies with gene expression (Pouyet et al. 2017), which may therefore lead to errors in the inference of optimal codons. Furthermore, in that situation, the method would systematically overestimate S for codons that are favored by NSPs in highly expressed genes. This probably explains why previous estimates of S in human and mice (respectively, 0.51 and 0.22) (dos Reis and Wernisch 2009) are higher than ours (respectively, 0.06 and 0.14). To limit this bias, we sought to predict optimal codons from the tRNA pool available in each species. For this, we estimated the abundance of each tRNA based on its gene copy number in the genome. In most species, we observed a strong correlation between the number of isoacceptor tRNA gene copies and the frequency of their cognate amino acid in the proteome (Fig. 2B). These strong correlations are consistent with the fact that cellular tRNA abundance is highly constrained to match the amino acid demand, and indicate that tRNA gene copy number is a good proxy to infer tRNA abundance, in agreement with previous experimental evidence from a limited set of species (Behrens et al. 2021). Based on our estimates of the tRNA pool, we predicted two sets of putative-optimal codons (POCs): For amino acids for which more than one isodecoder tRNA is available, optimal synonymous codons were defined as those decoded by the most abundant tRNA (POC1); for amino acids encoded by NNC/NNU duet codons and with one single isodecoder tRNA (GNN), the NNC codons were predicted to be optimal (POC2), based on previous studies showing that the WBp GNN:NNU was less efficient than the WCp GNN:NNC (Fig. 3B; Stadler and Fire 2011; Chan et al. 2017).

    Several lines of evidence indicate that our predictions of translationally optimal codons are accurate. First, our sets of POCs are consistent with previous predictions: Among the optimal codons that had been inferred based on differential usage between highly and lowly expressed genes in C. elegans (N = 26) and in D. melanogaster (N = 25) (Duret and Mouchiroud 1999), 88.4% and 88.0%, respectively, match with our POCs (25 POCs in C. elegans and 27 in D. melanogaster). Second, we observed that although the definition of POC1 and POC2 relies on very different principles, the two sets of codons show very similar signatures of TS (Fig. 4C). Furthermore, the analysis of substitution patterns and polymorphism in D. melanogaster confirmed that selection favors POC alleles over non-POC alleles in highly expressed genes (Supplemental Text 1). Finally, optimal codons are also expected to be selected for their impact on translation accuracy: Consistent with this prediction, we observed that within genes, POCs are enriched at the more constrained amino acid sites (Supplemental Text 2).

    Variation in the intensity of selection in favor of translationally optimal codons across metazoans

    For each species, we measured the frequency of optimal codons (combining POC1 and POC2) in highly expressed genes (top 2%) to estimate the population-scaled selection coefficient in favor of translationally optimal codons (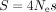Formula), using weakly expressed genes as a reference to account for the NSP (Sharp et al. 2005). Across the 223 species, the highest values of S are observed in Caenorhabditis nematodes (S = 1.25 in C. elegans and S = 1.00 in C. nigoni). We also found a clear signal of TS in Diptera (mean S = 0.63, N = 19 species) and, to a lesser extent, in Lepidoptera (mean S = 0.41, N = 8 species). Overall, estimates of S are weaker in other clades (Fig. 5). The weakness of TS in vertebrates (mean S = 0.15, N = 119 species) was a priori expected given that these organisms tend to have relatively small Ne. But what is surprising is that most of the invertebrate species show very weak TS. Besides Caenorhabditis and Diptera, our data set included 83 invertebrate species covering a wide range of clades (58 other insects, 12 other Ecdysozoa, six Spiralia, four Cnidaria, three Deuterostomia) that all show S-values lower than that of Diptera. This implies that the high values of S observed in Caenorhabditis and in Diptera represent exceptions rather than the rule and that TS is weak in most metazoan lineages.

    If the selection coefficient in favor of optimal codons (s) was constant across metazoans, then S should scale linearly with Ne. To test this prediction, we used silent-site polymorphism and germline mutation rate data (Lynch et al. 2023) to estimate the effective population size (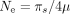Formula; hereafter noted as 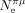Formula) in 41 species. As expected, S tends to increase with 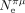Formula, but the correlation is not significant after accounting for phylogenetic inertia (Fig. 5D). 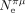The weakness of the correlation might be because these two parameters evolve on different timescales: Formula is indicative of the recent effective population size (on the order of Ne generations) and hence can change quite rapidly compared with S, which is estimated from the codon composition of genomes, resulting from a long-term accumulation of substitutions. This can explain why C. nigoni and C. 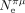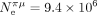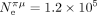elegans display similar values of S, despite a 75-fold difference in Formula (respectively, Formula and Formula). This difference in 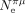Formula is because C. nigoni is an outcrossing species, like most other Caenorhabditis species, whereas the C. elegans lineage evolved toward selfing hermaphroditism (Li et al. 2014; Vielle et al. 2016). This transition in reproductive mode is recent, and hence, the SCU of C. elegans still retains the signature of strong TS inherited from its outcrossing ancestors. Thus, we can predict that the SCU of C. elegans is not at selection-mutation-drift equilibrium.

    To further test the relationship between S and Ne, we considered three additional parameters (longevity, body length, and dN/dS) that are all correlated with 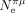Formula (Supplemental Fig. 7) but that are expected to reflect Ne over a longer timescale. A further interest of these proxies is that they can be estimated on much larger data sets (150 to 223 species). But, here again, we obtained similar results: S tends to increase with Ne, but correlations are weak, marginally significant after accounting for phylogeny (Fig. 5A–C). The weakness of the correlation is mainly because some species have a low S, despite life-history traits or dN/dS values indicative of a high Ne.

    Not only the correlations between Ne and S are weak, but also the range of variation in S appears to be quite limited compared to what would be expected given the variance in Ne. For instance, the mean value of 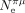Formula is about 15 times higher in Diptera than in mammals (based on, respectively, six and 41 species for which 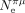Formula can be estimated) (Lynch et al. 2023). Yet, the mean value of S is only 5.3 times higher in Diptera (mean S = 0.63, N = 19 species) than in mammals (mean S = 0.12, N = 65 species). Thus, the difference in S between Diptera and mammals is smaller than what would be expected if S scaled linearly with Ne.

    One possible explanation for this discrepancy is that S is overestimated in mammals. As discussed by dos Reis and Wernisch (2009), the estimate of S is based on the assumption that NSPs are constant across genes, namely, that the difference in optimal codon frequency between highly and weakly expressed genes is entirely owing to TS. In reality, in some species, NSPs vary with gene expression (e.g., in humans) (Supplemental Fig. 10; Pouyet et al. 2017). To try to account for these variations, we measured the differences in POC frequency between highly and weakly expressed genes, controlling for differences in the corresponding triplet frequencies in introns. It is, however, possible that the base composition of introns is not a perfect predictor of NSPs, notably because introns are affected by indels and transposable elements, which are not allowed in coding regions. This is well illustrated by POC2 codons in humans, whose frequency clearly covaries with their noncoding controls, but with a wider amplitude in exons than in introns (Fig. 4A).

    An alternative hypothesis is that the discrepancy might result from a strong heterogeneity in the fitness effect of synonymous mutations. Indeed, the analysis of synonymous polymorphism in D. melanogaster indicated that a majority of codons are under weak selection in favor of translationally optimal codon (|Nes| ≈ 1) but that a small fraction (10%–20%) are under strong selection (|Nes| > 10) (Machado et al. 2020). With a Ne value 15 times lower, the first class of codons is expected to evolve neutrally in mammals. But the second class of codons would still appear under effective TS, which might explain the small but nonnull value of S measured in mammals.

    Another unexpected observation is that many species predicted to have a high Ne (based on their LHTs or dN/dS) show very weak S (Fig. 5A–C). In some species, this could be explained by the heterogeneity of NSPs along chromosomes, inducing a strong variance in SCU that precludes a coadaptation of the tRNA pool. This might be the case notably for some Hymenoptera, which, like tetrapods, are subject to gBGC (Wallberg et al. 2015) and present a very strong heterogeneity in NSPs (Fig. 7C). However, our data set also includes some species with small S values, despite a high Ne proxy and homogenous NSPs. So finally, we are left with the conclusion that variation in S across metazoans are not driven simply by the drift barrier and by gBGC but that they are also probably owing to variation in S, the selection coefficient in favor of translationally optimal codons. There is evidence that in unicellular organisms, the selective force for the optimization of SCU is the maximization of cellular growth (Rocha 2004; Sharp et al. 2005). It is possible that the selective pressure on cellular growth also varies across metazoans. Most Caenorhabditis species grow in ephemeral environments (rotting vegetation) and hence have been selected for their capacity to proliferate very rapidly (Cutter 2015). Manthey et al. (2024) recently quantified growth rates in 33 insects. The only Diptera present in their data set (Lucilia sericata) is the species that presented the highest growth rate, 12 times higher than the average growth rate of other holometabole insects (N = 10) and 52 times higher than the average growth rate of hemimetabole insects (N = 22). If the L. sericata is representative of other Diptera, this might explain why TS is particularly strong in that clade compared with other insects. It is noteworthy that the two invertebrate species that have been historically used as model organisms (D. melanogaster and C. elegans) both belong to the very rare metazoan clades with clear evidence of TS. This might reflect the fact that they have been chosen as model organisms for the very reason that they can grow very fast in the laboratory.

    Previous SectionNext Section

    Methods

    Gene expression and data collection

    The reference genome assemblies and genome annotations were downloaded from the National Center for Biotechnology Information (NCBI; https://www.ncbi.nlm.nih.gov) (Sayers et al. 2022). We obtained gene expression data for 257 metazoan species from GTDrift (Bénitière et al. 2024), in which gene expression levels (in fragment per kilobase of exon per million mapped reads [FPKM]) were estimated over 8362 RNA-seq samples. For each species, we considered the per-gene median expression level across all analyzed RNA-seq samples. Additionally, a phylogenetic tree was retrieved from GTDrift to account for phylogenetic inertia (Bénitière et al. 2024).

    tRNA gene annotation

    The genomic coordinates of tRNA genes were extracted from the NCBI annotation file (N = 44 species). For species in which tRNA annotations were not available (N = 213 species), we predicted tRNA gene copies using the program tRNAscan-SE 2.0.12 (November 2022), with the -E option specifically designed for eukaryotic tRNA identification (Chan et al. 2021). To avoid tRNA pseudogenes, we retained only tRNA gene predictions with a score exceeding 55, threshold based on the method of Chan et al. (2021).

    Analysis of codon usage

    We analyzed codon usage only in genes detected as being expressed (>0 FPKM) to avoid erroneously annotated genes. For each gene, we counted codons of the longest annotated coding sequences (CDSs). To control for variation in NSPs, we measured the frequency of corresponding nucleotide triplets within the intron (excluding the acceptor and donor splice sites that are highly constrained).

    Estimating ΔPOCexp

    We calculated ΔPOCexp by subtracting the frequency of POCs in the 50% least-expressed genes from the frequency of POCs in the top 2% most-expressed genes. We then adjusted for this estimate by removing the observed differences in corresponding triplet frequencies within introns between the 2% most-expressed and the 50% least-expressed genes.

    Estimates of effective population sizes

    We retrieved proxies for the effective population size from the GTDrift data resource (Bénitière et al. 2024), which included life history traits such as body length, longevity, and the ratio of nonsynonymous to synonymous substitutions rate (dN/dS). It is expected that the genome-wide dN/dS ratio increases during prolonged periods of small Ne, attributed to the fixation of slightly deleterious mutations (Ohta 1992; Galtier 2016).

    GTDrift also provides measures of Ne based on the germline mutation rate (μ) and the level of neutral diversity (πs) published by Lynch et al. (2023) (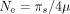Formula). We retrieved this estimate for 45 species, comprising 27 species within our data set and 18 for which species from the same genus were available.

    Analyses of correlations between traits across species

    To take into account the phylogenetic structure of the data, we used phylolm (Tung Ho and Ané 2014), which implements Pagel's lambda model (Pagel 1997) within a phylogenetic generalized least square framework (PGLS). For this, we used the phylogenetic tree of the 257 studied species, inferred from the alignment of 731 genes (Bénitière et al. 2024). We considered two versions of that tree: the phylogram (i.e., with branch lengths proportional to substitution rate) and the chronogram (i.e., a tree with branch lengths proportional to time). The chronogram was inferred from the phylogram using a penalized likelihood model with a relaxed molecular clock (Sanderson 2002) with APE (Paradis and Schliep 2019). The results of both approaches are shown in Supplemental Table S1 for each analysis. In all cases, both trees gave consistent results, but the PGLS models using the phylogram systematically gave a better fit (as judged by lower AICs). We therefore present in the main text the results obtained with the phylogram.

    Previous SectionNext Section

    Data access

    All processed data generated in this study, as well as the scripts used to analyze the data and to generate the figures, are available at Zenodo (https://doi.org/10.5281/zenodo.12669922). The scripts are also available as Supplemental Code.

    Previous SectionNext Section

    Competing interest statement

    The authors declare no competing interests.

    Previous SectionNext Section

    Acknowledgments

    Computational analyses were performed using the computing facilities of the Centre de Calcul du Laboratoire de Biométrie et Biologie Evolutive et du Pôle Rhône-Alpin de Bioinformatique (CC LBBE/PRABI) and the Core Cluster of the Institut Français de Bioinformatique (IFB; ANR-11-INBS-0013). Silhouette images of taxonomic Families originate from PhyloPic developed and maintained by Mike Keesey available at https://www.phylopic.org/. This work was funded by the French National Research Agency (ANR-20-CE02-0008-01 “NeGA”).

    Author contributions: L.D., T.L., and F.B. designed the project. F.B. conceived the pipeline and conducted the analyses. L.D., F.B., and T.L. wrote the manuscript.

    Previous SectionNext Section

    Footnotes

    • Received July 22, 2024.
    • Accepted January 30, 2025.

    This article is distributed exclusively by Cold Spring Harbor Laboratory Press for the first six months after the full-issue publication date (see https://genome.cshlp.org/site/misc/terms.xhtml). After six months, it is available under a Creative Commons License (Attribution-NonCommercial 4.0 International), as described at http://creativecommons.org/licenses/by-nc/4.0/.

    Previous Section
     

    References

    1. ↵
      Akashi H. 1994. Synonymous codon usage in Drosophila melanogaster: natural selection and translational accuracy. Genetics 136: 927–935. doi:10.1093/genetics/136.3.927
      Abstract/FREE Full Text
    2. ↵
      Behrens A, Rodschinka G, Nedialkova DD. 2021. High-resolution quantitative profiling of tRNA abundance and modification status in eukaryotes by mim-tRNAseq. Mol Cell 81: 1802–1815.e7. doi:10.1016/j.molcel.2021.01.028
      CrossRefMedlineGoogle Scholar
    3. ↵
      Bénitière F, Duret L, Necsulea A. 2024. GTDrift: a resource for exploring the interplay between genetic drift, genomic and transcriptomic characteristics in eukaryotes. NAR Genom Bioinform 6: lqae064. doi:10.1093/nargab/lqae064
      CrossRefGoogle Scholar
    4. ↵
      Buhr F, Jha S, Thommen M, Mittelstaet J, Kutz F, Schwalbe H, Rodnina MV, Komar AA. 2016. Synonymous codons direct co-translational folding towards different protein conformations. Mol Cell 61: 341–351. doi:10.1016/j.molcel.2016.01.008
      CrossRefMedlineGoogle Scholar
    5. ↵
      Bulmer M. 1987. Coevolution of codon usage and transfer RNA abundance. Nature 325: 728–730. doi:10.1038/325728a0
      CrossRefMedlineGoogle Scholar
    6. ↵
      Bulmer M. 1991. The selection-mutation-drift theory of synonymous codon usage. Genetics 129: 897–907. doi:10.1093/genetics/129.3.897
      Abstract/FREE Full Text
    7. ↵
      Chan S, Ch'ng J-H, Wahlgren M, Thutkawkorapin J. 2017. Frequent GU wobble pairings reduce translation efficiency in Plasmodium falciparum. Sci Rep 7: 723. doi:10.1038/s41598-017-00801-9
      CrossRefMedlineGoogle Scholar
    8. ↵
      Chan P, Lin B, Mak A, Lowe T. 2021. tRNAscan-SE 2.0: improved detection and functional classification of transfer RNA genes. Nucleic Acids Res 49: 9077–9096. doi:10.1093/nar/gkab688
      CrossRefMedlineGoogle Scholar
    9. ↵
      Cope AL, Shah P. 2022. Intragenomic variation in non-adaptive nucleotide biases causes underestimation of selection on synonymous codon usage. PLoS Genet 18: e1010256. doi:10.1371/journal.pgen.1010256
      CrossRefMedlineGoogle Scholar
    10. ↵
      Courel M, Clément Y, Bossevain C, Foretek D, Vidal Cruchez O, Yi Z, Bénard M, Benassy M-N, Kress M, Vindry C, et al. 2019. GC content shapes mRNA storage and decay in human cells. eLife 8: e49708. doi:10.7554/eLife.49708
      CrossRefMedlineGoogle Scholar
    11. ↵
      Cutter AD. 2015. Caenorhabditis evolution in the wild. BioEssays 37: 983–995. doi:10.1002/bies.201500053
      CrossRefMedlineGoogle Scholar
    12. ↵
      de Oliveira JL, Morales AC, Hurst LD, Urrutia AO, Thompson CRL, Wolf JB. 2021. Inferring adaptive codon preference to understand sources of selection shaping codon usage bias. Mol Biol Evol 38: 3247–3266. doi:10.1093/molbev/msab099
      CrossRefGoogle Scholar
    13. ↵
      Dong H, Nilsson L, Kurland CG. 1996. Co-variation of tRNA abundance and codon usage in Escherichia coli at different growth rates. J Mol Biol 260: 649–663. doi:10.1006/jmbi.1996.0428
      CrossRefMedlineGoogle Scholar
    14. ↵
      dos Reis M, Wernisch L. 2009. Estimating translational selection in eukaryotic genomes. Mol Biol Evol 26: 451–461. doi:10.1093/molbev/msn272
      CrossRefMedlineGoogle Scholar
    15. ↵
      Drummond DA, Raval A, Wilke CO. 2006. A single determinant dominates the rate of yeast protein evolution. Mol Biol Evol 23: 327–337. doi:10.1093/molbev/msj038
      CrossRefMedlineGoogle Scholar
    16. ↵
      Duret L. 2000. tRNA gene number and codon usage in the C. elegans genome are co-adapted for optimal translation of highly expressed genes. Trends Genet 16: 287–289. doi:10.1016/S0168-9525(00)02041-2
      CrossRefMedlineGoogle Scholar
    17. ↵
      Duret L, Galtier N. 2009. Biased gene conversion and the evolution of mammalian genomic landscapes. Annu Rev Genomics Hum Genet 10: 285–311. doi:10.1146/annurev-genom-082908-150001
      CrossRefMedlineGoogle Scholar
    18. ↵
      Duret L, Mouchiroud D. 1999. Expression pattern and, surprisingly, gene length shape codon usage in Caenorhabditis, Drosophila, and Arabidopsis. Proc Natl Acad Sci 96: 4482–4487. doi:10.1073/pnas.96.8.4482
      Abstract/FREE Full Text
    19. ↵
      Galtier N. 2016. Adaptive protein evolution in animals and the effective population size hypothesis. PLoS Genet 12: e1005774. doi:10.1371/journal.pgen.1005774
      CrossRefMedlineGoogle Scholar
    20. ↵
      Galtier N, Roux C, Rousselle M, Romiguier J, Figuet E, Glémin S, Bierne N, Duret L. 2018. Codon usage bias in animals: disentangling the effects of natural selection, effective population size, and GC-biased gene conversion. Mol Biol Evol 35: 1092–1103. doi:10.1093/molbev/msy015
      CrossRefMedlineGoogle Scholar
    21. ↵
      Gouy M, Gautier C. 1982. Codon usage in bacteria: correlation with gene expressivity. Nucleic Acids Res 10: 7055–7074. doi:10.1093/nar/10.22.7055
      CrossRefMedlineGoogle Scholar
    22. ↵
      Grantham R, Gautier C, Gouy M, Mercier R, Pavé A. 1980. Codon catalog usage and the genome hypothesis. Nucleic Acids Res 8: r49–r62. doi:10.1093/nar/8.1.197-c
      CrossRefMedlineGoogle Scholar
    23. ↵
      Ikemura T. 1985. Codon usage and tRNA content in unicellular and multicellular organisms. Mol Biol Evol 2: 13–34. doi:10.1093/oxfordjournals.molbev.a040335
      CrossRefMedlineGoogle Scholar
    24. ↵
      Kanaya S, Yamada Y, Kudo Y, Ikemura T. 1999. Studies of codon usage and tRNA genes of 18 unicellular organisms and quantification of Bacillus subtilis tRNAs: gene expression level and species-specific diversity of codon usage based on multivariate analysis. Gene 238: 143–155. doi:10.1016/S0378-1119(99)00225-5
      CrossRefMedlineGoogle Scholar
    25. ↵
      Kessler MD, Dean MD. 2014. Effective population size does not predict codon usage bias in mammals. Ecol Evol 4: 3887–3900. doi:10.1002/ece3.1249
      CrossRefMedlineGoogle Scholar
    26. ↵
      Kudla G, Lipinski L, Caffin F, Helwak A, Zylicz M. 2006. High guanine and cytosine content increases mRNA levels in mammalian cells. PLoS Biol 4: e180. doi:10.1371/journal.pbio.0040180
      CrossRefMedlineGoogle Scholar
    27. ↵
      Leppek K, Byeon GW, Kladwang W, Wayment-Steele HK, Kerr CH, Xu AF, Kim DS, Topkar VV, Choe C, Rothschild D, et al. 2022. Combinatorial optimization of mRNA structure, stability, and translation for RNA-based therapeutics. Nat Commun 13: 1536. doi:10.1038/s41467-022-28776-w
      CrossRefMedlineGoogle Scholar
    28. ↵
      Li S, Jovelin R, Yoshiga T, Tanaka R, Cutter AD. 2014. Specialist versus generalist life histories and nucleotide diversity in Caenorhabditis nematodes. Proc R Soc B: Biol Sci 281: 20132858. doi:10.1098/rspb.2013.2858
      CrossRefMedlineGoogle Scholar
    29. ↵
      Lim V, Curran J. 2001. Analysis of codon:anticodon interactions within the ribosome provides new insights into codon reading and the genetic code structure. RNA 7: 942–957. doi:10.1017/S135583820100214X
      Abstract
    30. ↵
      Lobry JR. 1995. Properties of a general model of DNA evolution under no-strand-bias conditions. J Mol Evol 40: 326–330. doi:10.1007/BF00163237
      CrossRefMedlineGoogle Scholar
    31. ↵
      Long H, Sung W, Kucukyildirim S, Williams E, Miller SF, Guo W, Patterson C, Gregory C, Strauss C, Stone C, et al. 2018. Evolutionary determinants of genome-wide nucleotide composition. Nat Ecol Evol 2: 237–240. doi:10.1038/s41559-017-0425-y
      CrossRefMedlineGoogle Scholar
    32. ↵
      Lynch M, Ali F, Lin T, Wang Y, Ni J, Long H. 2023. The divergence of mutation rates and spectra across the tree of life. EMBO Rep 24: e57561. doi:10.15252/embr.202357561
      CrossRefMedlineGoogle Scholar
    33. ↵
      Machado HE, Lawrie DS, Petrov DA. 2020. Pervasive strong selection at the level of codon usage bias in Drosophila melanogaster. Genetics 214: 511–528. doi:10.1534/genetics.119.302542
      Abstract/FREE Full Text
    34. ↵
      Manthey C, Metcalf CJE, Monaghan MT, Steiner UK, Rolff J. 2024. Rapid growth and the evolution of complete metamorphosis in insects. Proc Natl Acad Sci 121: e2402980121 doi:10.1073/pnas.2402980121
      CrossRefMedlineGoogle Scholar
    35. ↵
      Medina-Muñoz SG, Kushawah G, Castellano LA, Diez M, DeVore ML, Salazar MJB, Bazzini AA. 2021. Crosstalk between codon optimality and cis-regulatory elements dictates mRNA stability. Genome Biol 22: 14. doi:10.1186/s13059-020-02251-5
      CrossRefMedlineGoogle Scholar
    36. ↵
      Mordstein C, Savisaar R, Young RS, Bazile J, Talmane L, Luft J, Liss M, Taylor MS, Hurst LD, Kudla G. 2020. Codon usage and splicing jointly influence mRNA localization. Cell Syst 10: 351–362.e8. doi:10.1016/j.cels.2020.03.001
      CrossRefMedlineGoogle Scholar
    37. ↵
      Moriyama EN, Powell JR. 1997. Codon usage bias and tRNA abundance in Drosophila. J Mol Evol 45: 514–523. doi:10.1007/PL00006256
      CrossRefMedlineGoogle Scholar
    38. ↵
      Ohta T. 1992. The nearly neutral theory of molecular evolution. Annu Rev Ecol Syst 23: 263–286. doi:10.1146/annurev.es.23.110192.001403
      CrossRefGoogle Scholar
    39. ↵
      Ohta T. 1996. The neutral theory is dead: the current significance and standing of neutral and nearly neutral theories. Bioessays 18: 673–677. doi:10.1002/bies.950180811
      CrossRefMedlineGoogle Scholar
    40. ↵
      Ou X, Cao J, Cheng A, Peppelenbosch MP, Pan Q. 2019. Errors in translational decoding: tRNA wobbling or misincorporation? PLoS Genet 15: e1008017. doi:10.1371/journal.pgen.1008017
      CrossRefMedlineGoogle Scholar
    41. ↵
      Pagel M. 1997. Inferring evolutionary processes from phylogenies. Zool Scr 26: 331–348. doi:10.1111/j.1463-6409.1997.tb00423.x
      CrossRefGoogle Scholar
    42. ↵
      Paradis E, Schliep K. 2019. Ape 5.0: an environment for modern phylogenetics and evolutionary analyses in R. Bioinformatics 35: 526–528. doi:10.1093/bioinformatics/bty633
      CrossRefMedlineGoogle Scholar
    43. ↵
      Parmley JL, Hurst LD. 2007. Exonic splicing regulatory elements skew synonymous codon usage near intron-exon boundaries in mammals. Mol Biol Evol 24: 1600–1603. doi:10.1093/molbev/msm104
      CrossRefMedlineGoogle Scholar
    44. ↵
      Percudani R. 2001. Restricted wobble rules for eukaryotic genomes. Trends Genet 17: 133–135. doi:10.1016/S0168-9525(00)02208-3
      CrossRefMedlineGoogle Scholar
    45. ↵
      Pouyet F, Mouchiroud D, Duret L, Sémon M. 2017. Recombination, meiotic expression and human codon usage. eLife 6: e27344. doi:10.7554/eLife.27344
      CrossRefGoogle Scholar
    46. ↵
      Rocha EP. 2004. Codon usage bias from tRNA's point of view: redundancy, specialization, and efficient decoding for translation optimization. Genome Res 14: 2279–2286. doi:10.1101/gr.2896904
      Abstract/FREE Full Text
    47. ↵
      Sanderson MJ. 2002. Estimating absolute rates of molecular evolution and divergence times: a penalized likelihood approach. Mol Biol Evol 19: 101–109. doi:10.1093/oxfordjournals.molbev.a003974
      CrossRefMedlineGoogle Scholar
    48. ↵
      Sayers EW, Bolton EE, Brister JR, Canese K, Chan J, Comeau DC, Connor R, Funk K, Kelly C, Kim S, et al. 2022. Database resources of the national center for biotechnology information. Nucleic Acids Res 50: D20–D26. doi:10.1093/nar/gkab1112
      CrossRefMedlineGoogle Scholar
    49. ↵
      Sémon M, Lobry JR, Duret L. 2006. No evidence for tissue-specific adaptation of synonymous codon usage in humans. Mol Biol Evol 23: 523–529. doi:10.1093/molbev/msj053
      CrossRefMedlineGoogle Scholar
    50. ↵
      Shah P, Gilchrist MA. 2011. Explaining complex codon usage patterns with selection for translational efficiency, mutation bias, and genetic drift. Proc Natl Acad Sci 108: 10231–10236. doi:10.1073/pnas.1016719108
      Abstract/FREE Full Text
    51. ↵
      Sharp PM, Tuohy TM, Mosurski KR. 1986. Codon usage in yeast: Cluster analysis clearly differentiates highly and lowly expressed genes. Nucleic Acids Res 14: 5125–5143. doi:10.1093/nar/14.13.5125
      CrossRefMedlineGoogle Scholar
    52. ↵
      Sharp PM, Stenico M, Peden JF, Lloyd AT. 1993. Codon usage: mutational bias, translational selection, or both? Biochem Soc Trans 21: 835–841. doi:10.1042/bst0210835
      FREE Full Text
    53. ↵
      Sharp PM, Bailes E, Grocock RJ, Peden JF, Sockett RE. 2005. Variation in the strength of selected codon usage bias among bacteria. Nucleic Acids Res 33: 1141–1153. doi:10.1093/nar/gki242
      CrossRefMedlineGoogle Scholar
    54. ↵
      Shields DC, Sharp PM, Higgins DG, Wright F. 1988. “Silent” sites in Drosophila genes are not neutral: evidence of selection among synonymous codons. Mol Biol Evol 5: 704–716. doi:10.1093/oxfordjournals.molbev.a040525
      CrossRefMedlineGoogle Scholar
    55. ↵
      Stadler M, Fire A. 2011. Wobble base-pairing slows in vivo translation elongation in metazoans. RNA 17: 2063–2073. doi:10.1261/rna.02890211
      Abstract/FREE Full Text
    56. ↵
      Subramanian S. 2008. Nearly neutrality and the evolution of codon usage bias in eukaryotic genomes. Genetics 178: 2429–2432. doi:10.1534/genetics.107.086405
      Abstract/FREE Full Text
    57. ↵
      Sun F-J, Fleurdépine S, Bousquet-Antonelli C, Caetano-Anollés G, Deragon J-M. 2007. Common evolutionary trends for SINE RNA structures. Trends Genet 23: 26–33. doi:10.1016/j.tig.2006.11.005
      CrossRefMedlineGoogle Scholar
    58. ↵
      Tung Ho Ls, Ané C. 2014. A linear-time algorithm for Gaussian and non-Gaussian trait evolution models. Syst Biol 63: 397–408. doi:10.1093/sysbio/syu005
      CrossRefMedlineGoogle Scholar
    59. ↵
      Tuorto F, Lyko F. 2016. Genome recoding by tRNA modifications. Open Biol 6: 160287. doi:10.1098/rsob.160287
      CrossRefMedlineGoogle Scholar
    60. ↵
      Vielle A, Callemeyn-Torre N, Gimond C, Poullet N, Gray JC, Cutter AD, Braendle C. 2016. Convergent evolution of sperm gigantism and the developmental origins of sperm size variability in Caenorhabditis nematodes. Evolution (N Y) 70: 2485–2503. doi:10.1111/evo.13043
      CrossRefMedlineGoogle Scholar
    61. ↵
      Wallace EW, Airoldi EM, Drummond DA. 2013. Estimating selection on synonymous codon usage from noisy experimental data. Mol Biol Evol 30: 1438–1453. doi:10.1093/molbev/mst051
      CrossRefMedlineGoogle Scholar
    62. ↵
      Wallberg A, Glémin S, Webster MT. 2015. Extreme recombination frequencies shape genome variation and evolution in the honeybee, Apis mellifera. PLoS Genet 11: e1005189. doi:10.1371/journal.pgen.1005189
      CrossRefMedlineGoogle Scholar
    63. ↵
      Walsh IM, Bowman MA, Soto Santarriaga IF, Rodriguez A, Clark PL. 2020. Synonymous codon substitutions perturb cotranslational protein folding in vivo and impair cell fitness. Proc Natl Acad Sci 117: 3528–3534. doi:10.1073/pnas.1907126117
      Abstract/FREE Full Text
    64. ↵
      Wang H, McManus J, Kingsford C. 2017. Accurate recovery of ribosome positions reveals slow translation of wobble-pairing codons in yeast. J Comput Biol 24: 486–500. doi:10.1089/cmb.2016.0147
      CrossRefMedlineGoogle Scholar
    65. ↵
      Wu Q, Medina SG, Kushawah G, DeVore ML, Castellano LA, Hand JM, Wright M, Bazzini AA. 2019. Translation affects mRNA stability in a codon-dependent manner in human cells. eLife 8: e45396. doi:10.7554/eLife.45396
      CrossRefMedlineGoogle Scholar
    66. ↵
      Zaborske JM, DuMont VLB, Wallace EWJ, Pan T, Aquadro CF, Drummond DA. 2014. A nutrient-driven tRNA modification alters translational fidelity and genome-wide protein coding across an animal genus. PLoS Biol 12: e1002015. doi:10.1371/journal.pbio.1002015
      CrossRefMedlineGoogle Scholar
    | Table of Contents

    This Article

    1. Published in Advance February 10, 2025, doi: 10.1101/gr.279837.124 Genome Res. 35: 446-458 © 2025 Bénitière et al.; Published by Cold Spring Harbor Laboratory Press

    Article Category

    ORCID

    1. Profile for Bénitière, F.http://orcid.org/0000-0001-7773-3542
    2. Profile for Lefébure, T.http://orcid.org/0000-0003-3923-8166
    3. Profile for Duret, L.http://orcid.org/0000-0003-2836-3463

    Share

    Preprint Server



    Navigate This Article

    Current Issue

    1. January 2026, 36 (1)
    1. Current Issue
    1. Alert me to new issues of Genome Research