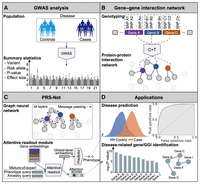
Modeling gene interactions in polygenic prediction via geometric deep learning

  1. Sai Zhang5,6
  1. 1School of Mathematical Sciences and LPMC, Nankai University, Tianjin, 300071, China;
  2. 2Institute for Interdisciplinary Information Sciences, Tsinghua University, Beijing, 100084, China;
  3. 3School of Engineering, Research Center for Industries of the Future, Westlake University, Hangzhou, 310030, Zhejiang, China;
  4. 4Department of Genetics, Center for Genomics and Personalized Medicine, Stanford University School of Medicine, Stanford, California 94304, USA;
  5. 5Department of Epidemiology, University of Florida, Gainesville, Florida 32603, USA;
  6. 6Departments of Biostatistics & Biomedical Engineering, UF Genetics Institute, University of Florida, Gainesville, Florida 32603, USA
  • Corresponding authors: zengjy{at}westlake.edu.cn, mpsnyder{at}stanford.edu, sai.zhang{at}ufl.edu
    •  
    Next Section

    Abstract

    Polygenic risk score (PRS) is a widely used approach for predicting individuals’ genetic risk of complex diseases, playing a pivotal role in advancing precision medicine. Traditional PRS methods, predominantly following a linear structure, often fall short in capturing the intricate relationships between genotype and phenotype. In this study, we present PRS-Net, an interpretable geometric deep learning–based framework that effectively models the nonlinearity of biological systems for enhanced disease prediction and biological discovery. PRS-Net begins by deconvoluting the genome-wide PRS at the single-gene resolution and then explicitly encapsulates gene–gene interactions leveraging a graph neural network (GNN) for genetic risk prediction, enabling a systematic characterization of molecular interplay underpinning diseases. An attentive readout module is introduced to facilitate model interpretation. Extensive tests across multiple complex traits and diseases demonstrate the superior prediction performance of PRS-Net compared with a wide range of conventional PRS methods. The interpretability of PRS-Net further enhances the identification of disease-relevant genes and gene programs. PRS-Net provides a potent tool for concurrent genetic risk prediction and biological discovery for complex diseases.

    Complex human diseases exhibit substantial polygenicity in their genetic architectures, characterized by a multitude of common genetic variants with moderate or minor effects accumulatively influencing the disease risk (Clarke et al. 2009; CKDGen Consortium et al. 2011; Orrù et al. 2013; Gaiteri et al. 2016). Polygenic risk scores (PRSs) (Torkamani et al. 2018; Choi et al. 2020; Lewis and Vassos 2020), also known as polygenic scores (PGSs), have been developed to quantitatively estimate the genetic susceptibility of individuals to specific traits or diseases based on common variants (i.e., variants with minor allele frequency [MAF] < 0.05 in the population). This methodology empowers several aspects of precision medicine, including disease prevention, early intervention, and personalized treatment (Gibson 2019; Konuma and Okada 2021; Polygenic Risk Score Task Force of the International Common Disease Alliance 2021).

    PRS is calculated based on summary statistics derived from the genome-wide association study (GWAS) (Euesden et al. 2015; Vilhjálmsson et al. 2015; Mak et al. 2017; Choi and O'Reilly 2019; Lloyd-Jones et al. 2019; Privé et al. 2021, 2022), a widely used statistical method for identifying disease-associated genetic variants (Wang et al. 2005; Korte and Farlow 2013; Uffelmann et al. 2021). Although GWAS enables genome-wide identification of risk variants, such as single-nucleotide polymorphisms (SNPs) and small insertions and deletions (indels), which exhibit significant differences in allele frequency between disease cases and healthy controls, these GWAS hits tend to have modest or even minor effects on the phenotype, resulting in limited prediction capability for individuals. In an effort to enhance predictive modeling, various statistical methods have been proposed to aggregate variants with a wide range of significance (e.g., GWAS P < 5 × 10−8), such as the clumping and thresholding (C + T) method (Purcell et al. 2007; Vilhjálmsson et al. 2015), PRSice-2 (Euesden et al. 2015), LDpred2 (Privé et al. 2021), and lassosum2 (Privé et al. 2022). However, these approaches mainly follow an additive structure and oversimplify the intricate relationship between genotype and phenotype.

    It has been broadly recognized that human phenotype is determined not solely by single genes but rather complex interactions among multiple genes or proteins, exhibiting additive or nonadditive genotype–phenotype (G2P) relationships (Cordell 2009; Zuk et al. 2012; Taylor and Ehrenreich 2015). Importantly, there is increasing evidence highlighting the significance of nonadditive G2P (Lenz et al. 2015; Varona et al. 2018; Guindo-Martínez et al. 2021). Epistasis is a prominent example that occurs when the impact of a gene variant depends on the presence or absence of variants in other genes (Cheverud and Routman 1995; Moore and Williams 2009; Lehner 2011). Several efforts have been made to consider such nonlinear genetic interactions in PRS calculation. These include tree-based methods such as random forests (Ho 1995; Breiman 2001), gradient boosting (Friedman 2001, 2002), and AdaBoost (Freund and Schapire 1997; Hastie et al. 2009), as well as deep learning–based models such as multiple-layer perceptrons (MLP) (Alzoubi et al. 2023) and convolutional neural networks (Sigurdsson et al. 2023). However, these methods only take a limited number of variants as their input and also lack the integration of prior knowledge regarding biological complexity. Indeed, existing nonlinear PRSs have demonstrated either comparable or, in many cases, inferior performance in predicting phenotypes compared with linear models (Bellot et al. 2018; Xu et al. 2022).

    In this study, we propose PRS-Net, a geometric deep learning–based framework tailored to effectively model nonlinear relationships among genetic factors, thus delivering more accurate and robust genetic risk prediction. Based on the GWAS summary statistics, PRS-Net first maps the genome-wide PRS onto a gene–gene interaction (GGI) network through the derivation of gene-level PRSs using the C + T method. Subsequently, a graph neural network (GNN) is employed to iteratively update the PRS embeddings of genes via message passing. An attentive readout module is introduced to enhance model interpretability. PRS-Net also integrates a mixture-of-expert module (Masoudnia and Ebrahimpour 2014) to improve prediction generalization across multiancestry data sets. Based on the UK Biobank (UKBB) database (Sudlow et al. 2015), extensive evaluations were performed for eight diseases—including Alzheimer's disease (AD), atrial fibrillation (AF), rheumatoid arthritis (RA), multiple sclerosis (MS), ulcerative colitis (UC), asthma, myocardial infarction (MI), and coronary artery disease (CAD)—and two traits, including height and body mass index (BMI). PRS-Net exhibited superior performance in predicting both diseases and traits compared with linear baseline methods, including PLINK C + T, PRSice-2, LDpred2, and lassosum2, as well as nonlinear models, including MLP and XGBoost (Chen and Guestrin 2016). Notably, we demonstrated the portability of PRS-Net across diverse ancestries. Through model interpretation, we further showcased the enhanced capacity of PRS-Net in pinpointing disease-relevant genes and gene programs. PRS-Net provides a potent framework for precise genetic risk prediction and systematic discovery of genetic and molecular underpinnings of complex traits and diseases.

    Previous SectionNext Section

    Results

    Overview of PRS-Net

    PRS-Net is a deep learning framework designed to enhance PRS prediction and gene discovery by modeling gene interactions using a GNN model (Methods). First, PRS-Net calculates gene-level PRSs based on GWAS summary statistics using a C + T method implemented by PLINK (Fig. 1A,B; Purcell et al. 2007; Vilhjálmsson et al. 2015). This method focuses on genetic variants within and near the gene body, encompassing both coding and noncoding genomic regions. By applying multiple P-value thresholds, several PRS values are generated for each gene, which then serves as features for corresponding genes. To characterize gene interactions in the biological system, PRS-Net incorporates a protein–protein interaction (PPI) network constructed from the STRING database (Fig. 1B; Szklarczyk et al. 2023). This network integration enables PRS-Net to capture high-order relationships between genotype and phenotype.

    Figure 1.
    View larger version:
    Figure 1.

    An illustrative diagram of PRS-Net. (A) The proposed framework is built upon GWAS summary statistics, including variants, risk alleles, P-values, and effect sizes. (B) A gene–gene interaction (GGI) network is constructed based on the protein–protein interactions (PPIs) in this study. Gene-level PRSs (various P-value thresholds applied) are calculated using the C + T method, serving as the node features within the network. (C) A graph neural network (GNN) is employed to update node features via message passing, and subsequently, an attentive readout module is introduced to facilitate model interpretation. (D) PRS-Net can be applied for both disease prediction and gene discovery. (GWAS) genome-wide association stuty, (C + T) clumping and thresholding.

    Next, gene-level PRSs and the PPI network are fed into a graph isomorphism network (GIN) (Fig. 1C; Xu et al. 2018), by which the gene features are updated iteratively by aggregating information from neighboring genes. Additionally, we adopt an attentive readout module to compute the global representation for each individual based on the attention mechanism, wherein the attention scores indicate gene importance to the phenotype of interest. This global representation is then used for making the final prediction. To address the challenge of cross-ancestry prediction, PRS-Net also incorporates a mixture-of-expert module (Masoudnia and Ebrahimpour 2014) with ancestry-specific attention modules.

    By integrating genetic data with biological network priors, PRS-Net offers as a powerful tool to the community with diverse downstream applications, ranging from disease prediction to biological discovery (Fig. 1D). In this study, the UKBB was used as the primary database for model training and testing (Methods). PRS-Net utilizes two cohorts: the base cohort analyzed in GWAS to estimate per-variant effect sizes and P-values (Fig. 1A), and the target cohort used to train and test PRS-Net. To prevent information leakage, we selected GWAS independent with UKBB for each disease and trait.

    PRS-Net improves disease risk prediction

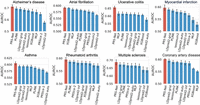
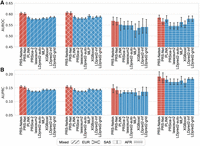
    We first benchmarked PRS-Net against multiple existing PRS methods in disease risk prediction (Methods) (Supplemental Table S1). Here, only UKBB Western European (EUR) samples were included in the analysis. Both metrics including the area under the receiver operating characteristic (AUROC) and the area under the precision-recall curve (AUPRC) were adopted for performance evaluation. Our results revealed that PRS-Net consistently outperformed all baseline methods, including nonlinear methods for all diseases, yielding relative improvements ranging from 0.7% to 6.9% in AUROC (Fig. 2) and 1.3% to 18.3% in AUPRC (Supplemental Fig. S1). Importantly, tests on two autoimmune diseases achieved the largest improvements, including UC (6.9% in AUROC and 18.3% in AUPRC) and MS (2.2% in AUROC and 8.4% in AUPRC), reinforcing the observed nonadditivity of genomic factors underlying these diseases (Lipsitch et al. 2003; Tsai and Santamaria 2013; Goyette et al. 2015; Lenz et al. 2015).We also compared PRS-Net with the best linear unbiased prediction (BLUP) using BOLT-LMM-inf (Loh et al. 2015) to generate the BLUP estimates, confirming the superiority of PRS-Net (Supplemental Fig. S2).

    Figure 2.
    View larger version:
    Figure 2.

    Prediction performance evaluation based on the area under the receiver operating characteristic curve (AUROC) for different diseases (41,175 test samples in total). The bar plot and error bar denote the mean and standard error, respectively. The training, validation, and testing procedure was conducted for six repeats with different random seeds for each model and each disease.

    To understand the suboptimal performance yielded by nonlinear baseline models, we developed two alternative versions of MLP and XGBoost, referred to as MLP_less_snp and XGBoost_less_snp, which only utilized GWAS variants included in PRS-Net (Supplemental Methods). We observed MLP_less_snp and XGBoost_less_snp displayed a performance comparable or even superior to that of the original MLP and XGBoost models (Supplemental Fig. S3). This suggests that existing nonlinear approaches may fail to effectively learn disease-variant associations.

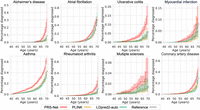
    We next utilized the Aalen–Johansen estimator (Aalen and Johansen 1978) to calculate the disease occurrence over the lifetime for individuals stratified into high-risk or low-risk groups, as determined by different PRS methods. High-risk individuals were defined as those with the highest 5% of PRSs, whereas low-risk individuals were identified as those with the lowest 5% of PRSs. High-risk individuals defined by PRS-Net exhibited an elevated risk of disease throughout their lifetime compared with those predicted by baseline methods, especially for UC, asthma, RA, and MS (Fig. 3). Meanwhile, low-risk individuals categorized by PRS-Net tended to maintain a lower risk of disease (Supplemental Fig. S4). These results underscore the potential of PRS-Net as an effective tool for disease risk stratification.

    Figure 3.
    View larger version:
    Figure 3.

    The cumulative incidence plots of high-risk individuals (with the highest 5% PRSs) identified by PRS-Net and baseline methods. Each plot illustrates the estimated percentage of individuals diagnosed with a specific disease at different ages. We provide cumulative incidence plots for the original data sets as references. The shaded area denotes the standard error estimated based on six repeats.

    PRS-Net enhances quantitative trait prediction

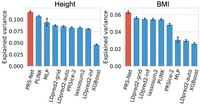
    We further applied PRS-Net on two quantitative traits, including height and BMI. Similarly, we focused on UKBB EUR samples in the analysis. Explained variance and R2 were used for performance evaluation (Methods). Again, PRS-Net exhibited superior prediction performance compared with all baseline methods for both traits (Fig. 4; Supplemental Fig. S5), with relative improvements of 8.50% and 11.64% for height and BMI in terms of explained variance, respectively. This highlights the generalizability of PRS-Net in predicting diverse phenotypes.

    Figure 4.
    View larger version:
    Figure 4.

    Prediction performance evaluation for quantitative traits (41,028 and 40,411 test samples for height and body mass index [BMI], respectively). Performance was measured in explained variance. The bar plot and error bar denote the mean and standard error, respectively. The training, validation, and testing procedure was conducted for six repeats with different random seeds for each model and each trait.

    PRS-Net boosts cross-ancestry prediction

    Next, we assessed the performance of PRS-Net and our multiple-ancestry model, PRS-NetMA, on the data set comprising individuals from diverse ancestral backgrounds. Specifically, we curated a mixed-ancestry UKBB data set encompassing EUR, South Asian (SAS), and African (AFR) for asthma, which contained a reasonable number of asthma cases (N > 1000) for each ancestry group (Supplemental Table S2). PRS-Net, trained solely on EUR samples, still outperformed baseline methods on the mixed and SAS test sets, suggesting that PRS-Net captured disease biology independently of ancestral backgrounds (Fig. 5). PRS-NetMA further improved cross-ancestry prediction and yielded a superior or comparable performance compared with PRS-Net on these ancestry-specific test sets (Fig. 5). These results demonstrate the portability of PRS-Net and PRS-NetMA across diverse ancestral groups in genetic risk prediction.

    Figure 5.
    View larger version:
    Figure 5.

    Prediction performance evaluation for asthma across multiple populations, including Western European (EUR), South Asian (SAS), and African (AFR) ancestries, measured by the area under receiver operating characteristic curve (AUROC; A) and the area under precision-recall curve (AUPRC; B), respectively. The results on the mixed ancestry test set were also reported. The bar plot and error bar denote the mean and standard error, respectively. The training, validation, and testing procedure was conducted for six repeats.

    PRS-Net identifies disease-relevant genes and GGIs

    Following the demonstration on the superiority of PRS-Net in disease prediction, we sought to examine its capability in gene discovery. Specifically, we applied the Mann–Whitney U test (Mann and Whitney 1947) to each gene assessing whether its attention scores for disease cases were significantly higher than those of healthy controls. For AD, this analysis yielded a gene set comprising 142 significant genes (adjusted P < 0.05, Bonferroni correction) (Supplemental Table S3). Gene set enrichment analysis (GSEA) (Subramanian et al. 2005) presented the enrichment of lipoprotein particles for PRS-Net-prioritized genes (Supplemental Fig. S6). This observation is in line with prior studies implicating lipoprotein particles as a risk factor of AD (Safieh et al. 2019; Zhou et al. 2020; Jin et al. 2021), with therapeutic potentials (Safieh et al. 2019; Jin et al. 2021).

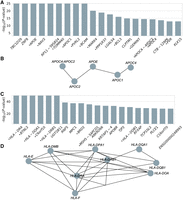
    From the results, 15 out of the top 20 genes (ranked by P-values) (Fig. 6A) have been identified as AD risk factors in previous studies. One notable example is APOE, which is the most prevalent high-density lipoprotein in the central nervous system (CNS) and has been consistently linked to AD in the literature (Tsai et al. 1994; Strittmatter and Roses 1995; Meyer et al. 1998; Green et al. 2009; Genin et al. 2011; Yamazaki et al. 2019). Other well-recognized AD genes interacting with APOE, including APOC1, APOC2, and APOC4, were also prioritized by PRS-Net (Fig. 6B).

    Figure 6.
    View larger version:
    Figure 6.

    PRS-Net identifies disease-relevant genes and gene modules for Alzheimer's disease and multiple sclerosis. (A) Top 20 genes ranked by P-values for Alzheimer's disease. P-value by the Mann–Whitney U test. An asterisk preceding the gene name signifies this gene has been reported to be associated with Alzheimer's disease in previous studies. (B) An example of PPIs among PRS-Net-identified genes for Alzheimer's disease. (C) Top 20 genes ranked by P-values for multiple sclerosis. (D) An example of PPIs among PRS-Net-identified genes for multiple sclerosis.

    For MS, our analysis identified 154 significant risk genes (adjusted P < 0.05, Bonferroni correction) (Supplemental Table S4). GSEA of PRS-Net-identified genes highlighted numerous immune-related pathways and the major histocompatibility complex (MHC) protein complex (Supplemental Fig. S7), agreeing well with the literature (Traugott 1987; Lee et al. 1990; Multiple Sclerosis Genetics Group et al. 1998; Dyment et al. 2005; Lincoln et al. 2005). A considerable number of HLA genes were prioritized by PRS-Net (Fig. 6C,D), reinforcing previous studies indicating that HLA interactions modulate the genetic risk of MS (The International Multiple Sclerosis Genetics Consortium 2015). Additionally, nonadditive interactions between HLAs have been widely reported to significantly affect the risk of autoimmune diseases (Lipsitch et al. 2003; Tsai and Santamaria 2013; Goyette et al. 2015; Lenz et al. 2015).

    To examine the contribution of GGIs in gene discovery, we trained a PRS-Net variation without the GGI network, denoted as PRS-Net-noPPI, and then applied it to identify disease genes using the same strategy. PRS-Net-noPPI identified a much smaller number of genes (N = 3 for AD and N = 1 for MS) (Supplemental Fig. S8) compared with PRS-Net. This supports the importance of GGIs in increasing the power of discovering disease genes.

    Ablation studies

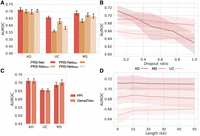
    To examine the contribution of different components in PRS-Net, we conducted extensive ablation studies. We first introduced multiple variations of PRS-Net, including PRS-NetSum, PRS-NetMean, and PRS-NetMax, replacing the attentive readout module with summation, averaging, and maximization operations, respectively. PRS-Net outperformed PRS-NetSum, PRS-NetMean, and PRS-NetMax (Fig. 7A; Supplemental Fig. S9A), with average relative improvements of 3.0%, 9.4%, and 5.7% in AUROC, respectively. This highlights the critical role of the attention module in boosting prediction performance.

    Figure 7.
    View larger version:
    Figure 7.

    The ablation results for PRS-Net. (A) The performance comparison between PRS-Net and its multiple variations. The bar plot and error bar denote the mean and standard error, respectively. (B) The performance of PRS-Net with PPI dropout. The line plot and shaded area denote the mean and standard error, respectively. (C) Comparison results of PRS-Net with different GGI networks. (D) The prediction performance of PRS-Net with different extension lengths. (AD) Alzheimer’s disease, (MS) multiple sclerosis, (UC) ulcerative colitis, (AUROC) the area under the receiver operating characteristic curve, (PPI) protein–protein interaction.

    Next, we assessed the impact of the GGI network on prediction. We tested it by randomly dropped PPIs with different ratios. As shown in Figure 7B and Supplemental Figure S9B, we observed a continuous decrease in prediction performance as the dropout ratio increased across different diseases, validating the contribution of GGIs in disease prediction. We also examined the impact of different PPI filtering thresholds on the prediction performance. PRS-Net yielded a comparable performance when we increased the threshold to 0.9 (Supplemental Fig. S10A); however, lowering the threshold below 0.8 resulted in a significant drop in performance. We further randomized the PPI network and, as expected, noticed a substantial performance decrease (Supplemental Fig. S10B). These results together highlight the contribution of a well-defined PPI network on the robustness and effectiveness of PRS-Net.

    Subsequently, we evaluated the performance of PRS-Net with different GGI networks. Specifically, we employed gene representations generated by Gene2vec (Du et al. 2019). This machine learning approach leverages gene coexpression information extracted from 984 NCBI Gene Expression Omnibus (GEO; https://www.ncbi.nlm.nih.gov/geo/) (Barrett et al. 2012) data sets to infer gene embeddings capturing the functional similarity between genes. We constructed a k-nearest neighbors graph based on the cosine similarity between gene embeddings as an alternative GGI network. We set k = 15 to match the number of interactions in our original PPI setting. We found that PRS-Net equipped with either GGI networks exhibited comparable prediction performance (Fig. 7C; Supplemental Fig. S9C), highlighting the robustness of PRS-Net against different GGI networks.

    In our model design, we extended gene bodies to incorporate genetic variants upstream of and downstream from individual genes. In addition to coding regions, these extended gene bodies (>20 kb) also covered noncoding regulatory regions, such as promoters and enhancers, which control the expression levels of target genes. We further explored the impact of different extension lengths (i.e., 0 kb, 5 kb, 10 kb, 20 kb, and 50 kb) on prediction. In general, PRS-Net displayed stable performance across different extension lengths (Fig. 7D; Supplemental Fig. S9D). It is noteworthy that the performance on MS was significantly reduced when no extension was employed (Fig. 7D), implicating the benefit of incorporating regulatory variants in genetic risk prediction for certain diseases.

    We further investigated how the gene extension length, in conjunction with R2 and clumping window size, impacts the model performance. In particular, we evaluated different combinations of R2 = 0.1 or 0.5, L = 0 kb or 10 kb, and window size = 25 kb or 250 kb, resulting in eight combinations in total. As shown in Supplemental Figure S11, the model performance was generally improved with a larger window size or gene extension length, whereas different values of R2 appeared to have a marginal effect on performance.

    To assess the impact of nonlinearity introduced by the MLP, we conducted a comparison between PRS-Net with a linear predictor (PRS-Net-Linear) and with an MLP predictor (PRS-Net-MLP). As shown in Supplemental Figure S12, both models achieved comparable results across different diseases, implicating that although MLP introduced additional nonlinearity, it was not necessary for boosting the performance in general. This further highlights the importance of the GNN module in enhancing the overall genetic prediction.

    Previous SectionNext Section

    Discussion

    In this study, we developed PRS-Net, a geometric deep learning–based framework that achieves in tandem disease prediction and biological discovery. By explicitly modeling GGIs using a GNN, PRS-Net enables the characterization of nonlinear relationships between genotype and phenotype. The integration of an attention module further improves model interpretability. Extensive tests on eight diseases and two quantitative traits demonstrate the superiority of PRS-Net over multiple baseline PRS methods in disease prediction and gene discovery.

    A standard clumping and thresholding (C + T) PRS integrates not only genome-wide significant (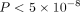Formula) variants but also marginal (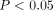Formula) or even nonsignificant (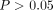Formula) ones to enhance the prediction performance (Choi et al. 2020). The P-value threshold, along with LD R2 threshold, determines the set of variants we want to include in a PRS model, as well as the best threshold varies for different diseases and traits. The design principle of PRS-Net is to decompose the genome-wide PRS into single-gene resolution to measure the contribution of each gene to the disease risk. This is achieved by calculating C + T PRS per gene and then integrating gene-level PRS features leveraging a GGI network. Because the best threshold is unknown in advance, here we chose to compute gene-level PRSs with multiple thresholds as the input node features and then integrated them using an embedding layer. This unbiased strategy enables us to assess the cumulative genetic contribution across various levels of statistical significance, capturing a broader spectrum of genetic information beyond top associations identified by GWAS. Although we have not experimented with other ways of initializing node features, we acknowledge the potential for further exploration in this aspect. We employed PLINK C + T, a most widely used method, to calculate gene-level PRSs in our implementation, but we recognize the possibilities of using alternative approaches, such as PRSice2, or even combinations of these approaches for gene-level PRS computation.

    One of the key motivations of our work is to empower biological discovery via model interpretation, which is lacking in traditional GWAS and PRS. By mapping a wide range of variants to their nearby genes, which has been demonstrated effective in nominating disease genes (Fulco et al. 2019; Nasser et al. 2021), we calculated gene-level PRS and then conducted GNN operations at the gene level. This layer-wise strategy achieves biology-informed disease prediction (Elmarakeby et al. 2021; Zhang et al. 2024), enabling a systematic investigation of the underlying disease biology. Of note, the flexibility of our framework also allows for the incorporation of distal intergenic variants (i.e., extending gene bodies to their linked distal regulatory regions) as long as their target genes are well defined. However, we leave this to the future work given the current challenges in linking distal variants to genes (Schnitzler et al. 2024).

    In the message passing phase of GNN, each node aggregates information from its neighboring nodes. In our context, each gene within the GGI network collects the genetic information from neighboring genes and refines its own features through this message passing process. This effect is desirable in our scenario because genes and proteins are not working in isolation but collaboratively to regulate various biological processes. The function of a gene may be compromised if the genes it interacts with experience a loss of function. This is exemplified by cases in which disease genes converge on particular gene modules or pathways (Berg and Geschwind 2012; Walker et al. 2023). Therefore, the propagation of PRS signals over GGIs facilitates the capture of inherent interdependencies among genes, contributing to a system understanding of disease etiology and enhanced risk prediction.

    In our tests, we specifically opt for the GIN (Xu et al. 2018) owing to its proven theoretical and empirical expressiveness. From a theoretical perspective, the seminal GIN paper established a theoretical framework by connecting GNNs with the Weisfeiler–Lehman (WL) graph isomorphism test. The WL test iteratively updates node feature vectors by aggregating neighbor features, providing a powerful tool for distinguishing between different graph structures. This theoretical analysis demonstrates GIN's outstanding expressiveness and supports our choice of GIN for its ability in effectively capturing complex interactions among elements. From an empirical perspective, GIN has demonstrated its efficacy across various applications, including but not limited to molecular representation learning (Wang et al. 2022), compound–protein interaction prediction (Lin et al. 2022), and spatial cellular modeling (Wu et al. 2022). The consistent superior performance shown in these studies underscores GIN's capability in modeling diverse graph-structured biological data.

    We reviewed several studies that reported the variance explained by polygenic models for height and BMI in the UKBB. Specifically, the variance explained is 1.5%, 1.6%, or 4.1% for BMI (Tyrrell et al. 2016; Sun et al. 2019; Vithayathil et al. 2021) and 5.5% or 12.3% for height (Tyrrell et al. 2016; Vithayathil et al. 2021), based on different studies. These data are consistent with our results. The performance of PRS models is considerably influenced by the discovery GWAS. In our tests, we utilized data from the GIANT consortium, a widely used standard database for height and BMI; however, it is important to note that the discrepancies between height GWAS from GIANT and from UKBB have been reported (Sohail et al. 2019), which could have contributed to the lower performance than expected. In addition, our initial analyses did not incorporate covariates such as age, sex, and principal components (PCs) into PRS modeling. When we included these covariates into the PRS-Net and baseline methods, we noticed a significant improvement across all methods (Supplemental Fig. S13).

    To examine the capacity of PRS-Net in modeling nonlinearity between genotype and phenotype, we performed a simulation study. We first designed a simulation approach allowing us to simulate phenotypes that exhibit nonlinear relationships with genetic features. In detail, we utilized a PRS-Net model with fixed weights (randomly initialized) to generate quantitative traits for individuals, using gene-level features derived from the height GWAS summary statistics as input. Because PRS-Net inherently models protein–protein interactions, the simulated traits reflect a nonlinear function of the input genetic features. We then trained PRS-Net based on this simulation data set and compared it with linear regression mimicking traditional PRS. As shown in Supplemental Figure S14A, PRS-Net significantly outperformed the linear model in phenotype prediction, demonstrating its effectiveness in modeling nonlinear G2P. As a negative control, we also generated traits from genotypes using a linear model. Specifically, we used effect sizes (i.e., β’s) derived from the height GWAS to compute a weighted sum of individuals’ genotypes, yielding their simulated traits. PRS-Net presented comparable prediction performance with linear regression (Supplemental Fig. S14B). Altogether, our results demonstrate PRS-Net is well behaved in enhancing PRS prediction by capturing nonlinear gene interactions, showing no significant false-positive effect.

    In summary, PRS-Net represents a novel biology-informed PRS framework, providing a potent tool for accurate genetic prediction and systematic biological discovery for complex traits and diseases.

    Previous SectionNext Section

    Methods

    Gene-level PRSs

    We first compute gene-level PRSs using the PLINK C + T method (Fig. 1B; Purcell et al. 2007; Vilhjálmsson et al. 2015). In particular, for each gene we focus on the variants residing within the extended gene body spanning from L bp upstream of its transcription start site (TSS) to L bp downstream from the transcription end site. In our study, we set L = 10,000, thereby encompassing variants located within noncoding regulatory regions, such as promoters and enhancers. The linkage disequilibrium (LD) estimated based on the 1000 Genomes European samples (The 1000 Genomes Project Consortium 2015) is adopted to perform clumping and remove correlated variants, wherein we set R2 = 0.5 and window size = 250 kb. Given a specific P-value threshold, the gene-level PRSs utilizing all variants with GWAS P-values below this threshold are computed across all genes for each individual in the target cohort. In this study, we set multiple P-value thresholds including 1 × 10−5, 1 × 10−4, 1 × 10−3, 1 × 10−2, 5 × 10−2, 0.1, 0.2, 0.3, 0.4, 0.5, and one, yielding 11 PRSs for each gene.

    GGI network

    We establish a GGI network that empowers PRS-Net to capture molecular interactions underlying the target phenotype (Fig. 1B). We construct our GGI network based on the high-confidence PPIs (with a confidence score > 0.8) derived from the STRING database (Szklarczyk et al. 2023). Formally, the GGI network is denoted as 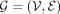Formula, where V stands for the set of nodes, and E represents the set of edges. Each node 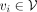Formula is a protein-coding gene and each edge 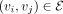Formula stands for an interaction between genes vi and vj with a STRING score greater than 0.8. Note that we add a self-loop (vi, vi) to each node 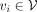Formula in the network. Finally, we obtain a GGI network encompassing 19,836 genes and 250,236 interactions.

    PRS-Net

    Graph neural network

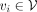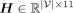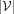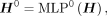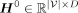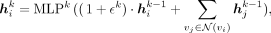    We utilize a GNN to integrate gene-level PRSs leveraging GGIs (Fig. 1C). In this study, we specifically opt for a GIN (Xu et al. 2018) owing to its demonstrated theoretical and empirical expressiveness. In particular, given input PRS features hi ∈ H for Formula, where Formula and Formula is the number of genes in G, we first perform feature embedding: Formula (1) where Formula and D is the dimension of hidden features. 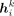Next, we apply multiple GIN layers to iteratively update the features of each node by aggregating neighboring information, as depicted below: Formula (2) where Formula is the hidden feature of vi at the kth layer, 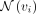Formula stands for the neighbors of vi in the GGI network, MLPk is the MLP at the kth layer, and ϵ is a learnable variable. After K steps of messaging passing, each gene effectively encapsulates the PRS information within its K-hop neighborhood.

    Attentive readout module

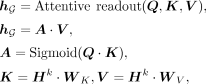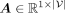    Following the GNN operation, we compute a global representation for each sample using an attentive readout module shown as follows: Formula (3) where WK ∈ ℝD×D and WV ∈ ℝD×D are trainable key (i.e., K) and value (i.e., V) matrices, respectively; Q ∈ ℝ1×D is the trainable query vector; Formula are the attention scores; and 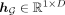Formula is the global representation. Note that a higher attention score indicates a greater disease-relevance of the corresponding gene.

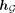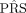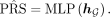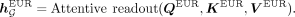    With the global representation Formula, we next employ an MLP to make the final prediction denoted as Formula: Formula (4) Additionally, we implement a mixture-of-expert module (Masoudnia and Ebrahimpour 2014) to handle cross-ancestry prediction. In particular, we introduce a separate attentive readout module for each ancestry (referred to as ancestry-specific attention module), and it is activated only if the input sample is with a matching ancestral origin. 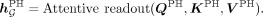For instance, when dealing with individuals of EUR ancestry, we calculate the ancestry-specific global representation as follows: Formula (5) The ancestry-specific readout module is designed to capture ancestry-specific disease associations. 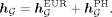We also introduce a shared readout module to learn general genetic patterns independent with ancestries: Formula (6) The final global representation is given by combining the aforementioned two representations: Formula (7) We refer to the single-ancestry model as PRS-Net and the multiancestry variation as PRS-NetMA.

    Model evaluation

    We constructed target cohorts for eight diseases, including AD, AF, RA, MS, UC, asthma, MI, and CAD, and two quantitative traits, including height and BMI, based on the UKBB database (Sudlow et al. 2015). The ICD-10 codes (World Health Organization et al. 1992) were utilized to define disease phenotypes (Supplemental Table S1). Quantitative traits (height: Data Field 12144; BMI: Data Field 21002) were averaged for individuals across multiple instances.

    In our experiments, we mainly focused on EUR individuals owing to the insufficient sample size of non-Europeans for certain diseases (Supplemental Table S2). After stringent quality controls (QCs) following the best practice (Supplemental Methods; Choi et al. 2020), each disease data set (target cohort) consisted of about 390,000 individuals. To prevent information leakage, we carefully chose GWAS not including UKBB samples in gene-level PRS calculation. GWAS summary statistics for diseases and traits are available from their original publications (Wood et al. 2014; Locke et al. 2015; The CARDIoGRAMplusC4D Consortium 2015; Christophersen et al. 2017; De Lange et al. 2017; International Multiple Sclerosis Genetics Consortium et al. 2019; Wightman et al. 2021; Ishigaki et al. 2022; Zhou et al. 2022).

    For each target cohort, we randomly partitioned it into training, validation, and test sets with a ratio of 8:1:1. The validation data set was used for early stopping, and the final performance was evaluated on the test data set. More PRS-Net training details can be found in Supplemental Methods.

    Following the best practice (Choi et al. 2020), we also implemented four traditional linear PRS models, including two C + T-based methods (PLINK [Purcell et al. 2007] and PRSice2 [Choi and O'Reilly 2019]), lassosum2 (Privé et al. 2022), and LDpred2 (LDpred2-auto, LDpred2-grid, and LDpred2-inf) (Privé et al. 2021), as well as two nonlinear models, including MLP and XGBoost, as our baseline methods. More implementation details can be found in Supplemental Methods. LD estimation used in baselines was the same as that adopted in PRS-Net.

    We adopted two metrics, AUROC and AUPRC, to measure the performance for disease classification and explained variance and R2 for quantitative trait regression. Performance of all methods was estimated based on six independent runs with different random seeds for both data partitioning and model initialization.

    Software availability

    The source code and the tutorial of PRS-Net are available at GitHub (https://github.com/lihan97/PRS-Net) and as Supplemental Code.

    Previous SectionNext Section

    Competing interest statement

    M.P.S. is a cofounder and the scientific advisory board member of Personalis, SensOmics, Qbio, January AI, Fodsel, Filtricine, Protos, RTHM, Iollo, Marble Therapeutics, Crosshair Therapeutics, NextThought, and Mirvie. He is a scientific advisor of Jupiter, Neuvivo, Swaza, Mitrix, Yuvan, TranscribeGlass, and Applied Cognition. The remaining authors declare no competing interests.

    Previous SectionNext Section

    Acknowledgments

    This work was supported by the National Natural Science Foundation of China (T2125007 to J.Z.), the National Key Research and Development Program of China (2021YFF1201300 to J.Z.), the New Cornerstone Science Foundation through the XPLORER PRIZE (J.Z.), the Research Center for Industries of the Future (RCIF) at Westlake University (J.Z.), and the Westlake Education Foundation (J.Z.). This research was conducted using the UK Biobank Resource under application number 41751; we thank all UK Biobank participants for sharing their data.

    Author contributions: S.Z. and H.L. conceived the concept and designed the study. H.L. and S.Z. developed the methodology and conducted data analysis. H.L., S.Z., M.P.S., and J.Z. are responsible for the data interpretation. S.Z., M.P.S., and J.Z. supervised the project. H.L. and S.Z. prepared the manuscript with the assistance from all other authors.

    Previous SectionNext Section

    Footnotes

    • [Supplemental material is available for this article.]

    • Article published online before print. Article, supplemental material, and publication date are at https://www.genome.org/cgi/doi/10.1101/gr.279694.124.

    • Freely available online through the Genome Research Open Access option.

    • Received June 14, 2024.
    • Accepted November 14, 2024.

    This article, published in Genome Research, is available under a Creative Commons License (Attribution 4.0 International), as described at http://creativecommons.org/licenses/by/4.0/.

    Previous Section
     

    References

    1. ↵
      The 1000 Genomes Project Consortium. 2015. A global reference for human genetic variation. Nature 526: 68–74. doi:10.1038/nature15393
      CrossRefMedlineGoogle Scholar
    2. ↵
      Aalen OO, Johansen S. 1978. An empirical transition matrix for non-homogeneous Markov chains based on censored observations. Scand J Statist 5: 141–150.
      Google Scholar
    3. ↵
      Alzoubi H, Alzubi R, Ramzan N. 2023. Deep learning framework for complex disease risk prediction using genomic variations. Sensors 23: 4439. doi:10.3390/s23094439
      CrossRefMedlineGoogle Scholar
    4. ↵
      Barrett T, Wilhite SE, Ledoux P, Evangelista C, Kim IF, Tomashevsky M, Marshall KA, Phillippy KH, Sherman PM, Holko M, et al. 2012. NCBI GEO: archive for functional genomics data sets—update. Nucleic Acids Res 41: D991–D995. doi:10.1093/nar/gks1193
      CrossRefMedlineGoogle Scholar
    5. ↵
      Bellot P, de Los Campos G, Pérez-Enciso M. 2018. Can deep learning improve genomic prediction of complex human traits? Genetics 210: 809–819. doi:10.1534/genetics.118.301298
      Abstract/FREE Full Text
    6. ↵
      Berg JM, Geschwind DH. 2012. Autism genetics: searching for specificity and convergence. Genome Biol 13: 247. doi:10.1186/gb4034
      CrossRefMedlineGoogle Scholar
    7. ↵
      Breiman L. 2001. Random forests. Mach Learn 45: 5–32. doi:10.1023/A:1010933404324
      CrossRefGoogle Scholar
    8. ↵
      The CARDIoGRAMplusC4D Consortium. 2015. A comprehensive 1000 Genomes–based genome-wide association meta-analysis of coronary artery disease. Nat Genet 47: 1121–1130. doi:10.1038/ng.3396
      CrossRefMedlineGoogle Scholar
    9. ↵
      Chen T, Guestrin C. 2016. XGBoost: a scalable tree boosting system. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, pp. 785–794. ACM, San Francisco. doi:10.1145/2939672.293978
      Google Scholar
    10. ↵
      Cheverud JM, Routman EJ. 1995. Epistasis and its contribution to genetic variance components. Genetics 139: 1455–1461. doi:10.1093/genetics/139.3.1455
      Abstract/FREE Full Text
    11. ↵
      Choi SW, O'Reilly PF. 2019. Prsice-2: polygenic risk score software for biobank-scale data. GigaScience 8: giz082. doi:10.1093/gigascience/giz082
      CrossRefMedlineGoogle Scholar
    12. ↵
      Choi SW, Mak TS-H, O'Reilly PF. 2020. Tutorial: a guide to performing polygenic risk score analyses. Nat Protoc 15: 2759–2772. doi:10.1038/s41596-020-0353-1
      CrossRefMedlineGoogle Scholar
    13. ↵
      Christophersen IE, Rienstra M, Roselli C, Yin X, Geelhoed B, Barnard J, Lin H, Arking DE, Smith AV, Albert CM, et al. 2017. Large-scale analyses of common and rare variants identify 12 new loci associated with atrial fibrillation. Nat Genet 49: 946–952. doi:10.1038/ng.3843
      CrossRefMedlineGoogle Scholar
    14. ↵
      CKDGen Consortium, KidneyGen ConsortiumEchoGen consortium CHARGE-HF consortium, Aspelund T, Garcia M, Chang Y-PC, O'Connell JR, Steinle NI, Grobbee DE. 2011. Genetic variants in novel pathways influence blood pressure and cardiovascular disease risk. Nature 478: 103–109. doi:10.1038/nature10405
      CrossRefMedlineGoogle Scholar
    15. ↵
      Clarke R, Peden JF, Hopewell JC, Kyriakou T, Goel A, Heath SC, Parish S, Barlera S, Franzosi MG, Rust S, et al. 2009. Genetic variants associated with Lp(a) lipoprotein level and coronary disease. N Engl J Med 361: 2518–2528. doi:10.1056/NEJMoa0902604
      CrossRefMedlineGoogle Scholar
    16. ↵
      Cordell HJ. 2009. Detecting gene–gene interactions that underlie human diseases. Nat Rev Genet 10: 392–404. doi:10.1038/nrg2579
      CrossRefMedlineGoogle Scholar
    17. ↵
      De Lange KM, Moutsianas L, Lee JC, Lamb CA, Luo Y, Kennedy NA, Jostins L, Rice DL, Gutierrez-Achury J, Ji S-G, et al. 2017. Genome-wide association study implicates immune activation of multiple integrin genes in inflammatory bowel disease. Nat Genet 49: 256–261. doi:10.1038/ng.3760
      CrossRefGoogle Scholar
    18. ↵
      Du J, Jia P, Dai Y, Tao C, Zhao Z, Zhi D. 2019. Gene2vec: distributed representation of genes based on co-expression. BMC Genomics 20: 82. doi:10.1186/s12864-018-5370-x
      CrossRefMedlineGoogle Scholar
    19. ↵
      Dyment DA, Herrera BM, Zameel Cader M, Willer CJ, Lincoln MR, Dessa Sadovnick A, Risch N, Ebers GC. 2005. Complex interactions among MHC haplotypes in multiple sclerosis: susceptibility and resistance. Hum Mol Genet 14: 2019–2026. doi:10.1093/hmg/ddi206
      CrossRefMedlineGoogle Scholar
    20. ↵
      Elmarakeby HA, Hwang J, Arafeh R, Crowdis J, Gang S, Liu D, AlDubayan SH, Salari K, Kregel S, Richter C, et al. 2021. Biologically informed deep neural network for prostate cancer discovery. Nature 598: 348–352. doi:10.1038/s41586-021-03922-4
      CrossRefMedlineGoogle Scholar
    21. ↵
      Euesden J, Lewis CM, O'Reilly PF. 2015. PRSice: Polygenic Risk Score software. Bioinformatics 31: 1466–1468. doi:10.1093/bioinformatics/btu848
      CrossRefMedlineGoogle Scholar
    22. ↵
      Freund Y, Schapire RE. 1997. A decision-theoretic generalization of on-line learning and an application to boosting. J Comput Syst Sci 55: 119–139. doi:10.1006/jcss.1997.1504
      CrossRefGoogle Scholar
    23. ↵
      Friedman JH. 2001. Greedy function approximation: a gradient boosting machine. Ann Stat 29: 1189–1232. doi:10.1214/aos/1013203451
      CrossRefMedlineGoogle Scholar
    24. ↵
      Friedman JH. 2002. Stochastic gradient boosting. Comput Stat Data Anal 38: 367–378. doi:10.1016/S0167-9473(01)00065-2
      CrossRefGoogle Scholar
    25. ↵
      Fulco CP, Nasser J, Jones TR, Munson G, Bergman DT, Subramanian V, Grossman SR, Anyoha R, Doughty BR, Patwardhan TA, et al. 2019. Activity-by-contact model of enhancer–promoter regulation from thousands of crispr perturbations. Nat Genet 51: 1664–1669. doi:10.1038/s41588-019-0538-0
      CrossRefMedlineGoogle Scholar
    26. ↵
      Gaiteri C, Mostafavi S, Honey CJ, De Jager PL, Bennett DA. 2016. Genetic variants in Alzheimer disease—molecular and brain network approaches. Nat Rev Neurol 12: 413–427. doi:10.1038/nrneurol.2016.84
      CrossRefMedlineGoogle Scholar
    27. ↵
      Genin E, Hannequin D, Wallon D, Sleegers K, Hiltunen M, Combarros O, Bullido MJ, Engelborghs S, De Deyn P, Berr C, et al. 2011. APOE and Alzheimer disease: a major gene with semi-dominant inheritance. Mol Psychiatry 16: 903–907. doi:10.1038/mp.2011.52
      CrossRefMedlineGoogle Scholar
    28. ↵
      Gibson G. 2019. On the utilization of polygenic risk scores for therapeutic targeting. PLoS Genet 15: e1008060. doi:10.1371/journal.pgen.1008060
      CrossRefMedlineGoogle Scholar
    29. ↵
      Goyette P, Boucher G, Mallon D, Ellinghaus E, Jostins L, Huang H, Ripke S, Gusareva ES, Annese V, Hauser SL, et al. 2015. High-density mapping of the MHC identifies a shared role for HLA-DRB1*01:03 in inflammatory bowel diseases and heterozygous advantage in ulcerative colitis. Nat Genet 47: 172–179. doi:10.1038/ng.3176
      CrossRefMedlineGoogle Scholar
    30. ↵
      Green RC, Scott Roberts J, Adrienne Cupples L, Relkin NR, Whitehouse PJ, Brown T, Eckert SL, Butson M, Dessa Sadovnick A, Quaid KA, et al. 2009. Disclosure of APOE genotype for risk of Alzheimer's disease. N Engl J Med 361: 245–254. doi:10.1056/NEJMoa0809578
      CrossRefMedlineGoogle Scholar
    31. ↵
      Guindo-Martínez M, Amela R, Bonàs-Guarch S, Puiggròs M, Salvoro C, Miguel-Escalada I, Carey CE, Cole JB, Rüeger S, Atkinson E, et al. 2021. The impact of non-additive genetic associations on age-related complex diseases. Nat Commun 12: 2436. doi:10.1038/s41467-021-21952-4
      CrossRefMedlineGoogle Scholar
    32. ↵
      Hastie T, Rosset S, Zhu J, Zou H. 2009. Multi-class adaboost. Stat Interface 2: 349–360. doi:10.4310/SII.2009.v2.n3.a8
      CrossRefGoogle Scholar
    33. ↵
      Ho TK. 1995. Random decision forests. In Proceedings of Third International Conference on Document Analysis and Recognition, Vol. 1, pp 278–282. IEEE, Montreal, QC, Canada.
      Google Scholar
    34. ↵
      The International Multiple Sclerosis Genetics Consortium. 2015. Class II HLA interactions modulate genetic risk for multiple sclerosis. Nat Genet 47: 1107–1113. doi:10.1038/ng.3395
      CrossRefMedlineGoogle Scholar
    35. ↵
      International Multiple Sclerosis Genetics Consortium, ANZgene, IIBDGC, WTCCC2. 2019. Multiple sclerosis genomic map implicates peripheral immune cells and microglia in susceptibility. Science 365: eaav7188. doi:10.1126/science.aav7188
      Abstract/FREE Full Text
    36. ↵
      Ishigaki K, Sakaue S, Terao C, Luo Y, Sonehara K, Yamaguchi K, Amariuta T, Too CL, Laufer VA, Scott IC, et al. 2022. Multi-ancestry genome-wide association analyses identify novel genetic mechanisms in rheumatoid arthritis. Nat Genet 54: 1640–1651. doi:10.1038/s41588-022-01213-w
      CrossRefMedlineGoogle Scholar
    37. ↵
      Jin Y, Chifodya K, Han G, Jiang W, Chen Y, Shi Y, Xu Q, Xi Y, Wang J, Zhou J, et al. 2021. High-density lipoprotein in Alzheimer's disease: from potential biomarkers to therapeutics. J Control Release 338: 56–70. doi:10.1016/j.jconrel.2021.08.018
      CrossRefMedlineGoogle Scholar
    38. ↵
      Konuma T, Okada Y. 2021. Statistical genetics and polygenic risk score for precision medicine. Inflamm Regen 41: 18. doi:10.1186/s41232-021-00172-9
      CrossRefMedlineGoogle Scholar
    39. ↵
      Korte A, Farlow A. 2013. The advantages and limitations of trait analysis with GWAS: a review. Plant Methods 9: 29. doi:10.1186/1746-4811-9-29
      CrossRefMedlineGoogle Scholar
    40. ↵
      Lee SC, Wayne Moore GR, Golenwsky G, Raine CS. 1990. Multiple sclerosis: a role for astroglia in active demyelination suggested by class II MHC expression and ultrastructural study. J Neuropathol Exp Neurol 49: 122–136. doi:10.1097/00005072-199003000-00005
      CrossRefMedlineGoogle Scholar
    41. ↵
      Lehner B. 2011. Molecular mechanisms of epistasis within and between genes. Trends Genet 27: 323–331. doi:10.1016/j.tig.2011.05.007
      CrossRefMedlineGoogle Scholar
    42. ↵
      Lenz TL, Deutsch AJ, Han B, Hu X, Okada Y, Eyre S, Knapp M, Zhernakova A, Huizinga TW, Abecasis G, et al. 2015. Widespread non-additive and interaction effects within HLA loci modulate the risk of autoimmune diseases. Nat Genet 47: 1085–1090. doi:10.1038/ng.3379
      CrossRefMedlineGoogle Scholar
    43. ↵
      Lewis CM, Vassos E. 2020. Polygenic risk scores: from research tools to clinical instruments. Genome Med 12: 44. doi:10.1186/s13073-020-00742-5
      CrossRefMedlineGoogle Scholar
    44. ↵
      Lin X, Xu S, Liu X, Zhang X, Hu J. 2022. Detecting drug–target interactions with feature similarity fusion and molecular graphs. Biology (Basel) 11: 967. doi:10.3390/biology11070967
      CrossRefMedlineGoogle Scholar
    45. ↵
      Lincoln MR, Montpetit A, Zameel Cader M, Saarela J, Dyment DA, Tiislar M, Ferretti V, Tienari PJ, Dessa Sadovnick A, Peltonen L, et al. 2005. A predominant role for the HLA class II region in the association of the MHC region with multiple sclerosis. Nat Genet 37: 1108–1112. doi:10.1038/ng1647
      CrossRefMedlineGoogle Scholar
    46. ↵
      Lipsitch M, Bergstrom CT, Antia R. 2003. Effect of human leukocyte antigen heterozygosity on infectious disease outcome: the need for allele-specific measures. BMC Med Genet 4: 2. doi:10.1186/1471-2350-4-2
      CrossRefMedlineGoogle Scholar
    47. ↵
      Lloyd-Jones LR, Zeng J, Sidorenko J, Yengo L, Moser G, Kemper KE, Wang H, Zheng Z, Magi R, Esko T, et al. 2019. Improved polygenic prediction by Bayesian multiple regression on summary statistics. Nat Commun 10: 5086. doi:10.1038/s41467-019-12653-0
      CrossRefMedlineGoogle Scholar
    48. ↵
      Locke AE, Kahali B, Berndt SI, Justice AE, Pers TH, Day FR, Powell C, Vedantam S, Buchkovich ML, Yang J, et al. 2015. Genetic studies of body mass index yield new insights for obesity biology. Nature 518: 197–206. doi:10.1038/nature14177
      CrossRefMedlineGoogle Scholar
    49. ↵
      Loh P-R, Tucker G, Bulik-Sullivan BK, Vilhjálmsson BJ, Finucane HK, Salem RM, Chasman DI, Ridker PM, Neale BM, Berger B, et al. 2015. Efficient Bayesian mixed-model analysis increases association power in large cohorts. Nat Genet 47: 284–290. doi:10.1038/ng.3190
      CrossRefMedlineGoogle Scholar
    50. ↵
      Mak TSH, Porsch RM, Choi SW, Zhou X, Sham PC. 2017. Polygenic scores via penalized regression on summary statistics. Genet Epidemiol 41: 469–480. doi:10.1002/gepi.22050
      CrossRefMedlineGoogle Scholar
    51. ↵
      Mann HB, Whitney DR. 1947. On a test of whether one of two random variables is stochastically larger than the other. Ann Math Stat 18: 50–60. doi:10.1214/aoms/1177730491
      CrossRefGoogle Scholar
    52. ↵
      Masoudnia S, Ebrahimpour R. 2014. Mixture of experts: a literature survey. Artif Intell Rev 42: 275–293. doi:10.1007/s10462-012-9338-y
      CrossRefGoogle Scholar
    53. ↵
      Meyer MR, Tschanz JT, Norton MC, Welsh-Bohmer KA, Steffens DC, Wyse BW, Breitner J. 1998. APOE genotype predicts when—not whether—one is predisposed to develop Alzheimer disease. Nat Genet 19: 321–322. doi:10.1038/1206
      CrossRefMedlineGoogle Scholar
    54. ↵
      Moore JH, Williams SM. 2009. Epistasis and its implications for personal genetics. Am J Hum Genet 85: 309–320. doi:10.1016/j.ajhg.2009.08.006
      CrossRefMedlineGoogle Scholar
    55. ↵
      Multiple Sclerosis Genetics Group, Haines JL, Terwedow HA, Burgess K, Pericak-Vance MA, Rimmler JB, Martin ER, Oksenberg JR, Lincoln R, Zhang DY, et al. 1998. Linkage of the MHC to familial multiple sclerosis suggests genetic heterogeneity. Hum Mol Genet 7: 1229–1234. doi:10.1093/hmg/7.8.1229
      CrossRefMedlineGoogle Scholar
    56. ↵
      Nasser J, Bergman DT, Fulco CP, Guckelberger P, Doughty BR, Patwardhan TA, Jones TR, Nguyen TH, Ulirsch JC, Lekschas F, et al. 2021. Genome-wide enhancer maps link risk variants to disease genes. Nature 593: 238–243. doi:10.1038/s41586-021-03446-x
      CrossRefGoogle Scholar
    57. ↵
      Orrù V, Steri M, Sole G, Sidore C, Virdis F, Dei M, Lai S, Zoledziewska M, Busonero F, Mulas A, et al. 2013. Genetic variants regulating immune cell levels in health and disease. Cell 155: 242–256. doi:10.1016/j.cell.2013.08.041
      CrossRefMedlineGoogle Scholar
    58. ↵
      Polygenic Risk Score Task Force of the International Common Disease Alliance. 2021. Responsible use of polygenic risk scores in the clinic: potential benefits, risks and gaps. Nat Med 27: 1876–1884. doi:10.1038/s41591-021-01549-6
      CrossRefMedlineGoogle Scholar
    59. ↵
      Privé F, Arbel J, Vilhjálmsson BJ. 2021. LDpred2: better, faster, stronger. Bioinformatics 36: 5424–5431. doi:10.1093/bioinformatics/btaa1029
      CrossRefMedlineGoogle Scholar
    60. ↵
      Privé F, Arbel J, Aschard H, Vilhjálmsson BJ. 2022. Identifying and correcting for misspecifications in GWAS summary statistics and polygenic scores. HGG Adv 3: 100136. doi:10.1016/j.xhgg.2022.100136
      CrossRefMedlineGoogle Scholar
    61. ↵
      Purcell S, Neale B, Todd-Brown K, Thomas L, Ferreira MA, Bender D, Maller J, Sklar P, De Bakker PI, Daly MJ, et al. 2007. Plink: a tool set for whole-genome association and population-based linkage analyses. Am J Hum Genet 81: 559–575. doi:10.1086/519795
      CrossRefMedlineGoogle Scholar
    62. ↵
      Safieh M, Korczyn AD, Michaelson DM. 2019. ApoE4: an emerging therapeutic target for Alzheimer's disease. BMC Med 17: 64. doi:10.1186/s12916-019-1299-4
      CrossRefMedlineGoogle Scholar
    63. ↵
      Schnitzler GR, Kang H, Fang S, Angom RS, Lee-Kim VS, Rosa Ma X, Zhou R, Zeng T, Guo K, Taylor MS, et al. 2024. Convergence of coronary artery disease genes onto endothelial cell programs. Nature 626: 799–807. doi:10.1038/s41586-024-07022-x
      CrossRefMedlineGoogle Scholar
    64. ↵
      Sigurdsson AI, Louloudis I, Banasik K, Westergaard D, Winther O, Lund O, Ostrowski SR, Erikstrup C, Pedersen OBV, Nyegaard M, et al. 2023. Deep integrative models for large-scale human genomics. Nucleic Acids Res 51: e67. doi:10.1093/nar/gkad373
      CrossRefGoogle Scholar
    65. ↵
      Sohail M, Maier RM, Ganna A, Bloemendal A, Martin AR, Turchin MC, Chiang CW, Hirschhorn J, Daly MJ, Patterson N, et al. 2019. Polygenic adaptation on height is overestimated due to uncorrected stratification in genome-wide association studies. eLife 8: e39702. doi:10.7554/eLife.39702
      CrossRefMedlineGoogle Scholar
    66. ↵
      Strittmatter WJ, Roses AD. 1995. Apolipoprotein E and Alzheimer disease. Proc Natl Acad Sci 92: 4725–4727. doi:10.1073/pnas.92.11.4725
      Abstract/FREE Full Text
    67. ↵
      Subramanian A, Tamayo P, Mootha VK, Mukherjee S, Ebert BL, Gillette MA, Paulovich A, Pomeroy SL, Golub TR, Lander ES, et al. 2005. Gene set enrichment analysis: a knowledge-based approach for interpreting genome-wide expression profiles. Proc Natl Acad Sci 102: 15545–15550. doi:10.1073/pnas.0506580102
      Abstract/FREE Full Text
    68. ↵
      Sudlow C, Gallacher J, Allen N, Beral V, Burton P, Danesh J, Downey P, Elliott P, Green J, Landray M, et al. 2015. UK biobank: an open access resource for identifying the causes of a wide range of complex diseases of middle and old age. PLoS Med 12: e1001779. doi:10.1371/journal.pmed.1001779
      CrossRefMedlineGoogle Scholar
    69. ↵
      Sun Y-Q, Burgess S, Staley JR, Wood AM, Bell S, Kaptoge SK, Guo Q, Bolton TR, Mason AM, Butterworth AS, et al. 2019. Body mass index and all cause mortality in HUNT and UK biobank studies: linear and non-linear Mendelian randomisation analyses. BMJ 364: l1042. doi:10.1136/bmj.l1042
      Abstract/FREE Full Text
    70. ↵
      Szklarczyk D, Kirsch R, Koutrouli M, Nastou K, Mehryary F, Hachilif R, Gable AL, Fang T, Doncheva NT, Pyysalo S, et al. 2023. The STRING database in 2023: protein–protein association networks and functional enrichment analyses for any sequenced genome of interest. Nucleic Acids Res 51: D638–D646. doi:10.1093/nar/gkac1000
      CrossRefMedlineGoogle Scholar
    71. ↵
      Taylor MB, Ehrenreich IM. 2015. Higher-order genetic interactions and their contribution to complex traits. Trends Genet 31: 34–40. doi:10.1016/j.tig.2014.09.001
      CrossRefMedlineGoogle Scholar
    72. ↵
      Torkamani A, Wineinger NE, Topol EJ. 2018. The personal and clinical utility of polygenic risk scores. Nat Rev Genet 19: 581–590. doi:10.1038/s41576-018-0018-x
      CrossRefMedlineGoogle Scholar
    73. ↵
      Traugott U. 1987. Multiple sclerosis: relevance of class I and class II MHC-expressing cells to lesion development. J Neuroimmunol 16: 283–302. doi:10.1016/0165-5728(87)90082-8
      CrossRefMedlineGoogle Scholar
    74. ↵
      Tsai S, Santamaria P. 2013. MHC class II polymorphisms, autoreactive T-cells, and autoimmunity. Front Immunol 4: 321. doi:10.3389/fimmu.2013.00321
      CrossRefMedlineGoogle Scholar
    75. ↵
      Tsai MS, Tangalos EG, Petersen RC, Smith GE, Schaid DJ, Kokmen E, Ivnik RJ, Thibodeau SN. 1994. Apolipoprotein E: risk factor for Alzheimer disease. Am J Hum Genet 54: 643.
      MedlineGoogle Scholar
    76. ↵
      Tyrrell J, Jones SE, Beaumont R, Astley CM, Lovell R, Yaghootkar H, Tuke M, Ruth KS, Freathy RM, Hirschhorn JN, et al. 2016. Height, body mass index, and socioeconomic status: Mendelian randomisation study in UK biobank. BMJ 352: i582. doi:10.1136/bmj.i582
      Abstract/FREE Full Text
    77. ↵
      Uffelmann E, Huang QQ, Munung NS, De Vries J, Okada Y, Martin AR, Martin HC, Lappalainen T, Posthuma D. 2021. Genome-wide association studies. Nat Rev Methods Primers 1: 59. doi:10.1038/s43586-021-00056-9
      CrossRefGoogle Scholar
    78. ↵
      Varona L, Legarra A, Toro MA, Vitezica ZG. 2018. Non-additive effects in genomic selection. Front Genet 9: 78. doi:10.3389/fgene.2018.00078
      CrossRefMedlineGoogle Scholar
    79. ↵
      Vilhjálmsson BJ, Yang J, Finucane HK, Gusev A, Lindström S, Ripke S, Genovese G, Loh P-R, Bhatia G, Do R, et al. 2015. Modeling linkage disequilibrium increases accuracy of polygenic risk scores. Am J Hum Genet 97: 576–592. doi:10.1016/j.ajhg.2015.09.001
      CrossRefMedlineGoogle Scholar
    80. ↵
      Vithayathil M, Carter P, Kar S, Mason AM, Burgess S, Larsson SC. 2021. Body size and composition and risk of site-specific cancers in the UK biobank and large international consortia: a Mendelian randomisation study. PLoS Med 18: e1003706. doi:10.1371/journal.pmed.1003706
      CrossRefMedlineGoogle Scholar
    81. ↵
      Walker JT, Saunders DC, Rai V, Chen H-H, Orchard P, Dai C, Pettway YD, Hopkirk AL, Reihsmann CV, Tao Y, et al. 2023. Genetic risk converges on regulatory networks mediating early type 2 diabetes. Nature 624: 621–629. doi:10.1038/s41586-023-06693-2
      CrossRefMedlineGoogle Scholar
    82. ↵
      Wang WY, Barratt BJ, Clayton DG, Todd JA. 2005. Genome-wide association studies: theoretical and practical concerns. Nat Rev Genet 6: 109–118. doi:10.1038/nrg1522
      CrossRefMedlineGoogle Scholar
    83. ↵
      Wang Y, Wang J, Cao Z, Farimani AB. 2022. Molecular contrastive learning of representations via graph neural networks. Nat Mach Intell 4: 279–287. doi:10.1038/s42256-022-00447-x
      CrossRefGoogle Scholar
    84. ↵
      Wightman DP, Jansen IE, Savage JE, Shadrin AA, Bahrami S, Holland D, Rongve A, Børte S, Winsvold BS, Drange OK, et al. 2021. A genome-wide association study with 1,126,563 individuals identifies new risk loci for Alzheimer's disease. Nat Genet 53: 1276–1282. doi:10.1038/s41588-021-00921-z
      CrossRefMedlineGoogle Scholar
    85. ↵
      Wood AR, Esko T, Yang J, Vedantam S, Pers TH, Gustafsson S, Chu AY, Estrada K, Luan J, Kutalik Z, et al. 2014. Defining the role of common variation in the genomic and biological architecture of adult human height. Nat Genet 46: 1173–1186. doi:10.1038/ng.3097
      CrossRefMedlineGoogle Scholar
    86. ↵
      World Health Organization. 1992. Icd-10. international statistical classification of diseases and related health problems: tenth revision 1992, volume 1 = cim-10. classification statistique internationale des maladies et des problèmes de santé connexes: dixième révision 1992, volume 1. Weekly Epidemiological Record = Relevé épidémiologique hebdomadaire 67: 203–204.
      MedlineGoogle Scholar
    87. ↵
      Wu Z, Trevino AE, Wu E, Swanson K, Kim HJ, Blaize D'Angio H, Preska R, Charville GW, Dalerba PD, Egloff AM, et al. 2022. Graph deep learning for the characterization of tumour microenvironments from spatial protein profiles in tissue specimens. Nat Biomed Eng 6: 1435–1448. doi:10.1038/s41551-022-00951-w
      CrossRefGoogle Scholar
    88. ↵
      Xu K, Hu W, Leskovec J, Jegelka S. 2018. How powerful are graph neural networks? In International Conference on Learning Representations, Vancouver, BC, Canada.
      Google Scholar
    89. ↵
      Xu Y, Vuckovic D, Ritchie SC, Akbari P, Jiang T, Grealey J, Butterworth AS, Ouwehand WH, Roberts DJ, Di Angelantonio E, et al. 2022. Machine learning optimized polygenic scores for blood cell traits identify sex-specific trajectories and genetic correlations with disease. Cell Genom 2: 100086. doi:10.1016/j.xgen.2021.100086
      CrossRefMedlineGoogle Scholar
    90. ↵
      Yamazaki Y, Zhao N, Caulfield TR, Liu C-C, Bu G. 2019. Apolipoprotein E and Alzheimer disease: pathobiology and targeting strategies. Nat Rev Neurol 15: 501–518. doi:10.1038/s41582-019-0228-7
      CrossRefMedlineGoogle Scholar
    91. ↵
      Zhang S, Shu H, Zhou J, Rubin-Sigler J, Yang X, Liu Y, Cooper-Knock J, Monte E, Zhu C, Tu S, et al. 2024. Deconvolution of polygenic risk score in single cells unravels cellular and molecular heterogeneity of complex human diseases. bioRxiv doi:10.1101/2024.05.14.594252
      Abstract/FREE Full Text
    92. ↵
      Zhou Z, Liang Y, Zhang X, Xu J, Lin J, Zhang R, Kang K, Liu C, Zhao C, Zhao M. 2020. Low-density lipoprotein cholesterol and Alzheimer's disease: a systematic review and meta-analysis. Front Aging Neurosci 12: 5. doi:10.3389/fnagi.2020.00005
      CrossRefMedlineGoogle Scholar
    93. ↵
      Zhou W, Kanai M, Wu K-HH, Rasheed H, Tsuo K, Hirbo JB, Wang Y, Bhattacharya A, Zhao H, Namba S, et al. 2022. Global biobank meta-analysis initiative: powering genetic discovery across human disease. Cell Genom 2: 100192. doi:10.1016/j.xgen.2022.100192
      CrossRefMedlineGoogle Scholar
    94. ↵
      Zuk O, Hechter E, Sunyaev SR, Lander ES. 2012. The mystery of missing heritability: genetic interactions create phantom heritability. Proc Natl Acad Sci 109: 1193–1198. doi:10.1073/pnas.1119675109
      Abstract/FREE Full Text

    Articles citing this article

    • PRSNet-2: End-to-end genotype-to-phenotype prediction via hierarchical graph neural networks bioRxiv November 26, 2025 0: 2025.11.22.689899v1-2025.11.22.689899
    • VADEr: Vision Transformer-Inspired Framework for Polygenic Risk Reveals Underlying Genetic Heterogeneity in Prostate Cancer medRxiv May 21, 2025 0: 2025.05.16.25327672v1-2025.05.16.25327672
    • Dissecting the genetic complexity of myalgic encephalomyelitis/chronic fatigue syndrome via deep learning-powered genome analysis medRxiv May 13, 2025 0: 2025.04.15.25325899v2-2025.04.15.25325899
    | Table of Contents
    OPEN ACCESS ARTICLE

    This Article

    1. Published in Advance November 19, 2024, doi: 10.1101/gr.279694.124 Genome Res. 35: 178-187 © 2025 Li et al.; Published by Cold Spring Harbor Laboratory Press

    Article Category

    ORCID

    1. Profile for Li, H.http://orcid.org/0000-0002-7380-6174

    Share

    Preprint Server



    Navigate This Article

    Current Issue

    1. January 2026, 36 (1)
    1. Current Issue
    1. Alert me to new issues of Genome Research