Examining the dynamics of three-dimensional genome organization with multitask matrix factorization
Abstract
Three-dimensional (3D) genome organization, which determines how the DNA is packaged inside the nucleus, has emerged as a key component of the gene regulation machinery. High-throughput chromosome conformation data sets, such as Hi-C, have become available across multiple conditions and time points, offering a unique opportunity to examine changes in 3D genome organization and link them to phenotypic changes in normal and disease processes. However, systematic detection of higher-order structural changes across multiple Hi-C data sets remains a major challenge. Existing computational methods either do not model higher-order structural units or cannot model dynamics across more than two conditions of interest. We address these limitations with tree-guided integrated factorization (TGIF), a generalizable multitask nonnegative matrix factorization (NMF) approach that can be applied to time series or hierarchically related biological conditions. TGIF can identify large-scale changes at the compartment or subcompartment levels, as well as local changes at boundaries of topologically associated domains (TADs). Based on benchmarking in simulated and real Hi-C data, TGIF boundaries are more accurate and reproducible across differential levels of noise and sources of technical artifacts, and are more enriched in CTCF. Application to three multisample mammalian data sets shows that TGIF can detect differential regions at compartment, subcompartment, and boundary levels that are associated with significant changes in regulatory signals and gene expression enriched in tissue-specific processes. Finally, we leverage TGIF boundaries to prioritize sequence variants for multiple phenotypes from the NHGRI GWAS catalog. Taken together, TGIF is a flexible tool to examine 3D genome organization dynamics across disease and developmental processes.
The three-dimensional (3D) organization of the genome refers to the packaging of DNA inside the nucleus. It has emerged as a key regulatory mechanism of cellular function and dysfunction across diverse developmental (Zheng and Xie 2019), disease (Lupiáñez et al. 2016), and evolutionary contexts (McCord 2017; Eres et al. 2019). High-throughput chromosomal conformation capture (Hi-C) technologies enable the study of 3D genome organization by experimentally measuring the tendency of genomic regions to spatially interact with one another (Mumbach et al. 2016; Kempfer and Pombo 2020; Dekker et al. 2023). The 3D genome is organized into structural units at multiple scales: compartments spanning several megabases, topologically associated domains (TADs) spanning hundreds of kilobases scale, and enhancer–promoter loops involving pairs of loci of a few thousand bases (Bouwman and de Laat 2015; Rowley and Corces 2018; Kempfer and Pombo 2020). Changes in 3D genome organization at different topological levels have been observed with transitions in both normal (Bonev et al. 2017; Stadhouders et al. 2018; Zheng and Xie 2019) and disease processes (Lupiáñez et al. 2016; Norton and Phillips-Cremins 2017; Wang et al. 2023). Through efforts from large-scale consortia such as the 4D Nucleome Project, Hi-C measurements are becoming increasingly common from multiple conditions corresponding to time points, cell types, and species (Dekker et al. 2017, 2023; Reiff et al. 2022; Roy et al. 2023). These data sets provide a unique opportunity to examine the dynamics of 3D genome organization across space and time and its impact on disease and normal processes.
The reliable detection of 3D genome dynamics at different units of organization is a significant computational challenge. Current computational approaches to examine dynamics in the 3D genome can be grouped into those that identify large-scale or compartmental-level changes (Fotuhi Siahpirani et al. 2016; Chakraborty et al. 2022), those that can identify TAD-scale changes or “differential TADs” (Cresswell and Dozmorov 2020; Wang et al. 2020), and those that examine changes at the level of loops or interactions (Lun and Smyth 2015; Djekidel et al. 2018; Ardakany et al. 2019; Stansfield et al. 2019; Galan et al. 2020). Compared with methods for detecting differences at the interaction level, there are relatively few approaches to detect TADs or compartment changes. The most common approach to study TAD dynamics across multiple conditions is to first apply a TAD-calling method to data from each condition, followed by postprocessing to identify TAD boundaries in one condition but not another (Bonev et al. 2017; Stadhouders et al. 2018; Zhang et al. 2019; Emerson et al. 2022; Wang et al. 2022). Although such a two-step approach can identify some meaningful differences, the unsupervised nature of TAD finding could make these approaches more susceptible to finding nonbiological differences and technical artifacts (Zheng et al. 2022; Kobets et al. 2023; Fletez-Brant et al. 2024). Numerous studies have shown that Hi-C count profiles obey cell type, time point, and species relationships, in which data sets from nearby contexts are more similar than those that are far away (Vietri Rudan et al. 2015; Bonev et al. 2017; Yang et al. 2017; Zhang et al. 2019). An approach that constrains the TAD and compartment finding based on such prior information about the relationships between the input data sets could be less prone to spurious differences. A few methods have been developed to directly identify TAD boundary differences, but they are focused on pairs of conditions (Wang et al. 2020) or are limited in their ability to compare more than two conditions (Cresswell and Dozmorov 2020).
To address the dearth of methods for identifying large-scale organizational changes, especially when considering more than two data sets, we developed tree-guided integrated factorization (TGIF). TGIF is a multitask, nonnegative matrix factorization (NMF) framework enabling joint embedding of multiple Hi-C matrices and identification of compartments and TADs across multiple conditions. NMF is a popular dimensionality reduction approach for analyzing nonnegative, genome-scale data sets (Stein-O'Brien et al. 2018; Kotliar et al. 2019; Lee and Roy 2021), in which the low-dimensional factors capture the biologically meaningful structure of the data. Multitask NMF frameworks factorize multiple input matrices simultaneously to yield low-dimensional embeddings in a shared latent space. They have been successfully applied to single-cell omics data to integrate matrices from multiple samples, experiments, and modalities by removing batch effect and technical noise (Welch et al. 2019; Liu et al. 2020; Kriebel and Welch 2022; Luecken et al. 2022; Hu et al. 2024). TGIF incorporates a hierarchical multitask NMF formulation to simultaneously factorize multiple Hi-C matrices from related biological conditions and constrain the factors from closely related conditions to be similar. The factors represent low-dimensional embeddings of genomic regions in an aligned latent space, representing their global or local chromatin architecture. We use such embeddings to identify changes at both the compartment and TAD levels. When applied to simulated and real time course Hi-C matrices, TGIF identifies fewer false positive differences in TAD boundaries and produces a more reproducible set of boundaries across biological replicates, normalization methods, depths, and resolutions compared with other methods. Differential boundaries and compartmental regions identified by TGIF show significant changes in relevant biological signals such as gene expression, histone modification, and chromatin accessibility. Finally, persistent boundaries identified by TGIF from a cardiomyocyte differentiation data set are enriched in sequence variants associated with cardiovascular disease (CVD). Together, these results demonstrate the versatility and utility of TGIF to examine changes in higher-order 3D genome organization across diverse types of dynamic processes.
Results
TGIF for examining dynamics in 3D genome organization
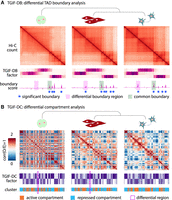
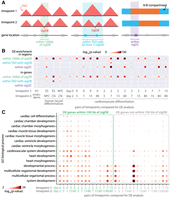
TGIF is a general-purpose framework to study 3D genome organization dynamics both at the TAD and compartment levels (Fig. 1). TGIF is based on multitask NMF. It takes as input a set of Hi-C matrices, each representing a biological condition, and a user-specified tree structure that can encode an arbitrary relationship among the conditions, such as time or cell type lineage (Fig. 1; Supplemental Fig. S1). TGIF uses a novel regularization term in its objective to jointly factorize the matrices such that input matrices from more closely related conditions result in more similar lower-dimensional representations, namely, factors.
Overview of TGIF. (A) TGIF for differential boundary analysis (TGIF-DB). TGIF-DB takes multiple Hi-C count matrices as input and simultaneously learns a lower-dimensional representation of genomic regions based on their interaction patterns. The input matrices are from related biological conditions with their relationship encoded as a tree. From the lower-dimensional factors, we measure the boundary score of each region and identify boundaries for each input condition and significantly differential boundaries (sigDBs) for every pair of conditions. (B) TGIF for differential compartment analysis (TGIF-DC). TGIF-DC converts input matrices into correlation matrices of observed-over-expected (O/E) counts and factorizes them to yield latent features, which are used to cluster the regions. Each cluster corresponds to a compartment or a subcompartment. TGIF-DC also identifies significantly differential compartmental regions (sigDCs) for every pair of input conditions.
To handle both compartment and TAD identification, we implemented two versions of TGIF: TGIF-DB and TGIF-DC. TGIF-DB identifies conserved and differential boundaries demarcating TADs under different conditions (Methods) (Fig. 1A; Supplemental Fig. S1A), whereas TGIF-DC identifies compartment-level changes in 3D genome organization (Fig. 1B). In TGIF-DB, the factorization is performed on submatrices along the diagonal of the intrachromosomal Hi-C matrices, as these diagonal submatrices capture the TAD-scale, the local topology of chromosomes. Each submatrix is factorized over a range of k, the hyperparameter specifying the rank of the lower-dimensional space (Supplemental Fig. S1B). TGIF-DB calculates a boundary score from the factors at each k, which are averaged to provide an overall boundary score (Supplemental Fig. S1C). Considering multiple k’s allows us to capture structural units or domains of different sizes in the lower-dimensional space and removes the need to specify the number of factors (Methods). TGIF-DB identifies regions with significant boundary scores by comparing the average boundary scores against a “null distribution” of boundary scores to calculate an empirical P-value (Supplemental Fig. S1D). TGIF-DB outputs the list of significant boundaries corresponding to each input data set and a list of significantly differential boundary regions for every pair of input count matrices (Methods) (Supplemental Fig. S1E).
TGIF-DC operates at the entire chromosome level and applies its multitask factorization on the observed-over-expected (O/E) counts matrix as described previously (Methods) (Lieberman-Aiden et al. 2009; Rao et al. 2014). To identify the two major compartments of active and repressive genomic regions, TGIF-DC factorizes the O/E matrices with parameter k = 2. The resulting factors are used to group the genomic regions into two different clusters. By specifying a higher parameter value, for example, k = 5, TGIF-DC can also identify more granular subcompartment structures, which can be interpreted using one-dimensional chromatin signals. Similar to TGIF-DB, TGIF-DC identifies significantly differential compartment and subcompartment regions for every pair of input conditions (Methods).
In cases in which the relationship between the input Hi-C data is not available (e.g., integrating Hi-C data sets from multiple studies or pseudobulk single-cell Hi-C data from cell clusters) (Zhou et al. 2019; Zhang et al. 2022) TGIF can infer a tree structure based on the pairwise similarity of the input Hi-C matrices measured by stratum-adjusted correlation coefficient (SCC; Methods) (Supplemental Fig. S2; Yang et al. 2017) or a similar distance-stratified metric.
TGIF-DB identifies fewer false-positive differential boundaries in simulated and real Hi-C data
TGIF-DB was benchmarked against four other TAD calling methods: three methods designed for calling TADs and boundaries from a single Hi-C matrix (which we refer to as single-task methods), and one designed specifically for differential boundary identification (Methods). The three single-task methods were GRiNCH (Lee and Roy 2021), SpectralTAD (Cresswell et al. 2020), and TopDom (Supplemental Methods; Shin et al. 2016). TADCompare (Cresswell and Dozmorov 2020) is a method designed for differential boundary detection.
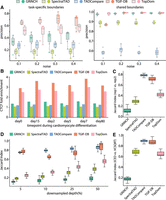
Because real Hi-C data sets do not have a ground-truth set of TAD boundaries, we first evaluated the quality of TAD boundaries identified by each method in simulated data sets. We generated four Hi-C matrices, each with its own set of ground-truth boundaries, based on the count simulation procedure from Forcato et al. (2017), and noise added to 10%, 20%, 30%, and 40% of interaction counts (Supplemental Methods). For every pair of matrices, we calculate the precision and recall of boundaries found only in one matrix (“task-specific” boundaries) and those shared between the two input matrices (shared boundaries). Across the different levels of noise, TGIF-DB has the highest precision on task-specific boundaries (Fig. 2A). With the exception in the lowest level of noise (10%), TGIF-DB is among the methods with the highest precision for shared boundaries along with GRiNCH and TopDom (Fig. 2A). For recall of task-specific boundaries (Supplemental Fig. S3A), TGIF-DB is second to TopDom in all but the lowest noise level. For shared boundaries, TGIF-DB and TopDom also have the highest recall in all but the lowest noise level.
Benchmarking TGIF-DB. (A) Precision on ground-truth boundaries in simulated Hi-C matrices. Each point represents the precision from a pair of input simulated data sets compared with yield task-specific boundaries (i.e., boundaries found in one input data set but not in the other) and shared boundaries. (B) CTCF peak enrichment in boundaries from different TAD-calling and differential-boundary-calling methods. (C) Boundary set similarity between biological replicates of hESCs (from day 0 of cardiomyocyte differentiation data). (D) Boundary set similarity measured by Jaccard index between GM12878 data and downsampled data, across different downsampling depths. (E) Boundary set similarity between ICE-normalized and VCSQRT-normalized input matrices of mESCs (from mouse neural differentiation data).
Next, we evaluated the quality of TAD boundaries identified by each method based on the enrichment of CTCF binding. CTCF is an architectural protein associated with establishing boundaries (Gómez-Díaz and Corces 2014; Cubeñas-Potts and Corces 2015; Merkenschlager and Nora 2016). We used the time-series data set of cardiomyocyte differentiation (Zhang et al. 2019), which profiled both genome-wide chromosome conformation with Hi-C and CTCF binding with ChIP-seq. The boundary regions predicted by each method for each time point were used to calculate their fold enrichment of CTCF peaks against the genomic background (Methods). Significant boundaries identified by TGIF-DB have the highest fold enrichment, followed by single-task methods, TopDom and GRiNCH (Fig. 2B).
We next measured the Jaccard score between the boundary sets from a pair of biological replicates of H1 human embryonic stem cell line (Methods) (Zhang et al. 2019); TADCompare and TGIF-DB had the highest scores, recovering a more similar set of boundaries between the biological replicates compared with other methods (Fig. 2C). Furthermore, differential boundaries between two time points (day 0 and day 2 of cardiomyocyte differentiation) identified by TADCompare and TGIF-DB had the fewest false positives based on overlap with differential boundaries between two biological replicates of the same time point (Supplemental Methods; Supplemental Fig. S3B). We also benchmarked the degree of false-positive, nonbiological differences identified by each method in (1) Hi-C data sets with different depths, (2) data sets from biological replicates, (3) data sets normalized using different methods, and (4) data sets at different bin resolutions. To this end, we downsampled a high-depth Hi-C data set from the GM12878 cell line with 4.01 billion reads (Rao et al. 2014; Reiff et al. 2022) by subsampling 5%, 10%, 25%, and 50% of the reads (Methods). We measured the Jaccard score between the boundary sets from the original high-depth input and the downsampled counterpart. The higher the Jaccard index, the fewer the false-positive differences identified by a method. Across all downsampled depths, TADCompare and TGIF-DB were the top-performing methods, with consistently high Jaccard scores (Fig. 2D). Single-task methods (GRiNCH, SpectralTAD, and TopDom) had much lower Jaccard scores, with discrepancy increasing with depth differences. We observed similar results with TADCompare and TGIF-DB obtaining the highest Jaccard score between TAD boundary sets from mouse embryonic stem cell (mESC) Hi-C data normalized using different methods (Methods) (Fig. 2E). Finally, we measured the stability of TAD boundaries to the changing resolution (10 kb, 25 kb, 50 kb) of input Hi-C matrices using the Jaccard score (Methods). TGIF-DB and GRiNCH yield the most stable or similar boundaries to changing resolution (Supplemental Fig. S3C), with the exception of 25 kb–50 kb, at which TopDom also performed well. These results demonstrate the advantages of using TGIF-DB to identify biologically relevant boundaries enriched in known boundary elements while minimizing false-positive differences.
TGIF-DC identifies compartment dynamics that are significantly enriched for differential regulatory signals
We compared TGIF-DC against three existing methods on the H1 hESC and endoderm differentiation data set (Supplemental Methods): PCA-based (Lieberman-Aiden et al. 2009), Cscore (Zheng and Zheng 2018), and dcHiC (Chakraborty et al. 2022).
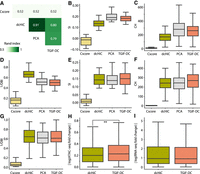
We first compared the similarity of compartment assignments between different methods using Rand index (Fig. 3A). The PCA-based method and dcHiC, which also utilizes PCA, produced the most similar compartments (Rand index: 0.91), followed by TGIF-DC (Rand index: 0.79–0.8). Cscore found a substantially different set of compartments (Rand index: 0.52). We assessed the quality of compartments with three cluster quality metrics, silhouette index (SI) (Fig. 3B), Calinski–Harabasz score (CH) (Fig. 3C), and Davies–Bouldin index (DBI) (Fig. 3D), using O/E counts as features of each genomic loci (Methods). In all three metrics, TGIF-DC, dcHiC, and PCA-based compartments are comparable in their quality and outperformed Cscore. We also measured compartment quality using chromatin accessibility, a key regulatory measurement that characterizes different compartment types (e.g., the active A and repressive B) (Lieberman-Aiden et al. 2009; Fortin and Hansen 2015). Briefly, we measured SI (Fig. 3E), CH (Fig. 3F), and DBI (Fig. 3G) using the mean base pair ATAC-seq signal for each 100 kb region as the feature (Methods). For all three metrics, the compartments from TGIF-DC, PCA-based method, and dcHiC are of similar quality.
Benchmarking TGIF-DC on data from H1 and H1 differentiated to definitive endoderm. (A) Similarity of compartment assignments from different methods measured by Rand index. (B–D) Quality of compartments based on O/E counts measured by the silhouette index (SI; B), Calinski–Harabasz score (CH; C), and Davies–Bouldin index (DBI; D). (E–G) SI (E), CH (F), and DBI (G) on accessibility (ATAC-seq) signal. (H) Magnitude of log fold change in accessibility between H1 and endoderm within sigDCs identified by dcHiC and TGIF-DC. (I) Magnitude of log fold change in gene expression between H1 and endoderm within sigDCs identified by dcHiC and TGIF-DC.
Finally, we compared TGIF-DC exclusively with dcHiC, the only other method that specifically identifies differential compartment regions. Significantly differential compartmental regions (sigDCs) identified by TGIF-DC have a significantly higher change in accessibility signal and gene expression compared with regions not part of sigDCs (Supplemental Fig. S5A,B). Compared with significantly differential regions identified by dcHiC, sigDCs from TGIF-DC also have a significantly higher change in accessibility signal (t-test P-value <1 × 10–2) (Fig. 3H) and are comparable in terms of the change in gene expression levels (Fig. 3I).
Taken together, TGIF-DC captures compartment structure consistent with established compartment-calling methods, while pinpointing differential regions with significant changes in regulatory signals such as chromatin accessibility.
TGIF-DC offers a unified framework to identify both compartment and subcompartment dynamics
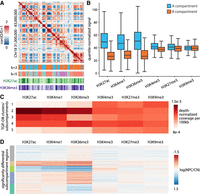
Although compartments provide a global partitioning of each chromosome, the genome is hierarchically organized with compartments further partitioned into smaller subcompartments that could represent functionally distinct set of regions (Rao et al. 2014; Xiong and Ma 2019). TGIF-DC has a tunable parameter (k, the rank of factors) that can be used to identify such subcompartments. To demonstrate TGIF-DC's ability to identify both compartments and subcompartments, we applied it to the mouse neural differentiation data set with three time points: embryonic stem cells (ESs), neural progenitors (NPCs), and cortical neurons (CNs) (Supplemental Figs. S4, S6, S7). This data set additionally measured six different histone modification signals for NPCs and CNs that were beneficial for additional biological interpretation of TGIF-DC results (Methods) (Fig. 4A). We first analyzed the compartment structure from TGIF-DC (k = 2) for each chromosome, based on GC content (mean GC percentage for each 100 kb bin; Methods), annotating the compartment with higher GC content as compartment A and the one with lower GC content as compartment B (Methods) (Supplemental Fig. S8). Regions annotated as the A compartment by TGIF-DC have significantly higher signal for marks associated with active enhancer (H3K27ac, H3K4me1) or elongation (H3K36me3) than those in the B compartment (Fig. 4B).
Characterizing compartments and subcompartments identified by TGIF-DC in mouse neural differentiation data. (A) A heatmap visualization of correlation matrix of O/E counts from cortical neuron (CN) Chr 18 regions at 100 kb resolution, followed by TGIF compartment assignments (i.e., clusters from k = 2) and subcompartments (e.g., clusters from k = 5), as well as H3K27ac/H3K36me3 ChIP-seq signal heatmaps. (B) Distribution of histone modification signal in A and B compartments in neural progenitors (NPCs) and CNs. (C) Mean histone modification signals across different subcompartments in NPCs and CNs. (D) Log fold change of histone modification signals between NPCs and CNs within significantly differential subcompartment regions identified by TGIF-DC. These regions were grouped based on their histone modification signal fold change patterns using k-means clustering and are visualized here.
We next applied TGIF-DC with k = 5 to identify subcompartment structure per chromosome, each k corresponding to a different subcompartment (Methods). We interpreted these subcompartments based on the mean histone modification signal of the genomic loci assigned to each subcompartment. The subcompartments exhibited distinct histone modification patterns (Fig. 4C, Chr 18), with subcompartments 1 and 5 associated with repressive marks (H3K9me3, H3K27me3), whereas the other three (subcompartments 2, 3, and 4) associated with active marks. Within these two groups, each subcompartment had a different signature of marks. For example, subcompartment 3 exhibits a relatively lower signal of H3K36me3 compared with subcompartments 2 and 4, whereas subcompartment 2 had a higher signal of all three activating marks (H3K27ac, H3K36me3, H3K4me1) compared with subcompartments 3 and 4. Between the two subcompartments, 1 and 5, with repressive mark association, one (subcompartment 1) exhibited higher H3K4me3 and H3K9me3 levels compared with the other one (subcompartment 5).
Finally, we assessed TGIF-DC's differential subcompartments by measuring the log fold change in histone modification signals between two time points, NPC and CN, and k-mean-clustering the regions based on this signal difference. We find distinct subgroups of regions with different fold change of the three activating marks H3K27ac, H3K36me3, and H3K4me1 (Fig. 4D). The repressive marks or the promoter specific mark, H3K4me3, did not vary substantially for these regions.
Taken together, these results demonstrate TGIF-DC's flexible framework to identify both compartment- and subcompartment-level dynamics that are associated with significant changes in regulatory activity between the time points or cell stages compared.
Changes in gene expression are associated with changes in boundaries during differentiation
Untangling the relationship between 3D genome organization and gene expression remains a key question in regulatory genomics. Although a direct mechanistic link between transcription and 3D genome organization has been observed (Heinz et al. 2018; van Steensel and Furlong 2019) during cell state transitions (Chen et al. 2024; Pollex et al. 2024), other studies found that changes in 3D genome organization are not a strong determinant of gene expression changes (Espinola et al. 2021; Ing-Simmons et al. 2021). To assess the extent to which changes in 3D genome structure are associated with changes in expression, we analyzed differential structures identified by TGIF with differential gene expression in multiple mammalian differentiation data sets.
We applied TGIF to the three time course data sets with both Hi-C and RNA-seq measurements (Supplemental Fig. S4; Supplemental Tables S1–S3): (1) H1 hESCs differentiated to endoderm (Supplemental Figs. S5C–F, S9; Reiff et al. 2022; Dekker et al. 2023), (2) a mouse neural differentiation time course from mESC to CNs (Supplemental Figs. S6, S7, S10; Bonev et al. 2017), and (3) a human cardiomyocyte differentiation time course from hESCs to ventricular cardiomyocytes (Supplemental Figs. S11, S12; Zhang et al. 2019). We performed pairwise comparison of differential boundary, compartment, and gene expression, for example, H1 versus endoderm, mESC versus NPC, and day 0 versus day 2 of cardiomyocyte differentiation. Within each pairwise comparison, we asked whether differentially expressed (DE) genes are enriched in three different sets of dynamic regions (Methods) (Fig. 5A): (1) regions near (i.e., within 100 kb of) significantly differential boundaries (sigDBs), (2) regions within a TAD with at least one sigDB, and (3) regions within sigDCs. Differential regions within 100 kb of sigDBs are consistently enriched for DE genes (Fig. 5B, top; Supplemental Tables S5–S7). Furthermore, genes within 100 kb of sigDBs are also enriched for DE compared with all genes (Fig. 5B, bottom). Regions in set (2) (within a TAD with at least one sigDB) do not show consistent enrichment, likely because of the permissive inclusion criteria for this set. Regions within sigDCs are significantly enriched in DE genes for the H1–endoderm differentiation and the majority of the comparisons in the cardiomyocyte differentiation data set. The enrichment for genes was lower, possibly owing to the large number of genes within compartments.
Differential gene expression near or within differential structural features. (A) Differential gene expression (DE) enrichment was measured in regions and genes near or within dynamic regions, that is, regions within 100 kb of significantly differential boundary (sigDBs), regions within TAD with at least one sigDB, and regions within sigDCs. (B) DE, sigDBs, and sigDCs were measured and identified in pairwise comparisons of time points across three mammalian differentiation data sets: H1 differentiated to endoderm, mouse neural differentiation (ESs, NPCs, CNs), and cardiomyocyte differentiation (day 0, 2, 5, 7, 15, 80). The negative log P-value of the enrichment hypergeometric test is visualized here. (C) GO biological process enrichment of genes within 100 kb of sigDB from cardiomyocyte differentiation data.
To assess the biological significance of DE genes near differential boundaries, we examined the biological processes enriched in DE genes near sigDBs compared with processes enriched in other genes (Methods). In the cardiomyocyte differentiation data, DE genes in general showed significant enrichment for generic developmental terms like multicellular organismal development (Fig. 5C; Supplemental Table S8). However, DE genes near sigDBs tended to be significantly enriched for processes specific to cardiac and heart development (e.g., cardiac cell differentiation, heart development and morphogenesis). DE genes near sigDBs between H1 and endoderm also showed significant enrichment in developmental terms (e.g., cell morphogenesis involved in differentiation, cellular component organization, or biogenesis) compared with those not near sigDBs (Supplemental Table S9). For the mESC-to-CN differentiation, DE genes near sigDBs were enriched for neuronal processes when comparing ESs versus CNs and ESs versus NPCs (Supplemental Table S10).
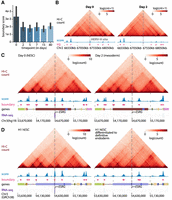
Finally, to characterize specific loci with differential 3D organization patterns, we prioritized regions based on the magnitude of change in their boundary scores and then overlapped them with genomic features such as retrotransposons. Human endogenous retrovirus subfamily H retrotransposons (HERV-H) in particular have been implicated in chromatin organization (Lawson et al. 2023) as a major determinant of TAD boundaries specific to hESCs (i.e., day 0 of cardiomyocyte differentiation) when transcriptionally active (Zhang et al. 2019). Boundary scores at the top 100 transcriptionally active HERV-H sites is higher in hESCs (day 0) compared with subsequent time points (Fig. 6A). We observe the presence of such a boundary unique to day 0 that disappears in subsequent time points at one of the top transcriptionally active HERV-H sites (Fig. 6B). Among the top-ranked sigDBs based on change in boundary scores, we found sigDB regions where a boundary is present in the pluripotent state but absent in the differentiated state (Fig. 6C,D). These sigDB instances are proximal to the ESRG gene, highly expressed in the pluripotent state compared with the subsequent differentiated states. ESRG is a HERV-H-containing long noncoding RNA (lncRNA) (Wang et al. 2014); in addition to demarcating domain boundaries in hESCs, this particular site may affect the pluripotency state on knockdown (Wang et al. 2014) and has known roles in developmental and embryonal carcinoma (Wanggou et al. 2012).
Human pluripotency-specific boundary elements. (A) Boundary scores of transcriptionally active HERV-H retrotransposon sites during each time point of cardiomyocyte differentiation. (B) The top HERV-H site based on its transcription level in day 0 pluripotent state (within somatic chromosomes) and the overlapping sigDBs identified by TGIF-DB. (C,D) ESRG, a HERV-H-containing DE gene, overlapping a sigDB in cardiomyocyte differentiation (C) and in H1 differentiated to endoderm (D).
Among other top-ranked sigDBs in cardiomyocyte differentiation, we found DE genes with known roles in cardiac development. For example, a boundary was found in primitive cardiomyocytes (day 15) but absent in ventricular cardiomyocytes (day 80) (Supplemental Fig. S13A). This boundary overlaps MYH6, highly expressed in day 15 compared with day 80, and is adjacent to MYH7, displaying the opposite expression change pattern to MYH6. Both genes are involved in cardiac muscle function (Ching et al. 2005; Warkman et al. 2012). Recently an enhancer cluster located downstream from MYH7 at Chr 14: 23,876,121–23,878,188 was identified as a switch that can downregulate expression of MYH7 while upregulating MYH6 (Gacita et al. 2021). We also identified a sigDB close to the Ncam1 gene, which is differentially expressed between ESs and CNs (Supplemental Fig. S13B); Ncam1 has known roles in neuron axon guidance and synapse formation (Shetty et al. 2013; Hata et al. 2018). These examples provide further evidence for TGIF-DB's ability to identify relevant dynamic boundaries that could impact overall cell state identity.
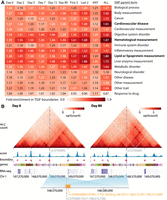
Persistent boundaries are enriched for SNPs from diverse disease phenotypes
Single-nucleotide polymorphisms (SNPs) identified from genome-wide association studies (GWAS) are frequently found in noncoding regions of the genome and have been implicated in disease phenotypes by affecting the 3D genome organization (Lupiáñez et al. 2015; Orozco et al. 2022). Specifically, such variants could disrupt TAD boundaries and cause promiscuous expression of genes (Lupiáñez et al. 2015; Chakraborty and Ay 2019). We investigated whether TGIF boundaries from the human cardiomyocyte differentiation data could be used to examine regulatory variants identified for diverse disease phenotypes in GWAS. We considered 17 phenotypic categories from the GWAS catalog and tested the enrichment of SNPs from each category in TGIF boundaries (Methods). SNPs across different categories were most enriched in the common set of boundaries across time points (i.e., persistent boundaries) than in other time point–specific or broader subsets of boundaries, with hematological measurement, CVD, and lipid or lipoprotein measurement being the most enriched phenotypic categories (Fig. 7A). Importantly, SNPs associated with CVD exhibited the second-highest enrichment. The traits that had lower enrichment included neurological disorders and nonspecific categories. We examined 66 persistent boundaries with at least one CVD-associated SNP. One such boundary had the SNP rs72705895, which is associated with venous thromboembolism (Fig. 7B; Lindström et al. 2019) and additionally overlaps a CTCF binding site (regulatory feature ENSR00000255184 from Ensembl regulatory build annotations) (Zerbino et al. 2015; Cunningham et al. 2022). Another boundary included rs9349379, which is found in the intronic region of PHACTR1 (Supplemental Fig. S14). Both the intronic variant and the gene are associated with coronary artery atherosclerotic disease (Koitsopoulos and Rabkin 2021; Kuveljic et al. 2021), whereas the SNP itself is on a predicted enhancer region (Ensembl regulatory build annotation ENSR00001107203), suggesting its putative role in disrupting an intronic enhancer. Genome editing experiments of boundary locations harboring these SNPs combined with Hi-C assays could help examine the role of dysregulated 3D genome organization as a possible mechanism by which regulatory variants impact phenotype.
SNP enrichment in persistent boundaries. (A) Fold enrichment of SNPs in different subsets of boundary regions, across different categories (SNP parent terms). We measured the enrichment of SNPs in time point–specific boundaries (day 0–80) of cardiomyocyte differentiation, in boundaries common to the first two or the last two time points, in the union of boundaries (ANY), and in the intersection of boundaries across all time points (ALL). (B) A SNP landing in a boundary persistent across all time points (only day 0 and day 80 visualized here) and a CTCF binding site.
Discussion
Systematic characterization of the dynamics of three dimensional genome organization can improve our understanding of how this layer of regulation impacts phenotypic and molecular changes across different biological contexts, such as species, time, and developmental stages. Advances in genomic tools and concerted consortia-level efforts have produced a growing compendia of high-throughput chromosome conformation capture data sets (Dekker et al. 2017, 2023; Reiff et al. 2022). However, systematic analysis of these data sets to quantify the extent of change is a challenge, because of the multiple layers at which the 3D genome is organized and the paucity of tools to analyze data sets from a large number of contexts. To address this challenge, we developed TGIF that combines multitask learning with matrix factorization to examine the dynamics of 3D genome organization across multiple structural scales and biological conditions.
TGIF's design is motivated by a number of considerations. First, TAD and compartment identification are unsupervised learning problems with no ground truth for real Hi-C data sets. Because Hi-C data can be sparse, identification of such structures and assessment of how much they change could be susceptible to statistical, nonbiological differences. Second, several studies from multiple cell types, time points, and species have shown that TAD and compartments are conserved across species (Dixon et al. 2012; Vietri Rudan et al. 2015). TGIF's hierarchical, multitask learning framework exploits this prior information to constrain the identification of organizational structures while being sensitive to the extent of relatedness of the data sets by using a tree structure. Finally, TGIF is motivated by a dimensionality reduction (matrix factorization) framework to reduce the noisy, high-dimensional count profile of each genomic locus into a low-dimensional space of different ranks. This enables TGIF to be a general framework that identifies TADs, compartments, and subcompartments and their dynamics. The application of TGIF and existing methods to simulated and read Hi-C time course data sets showed that TGIF can accurately recover structural units such as compartments and TADs, while having a lower false-positive rate and greater robustness to technical differences between data sets such as depth, normalization, and resolution. TGIF also identifies biologically meaningful differences in 3D genome organization that are supported by numerous one-dimensional features such as architectural protein enrichment, histone modification, and differential expression.
An open question with topological domain changes is how they relate to changes in gene expression (Ghavi-Helm et al. 2019; Greenwald et al. 2019; Cavalheiro et al. 2021; McArthur and Capra 2021). At the TAD level, fusion or inversion of TADs could result in gene expression change, although the extent to which such changes are genome-wide or are specific to disease-associated genes is still unclear (Cavalheiro et al. 2021). Evidence suggests that RNA polymerase elongation or the binding of the preinitiation complex to DNA during transcription can give rise to domain structures, providing a direct mechanistic link between transcription and 3D genome organization (Heinz et al. 2018; van Steensel and Furlong 2019). This relationship can further depend upon the developmental stage or differentiation status of cells (Chen et al. 2024; Pollex et al. 2024). However, this has been debated in other studies, for example, during Drosophila development (Espinola et al. 2021; Ing-Simmons et al. 2021).
Using multisample mammalian data sets, we examined the propensity of DE genes to be close to differential boundaries and compartments. The enrichment of DE genes near differential boundaries is indicative of the impact of TAD changes to gene expression changes; furthermore, DE genes that were near differential boundaries were more significantly enriched for context-specific processes, which could indicate that such changes are associated with fine-tuning of gene expression during cellular differentiation. Finally, we observe a similar trend in regions participating in differential compartments, although to a lesser extent that TAD changes. Follow-up experiments that perturb boundaries and compartment structures coupled with gene expression measurements would be beneficial for teasing apart causal versus correlational relationships between chromatin organization and gene expression changes.
Regulatory sequence variants can misregulate gene expression by disrupting TAD boundaries (Lupiáñez et al. 2015; Chakraborty and Ay 2019). We used our TAD boundaries to examine the impact of this variation. We found the greatest enrichment in boundaries that did not change over time, namely, the persistent boundaries. Furthermore, we found several cardiovascular and metabolic disease trait SNPs to be enriched in these boundaries. These persistent boundaries may be specific to the entire cardiac tissue as a whole rather than a specific developmental time or stage. As future work, it would be worth investigating persistent boundaries in other developmental lineages and their propensity to prioritize SNPs for diseases in a tissue-specific manner. Additionally, this provides a way to prioritize variants for downstream functional experiments that could be important to identify the mechanisms by which variants disrupt gene regulatory processes.
There are a number of directions in which TGIF could be extended. One direction is to consider our benchmarking results and identify areas of improvement in which TGIF-DB is currently not the best method. For example, TGIF-DB has higher precision for task-specific boundaries in simulated data but at the cost of lower recall compared with that of TopDom. TGIF also finds a higher percentage of false-positive differential boundaries between biological replicates compared with TADCompare and does not significantly outperform dcHiC when comparing gene expression change within differential compartments. Such nonoptimal performance could be because of TGIF's regularization scheme, which shares information across contexts but does not explicitly capture differences between them. To address this limitation, TGIF's loss function could be extended to include a contrastive term. Another direction is to enable greater flexibility in capturing data set relatedness. Currently, TGIF uses the same hyperparameter value for all branches of the tree, which could be limiting when a more granular control is desirable to define the relationship between the data sets. An extension to TGIF could allow varying hyperparameter values depending upon the position in the hierarchy, as informed by auxiliary information such as phylogenetic branch length across species or gene expression similarity across cell types. A third direction of research is to consider auxiliary measurements, including sequence, to inform the inference of the topological units using techniques such as semisupervised clustering (Bondell and Reich 2008; Bair 2013).
Overall, TGIF is a flexible and robust framework to examine changes in genome organization at the compartment and TAD level across a large number of Hi-C data sets. As more data sets across diverse biological contexts become available, methods like TGIF are expected to be increasingly helpful to examine 3D genome organization dynamics and its impact on normal and disease processes.
Methods
TGIF
TGIF is based on multitask NMF (Lee and Seung 2000) and can be used to identify low-dimensional structures across multiple Hi-C data sets. The tasks in TGIF correspond to Hi-C data sets that in turn are from hierarchically related contexts, such as cellular stages, species, and time points. TGIF extends an existing framework, multiview NMF (Supplemental Methods; Liu et al. 2013; Baur et al. 2022), which assumes all the tasks are equally related. TGIF generalizes multiview NMF to allow for integration of data sets from different biological contexts such as time or developmental stage, and therefore, they may not all be equally related to each other.
Formally, TGIF takes as input t ∈ {1, …, T} matrices representing T tasks. Each matrix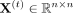 
is a symmetric Hi-C count matrix over n genomic loci. TGIF also requires as input a task tree that describes parent–child relationships between the tasks (Fig. 1A). Given these inputs, TGIF optimizes the following objective:
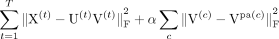(1)
The objective aims to
-
constrain a task-specific latent factor V(t) in a leaf node of the task hierarchy to be similar to VPa(t) in its parent node;
-
constrain an internal node's latent factor V(b) to be similar to its direct child nodes’ V(c) and its parent node's VPa(b); and
-
constrain the root node's latent factor V(r) to be similar to all of its direct child nodes’ V(b)s.
The hyperparameter α controls the strength of the constraints such that the higher the α, the more the factor V(c) is encouraged to be similar to its parent. Selection of α is discussed in the Supplemental Methods (see Supplemental Figs. S18–S21).
TGIF uses a block coordinate descent (BCD) optimization scheme to learn these factors because BCD guarantees convergence to a local optimum (Kim et al. 2014). Additional details of the TGIF algorithm can be found in the Supplemental Methods.
TGIF's factors can be used to find changes in compartments as well as changes in boundaries of finer-scaled TADs. TGIF-DB for differential boundary identification and TGIF-DC for identifying differential compartment regions are described in detail in subsequent sections.
TGIF-DB for differential boundary identification
TGIF-DB identifies TAD boundaries in four major steps: (1) multitask factorization of input Hi-C matrices, (2) boundary score computation, (3) empirical P-value calculation and FDR correction to detect significant boundaries, and (4) identification of sigDBs.
Multitask factorization of input Hi-C matrices
TGIF-DB applies TGIF to small partially overlapping submatrices along the diagonal of the symmetric intrachromosomal interaction count matrices (Supplemental Fig. S1A,B). This mirrors the approaches taken by existing TAD-calling methods (Lieberman-Aiden et al. 2009; Cresswell and Dozmorov 2020; Li et al. 2021). By default, each submatrix spans 2 Mb × 2 Mb with an overlap “step size” of 1 Mb between consecutive submatrices. The exact dimension of the submatrix, namely, the number of rows and columns, will depend on the resolution of the Hi-C data. The minimum size of the submatrices is bound at 100 (and the corresponding step size at 50) genomic regions to prevent overfragmentation of the input matrices, especially for lower-resolution input Hi-C matrices. Regions with interaction values missing for more than half of its neighbors in the radius defined by the window size in any of the input matrices are filtered out from the original input intrachromosomal matrices before any submatrices are formed. In NMF, usually the rank k of the lower-dimensional factors is user-specified. However, TGIF does not require this because a single k value may not be appropriate across all task-specific input submatrices. Instead TGIF scans a range of k values, with k ∈ {2, …, 8}, to recover lower-dimensional factors at multiple resolutions and defines boundaries based on a consensus of these factors (as described below). Because the submatrix size is small, it is computationally tractable to scan a range of k.
Boundary score calculation
After factorization, the next step is to identify genomic regions representing conserved or dynamic TAD boundaries across
conditions. We define a boundary as a region whose low-dimensional representation changes significantly compared with its
immediate preceding neighbor bin. To this end, we define a boundary score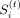 
using the output factors for each of the t tasks from TGIF. Because X(t) is symmetric, either U(t) or V(t) could be used to estimate these boundary scores. Assuming we use U(t), the score 
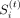for each region i in task t is the cosine distance between the low-dimensional representation of region i and region i − 1:
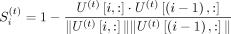(1)
The final boundary score for region i in task t is the mean of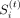 
estimated from factors across the range of k ∈ {2, …, 8} (Supplemental Fig. S1C). For regions that are in the overlapping window between two consecutive count submatrices, the final boundary score is averaged
from across all submatrix factors.
Empirical P-value calculation and FDR correction
Once the scores are calculated, we estimate a “null” distribution of boundary scores and use it to determine the empirical P-value of boundary scores and find significant boundaries. The null distribution is computed from a randomized background matrix (Supplemental Methods). We calculate the empirical P-value for each region i in task t as the proportion of “null” background scores higher than the given region's boundary score. Finally, to find significant boundaries and to correct for multiple significant testing, we perform the Benjamini–Hochberg procedure (Benjamini and Hochberg 1995). The output of the P-value and FDR estimation step is a binary value for each region i and task t, indicating whether the region has a significant boundary score (one) or not (zero). The significant boundaries identified in this manner may still be susceptible to noisy, low-count regions of the genome. Therefore, we additionally filter the boundaries to find “summit-only” versions of the significant boundaries; that is, if there is more than one consecutive significant boundary region along the linear genome, only the region with the highest significant score is called a boundary. To characterize the boundaries excluded by the summit-only approach, we compared both summit and nonsummit boundaries in H1–endoderm data. Nonsummit boundaries tend to be shared across cell types and comprise ∼50% of the total significant boundaries (Supplemental Fig. S15). The current implementation of TGIF-DB outputs both summit-only and all significant boundaries, allowing the user to use their own cut-offs.
sigDB regions in pairwise comparison of conditions
We provide a statistically significant subset of pairwise differential boundary regions (sigDBs). For a pair of conditions
with input Hi-C matrices, A and B, and for each genomic region i, we calculate the absolute difference in boundary scores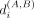 
between the two conditions. We estimate a null Gaussian distribution using the absolute difference of boundary scores of
genomic regions that do not have significant boundaries in either A and B. We calculate the Z-score and corresponding P-value of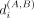 
for all regions using this null distribution. After FDR correction, we report the regions with an adjusted P-value <0.05 as sigDB regions. We further annotate the type of change represented by each sigDB between conditions A and B:
a boundary created in B, deleted in B, or shifted in B within five genomic bins (Supplemental Methods).
TGIF-DC for differential compartment and subcompartment identification
Identification of compartments with TGIF-DC
To identify compartments, we apply TGIF to a 100 kb resolution intrachromosomal Hi-C matrix that is first converted into an
O/E count correlation matrix as described previously by Rao et al. (2014). We upshift the correlation matrix by one so that all values are nonnegative. To identify compartments, we apply TGIF with
the input tree structure to these matrices with rank k = 2. After factorization, we infer each region i’s cluster assignment,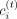 
, for each task t, such that 
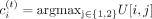. We refer to these clusters as compartments. To identify subcompartments and differential subcompartment regions, a higher
k value, for example, five, can be used, and TGIF-DC will generate more granular cluster assignments, for example, five clusters
of regions instead of two clusters. Each of these clusters corresponds to a subcompartment.
Detecting differential compartments with TGIF-DC
We provide a statistically significant subset of pairwise differential compartment regions. We utilize the lower-dimensional
representation of each genomic region from the factors in this step. For a pair of conditions or time points being compared,
A and B, we calculate the cosine distance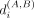 
between U(A)[i,:] and U(B)[i,:] for each genomic region i. Using the cosine distance of regions that do not change their cluster assignment between the conditions (i.e., static regions),
we estimate the mean and standard deviation of a Gaussian null distribution. The null distribution is used to calculate the
Z-score and P-value for the remaining (dynamic/differential) regions. Statistically significant differential regions are those with an
FDR < 0.05. Significantly differential subcompartment regions are identified in the same way as the differential compartment
regions.
Post hoc annotation of TGIF-DC clusters into A and B compartments
TGIF-DC by default uses k = 2 and segments the given chromosome into two clusters of regions. In our analysis, we use GC content and chromatin accessibility to annotate each cluster as an A or B compartment, in a manner similar to existing analysis and tools (Fortin and Hansen 2015; Kruse et al. 2020). Briefly, the cluster with higher mean accessibility signal (measured by ATAC-seq or DNase-seq) or GC content is assigned to an A compartment and the other cluster to a B compartment. Detailed annotation process for each of the developmental time course data sets can be found in the Supplemental Methods (see Supplemental Figs. S24, S25).
Estimating tree structure from input Hi-C matrices for unknown inter-data set relationships
When prior information about the relationship among the input matrices is not available, a tree structure can be estimated using pairwise similarity of the input Hi-C matrices, converting to distance followed by hierarchical clustering. We suggest the use of a distance-stratified similarity measure, such as the SCC (Supplemental Fig. S2A; Yang et al. 2017), which we have also used for our hyperparameter analysis (Supplemental Methods). Once SCC is calculated for each pair of input matrices, it is converted to a distance by subtracting from one (Supplemental Fig. S2B), which in turn is used as input to hierarchical clustering with average linkage. We tested this approach for the mouse neural differentiation data set and found that the output tree of hierarchical clustering is similar to the known biological relatedness of this data set (Supplemental Fig. S2C; Bonev et al. 2017) and is identical to the tree we used as input to TGIF for our experiments. The current implementation of TGIF offers this functionality as a preprocessing script (see Software Availability section).
Data sets used in analysis
We applied TGIF to three Hi-C time course data sets: H1 hESC differentiated to endoderm (Reiff et al. 2022; Dekker et al. 2023), mouse neural differentiation data from Bonev et al. (2017), and human cardiomyocyte differentiation data from Zhang et al. (2019). For processing, application of TGIF, and a list of accession numbers, see Supplemental Methods; Supplemental Figure S4, and Supplemental Tables S1–S4.
Benchmarking methods for identifying differential domain boundaries
Existing methods used in benchmarking TGIF-DB
TGIF-DB was benchmarked against four other methods for identifying differential TAD boundaries: GRiNCH (Lee and Roy 2021), SpectralTAD (Cresswell et al. 2020), TADCompare (Cresswell and Dozmorov 2020), and TopDom (Shin et al. 2016). GRiNCH, SpectralTAD, and TopDom are single-task TAD identification methods accepting a single input matrix individually followed by pairwise comparison of identified boundaries. TADCompare is a differential TAD identification method that can take as input a pair of Hi-C matrices as well as a time series of Hi-C matrices. These methods are described in more detail in the Supplemental Methods (see Supplemental Fig. S22).
Benchmarking on simulated data with known boundaries
To benchmark methods that can detect TAD-level changes, we generated simulated contact matrices with known TADs and TAD changes for four hierarchically related conditions (Supplemental Fig. S16). The TAD changes can fall into one of three categories: a TAD split creating a new boundary, a TAD merge removing a boundary, and a TAD shift, in which the location of a boundary is moved up or down the linear chromosome (Supplemental Fig. S16A; Cresswell and Dozmorov 2020). We first generate a set of TADs with known change patterns and then populate contact matrices following the Hi-C count simulation procedure in the benchmarking study by Forcato et al. (2017). The simulation procedure is detailed in the Supplemental Methods. We applied GRiNCH, SpectralTAD, TADCompare, TGIF-DB, and TopDom to the simulated data sets to assess their ability to recover shared and differential boundaries. We applied TADCompare to each pair of the four simulated matrices. TADCompare outputs differential boundaries, including the task in which the boundary is significant, and nondifferential boundaries, which we consider as shared boundaries. We applied single-task methods (GRiNCH, SpectralTAD, TopDom) to each of the four simulated matrices independently to identify the TADs for each input matrix. The resulting TAD boundaries for each pair of input matrices were compared to identify task-specific and shared boundaries. TGIF was applied to all four simulated matrices together with the known tree structure used to generate the simulated data (Supplemental Fig. S16C). We calculated the precision and recall of task-specific and shared boundaries in every pair of simulated matrices. Shared boundaries between simulated matrices A and B are boundaries found or identified in both A and B. Task-specific boundaries are boundaries found in A but not in B and vice versa.
Measuring CTCF enrichment in boundaries
To evaluate the boundaries identified by various TAD-calling methods, we measured CTCF peak enrichment in boundaries found in the cardiomyocyte differentiation data set (Supplemental Table S3). Using MACS2 (Zhang et al. 2008), we first called peaks on CTCF ChIP-seq data from each of the six time points (day 0, 2, 5, 7, 15, 80) of the cardiomyocyte differentiation time course. Replicates from each time point were collapsed by intersecting overlapping peaks with BEDTools (Quinlan and Hall 2010). Each peak was then assigned to a 10 kb uniform bin again using BEDTools. TAD-calling methods GRiNCH, SpectralTAD, and TopDom were applied to 10 kb Hi-C matrices from each of the six time points. TGIF-DB was applied to Hi-C matrices from all six time points using the tree structure in Supplemental Figure S4, and significant boundaries from each time point were used for enrichment analysis. TADCompare was applied to each pair of consecutive time points: day 0 versus day 2, day 2 versus day 5, day 5 versus day 7, day 7 versus day 15, and day 15 versus day 80. As TADCompare outputs both nondifferential and differential boundaries for every pairwise comparison, we define a boundary set specific to a time point as follows: (1) for day 0, the union of differential boundaries in day 0 and nondifferential boundaries between day 0 and 2; (2) for day 80, the union of differential boundaries in day 80 and nondifferential boundaries between day 15 and 80; and (3) for all intermediate time points t, the union of differential boundaries in t, nondifferential boundaries between day t and tprevious, and non−differential boundaries between day t and tfollowing. The CTCF peak fold enrichment ratio for a given time point was calculated as (q/M)/(s/N), where q is the number of boundaries with at least one CTCF peak, M is the number of boundary regions, s is the number of regions with at least one CTCF peak, and N is the total number of genomic regions.
Benchmarking with downsampled data to assess robustness to depth
We downloaded the high-depth Hi-C data set of GM12878 cell line (Rao et al. 2014) with 4.01 billion total reads from the 4D Nucleome data portal (Supplemental Table S4; Dekker et al. 2017; Reiff et al. 2022). We then subsampled 5%, 10%, 25%, and 50% of the reads, generated 10 kb-resolution intrachromosomal Hi-C matrices using Juicer (Durand et al. 2016), and ICE-normalized the intrachromosomal interaction matrices from each downsampled data set. We calculated Jaccard index by dividing the number of boundaries found at both depths by the number of boundaries identified in either depth for the GM12878 data set. The higher the Jaccard Index, the fewer the false-positive differences. Three TAD-calling methods, GRiNCH, SpectralTAD, and TopDom were applied individually to five data sets: original high-depth GM12878 data and four low-depth GM12878 data downsampled to 5%, 10%, 25%, and 50% depths, respectively. TADCompare and TGIF-DB were applied to four pairs of data sets, each pair including the original high-depth GM12878 data set and the downsampled low-depth data set (e.g., GM12878 data downsampled to 50% depth) (Supplemental Fig. S4). For TADCompare, the Jaccard index was calculated for each pair of data sets as the ratio of number of nondifferential boundaries and the number of differential and nondifferential boundaries. Similarly, for TGIF-DB, the Jaccard index was calculated as the ratio of the number of non-sigDB regions divided by the size of the union of boundary regions from the original-depth and subsampled data set.
Measuring stability of boundary sets across multiple resolutions of input data
We used the mouse neural differentiation data set (Bonev et al. 2017) to assess the stability of boundary sets identified by different TAD boundary identification methods at different resolutions, 10 kb, 25 kb and 50 kb, because this data set was readily available at these resolutions. We focused our comparisons only for the mESC time point. The single-task boundary calling methods (GRiNCH, SpectralTAD, TopDom) were applied individually to 10 kb, 25 kb, and 50 kb intrachromosomal matrices from mESCs. TADCompare was applied to a pair of time points including mESCs, both at the same resolution: mESCs versus NPCs and mESCs versus CNs. To find mESC boundaries from the outputs of the pairwise TADCompare comparisons at each resolution, we took the union of nondifferential boundaries and differential boundaries enriched in mESCs. We applied TGIF-DB to a tree with all three time points from mouse neural differentiation data set at a specific resolution, and we took the significant boundaries from mESCs (Supplemental Fig. S4). This was repeated for each resolution. To allow for comparison of boundaries from different resolutions, we projected the higher resolution bins to the coarsest resolution, namely, 50 kb. For instance, in the 25 kb versus 50 kb comparison, each 50 kb bin is composed of two 25 kb bins and is considered to have a boundary if either of the 25 kb bins had a boundary. Similarly, for the 10 kb versus 50 kb comparison, any of the five comprising 10 kb bins would be used to define a boundary in the 50 kb bin spanning them. In the 10 kb versus 25 kb comparison, if any of the 10 kb bins or the 25 kb bins have a boundary in the shared 50 kb bin, we define the 50 kb bin as a boundary. We then measure Jaccard index of boundaries at this lowest resolution.
Comparison of TGIF-DC to existing compartment-calling methods
We compared TGIF-DC to two established methods for calling compartments, namely, a principal component analysis (PCA)–based method (Lieberman-Aiden et al. 2009) and Cscore (version 1.1) (Zheng and Zheng 2018), as well as a method designed specifically for differential compartment analysis, dcHiC (version 2.1) (Chakraborty et al. 2022). Each method is described in detail in the Supplemental Methods (see Supplemental Fig. S23). We applied all four methods to 100 kb intrachromosomal count matrices from a H1 hESC cell line. TGIF-DC and dcHiC were additionally applied to 100 kb intrachromosomal count matrices from H1 differentiated to endoderm. Both data sets were downloaded from 4D Nucleome consortium (Reiff et al. 2022; Dekker et al. 2023). To compare the compartment results across the different methods, we measured the Rand index between compartment assignments to each genomic region. To measure the quality of the compartments, we used three well-known cluster quality metrics: SI, CH, and DBI, measured on the O/E matrices for each chromosome, as well as the accessibility signal for each 100 kb genomic region. The accessibility signal was defined as the mean ATAC-seq reads per base pair. Finally, to compare dcHiC and TGIF-DC for significantly differential compartments between H1 and the endoderm, we calculated the log ratio of the accessibility signal and gene expression (from RNA-seq, in TPM) in H1 over that of the endoderm for each significantly differential region.
Assessing differential gene expression near or within significantly differential boundaries and compartments
We used RSEM (Li and Dewey 2011) on the raw RNA-seq data from the cardiomyocyte differentiation and the mouse neural differentiation time course to obtain expected counts for each replicate at each time point. We also downloaded the RNA-seq data for a H1 hESC cell line and endoderm differentiated from H1 from 4D Nucleome (Reiff et al. 2022; Dekker et al. 2023). We used these values as input to DESeq2 (Love et al. 2014) to identify DE genes for every pair of time points in each data set (e.g., H1 vs. endoderm; mESC vs. NPC; day 0 vs. day 2 in cardiomyocyte differentiation). DE genes were defined by using a threshold of adjusted P-value <0.05.
For every pair of time points, we tested the enrichment of these DE genes within regions of interest (Fig. 5A): (1) regions near (i.e., within 100 kb) sigDBs, (2) regions within a TAD with at least one sigDB, and (3) regions within sigDCs. For set 2, we defined all regions bounded within a pair of shared boundaries and containing at least one sigDB within those bounds as belonging to a “TAD with at least one sigDB.”
The fold enrichment of DE genes in these regions was computed as (q/M)∕(s/N), where N is number of all regions; s=|set of regions with at least one DE gene|; M=|a subset regions of interest as defined above, for example, regions near sigDB|; and q=|regions of interest with at least one DE gene, for example, regions near sigDB with a DE gene|. We also performed gene-centric fold enrichment calculations: (qg/Mg)/(sg/Ng), where Ng is total number of genes with expression; sg=|DE genes|; Mg=|genes overlapping with a region of interest, for example, region near sigDB|; and qg=|DE genes overlapping with a region of interest|. A hypergeometric test was additionally performed to calculate the significance of this fold enrichment value for each pair of time points. We additionally examined the correlation between a gene's RNA-seq fold change and the raw boundary score change (positive or negative) of its nearest sigDB in the H1–endoderm data set. We found little to no correlation in the magnitude or the direction of change in gene expression and boundary strength (Pearson's corr = 0.03) (Supplemental Fig. S17).
Gene Ontology (GO) term enrichment analysis was performed for two different subsets of genes based on their DE status and whether they were close to (within 100 kb of) sigDB: (1) DE genes not close to a sigDB and (2) DE genes close to a sigDB. The significance of enrichment was determined with a FDR-corrected hypergeometric test P-value <0.05. To select candidate differential boundaries for visualization, we ranked a sigDB based on two criteria: (1) adjusted P-value of the change in TGIF-DB boundary score and (2) the significance of the nearby differential expression measured by the nearest DE gene's adjusted P-value. We converted these values into ranks and used the mean rank of a boundary to select the top 10 regions with promising differential boundaries.
SNP enrichment within TGIF boundaries from cardiomyocyte differentiation data
We downloaded SNPs in the GWAS catalog (Sollis et al. 2023) and mapped each SNP's associated trait to its parent phenotype, based on experimental factor ontology (EFO). We refer to these parent terms as SNP categories in our analysis. In total, we had 17 such categories (e.g., CVD), for which we tested enrichment of SNPs in TGIF-DB boundaries. For each category, we calculated the fold enrichment of associated SNPs in different subsets of TGIF-DB boundaries across different time points: boundaries found in a specific time point, boundaries found in the first two or the last two time points, boundaries found across all time points (ALL) (Fig. 7A), and boundaries found in any of the time points (ANY) (Fig. 7A). We used the following formula to calculate fold enrichment: (q/M)∕(s/N). Here, q is the number of boundaries of a particular type (e.g., ANY) with at least one SNP of interest, M is the number of boundaries of a particular type (e.g., ANY), s is the number of regions containing at least one SNP, and N is the total number of genomic regions.
Software availability
TGIF-DC and TGIF-DB, along with scripts used for evaluation, analysis, and visualization are available as Supplemental Codes S1, S2, and S3; at GitHub (https://github.com/Roy-lab/tgif); and at Zenodo (https://doi.org/10.5281/zenodo.13323898).
Competing interest statement
The authors declare no competing interests.
Acknowledgements
This work is supported by the National Institutes of Health (NIH) through the grant NIH National Human Genome Research Institute R01-HG010045-01 and by the Computation and Informatics in Biology and Medicine (CIBM) training program (U.S. National Library of Medicine 5T15LM007359). We thank the Center for High-Throughput Computing at the University of Wisconsin–Madison for computational resources. We also thank Yanxiao Zhang and Bing Ren for providing the list of HERV-H retrotransposon site coordinates and their expression levels.
Author contributions: D.-I.L. and S.R. conceptualized the overall framework and algorithm. D.-I.L. implemented the algorithm, designed and performed experiments, and wrote the manuscript. S.R. designed the experiments and wrote the manuscript.
Footnotes
-
[Supplemental material is available for this article.]
-
Article published online before print. Article, supplemental material, and publication date are at https://www.genome.org/cgi/doi/10.1101/gr.279930.124.
- Received August 15, 2024.
- Accepted February 20, 2025.
This article is distributed exclusively by Cold Spring Harbor Laboratory Press for the first six months after the full-issue publication date (see https://genome.cshlp.org/site/misc/terms.xhtml). After six months, it is available under a Creative Commons License (Attribution-NonCommercial 4.0 International), as described at http://creativecommons.org/licenses/by-nc/4.0/.
