Theoretical framework for the difference of two negative binomial distributions and its application in comparative analysis of sequencing data
Abstract
High-throughput sequencing (HTS) technologies have been instrumental in investigating biological questions at the bulk and single-cell levels. Comparative analysis of two HTS data sets often relies on testing the statistical significance for the difference of two negative binomial distributions (DOTNB). Although negative binomial distributions are well studied, the theoretical results for DOTNB remain largely unexplored. Here, we derive basic analytical results for DOTNB and examine its asymptotic properties. As a state-of-the-art application of DOTNB, we introduce DEGage, a computational method for detecting differentially expressed genes (DEGs) in scRNA-seq data. DEGage calculates the mean of the sample-wise differences of gene expression levels as the test statistic and determines significant differential expression by computing the P-value with DOTNB. Extensive validation using simulated and real scRNA-seq data sets demonstrates that DEGage outperforms five popular DEG analysis tools: DEGseq2, DEsingle, edgeR, Monocle3, and scDD. DEGage is robust against high dropout levels and exhibits superior sensitivity when applied to balanced and imbalanced data sets, even with small sample sizes. We utilize DEGage to analyze prostate cancer scRNA-seq data sets and identify marker genes for 17 cell types. Furthermore, we apply DEGage to scRNA-seq data sets of mouse neurons with and without fear memory and reveal eight potential memory-related genes overlooked in previous analyses. The theoretical results and supporting software for DOTNB can be widely applied to comparative analyses of dispersed count data in HTS and broad research questions.
Following the completion of the Human Genome Project in 2001, high-throughput sequencing (HTS) emerged as one of the most important and fundamental techniques in the biological sciences, supporting a wide range of research projects (Hawkins et al. 2010; Metzker 2010; McCombie et al. 2019). Since 2003, HTS techniques have been applied to many novel, high-throughput experiments, including RNA-seq (Wang et al. 2009), ChIP-seq (Park 2009), whole-genome sequencing (WGS) (Cirulli and Goldstein 2010), ATAC-seq (Buenrostro et al. 2015), CAPTURE-3C-seq (Liu et al. 2017), and Hi-C (Dixon et al. 2012; Rao et al. 2014). These bulk omics experiments significantly increased our understanding of complex biological processes, including gene expression, transcriptional regulation, and 3D genomic architecture. Recently, HTS has also been applied to single-cell omics experiments, such as scRNA-seq (Ding et al. 2020; Vandereyken et al. 2023), scATAC-seq (De Rop et al. 2023), and scHi-C (Ramani et al. 2017; Lee et al. 2019), enabling the study of biological systems at the single-cell level. Single-cell applications of HTS provided us with new insights into cellular heterogeneity, cell-to-cell variability, and rare cell populations that are difficult to detect using bulk-based methods. Comparing data sets sampled from different experimental conditions is a common analytical approach for both single-cell and bulk HTS data analysis and is critical for delineating the molecular dynamics underlying fundamental biological processes and disease pathology. In current computational tools of comparative analysis, the negative binomial (NB) is the most widely used distribution to model the abundance of read counts within genes or chromosomal regions (Grün et al. 2014; Svensson 2020). Therefore, the comparison of two data sets involves testing for a significant difference between two NB distributions. Consider the following example of comparative analysis, which is standard in the field: In scRNA-seq data, read counts within a gene region are considered to represent the expression level of that gene in a cell, and the expression levels among a group of cells (i.e., a cell type) are fitted as an NB distribution. For each gene, the changes in its expression between two groups of cells can be tested for statistical significance by using the distribution of the difference of two NB distributions (DOTNB). However, basic theoretical results on DOTNB are still lacking in statistics.
The NB distribution, denoted by NB(λ, p), is an important probabilistic model that represents the distribution of the number of trials until the first λ failures in Bernoulli trials with the failure probability p. It was first initiated by Pascal in 1679 and given its earliest concrete formulation in 1741 by Montmort (Bartko 1962). Over the past century, NB distribution has been extensively examined, and several generalizations have been studied (Patil et al. 1986; Gupta and Ong 2004; Vellaisamy and Upadhye 2007; Zörnig 2014). For instance, when given a finite set of probability mass functions (PMFs) of NB distributions, the weighted NB is defined
as their convex combination 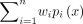 , where
, where 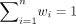 and wi > 0. Such a convex combination of NB PMFs preserves properties such as nonnegativity and integrating to 1, and thus, mixture
densities are themselves PMFs. However, the nonconvex combination of PMFs is more challenging and limited results are available
for review. Specifically, if
and wi > 0. Such a convex combination of NB PMFs preserves properties such as nonnegativity and integrating to 1, and thus, mixture
densities are themselves PMFs. However, the nonconvex combination of PMFs is more challenging and limited results are available
for review. Specifically, if 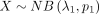 and
and 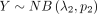 , what is the distribution for DOTNB, Z = X − Y? In 2014, Lekshmi and Sebastian (2014) provided partial analytic results for a special case, in which two independently distributed NB random variables have the
same dispersion parameter λ1 = λ2. However, the derivation of basic analytic results of the general case, in which λ1 ≠ λ2, remains an open question. This leaves a major gap in comparative analysis of HTS data sets, in which the distributions of
read counts for genes or chromosomal regions from two experiments should be reasonably considered independent.
, what is the distribution for DOTNB, Z = X − Y? In 2014, Lekshmi and Sebastian (2014) provided partial analytic results for a special case, in which two independently distributed NB random variables have the
same dispersion parameter λ1 = λ2. However, the derivation of basic analytic results of the general case, in which λ1 ≠ λ2, remains an open question. This leaves a major gap in comparative analysis of HTS data sets, in which the distributions of
read counts for genes or chromosomal regions from two experiments should be reasonably considered independent.
The lack of theoretical results on DOTNB significantly limits the comparative analysis of diverse bulk and single-cell omics data types. Take scRNA-seq as an example: Various methods are available for detecting differentially expressed genes (DEGs) in case-versus-control scRNA-seq data sets, including SCDE (Kharchenko et al. 2014), scDD (Korthauer et al. 2016), D3E (Delmans and Hemberg 2016), Monocle3 (Qiu et al. 2017), DyNB (Äijö et al. 2014), SINCERA (Guo et al. 2015), DEsingle (Miao et al. 2018), SigEMD (Wang and Nabavi 2018), EMDomics (Nabavi et al. 2016), edgeR (Robinson et al. 2010), DESeq2 (Anders and Huber 2010), glmmTMB (Brooks et al. 2017), DEGman (Zhang et al. 2022), NEBULA (He et al. 2021), and MAST (Finak et al. 2015). Although most of these methods use the NB distribution to model gene expression levels in a group of cells, they all rely on heuristic approximations or empirical distributions to test the significance of the difference in gene expression between two cell groups. For example, SCDE calculates an empirical P-value for testing differential expression, whereas MAST uses a test with asymptotic chi-square null distribution and a false-discovery rate (FDR) adjustment control to determine whether a gene is differentially expressed. DyNB uses NB distributions and Gaussian processes to model gene expression levels and uses Markov chain Monte Carlo (MCMC) sampling for DEG detection. edgeR models gene counts as NB distributions and then uses an empirical test with FDR control to determine DEGs. DESeq2 is also based on NB distribution and uses generalized linear models (GLMs) as well as a likelihood ratio test (LRT) for detecting DEGs. However, these testing strategies are affected by different noise levels, different sequencing depths, low sensitivities for small sample/cell sizes (Wang et al. 2019), and high false-positive (FP) rates (Squair et al. 2021; Das et al. 2022). Notably, they lead to substantial disagreement between DEG analysis methods (Mou et al. 2019; Wang et al. 2019) and can result in different DEG sets even when using the same method of analysis (Lytal et al. 2020). Furthermore, existing methods have limited capabilities for comparative analysis of rare cell types for which cell numbers are in the tens, because small cell numbers usually cannot provide effective random sampling (e.g., MCMC sampling) for heuristic approximations or estimating empirical distributions. Finally, these methods are time-consuming when applied to large single-cell data sets (i.e., tens of thousands of cells) because of the large iterations in sampling processes. In addition to scRNA-seq, these technical limitations are also observed in scHi-C and in bulk omics data such as RNA-seq, ChIP-seq, and Hi-C.
To address the theoretical and practical limitations, we derive the basic analytic properties of DOTNB, including its PMF, cumulative distribution function (CDF), moments, and asymptotic behaviors. As a state-of-the-art application of DOTNB, we introduce DEGage, a novel method for detecting DEGs between two scRNA-seq data sets. DEGage accepts raw counts as inputs, effectively avoiding biases introduced by artificial normalization steps prevalent in existing methods. Extensive validations on both the simulated and real scRNA-seq data sets indicate that DEGage surpasses the performance of five popular DEG analysis tools. Notably, DEGage displays exceptional robustness against high dropout noise levels, offers rapid processing for scRNA-seq data containing large numbers of cells, and displays high sensitivity when applied to rare cell types with small numbers. These findings indicate that the theoretical advancements in DOTNB facilitate more precise statistical testing and enriched result interpretations. To promote broader application of DOTNB, we implemented basic functions for DOTNB across several programming languages (Python, R, Perl, MATLAB, and C++), which can be seamlessly integrated to augment existing computational methods and catalyze the inception of novel strategies for comparative analysis in HTS data and beyond.
Results
Analytic results for DOTNB and comparative analysis of HTS data
Here, we first derive basic probability functions for the DOTNB distribution that describes the difference between two independent
NB distributions 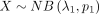 and
and 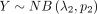 ; that is,
; that is, 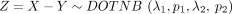 .
.
Suppose that 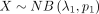 and
and 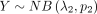 are independent variables, the variable Z = X − Y follows DOTNB (λ1, p1, λ2, p2) distribution. We have the following:
are independent variables, the variable Z = X − Y follows DOTNB (λ1, p1, λ2, p2) distribution. We have the following:
-
Its PMF is
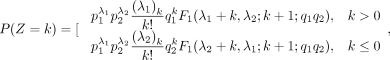 where
where 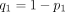 ,
, 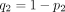 ,
, 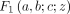 is a Gaussian hypergeometric function (GHF), and (q)n is the Pochhammer symbol, that is,
is a Gaussian hypergeometric function (GHF), and (q)n is the Pochhammer symbol, that is,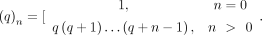
-
Its mean is
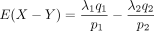 , and the variance is
, and the variance is 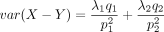 .
.
Theorem 1 establishes the PMF function and moments of DOTNB (see proofs in Methods). The results describe that DOTNB is an
asymmetric distribution defined over integers. Its CDF can be calculated as 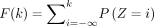 . Because 0 < p1 < 1, we have
. Because 0 < p1 < 1, we have 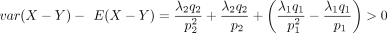 ; that is, its variance is greater than the mean. Thus, the DOTNB distribution is suitable for modeling overdispersed data
sets.
; that is, its variance is greater than the mean. Thus, the DOTNB distribution is suitable for modeling overdispersed data
sets.
We also obtain two corollaries to describe DOTNB's asymptotic properties, indicating that the long-tail shapes are asymptotically defined by the two NB distributions respectively (see proofs in Methods).
When k → +∞, 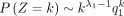 and k → −∞,
and k → −∞, 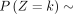
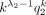 .
.
When k → +∞, 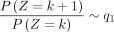 and k → −∞,
and k → −∞, 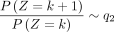 .
.
Here, Corollary 1 states that the probability is asymptotically determined by the subtrahend NB when k goes to positive infinity, whereas the probability is asymptotically determined by the minuend NB when k goes to negative infinity. Corollary 2 estimates the probability changes for large k, that is, it converts to q1 for positive k and to q2 for negative k.
Although the DOTNB can be simulated using two NB distributions, the accuracy of empirical distribution estimations is significantly
influenced by sample sizes. In Supplemental Figure S1, histograms show simulation examples of the random differences of two NB distributions (black lines), and their corresponding
theoretical DOTNB PMFs are shown as red lines. In particular, Supplemental Figure S1A shows 100,000 samples of 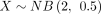 and
and 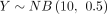 . The theoretical distribution DOTNB(2, 0.5, 10, 0.5) is skewed to the second quadrant and simulated by the two NB distributions. Supplemental Figure S1B shows 100,000 samples of
. The theoretical distribution DOTNB(2, 0.5, 10, 0.5) is skewed to the second quadrant and simulated by the two NB distributions. Supplemental Figure S1B shows 100,000 samples of 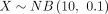 and
and 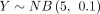 and the DOTNB(10, 0.1, 5, 0.1). Please note that when the sample sizes are reduced from 100,000 (Supplemental Fig. S1B) to 10,000 (Supplemental Fig. S1C) and 2000 (Supplemental Fig. S1D), the histograms of DOTNB simulations show increased noise variations (black signals), which will significantly affect the
precision of fitting empirical distributions. This observation partially explains why these comparative analysis methods usually
rely on large random sampling iterations and have low sensitivity when small samples are used. Thus, applying our closed forms
of DOTNB can achieve high sensitivity for small samples and can avoid large runtimes for large sample sizes, improving the
reliability and performance of comparative analysis of HTS data.
and the DOTNB(10, 0.1, 5, 0.1). Please note that when the sample sizes are reduced from 100,000 (Supplemental Fig. S1B) to 10,000 (Supplemental Fig. S1C) and 2000 (Supplemental Fig. S1D), the histograms of DOTNB simulations show increased noise variations (black signals), which will significantly affect the
precision of fitting empirical distributions. This observation partially explains why these comparative analysis methods usually
rely on large random sampling iterations and have low sensitivity when small samples are used. Thus, applying our closed forms
of DOTNB can achieve high sensitivity for small samples and can avoid large runtimes for large sample sizes, improving the
reliability and performance of comparative analysis of HTS data.
With this general framework established, we can apply DOTNB to various HTS data types for the comparative analysis of two independent data sets. Typical examples include but are not limited to
-
DEG analysis for scRNA-seq. In this application, the expression counts of each gene in two data sets are fit as independent NB distributions. Then the DOTNB is used to estimate the theoretical difference, and significance testing can be performed to detect DEGs. As a state-of-the-art application, we introduce DEGage in the following section for the DEG analysis of two scRNA-seq data sets.
-
Comparative analysis of chromosomal regions/peaks across two ChIP-seq data sets. Peak densities of ChIP-seq data are usually estimated as NB distributions in multiple ChIP-seq analysis tools, including MACS2 (Zhang et al. 2008). Thus, the comparative analysis of a chromosomal region/peak across two ChIP-seq data sets is also a test of the difference between two NB distributions. Here, similar to application 1, the NB distributions of raw read counts of peaks for multiple samples under different conditions can be estimated.
-
Chromatin interaction dynamics. In computational analysis of 3D chromatin interaction data, for example, Hi-C (Dixon et al. 2012) or CAPTURE-3C-seq (Liu et al. 2017), the chromatin interaction strengths among bin-pairs are described as NB distributions in several computational tools (Rao et al. 2014; Liu et al. 2017; Chen et al. 2020; Sahin et al. 2021). The chromatin interaction dynamics of enhancer–promoter interactions, or of loop bin-pairs among two biological conditions, can be tested by using the DOTNB model.
It is important to note that applying DOTNB to HTS data analysis has a significant advantage in that sequence depths of two data sets do not need to be normalized by total sequence reads. This is important because normalization strategies employed by existing analysis tools can introduce distinct genome-wide biases. These biases may be further amplified when analyzing genes that exhibit exceptionally high or low expression levels. In contrast, DOTNB operates under the assumption that the model parameters for the two data sets are independent, leading to a framework better suited for calculations involving read counts. Furthermore, DOTNB allows for the direct estimation of parameters from the raw reads, effectively circumventing artificial effects introduced by normalizing individual genes based on total sequencing reads.
DEGage shows high performance on simulated and real scRNA-seq data
To demonstrate the practical application of DOTNB to analysis of HTS data, we developed DEGage, a new computational tool for identifying DEGs in scRNA-seq data (for further details, see Methods) (Fig. 1). After performing quality control processes that remove genes with lower expression and outlier cells, the expression levels of each gene (raw counts) are modeled as two independent NB distributions for the two conditions that will be compared. A P-value for each gene is then calculated using the DOTNB CDF function to test the significance of differences in gene expression. Unlike other methods that rely on approximation or empirical techniques, DEGage directly estimates NB distributions for two scRNA-seq data sets and conducts significance testing using DOTNB.
Computational workflow of DEGage. DEGage takes two scRNA-seq data sets as inputs and utilizes the DOTNB distribution as the core statistical model to test the significance of gene expression profiles of the two data sets. It outputs multiple types of information suitable for downstream analysis.
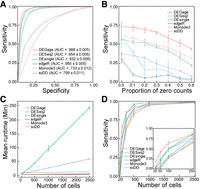
To evaluate the performance of DEGage, we analyzed multiple large-scale scRNA-seq data sets and compared the results to those obtained with five popular methods for DEG analysis: DEsingle, DESeq2, edgeR, Monocle3, and scDD (Supplemental Table S1). Initially, we benchmarked the performance of DEGage on simulated data sets with varying gene expression levels across two conditions by generating 10 data sets containing 2000 DEGs and 18,000 equivalently expressed (EE) genes using scDD's simulation framework (Korthauer et al. 2016). We applied these six DEG analysis tools to the simulated data and computed their average performances. The benchmarking results demonstrate the superior performance of DEGage across multiple critical evaluation metrics, including the number of detected DEGs, sensitivity, specificity, precision, accuracy, and the F1 score (Supplemental Table S2). Notably, DEGage stands out with the highest sensitivity score (0.812), highlighting its ability to correctly identify a substantial portion of DEGs. Furthermore, DEGage achieves the highest F1 score (0.765), effectively striking a harmonious balance between sensitivity and specificity. In contrast, edgeR, Monocle3, and scDD exhibit the lowest sensitivities among all evaluated packages, each falling below the 0.600 threshold. Additionally, Monocle3 presents notably low specificity and a markedly low F1 score (0.222), emphasizing its limitations in correctly classifying DEGs. To provide a visual representation of the performance, we calculated the receiver characteristic curves (ROCs) (Fig. 2A) to illustrate the trade-off between true-positive (TP) and true-negative (TN) rates. Among the area under the curve (AUC) values for the six methods, DEGage emerges with the highest AUC value (0.968). Conversely, Monocle3 records the lowest AUC value (0.733), mirroring its suboptimal sensitivity and specificity. The elevated sensitivity demonstrated by DEGage aligned with our expectations, as the theoretical foundations of DOTNB are designed to yield enhanced statistical power, bolstering its ability to identify DEGs accurately.
Computational performance of DEGage. (A) ROCs show the performances of six methods on simulated data. (B) The effect of dropout proportions on the sensitivities of the six methods. (C) Runtimes of each method with varying numbers of cells. (D) Sensitivities of each method with different numbers of cells.
In addition to the simulated data analysis, we also evaluated the six tools on positive and negative control data sets derived from real scRNA-seq experiments. The positive control data set contained 48 mouse embryonic stem cells and 44 mouse embryonic fibroblasts (Islam et al. 2011). We used a gold-standard gene set, which contains DEGs validated by PCR experiments (Moliner et al. 2008; Kharchenko et al. 2014), to evaluate the sensitivity of each tool. DEGage displays strong performance by identifying 6626 genes with an FDR < 0.05 in the positive control data set, achieving an acceptable level of sensitivity (0.501) (Supplemental Table S3). Although the sensitivity of DEGage ranks slightly lower than that of DEsingle (0.610), it is important to note that DEsingle returns significantly more DEGs, surpassing DEGage by 2003 genes. This increased sensitivity of DEsingle comes at the cost of lower specificity, as indicated by its results. In the context of the negative control data set, DEGage returns a minimal number of detected DEGs (198.5) and a high specificity score (0.984). This highlights the ability of DEGage to accurately discern the absence of differential gene expression and prevent FP identifications. In summary, DEGage demonstrates robust and reliable performance in distinguishing true differential gene expression from random noise.
DEGage is robust against dropouts and supersensitive to DEGs in rare cell types
Dropout counts occur when a gene is detected in one cell but not in another cell of the same type, a phenomenon caused by the low capture efficiency of scRNA-seq methods. This creates count sparsity, limiting the view of the transcriptomic characteristics of a gene and posing a major challenge in scRNA-seq data analysis (Qiu 2020; Xu et al. 2022). We evaluated the robustness of the six methods against different levels of dropout noise using data simulated according to an NB distribution with zeros randomly introduced to simulate dropout events. Among the six methods, DEGage is the most robust against dropout noise across all proportions (Fig. 2B). Monocle3 is the second most robust method against dropouts and performs better than DEsingle. Notably, methods that are specifically designed for scRNA-seq data (DEGage, DESingle, Monocle3, and scDD) tended to show linear rates of decline in sensitivity. Meanwhile, methods that were developed for bulk RNA-seq (DESeq2, edgeR) show steeper rates of decline initially and leveled out at larger dropout proportions, suggesting they may be less suitable for use on scRNA-seq data sets with high proportions of dropouts.
Next, we investigated the effect of cell numbers on runtimes, as scRNA-seq data sets can include tens of thousands of cells. Because DEGage leverages the advantages of the closed forms of DOTNB, it is expected to offer fast runtimes in data processing. We compared the runtimes of the six packages on simulated data sets and found that DEGage is faster than other DEG analysis tools. We varied cell numbers from 20 to 2500, where 20 represents the typical number of cells for rare cell types. Results show that DEGage has similar runtimes to those of edgeR and Monocle3 across all numbers of cells (<20 min per 2500 cells), which are based on heuristic testing methods. Meanwhile, DESingle and scDD are significantly slower than other packages (Fig. 2C). Additionally, we observed that DEGage exhibits very small variation among runtimes for different cell numbers, whereas other methods show larger variances. Taken together, the results show that DEGage is robust against dropout noise while maintaining relatively high running speed for processing scRNA-seq data sets.
Although scRNA-seq data has been used to identify rare cell types (Wegmann et al. 2019; Fa et al. 2021), DEG analysis for those rare cell types remains challenging because the limited sample sizes reduce the power to detect statistically significant differences (Das et al. 2022). With the introduction of DOTNB distribution, we predict that DEGage will remain sensitive even for rare cell types with small sample sizes. To test this, we benchmarked the sensitivities of six tools on cell numbers ranging from 20 to 2500 (Fig. 2D). DEGage has the highest sensitivity between 20 and 250 cells, suggesting it is an effective tool for detecting DEGs in rare cell populations. Furthermore, the sensitivities of all packages increased with cell numbers, and the curves come to mature around 1000 cells, indicating that 1000 could be an ideal sample size for testing with these methods.
DEGage performs well on imbalanced data sets
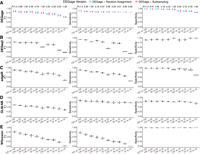
Many biological experiments frequently obtain different sample sizes, leading to imbalanced scRNA-seq data sets for comparative analysis. This imbalance presents a significant issue as it can impact statistical power and reduce reproducibility across different runs (Mou et al. 2019; Lytal et al. 2020). Subsampling strategy is frequently used in many available tools for comparative analysis to address the imbalance in sample sizes (Anders and Huber 2010; Robinson et al. 2010). However, subsampling can leave a numerous cell in a large data set unused. To address this challenge, we implemented two sampling strategies with DEGage: One, by default, involves subsampling the large data set to pair with each cell in the small data set (named subsampling), whereas the other involves pairing each cell in the large data set with a randomly selected cell in the smaller data set (named random assignment). We conducted tests to assess how these two sampling strategies affect DEGage's performance on imbalanced sample sizes, ranging from 10 to 100 cells. To better mimic the complexity in real scRNA-seq data, we also included three other parameters in the simulation: effect size, dispersion, and dropout levels. The effect size is defined as the log2 fold changes of expression levels of a gene between two conditions, and the dispersion controls the variability or spread of the data around the mean of an NB distribution (Love et al. 2014). Here, the effect size was uniformly sampled in the range of (1, 7.5), and the dispersion was uniformly sampled in the range of (0.1, 10). Meanwhile, each gene in all data sets was randomly assigned dropout levels in the range of (0.1, 0.5). The validation results demonstrate that DEGage performs well with both sampling strategies but exhibits slight differences across different imbalanced data sets (Fig. 3A; Supplemental Tables S4–S6). First, we confirmed that, for both sampling strategies, DEGage achieves high performance according to the criteria of F1, sensitivity, and specificity while maintaining small variances in 10 replicates. Specifically, in all seven combinations of different cell sizes, sensitivity scores exceed 0.8. Specificity scores exceed 0.8, and F1 scores exceed 0.65, except for very small cell sizes of 10 versus 10 (specificity of 0.79 and F1 of 0.51). Second, we observed slightly varied performance in imbalanced data sets when employing different sampling strategies. Specifically, the subsampling strategy yielded generally higher sensitivity scores than the random assignment strategy, and the random assignment strategy exhibits slightly higher specificity scores. F1 scores, which balance both sensitivity and specificity, show that the random assignment strategy performs slightly better than the subsampling for imbalanced data sets. However, no significant difference in F1, sensitivity, and specificity scores was obtained between the two subsampling strategies (Student's t-test, two-sided) (Fig. 3A). These results suggest that random assignment is a useful approach for fully utilizing gene expression signals across all cells in the large data set when comparing with a relatively small data set.
Performance evaluation of DEGage on imbalanced data sets. (A) Comparison of DEGage's performance between the random assignment and the subsampling strategy. F1, sensitivity, and specificity scores were calculated for 10 combinations of balanced and imbalanced data sets. Each boxplot represents the scores across 10 replicates. The P-values were calculated using a two-sided Student's t-test. Performance of DESeq2 (B), edgeR (C), GLM.NB (D), and Wilcoxon test (E) on imbalanced data sets. Detailed scores are presented in Supplemental Tables S4–S6.
We compared DEGage's performance with four other popular methods (DESeq2, edgeR, the Wilcoxon test, and the GLM.NB method) using different parameter settings for effect size, dispersion, and imbalanced sample sizes. We included the Wilcoxon test because it is a nonparametric method widely used for comparing two imbalanced data sets. Meanwhile, MASS's GLM offers a regression-based LRT for the difference in the mean rates of two NB distributions (named GLM.NB) (Venables and Ripley 2002). First, we observed that DEGage achieves the highest F1 and sensitivity scores across combinations of small and strong imbalanced data sets: 10 versus 10, 25 versus 10, 25 versus 25, 50 versus 10, 50 versus 25, 50 versus 50, and 100 versus 10 (Fig. 3A–E; Supplemental Tables S4–S6). Meanwhile edgeR has slightly better F1 scores for two relatively large data sets: 100 versus 50 and 100 versus 100 (Fig. 3C), and DESeq2 has better sensitivity scores for 100 versus 25, 100 versus 50, and 100 versus 100 (Fig. 3B). Additionally, we observed that edgeR maintains better F1 scores than DESeq2 across most combinations. The Wilcoxon test exhibits the highest specificity across all combinations, but the poorest sensitivity (Fig. 3E), eventually resulting in lower F1 scores than those of parametric test methods like edgeR, DESeq2, and DEGage. The GLM.NB method achieves fair sensitivity and specificity scores (Fig. 3D), resulting in slightly better F1 scores than Wilcoxon but lower than DEGage and edgeR. Considering that both DEGage and GLM.NB utilize the same procedure to estimate gene expression levels as NB distributions, the better performance of DEGage across all 10 combinations indicates that the usage of closed forms of DOTNB is more effective than the LRT in testing the difference between NB-based scRNA-seq data sets.
We then investigated how different effect sizes and dispersions affect the performance of DEG detection by plotting the F1, sensitivity, and specificity scores for different parameter combinations. First, we observed that DEGage generally achieves better F1 scores for different dispersion settings of 0.1, 0.5, one, five, and 10, especially for small effect sizes of 1.5 and small sample sizes of 10 versus 10 (Supplemental Fig. S2). The GLM.NB shows decreasing F1 scores for large dispersions of five and 10, whereas Wilcoxon has the poorest F1 scores for small dispersions of 0.1 and 0.5. Second, all methods show increasing sensitivity for larger dispersions (Supplemental Fig. S3). DEGage and GLM.NB have better sensitivity scores than edgeR, DESeq2, and Wilcoxon on small sample sizes, that is, 10 versus 10 and 25 versus 10. Wilcoxon has the poorest sensitivity scores, especially for small dispersions of 0.1. Third, all methods generally show good specificity scores for different dispersions, sample sizes, and effect sizes (Supplemental Fig. S4). Among them, Wilcoxon has the best and most stable specificity scores (greater than 0.99) for different dispersions. Notably, GLM.NB achieves decreased F1 and specificity for large dispersions (Supplemental Figs. S2, S4). Taken together, these results on small imbalanced data sets (100 or fewer cells) and different parameter settings indicate that both the subsampling strategy and random assignment strategy integrated in DEGage outperform other methods. Moreover, these findings corroborate our observations in Figure 2D, further demonstrating DEGage's superior performance in detecting DEGs when comparing small data sets.
DEGage detects marker genes across diverse cell types in prostate cancer
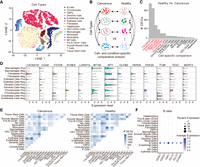
To further assess the potential value of DEGage for analyzing real scRNA-seq data, we tested it on a data set of human prostate cells taken from patients and healthy controls (Heidegger et al. 2022). After quality control, a total of 24,926 cells remained. First, we annotated cell types with SingleR (Aran et al. 2019), resulting in a total of 17 cell types for both cancerous and healthy conditions (Fig. 4A). Next, we used DEGage to assess DEGs under two scenarios: (1) in the same cell types under cancerous and healthy conditions and (2) across different cell types within same condition (Fig. 4B). It is worth noting that the sample sizes of these cell types vary greatly, ranging from 25 (HSC CD34+ cells) to 8404 (epithelial cells). This includes five cell types with fewer than 100 cells and five cell types with more than 1000 cells (Supplemental Table S7). Thus, the comparisons among these cell types represent varying degrees of imbalance, particularly between frequent and rare cell types.
DEGage detects canonical prostate cancer markers across multiple cell types. (A) t-SNE embeddings of 24,926 human prostate cancer cells. (B) Organization of analyses with DEGage on the Heidegger data set. (C) The number of DEGs detected between cancerous and healthy conditions of the same cell type. The HVCTs are indicated in red. (D) Prostate cancer marker genes detected by DEGage in HVCTs. Expression levels of each gene are shown for both cancerous and healthy conditions of each cell type. (E) The number of DEGs detected between each cell type under cancerous and healthy conditions, respectively. (F) Marker genes detected by DEGage in healthy B cells.
Results for the first scenario reveal six cell types that exhibit a significantly higher number of DEGs: fibroblasts (716), dendritic cells (615), epithelial cells (266), macrophages (178), chondrocytes (99), and endothelial cells (99) (Fig. 4C; Supplemental Table S8). Because of the relatively large number of DEGs in these cell types compared with others, we categorized them as highly variable cell types (HVCTs) in prostate cancer. Upon manual examination of these DEGs, we discovered that many of them had been previously detected in other research studies (Supplemental Table S9). Out of all these markers, we consistently observed overexpression of NPY across HVCTs under cancerous conditions (Fig. 4D). Additionally, other markers were associated with more cell type–specific processes, such as CACNA1D overexpression, which modulates androgen receptor transactivation in fibroblasts (Chen et al. 2014), resulting in transcriptional regulation of cancer-associated fibroblast activation (Clocchiatti et al. 2018).
When comparing different cell types, DEGage consistently detects reasonable numbers of DEGs in line with the dissimilarity between the cell types (Fig. 4E). For instance, 2517 DEGs are identified between epithelial cells and common myeloid progenitors, indicating substantial differences in gene expression patterns between these two distinct cell types. In contrast, T cells and NK cells, known to have similar expression patterns (Narni-Mancinelli et al. 2011), yield only 118 DEGs between them. Full DEG lists for each of the cell type comparisons are available in Supplemental Table S10. These comparisons allow DEGage to identify well-known marker genes for each cell type. For example, IGHA1, IGHG3, IGKC, IGLC2, IGLC3, and JCHAIN are established markers for B cells (Fig. 4F). These markers primarily consist of immunoglobulin isotypes, with the exception of JCHAIN, which plays a pivotal role in the formation of immunoglobulin multimers (Castro and Flajnik 2014). The comprehensive sets of marker genes detected by DEGage for tumor-positive and tumor-negative cells can be found in Supplemental Figures S5 and S6.
DEGage detects memory-related genes in engram neurons
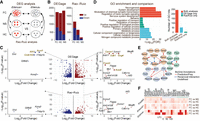
After demonstrating the efficacy of DEGage for analyzing large scRNA-seq data sets, we further tested its performance for detecting DEGs on small cell numbers by using a neuronal data set containing only 38 Arc::dVenus mouse neurons from Rao-Ruiz et al. (2019). In their paradigm, mice were subjected to three conditions: fear-conditioned with foot shock (FC), no shock (NS), and home cage (HC), which each includes 24, eight, and six brain frontal cortex cells, respectively, with half of the cells in each condition expressing dVenus (dVenus+), and the other half not expressing dVenus (dVenus−). In Arc::dVenus mice, a destabilized fluorescent reporter (dVenus) is coupled to the promoter for Arc, whose expression is strongly associated with memory formation (Gouty-Colomer et al. 2016). Therefore, dVenus+ cells express Arc in response to conditioning, whereas dVenus− cells do not. In Rao-Ruiz's initial analysis, comparisons between dVenus+ and dVenus− cells were sought individually. Here we apply DEGage to not only reproduce the author's initial analysis but also compare dVenus+ and dVenus− between FC and HC mice and between FC and NS mice (Fig. 5A).
DEGage detects DEGs related to remote memory formation. (A) Organization of the analyses performed by Rao-Ruiz and DEGage. (B) Comparison of the numbers of DEGs detected by DEGage and Rao-Ruiz. (C) Volcano plots of DEGs showcase DEGs detected by DEGage and Rao-Ruiz. Subfigures highlight DEGs with log2 fold changes (LFCs) less than −6 and greater than six. DEGs uniquely identified by DEGage are marked in gold. (D) The enrichment of GO biological process of the DEGs identified by both DEGage and Rao-Ruiz. The bar plot shows the number of GO biological process hits for each of the previously listed conditions. (E) Networks retrieved from STRING, with their corresponding BioGrid annotations, derived from DEGs uniquely identified by DEGage. These genes primarily fall into three major functional groups of GO biological processes (shown in light blue, red, and green). LFCs of these genes are presented in F.
In comparisons between the dVenus+ and dVenus− cells, DEGage identified 1717 FC DEGs, 1655 HC DEGs, and 1803 NS DEGs, whereas the Rao-Ruiz analyses found 1082 FC DEGs, 639 HC DEGs, and 175 NS DEGs (Fig. 5B; Supplemental Table S11). Among these DEGs, the two analyses shared 69.5% of their FC DEGs, 24.1% of their HC DEGs, and 4.0% of their NS DEGs. Rao-Ruiz's analyses were performed with DESeq2, and these discrepancies are likely attributable to methodological differences in handling small sample sizes. We plotted the P-values of genes outputted by DEGage and DESeq2, respectively (Fig. 5C). We found that DESeq2 calculated P-values mainly ranging from 10−40 to one, whereas DEGage outputted more even smaller P-values, ranging from 10−120 to 10−40 (Fig. 5C, y-axis). This suggests that DEGage is quite sensitive, particularly for genes with log2 fold-changes between two and six (Fig. 5C, x-axis). Additionally, we observed that DEGage is also sensitive to genes with larger fold-changes. For upregulated genes with log2 fold-changes greater than six, DEGage detects 15 DEGs, which is five more than DESeq2 (i.e., Cavin1, Sdk1, Gng4, Fmnl3, and Acadl) (Fig. 5C). Because these genes exhibit significant fold-changes exceeding six between the two conditions, they are more likely to be true DEGs. Furthermore, for down-regulated genes with log2 fold changes less than −6, DEGage identified three DEGs that were missed by DESeq2 (i.e., Ccdc103, Itih3, and Acot1). Among these eight genes, we found that seven of them could be potentially involved in memory functions or neural circuits, leaving only Cavin1 functionally uncharacterized (Supplemental Table S12). For example, Ccdc103 enables protein homodimerization in axonemal dynein complex assembly and cilium movement, and such cilium-related genes play a substantial role in remote memory (Jovasevic et al. 2021). Itih3 encodes the heavy chain subunit of the pre-alpha-trypsin inhibitor complex, stabilizing the extracellular matrix by binding hyaluronic acid. Its variants have been associated with memory consolidation and hippocampal connectivity deficits in autism (Xie et al. 2020). Acot1 catalyzes the hydrolysis of acyl-CoAs into free fatty acids and coenzyme A, regulating their respective intracellular levels. Although Acot1’s relationship to fear memory formation has not been directly characterized, the regulation of acetyl-CoA during histone acylation in neurons plays a critical role in memory formation (Alexander et al. 2022). These results indicate that DEGage demonstrates higher sensitivity than DESeq2 for detecting DEGs in real applications.
To assess the biological relevance of the identified DEGs in each analysis, we conducted an evaluation of GO biological process annotations for the following subsets of FC DEGs: genes detected by both methods, genes exclusively detected by Rao-Ruiz, and genes exclusively detected by DEGage. Both methods uncovered DEGs strongly associated with neural functioning and memory formation. DEGs detected only by DEGage exhibit specificity toward various metabolic processes, whereas Rao-Ruiz's DEGs map to less specific GO terms with lower significance levels (Fig. 5D). Among the DEGs unique to each method, DEGage's DEGs are associated with a broader range of GO terms, suggesting a higher level of biological relevance compared with DEGs unique to Rao-Ruiz's analysis (Fig. 5D, right side). Furthermore, we constructed the network associations among DEGs uniquely detected by DEGage through the STRING database (Szklarczyk et al. 2021). These associations are subsequently annotated based on available information from the BioGrid database (Oughtred et al. 2019). We identified three networks with reasonably high-confidence levels (>0.650), each seemingly related to a distinct metabolic process (Fig. 5E). These processes appear to be upregulated primarily in dVenus− cells (Fig. 5F), suggesting that non-memory-forming cells may engage in additional metabolic functions alongside memory-forming cells.
Discussion
In this study, we introduced DOTNB, a novel distribution family with analytical results and supportive software. Development
of DOTNB successfully bridges a longstanding theoretical gap surrounding the exploration of NB distributions. We derived statistical
properties of the DOTNB, including its PMF, CDF, and moments, providing a new discrete distribution to model and analyze dispersed
count data. It is worth noting that the DOTNB PMF can be partially expressed using the 2F1 GHF. Therefore, more analytic properties of the DOTNB PMF could be explored by applying the available theories related to
GHF (Aomoto and Kita 2011). In Theorem 1, the DOTNB PMF is represented using the 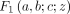 function with the four parameters a, b, c, z, which are different for k > 0 and k ≤ 0; that is,
function with the four parameters a, b, c, z, which are different for k > 0 and k ≤ 0; that is, 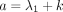 ,
, 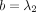 ,
, 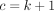 , and
, and 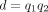 for k > 0;
for k > 0; 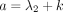 ,
, 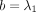 ,
, 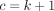 , and
, and 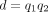 for k ≤ 0. Although the 2F1 GHF provides a mathematical description of the DOTNB PMF, it is hard to provide a direct biological interpretation for the
GHF parameters outside of the PMF's context. We also obtained two asymptotic behaviors that describe how the dynamic changes
of DOTNB probability can be determined by the two NB distributions for large k values. We hope these results can help researchers understand properties of DOTNB and continue theoretical research in the
future. By implementing basic functions for DOTNB across several programming languages (Python, R, Perl, MATLAB, and C++),
we aim to facilitate its widespread use in computational methods and catalyze the development of novel strategies for comparative
data analysis. Based on this work, it is also valuable to study the difference of two “zero-inflated” NB (ZINB) distributions,
which were recently used as an alternative distribution to fit scRNA-seq counts with dropouts (Lopez et al. 2018; Risso et al. 2018; Eraslan et al. 2019). The ZINB distribution is a mixture of an NB distribution and inflated zeros that are affected by a latent variable interpretation
(Garay et al. 2011; Miao et al. 2018). Let
for k ≤ 0. Although the 2F1 GHF provides a mathematical description of the DOTNB PMF, it is hard to provide a direct biological interpretation for the
GHF parameters outside of the PMF's context. We also obtained two asymptotic behaviors that describe how the dynamic changes
of DOTNB probability can be determined by the two NB distributions for large k values. We hope these results can help researchers understand properties of DOTNB and continue theoretical research in the
future. By implementing basic functions for DOTNB across several programming languages (Python, R, Perl, MATLAB, and C++),
we aim to facilitate its widespread use in computational methods and catalyze the development of novel strategies for comparative
data analysis. Based on this work, it is also valuable to study the difference of two “zero-inflated” NB (ZINB) distributions,
which were recently used as an alternative distribution to fit scRNA-seq counts with dropouts (Lopez et al. 2018; Risso et al. 2018; Eraslan et al. 2019). The ZINB distribution is a mixture of an NB distribution and inflated zeros that are affected by a latent variable interpretation
(Garay et al. 2011; Miao et al. 2018). Let 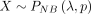 , and the ZINB PMF is presented as
, and the ZINB PMF is presented as 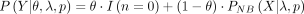 . Here
. Here 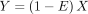 , and E denotes the zero-inflation indicator, taking the value of one with a probability of θ and zero otherwise, independently of
X. Please note the NB part can also have zero values, and the observed zero values are the mixture of inflated zeros and zeros
from the NB distribution. Given two ZINB variables,
, and E denotes the zero-inflation indicator, taking the value of one with a probability of θ and zero otherwise, independently of
X. Please note the NB part can also have zero values, and the observed zero values are the mixture of inflated zeros and zeros
from the NB distribution. Given two ZINB variables,  and
and  , their difference
, their difference 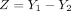 can be rewritten as (X1 − X2) − (E1X1 − E2X2). The first part follows a DOTNB, and the second part is the difference of zeros between two conditions. Thus, we can still
test the significance of the DOTNB part; however, more analytic results about the difference of two ZINBs are yet to be derived.
can be rewritten as (X1 − X2) − (E1X1 − E2X2). The first part follows a DOTNB, and the second part is the difference of zeros between two conditions. Thus, we can still
test the significance of the DOTNB part; however, more analytic results about the difference of two ZINBs are yet to be derived.
Using the DOTNB model, we developed DEGage, a novel NB-based method for identifying DEGs. Rigorous benchmarking of DEGage against five popular DEG analysis methods utilizing both simulated and control data sets shows that DEGage has the highest sensitivity and F1 scores, especially for comparing small data sets. Furthermore, DEGage, advanced in the closed forms of the DOTNB model, boasts expedited runtimes for processing large data sets. As imbalanced data sets are frequently encountered in biological experiments, we equipped DEGage with two sampling strategies: random assignment and subsampling. Upon testing them on imbalanced data sets, we observed that the subsampling strategy has slightly higher sensitivity on imbalanced data sets, whereas the random assignment strategy performs better for small imbalanced data sets in terms of specificity. However, neither of them consistently yields better performance in terms of F1, sensitivity, and specificity across all scenarios. Thus, the results suggest that users can select a suitable sampling strategy based on performance preference and data scale. As an NB model–based method, DEGage may have reduced power when the true distributions exhibit two peaks or two classes (Hebenstreit et al. 2011). By default, DEGage fits an NB distribution for each gene in a cell population, even if the ground truth exhibits a bimodal distribution. Consequently, this fitting process may reduce the testing precision in such scenarios. Another practical consideration for improving DEGage's performance is to control covariates and confounders in scRNA-seq data sets, such as sequencing depth, cell cycle effects, and lowly and highly expressed genes (Chen and Zhou 2017; Lun and Marioni 2017; Hafemeister and Satija 2019; Choudhary and Satija 2022). DEGage uses the GLM method to directly estimate the parameters of NB distributions (Venables and Ripley 2002); however, such estimation may lead to overfitting, mainly owing to covariates and confounders in the sequencing data (Hafemeister and Satija 2019). To obtain precise and stable parameter estimates, an alternative procedure could involve “regularized NB regression,” which can efficiently remove the influence of covariates while preserving biological heterogeneity in scRNA-seq data (Hafemeister and Satija 2019). For example, we can initially fit model parameters for each gene using a GLM, with sequencing depth as a covariate. Kernel regression can then be applied to the resulting parameter estimates to learn regularized parameters that depend on a gene's average expression and are robust to sampling noise. A second round of NB regression can be performed to constrain the model parameters to those learned in the previous step. Consequentially, DEGage can utilize the regularized parameters of two NB distributions for the DOTNB-based test and further improve performance.
Although the DOTNB model has been applied in scRNA-seq data analysis, we believe it can be integrated for comparative analysis of other single-cell or bulk omics data, such as scHi-C (Ramani et al. 2017; Lee et al. 2019), bulk RNA-seq (Wang et al. 2009), ChIP-seq (Park 2009), and more. Taking bulk RNA-seq as an example, it is methodologically feasible to directly prepare gene expression profiles from case and control RNA-seq data sets and input them into DEGage for DEG analysis. However, preprocessing and normalization procedures for raw RNA-seq data sets differ from those for scRNA-seq and require careful consideration for controlling confounding factors such as count normalization, age, gender, disease status, and others (Oshlack et al. 2010; Kumar et al. 2018). This is important for comparative analysis of real clinical data sets, such as large samples from the TCGA database (The Cancer Genome Atlas Research et al. 2013). In summary, DOTNB is a novel discrete distribution for modeling dispersed count data, and we expect that it can be widely utilized not only in sequencing data analysis but also in various research questions for the comparison of count data between groups to test significant differences.
Methods
Theorems and proofs of DOTNB distribution
Given 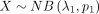 and
and 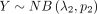 , we consider the difference between two independently distributed NB random variables, which is defined as
, we consider the difference between two independently distributed NB random variables, which is defined as 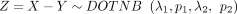 . It is worth noting that although X and Y are nonnegative variables, Z is a variable defined on all integers. To calculate its PMF, we start with the derivation of the necessary formulas.
. It is worth noting that although X and Y are nonnegative variables, Z is a variable defined on all integers. To calculate its PMF, we start with the derivation of the necessary formulas.
Suppose that 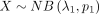 and
and 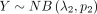 are independent variables; the variable
are independent variables; the variable 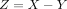 follows DOTNB (λ1, p1, λ2, p2) distribution. We have
follows DOTNB (λ1, p1, λ2, p2) distribution. We have
-
Its PMF is
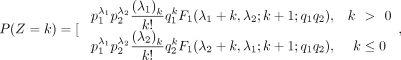 where
where 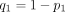 ,
, 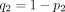 ,
, 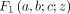 is a GHF, and (q)n is the Pochhammer symbol, that is,
is a GHF, and (q)n is the Pochhammer symbol, that is,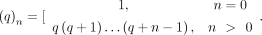
-
Its mean is
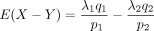 , and the variance is
, and the variance is 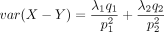 .
.
-
Because
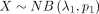 and
and 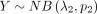 , we have
, we have 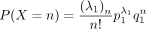 and
and 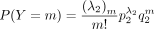 . We shall calculate the moment generating function of X − Y.
. We shall calculate the moment generating function of X − Y.
Note that
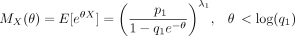
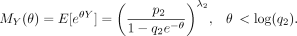
Then,
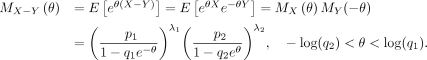
We next calculate the generating function of X − Y. Note that
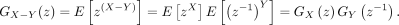
Recall that
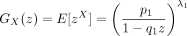
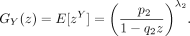
Then,
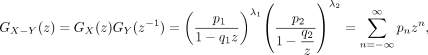 where
where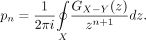
Note that
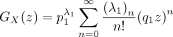
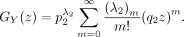
Then,
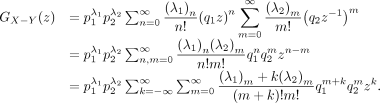
Then,
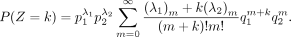
If k ≥ 0, then
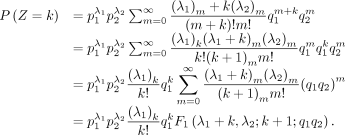
By symmetry, when k < 0, we have
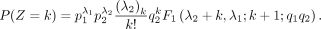
-
We next calculate the moments of X − Y. Note that
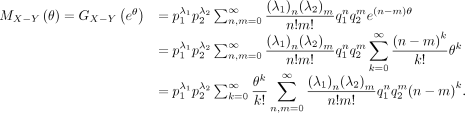
Then,
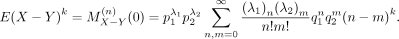
We have
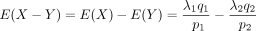
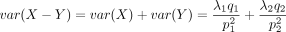
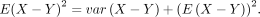
End of proof.
When the observations X and Y are available, the parameters of the DOTNB distribution can be obtained by estimating the NB parameters of the two data sets accordingly. In this study, the parameters are calculated using NB regression with MASS's GLM (Venables and Ripley 2002). Additionally, we consider the asymptotic behaviors of DOTNB distribution.
When k → +∞, 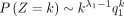 and k → −∞,
and k → −∞, 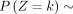
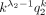 .
.
When k > 0, we have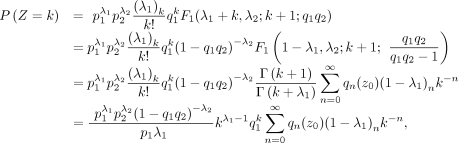 where q0(z0) = 1 and qn(z0), n ≥ 1 are defined by
where q0(z0) = 1 and qn(z0), n ≥ 1 are defined by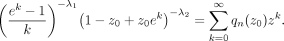
Then, we have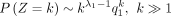
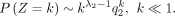
End of proof.
When k → +∞, 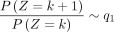 and k → −∞,
and k → −∞, 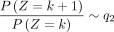 .
.
When k ≫ 1, we have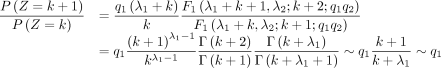
Similarly, we have 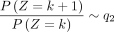 , when k ≪ −1.
, when k ≪ −1.
End of proof.
DEGage workflow
NB distributions are widely used in analyzing bulk RNA-seq data and, more recently, scRNA-seq data. In scRNA-seq experiments, gene expression levels are quantified by counting the number of sequencing reads that align to each gene in a cell. The resulting counts represent discrete, nonnegative data. Each gene's counts (successes) can be modeled as a random variable following an NB distribution. For example, if a gene's counts follow NB(10, 0.1) for a cell population under one condition, the parameters λ = 10 and p = 0.1 could be intrinsically determined by the biological conditions and experimental procedures. Once the scRNA-seq experiments are completed and the data are obtained, these two parameters can be estimated. Furthermore, if a gene's counts follow NB(10, 0.1) and NB(5, 0.1) in two different experiments, the expression difference of the gene is also a variable that follows DOTNB(10, 0.1, 5, 0.1). Therefore, DOTNB(10, 0.1, 5, 0.1) can be employed to calculate the probability for the observed expression difference of the gene between the two scRNA-seq data sets.
In this study, we propose a novel method called DEGage to detect DEGs from paired scRNA-seq data sets by utilizing the theoretical results of the DOTNB model (Fig. 1). Initially, DEGage takes the raw count matrices of two scRNA-seq conditions that could correspond to two samples, cell types, or one cell type on two biological conditions (i.e., two groups of cells, C1 and C2). Low-quality cells with a low number of detected genes will be filtered as suggested in Seurat (Butler et al. 2018; Hao et al. 2021). Initial filtering takes place to remove genes with low or undetectable expression levels. Genes are prefiltered with a nonparametric permutation test (i.e., shuffle test) (Moore 1999), so that only those genes below a significance level are kept for downstream analysis. Specifically, cells in two data sets are randomly relabeled, and the difference between the means of the two relabeled data sets is calculated. Subsequently, the cells from the two data sets are pooled, and the difference in sample means is calculated and recorded for 2000 permutations of the pooled values into two groups of equal size. Each time the difference between means exceeds that of the mean difference under the original labels, it is considered extreme. The proportion of occurrences in which this happens out of the total number of permutations determines the P-value. Genes below a significance level (α = 0.1 by default) are then selected for downstream analysis. For each remaining gene, the expression levels (raw counts) are fitted as NB distributions for both conditions using the MASS's GLM (Venables and Ripley 2002). Once the parameters have been estimated, a P-value for each gene will be calculated using the DOTNB CDF to test the significance of gene-wise expression differences. Specifically, we randomly select and order the same numbers of cells in C1 and C2 (i.e., min(|C1|, |C2|)), calculate the difference for the ordered pairs of cells of the X and Y, and then determine the mean of the differences. Next, the P-value for the mean of the ordered difference is calculated by using DOTNB CDF. If the P-value is less than a prespecified threshold (e.g., 0.05), the gene is considered as significantly differentially expressed. To control the FDR, P-values are adjusted according to the Benjamini adjustment for multiple tests (Benjamini and Hochberg 1995). The detailed results of DEGage calculations are outputted, including the lists of DEGs, their expression profiles, P-values, FDRs, and the regression parameters in estimating the NB distributions.
The DEGage software was implemented in R language (R Core Team 2023) with user-friendly operations. Its input consists of two scRNA-seq data sets, and the software outputs the DEG list along with their calculated P-values, which can be utilized for downstream enrichment analysis and other applications. To process large data sets, DEGage employs CPU + GPU hybrid parallel computing techniques by utilizing the “gpuR” package (Rupp et al. 2016). The source code, demo examples, and detailed usage instructions for DEGage are publicly available at GitHub (https://github.com/chenyongrowan/DEGage). To promote the broad usage of DOTNB, its PMF, CDF, mean, and variance functions have been implemented using several languages (Python, R, Perl, MATLAB, and C++) and are publicly available at GitHub (https://github.com/chenyongrowan/DOTNB). All the code for DOTNB and DEGage was implemented and tested under the Linux environment (Ubuntu 22.04) and Windows system (Windows 11 pro).
Simulated data
In biological data, it is not possible to fully validate TP and TN rates, so simulated data sets are generated to assess absolute TPs and TNs. We used the simulateSet() function from scDD (Korthauer et al. 2016), a method previously used in several benchmarking studies (Wang et al. 2019; Squair et al. 2021; Das et al. 2022). We used a data set containing information about pluripotent stem cells from previous research (Tung et al. 2017) as seed data for scDD package to model counts. Then, we randomly generated 10 data sets, each containing 2000 DEGs and 18,000 EE genes. The data sets had a total of 150 cells, with 75 cells allocated to each of the two respective conditions.
To further assess the performance and runtimes of DEGage and several popular DEG analysis tools, we also generated scRNA-seq data sets with different numbers of cells. The number of cells in each data set ranged from 20 to 2500 cells. For each cell population size, we generated five replicate data sets that each had 2000 DEGs and 18,000 EE genes. Runtimes were measured on a laptop with an Intel Core i7 processor and 16 GB memory. We calculated the average runtimes of five replicates to represent the speed performance for different cell sizes, respectively.
Simulation for testing robustness against dropout noise
To test the robustness of DEGage against dropout noise, we implemented a novel simulation framework by generating counts according to NB distributions with specified dropout proportions. This framework generates integer counts that follow an NB distribution and introduces a predetermined proportion of dropout counts. To introduce dropouts, a number of counts equal to the desired dropout proportion were replaced with artificial zeros. We independently generated a total of 13 data sets, with dropout proportions ranging from zero to 0.6 in increments of 0.1. Five replicates of each data set were generated, and each data set had a total of 150 cells with 75 cells allocated to two respective conditions. Furthermore, each data set contained 1500 DEGs and 15,000 EE genes.
Performance testing for different sampling strategies on imbalanced data sets
DEGage includes two different subsampling strategies for handling imbalanced data sets. By default, it randomly selects the same numbers of cells in the large data set to pair with those in the small data set for testing. Additionally, to fully utilize the cells in the large data set, DEGage offers another sampling option: random assignment, which pairs each cell in the large data set with a randomly selected cell in the smaller data set. We evaluated DEGage's performance using both sampling strategies on simulated scRNA-seq data sets with both balanced and imbalanced cell numbers. Ten cases of balanced/imbalanced data sets were simulated, each with the following numbers assigned to the first condition versus the second condition: 100 versus 100, 100 versus 75, 75 versus 75, 100 versus 50, 50 versus 50, 100 versus 25, 25 versus 25, 100 versus 10, 50 versus 10, and 10 versus 10. Here, the balanced data sets with reduced sample sizes, including 75 versus 75, 50 versus 50, 25 versus 25, and 10 versus 10, served as balanced controls for the imbalanced cases. DEGage's simulation framework was used to control effect sizes, dispersions, and imbalance across the simulated NB distributions for two samples. We constructed two types of simulation data sets using grid combinations of parameters and merged combinations of parameters. First, the parameter grid-combination analysis surveyed dispersions of 0.1, 0.5, one, five, and 10. DEGs were simulated with log2 fold changes of 1.5, 2.5, 3.5, 4.5, 5.5, 6.5, and 7.5, whereas non-DEGs had no effect size differences. Sample sizes for each condition were either 10, 25, 50, or 100. Simulation data were constructed for each combination of dispersion, effect size, and imbalance sample size. Second, dispersions and effect sizes were uniformly sampled and merged in each of the 10 imbalanced sample size combinations. This serves to average the dispersion and effect sizes, which are preliminarily used to investigate the effects of imbalanced sample sizes. Both types of simulation data sets included dropout proportions that were randomly sampled on a gene-wise basis and ranged from 0.1 to 0.5. Ten replicate data sets were generated for each grid combination of three parameters. Each data set was simulated with 10,000 genes, 1000 of which were differentially expressed. DEGage versions with the random assignment and subsampling protocols were compared with edgeR, DESeq2, the Wilcoxon test, and the GLM.NB LRT test. Each tool was run 10 times on each of the 10 data cases, and sensitivity, specificity, and F1 scores were calculated for performance evaluation. The performance difference between the two sampling strategies was tested by using a two-sided Student's t-test.
Real positive and negative control data sets
Although simulated data are useful for evaluating the performance of DEG analysis packages and controlling for true positives and negatives (Gagnon et al. 2022), they fail to capture the heterogeneity present in real data sets. Therefore, we used multiple real data sets to further examine the selected DEG analysis packages. To assess TP rates in real data, we used a positive control data set provided by Islam et al. (2011), which contains 22,928 genes across 48 mouse embryonic stem cells and 44 mouse embryonic fibroblasts. The data set is available from the NCBI Gene Expression Omnibus (GEO; https://www.ncbi.nlm.nih.gov/geo/) under accession number GSE29087. The TPs of the data set were assessed with the top 1000 DEGs validated with qRT-PCR experiments (Moliner et al. 2008; Kharchenko et al. 2014).
To assess FP rates, we employed a procedure similar to previous research (Wang et al. 2019). We retrieved a negative control data set, which contains 80 pool-and-split cells under the same condition (GEO; GSE54695) (Grün et al. 2014). We randomly selected 40 cells to represent condition-1 and 40 cells to represent condition-2. We repeated this process 10 times to generate 10 random data sets.
Applications to real scRNA-seq data sets
We further assessed DEGage's performance by applying it to two scRNA-seq studies, one on cancer cells and one on neurons. First, we collected the data set containing cancerous and healthy cells from human prostate cancer samples across four patients (GEO; GSE193337) (Heidegger et al. 2022). After performing basic quality control, we clustered 24,926 cells with Seurat and generated cell type annotations with SingleR (Aran et al. 2019). We used DEGage to assess differential gene expression for two scenarios: (1) on same cell types under cancerous and healthy conditions and (2) across different cell types within same condition. The second data set is from Rao-Ruiz et al. (2019) and contains 38 engram neurons from fear-conditioned mice (GEO; GSE129024). These neurons are classified into three treatment categories: mice that were fear-conditioned and subjected to recall conditions (FC), mice that were not fear-conditioned but subjected to recall (NS), and mice that were neither conditioned nor subjected to recall (HC). For each of these three conditions, neurons were marked as dVenus+ or dVenus− to note activation in response to recall stimuli. Genes with an FDR < 0.05 were labeled significant. We used PANTHER (Mi and Thomas 2009; Mi et al. 2019; Thomas et al. 2022) to retrieve pathway and functional enrichment annotations for the DEGs of both data sets. The complete lists of FC dVenus+/− DEGs generated by both DEGage and Rao-Ruiz's analyses were separately entered into PANTHER. Enriched GO terms were identified using the built-in statistical overrepresentation test (Fisher's exact test, FDR < 0.05), with the default gene list for Mus musculus from PANTHER used as the background gene set. To construct DEG networks, all DEGs from the FC dVenus+/− subset were queried in the STRING database (Szklarczyk et al. 2021). Only edges with confidence scores greater than 0.75 were retained, and any isolated DEG nodes were filtered out. For each remaining DEG, functional profiles in the BioGRID database (Oughtred et al. 2019) were manually examined to identify predator/prey relationships between DEGs and to confirm their interactions. The final network visualization was created using Cytoscape (Shannon et al. 2003).
Comparative analysis and benchmarking metrics
We compared DEGage to five popular DEG analysis packages, namely, DEGseq2, DEsingle, edgeR, Monocle3, and scDD (for details,
see Supplemental Table S1). We also evaluated the performance of DEG detection using a Wilcoxon test, a nonparametric method widely employed for comparing
two imbalanced data sets. The “wilcox.test” function in R was utilized to compute P-values, which were subsequently adjusted using the FDR procedure with “p.adjust.” Furthermore, we compared DEGage with the
GLM.NB method from the MASS R package that can test for the difference in the mean rates of two NB distributions by LRT (Venables and Ripley 2002). No subsampling occurred during the preparation of any benchmarking or real data sets. The subsampling procedure contained
within the DEGage pipeline was not applied to any other methods for any data set. We assessed the performance of each package
on the data sets described earlier, following the example workflows published in their respective Bioconductor links. For
each data set, we ran all seven methods to identify DEGs. We classified any EE gene identified as a DEG as a FP, while classifying
any DEG identified as an EE gene as a false negative (FN). The sensitivity, specificity, precision, accuracy, and F1-score
were calculated using the following formulas: (1) sensitivity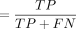 ; (2) specificity
; (2) specificity 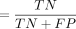 ; (3) precision
; (3) precision 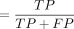 ; (4) accuracy
; (4) accuracy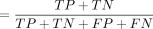 ; and (5) F1
; and (5) F1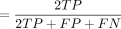 . We also calculated the ROCs and AUCs for each package by using the package pROC (Robin et al. 2011).
. We also calculated the ROCs and AUCs for each package by using the package pROC (Robin et al. 2011).
Software availability
The DOTNB implementation is available at GitHub (https://github.com/chenyongrowan/DOTNB), and DEGage is available at GitHub (https://github.com/chenyongrowan/DEGage). The DEGage tutorial, which includes descriptions of the functionalities, installation, usage instructions, demo examples, and data sets, is publicly released on RPubs by RStudio at https://rpubs.com/aliciaprowan/1043456. The demo code for running and comparing DEGage with other methods is publicly released at https://rpubs.com/aliciaprowan/1202999. All the source code of DOTNB and DEGage, demo examples, usage instructions, and custom scripts for data analysis is also available as Supplemental Code.
Competing interest statement
The authors declare no competing interests.
Acknowledgments
We thank Dr. Thomas N. Ferraro and Dr. Alma Faust for critically reading the manuscript and for helpful discussions. This work was supported by the National Science Foundation CAREER award DBI-2239350 for Y.C., a key project of Natural Science Foundation of Tianjin City (19JCZDJC35100), and the National Natural Science Foundation of China (61572358) to S.Z.
Author contributions: Y.C. and S.Z. conceived and designed the algorithms and experiments. A.P., R.C., and S.Z. implemented the software. A.P., R.C., and Y.C. preprocessed the data and analyzed the results. Y.C., S.Z., and A.P. drafted and reviewed the paper. All authors have read and approved the final manuscript.
Footnotes
-
[Supplemental material is available for this article.]
-
Article published online before print. Article, supplemental material, and publication date are at https://www.genome.org/cgi/doi/10.1101/gr.278843.123.
-
Freely available online through the Genome Research Open Access option.
- Received December 11, 2023.
- Accepted September 10, 2024.
This article, published in Genome Research, is available under a Creative Commons License (Attribution-NonCommercial 4.0 International), as described at http://creativecommons.org/licenses/by-nc/4.0/.