Accurate quantitation of allele-specific expression patterns by analysis of DNA melting
Abstract
Epigenetic and genetic mechanisms can result in large differences in expression levels of the two alleles in a diploid organism. Furthermore, these differences may be critical to phenotypic variations among individuals. In this study, we present a novel procedure and algorithm to precisely and accurately quantitate the relative expression of each allele. This method uses the differential melting properties of DNAs differing at even a single base pair. By referring to the melting characteristics of the two pure alleles, the fractional contribution of the two alleles to any unknown mixture can be mathematically resolved. These methods are highly accurate and precise because each single melting reaction yields multiple data points for analysis. Finally, we discuss how this approach can be used more generally to accurately quantitate gene expression relative to known standards.
The two alleles of a gene in diploid organisms are not always expressed equally. This unequal expression can be due to epigenetic or to genetic processes. Epigenetic mechanisms that lead to unequal allele expression include genomic imprinting and X-inactivation. In addition, an increasing number of genes are being identified that are subject to allelic exclusion but where the choice of allele appears to be stochastic. Some examples of genes thus regulated include immunoglobulin and odorant receptors in mammals. Genetic mechanisms can also account for differences in allele expression levels. Polymorphism in cis regulatory sequences that control RNA synthesis and/or stability can result in differential expression of two alleles (Pastinen and Hudson 2004). All these differences in mRNA expression levels between alleles have the potential to give rise to differences in the total biochemical or biophysical activity of the expressed molecules (Yan et al. 2002a; Ueda et al. 2003) and, therefore, confer variable fitness to their host organism. Thus understanding polymorphic alleles with respect to their relative expression level may provide insights into the mechanisms of phenotypic variation of biomedical significance.
Analysis of allelic expression variation depends on identification of a single nucleotide polymorphism (SNP) within the RNA coding sequence. Based on the SNP, the relative expression levels have been assessed by several methods including RNase Protection Assay (Winter et al. 1985) and Single Nucleotide Primer Extension assayed by radioactive nucleotide incorporation (SNuPE) (Kuppuswamy et al. 1991), or by mass spectrophotometry (rcPCR) (Knight et al. 2003). These methods are all technically challenging and, more importantly, limited in their ability to precisely quantitate variations in allelic expression.
We have developed a novel theorem for the quantification of a mixture of two different cDNAs by exploiting the unique melting properties of the cDNA variants. In this study, we successfully apply this analysis to establish a very rapid and accurate procedure for the quantitative determination of the allelic variation between two polymorphic alleles. In addition, we discuss the general applicability of our procedure in quantitating gene expression.
Results
A double-stranded DNA (dsDNA) molecule melts to two molecules of single-stranded DNA (ssDNA) under conditions that abrogate the interacting forces between bases. Melting of a dsDNA by continual increase of temperature is easily achieved with the aid of a conventional real-time themocycler and yields a sigmoidal melting curve when the amount of dsDNA is plotted against temperature.
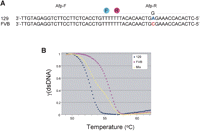
Even DNAs carrying a single nucleotide polymorphism (SNP) can be distinguished based on their unique melting curves (Fig. 1). We have identified an SNP in the 3′-UTR of murine alpha-fetoprotein (Afp) cDNA that distinguishes 129 and FVB strains (Fig. 1A). A probe pair, Afp-F and Afp-R, was designed to hybridize to the SNP-containing region. The Afp-R probe emits red light with maximum intensity at 640 nm from its Red640 dye by fluorescence resonance energy transfer (FRET) from the activated fluorescein dye of Afp-F. This energy transfer can occur only when the two dyes are in close proximity as when they each hybridize to their adjacent cognate sequences on the DNA. Thus the intensity of emitted fluorescent light from Red640 reflects the amount of probe–DNA hybridization.
Characteristic melting curves distinguish DNAs differing at only a single base pair. (A) FRET probes Afp-F and Afp-R are labeled with fluorescein and with Red640, respectively. The SNP distinguishing 129 and FVB alleles is highlighted with bold type. (B) The melting of FRET probe Afp-R from mouse Afp cDNAs derived from 129 mice (blue diamonds), FVB mice (purple squares), or from a 1:1 volume mixture of 129 and FVB cDNAs (yellow triangles). DNA melting is assayed by loss of fluorescence at 640 nm and then normalized as described in the text so that the Y-axis reflects the relative fraction of remaining dsDNA [γ(dsDNA)]. Note the leftward shift of the 129 cDNA melting, consistent with its single base-pair mismatch of probe Afp-R.
The PCR-amplified Afp cDNA amplicons of FVB (Fig. 1B, purple squares) and of 129 (Fig. 1B, blue diamonds) origins were each separately annealed with FRET probes and their melting behaviors analyzed (Fig. 1B). The resulting melting curves were then normalized by converting the maximum fluorescence value for each amplicon to 1 and the minimum fluorescence value to 0, with all other values adjusted proportionally. This normalization converts the Y-axis into the fraction of dsDNA [γ(dsDNA)] at a given temperature in each melting, and enables different samples and runs to be compared and analyzed in a standardized manner. The Afp-R probe matches perfectly with the FVB amplicon but carries a 1-bp mismatch with the 129 amplicon (Fig. 1A). Accordingly, the probe more readily melts away from the 129 amplicon, thus shifting the 129 melting curve to the left relative to the melting curve for the FVB amplicon. We also generated a melting curve for amplicons generated by PCR amplification of a 1:1 mixture of FVB and 129 cDNAs (Fig. 1B, yellow triangles). Note that this melting curve is a composite of the pure FVB and pure 129 curves.
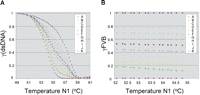
We anticipated that the melting characteristics of any mixture of 129 and FVB amplicons would reflect the relative contributions of each amplicon to the total mixture. To test this hypothesis, we mixed cDNAs in known proportions, amplified them by PCR, and then generated melting curves for each amplicon mixture. Figure 2A shows one experiment in which FVB cDNA contributions to the starting mixtures varied incrementally from 10% to 90% of the total cDNA volumes added. As in all experiments, melting curves for pure FVB and pure 129 cDNAs were also generated. Note that the normalized melting curves of each mixture are distributed in an ordered manner according to the contribution of each component to the mixture. These results support the notion that the melting curves might be useful in actually quantitating the relative allelic contributions in a two-allele mixture.
Melting curves for composite mixtures reflect the relative contribution of each of the two alleles. (A) Melting of FRET probe Afp-R from PCR amplicons of pure 129 (curve A), pure FVB (curve K), and of 129 + FVB mixtures (curves B–J). Mixes were generated prior to PCR amplification by pooling FVB and 129 cDNAs in proportions defined in Table 1. Note the ordered leftward shift (decreased Tm values) as the fractional value of 129 cDNA increases. (B) The calculated fractional values for FVB (γFVBs) at given temperatures were averaged and plotted. γFVBs were calculated using Equation 1, as described in the text, comparing every temperature pair that falls within the parameters described in Methods. Specifically, we used temperatures in which <90% but >10% of 129 amplicons were still double-stranded. For example, in this experiment, we used melting data from between 51.9°C and 55.5°C.
Equation 1 describes how a melting curve can be used to deduce allelic contribution in a mixture of dsDNAs A and B.
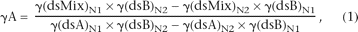where γA is the fraction of A in the mixture, γ(dsMix)N is the fraction of the total DNA that is doubled-stranded at temperature N; and γ(dsA)N and γ(dsB)N are fractions of DNAs A and B, respectively, that are double-stranded at temperature N. The derivation of Equation 1 is presented
in Methods. With Equation 1, the fractional contribution of any allele to a given DNA mixture can be calculated by obtaining
the melting curves for that mixture and for the two pure DNAs.
In the derivation of Equation 1, we make one empirical (i.e., nonmathematical) assumption. Specifically, we presume that the two alleles behave independently during the melting process. That is, Equation 1 assumes that the melting curve for allele A is independent of the presence of allele B amplicons (and vice versa). To test our assumption empirically, we used Equation 1 to calculate the dsDNA fractions using every possible temperature pair that meets the conditions described in Methods. If the melting process meets the assumption we made above, we expect that the resulting fraction values derived for each sample should be comparable using any two temperature points. As seen in Figure 2B, where calculated fractional values of FVB (γFVΒs) at given temperatures were averaged and plotted, the γFVΒs are, in fact, highly similar within each sample and independent of the temperature used for calculations, indicating that the data acquisition during the melting is quite reliable and the conditions for the melting process fit with our assumption about the melting. Thus, we conclude that the characteristics of the melting curve can be used to evaluate the relative contributions of the two alleles to a cDNA mixture, and the melting curves faithfully reflect the relative input of each cDNA. The γFVB values for each temperature pair from one melting analysis are averaged and presented in Table 1 as γFVB(Ob).
DNA melting curves can be used to calculate the fractional value of each allele in a two-allele mixture
We next took into consideration the possibility that there might be a bias in the binding of the Afp-R probe to each of the
two alleles. Specifically, under our annealing conditions, it seemed likely that a relatively greater fraction of the FVB
amplicons might anneal to the perfectly matched Afp-R probe. This would result in an underestimate of the number of 129 alleles
in the starting mixture. In other words, our γA(Ob) values actually represent the fraction of A that is annealed to the FRET
probes (relative to the fraction of B that is annealed) and not truly the fraction of A in the DNA pool. To address this issue,
we realized that our assay required a 1:1 mixture of A and B cDNAs as a third reference standard. The observed γA and γB values
for this reference are referred to as γAH and γBH, respectively (where H stands for the “half and half”). Because the value for γAH must, by definition, be 0.5 once bias is corrected, we can obtain the following equation to correct for probe bias:
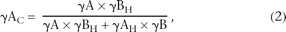where γAC is the bias-corrected fraction of dsDNA A in the mixture; and γAH and γBH are the γA and γB, respectively, of the 1:1 mixture. The derivation of Equation 2 is presented in Methods.
We applied the correction equation to the data shown in Table 1, and the corrected values and their standard deviations are reported in the bottom two rows. Comparing calculated (γFVBC) with expected [γFVB(Ex)] values, we conclude that the melting curve analysis is both highly reproducible and precise and, moreover, is highly accurate in calculating the allelic composition over a wide range of relative fractions.
Note that in these experiments, we use a 1:1 volume mixture of A and B cDNAs as our bias correction reference. This reference is appropriate in these initial studies, where we are seeking to demonstrate that our assay accurately ascertains the relative fractions of A and B alleles added. As described below, an appropriate control for most studies is not a 1:1 volume mixture but a 1:1 molar mixture.
We next wished to determine the ability of our method to resolve the mixing ratio when one allele is overwhelmingly dominant as is often the case with genes that are subject to genomic imprinting, X chromosome inactivation, and allelic exclusion. We therefore prepared incremental cDNA mixtures in which 129 alleles represented only a small fraction of the starting material. After PCR amplification and melting curve analysis, using as references only pure 129, pure FVB, and a 10 μL:10 μL mixture, we calculated the values shown in Table 2. Again, the calculated γFVBC values support the notion that this is a highly precise assay with which to quantitate allele usage even when the samples are highly skewed toward one allele. Together, the results in Tables 1 and 2 demonstrate that the melting analysis faithfully determines the relative contribution of each allele in a two-allele mixture.
DNA melting curves can be used to calculate the fractional value of each allele in a two-allele mixture where one allele is grossly under-represented
It was also critical to address directly the accuracy of our method using independently derived standards. That is, we needed to demonstrate that the assay not only reflects the relative changes in fractional representation of A and B but also that the absolute values derived for γA and γB can be correctly ascertained. We therefore constructed several plasmids that each carries a defined number of FVB and 129 cDNA inserts. In other words, we derived several independent samples in which the starting proportions of FVB and 129 cDNAs were known with certainty. We amplified these plasmids and then assayed the amplicon mixture as described above. In this experiment, we used a plasmid (pTG1) that has a single-copy insertion of each cDNA as our bias control. This plasmid provides, by its nature, the equimolar control for the bias correction and means that the assay will yield fractional values reflecting the real allelic distribution. Our results (Table 3) demonstrate that melting curve analysis accurately and precisely quantitates the relative contributions of each allele in a two-allele mixture.
Melting curve analysis can accurately ascertain the fractional representation of each allele in a two-allele mixture
DNA melting curves can be used to calculate the fractional value of domesticus and castaneus alleles of H19 and Kcnq1
We next wanted to examine allele-specific expression of H19 and Kcnq1 in real tissues equivalent to those previously characterized in earlier published studies. Previous reports have demonstrated that H19 is expressed almost exclusively from the maternal allele and that paternal repression is dependent on the presence of the H19ICR (also called the H19DMR) on the paternal chromosome. In liver RNAs prepared from wild-type mice where the maternal allele is castaneus and the paternal allele is FVB domesticus, we saw that the paternal chromosome contributes only 1.5% ± 1.1% (N = 4 mice) of the total RNA. However, upon paternal deletion of the H19ICR, the paternal contribution is 39.8% ± 0.8% (N = 3 mice), consistent with results using RNase Protection (Thorvaldsen et al. 1998) and by SNuPE (Kaffer et al. 2000; Srivastava et al. 2000) but with considerably greater precision. Expression of Kcnq1 is also biased toward the maternal chromosome, but imprinting of Kcnq1 is gradually lost during embryonic development (Gould and Pfeifer 1998). Using RNAs isolated from wild-type castaneus/domesticus mice, we found that the maternal chromosome accounted for the following percentages of total Kcnq1 RNA: e13.5, 95.8% ± 0.3%; e14.5, 90.4% ± 0.8%; e15.5, 77.9% ± 1.2%; e16.5, 75.1% ± 4.1%; p2, 61.3% ± 3.0%; and p21, 58.7% ± 0.9% (N = 3 mice). Again, these results are entirely consistent with previous studies that used differential sensitivity to NlaIII digestion to distinguish the two alleles, which were then each quantitated by densitometry scans (Gould and Pfeifer 1998). Note that the precision of results associated with DNA melting analysis is much improved, allowing the investigator the ability to distinguish subtle differences otherwise not discernible, even while the hands-on labor required is drastically reduced. In fact, once the cDNAs are acquired, analysis is complete within ∼1 h.
Discussion
It is now clear that numerous loci show strong allele-specific biases in gene expression. Some genes show disparate expression of the two alleles due to epigenetic mechanisms. Examples include not only genes regulated by genomic imprinting and X-inactivation, but also many biologically important cases where allelic exclusion is random in terms of the choice of allele. Some examples of genes subject to allelic exclusion include those encoding odorant receptors, immunoglobulins, T-cell receptors, interleukins, Natural Killer cell receptors, and p120 catenin (Held et al. 1995; Goldmit and Bergman 2004; Gimelbrant et al. 2005; Shykind 2005). Moreover, it is becoming clear that even among genes that are biallelically expressed, there may be large allelic variations in the RNA levels based on genetic variations between alleles (Yan et al. 2002b; Lo et al. 2003). These variations are presumably associated with natural polymorphisms in critical cis-acting elements at these loci. Such differences can affect phenotype and may account for some of the enormous natural variation seen between individuals in outbred populations as well as some experimentally interesting variations seen when crossing inbred lines of laboratory animals.
In this study, we present a methodology for accurate, precise, and reproducible quantitation of allele-specific expression. Our primary model system for this protocol development was the mouse Afp gene. In order to study imprinting mechanisms, we have recently established several mouse models in which the Imprinting Control Region (ICR) from the Igf2/H19 locus on distal chromosome 7 was moved to the nonimprinted Afp locus on mouse chromosome 5 (Park et al. 2004). We have already shown that these insertions result in paternal-specific methylation of the mutant chromosomes. However, to determine whether these differential methylation patterns also resulted in parent-of-origin functional differences in Afp expression, we needed the ability to accurately quantitate the expression of Afp from mutant chromosomes relative to that of the wild-type allele. Because some of the insertions carried subtle mutations in the ICR, we wanted to be sure our quantitation could detect subtle changes in allele preferences. Thus, we developed the methodology described in this report.
This new method is simple, fast, and readily adaptable by any molecular biology lab that has access to a real-time PCR system capable of using FRET probes. This method is based on the differential melting behaviors of DNAs that vary at even a single nucleotide. In this technique, the melting of FRET probes is assayed and normalized, and these data are used to calculate the allelic composition through the use of three reference curves. Two of the reference standards are the pure samples of each of the two alleles. The third standard is a 1:1 mixture of the two alleles and corrects for potential bias of the FRET sensor probe for its perfect match. The actual bias we observed varied from probe to probe. For the AFP assay, a true 50:50 mix would appear to be ∼60:40 without correction. For other probes tested, the mix would appear something like 52:48 without correction. Due to slight shifts in melting curves between runs, for the most accurate calculations, all three standards need to be included with each sample run.
If the third standard is a 1:1 volume mixture, then one can readily correct for biases in FRET probe hybridization and therefore accurately determine the relative fractional composition of various samples. For example, one can accurately measure that sample 1 has twice the fractional input of allele A as compared to sample 2. This is actually what is being accomplished in most allele-specific RNA assays (albeit usually without quantitation). More useful, however, if the third reference standard is a 1:1 molar mixture, then one is able to correct for probe bias and also accurately determine the absolute fractional value for each of two alleles in the mixture.
Any laboratory can readily obtain a 1:1 molar mixture reference standard. In the experiments presented here, we obtained this control by subcloning the amplicon for each allele into a single plasmid vector. Restriction enzyme digestion released the inserts as separate but equimolar fragments. Alternatively, genomic DNA can be used as the 1:1 molar reference standard. In this case, the PCR primers used to generate the amplicons for melting analysis should be designed so that they are internal to the exon carrying the relevant SNP.
We have tested various types of samples including plasmid DNA and RT-PCR-generated cDNA, and we have varied the initial substrate concentrations over orders of magnitude and in all cases have obtained reliable and accurate results with the protocol described here (data not shown). However, we have noted that it is quite important to complete the analysis as a two-step process in order to obtain optimal results. After PCR amplification, a part of the sample is removed to an EDTA solution carrying the FRET probes for melting analysis. In contrast, inclusion of the FRET probes in the original PCR reaction gave results with significantly larger standard errors and that deviated more from the expected values.
We have developed a highly functional assay for determining the fractional composition of a two-allele mixture. The accuracy of this methodology is clearly evident in a comparison of expected [γ(Ex)] and calculated (γC) values in Tables 1–4. The reproducibility and precision of the assay is evident in the small standard deviations associated with these calculated γFVB values. We expect that the extraordinary precision is due both to the inherent advantages of the real-time PCR technology and also to the nature of the algorithm for calculating γ. Because there are multiple N1 and N2 temperature data sets for each melting experiment, multiple values for γA are calculated and then averaged in each melting experiment. Thus, the final γA value is a function of multiple measurements taken at various times during the melting experiment and does not rely on any one potentially faulty measurement.
Compared with other methods available for quantitating allele-specific expression, our method becomes most advantageous when one is either assaying many samples or, alternatively, assaying small numbers of samples but in many batches over a period of time. This is because our method does require the initial investment of money to purchase the two FRET probes. There is also an initial investment of effort to subclone the cDNA fragments that will serve as the reference standards: pure allele A, pure allele B, and a 1:1 molar standard. (Note, however, equivalent standards are required for any quantitative assay.) Once these reagents are generated, our method is particularly inexpensive in terms of labor, money, and time as new RNA samples can be easily analyzed in less than half a day. The approach is technically straightforward and can be readily followed by any molecular biology lab with access to a real-time PCR system. The mathematical analysis for quantitation is easy to use. Our own software is specifically designed to interface with the Roche Light Cycler and is available to the research community at http://pfeiferlab.nichd.nih.gov.
In addition to the Afp, H19, and Kcnq1 genes described in this report, we have additionally generated assays to quantitate three housekeeping genes (Ubc, G6pdx, and Rps27) and the H19ICR, as well as to measure promoter usage at the Igf2 locus (S.Y. Jeong and K. Pfeifer, unpubl.). In developing these eight assays, we have noted that there is a large flexibility in the design of the primers used to generate the substrates for melting analysis. However, careful design of the FRET probes is critical. The rules we observed in designing FRET probes are straightforward. First, the calculated melting temperature (Tm) for the donor probe should exceed the Tm for the sensor probe by 3°–5°C. Second, the difference in the melting temperatures of the sensor probe annealed to the perfect and the 1-bp mismatch DNAs should as great as possible. This is accomplished by designing the sensor probe to be an exact match to whichever allele will give the higher calculated melting temperature. Most importantly, to obtain an adequate signal, the FRET probes should not be likely to form any stable hairpins. There has been no apparent restriction on the nature of the SNPs that will work with this assay as we have distinguished A/C, T/C, G/T, C/G, A/T, and A/G polymorphisms.
Our methodology represents a novel use of DNA melting to analyze gene expression. Our methodology allows molecular biologists to accurately measure allele bias in wild-type and mutant cells in such cases as genomic imprinting, X-inactivation, and allelic exclusion. Likewise, this approach offers a simple way to screen multiple samples for allelic bias in order to study the potential effects of such bias in determining phenotype. For example, the role of allele bias in QTL candidate gene expression can be readily ascertained using these approaches (Farrall 2004). In addition, our approach can be extended to quantitate the absolute expression levels of any genes of interest. That is, the level of any nucleic acid of interest can be determined by introducing an artificially generated SNP-carrying competitor of known concentration to a cDNA mix of interest prior to PCR amplification. Given its simplicity, quickness, and accuracy, this DNA melting analysis approach will provide a straightforward paradigm to compare gene expression levels across cell types and developmental stages.
Methods
Derivation of Equation 1 to calculate the fractional representation of each allele in a two-allele mixture
In a mixture of dsDNAs A and B, the fraction of the total DNA corresponding to DNA A, γA, can be defined as γA = [A]/([A] + [B]). Likewise, γB = [B]/([A] + [B]). In a mixture of only two DNAs, then γA + γB = 1.
During the melting of this DNA mixture, the fraction of the total DNA that is double-stranded at any temperature N [γ(dsMix)N] will be a function of the amount of each of the two components, A and B, that remain double-stranded at this temperature,
weighted by the fractional contributions of A and B to the mixture:
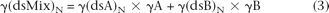The values of dsDNA fractions of the mixture and of the pure A and B DNAs at a given temperature can easily be obtained from
the normalized melting curve. Therefore, γA, the fractional contribution of DNA A to the mixture, can be readily calculated
using the dsDNA fraction values at any two temperature points, N1 and N2, as below,
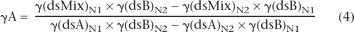Because there are multiple N1 and N2 data sets in each melting experiment, multiple values for γA can be calculated and averaged
in each melting analysis, increasing the precision of the calculated γA.
Alternatively, since γA + γB = 1, γA can be calculated by substituting 1 − γA for γB in Equation 3:
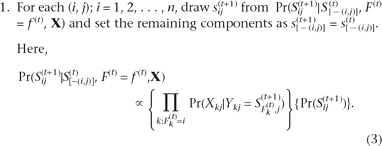In sum, γA, the fraction of DNA A in the two-part mixture, represents the ratio between the distances from the pure DNA B
to the mixture and from the pure DNA A to B on the normalized melting curve at any temperature and can be calculated from
the experimentally obtainable values during the DNA melting. When Equation 5 is used, γA can be calculated for multiple temperature
values (N), corrected for probe bias (as described below), and then averaged to obtain a γA(ob) for that sample. Thus, as
with Equation 4 above, the final γA value for each sample represents multiple experimental data points, thus increasing the
precision and reproducibility of the melting curve analysis assay. In several experiments, analysis of melting curves using
Equations 4 and 5 have given essentially identical results.
Derivation of the bias-correction equation (Equation 2)
As described above, γA is the fractional component of DNA A in a mixture of DNAs A and B and can be mathematically defined: γA = [A]/([A] + [B]). Equation 1 describes algorithms for using the results of DNA melting analysis to calculate γA [i.e., to obtain γA(Ob)]. The melting analysis depends on hybridization of two FRET probes to DNAs A and B. γA(Ob) will represent the real γA insofar as the DNAs A and B hybridize equally well to these FRET probes. Because one of the FRET probes matches perfectly with DNA A but has a 1-bp mismatch with DNA B, we presume that the FRET probe might hybridize better to DNA A and therefore that γA(ob) will incorrectly overstate γA. In fact, it is more accurate not to represent γA(ob) as equal to [A]/([A] + [B]) but, rather, to state that γA(Ob) = [A*]/([A*] + [B*]), where [A*] and [B*] represent the concentrations of DNAs A and B, respectively, hybridized to FRET probes.
Given the potential for this bias, we use the term γAC to represent γA(Ob) that has been corrected for probe bias. To correct for probe bias, we can use the 1:1 or half (H) mixture
because we can calculate the degree of bias by observed γA(ob) for this 1:1 mixture (hereafter called γAH) and compare this value to 0.5, the γA of a 1:1 mixture if there is no probe bias. Let us define γAH and γBH as the observed γA and γB values, respectively, in a true 1:1 mixture of A and B DNAs. Then the observed γA value [γA(Ob)]
is related to the observed γAH as described:
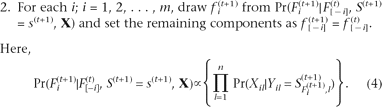Through algebraic manipulations, Equation 6 can be used to define [B]/[A]:
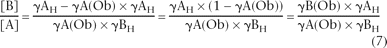Since γAC = [A]/([A] + [B]) or, alternatively, γAC = 1/(1 + [B]/[A]), then substitution for [B]/[A] using Equation 7 yields the following function, which can be used to correct
for bias:
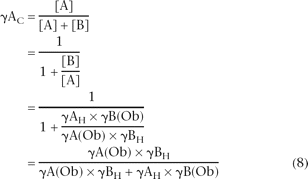Note that the critical experimental decision is what to use as the 1:1 mixture for measuring γAH.
Plasmids
Reference plasmids pcAFP-T (129 cDNA) and pcAFP-G (FVB cDNA) each carry a 236-bp insert including the 5′-UTR of mouse Afp generated by RT-PCR of total liver RNA using primers Afp-4F, 5′-AGATTTCTCGGGCCTTTT-3′; and Afp-2R, 5′-GGTATAGA AATCTCACATGG-3′. Additional plasmids, carrying multiple insertions of this cDNA fragment (see Table 3) were generated by subcloning.
Reverse transcription and PCR
Reverse transcription was carried out on 2 μg of total liver RNAs using Superscript II (Invitrogen) cDNA synthesis kits following the manufacturer’s instructions. Amplicons for melting analysis of Afp were generated starting with ∼0.1 ng of DNA template and using 10 pmol of primers Afp-5F (5′-AAGTTGATTTCCAA AACTCG-3′) and Afp-2R to generate a 163-bp product. Amplicons for analysis of H19 were generated using primers 5′-GC CTCAAGCACACGGCCACA and 5′-GCACTAAGTCGATTGCACT GG to generate a 164-bp product. Amplicons for analysis of Kcnq1 were generated using primers 5′-CATCGGTGCCCGTCTG AACAG and 5′-TGCTGGGTAGGAAGAGCTCAG to generate a 188-bp product.
DNA melting analysis
Ten microliters of PCR amplicons was mixed with 10 μL of 10 mM EDTA and with 4 pmol of FRET probes, Afp-R and Afp-F (see Fig. 1B). DNA melting was performed using a Roche LightCycler under the following conditions: 30 sec at 95°C, 8 min at 49°C, and 0.2°C stepwise increases in temperature until 65°C was achieved. Assay results are essentially insensitive to the rate of temperature increase. However, it is important to measure fluorescence after stepwise increases and not during a continuous increase. The background-adjusted fluorescence values (F2/F1) from the Red640 dye were extracted using the LightCycler3 Data Analysis (Version 3.5.28) and then submitted to our analysis program. Due to the likelihood that the very small differences in the normalized values between samples and references at the beginning and at the ending of the melting curves would not be well resolved by the machine, only the values at the temperatures in a range defined by dsDNA fractions from 5% to 90 % of the fastest melting reference (129 cDNA) were used for subsequent analysis. Within this range, all temperature pairs with a ΔT of ≥1°C were subjected to calculation to yield a fractional component for that sample. The fractional values for all the temperature pairs were then averaged to yield γDNA(Ob) (observed fractional value) for that sample. These γDNA(Ob) values were then corrected using the fraction value of the 1:1 mixture to yield the bias-corrected fraction value, γDNAC. When the 1:1 mixture is a true 1:1 mass mixture of the two alleles, this γDNAC is an accurate representation of the true allelic fraction. We have developed software to directly interface with data acquired by the Roche Light Cycler and will readily share this or advise on interfaces with other equipment.
For analysis of H19 gene expression, FRET probes 5′-CCTCTTTGGCAATGCTGCCCCA-Fluorescein and 5′-LC Red640-ACCCACCTGTCGTCCATCTCCG-C3 Blocker were used as described above. The underscored G is an A residue in domesticus animals. For analysis of Kcnq1 gene expression, we used FRET probes 5′-GTGATCATCACAGACATGCTCCACCAGC-Fluorescein and 5′-LC Red640-GCTGTCCCTGCAACAAGGTG-C3 Blocker. The underscored C is an A residue in domesticus animals. All FRET probes were obtained from Idaho Technology, Inc.
Acknowledgments
This work was supported by the NICHD Intramural Research Program. The NICHD ACUC approved all animal experimentation. We thank Claudia Gebert for many helpful discussions, especially in the design of FRET probes; John Van Druff for construction of the Kcnq1 reference plasmids; and Lamar Roos for advice on FRET probe design.
Footnotes
-
↵3 Corresponding author.
↵3 E-mail kpfeifer{at}mail.nih.gov; fax (301) 402-0543.
-
[Supplemental material is available online at www.genome.org and at http://pfeiferlab.nichd.nih.gov.]
-
Article published online before print. Article and publication date are at http://www.genome.org/cgi/doi/10.1101/gr.6028507
-
- Received October 11, 2006.
- Accepted April 10, 2007.
- Copyright © 2007, Cold Spring Harbor Laboratory Press
