Homotypic Regulatory Clusters in Drosophila
Abstract
Cis-regulatory modules (CRMs) are transcription regulatory DNA segments (∼1 Kb range) that control the expression of developmental genes in higher eukaryotes. We analyzed clustering of known binding motifs for transcription factors (TFs) in over 60 known CRMs from 20 Drosophila developmental genes, and we present evidence that each type of recognition motif forms significant clusters within the regulatory regions regulated by the corresponding TF. We demonstrate how a search with a single binding motif can be applied to explore gene regulatory networks and to discover coregulated genes in the genome. We also discuss the potential of the clustering method in interpreting the differential response of genes to various levels of transcriptional regulators.
One of the most intriguing questions for understanding protein-DNA recognition is how a low-abundant transcription factor (TF) quickly finds a short recognition motif at the correct place in the genome (Berg and von Hippel 1987, 1988). This important problem of TF recruitment to its functional binding site can be considered from the informational and the molecular points of view. From the informational point of view, regulatory regions must differ strikingly from the rest of the genome to facilitate the recruitment. The amount of regulatory information encoded by a single binding site is much smaller than that encoded by an array of similar binding sites, that is, a ‘homotypic’ binding site cluster. This informational advantage of the homotypic clusters might be utilized by molecular mechanisms such as high-affinity cooperative binding (Hertel et al. 1997) or lateral diffusion of a TF along the regulatory region from low- to high-affinity binding sites (Kim et al. 1987; Khory et al. 1990; Coleman and Pugh 1995). Indeed, the presence of multiple copies of binding sites of the same type in promoter and enhancer regions is a widely spread phenomenon in nature (Stanojevic et al. 1991; Arnone and Davidson 1997; Papatsenko et al. 2002). Most transcription regulatory regions, however, contain different types of binding motifs; therefore, the major efforts in exploring binding-site clustering have thus far focused on the extraction of ‘heterotypic’ clusters (clusters containing different binding motifs).
Several conceptually different strategies have been employed for evaluation of clustered signals in regulatory regions. The majority of these studies describe a cluster as a series of closely spaced binding sites for a number of different TFs. The ‘fuzzy clustering’ (Pickert et al. 1998) and related algorithms (Kondrakhin et al. 1995; Wasserman and Fickett 1998) estimate the quality of the binding motifs (weaker and stronger sites) and cluster matches with similar position weight matrix (PWM) scores in a fixed window. Hidden Markov model (HMM)-based methods require parameter settings for the window size and the number of expected motifs (Crowley et al. 1997; Frith et al. 2001). R-scan algorithms assess distance distribution between PWM (or consensus) matches to binding motifs and compare cluster significance in all possible window sizes (Wagner 1997, 1999; Su et al. 2001).
Using R-scan algorithms, it was demonstrated that upstream segments of yeast genes contain homotypic clusters of binding sites for transcriptional regulators (Wagner 1997). In higher eukaryotes, however, many genes are regulated by distant regulatory elements, which can be well separated from the coding regions. It was recently reported by Berman et al. (2002) that the clustering of binding motifs provides sufficient information for localization of these distantcis-regulatory modules (CRMs) within the genome ofDrosophila. It was also shown that even clustering of a single binding motif might provide a significant basis for evaluation of CRM sequences in developmental genes of Drosophila (Markstein et al. 2002; Papatsenko et al. 2002).
The early Drosophila developmental genes encode TFs that control pattern formation of the developing fly embryo. They form a spatiotemporal cascade of direct transcriptional interactions (Kassis 1990; Small et al. 1992; Nasiadka and Krause 1999). CRMs control the expression of these developmental genes and represent regions containing binding sites for multiple upstream factors, which are themselves the products of other developmental genes in the cascade. For many of these modules (e.g., stripe enhancers fromeven-skipped) (Stanojevic et al. 1991; Small et al. 1992), an extensive characterization is available at the genetic, biochemical, and evolutionary (comparison between species) levels, which makes them one of the best model systems in higher eukaryotes. Another advantage of the developmental cascade is that all genes are directly connected in this regulatory network: (1) they all encode TFs, and (2) they act as gradients in the cell-free environment of the developing fly embryo (syncytium). Therefore, these genes also represent a unique opportunity to study differential gene responses to the concentration of TFs (Driever and Nusslein-Volhard 1988a,b; Driever et al. 1989).
The main goals of the present study were to analyze the clustering of individual binding motifs in CRMs of Drosophila developmental genes and to confirm that the homotypic clusters are statistically significant in this model system. Another objective was to explore the dependence of the cluster significance and the fidelity of CRM recognition in the genome on the relative site affinity and the size of the resolution window. We also demonstrate here that the analysis of clustering can be applied for quantitative description of transcriptional regions through the relative site density and the relative site affinity.
Transcription regulatory modules and promoter sequences of higher eukaryotes contain more than one type of recognition motif. In this respect, CRM identification in the context of genome annotation appears to be most successful using heterotypic clustering models (Berman et al. 2002; Halfon et al. 2002). However, construction of biologically relevant, complex heterotypic cluster models represents a challenging problem. Here we demonstrate that homotypic clustering models, the simplest of all possible combinatorial models, can also produce very impressive results and may serve to complement the heterotypic approach. Moreover, description of each individual binding motif in the context of a homotypic cluster seems to be very convenient for biological analysis of sophisticated regulatory units.
RESULTS
Annotation for CRM Sequences
To explore binding site clustering in known DrosophilaCRMs, we assembled and annotated all published experimental data for the early developmental gene enhancers. These data include three major types of information: (1) known binding motifs for TFs, (2) known CRM regions, and (3) known regulatory interactions.
First, we aligned footprint data for 28 binding motifs, representing the majority of the maternal, gap, pair rule, and some segment polarity genes. For each alignment, we established the optimal motif width, and outlined a well defined core formed by positions with high information content. Second, we retrieved published deletion analysis data for more than 60 CRMs from 20 different target genes that are regulated by these 28 TFs. Third, we annotated the known regulatory interactions for each CRM using published data that describe changes in CRM functions in mutant embryos lacking specific TFs.
To navigate through this collected data, we generated an interactive database containing several structural levels. The top level comprises a list of genes, and references to the corresponding sources in the literature. The second level consists of an interactive map, which describes the position of all functional elements (coding sequences and enhancers) in each gene locus (loci ranged in size from 16–120 Kb). The exact location of each functional element is presented in a table below the map, along with a description of any known regulatory interactions mediated by the element. The third level contains the annotated locus sequence with highlighted functional regions. In comparison with existing dedicated databases, such as GeNet (Kolpakov et al. 1998; Serov et al. 1998), our compilation is focused on available deletion and footprinting data and it is convenient for: (1) fast navigation and retrieving of CRMs, and (2) fast retrieving of the binding motifs involved in a given regulatory interaction. All annotated data are publicly accessible from the Web site (http://homepages.nyu.edu/∼dap5/PCL/appendix2.htm).
Representation of Clustered Recognition Motifs
We adopted position weighted matrices (PWM) as a model description of binding motifs for TFs (see Methods). For a selected motif quality (the PWM cutoff value), we identified all putative binding sites in the locus sequences from our database.
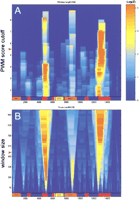
To generate a simple, biologically relevant cluster representation, we counted the number of the sites in a sliding window and considered both the window length and the PWM cutoff values as parameters. It was found that these parameters dramatically alter the statistical significance and the position of the clusters. For each position in a sequence, each PWM cutoff, and each window length, we found the number of PWM matches within the window and evaluated the significance of the clusters adopting the Poisson distribution for the number of PWM matches in the window (see Methods). Figure 1 illustrates clusters of Bicoid binding motif in the even-skipped locus evaluated in a broad range of parameter values. This representation allows a quantitative description of clusters and provides information on compositional (structural) cluster structure, as it (1) shows the ratio between the low- and the high-affinity sites in the cluster, and (2) reflects the presence of subclusters in the context of larger clusters (Fig. 1B).
Representation of clustered recognition motifs. The distribution of clusters for the Bicoid motif in the locus of even-skipped is shown. The color intensity scale represents statistical significance of constitutive clusters. A map of known functional elements in theeve locus is given on the bottom of each panel (X-axis: relative position in the locus in base pairs). (A) Dependence of the cluster significance on the PWM site score cutoff (Y-axis) at the fixed window size (500 bp, see also the red mark on B). (B) How the size of the resolution window (Y-axis) affects the cluster significance at the fixed PWM cutoff (red mark on A). The representation given shows that Bicoid clusters in eve stripe 2 and eve stripe 1+5 regions have distinct ratios of high- and low-affinity binding sites (the cluster composition). Both of these regions in the evelocus have been shown to be responsible for formation of correspondingeve expression stripes in a fly embryo. The weak ‘Bicoid’ cluster inside the eve late1 element indicates the presence of the clustered motif related, but not identical to Bicoid. It is known, however, that the eve late2 region is under control of other homeodomain proteins (such as Eve itself) that also have the conserved core consensus sequence TAAT. The best correlation obtained for Bicoid clusters with their cognate CRMs is 0.76 for the eve locus (Table 2, eve locus vs. Bicoid motif).
Homotypic Clusters Correlate With Functional CRMs
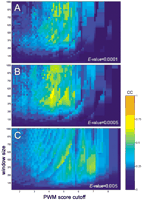
Figure 1 shows that the positions of the most significant Bicoid clusters in the eve locus agree well with the positions of the known Bicoid-regulated CRMs, the eve stripe 2 and theeve stripe 5+1 enhancers. To test how general this correlation is, we selected from our annotation nine recognition motifs for TFs with the most robust PWMs (built from the most reliable alignments; Table 1 and see the Web site Appendix), and we measured the correlation between the position of experimentally verified CRMs and the position of identified homotypic clusters. One can see that the correlation depends on parameters of our clustering function: the window size, the PWM cutoff, and the cluster significance (see Methods). We then searched for the global maximum of the correlation for each motif in the space defined by these three parameters (Fig. 2). For example, we searched for the global maximum of the correlation between positions of Bicoid clusters and positions of all Bicoid-driven CRMs in loci oftll, otd, btd, sal, hb,kr, kni, and eve (bicoid-dependent genes; see Web site Appendix).
Parameter Values in the Point of Global Agreement
Search for the maximum of the correlation between the location of Bicoid clusters and the location of Bicoid-driven CRM sequences in eight different genes. Y-axis shows the size of the resolution window; X-axis shows the PWM cutoff values; the color intensity scale shows the correlation (the Pearson association coefficient) value. The correlation also depends on the cluster significance (theE-value cutoff), which is shown by three consequent projections with the increasing E-value cutoff (A–C). The global maximum of correlation for the Bicoid motif is found at the PWM cutoff values 4.1–4.3, for the windows ∼500–600 bp and at the E-value cutoff 0.0005 (B). The CC maximum has nonmonotonous distribution in the parametric space, caused, in part, by a specific ratio between low- and high-scoring PWM matches, i.e., by specific ‘cluster composition.’
We found that for most of the motifs considered, both the correlation coefficient and the cluster significance (cluster E-value cutoff) take high values simultaneously at the point of the global maximum. This suggests that the optimal parameter settings (i.e., cluster composition) are similar for distinct CRMs regulated by the same TF. Therefore, selectivity of cluster recognition can be improved if a particular set of parameters is obtained from analysis of known functional regions (window/PWM score/cluster significance). If clusters do not pass these parameters, their composition (structure) appears to be dissimilar from the functional cluster, and the likelihood that they belong to the given binding motif is lower.
The summarized data of the described correlation test for nine binding motifs (Table 1) strongly confirmed that statistically significant homotypic clusters indeed coincided with their cognate regulatory regions. In addition, the search for the maximum of the correlation resulted in optimized parameter values, which one can use to search for the homotypic clusters in the genome. Thus, we observed that for the majority of the motifs, the optimal resolution window fell within a surprisingly narrow range of 500–600 bp at the point of the global maximum. We defined this value as the size of the functional binding site cluster, and it appeared to be very close for all binding motifs studied. Indeed, there are very few examples in our database of a CRM smaller than 500 bp. Another important parameter that we obtained using the described optimization procedure was the optimal PWM score cutoff, which delimited the border between the functional high-scoring binding site matches and the false positives.
Once confirmed, the homotypic cluster representation can be implemented in genomics and biological applications including: (1) constructing regulatory gene networks, and (2) discovering similarly regulated genes in the genome.
Construction of Regulatory Gene Networks
One of the main questions in exploring gene networks is whether a given TF regulates a particular gene. Our data suggest that if this is the case, a significant binding site cluster for this transcriptional regulator should be present in the regulatory region of the gene. Therefore, one can explore regulatory networks by testing the presence of regulatory clusters for potential upstream regulators in known CRMs of putative target genes.
We demonstrated the potential of this approach by testing known regulatory interactions with parameters obtained from the optimization procedure described above (Table 1, Fig. 2). Consideration of the nine motifs with best alignments suggests an optimal window size of 575 bp. The same results show that all functional clusters contain sites having the PWM cutoff value corresponding to the site E-value (see Methods) cutoff of ∼10−3. Using these estimations for the window size and the PWM cutoff (the site E-value cutoff), we can now scan a number of known genes with a number of binding motifs for putative upstream regulators and reveal the potential interactions between genes in the network.
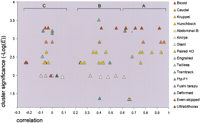
To this end, we decided to carry out a recognition test for all annotated regulatory interactions in the developmental cascade, which are present in our literature compilation (more than 60 interactions; see Web site Appendix). In fact, these interactions represent combinations of 20 annotated developmental genes and 16 TFs with known regulatory motifs, mainly encoded by the same developmental genes, as noted earlier. For each motif/locus combination, we measured two statistical values: the correlation between positions of the predicted clusters and positions of their cognate CRMs, and the cluster significance (cluster E-value cutoff). Table2 shows statistical values obtained for more than 60 regulatory interactions tested. Graphic representation of the recognition test is given in Figure 3. One can see that the correlation value and the cluster significance (cluster E-value) represent two independent validation criteria for a given regulatory interaction. This two-statistics representation allows not only testing of the relevance of each regulatory interaction, but also comparing the relative performance of different binding motifs.
Correlation of Clusters With Their Cognate CRM Sequences
Recognition of known regulatory interactions. The data from Table2 are represented as a scatter plot. The correlation values (X-axis) for tested motif/gene locus combinations are plotted vs. the cluster significance (-Log[E], Y-axis). Motifs are shown on the right side; data points for each motif have the same color. Brackets (A–C) mark three distinct correlation groups. The cluster significance cutoff (the cluster E-value cutoff) was set for each motif on the basis of a global training procedure (see Table 1). Data points in the upper right corner correspond to the best confidence of recognition; poorly performing motifs have a consistently low E-value (Gt, Eve).
All considered motif/locus combinations fall into three main categories: good recognition (Fig. 3, group ‘A’), moderate recognition (Fig. 3, group ‘B’) and no recognition (Fig. 3, group ‘C’). Group ‘A’ comprises cases where the experimental data are in perfect agreement with computationally predicted binding site clusters, and all combinations in this group typically have very high cluster significance as well. Note that the value of the correlation coefficient in our recognition test is comparable to that observed for gene recognition in long genomic sequences (Guigó et al. 2000). Examples in group ‘C’ show no significant correlation and represent the rate of false negatives (FNs) for the method (35%). For example, we failed to confirm regulation of otd by Bicoid, although this regulatory interaction has experimental support (Gao et al. 1996;Gao and Finkelstein 1998). Based on cluster occurrence in theDrosophila genome, we also estimated the false positive rate (FP; see also the Web site Appendix). Thus, for the Bicoid binding motif, with parameter values set to the optimal (Table 1), we detected ∼550 clusters in the genome. At the same time, the total length of the locus sequences for 20 considered developmental genes covers 0.4% of the genome at most, which corresponds to ∼2 FP Bicoid clusters in this group of genes. Taking into account the 10 functional Bicoid clusters present (Table 2), the FP rate for Bicoid should not exceed 20% in the considered developmental cascade.
The high fidelity of recognition observed in the described test allows construction of reliable networks for direct transcriptional gene interactions as long as the reliable recognition motifs are available.
Discovery of Similarly Regulated Genes in the Genome
Finding coregulated genes through analysis of similar signals in their cis-regulatory regions is an extremely important task for exploring gene networks in higher eukaryotes (Arnone and Davidson 1997). The identification of similarly regulated genes in the genome is a well explored area with multiple algorithms developed. However, site clustering yields a new insight into the problem.
Defined sets of binding motifs might now serve to build recognition models on the basis of site clustering (heterotypic clusters) and to extract similarly regulated genes from the genome using these models. In many cases, this approach appears to be extremely efficient (Berman et al. 2002). Some attempts were also made to search the genome using clustering of single binding motifs (Markstein et al. 2002) or homotypic clusters. In fact, a search for homotypic clusters, which requires clustering of each binding motif, might be more selective than searching with heterotypic cluster models. Homotypic clustering is also of special biological interest as it allows construction of very specific recognition models. In particular, extraction from the genome might require specific features such as ratios between distinct binding motifs, the presence of binding motifs with defined affinity, etc. (Small et al. 1992; Ludwig et al. 1998, 2000). In this case, the initial separate consideration of distinct binding motifs gives significant flexibility, as one can describe the final heterotypic clustering model as combined specific homotypic clustering models, built for each motif separately.
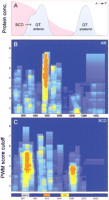
To demonstrate the difference between programs based on heterotypic and homotypic cluster considerations, we analyzed the distribution of regulatory regions in the locus of giant. Giant is a gap gene that is expressed in embryos in two broad domains, the anterior and the posterior. The enhancer region responsible for the expression of the posterior giant domain was identified (Berman et al. 2002) using a search with several binding motifs (a heterotypic cluster). The region in the giant locus responsible for anterior giant expression is not known; however, this expression is sensitive to Bicoid and is not observed in bicoid −mutants (Eldon and Pirrotta 1991; Kraut and Levine 1991). We scanned the giant locus (16 Kb) for the presence of Bicoid binding site clusters and identified one striking region upstream of thegiant coding sequence (Fig. 4), which is different from the previously identified posterior enhancer. The identified region is a strong candidate CRM that responds to the Bicoid gradient.
Discovery of CRM sequences using clustering of single motifs. Results of mapping of cis-regulatory modules in the giantlocus are shown in comparison with the distribution of known functional elements. (A) Relative distribution of Bicoid and Giant expression patterns along the embryo. (B) The distribution of Kruppel and (C) the distribution of Bicoid clusters. Besides the known posterior enhancer (Berman et al. 2002), the method indicates the presence of two Bicoid clusters upstream and downstream of the gene. Notice that the Bicoid cluster located downstream of thegiant CDS (B, in position ∼10000) contains low-affinity Bicoid sites (PWM is below 4.2, the established optimal cutoff for Bicoid; see Table 1) and does not represent a candidate CRM. We also found that this sequence consists of several long direct repeats (∼100 bp), which is not typical for DrosophilaCRMs. In contrast, the upstream candidate region contains a very strong cluster of closely spaced high-affinity Bicoid sites.
This example demonstrates that the separate consideration of binding motifs might be an excellent complement to the consideration of heterotypic clusters. Positions of predicted CRMs in 20 developmental genes using homotypic cluster consideration are available from our Web resource.
DISCUSSION
Interpreting Gene Response to Upstream Regulators
The description of a regulatory module in the form of overlapping homotypic clusters presents the possibility to explore and interpret the differential responses of CRMs to various concentrations of upstream regulators. The differential gene response to upstream regulators depends on the number and affinity of binding motifs (Driever and Nusslein-Volhard 1988a,b; Driever et al. 1989), which one can describe through parameters of corresponding homotypic clusters. In our case, the number of sites (the site density) in a CRM is related to the statistical significance of the cluster, whereas the affinity of these sites and the ratio between the high-affinity and low-affinity sites is described by the PWM cutoff values. Finally, the true size of the CRM can be obtained from the optimal resolution windows for overlapping homotypic clusters that comprise this CRM.
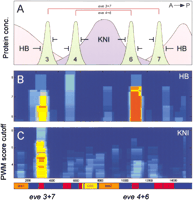
How can one use this quantitative information for interpreting CRM response to the upstream regulators? For example, one can compare the differential response of clusters with distinct ratios of the high- and low-affinity sites. To illustrate this example we considered the regulation of the even-skipped enhancers by Hunchback and Knirps. Genetic analysis (Small et al. 1996; Kosman and Small 1997; Fujioka et al. 1999; Sackerson et al. 1999) indicates that the repressors Knirps and Hunchback delimit the expression borders of the even-skipped stripes 3, 4, 6, and 7 (Fig.5A). The eve stripes 4 and 6 are formed in the regions of the embryo with a lower concentration of Hunchback and a higher concentration of Knirps. In contrast,eve stripes 3 and 7 are formed in regions where the Hunchback concentration is greater than that of Knirps. The two corresponding CRM regions, for eve 4+6 and eve 3+7, contain all transcriptional information for these four stripes.
Quantitative description of gene response to TFs. Overlapping Hunchback and Knirps gradients combine two symmetrical zones, where theeven-skipped expression stripes 4+6 and 3+7 are formed (A). The Hunchback cluster in the eve 3+7 enhancer has a lower PWM cutoff (site affinity) and a lower statistical significance (less sites) than that in the eve 4+6. In contrast, the Knirps cluster in eve 3+7 enhancer has more high-affinity sites than that in the eve 4+6 (B). The detected composition of clusters for Hunchback and Knirps in theeven-skipped locus supports the existing biological model and might be used for interpretation of gene response to the upstream regulators.
Investigation of clusters for Hunchback and Knirps motifs in these two enhancer regions reveals that the 3+7 enhancer has a much stronger (more sites with a higher affinity) cluster of Knirps sites, but a weaker cluster for Hunchback than the 4+6 region (Fig. 5B). This distribution of Hunchback and Knirps clusters fits well with the expected response levels of the two enhancers. The poor Hunchback cluster in the eve 3+7 region may be related to its lower response to Hunchback repression. As a result, eve stripes 3 and 7 are formed in the embryonic domains with a higher concentration of Hunchback. Conversely, a powerful cluster of Knirps sites delimits the position of these two stripes relative to the Knirps gradient. The reverse situation takes place in the case of the eve 4+6 enhancer, which has a weak Knirps cluster, acting only in response to a higher dose of Knirps.
Prediction of the differential gene response through quantitative description of a gene regulatory region is a difficult task. In the general case one has to account not only for the number and the affinity of binding motifs present in the region, but also for potential input from various TFs involved in the regulation and perhaps many other circumstances.
Strategies for Exploring Drosophila Gene Networks
The distribution and the dynamics of gene products in multicellular organisms vary significantly from one cell to another, and obtaining a series of expression data for each cell or even small groups of cells in this case is much more difficult than for unicellular organisms. Therefore, finding coregulated genes through analysis of similar signals in theircis-regulatory regions can be very fruitful for exploring gene networks in higher eukaryotes. In this context, theDrosophila developmental enhancers represent an excellent model for exploration, due to the large amount of accumulated experimental data for the system.
How one can handle such valuable datasets, and what information can be obtained from computational analysis of the data? In our recent work (Papatsenko et al. 2002), we demonstrated how to calculate the relative affinity (the optimal PWM score cutoff) for functional binding sites on the basis of agreement within original footprint data for transcriptional regulators obtained from different literature sources. In the present study, we show that this strategy can be extended to agreements established between different types of data. For instance, we use binding motifs (in vitro footprinting data) and positions of CRMs (in vivo deletion data) as the input for our correlation function described above (Table 1, Fig. 2). In fact, the optimal PWM cutoff values obtained using this correlation analysis (based on clustering phenomena) fell very close to the PWM, obtained previously (Papatsenko et al. 2002) using comparison of different footprints only.
In this paper we demonstrate (see the Construction of Regulatory Gene Networks section above) that the optimized parameters obtained by comparing various types of data can be efficiently used for further exploration of the network. In the case of Drosophiladevelopmental genes, the network is still incomplete, as in some genes cis-regulatory modules are not known, and in others it is not known what exact function they perform. Some of these informational gaps in the developmental gene network can be filled using cluster analysis of known binding motifs, similar to the one described in the present work. Experimental evidence still must be obtained to confirm the proposed interactions between genes, but the computational strategy presented here allows the performance of these tests in a systematic manner.
Motif Clustering in Transcription Regulatory Systems
How common is the clustering of binding sites, and what type of recognition motifs form significant clusters in the genome? To answer these questions, we first calculated how often a given regulatory interaction in the developmental network results in a cluster of binding motifs in the target CRM region (see the data on our Web site). We found that positive hits for homotypic binding motifs (i.e., presence of statistically significant clusters) comprise more than 70% of all regulatory interactions tested. Moreover, regulatory interactions within the network that produce no clusters (negative hits) in CRM regions belong to poorly characterized genes (btd, prd) or are described by poorly performing motifs (Gt, Eve; Fig. 3). Second, we investigated motif clustering in another model system, the Drosophila rhodopsin promoters. The regulatory regions of these genes represent typical proximal promoters with TATA box and transcription start site (TSS) motifs and participate in the regulation of terminal differentiation genes, the visual pigments rhodopsins. There are several known binding motifs for transcriptional regulators in the rhodopsinpromoters (Mismer and Rubin 1989; Fortini and Rubin 1990; Papatsenko et al. 2001). We analyzed the distribution of clusters for Orthodenticle and Prospero in several rh promoters and found corresponding significant clusters to be specifically present in the promoter regions (see Web site Appendix).
The results described herein suggest that clustering of recognition motifs for spatiotemporal and tissue-specific transcriptional regulators seems to be a common phenomenon in higher eukaryotes, independent from the nature of the gene and its position in the regulatory hierarchy. We believe that the consideration of homotypic clusters is a very powerful approach that can be efficiently implemented to a broad variety of genomics and biological applications.
METHODS
Initial alignments for recognition motifs were built using the ClustalW method and adjusted manually. For each type of recognition
motif, we outlined a well defined core made of positions with high information content (see Web site Appendix). In this procedure,
the threshold levels were set to the same value for all motifs considered. Based on the resulting alignments, we built position
weighted matrices for motifs using a formula with a pseudocount parameter: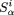
where Si
α is the score of the letter α (α∈{A,C,G,T}) in the position i,ni
α is the number of letters α in column i of the motif alignment, qα is the frequency of letter α in the Drosophila genome, anda is the pseudocount parameter, which we put equal to 1.
For each PWM cutoff value, we estimated the site E-value as the total number of motif matches above the PWM cutoff in the entireDrosophila genome normalized to the length of the genome. The sequence of the complete genome for Drosophila melanogasterwas obtained from the BDGP database (Rubin and Lewis 2000) and filtered for low-information regions, such as satellite DNA.
To measure the statistical significance of a cluster, the probabilityp of k PWM hits within n-window for random Bernoulli sequence was approximated by the Poisson distribution (Wagner 1997, 1999). To measure the cluster significance, we considered a conditional probability of observing k sites in then-window, where one site is already present: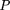
Thus in this case, a cluster should contain at least two sites. An extension of this formula can be readily obtained from
the Poisson distribution for clusters which contain at least k sites, knowing that l sites are already present. The resulting cluster E-values were then calculated for clusters that contained more than m sites (m ≥ k):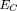
These conditional cluster E-values were assigned to each position of the test sequence and plotted then as n-width windows centered on the corresponding positions (in Fig. 1, log(EC
) values are shown).
The site E-value ES and the conditional cluster E-value EC allow one to calculate the average expectation of the cluster in the window as ν = ESEC . Statistical significance of the appearance of one cluster in a locus by chance can be calculated from ν with the correction for the number of independent observations (independent resolution windows). We approximated the number of independent observations to be roughly equal to 2N/L, where N is the length of the locus sequence and L is the length of the window. In this case, the statistical significance of a cluster in a locus can be estimated as 2Nν/L(correction Bonferroni, see Table 1).
To estimate the agreement between the cluster location (predicted map) and the location of enhancer regions (experimental
map), we monitored the Pearson association coefficient (Waterman 1995):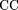
where TP is the number of positions covered by both the predicted clusters and the experimental CRM, TN is the number of positions covered by neither of them, FP is the number of positions covered only by the prediction, and FN is the number of positions covered only by the CRM. In the case of global optimization, we calculated the numbers of TP, TN,FP, and FN for all genes regulated by one motif at once. This value is accepted as standard for an assessment of gene prediction accuracy
(Guigó et al. 2000).
Because of the diversity of cluster composition, we decided to explore the entire parametric space of our clustering and correlation functions. When assessing motif clustering, we chose cluster significance (cluster E-value) as the dependent variable in the 3D data array, with the PWM score, the window length, and the window position in the sequence as coordinate variables. In the case of the correlation function, we adopted correlation coefficient (CC) as the dependent variable in another 3D data array, with the PWM score, the window length, and the clusterE-value as coordinate variables. The example shown in Figure1A represents projection of the cluster E-value 3D data array onto the surface defined by the window position in a sequence and the PWM cutoff. The window size in this case is fixed. Another projection of the same 3D data array is shown in Figure 1B. In this case, the PMW cutoff is fixed and the cluster E-value depends on the window position in a sequence and the window length only. Figure 2 shows three consequent projections of 3D CC data array onto a surface defined by the PWM score cutoff and the window size.
WEB SITE REFERENCES
http://homepages.nyu.edu/∼dap5/PCL/appendix2.htm; The CRM annotation, software, and related resources are available at this Web site.
Acknowledgments
We thank Ben Berman for sharing his unpublished results, and stimulating discussion. We thank Stephen Small for his ideas regarding differential gene response and his suggestion to explore this issue on the example of even-skipped stripe 4+6 and 3+7 enhancers. We also thank Claude Desplan and Bud Mishra for careful reading of the manuscript and helpful discussion. This work was supported by a grant from the NIH/National Eye Institute (EY13010) to Claude Desplan. V.M. and A.L. were also supported in part by grants from the Ludwig Institute for Cancer Research, HHMI East Europe (#55000309), and RFBR (#02-04-49111).
The publication costs of this article were defrayed in part by payment of page charges. This article must therefore be hereby marked “advertisement” in accordance with 18 USC section 1734 solely to indicate this fact.
Footnotes
-
↵4 Corresponding author.
-
E-MAIL dap5{at}nyu.edu; FAX (212) 995-4710.
-
Article and publication are at http://www.genome.org/cgi/doi/10.1101/gr.668403.
-
- Received July 26, 2002.
- Accepted January 22, 2003.
- Cold Spring Harbor Laboratory Press
