Distribution of Protein Folds in the Three Superkingdoms of Life
- 1National Center for Biotechnology Information, National Library of Medicine, National Institutes of Health, Bethesda, Maryland 20894 USA; 2Department of Structural Biology, Stanford University, Stanford, California 94305-5126 USA; 3Department of Molecular Pharmacology and Biological Chemistry, Northwestern University, Chicago, Illinois 60611 USA
Abstract
A sensitive protein-fold recognition procedure was developed on the basis of iterative database search using the PSI-BLAST program. A collection of 1193 position-dependent weight matrices that can be used as fold identifiers was produced. In the completely sequenced genomes, folds could be automatically identified for 20%–30% of the proteins, with 3%–6% more detectable by additional analysis of conserved motifs. The distribution of the most common folds is very similar in bacteria and archaea but distinct in eukaryotes. Within the bacteria, this distribution differs between parasitic and free-living species. In all analyzed genomes, the P-loop NTPases are the most abundant fold. In bacteria and archaea, the next most common folds are ferredoxin-like domains, TIM-barrels, and methyltransferases, whereas in eukaryotes, the second to fourth places belong to protein kinases, β-propellers and TIM-barrels. The observed diversity of protein folds in different proteomes is approximately twice as high as it would be expected from a simple stochastic model describing a proteome as a finite sample from an infinite pool of proteins with an exponential distribution of the fold fractions. Distribution of the number of domains with different folds in one protein fits the geometric model, which is compatible with the evolution of multidomain proteins by random combination of domains.
[Fold predictions for proteins from 14 proteomes are available on the World Wide Web atftp://ncbi.nlm.nih.gov/pub/koonin/FOLDS/index.html. The FIDs are available by anonymous ftp at the same location.]
Knowledge of the three-dimensional structures of proteins is indispensable for understanding biological processes. Ideally, determination of the structures of all proteins encoded in a genome should follow genome sequencing promptly. In reality, the recent substantial progress in experimental structural biology notwithstanding, structures are being determined for only a miniscule fraction of the gene products even for a bacterial genome containing a few thousand genes, not to mention the human genome with its estimated 100,000 genes (Holm and Sander 1996). Fortunately, however, considerable information on protein structure can be extracted by computer from sequence alone. This stems from two related principles of protein sequence-structure relationships: (a) there is only a limited number of distinct protein folds, perhaps no more than 1000 altogether, and ∼400, presumably the most common ones, are already represented by experimentally determined structures (Dorit et al. 1990; Chothia 1992; Hubbard et al. 1997); (b) proteins with similar sequences tend to have similar structures; in homologous proteins, structure is generally more conserved than sequence, and therefore even subtle but reliable sequence similarity is likely to signify structure conservation (Doolittle 1981; Holm and Sander 1996, 1997).
The latter principle is essentially a recast of the Anfinsen’s postulate: A protein’s sequence determines its structure (Anfinsen and Scheraga 1975). Theoretically, structure should thus be predictable from sequence. Currently, however, such ab initio prediction is possible only for peptides and very small proteins (Abagyan 1997; Ortiz et al. 1998). Therefore for typical proteins, the only practical route to deriving structural information from sequence is through similarity to proteins with known structures, and success of structure prediction critically depends on the resolution and robustness of the methods used to detect such similarity. There are two basic categories of such methods: (1) sequence similarity analysis; and (2) sequence–structure threading (Godzik and Skolnick 1992; Bryant and Altschul 1995; Murzin and Bateman 1997). The threading approaches have been designed to address the problem of sequence-based structure prediction directly by assessing the compatibility of a given sequence with each known structure. These methods, however, generally lack statistical rigor and are computationally expensive (Lathrop 1994; T.F. Smith et al. 1997). Sequence similarity search is much faster, and at least the most popular method, BLAST, has a solid statistical foundation (Karlin and Altschul 1990; Karlin et al. 1991). The problem with these methods is that, as shown by a recent extensive evaluation, they detect only a small fraction of all homologous relationships that can be inferred from the comparison of the known protein structures (Brenner et al. 1998).
Accumulation of complete genome sequences from several bacteria, archaea, and eukaryotes creates new possibilities for assessing the phylogenetic distribution of protein folds in connection to organism phenotypes. Clearly, such a survey will be meaningful only if for each known fold, the majority of the representatives are recognized correctly. Recently several attempts have been made to analyze fold distribution in the complete protein sequence database (Gerstein and Levitt 1997) or in individual proteomes (Fischer and Eisenberg 1997;Gerstein 1997). These efforts relied primarily on standard methods for sequence comparison whose relatively low performance in fold recognition has been demonstrated (Brenner et al. 1998), with an additional contribution from secondary structure-based threading (Fischer and Eisenberg 1997). We sought to increase the sensitivity of fold recognition by using position-dependent weight matrices that are produced by the PSI-BLAST program concomitantly with database search (Altschul et al. 1997). In several studies on individual protein families, PSI-BLAST has demonstrated its ability to detect subtle sequence similarities that led to fold prediction, in part already confirmed by experiment (Mushegian et al. 1997; Aravind et al. 1998a,b;Aravind and Koonin 1998). We reasoned that matrices produced by PSI-BLAST could serve as sensitive identifiers for protein folds and proceeded to develop such identifiers for all folds present in the Structural Classification of Proteins (SCOP) database (Murzin et al. 1995; Hubbard et al. 1997) and to apply them for a comparative analysis of fold distribution in complete proteomes of bacteria, archaea, and eukaryotes.
RESULTS AND DISCUSSION
The Fold Recognition Procedure
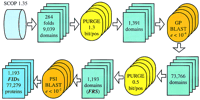
The starting material for our fold recognition protocol (Fig.1) was the set of protein sequences represented in SCOP 1.35, in which individual structural domains have been isolated. With the goal of increasing the resolution power of the resulting profiles, these domain sequences were enriched with those of obvious homologs from the nonredundant (NR) protein sequence database at the National Center for Biotechnology Information (NCBI) and then clustered by sequence similarity to select representative sequences for fold recognition (see Methods). The resulting 1193 domains belong to significantly different proteins with reliable fold assignment, classified by fold (fold representative sequences or FRS). Each FRS was used as a starting point for iterative PSI-BLAST search of the NR database, producing significant hits to 77,279 proteins, which comprises ∼27% of the entire database. Compared to single-pass searches, the iterative searches retrieved a total of 26,275 extra hits corresponding to 228 out of the 284 folds. The current version of PSI-BLAST has the option of saving position-dependent weight matrices constructed during the iterative search. Such a matrix contains information on all the database sequences significantly similar to a FRS and can be used to search another database, greatly increasing the sensitivity and selectivity compared to a search with a single query sequence. Thus the 1193 matrices produced for each of the FRS by the PSI-BLAST searches were stored for subsequent use as fold identifiers (FIDs).
Under this approach, a fold may be represented by one or multiple FIDs, depending on the number of FRS. Cross-recognition between FIDs (in other words, overlap between PSI-BLAST outputs) within one fold measures the ability of the method to detect subtle similarities that escape standard sequence comparison procedures. Of the 176 folds with more than one FRS, 74 (42%) showed perfect intrafold recognition (there was overlap within each pair of outputs), 58 (33%) showed partial intrafold recognition, and in the remaining 44 (25%), there was no recognition between different FIDs.
In contrast, recognition between different folds typically is false; thus overlaps between the database search results for FRS representing different folds should be considered false positives for one or both of the two folds involved. To estimate the error rates conservatively, both assignments were counted as false positives. (Parenthetically, it should be noticed that this may not be true in the rare cases in which certain folds in the SCOP classification seemed to have been split artificially. Thus it was noticed that two pairs of folds, namely seven- and eight-bladed β-propellers and two Rossmann-like nucleotide-binding folds, are in fact related closely at the sequence level. These folds were combined for the purpose of this analysis). Of the 284 folds included in our analysis, for 198 (70%), no false positives were detected. For the remaining folds, point estimates of the false-positive rates were obtained after clustering the complete sets of hits and the sets of overlaps, to account for nonindependent (homologous) sequences.
A point estimate of the error rate may give false confidence when the number of involved cases is small. To obtain an interval estimate, we assumed that clusters of database hits for each FRS were obtained independently (a realistic assumption given the low cut-off used for clustering; see Methods). A Bernoulli model was then applied to find the upper limit for a background error rate that may lead to the given number of independent false positives out of the given number of independent clusters. The upper limits of the 95% confidence interval of the false positive rate for the most common folds are shown in Table1. With the exception of two cases, the maximum expected error rate is well below 10%. This is in a good agreement with the empirical results (see below).
Upper Limit of 95% Confidence Interval for False-Positive Rate
Whereas the evaluation of the false-positive rate in fold recognition is more or less straightforward, the critical issue of false negatives (that is, how many proteins with a known fold are missed) is much harder to address. Some estimates, however, could be made concomitantly with a detailed analysis of the distribution of predicted folds in complete proteomes as discussed below.
Phylogenetic Distribution of Protein Folds
At the time of this analysis (April 1998), 13 complete genome sequences were publicly available: Haemophilus influenzae(Fleischmann et al. 1995), Mycoplasma genitalium (Fraser et al. 1995), Mycoplasma pneumoniae (Himmelreich et al. 1996),Synechocystis sp. (Kaneko and Tabata 1997), Helicobacter pylori (Tomb et al. 1997), Escherichia coli (Blattner et al. 1997), Bacillus subtilis (Kunst et al. 1997),Borrelia burgdorferi (Fraser et al. 1997), Aquifex aeolicus (Deckert et al. 1998), Methanococcus jannaschii(Bult et al. 1996), Methanobacterium thermoautotrophicum (D.R.Smith et al. 1997), Archaeoglobus fulgidus (Klenk et al. 1997), and Saccharomyces cerevisiae (Goffeau et al. 1996). In addition, the proteome of the nematode Caenorhabditis elegansthat was ∼85% complete (Kuwabara 1997) also was included in the analysis (Table 2).
Fold Assignment in Complete Proteomes
Fold assignment was performed by searching the sequences from each of these proteomes using the PSI-BLAST program (a single pass), with each of the 1193 FIDs as the query. All hits with an e-value ≤10−2 after an adjustment to the NR database size were considered automatic fold assignments. For the 30 most common folds, additional, case-by-case analysis was performed by searching for the conservation of motifs typical of known protein families in the outputs of the FID-initiated searches (regardless of the statistical significance). Additionally, all the sequences from complete proteomes were searched against the NR database using PSI-BLAST and the outputs were examined in the same fashion.
The results of this analysis (Table 2) show that the fraction of false positives (erroneous fold assignments) among automatic predictions typically was ∼1%–2% (maximum 3.2%); the detected fraction of false negatives (additional assignments made by the case-by-case screening) was 9%–13% (maximum 13.3%). These findings suggest that FIDs predict protein folds at a genome scale with a reasonable reliability.
The overall fraction of proteins with fold assignments in the proteomes typically varied in the range of 24%–35% with a few exceptions: the highly compositionally biased proteome of B. burgdorferi and the incomplete proteome of C. elegans, which was analyzed only automatically, have the lowest fraction of proteins with assigned folds (19% and 21%, respectively), whereas the smallest known proteome ofM. genitalium has the highest (39%). This prediction rate is considerably higher than those reported in the previous studies (Fischer and Eisenberg 1997; Gerstein 1997; Gerstein and Levitt 1997). Furthermore, the information is now available for a greater number of genomes, at least for bacteria and archaea. Thus, though the prediction evidently is still incomplete, it was of interest to explore some patterns in the fold distribution.
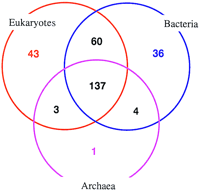
Figure 2 shows the distribution of predicted folds in the three superkingdoms of life, Bacteria, Archaea, and Eukarya. Almost one-half of the folds are universal. It is remarkable that nearly all folds found in archaea belong to this ubiquitous set, whereas a very small number is shared by archaea with bacteria or eukaryotes, to the exclusion of the third superkingdom. By contrast, over 20% of the recognized folds are shared by bacteria and eukaryotes, but not by archaea, most likely caused by the transfer of bacterial genes from organellar genomes to the nuclear genomes of eukaryotes, and perhaps to additional horizontal transfer events. Whereas major gene exchange has most likely occurred also between bacteria and archaea (Koonin et al. 1997), it appears that these events involved primarily genes encoding proteins with ubiquitous folds, for example., central metabolic enzymes. The near absence of archaea-specific folds, which contrasts the considerable and almost equal number of specifically bacterial and eukaryotic folds, probably reflects the currently insufficient structural characterization of archaeal proteins.
Distribution of the recognized folds in bacteria, archaea, and eukaryotes. The number of recognized folds is indicated for each part of the diagram.
In all three superkingdoms, the most common fold is the P-loop NTPase. Four folds, namely P-loop NTPases, TIM barrels, ferredoxin-like domains, and Rossmann fold domains, are present in all three top 10 lists (Table 3). The abundance of each of the common folds, but particularly P-loop NTPases and SAM-dependent methyltransferases (the third and fourth-ranking fold in bacteria and archaea, respectively), seems to have been underestimated in the previous studies (Gerstein 1997; Gerstein and Levitt 1997). The P-loops have not been detected as the most common fold in any genome or taxonomic division, whereas the methyltransferases never made the top 10 list at all, apparently because of the relative difficulty of their recognition. In agreement with the previous findings reported for a small set of complete genomes (Gerstein 1997), all top folds in bacteria and archaea, and 8 out of the top 10 folds in eukaryotes belong to two structural classes: α/β and mixed α + β proteins.
Top 30 Folds in Complete Proteomes
The distributions of the most common folds in bacterial and archaeal proteomes are very similar (8 of the top 10 folds are the same; Table3), though the much higher abundance of ferredoxin-like proteins and metallo-β-lactamase-like proteins and the under-representation of the Rossmann fold in archaea are notable. Eukaryotes show a different ranking of folds—five of the folds among the eukaryotic top 10 hits are not in the bacterial or archaeal top 10 lists, and one, namely the ligand-binding domains of nuclear receptors, is unique for eukaryotes (Table 3). In bacteria and archaea, the most common folds correspond to enzymes involved in genome replication and expression (e.g., ATPases and GTPases) and metabolic enzymes. Particularly notable is the abundance of methyltransferases (Table 3; see above), most of which are involved in modification of nucleic acids and proteins. By contrast, among the eukaryotic top 10 folds, proteins involved in regulation and signal transduction, such as protein kinases and β-propellers, are prominent; it is of further note that in the multicellular eukaryoteC. elegans, protein kinases are the most common fold (Table3). Perhaps unexpectedly, in spite of the great importance of methylation in the regulation of eukaryotic gene expression, the methyltransferases are relatively much less abundant in eukaryotes than in prokaryotes (rank 12; Table 3).
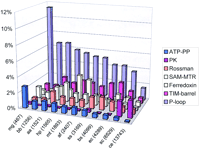
The fraction of proteins with the P-loop fold strongly depends on the proteome size—the smaller the proteome, the larger the share of P-loop-containing proteins (Fig. 3). This reflects the fact that many ATPases and GTPases are involved in housekeeping processes (e.g., translation and replication), and their loss is incompatible with life. The other common folds do not show a similar distribution, and their contribution to a given proteome seems to depend more on the respective organism’s lifestyle than on the total number of proteins. Thus the fraction of TIM barrels is the greatest in heterotrophic bacteria with diverse metabolism, for example, E. coli, whereas ferredoxins are most prominent in autotrophs with long electron transfer chains such as archaea andSynechocystis sp. Even more specifically, in the free-living bacterium A. aeolicus, whose proteome size is close to those of the parasites B. burgdorferi and H. pylori, the folds involved in metabolic functions, namely TIM barrels and Rossmann fold domains, are clearly more abundant (Fig. 3). Some observations, however, for example the obvious over-representation of methyltransferases in H. pylori (Fig. 3), are not so easily explained and may hint at completely unknown aspects of the organism’s physiology.
Distribution of the most common folds in selected bacterial, archaeal, and eukaryotic proteomes. (ATP-PP) ATP pyrophosphatases; (PK) serine–threonine protein kinases; (SAM-MTR) S-adenosyl methionine-dependent methyltransferases. (mg) Mycoplasma genitalium; (bb) Borrelia burgdorferi; (aa) Aquifex aeolicus; (hp) Helicobacter pylori; (mt)Methanobacterium thermoautotrophicum; (af) Archaeoglobus fulgidus; (ss) Synechocystis sp.; (bs) Bacillus subtilis; (ec) Escherichia coli; (sc) Saccharomyces cerevisiae; (ce) Caenorhabditis elegans. For each genome, the total number of encoded proteins is indicated in parenthesis.
Clustering of Organisms on the Basis of Fold Composition
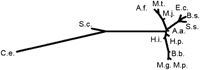
Even a superficial inspection of the distributions of the top 30 folds reveals certain similarities between different organisms (Table3). To address the issue in a systematic manner, a matrix of correlation coefficients between the fold distributions was constructed and used to produce a similarity dendrogram (Fig. 4). The dendrogram emphasizes the already mentioned dramatic difference in the fold composition between eukaryotes and prokaryotes (bacteria and archaea). Archaea form a distinct branch, whereas bacteria fall into two clusters—free-living and parasitic ones. The hyperthermophilic bacterium A. aeolicus is close to the common branching point on the dendrogram, which may reflect massive horizontal gene transfer from archaea, resulting in a chimeric composition of its genome (Aravind et al. 1998c).
It should be emphasized that the observed clustering is clearly different from that observed in phylogenetic reconstructions; for example, such phylogenetically close bacteria as E. coli andH. influenzae (Fleischmann et al. 1995) are in different branches of the fold composition dendrogram. It appears that the observed clustering of parasitic bacteria and their separation from the free-living ones reflects the elimination of a similar subset of folds in the course of a genome-scale adaptation to parasitism that has occurred independently in different bacterial lineages.
Ranking and Diversity of Protein Folds in Proteomes
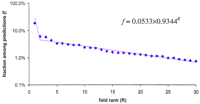
To explore the general features of protein-fold distribution in all organisms, the unweighted average fraction of each fold was calculated first within the superkingdoms and then between them (Table 3). This procedure gives equal weights to each proteome within a superkingdom and to each superkingdom in the total count, regardless of the sample size. A plot of the average fraction of the given fold representatives in a proteome versus fold rank (Fig. 5) shows that at least 29 of the top 30 folds fit an exponent with a strong statistical support [P(χ2) >> 0.1] (extending this plot to the rest of the 239 folds detected in 14 proteomes is statistically unfeasible since most of them are represented by only a few proteins). The first point that does not fit the curve in Figure 5corresponds to the top-ranking P-loop ATPase fold, which is clearly over-represented, given the exponential distribution. Computer simulations based on very simple models of protein fold evolution (assuming a constant rate of protein duplication within a fold and in time, but different rates for different folds) show that the fraction versus rank plots fit exponent when the background probability of protein duplication (i.e., the growth rate of the number of fold representatives) is uniformly distributed among the folds (not shown).
Rank distribution of the unweighted average fraction of the top 30 protein folds in proteomes. (Blue diamonds) The observed unweighted average fractions of folds; (magenta line) The best-fitting exponent approximation.
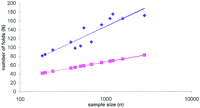
The larger the proteome, the more different folds it contains (Table 2; Fig. 6). This reflects the intuitively obvious fact that proteomes of more complex organisms show a greater structural diversity. On the other hand, the increase of diversity follows from a purely stochastic model that describes a proteome as a finite sample from an infinite pool of proteins with a particular distribution of fold fractions (a bag of proteins). A series of numerical experiments was performed, simulating random sampling from a protein pool. The pool contained an infinite number of proteins, with fold fractions distributed exponentially except for one special point (the top-ranking fold); the parameters of the simulated distribution were optimized to fit the exponential part of the distribution of the top 30 folds from the 14 proteomes (Fig. 5). A comparison of the simulated and observed data (Fig. 6) shows that, whereas both real and simulated diversity seem to follow the logarithm law, the stochastic model underestimates the number of different folds approximately twofold. From the statistical viewpoint, these observations suggest that the distribution of lower-ranking folds (that can not be assessed directly because of the lack of statistically representative data) does not fit the exponential distribution observed for the higher-ranking folds (Fig.5). In other words, the fold composition of the real proteomes does not seem to follow the protein bag model; their higher than expected diversity is likely to be a product of natural selection.
Observed and simulated fold diversity in complete proteomes. (Blue diamonds) Observed number of different folds in the proteomes, plotted against the number of proteins with predicted folds (sample size). (Magenta squares) The results of computer simulations under the stochastic model (see text). (Dotted lines) The respective best-fitting logarithm approximations.
Multidomain Proteins
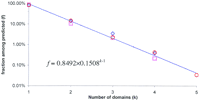
Whereas most proteins contain only one recognizable domain, complex, multidomain proteins are not uncommon (Doolittle 1995). Aggregation of different domains within a single polypeptide chain obviously serves the purpose of bringing several different activities into spatial proximity to ensure proper coordination and regulation. One could speculate that evolution favors the formation of such multidomain proteins, or that their abundance should increase along with increasing complexity of the cellular machinery. To address these questions quantitatively, we examined the distribution of the number of domains in proteins from the three superkingdoms. The number of different folds predicted in each protein in the complete proteomes was counted, and the unweighted average fraction of the proteins with each given number of domains was calculated for each superkingdom (Fig.7). Somewhat surprisingly, the three distributions do not significantly differ from each other [P(χ2) > 0.1 in all comparisons between superkingdoms], indicating that neither the proteome size nor the average protein length [both of which are considerably greater in eukaryotes (Das et al. 1997)] affect the statistics of domain composition. All distributions show a very good fit [P(χ2) >> 0.1] to an exponential model (Fig. 7), where each next class contains approximately seven times less entries then the previous one. Such geometric distribution is typical of series of random independent events with the same background probability. This observation further supports the notion that the selective forces that affect the formation of multidomain proteins, if they exist, are well balanced by the forces that favor splitting of such proteins.
Distribution of multidomain proteins in complete proteomes. (Blue diamonds) Bacteria; (magenta squares) Archaea; (red circles) Eukarya. (Dotted line) Best-fitting exponent approximation (geometric distribution) for the data, averaged across the three superkingdoms.
General Notes and Conclusions
We developed a computer system for protein fold recognition that is based on position-dependent weight matrices constructed using the iterative PSI-BLAST methods, with structurally characterized domains from the SCOP database as starting points. A collection of 1193 position-dependent weight matrices that can serve as fold identifiers was constructed and is available for use. Folds were predicted for 20%–30% of the proteins in each of the 13 analyzed complete proteomes, with a greater prediction rate (39%) for the minimal proteome of M. genitalium. After this analysis was completed, two independent studies have been published that give a very close number of predicted folds for M. genitalium using PSI-BLAST with proteins from this bacterium as starting points (Huynen et al. 1998; Rychlewski et al. 1998). The congruence between the two approaches suggests that PSI-BLAST is a reasonably robust tool for fold prediction.
Given that another 20%–30% of each proteome seem to be comprised by integral membrane proteins and soluble nonglobular proteins (e.g.,Koonin et al. 1997), 30%–50% of all predictable globular domains may be covered by the present analysis. Although incomplete, this coverage suggests that conclusions drawn from the comparative analysis of fold distributions among different phylogenetic lineages may be meaningful. These distributions show major differences between eukaryotes and prokaryotes (bacteria and archaea) in terms of the predominant folds. The most common folds in prokaryotes are those involved in housekeeping functions, such as P-loop-containing NTPases and TIM barrels, whereas the eukaryotic distribution is marked by the prominence of domains with primarily regulatory functions, such as protein kinases and β-propellers. Within the bacteria, there is a remarkable correlation in the fold distributions between phylogenetically distant parasitic species as opposed to their free-living relatives.
Computer simulation of the rank distribution of folds, when compared to the actual observations, indicates that the diversity of folds in each of the analyzed proteomes is about twice as great as that predicted on the basis of the exponential distribution seen among the top 30 folds. It is speculated that structural diversity may be selected for in the course of evolution. The observed distribution of the number of multidomain proteins fits the model of their origin by random domain combination. Further improvements in domain recognition, together with the experimental identification of new folds, will show how general these trends are.
It should be kept in mind that our conclusions may be to some extent affected by the existing biases both in the database of protein structure and in the available collection of complete genome sequences. In particular, folds that are specific to archaea and to multicellular eukaryotes are likely under-represented. Nevertheless, given that the most common folds are already clearly present in SCOP and that at least two genomes from each of the three superkingdoms are available, we do not expect that the ranking of the most abundant folds changes significantly.
METHODS
Databases
The sequences of individual domains from the SCOP 1.35 database were used as the learning set for the fold recognition procedure. All database searches were performed with the NCBI NR database (288,947 protein sequences) in which the regions with low compositional complexity have been masked using the SEG program [window length 60, trigger complexity threshold 3.4, extension complexity threshold 3.8 (Wootton 1994; Wootton and Federhen 1996)]. This version of the NR database is available on request. Proteome sequence data were extracted from the NCBI database of genomes (http://ncbi.nlm.nih.gov/Entrez/Genomes/org.html).
Sequence Analysis
All searches were performed using the PSI-BLAST program, version 2.0.4 (Altschul et al. 1997). The fold recognition protocol (Fig. 1) was developed using the domain sequences representing 284 folds from SCOP 1.35. The nonprotein, oligopeptide, and coiled–coil folds were excluded for obvious reasons; folds so far found only in viral proteins were irrelevant for the analysis of proteomes of cellular life forms and were not analyzed either; the immunoglobulin fold was excluded because of the over-representation of immunoglobulin-like sequences in the NR database that made the analysis of this fold very computationally intensive. To purge redundant entries, sequences belonging to each fold were clustered by a single-linkage algorithm. The pairwise BLAST alignment score divided by the length of the shorter sequence was used as the linkage criterion) with the linkage threshold of 1.3 bit/position; the longest sequence from each cluster was selected for further analysis, and the remaining sequences were discarded. With the goal of increasing the resolution power of the procedure, the resulting sequence set was used to search the NR database using the gapped BLASTP program. Database entries with highly significant (e ≤ 10−4) similarity to the query sequences were considered to be indisputable homologs with the same structural fold. The portions of the respective proteins that aligned with the query were extracted from the database and clustered again using the linkage threshold of 0.5 bit/position. The longest sequence was again retained and used as a query to initiate a PSI-BLAST search of the NR database that was run to convergence or to a maximum of 10 iterations, whichever comes first; the cutoff for inclusion of a sequence in matrix construction was set ate ≤ 10−2. In addition to the search results themselves, a position-specific weight matrix was saved for each search and stored for subsequent use.
For the construction of fold composition dendrogram, the matrix of correlation coefficients (r) between the species-specific fold composition vectors was converted into a distance matrix using the 1 − r 2 transformation. The dendrogram was constructed from this distance matrix using the FITCH program from the PHYLIP package (Felsenstein 1996), which is based on the least-square algorithm of Fitch and Margoliash (Fitch and Margoliash 1967).
Acknowledgments
We thank L. Aravind and Roland Walker for valuable help with case-by-case fold prediction and automated database searches, respectively, and L. Aravind, Steven Bryant, Michael Galperin, David Landsman, David Lipman, Kira Makarova, and Roland Walker for critical reading of the manuscript.
The publication costs of this article were defrayed in part by payment of page charges. This article must therefore be hereby marked “advertisement” in accordance with 18 USC section 1734 solely to indicate this fact.