The Relative Power of Family-Based and Case-Control Designs for Linkage Disequilibrium Studies of Complex Human Diseases I. DNA Pooling
Abstract
We consider statistics for analyzing a variety of family-based and nonfamily-based designs for detecting linkage disequilibrium of a marker with a disease susceptibility locus. These designs include sibships with parents, sibships without parents, and use of unrelated controls. We also provide formulas for and evaluate the relative power of different study designs using these statistics. In this first paper in the series, we derive statistical tests based on data derived from DNA pooling experiments and describe their characteristics. Although designs based on affected and unaffected sibs without parents are usually robust to population stratification, they suffer a loss of power compared with designs using parents or unrelateds as controls. Although increasing the number of unaffected sibs improves power, the increase is generally not substantial. Designs including sibships with multiple affected sibs are typically the most powerful, with any of these control groups, when the disease allele frequency is low. When the allele frequency is high, however, designs with unaffected sibs as controls do not retain this advantage. In designs with parents, having an affected parent has little impact on the power, except for rare dominant alleles, where the power is increased compared with families with no affected parents. Finally, we also demonstrate that for sibships with parents, only the parents require individual genotyping to derive the TDT statistic, whereas all the offspring can be pooled. This can potentially lead to considerable savings in genotyping, especially for multiplex sibships. The formulas and tables we derive should provide some guidance to investigators designing nuclear family-based linkage disequilibrium studies for complex diseases.
Over the last decade, attention has turned from positional cloning of Mendelian disease genes to the dissection of multifactorial or complex diseases. These are the common disorders that do not display simple patterns of inheritance but are more consistent with the interactive effects of multiple contributing loci. The ability to detect such loci depends on the magnitude of their effects.
At the same time, it has also become clear that conventional linkage analysis as a tool for mapping disease loci is of limited potential and, from a practical standpoint, can only be expected to succeed when the gene effect is moderate to large. One way of quantitating the effect of a locus is by the parameter γ, the genotype risk ratio associated with heterozygosity or homozygosity for a disease susceptibility allele. In a recent perspective, Risch and Merikangas (1996) and Camp (1997) demonstrated that linkage analysis was likely to be successful only for loci with γ values in the range of four or larger but not for loci with γ values of two or less. However, even for loci that confer risks associated with γ values of four or larger, positional cloning may still be a daunting task, as the confidence region for such loci is likely to be large. In such cases, linkage disequilibrium analysis becomes a critical tool for attempting to narrow the inclusion region.
As an alternative approach to linkage screens, Risch and Merikangas (1996) suggested genome-wide linkage disequilibrium studies to search for loci contributing to disease susceptibility. We use the term linkage disequilibrium to refer to a population association between two loci that are linked. In the limiting case, the two loci are in complete disequilibrium or identical, whereby we assume that the tested marker is actually disease predisposing. We refer to association between unlinked loci as allelic association. Risch and Merikangas (1996) showed that even if one needs to test 1,000,000 polymorphic alleles and allows for a conservative significance level of 5 × 10−8, gene effects with γ values of as low as 1.5 could be readily detected in realistically sized samples (<1000 families).
If genome screens by linkage disequilibrium analysis with a large number of tested loci are to become feasible, it will be necessary to develop efficient methods for genotyping a large number of loci. One approach that can greatly reduce genotyping efforts is DNA pooling, which has been shown to be quite effective in identifying disease-causing loci in several settings, including Mendelian founder mutations (Carmi et al. 1995; Barcellos et al. 1997) as well as complex diseases (Arnheim et al. 1985).
DNA pooling may ultimately be the critical difference between linkage and linkage disequilibrium studies. By DNA pooling, we assume that multiple individual DNAs are pooled before genotyping. In linkage studies, individual genotypes need to be constructed, or at least, pairs of individuals need to be compared for identity by descent, by such methods as GMS (Nelson et al. 1993). In contrast, in linkage disequilibrium studies, affected individuals can be grouped, as can unaffected individuals. It then remains only to compare allele frequency estimates in the two groups. If allele frequencies can be accurately estimated by genotyping only two pools of DNA rather than a large number of subjects individually, tremendous savings can be obtained.
It is of considerable importance to examine the relative power and robustness of different study designs for approaching linkage disequilibrium analysis. In general, we propose a two-stage approach. We suggest that initial screens be conducted by DNA pooling; loci that provide positive results in this initial screen can then be subjected to individual genotyping for confirmation. In this way, time-consuming individual genotyping can be reserved only for the most promising loci. However, efficiencies are still possible under individual genotyping, as described below.
The simplest linkage disequilibrium study is the epidemiologic case–control design, where unrelated affected (cases) and unaffected (controls) individuals are typed. The major limitation of this design, however, is the potential for confounding, or an artifactual result. If the population under study is heterogeneous and not randomly mating and the cases and controls are not ethnically balanced, an allele frequency difference can emerge that is coincidental. Such an artifact is most likely to happen when the disease occurs more frequently in an undetected subpopulation, which also differs, by chance, from the remaining population in the frequency of the tested allele.
Because of this potential for confounding, the case–control design has lost favor with geneticists, perhaps unduly so. Confounding requires undetected heterogeneity within the population studied, including nonrandom mating and allele frequency differences between subpopulations. Any known ethnic subgrouping can be controlled by matching controls to cases by ethnicity, provided this is known, or by focusing on a single ethnic subgroup.
In any event, over the past decade, family-based linkage disequilibrium study designs have become popular because they offer complete robustness to potential population heterogeneity. Also, the samples are often simple to collect and can approach case–control designs in terms of power. Perhaps the most popular of such designs is the single affected child with parents. Several statistics have been formulated to analyze such studies. The original proposal was the haplotype relative risk (HRR) of Falk and Rubinstein (1987), who calculated genotype frequencies in the affected children and compared them with the frequency of genotypes formed by merging the parental alleles not transmitted to the affected child (effectively creating a “control” genotype from the alleles not transmitted to the affected child).
Terwilliger and Ott (1992) subsequently considered several different test statistics for this same design. They referred to the Falk–Rubinstein statistic as a genotype-based haplotype relative risk (GHRR); they also formulated a test statistic based on allele frequencies, rather than genotype frequencies observed in the affected child versus the parental alleles not transmitted. They referred to this statistic as the haplotype-based haplotype relative risk (HHRR). They also described an alternative method of analyzing the family genotype data based on McNemar’s test. This entails ignoring homozygous parents and considering only the alleles transmitted by heterozygous parents. Conditional on parental heterozygosity, each allele has a 50% probability of transmission, leading to a simple symmetric χ2 test. Spielman et al. (1993) and Ewens and Spielman (1995) showed that this test is completely robust to nonrandom mating and that it can readily be extended to families with more than one affected child, because under the null hypothesis of no linkage disequilibrium, every child in a family has an independent probability of 50% of inheriting each of the two alleles from a heterozygous parent. Spielman et al. (1993) described this test as a transmission disequilibrium test (acronym TDT), which is now in common usage. Other tests for families with multiple affected sibs have been developed, such as a maximum likelihood test (Risch 1984; Schaid and Sommer 1993,1994) and the AFBAC test (Thomson 1995), which compares the frequency of alleles transmitted to affected children versus alleles never transmitted to an affected child. The relative power of the AFBAC test versus the TDT depends on the precise genetic model and population mating pattern; however, Ewens and Spielman (1995) showed that only the TDT is robust to all possible mating patterns, although the HHRR is also robust under population stratification, the usual concern in nonrandomly mating populations.
Although family designs based on affected children and parents have been widely used, it is sometimes difficult or impossible to obtain blood samples from parents, especially for late onset disorders where the parents will often be deceased. Therefore, it is important to consider designs involving affected and unaffected sibs (Clarke et al. 1956; Eaves and Meyer 1994; Risch and Zhang 1995; Risch and Merikangas 1997; Curtis 1997). Using unaffected sibs as controls for affected sibs offers the advantage that test statistics independent of population mating type patterns can be constructed, similar to the TDT, eliminating the possibility of stratification artifact. Below, we consider various tests and the power of these tests for sibling-based association studies, in particular in comparison to designs involving parents or unrelated controls.
Our goal in this series of papers is to evaluate the power of various family-based and nonfamily-based study designs for detecting linkage disequilibrium, based on both DNA pooling and individual genotyping. As we describe, DNA pooling precludes the possibility of calculating certain test statistics (such as the TDT). In the first paper of the series, we focus on analyses based on DNA pooling; in a subsequent paper, we consider individual genotyping. In considering power, we initially consider the case of complete disequilibrium, wherein the marker tested is identical to the disease susceptibility locus; subsequently, we examine the implications of incomplete disequilibrium. We begin by introducing our notation and genetic model and show that all of the disequilibrium statistics are a function of the allele frequency difference between affecteds (cases) and an appropriate control group.
GENETIC MODEL
We consider a disease locus with alleles D and d, and a marker locus with alleles A and a. D is the predisposing allele. A general model for penetrances at the disease locus is assumed, in which the disease genotypes and penetrances areDD, f 2; Dd, f 1; and dd, f 0. We assume throughout that penetrances are low, so that unaffected individuals can be treated as random, or phenotype “unknown.” This will generally be a reasonable assumption when multiple loci contribute to susceptibility and especially when the monozygotic twin concordance is <30%, as the genotype distribution for an unaffected sib at any particular locus will deviate little from a “random” sib. For a major locus with high penetrance, our calculations are conservative because unaffected individuals are more likely to be genotypically discordant with their affected sibs than random individuals. Under these assumptions, the penetrance parameters can be reduced to “relative penetrances,” or genotypic risk ratios (Risch and Merikangas 1996). In terms of our modeling, this is equivalent to fixing f 0 = 1; then, f 1 = the risk associated with genotypeDd relative to genotype dd, andf 2 = the risk associated with genotype DDrelative to genotype dd. Various models can be defined in terms of f 2 and f 1. For example, a dominant model is characterized byf 2 = f 1, a recessive model byf 1 = 1, an additive model byf 2 = 2f 1 − 1, and a multiplicative model byf 2 = f 1 2.
STATISTICS
To test the null hypothesis of no linkage disequilibrium between the marker locus and disease locus, we compare the allele
frequencies ofA in the affected population and a control population, which may be based on unrelated individuals, parents, or unaffected
siblings of the affecteds. We use statistics of the form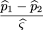 where ^p
1 is the sample frequency of allele A among the affected,^p
2 is the sample frequency of A among the controls, and ς̂2is an estimator of the variance of^p
1 −^p
2.
where ^p
1 is the sample frequency of allele A among the affected,^p
2 is the sample frequency of A among the controls, and ς̂2is an estimator of the variance of^p
1 −^p
2.
Suppose we have a sample of n families of identical structure. Consider the case where each family consists of an affected child and his/her parents. For
this case we consider the parents as the comparison group. For the ith family, letX
(i),X
f
(i), andX
m
(i) denote the number of A alleles in the child, father, and mother, respectively. Then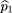 and
and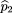 Under the null hypothesis of no linkage disequilibrium, all alleles have a 50% chance of being transmitted from a heterozygous
parent to the child, and the alleles transmitted from the two parents are independent. Thus,^p
1 −^p
2 has mean 0 and variance h/8n, where h is the probability of a parent being heterozygous. This is because^p
1 −^p
2 is just (1/4n) times the sum over 2n parents of the number of A alleles transmitted versus nontransmitted to a child. For homozygous parents, the variance of the difference in number of
transmitted versus nontransmitted A alleles is 0, whereas for heterozygous parents the variance is 1. Thus, the total variance is (1/16n
2)(2n)h =h/8n.
Under the null hypothesis of no linkage disequilibrium, all alleles have a 50% chance of being transmitted from a heterozygous
parent to the child, and the alleles transmitted from the two parents are independent. Thus,^p
1 −^p
2 has mean 0 and variance h/8n, where h is the probability of a parent being heterozygous. This is because^p
1 −^p
2 is just (1/4n) times the sum over 2n parents of the number of A alleles transmitted versus nontransmitted to a child. For homozygous parents, the variance of the difference in number of
transmitted versus nontransmitted A alleles is 0, whereas for heterozygous parents the variance is 1. Thus, the total variance is (1/16n
2)(2n)h =h/8n.
Different estimators of Var(^p
1 −^p
2), or equivalently, different estimators of parental heterozygosityh, result in different test statistics. For example, if we use ^h, the proportion of heterozygous parents in the sample, as an estimator of h,the test statistic is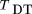 the usual TDT of Spielman et al. (1993), or McNemar’s test as described by Terwilliger and Ott (1992). Here, we use D as a subscript to denote that we do not use a Hardy–Weinberg assumption, and the subscript T denotes that p
2 is estimated from parents’ genotypes. If we use 2^p
2 (1 −^p
2) as an estimator of h, the test statistic is
the usual TDT of Spielman et al. (1993), or McNemar’s test as described by Terwilliger and Ott (1992). Here, we use D as a subscript to denote that we do not use a Hardy–Weinberg assumption, and the subscript T denotes that p
2 is estimated from parents’ genotypes. If we use 2^p
2 (1 −^p
2) as an estimator of h, the test statistic is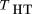 Here, we use the subscript H to denote the use of theHardy–Weinberg assumption. This is equivalent to the HHRR statistic of Terwilliger and Ott (1992). This estimator of his calculated under the assumption of Hardy–Weinberg frequencies for the parents. So, if the sample is from a stratified population,
2^p
2(1 − ^p
2) will be an overestimate of h, and as a result, this statistic leads to a conservative test if the statistic 5 is used as a zscore. Under other types of population structure, 2^p
2(1 − ^p
2) could underestimate h and lead to an anticonservative test [Ewens et al. (1995) give examples of different population structures that lead to an excess of heterozygotes]. Several authors have made comparisons
of these two statistics. Although when random mating is assumed, the HHRR test is more powerful than the TDT (Terwilliger and Ott 1992), this is not true when mating is not at random (Schaid and Sommer 1993). When population stratification exists, HHRR test would be less powerful than the TDT. However, it is only with very large
stratification effects that the power of the TDT is substantially larger than that of the HHRR test (Thomson 1995).
Here, we use the subscript H to denote the use of theHardy–Weinberg assumption. This is equivalent to the HHRR statistic of Terwilliger and Ott (1992). This estimator of his calculated under the assumption of Hardy–Weinberg frequencies for the parents. So, if the sample is from a stratified population,
2^p
2(1 − ^p
2) will be an overestimate of h, and as a result, this statistic leads to a conservative test if the statistic 5 is used as a zscore. Under other types of population structure, 2^p
2(1 − ^p
2) could underestimate h and lead to an anticonservative test [Ewens et al. (1995) give examples of different population structures that lead to an excess of heterozygotes]. Several authors have made comparisons
of these two statistics. Although when random mating is assumed, the HHRR test is more powerful than the TDT (Terwilliger and Ott 1992), this is not true when mating is not at random (Schaid and Sommer 1993). When population stratification exists, HHRR test would be less powerful than the TDT. However, it is only with very large
stratification effects that the power of the TDT is substantially larger than that of the HHRR test (Thomson 1995).
ANALYSES BASED ON DNA POOLING
In the following, we consider a general pooling strategy whereby all the affected offspring comprise one pool and either the parents, unaffected sibs, or unrelated controls form the second pool. The data, in this case, are the allele frequencies in each pool and the number of individuals in each pool. A direct estimate of h from the parents is not available, so the Hardy–Weinberg assumption must be made. Thus, the HHRR statistic (formula 5) will be considered. Note that the HHRR statistic depends only on the (pooled) allele frequencies in each of the two groups and the sample sizes. Because we consider a number of cases in terms of affected and unaffected sibs, with and without parents, and unrelated controls, we introduce some notation. We generally denote the test statistic used for these forms of data byQ and will use properties of this statistic under null and alternative hypotheses to calculate the power of each test. WhenQ is based on a family with r affected and sunaffected sibs and x available parents and uunrelated controls, we let μr,s,x,u = E(Q) and σ2 r,s,x,u = Var(Q).
The tests considered below concern cases in which samples are pooled into two groups. As noted above, the TDT statistic cannot be calculated when this is done, because for this statistic the proportion of parents that are heterozygous is required to calculate^h. However, to calculate a TDT, individual genotypes of the offspring samples are not required to estimate ^p 1(formula 4); thus, the offspring samples can still be pooled, leading to a significant reduction in genotyping, especially for multiplex sibships. Furthermore, it is also clear that to calculate a TDT does not require having the nuclear families intact.
r Affected Children with Parents
To study the power of the THT
statistic, we need to calculate the mean μ and variance σ2 of statistic 5 under the alternative hypothesis. We first consider the case that the marker locus and the disease locus are
in complete disequilibrium or that the disease-predisposing locus is being assayed. For a single family with one affected
child, let Here, the superscript (i) is suppressed for simplicity. LetG = (Xm,Xf
) denote the mating type.
Here, the superscript (i) is suppressed for simplicity. LetG = (Xm,Xf
) denote the mating type.
Given G = (1,1), that is, both parents are heterozygous, the possible values of Q are Q = −1/2, 0, 1/2 with respective probabilities 1 / (1 + 2f
1 +f
2), 2f
1 / (1 + 2f
1 + f
2) andf
2 / (1 + 2f
1 +f
2). Therefore,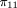 and
and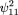 Similarly,
Similarly,
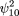 and
and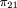
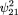 For all other mating types, Q = 0. So
For all other mating types, Q = 0. So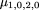 and
and

 where gij
is the population frequency of mating type (i,j) and mij
is the conditional probability of G = (i,j) given one affected child in the family; these values are given in Table1, setting r = 1. Here,m
(ij) =mij
+ mji
whenj ≄′ i. Under H
0, the mean ofQ is 0 and its variance is p(1 − p)/4. For any given locus, we test each allele individually. Hence, forn independent families and using a one-sided test, assuming asymptotic normality, the power to reject the null hypothesis with
significance level α is given by
where gij
is the population frequency of mating type (i,j) and mij
is the conditional probability of G = (i,j) given one affected child in the family; these values are given in Table1, setting r = 1. Here,m
(ij) =mij
+ mji
whenj ≄′ i. Under H
0, the mean ofQ is 0 and its variance is p(1 − p)/4. For any given locus, we test each allele individually. Hence, forn independent families and using a one-sided test, assuming asymptotic normality, the power to reject the null hypothesis with
significance level α is given by in which
in which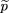 is the expected frequency of allele A in the parents under the alternative hypothesis, Φ is the cumulative standard normal
distribution function, z
α is the 100α percentile of the standard normal distribution, and i andj range from 0 to 2. In using a one-sided test, we are assuming that all alleles at a locus are tested (e.g., both alleles
at a two-allele locus).
is the expected frequency of allele A in the parents under the alternative hypothesis, Φ is the cumulative standard normal
distribution function, z
α is the 100α percentile of the standard normal distribution, and i andj range from 0 to 2. In using a one-sided test, we are assuming that all alleles at a locus are tested (e.g., both alleles
at a two-allele locus).
Conditional Probability [m (r) ij] of Mating Type G Given r Affected Children
The analysis of r affected children is completely analogous to the previous case of one affected child. LetX
1
(i),X
2
(i), … ,X
r
(i) be the number of A alleles in each affected child.X
f
(i) andX
m
(i) are defined as before. If we have a sample of n families with r affected children and parents, then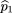
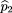 and the test statistic is
and the test statistic is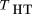 Let
Let Notice that, given G, X
1, X
2, … , Xr
are independent and have the same distribution as before, so
Notice that, given G, X
1, X
2, … , Xr
are independent and have the same distribution as before, so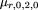 also, E(Q‖G) is the same as before, so that
also, E(Q‖G) is the same as before, so that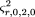

 in which m
(r)
ij is the conditional probability of G = (i,j) givenr affected children; these probabilities are given in Table1. The power for n such families is
in which m
(r)
ij is the conditional probability of G = (i,j) givenr affected children; these probabilities are given in Table1. The power for n such families is in which, in this case,
in which, in this case,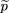
r Affected Children and s Unaffected Sibs without Parents
We then consider families with r affected children ands unaffected sibs in which the parents are unavailable; each family has the same numbers of unaffected sibs. Thus, all sibships are of size s + r. Again, we assume the absolute penetrances are low so that the distribution of parental mating type depends only on the number of affected children in each family and not on the number of unaffected; also, all alleles should have a 50% chance of being transmitted to the unaffected children from heterozygous parents.
We first consider the case of r = 1. LetY
1
(i),Y
2
(i), ...,Y
s
(i) be the number of A alleles in the unaffected sibs who are enumerated from 1 to s. For this case, the comparison group is the unaffected sibs. Then, forn independent families of identical structure,^p
1 is defined the same as before (formula 2) and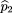 Under the null hypothesis,^p
1 −^p
2 has mean 0 and variance (s + 1)h/(8sn). The test statistic 1 is then given by
Under the null hypothesis,^p
1 −^p
2 has mean 0 and variance (s + 1)h/(8sn). The test statistic 1 is then given by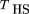 in which
in which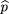 is the sample frequency of allele A. Here, we are using 2^p(1 −^p) as an estimator ofh. As in the case of an affected child with parents, this estimator is derived under the Hardy–Weinberg assumption and could
overestimate h in a stratified population. The subscriptS on T in formula 15 indicates that the comparison allele frequency is based on sibs.
is the sample frequency of allele A. Here, we are using 2^p(1 −^p) as an estimator ofh. As in the case of an affected child with parents, this estimator is derived under the Hardy–Weinberg assumption and could
overestimate h in a stratified population. The subscriptS on T in formula 15 indicates that the comparison allele frequency is based on sibs.
To study the power of this test, let By an argument similar to that used for the previous case, we can compute the mean and variance of Q under the alternative hypothesis. Note that by assumption the distribution of the mating typeG will not change (Table 1) and the conditional expectation of Q given G is the same as before, so only the conditional variances change. After some simple algebra, we have
By an argument similar to that used for the previous case, we can compute the mean and variance of Q under the alternative hypothesis. Note that by assumption the distribution of the mating typeG will not change (Table 1) and the conditional expectation of Q given G is the same as before, so only the conditional variances change. After some simple algebra, we have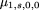 and
and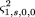 in which ς2
1,0,2,0 is given by formula 8.
in which ς2
1,0,2,0 is given by formula 8.
Hence, by analogy with formula 9, n such families give the power (for a one-sided test) in which
in which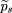 If each family consists of r affected and sunaffected sibs, by analogy with formula 15, the statistic 1 is given by
If each family consists of r affected and sunaffected sibs, by analogy with formula 15, the statistic 1 is given by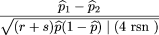 in which
in which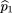 is the frequency of allele A in the r affected sibs,
is the frequency of allele A in the r affected sibs,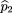 is the frequency of allele A in the s unaffected sibs, and
is the frequency of allele A in the s unaffected sibs, and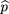 is the sample frequency of allele A. By analogy to the derivation of formula 19, the power for this test is
is the sample frequency of allele A. By analogy to the derivation of formula 19, the power for this test is in which
in which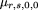
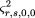 and
and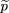 is the sample frequency of allele A under the alternative hypothesis, and μr,0,2,0 and ς2
r,0,2,0 are given in formulas 10 and 11, respectively.
is the sample frequency of allele A under the alternative hypothesis, and μr,0,2,0 and ς2
r,0,2,0 are given in formulas 10 and 11, respectively.
r Affected Sibs, s Unaffected Sibs, and One Available Parent
Now, we consider families with r affected children,s unaffected sibs, and one available parent (say the father without loss of generality). We first consider the caser = 1. Let Xf
(i)denote the number of A alleles in the available parent. For this case, the comparison group is the available parent plus the unaffected sibs. Then,
using the same notation as before, we define^p
1 as in formula 2 and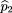 To calculate the mean and variance of^p
1 −^p
2, let
To calculate the mean and variance of^p
1 −^p
2, let Again, the distribution of G will not change, and the conditional expectation of Q given G is the same as before, so only the conditional variances change. After some algebra, we have
Again, the distribution of G will not change, and the conditional expectation of Q given G is the same as before, so only the conditional variances change. After some algebra, we have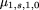 and
and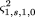


 Under the null hypothesis,^p
1 −^p
2 will have mean 0 provided the available and missing parents are random with regard to the frequency of allele A, and variance {(s + 2)h / [8(s + 1)] + (2m
(20) − m
11) / [8(s + 1)2]}/n, or equivalently {(s + 2)h / [8(s + 1)] + (hc
− h) / [4(s + 1)2]}/n, where hc
is the probability of a child being heterozygous. If we further assume Hardy–Weinberg equilibrium and random mating, the
variance can be simplified to (s + 2)pq / [4(s + 1)n]. So, we could define the test statistic to be
Under the null hypothesis,^p
1 −^p
2 will have mean 0 provided the available and missing parents are random with regard to the frequency of allele A, and variance {(s + 2)h / [8(s + 1)] + (2m
(20) − m
11) / [8(s + 1)2]}/n, or equivalently {(s + 2)h / [8(s + 1)] + (hc
− h) / [4(s + 1)2]}/n, where hc
is the probability of a child being heterozygous. If we further assume Hardy–Weinberg equilibrium and random mating, the
variance can be simplified to (s + 2)pq / [4(s + 1)n]. So, we could define the test statistic to be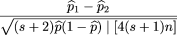 in which
in which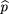 Then, n such families give the power (for a one-sided test)
Then, n such families give the power (for a one-sided test) (25)
(25)
where˜p 1,s = ^p + μ1,s,1,0 / (s + 2) is the frequency of allele A in the typed parent ands + 1 sibs under the alternative hypothesis. We note that (2m (20) −m 11) / [8(s + 1)2] equals 0 under random mating and Hardy–Weinberg. Also, unless the deviation from the above assumptions is large, this term would be small and σ1,s,1,0 2 would be quite close to σ1,s + 1,1,0 2. Thus, the required sample size for families with one affected sib,s unaffected sibs, and one parent would be approximately equal to families with one affected and s + 1 unaffected sibs. If each family consists of r affected sibs, s unaffected sibs, and one available parent, similar arguments apply, namely, the power can be expected to be comparable to families with raffected and s + 1 unaffected sibs without parents. Numerical examples (data not shown) bear this out. It is important to note that the expectation of Q is 0 under the null hypothesis only when the available and missing parents can be assumed to have the same frequency of allele A, which may be unprovable.
Families with an Affected Parent
So far, for families with parents, we have assumed the parents to be random with respect to disease status (i.e., unknown). When the disease prevalence in parents is low, these results are comparable to a sample of families with unaffected parents. Here, we consider the question of power for families with an affected parent. This would entail analyzing these families separately from those without affected parents under random sampling, or, specifically, sampling to enrich for families with affected parents.
We consider families with one affected parent, one unknown parent, andr affected children. We use the same statistic as formula 5, that is, comparing the allele frequency of the affected children with that of the parents (both affected and unaffected).
Given G, the distribution of the child’s genotype would be the same as before. However, the conditional distribution of Ggiven r affected children would change to take into account the affected parent. So the mean and variance will have the same forms as in formulas 4 and 5 but with different values ofmij , which are given in Table 2. The power is also as given in formula 9, but with the modified values of μ, σ2, and^p.
Conditional Probability of Mating Type G Given rAffected Children and an Affected Parent
r Affected Sibs with u Unrelated Controls
In contrast to the designs considering unaffected sibs or parents along with the affected sibs, we also evaluate affected sibships (withr affecteds) using u unrelated subjects as controls. Using unrelateds raises the issue of confounding owing to population stratification; however, we show below that using sib controls also entails less power than the use of unrelated individuals.
To examine the relative power obtained by using unaffected unrelated controls as opposed to unaffected sibs, consider n family sets each with r affected sibs and u unrelated controls. Then, we can define the test statistic as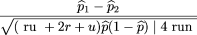 in which
in which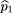
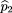
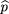 and Y
1
(i), … ,Yu
(i) are the number ofA alleles in the u unrelated controls. The respective variances of^p
1 and^p
2 arepq(r + 1) / 4 and pq / 2u.These are used as weights in the standard statistical way in the definition of ^p.
and Y
1
(i), … ,Yu
(i) are the number ofA alleles in the u unrelated controls. The respective variances of^p
1 and^p
2 arepq(r + 1) / 4 and pq / 2u.These are used as weights in the standard statistical way in the definition of ^p.
To calculate the power, we first need to determine the expectation and variance of (X 1 + X 2 + … + Xr ) / 2r under the alternative hypothesis (again the superscript (i) is suppressed for convenience). Here, we define ɛij= E[(X 1 + … +Xr )/2r‖(i,j)], that is, the conditional expectation of (X 1 + … +Xr ) / 2r given parental mating type (i,j). Then, ɛ22 = 1, ɛ21 = ɛ12 = (2f 2 + f 1) / (2f 2 + 2f 1), ɛ20 = ɛ02 = 1/2, ɛ11 = (f 2 + f 1) / (f 2 + 2f 1 + 1), ɛ10 = ɛ01 = f 1 / (2f 1 + 2), and ɛ00 = 0.
We also require the variance of (X
1 + … +Xr
) / 2r conditional on mating type. Here, we define τij
2 = Var[(X
1/2) ‖ (i,j)]. Then, τ22
2 = τ20
2 = τ00
2 = 0, τ21
2 = τ12
2 =f
2
f
1 / 4(f
2 + f
1)2, τ11
2 = (f
2
f
1 + 2f
2 + f
1) / 2(f
2 + 2f
1 + 1)2, τ10
2 = τ01
2 =f
1 / 4(f
1 + 1)2. Then, the power is given by in which
in which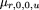
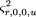
 and
and
Numerical Results—Comparison of Sample Sizes
We now evaluate the relative efficiency of different family structures for detecting linkage disequilibrium. We base relative efficiency on the relative number of families, or subjects, required to obtain a given power. Which use is more appropriate, that is, in terms of families or subjects, will depend on whether the primary expense is in identifying and recruiting families or individual subjects within families. We consider affected sibships of size one to four with parents, a sibship of size one with an affected parent, sibships without parents with up to four affected sibs and two unaffected sibs, and affected sibships up to size four compared with two unrelated controls.
We calculate the sample size necessary to obtain power of 80% (z
1 − β = −0.84) with a significance level of 5 × 10−8(z
α = 5.33), which yields a posterior false-positive rate of ∼5% after 1,000,000 independent tests (Risch and Merikangas 1996). To do so, we use the power formulas given above for the various family structures (formulas 9, 12, 19, 20, 25, and 27).
To obtain the formula for sample size n, these formulas are set equal to 1 − β and then solved for n. For example, for formula 9, we get (suppressing the subscripts of μ and σ) Similar formulas for n are easily derived from the other power formulas.
Similar formulas for n are easily derived from the other power formulas.
Table 3 provides the required number of families for detection of linkage disequilibrium for dominant, recessive, multiplicative, and additive models for sibships with parents. For each model we have included only a single set of genotypic risk ratios (withf 2 fixed at four) and three gene frequencies (P = 0.05, 0.20, and 0.70). The actual genotypic risk ratios for each model are given in the footnote to Table 3. Results were similar for other genotypic risk ratios (in terms of the relative magnitudes of the various sample sizes).
Number of Families Required to Detect Linkage Disequilibrium for Sibships with Parents for Four Genetic Models Using Pooling
The results for sibships without parents, comparing affected to unaffected sibs, are given in Table 4. We consider sibships with up to four affected and two unaffected sibs. In Table5 we present results comparing affected sibships up to size four with two unrelated controls. Comparing Tables 3 and 4, it is apparent that among the family-based designs, sampling parents is always optimal. The number of discordant sib pairs required to give the same power as a child with parents is roughly twofold across models (Table 3, column 1, vs. Table 4, column 1). However, per individual sampled, this ratio is 1.33-fold. Adding an additional unaffected sib gives a family sample size ratio of ∼1.5 compared with affecteds with parents and is the same per person sampled (Table 3, column 1, vs. Table 4, column 2). We also note that per person sampled, the relative efficiency of an affected child and one unaffected sib is the same as an affected child and two unaffected sibs. In general, for families with one affected child, using s unaffected sibs would be approximately s ÷ (1 + s) as efficient in terms of the relative numbers of families required as using parents as controls. Thus, the gain, per person sampled, diminishes with each additional unaffected sib sampled. Thus, if affecteds are readily available, there is not much advantage in sampling additional unaffected sibs beyond the first. The same is true for sibships withr affected sibs (r > 1), where the corresponding formula is s ÷ (r + s). For affected sib pairs, the required number using two unaffected sibs is double the number of such pairs with parents. As the number affected increases to three and four, this ratio increases from two to about threefold, whereas the number of individuals sampled is the same for both designs.
Number of Families Required to Detect Linkage Disequilibrium for Sibships with r Affected and s Unaffected Sibs, without Parents, Using Pooling
Number of Families Required to Detect Linkage Disequilibrium for Sibships with r Affected Sibs Compared with Two Unrelated Controls Using Pooling
What is the impact of one parent being affected in families with one affected child and parents available? The answer depends primarily on the frequency of the susceptibility allele but also to some extent, the genetic model and penetrances (Table 3, column 1 vs. column 5). Typically, when the allele frequency is low (<20%), families with an affected parent are more powerful but only largely so at very low allele frequencies (<5%). For high allele frequencies (>50%), however, the opposite is the case; such families are less powerful. Again, this is most true when the allele frequency is very high (>70%). These results are easily seen in terms of heterozygosity for the disease allele in the affected parent. At low allele frequency, the parent being affected will increase the probability that (s)he is heterozygous; at high allele frequency it will reduce that probability. Maximum power is obtained when parents are heterozygous.
From Tables 3 and 4 we can also contrast the relative efficiency of families with different numbers of affected children. First, we consider families with parents. For most models, the relative efficiency of families with two affected compared to singletons ranges from ∼3-fold at low allele frequency to ∼1.5-fold at high allele frequency, depending to some extent on the genetic model. The only substantial deviation from these ratios is for a rare recessive gene, in which the efficiency of multiplex families is substantially greater (up to fivefold). In any event, because families with two affected children have only 4:3 as many subjects to sample as families with one affected child, such families will generally also be more efficient per person sampled. For families with three affected, the relative efficiency compared with sib pairs ranges from ∼1.2 at high allele frequency to 2 at low allele frequency. The sample size ratio is 5:4 = 1.25, which suggests those will also be a useful family structure. For families with four affected, the relative efficiency, compared with trios, ranges from 1.0 at high allele frequency to ∼1.8 at low allele frequency. Thus, quartets will also be generally useful families. It is likely, however, that families with more affecteds are more difficult and expensive to recruit. Thus, a reasonable strategy might be to collect all families with at least two affected sibs.
The situation is somewhat different when comparing families without parents. For example, consider sibships with one affected and two unaffected versus two affected and one unaffected. The relative efficiency of these two family structures, which have the same number of individuals, depends on the model and allele frequency. Families with two affected are more efficient for low allele frequencies but not necessarily so for high allele frequencies. This is particularly true for dominant or additive models, in which families with one affected are more efficient at high allele frequencies and even at moderate allele frequencies if the penetrance ratio is high. The trend toward increasing efficiency with number of affected sibs seen in the case of parents included does not generally apply to families without parents. For example, comparing families with one to four affected sibs, each with two unaffected sibs, the required sample sizes decrease only at low allele frequency (P = 0.05); at high allele frequency (P = 0.70), the numbers increase with number affected. At intermediate allele frequencies, the sample sizes decrease only for the recessive model but are roughly similar for the other models.
To examine the loss of power by using unaffected sibs or parents as controls, we considered the power for affected sibships using unrelated unaffecteds as controls. The loss of power using relatives for controls is substantial. Affected sib pairs with two unrelated controls are typically 3–3.5 times as efficient as sib pairs with two unaffected sibs. Even for affected sib pairs with parents, the loss of efficiency is approximately twofold. The disadvantage of family-based controls grows with the number of affected sibs. For affected sib trios, families with two unaffected sibs are ∼5 times less efficient than using two unrelated controls; families with parents are ∼2 times less efficient. For families with four affected, the situation is even worse. Using unaffected sibs is ∼6 times less efficient than using two unrelated controls; using parents is ∼40% as efficient. Upon reflection, the explanation for these trends should be clear. With more affected in the sibship, the frequency of allele A increases, creating a greater difference from unrelated controls. With family-based designs, however, the allele frequency is also increasing in the relatives (unaffected sibs or parents), leading to a smaller difference between the affecteds and their normal sibs or parents. The disadvantage of using unrelated controls is the potential for artifact owing to population stratification. However, it is important to note that the robustness obtained from using family-based controls comes at a substantial price—a loss of efficiency of two- to sixfold using unaffected sibs or two- to threefold using parents.
Examination of Tables 3 T4 T5 reveals that remarkable savings in total sample size can be achieved by sampling families with more affected sibs, especially at lower disease allele frequencies and when unrelated controls are used. Furthermore, the number of multiplex families required can be reduced even further if one uses additional unrelated controls. For example, by using three controls for sibships with three affected sibs, the required sample size can be reduced by ∼15%; by using four unrelated controls in families with four affected sibs, the sample sizes can be reduced by ∼30% (calculations performed but not shown). This is an additional advantage to using unrelated controls that cannot be realized by using family-based controls. Generally, it is simpler to obtain a large unrelated control group than related controls.
We also wanted to determine the extent to which the sample size reduction from using sibships with more affecteds was owing to the larger sample size, versus the expected increase in susceptibility allele frequency in such families. Therefore, we considered the design of selecting a single affected from sibships with two, three, or four affected along with two unrelated, unaffected controls. For this design, the required number of cases was increased by ∼60% over the numbers given in Table 5 for sibships of size 2, 70% for sibships of size 3, and 80% for sibships of size 4. Thus, much of the substantial increase in power using larger sibships derives from the excess allele frequency expected in the affected individuals from such families, rather than the larger number of subjects included.
Finally, we note that although the actual numbers in Tables 3 T4 T5 are based on a significance level of 5 × 10−8(Z α = 5.33) and power of 80% (Z 1 − β = −0.84), the ratio of sample sizes for different designs is reasonably stable for other levels of significance and power. This is because in the sample size formulas, the coefficients of Z α andZ 1 − β are nearly equal, representing the standard deviation of the statistic under the null and alternative hypotheses. When considering alternative hypotheses close to the null, these standard deviations are very similar; thus, the sample size is nearly a function of (Z α + Z 1 − β)2. Therefore, other values of Z α andZ 1 − β will give sample size ratios that are similar to those we have derived.
Combining Families of Different Structure
In all the calculations derived above, we have assumed pooling of families of identical structure. Typically, an investigator may, in practice, have families of differing structure—for example, some singleton families with parents, some sibships without parents with different numbers of affecteds and unaffecteds. Simple pooling of families of different structure (e.g., placing all unaffecteds and/or parents together and all affecteds together) is not a robust procedure, because population stratification could lead to an artifactual difference between the “affected” and control pools. For example, suppose we have sibships without parents: Some of the sibships have one affected and two unaffected, and the others have two affected and one unaffected. Then, if the sibships come from populations with different allele frequencies, the pooled samples will not necessarily have the same frequency. This is because the affected pool will be weighted toward the populations from which the sibships with two affected are derived, whereas the control pool will be weighted toward the populations from which the sibships with one affected derive. For example, suppose the frequency of allele A in the population from which the sibships with two affected and one unaffected sib derive is 0.6, whereas its frequency in the populaton from which the sibships with one affected and two unaffected derive is 0.3. Then the frequency of alleleA in the affected pool (assuming equal representation of the two sibship types) is (2/3)(0.6) + (1/3)(0.3) = 0.5, while the frequency in the pool of unaffected sibs is (1/3)(0.6) + (2/3)(0.3) = 0.4. Thus, the affected pool appears to have a higher frequency of allele A owing simply to population stratification and unbalanced sibships.
There are two potential solutions to this problem. First, only families of identical structure are pooled. Statistics can be derived from each of these individual experiments and subsequently combined (as described below). However, there is a second possibility allowing for combining all families. To combine across families, the ratio of number affected to number unaffected must be constant. One way to accomplish this is to have an equal number of affecteds and unaffecteds from each family. This can be done by duplicating some samples placed in the pools. For example, suppose we have families with one affected and two parents (type 1), one affected and one unaffected sib (type 2), one affected and two unaffected sibs (type 3), two affected with two parents (type 4), two affected and one unaffected sib (type 5), and two affected and two unaffected sibs (type 6). Families of type 2, 4, and 6 can be pooled together as is; for families of type 1, the affected child is first duplicated before this family is pooled; for families of type 3, again the affected sib is duplicated before pooling; for families of type 5, the unaffected sib is duplicated before pooling. This strategy will create balanced pools between affecteds and controls, eliminating confounding owing to allele frequency variation among families of different structure. In the example given above, suppose we duplicate the unaffected sib in the sibships with two affected and one unaffected and duplicate the affected sib in the sibships with one affected and two unaffected in forming pools. The pooled allele frequency for affecteds will be (1/2)(0.6) + (1/2)(0.3) = 0.45, and the pooled allele frequency for unaffecteds will be the same, 0.45.
We then consider the statistics derived from these two approaches of combining families of different structure. In the first scenario, we have k pairs of allele frequencies from the kdifferent family structures. There is an infinite number of ways of combining these estimates; the optimal one, in terms of power, depends on the specific alternative model. As a simple, practical approach, we suggest taking the weighted sums of the allele frequencies, where the weights are based simply on the number of affected individuals going into that pool.
For the second scenario, we have just a single, pooled allele frequency difference for two pools; we need to calculate the variance of this difference. This can be accomplished by summing the variances for each family before duplication of individuals, using the formulas derived in the sections above. In these formulas we require a sample estimate ofp, the population frequency of allele A. This estimate varies according to family structure (e.g., it is estimated from parents only for affecteds with parents but from all sibs in families without parents). In this case, we suggest using ½(^p 1 + ^p 2), where ^p 1 and^p 2 are the estimated allele frequencies for the affected and control pools, respectively. This may lead to a conservative test and some loss of power; however, using only^p 2 as an estimator of p can lead to an inflated type 1 error frequency, especially if families without parents predominate in the sample.
The choice of which approach to take, scenario 1 or scenario 2, will depend on experimental considerations. Scenario 2 requires forming only two pools, although some individuals will need to be duplicated. Scenario 1 requires multiple pools, depending on the number of different family structures in the sample, but allows for analyzing the families as is.
Level of Resolution of Allele Frequencies in Pooling
An important issue in the power of DNA pooling strategies for detecting allelic associations with disease is the level of resolution of allele frequencies in DNA pools as a function of sample size. Imprecise estimation of allele frequencies in pooled samples leads to a source of variation for which we have not accounted in our formulas; we have only allowed for sampling variance. Assuming that the error of estimation is not systematically different between pools, the expected difference in allele frequencies between pools (i.e.,p 1 − p 2) will remain unchanged, but the variance of the estimated difference will be greater than what we have calculated. This will lead to an inflated type 1 error, because a greater proportion of the distribution, under the null hypothesis, will be beyond the threshold for significance. Thus, to retain the same significance level, the threshold for the observed allele frequency difference needs to be raised, leading also to a consequent decrease in power.
Evaluation of this problem requires both experimental and theoretical considerations. Presumably, the variability in allele frequency estimation increases with the number of samples in the pool; thus, there will be a trade-off between increasing the number of pools to improve resolution at the expense of creating more pools for genotyping. An exact analysis of this problem can be performed once the parameters of resolution for DNA pooling are obtained. Preliminary evidence from microsatellites indicates good reliability of allele frequency estimation in pools up to 75 individuals, indicating the feasibility of pooling for this class of marker (Barcellos et al. 1997). For SNP markers, these studies remain to be performed.
Incomplete Linkage Disequilibrium
The calculations we have presented above represent the case of complete linkage disequilibrium (i.e., the disease and marker loci are the same). It is important to consider also the power when examining a nearby marker in incomplete disequilibrium with the disease locus. As has been pointed out elsewhere (Muller-Myhsok and Abel 1997), the power to detect a disease susceptibility locus can decrease considerably with diminishing linkage disequilibrium between a tested marker and the disease locus.
We consider the following model: Let D and d be the alleles at the disease locus with allele frequencies p and q, respectively. Let A and a be the alleles at the marker locus, with allele frequencies p′ andq′, respectively, where A is positively associated with D. We define the linkage disequilibrium parameter δ (Bengtsson and Thomson 1981) by Furthermore, we define φ = qp‘/pq‘ as the odds ratio of the allele frequencies at loci D and A.We also note that, in general, 0 ≤ δ ≤ 1. However, ifp‘ < p, then δ has a smaller upper bound, namely φ, which is <1. If p‘ > p, then φ > 1, and δ has an upper bound of 1. From formula 28, we can derive the conditional probabilities:
Furthermore, we define φ = qp‘/pq‘ as the odds ratio of the allele frequencies at loci D and A.We also note that, in general, 0 ≤ δ ≤ 1. However, ifp‘ < p, then δ has a smaller upper bound, namely φ, which is <1. If p‘ > p, then φ > 1, and δ has an upper bound of 1. From formula 28, we can derive the conditional probabilities: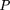
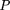
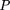
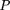 Assuming the relative penetrances f
2 andf
1 correspond to the disease locus genotypesDD and Dd, we can calculate relative penetrances f
2‘ and f
1‘ corresponding to the marker locus genotypes AA andAa by using the conditional allele probabilities given above, along with the formulaP(Aff‖AA) =P(Aff‖DD)P(DD‖AA) +P(Aff‖Dd)P(Dd‖AA) +P(Aff‖dd)P(dd‖AA), and similar formulas for genotypes Aa and aa. We then obtain
Assuming the relative penetrances f
2 andf
1 correspond to the disease locus genotypesDD and Dd, we can calculate relative penetrances f
2‘ and f
1‘ corresponding to the marker locus genotypes AA andAa by using the conditional allele probabilities given above, along with the formulaP(Aff‖AA) =P(Aff‖DD)P(DD‖AA) +P(Aff‖Dd)P(Dd‖AA) +P(Aff‖dd)P(dd‖AA), and similar formulas for genotypes Aa and aa. We then obtain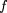
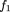 in which w = pq‘/p‘. If we assume a multiplicative model, namely f
1 = γ andf
2 = γ2, then the above formulas forf
2‘ and f
1‘ reduce also to a multiplicative model, f
1‘ = η,f
2‘ = η2, where
in which w = pq‘/p‘. If we assume a multiplicative model, namely f
1 = γ andf
2 = γ2, then the above formulas forf
2‘ and f
1‘ reduce also to a multiplicative model, f
1‘ = η,f
2‘ = η2, where It is then straightforward to calculate the sample size increase owing to incomplete disequilibrium for a multiplicative model,
using the design of a single affected with parents. From formulas derived previously, the required sample size when testing
the disease locusD is given by
It is then straightforward to calculate the sample size increase owing to incomplete disequilibrium for a multiplicative model,
using the design of a single affected with parents. From formulas derived previously, the required sample size when testing
the disease locusD is given by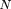 The comparable formula, using locus A instead ofD, is given by
The comparable formula, using locus A instead ofD, is given by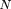 From formulas 30 and 31, if we assume z
1−β = 0 (corresponding to 50% power), or the term involving z
1 − β is relatively small or constant, then the ratioN‘/N can be well represented by
From formulas 30 and 31, if we assume z
1−β = 0 (corresponding to 50% power), or the term involving z
1 − β is relatively small or constant, then the ratioN‘/N can be well represented by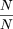 First we note that
First we note that and
and Thus,
Thus,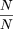 Formula 33 shows the sensitivity to incomplete disequilibrium. For example, if p = 0.1 and p′ = 0.2 but δ = 1, then N′/N = Φ = 2.25, that is, about twice the sample size is required. If δ = 0.7 instead of 1, then this figure can be multiplied
by ∼2, to give a sample size ratio of 4.5-fold. Similarly, if p = 0.2 andp′ = 0.1 and δ = Φ, thenN′/N = 1/Φ = 2.25. Of course, the greater the disparity between p and p′, or the smaller the value of δ, the greater the sample size increase.
Formula 33 shows the sensitivity to incomplete disequilibrium. For example, if p = 0.1 and p′ = 0.2 but δ = 1, then N′/N = Φ = 2.25, that is, about twice the sample size is required. If δ = 0.7 instead of 1, then this figure can be multiplied
by ∼2, to give a sample size ratio of 4.5-fold. Similarly, if p = 0.2 andp′ = 0.1 and δ = Φ, thenN′/N = 1/Φ = 2.25. Of course, the greater the disparity between p and p′, or the smaller the value of δ, the greater the sample size increase.
The calculation for other study designs, for example, those involving more affected sibs, is somewhat more complicated. To some extent, the sample size increase will be proportionately greater with more affected sibs, owing to lack of independence of the allele frequency difference (between affecteds and “controls”) among affected sibs, even within mating type. However, for near to complete disequilibrium, these effects will be modest.
DISCUSSION
We have presented statistics that can be applied to test for linkage disequilibrium in nuclear families based on DNA pooling, either when parents are available or unavailable. We have shown that increasing the number of affecteds in the sibship can lead to a substantial increase in power but will depend to some extent on the genetic model and allele frequencies. The greatest advantage occurs when the susceptibility allele frequency is low; when the allele frequency is high, designs incorporating unrelated controls maintain this advantage, whereas designs with unaffected sibs lose the advantage. Families with parents are intermediate, with neither a great loss nor advantage.
Using unaffected sibs as controls suffers a loss of power compared with using parents or unrelateds, especially as the number affected in the sibship increases. Additional benefit can be obtained by increasing the number of unaffected sibs in the family; however, on a per person basis, increasing this number past two will generally not greatly enhance the power.
Pooling provides the great advantage of reducing the amount of molecular work required but cannot guarantee the absolute robustness possible when individual genotyping is performed and analyzed by statistics such as the TDT. In the subsequent paper, we consider other statistics based on individual genotyping and their power.
Our motivation for these analyses is the recent demonstration of the limited power of linkage analysis to detect susceptibility loci of modest effect, which are likely to predominate for complex disorders (Risch and Merikangas 1996). The approach of genome-wide linkage disequilibrium studies is also not of unlimited potential. The primary limitation is the lack of complete disequilibrium with any tested candidate allele, which can substantially reduce power (Muller-Myhsok and Abel 1997). The original proposal by Risch and Merikangas (1996)was to test potentially functional variations in known genes. The limitation of this approach is the small proportion of known genes and the considerable future effort required to identify and sequence all human genes.
An alternative approach is to use a very dense map of anonymous polymorphisms, perhaps spaced 100 kb apart. It is as yet difficult to predict how successful this type of approach would be, owing to lack of knowledge of the distribution of linkage disequilibrium in the human genome. This distribution is certainly not uniform across chromosomes nor across populations. With the addition of further empirical studies of linkage disequilibrium in different populations in the future, it may be possible to better predict the power of this type of strategy. However, the considerations given in the final section of this paper and, in particular, formula 31 should serve as a warning that this latter approach will not automatically be successful, unless an extremely dense map of markers is used.
Given the large amount of genotyping likely to be required by either of the above strategies, our conclusions regarding number of families of different designs is quite relevant. We emphasize that multiplex families, that is, those with many affected sibs, are optimal and can greatly reduce the total sample size, but only if parents are available or by using unrelated controls.
Although there has been considerable emphasis of late on using family-based controls, we have shown that using unaffected sibs as controls may lead to an unacceptable loss of power when compared with designs using unrelated controls. Case-control association studies have often been criticized by geneticists for lack of robustness to stratification artifact. However, few direct examples of this explanation for spurious or nonreplicable genetic associations have been offered. Instead, the culprit may simply be type 1 error, resulting from large numbers of tests of this type being conducted, with few true underlying genetic associations. If so, using family-based designs will not eliminate nor even reduce the rate of false-positive claims. Using a design with low power may actually lead to an increased frequency of false positives among reported significant associations.
Thus, for early onset diseases, when parents are readily available, using multiplex families with parents as controls is a reasonable strategy. However, when parents are missing, we recommend using unrelated controls, at least as a first step, to retain high power to detect susceptibility loci of modest effect.
Acknowledgments
This work was supported, in part, by grants from National Human Genome Research Institute (NHGRI) (HG00348) and the Nancy Pritzker Foundation. We are grateful to Dr. Michael Boehnke for many helpful comments and suggestions on this manuscript and to Drs. David Curtis and Cedric Clarke for pointing out the Clarke et al. (1956) reference.
The publication costs of this article were defrayed in part by payment of page charges. This article must therefore be hereby marked “advertisement” in accordance with 18 USC section 1734 solely to indicate this fact.
Footnotes
-
↵4 Corresponding author.
-
E-MAIL Risch{at}lahmed.stanford.edu; FAX (650) 725-1534.
-
- Received December 30, 1997.
- Accepted November 10, 1998.
- Cold Spring Harbor Laboratory Press











