Fast sequence alignment for centromeres with RaMA

  1. Yansu Wang1,2
  1. 1Institute of Fundamental and Frontier Sciences, University of Electronic Science and Technology of China, Chengdu 611731, China;
  2. 2Yangtze Delta Region Institute (Quzhou), University of Electronic Science and Technology of China, Quzhou 324003, Zhejiang, China;
  3. 3School of Computer Science and Technology, Xidian University, Xi'an 710126, Shaanxi, China
  • Corresponding author: wangyansu{at}uestc.edu.cn
    •  
    Next Section

    Abstract

    The release of the first draft of the human pangenome has revolutionized genomic research by enabling access to complex regions like centromeres, composed of extra-long tandem repeats (ETRs). However, a significant gap remains as current methodologies are inadequate for producing sequence alignments that effectively capture genetic events within ETRs, highlighting a pressing need for improved alignment tools. Inspired by UniAligner, we developed a rare match aligner (RaMA), using rare matches as anchors and two-piece affine gap cost to generate complete pairwise alignment that better captures genetic evolution. RaMA also employs parallel computing and the wavefront algorithm to accelerate anchor discovery and sequence alignment, achieving up to 13.66 times faster processing using only 11% of UniAligner's memory. Downstream analysis of simulated data and the CHM13 and CHM1 higher-order repeat (HOR) arrays demonstrates that RaMA achieves more accurate alignments, effectively capturing true HOR structures. RaMA also introduces two methods for defining reliable alignment regions, further refining and enhancing the accuracy of centromeric alignment statistics.

    Advances in long-read sequencing technologies and assembly algorithms, highlighted by the Telomere-to-Telomere (T2T) Consortium's recent assembly of the first complete human genome (Liao et al. 2023), have enabled the complete assembly of complex repetitive regions such as centromeres. In the T2T–CHM13 genome assembly (Nurk et al. 2022), satellite repeats account for 6.2%, with alpha satellite being the predominant component, constituting 2.8% of the genome (Altemose et al. 2022). Studies on tandem repeats have further highlighted their critical role in various cellular processes and indicated that mutations within these repeats can lead to genetic disorders (Giunta and Funabiki 2017; Black and Giunta 2018; Song et al. 2018). Human centromeres consist of large arrays of alpha satellite DNA, often spanning millions of base pairs on each chromosome, and are characterized by extra-long tandem repeats (ETRs) known as monomers, primarily composed of ∼171 bp alpha satellite DNA (Manuelidis and Wu 1978). Monomers are organized into higher-order repeat (HOR) units, varying significantly across different species (Henikoff et al. 2001). Within these HOR units, monomers share sequence identities ranging from 50% to 90%, while the sequence identity between different HOR units within the same centromere can be as high as 95% to 100% (Bzikadze and Pevzner 2020; Gao et al. 2023). Centromeres are critical for genome stability, fertility, and healthy development as they ensure the proper distribution of genetic material during cell division; thus, given their detailed assembly, deep analysis is essential to understand their roles in genomic integrity and their associations with cancer and infertility (Schueler et al. 2001; Shepelev et al. 2009; McKinley and Cheeseman 2016; Giunta and Funabiki 2017; Black and Giunta 2018; Miga and Alexandrov 2021; Altemose et al. 2022; Tian et al. 2024).

    Human centromeres, among the most diverse and rapidly evolving regions of the genome, exhibit significant variation in tandem repeat copy numbers across the human population (Cechova et al. 2019). These variations, driven by mechanisms like unequal crossing over, concerted evolution, and saltatory amplification (Smith 1976; Miga and Alexandrov 2021; Logsdon and Eichler 2023), highlight the limitations of classical alignment models that focus solely on single-nucleotide insertions and deletions. Consequently, aligning ETRs across different human genomes poses a significant algorithmic challenge. Due to these complexities, centromeres and other ETRs have been excluded from the recently constructed human pangenome graph by the Human Pangenome Reference Consortium, as constructing the pan-centromere creates a significant bottleneck in the development of the human pangenome (Liao et al. 2023). Nevertheless, aligning centromeres is crucial for studies aimed at exploring their variation and evolution. In this pursuit, researchers sequenced, assembled, and compared all centromeres from a second human genome (Logsdon et al. 2024) to the finished reference genome (Altemose et al. 2022; Nurk et al. 2022; Liao et al. 2023).

    To align centromeres, researchers used three methods. Initially, they directly aligned sequences using minimap2 (Li 2018) with the parameters “minimap2 -I 15G -K 8G -t threads -ax asm20 –secondary = no –eqx -s 2500 ref.fasta query.fasta,” which were found optimal for centromeric regions. The second approach involved segmenting sequences into 10 kb fragments for alignment with minimap2. Lastly, they employed UniAligner (Bzikadze and Pevzner 2023), a new tool providing fast, efficient alignment of ETRs by focusing on rare substrings. Although UniAligner excels in aligning tandem repeat arrays and highlighting key genomic events, it performs only partial alignments and is not optimized for complete sequence alignment across other genomic regions. Enhancements in speed and memory efficiency could further extend its utility.

    Inspired by UniAligner, we developed the rare match aligner (RaMA) for pairwise centromere alignment, which leverages suffix and longest common prefix (LCP) arrays (Louza et al. 2020) to recursively identify rare matches as anchors based on their rarity. Following segmentation by these rare matches, the sequences are aligned using a two-piece affine gap cost (Gotoh 1990) implemented via a wavefront algorithm (Marco-Sola et al. 2021). This scoring system favors the insertion of longer gaps, thereby mirroring the genetic evolutionary events in centromeres, ultimately producing refined alignment results. Additionally, RaMA significantly enhances operational efficiency by employing parallel computing and implementing various algorithmic optimizations during anchor point detection, surpassing the performance of UniAligner. Analyses of simulated data and the CHM13 and CHM1 HOR arrays demonstrate that RaMA achieves greater alignment accuracy, effectively capturing authentic HOR structures. Furthermore, RaMA introduces two methodologies for defining reliable alignment regions, which further refine and enhance the accuracy of centromeric alignment statistics.

    Previous SectionNext Section

    Results

    Overview of RaMA

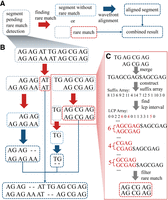
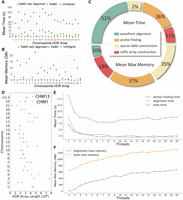
    RaMA is a rapid pairwise alignment tool designed for extremely long tandem repeat sequences like centromeres. RaMA accepts two assembled centromeric sequences as input. This implies that when aligning a chromosome-level reference to a contig-based assembly, users must first assign contigs to chromosome with another aligner (e.g., minimap2). RaMA then identifies rare matches as anchors and uses wavefront alignment to generate global pairwise alignment. Rare matches, infrequent within the input sequences, are prioritized by RaMA, which focuses on those with fewer occurrences. As depicted in Figure 1A, RaMA first identifies rare matches to serve as anchors, segments the sequences by these anchors, and repeats the process until no further anchors can be found. The resulting segments are then aligned using a wavefront alignment algorithm with a two-piece affine gap cost, and the final alignment results are synthesized.

    Figure 1.
    View larger version:
    Figure 1.

    Workflow of RaMA. (A) Recursive logic of RaMA: light gray boxes indicate segments awaiting rare match detection. After the search (red arrow), two scenarios arise: If no rare match is found, the segment turns light blue, undergoes wavefront alignment (blue arrow), and becomes a dark blue aligned segment. If a rare match is identified, it acts as an anchor, splitting the segment while leaving the rest in search mode. The final alignment is formed by combining all detected rare matches and aligned segments. (B) Alignment case: sequences “AG AG AT TG AG CG AG” and “AG CG AG AT AG CG AG,” each containing “AG” as a tandem repeat unit, are aligned using “AT” as a rare match anchor. The sequence is divided; the left part, without further anchors, proceeds to alignment. The right continues to search, finding “AG CG AG” as another anchor. Final results are achieved by merging these segments. (C) Rare match detection: sequences are combined with “$” as a delimiter, then processed to build suffix and LCP arrays. LCP intervals of length 1 are identified, with the longest rare match selected from conflicting results as the final anchor.

    In Figure 1B, an alignment case shows “AT” rare matches appearing twice and “AGCGAG” appearing three times. Despite its length, RaMA initially prioritizes “AT” as the anchor and considers “AGCGAG” later. RaMA uses dynamic programming to select optimal, colinear rare matches as anchors, detailed in Figure 1C and further elaborated in the Methods sections “Finding rare match via LCP interval” and “Filtering anchors using dynamic programming.” RaMA's efficiency is enhanced by parallel computing, which accelerates both the recursive anchor search and sequence alignment, resulting in rapid and accurate alignments.

    Comparison of RaMA and other methods on repetitive sequences

    Due to the arrangement of consecutive alpha satellite repeats into HOR units, which are repeated hundreds or thousands of times in each centromere, and the sequence identity between different HOR units within the same centromere being as high as 95% to 100%, existing sequence alignment methods can produce alignment results but struggle to reflect the variation and evolutionary information of centromeres. To demonstrate RaMA's superiority in centromere alignment, we conduct comparisons with three other methods: minimap2 (Li 2018), wfmash (https://github.com/waveygang/wfmash), and UniAligner (Bzikadze and Pevzner 2023). minimap2 is executed using the same parameters as the previous study (Logsdon et al. 2024). UniAligner, wfmash, and RaMA operate with its default settings (see Supplemental Method).

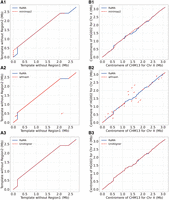
    We employed both simulated and real data sets to compare different methods’ capabilities in capturing centromeric genetic evolution. Inspired by UniAligner, we generated simulated data (see Supplemental Method). For the simulated data, alignment results have ground truth. As shown in Figure 2A, RaMA and UniAligner were able to accurately capture the regions that were removed from the simulated data, particularly in subfigures A1, A2, and A3. The alignment paths of both RaMA and UniAligner clearly reflect the existence of the two removed regions, demonstrating their ability to handle these genomic alterations effectively. In contrast, minimap2 (A1) and wfmash (A2) failed to identify these removed regions. Specifically, wfmash showed a nearly straight alignment path, indicating that it was unable to capture the deleted segments. Similarly, minimap2 missed part of the removed regions, with its alignment path showing gaps or soft clipping instead of reflecting the structural changes. Thus, RaMA and UniAligner outperform wfmash and minimap2 in accurately capturing centromeric evolutionary events.

    Figure 2.
    View larger version:
    Figure 2.

    Comparison of alignment paths between RaMA and other methods on real and simulated centromere sequences. Series A uses a template with region 1 removed as the reference and a template with region 2 removed as the query. Series B shows the X Chromosome centromere of CHM13 as the reference and HG002 as the query. Labels 1, 2, and 3 correspond to RaMA compared with minimap2, wfmash, and UniAligner, respectively.

    The performance of the four methods on the real data set mirrors their performance on the simulated data set. As shown in Figure 2B, RaMA and UniAligner share similar alignment paths but differ in detail. UniAligner performs rare alignment, only aligning within anchors and using match runs, insertions, and deletions. In contrast, RaMA employs WFA for comprehensive alignment, providing complete outcomes. While minimap2's alignment path is broadly similar to RaMA's, there are notable differences between the two. In contrast, wfmash only shares a small portion of the alignment path with RaMA, with the majority of its alignment results deviating substantially from RaMA's. We also applied the WFA with a dual-affine gap penalty using different parameter settings to align both the simulated and real data sets (see Supplemental Fig. S1). We tested various parameters of WFA to explore whether more optimized settings could improve centromere alignment. However, even with short insertion extension penalties and long insertion extension penalties set as high as 50, WFA's alignment results still produced straight lines, rendering the alignments biologically meaningless. Overall, RaMA demonstrates superior performance in capturing centromeric genetic evolutionary events compared to WFA, minimap2, and UniAligner.

    We also compared RaMA and UniAligner on nonrepetitive sequences. Our results show that RaMA performs comparably to or better than WFA at moderate to high similarity levels, while UniAligner consistently underperforms across all similarity ranges (Supplemental Figs. S10–S14). The average anchor coverage of RaMA is 32% in centromeres, reaching a peak of 76% on Chromosome 19 (see Supplemental Table S7). In contrast, nonrepetitive sequences with 70% similarity demonstrate a minimum coverage of 88%. Notably, even the centromere of Chromosome 19, which has the highest coverage, is still lower than that of nonrepetitive sequences at 70% similarity. This underscores a greater prevalence of rare matches in nonrepetitive regions (see Supplemental Method). RaMA's superior performance in nonrepetitive regions arises from identifying rare matches, analogous to MUMmer's maximal unique matches (MUMs). This observation aligns with Bzikadze and Pevzner's assertion (Bzikadze and Pevzner 2023) that “UniAligner performs comparably to other alignment tools on nonrepetitive sequences.” RaMA further outperforms UniAligner by integrating the WFA algorithm to resolve alignments in regions that are difficult for parameter-free methods to handle. RaMA also demonstrates slightly higher alignment quality than UniAligner on sequences combining tandem and nontandem repeat regions, showing strong potential for accurate alignment in these hybrid regions (see Supplemental Method; Supplemental Fig. S15; Supplemental Tables S6, S8).

    Indel analysis of X-Chromosome alignment between CHM13 and CHM1

    We conducted an in-depth analysis of indel events using the HOR array of the X Chromosome from CHM13 as the reference and CHM1 as the query. This analysis was aimed at better understanding the dynamics of structural variation (SV) between these two genomes, with a particular focus on indel events. Detailed statistics for the indels detected by both RaMA and UniAligner are presented in Supplemental Tables S1 and S2, providing a comprehensive comparison of the capabilities of these alignment tools.

    We defined two categories of reliable regions based on sequence identity and rare matches. For identity assessment based on previous work (Logsdon et al. 2024), the reference sequence was divided into 10 kb nonoverlapping windows, and sequence identity was calculated for each window. The mean value represented the overall sequence identity. The formula used was (number of matches)/(number of matches + number of mismatches + number of insertion events + number of deletion events). A window with an identity above 90% was classified as a reliable alignment region. The identity-based reliable alignment regions consist primarily of continuous, stable match areas, making them well-suited for mutation estimation. For the identification of rare match-based reliable regions, the approach for confirming rare match-based reliable regions is: Assuming rare matches are correctly aligned, if an interval segmented by them requires further alignment, it is considered unreliable; otherwise, it is reliable. Thus, all rare matches were directly classified as reliable regions. Moreover, alignment intervals between rare matches were also deemed reliable if they contained only simple insertions, simple deletions, or perfect matches. The rare match-based reliable alignment regions are mostly indels, making them suitable for indel-related estimation. Although UniAligner also uses rare matches and should theoretically yield similar reliable regions to RaMA, its output does not allow verification.

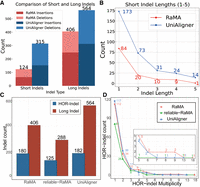
    As illustrated in Figure 3A, RaMA detected 124 short indels with a cumulative length of 195 bp, whereas UniAligner identified 315 short indels with a total length of 578 bp. Figure 3B further demonstrates that RaMA consistently reduces the number of short indels across all length categories, particularly for indels of length 1 bp, which occur at a frequency of ∼0.4 per 10,000 bp, compared to UniAligner's frequency of 1 per 10,000 bp. This observation suggests that short indels are infrequent in the evolutionary changes of the centromeric region. In this subsection, we primarily focus on analyzing indels, so we only use reliable regions based on rare matches.

    Figure 3.
    View larger version:
    Figure 3.

    Statistical results of centromere alignment on the X Chromosome for CHM13 and CHM1. (A) Comparison of the number of short and long indels, as well as insertions and deletions, in the alignment results of the two methods. (B) Comparison of the distribution of short indels (≤5 bp) by length in the alignment results of the two methods. (C) Comparison of the number of long indels and HOR-indels in RaMA alignment results, reliable regions of RaMA based on the rare match and the UniAligner alignment results. (D) Distribution of the multiplicity of HOR indels in RaMA alignment results, reliable regions of RaMA based on the rare match, and the UniAligner alignment results.

    For long indels, given that the canonical HOR on the X Chromosome is 2057 bp (Miga et al. 2020), we define a long indel as a HOR-indel if its length is a multiple of 2057, which lends greater reliability to it in the centromeric alignment analysis. We performed a statistical analysis of long indels and HOR-indels in the RaMA alignment results, the reliable regions of RaMA based on the rare match, and the UniAligner alignment results. As shown in Figure 3C, RaMA identified 406 long indels (180 of which are HOR-indels) in the full alignment, with 288 long indels (125 HOR-indels) in the reliable regions. In comparison, UniAligner identified 564 long indels, including 182 HOR-indels. The distribution of HOR-indel multiplicities is detailed in Figure 3D. RaMA's alignment results include 112 HOR-indels with multiplicity 1, 34 with multiplicity 2, and 34 with multiplicity above 2. In the reliable regions, there are 81 HOR-indels with multiplicity 1, 26 with multiplicity 2, and 18 with multiplicity above 2. Similarly, UniAligner's results show 117 HOR-indels with multiplicity 1, 39 with multiplicity 2, and 26 with multiplicity above 2. Both methods show similar multiplicity distributions, but RaMA identifies more larger multiplicities, for example, RaMA identified an 18-multiplicity long indel in a reliable region, which UniAligner missed.

    RaMA identified 28% fewer long indels than UniAligner, yet the number of HOR-indels remained nearly the same. However, the total multiplicity of HOR-indels identified by RaMA, at 372, was significantly higher than UniAligner's total multiplicity of 312, suggesting that RaMA's alignment results are more accurate than UniAligner in capturing true HOR structures. RaMA identified 71% of long indels and 70% of HOR-indels within the reliable region, indicating that most of these indels in the alignment are reliable. The concentration of HOR-indels in reliable regions further provides a solid basis for further structural analysis and validation.

    In UniAligner, the estimated rate of HOR-indels (over 2 kb in length) is one per 10 kb in centromeric regions. By comparison, the average SV rate in the human genome for variants exceeding 50 bp is one per 150 kb, with SVs over 2 kb accounting for only 10% of total SVs. Based on these estimates, UniAligner concludes: “Thus, the rate of large SVs in human centromeres exceeds the rate of large SVs in the rest of the human genome by two orders of magnitude.” However, our findings challenge this conclusion. We identified 125 reliable HOR-indels and 277 reliable long indels over 50 bp in centromeric regions, with HOR-indels comprising over 49% of all long indels, which is notably higher than the 10% typically observed genome-wide. These findings suggest a rate of one long indel per 11 kb in centromeric regions, ∼13 times the genome-wide average SV rate—substantially lower than the two orders of magnitude proposed by UniAligner.

    Statistical analysis of centromere alignments between CHM13 and CHM1

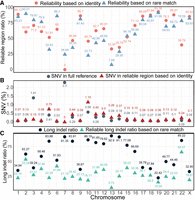
    The complete assembly of each CHM1 centromere allows for a comprehensive comparison of centromeric allelic sequences and structures between two human genomes. We used RaMA to align CHM13 and CHM1 centromeres, with a focus on analyzing the reliability of alignment regions. Figure 4 presents the RaMA alignment results, using the CHM13 centromere as the reference and the CHM1 centromere as the query. Figure 4A shows the proportion of two reliable region types across chromosome centromeres. Chromosome 7 has 0% identity-based reliable regions, and Chromosome 13 has only 7.88% rare match-based reliable regions, indicating unreliable alignments. Thus, Chromosomes 7 and 13 are excluded from corresponding average calculations. In the RaMA alignment with CHM13 as the reference, the average proportion of identity-based reliable regions is 66.38% and rare match-based is 63.64%. In comparison, UniAligner's identity-based reliable regions average 65.94%, indicating RaMA aligns slightly more reliably than UniAligner (see Supplemental Table S9).

    Figure 4.
    View larger version:
    Figure 4.

    Statistical analysis of centromere alignment results between CHM13 and CHM1 using RaMA. (A) Proportion of two types of reliable regions, based on identity and rare matches, across different chromosomes relative to the reference sequence length. (B) Comparison of the single-nucleotide variant (SNV) rates between the entire reference sequence region and identity-based reliable regions. (C) The proportion of total long indel length and the total length of reliable long indels based on rare matches in the full alignment length.

    As shown in Figure 4B, we calculated the single-nucleotide variant (SNV) rate for RaMA across the full reference sequence and within identity-based reliable regions, then compared it with UniAligner results. The calculation is mismatches divided by the length of the corresponding reference region. RaMA's average SNV rate is 0.21% across the full sequence and 0.25% in reliable regions, compared to UniAligner's 0.09% and 0.15%, respectively (see Supplemental Table S9; Supplemental Fig. S2). The estimated SNV rate in reliable regions is higher than in the full sequence, with RaMA's estimate being higher than UniAligner's. This suggests that existing centromere alignment methods may underestimate true SNV rates, missing key variations in centromere diversity and function. RaMA's higher SNV estimates help correct this, offering a clearer view of centromeric variability and supporting studies on centromere evolution and function. RaMA alignment results with CHM1 as the reference and UniAligner results both reach the same above conclusion (see Supplemental Table S9; Supplemental Figs. S3, S4).

    As shown in Figure 4C, we calculated the proportion of long indels (over five bases) in the full alignment length and their proportion within rare match-based reliable regions relative to the full length, comparing these results with UniAligner. UniAligner does not account for the alignment of insertion–deletion runs, resulting in its estimated proportion of long indels being a theoretical upper limit, averaging 77.2% (see Supplemental Table S10). In contrast, RaMA offers an estimated average proportion of long indels within reliable regions, which serves as a theoretical lower limit at 29.52%. The overall proportion of long indels reported by RaMA is an exploratory estimate that falls between these two bounds, averaging 60.78%. The higher proportion reported by UniAligner indicates an overestimation that may mislead interpretations of genomic variability in evolutionary studies and population genetics. This analysis narrows the range of long indels and offers a more accurate estimate, potentially enhancing our understanding of the evolutionary processes driving genetic diversity.

    Comprehensive performance analysis of RaMA

    RaMA achieves significant optimizations in both time and memory compared to UniAligner through enhancements in data structures, algorithms, and parallel computing techniques. While UniAligner is a rare-alignment method where the rare-alignment time equals the total alignment time, RaMA operates in two phases: rare match finding and WFA alignment. We conducted 10 alignments of the HOR arrays for the 23 chromosomes using CHM13 as the reference and CHM1 as the query. The length distribution of the HOR arrays for each chromosome is shown in Figure 5D. The experiments were run with Ubuntu 20.04.4 LTS, an Intel(R) Xeon(R) Gold 6230 CPU @2.10 GHz, 80 CPUs, and ∼1 TB of memory. RaMA was run using a single thread, with alignment times and memory usage shown in Figure 5A and B. RaMA's rare-alignment phase achieved a speedup of 94.99 times compared to UniAligner's total alignment time, and its total alignment time showed a speedup of 13.66 times. For memory usage, RaMA's rare match finding phase used 11.02% of UniAligner's memory peak, while the complete process used 11.15%. The significant speedup and reduced memory usage are due to RaMA's approach of constructing only the initial suffix array (SA) and LCP array. We also aligned the complete chromosomes of CHM13 and CHM1 to compare the performance of RaMA, minimap2, and wfmash with 32 threads. The time comparison in Supplemental Figure S5 shows that RaMA is faster than minimap2 on most chromosomes and is comparable to wfmash, except for the very long chromosomes. In terms of memory usage, as shown in Supplemental Figure S6, RaMA typically consumes more memory due to its reliance on the SA compared to minimap2 and wfmash, which use minimizers; however, this consumption remains within an acceptable range.

    Figure 5.
    View larger version:
    Figure 5.

    Comprehensive performance evaluation of RaMA: time and memory efficiency metrics. (A) Comparison of the average alignment time for HOR arrays across different chromosomes of CHM13 and CHM1 using RaMA and UniAligner. (B) Comparison of the average maximum memory usage for HOR arrays across different chromosomes of CHM13 and CHM1 using RaMA and UniAligner. (C) Comparison of the time and memory required for different algorithm stages of RaMA. (D) Comparison of HOR array lengths across different chromosomes between CHM13 and CHM1. (E) Variation in RaMA's anchor finding time, alignment time, and total time with the number of threads. (F) Variation in RaMA's alignment memory and total memory usage with the number of threads.

    In Figure 5C, the time and memory usage proportions for different stages of RaMA are presented. The initial phase accounts for 13% of the total time and 53% of the memory usage, the rare match finding phase takes up 36% of the time and 37% of the memory, and the wavefront alignment phase consumes 51% of the total time but only 10% of the memory. These findings highlight RaMA's memory intensity in its initial stages, with a shift toward time consumption during alignment. We also evaluated RaMA's performance with multithreading. Using the HOR array of Chromosome 11, we conducted 10 experiments and averaged the results. Figure 5E shows the variation in RaMA's processing time across different stages as the number of threads increases. The curves for total time and anchor finding time level off at six threads, achieving a 2.3-fold speedup compared to the single-threaded version. The wavefront alignment phase levels off at three threads. Figure 5F depicts the changes in memory peak values across different stages as the number of threads increases, showing a steady increase in both alignment memory peak and total memory peak with more threads. The runtime and memory usage of RaMA and UniAligner with varying sequence similarity can be found in Supplemental Figures S7 and S8.

    Previous SectionNext Section

    Discussion

    High-precision, long-read sequencing technologies have transformed human genome assembly, exemplified by T2T–CHM13, the first complete genome. Both T2T–CHM13 and CHM1 provide invaluable insights into complex centromeric regions, though aligning these regions remains challenging and has limited their inclusion in pangenome studies. Recently, UniAligner introduced a centromere-focused alignment framework, but its rare-alignment approach restricts its application to tandem repeats, leaving room for optimization in speed and memory efficiency. Inspired by UniAligner, we developed RaMA, incorporating a two-piece affine gap penalty wavefront alignment algorithm. RaMA significantly outperforms UniAligner, achieving 94.99 times faster rare-alignment and a 13.66-fold overall speedup with just 11% of UniAligner's memory usage. Multithreading further accelerates RaMA, peaking at six threads with a 2.3-fold increase in speed. RaMA thus offers substantial gains in alignment efficiency and resource usage over UniAligner.

    Assessing centromeric alignment quality remains a significant challenge in centromere sequence analysis. Currently, no quantitative metrics directly measure alignment accuracy, so quality is often inferred from simulated data sets and downstream analyses. Our tests with simulated data showed that only RaMA and UniAligner produced results consistent with the ground truth, while other methods failed to accurately identify removed regions. When applying RaMA and UniAligner to align the X Chromosome in real data sets CHM13 and CHM1, we found that both methods identified a similar number of HOR-indels. However, RaMA detected a significantly higher total HOR-indel multiplicity of 372 compared to UniAligner's 312 and identified an 18-multiplicity long indel that UniAligner missed, suggesting that RaMA's alignment more accurately captures true HOR structures.

    We used RaMA and UniAligner to align the HOR arrays of CHM13 and CHM1. Determining reliable alignment regions is crucial for centromeric analysis. We propose an identity-based method for reliable mutation calculation and a rare match-based method for reliable long indel assessment. RaMA's average SNV rate is 0.21% across the full sequence and 0.25% in identity-based reliable regions, compared to UniAligner's 0.09% and 0.15%. The SNV rate in identity-based reliable regions exceeds that of the full sequence, with RaMA's estimate higher than UniAligner's. In the X Chromosome HOR array alignment, RaMA identified 124 short indels, significantly fewer than UniAligner's 315, suggesting existing methods may underestimate SNV rates and overestimate indel counts. RaMA corrects these biases, providing more accurate estimates. We also calculated the proportion of long indels (over five bases) across the full alignment and within rare match-based reliable regions, comparing RaMA and UniAligner. UniAligner, without accounting for insertion–deletion runs, gives an upper limit at 77.2%, while RaMA provides a lower limit at 29.52% and an overall average of 60.78%. UniAligner's higher estimate suggests potential overestimation, while RaMA's narrower range offers a more accurate perspective on long indels, aiding insights into evolutionary processes and genetic diversity. Our findings challenge UniAligner's conclusion by showing a rate of one long indel per 11 kb in centromeric regions—13 times the genome-wide average, yet far below the two orders of magnitude difference previously estimated.

    Our research advances centromere alignment algorithms with two methods for reliable region identification, providing more precise alignment estimates. Despite RaMA's advancements in centromere sequence alignment, it cannot fully capture the genetic evolutionary events of centromeres due to limitations in recognizing specific monomer arrangements in HORs. To address this, we plan to optimize the algorithm to better capture monomer order. Additionally, we will develop a multiple sequence alignment method to support the simultaneous alignment of multiple centromeres. Experiments on nonrepetitive sequences show that RaMA's rare match achieves high alignment quality on over 90% of non-low-similarity sequences, demonstrating its potential for further extension.

    Previous SectionNext Section

    Methods

    Data set

    We extracted the assembled satellite centromeres from all chromosomes of the effectively haploid genomes CHM13v2.0 (Nurk et al. 2022) (available from https://s3-us-west-2.amazonaws.com/human-pangenomics/index.html?prefix=T2T/CHM13/assemblies/analysis_set/chm13v2.0.fa.gz) and CHM1v1.0 (Logsdon et al. 2024) (available from https://ftp.ncbi.nlm.nih.gov/genomes/all/GCA/037/575/895/GCA_037575895.1_UW_CHM1_v1.0/GCA_037575895.1_UW_CHM1_v1.0_genomic.fna.gz), as well as the diploid male genome HG002v1.0 (Jarvis et al. 2022; Rhie et al. 2023) (available from https://s3-us-west-2.amazonaws.com/human-pangenomics/index.html?prefix=T2T/HG002/assemblies/hg002v1.0.fasta.gz). After downloading the data, we extracted the centromere sequences based on their specific starting and ending coordinates (Supplemental Tables S3–S5). All test data sets used can be found at Zenodo (https://zenodo.org/records/14061939).

    To evaluate the performance of different methods on repetitive sequences, we created a simulated data set using the X Chromosome HOR array of CHM13 as a template, removing regions 1 (182,368–547,935) and 2 (2,417,322–2,773,488) to produce two new sequences (see Supplemental Method). To evaluate RaMA's performance on tandem and nontandem repeat sequences, we used INDELible to simulate two 1,000,000-length nonrepetitive sequences with 95% similarity, inserting CHM13 and CHM1 centromeres from Chromosomes 16 and 20 at positions 300,000 and 800,000 (see Supplemental Method).

    Constructing suffix and LCP array

    Identifying rare matches is fundamental to RaMA, as these matches are closely linked to genetic evolutionary events within ETRs. When analyzing two sequences, S1 and S2, they are combined into a single sequence S = S1$S2, with “$” serving as a delimiter. A “rare match” is defined as a subsequence that appears k times (where 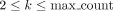Formula) within S and at least once in both sequences S1 and S2 independently. The parameter max_count is fixed, set to a default of 20. RaMA prioritizes rare matches with fewer occurrences for use as anchors. For instance, if a rare match that appears only twice is found in a pair of sequences, RaMA will not continue searching for a rare match that appears three times.

    The detection of these rare matches relies on the use of SAs and LCP arrays. A SA is composed of the indices of the lexicographically sorted suffix strings of sequence S. Conversely, the LCP array provides the lengths of the shared prefixes between consecutive suffixes in the SA, offering a precise and efficient means to identify potential rare matches. RaMA uses the gSACA-K (Louza et al. 2020) method to construct SA and LCP array of the concatenated string S with O(N) time complexity.

    Finding rare match via LCP interval

    An LCP interval is an interval [i..j] in the LCP array, where lmin is the minimum value in the subarray LCP[i], …, LCP[j]. The interval is defined by the condition that the LCP values immediately before and after this subarray, LCP[i − 1] and LCP[j + 1], are both <lmin. After identifying the LCP interval, left extension is required to eliminate duplicates (Zhang et al. 2024). This process involves iteratively comparing nucleotides to the left of the common substrings across all sequences until a mismatch occurs or a sequence boundary is reached, expanding lmin to l. For instance, the three intervals identified in Figure 1C are essentially the same, and by performing left extension, they produce identical results, effectively removing duplicates. If an LCP interval has a length of n, it indicates that a match of length l appears only n + 1 times within the entire sequence S. Thus, identifying rare matches can be modeled as finding LCP intervals, where the rarity of a rare match is determined by the length of the LCP interval. After constructing the LCP array, RaMA first searches for LCP intervals of length 1. If found, the search stops; otherwise, it continues searching for LCP intervals of length 2, and so forth, until an interval is found or the interval length exceeds max_count.

    Filtering anchors using dynamic programming

    The next step after identifying all rare matches is to convert them into anchors. A rare match is a match that occurs multiple times, whereas an anchor is a pair of matches appearing in both sequences. Therefore, for a given set of rare matches, all possible pairs can be combined to yield multiple anchors. For instance, if a rare match appears twice in the first sequence and three times in the second sequence, it can be converted into 2 × 3 = 6 anchors. Once we have the set of anchors, we need to determine the optimal chaining of these anchors to achieve the best alignment between the sequences. This involves calculating the chaining scores using dynamic programming, where each anchor's score is influenced by its matching bases and the gap cost between anchors.

    An anchor is defined as a three-tuple (x, y, w), representing the interval [x, x + w − 1] on the reference sequence S1 and the corresponding interval [y, y + w − 1] on the query sequence S2. Given a list of anchors sorted by their starting positions on the reference sequence x, let f(i) denote the maximum match chaining score up to the i-th anchor in the list (Zhou et al. 2024). 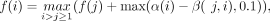The value of f(i) can be determined using dynamic programming: Formula (1) where α(i) is the length of rare match and β(j, i) is the gap cost between the colinear anchor j and i. 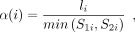In implementation, the α(i) is defined as follows: Formula (2) where li is the length of i-th rare match, and S1i denotes the occurrence counts of the i-th rare match in the reference and S2i denotes the query sequence, respectively. 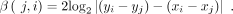As for β(j, i), if |(yi − yj) − (xi − xj)| = 0, β(j, i) = 0; otherwise, its value is Formula (3) As shown in Supplemental Figure S9, following the dynamic programming step, RaMA identifies a set of n collinear optimal anchors between the two sequences. These n anchors divide the sequences into n + 1 subsequences. The process of finding and determining anchors is then recursively repeated for each of these subsequences.

    Splitting sequences and their suffix and LCP arrays based on anchors

    In UniAligner, the suffix and LCP arrays for divided subsequences are reconstructed during each recursive search for anchors, which is unnecessary. In RaMA, we optimized the algorithm to construct the suffix and LCP arrays only once for the entire process, eliminating redundant computations. Thus, the challenge becomes how to construct the SA and LCP array for two new concatenated subsequences based on the existing SA and LCP array of the initial concatenated sequences. To facilitate this process, we constructed the inverse suffix array (ISA). The ISA is defined such that for each position i in the sequence, ISA[SA[i]] = i, meaning that the ISA maps each SA index to its original position in the sequence. For each position in the given subsequences, RaMA first uses the ISA to map each position to its corresponding index in the SA. These indices are then sorted in ascending order and mapped back to the SA to obtain the new SA.

    For constructing the new LCP array, we need to use a property of the LCP array 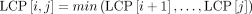Formula. This means that the value of the LCP between the i-th and j-th suffixes is the minimum value in the range from LCP[i + 1] to LCP[j]. To obtain the new LCP array, we perform a minimum value query on the intervals between the indices of the new SA in the original LCP array. Because we need to perform a large number of minimum value queries, we employed a linear range minimum query strategy using block sparse table to parallelly construct the enhanced SA of subsequences (see Supplemental Fig. S16), which achieved approximately a twofold speedup compared to UniAligner's direct SA construction method under a 16-thread setup (see Supplemental Method; Supplemental Figs. S17–S21). This allows us to index data with O(N) time and space complexity, enabling O(1) time complexity for minimum value queries. For details on linear range minimum query, see Supplemental Method.

    Wavefront alignment with two-piece affine gap cost

    After identifying all the anchors, the remaining task is to align the split subsequence segments. Given that these subsequences can still be very long and that longer gaps are more permissible in centromere alignment, we ultimately chose to use wavefront alignment with two-piece affine gap cost for aligning the subsequence segments. The wavefront alignment (Marco-Sola et al. 2021) is a recently proposed tool for pairwise sequence alignment that leverages homologs regions between sequences to accelerate the alignment process. It operates in O(ns) time, where n is the read length and s is the alignment score. This makes it significantly faster than traditional dynamic programming methods, particularly for long and noisy reads. The two-piece affine gap cost model is an extension of the affine gap cost model, introducing a secondary penalty for longer gaps to better capture the biological relevance of indel events. 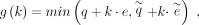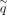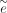It is defined as Formula (4) where q and e are the penalties for short gaps, and Formula and Formula are the penalties for long gaps. This scheme helps to recover longer insertions and deletions by applying different costs based on the gap length.

    Parallel acceleration of RaMA

    RaMA employs parallel acceleration in two modules: rare match anchor search and wavefront alignment. At the start of the anchor search module, we create a thread pool. The two input centromeric sequences are treated as an initial interval, and a thread is allocated from the pool to search for anchors. For each interval, we construct the enhanced SA (accelerated through parallel querying) and the block sparse table, using these data structures to identify rare matches as anchors. From n anchor points, we generate n + 1 new intervals, which are assigned corresponding threads to recursively search for additional rare matches until none are detected. Finally, all rare match anchors are merged into the final anchor points using a preorder traversal of a multiway tree structure. For the wavefront alignment module, if there are n final anchors, this results in n + 1 intervals that require wavefront alignment, which is also performed using the thread pool.

    Software availability

    RaMA code is available at GitHub (https://github.com/malabz/RaMA) and as Supplemental Code. Version 1.0 of RaMA can be found at Zenodo (https://zenodo.org/records/14061939).

    Previous SectionNext Section

    Competing interest statement

    The authors declare no competing interests.

    Previous SectionNext Section

    Acknowledgments

    The work was supported by the National Natural Science Foundation of China (nos. 62425107, 62450002, and 62131004) and the Municipal Government of Quzhou (no. 2023D036).

    Author contributions: P.Z. conceived and designed the study, developed the software implementation, conducted the experiments, and drafted the manuscript. Y.W. contributed to the development of the sequence alignment algorithm. Q.T. participated in experimental execution and data collection. Q.Z. provided critical revisions to the manuscript and secured funding support. Y.W. supervised the entire research project, contributed to experimental design and manuscript revision, and acquired funding. Additionally, we acknowledge Xiaofei Yang from Xi'an Jiaotong University for his valuable support and assistance.

    Previous SectionNext Section

    Footnotes

    • Received July 8, 2024.
    • Accepted February 6, 2025.

    This article is distributed exclusively by Cold Spring Harbor Laboratory Press for the first six months after the full-issue publication date (see https://genome.cshlp.org/site/misc/terms.xhtml). After six months, it is available under a Creative Commons License (Attribution-NonCommercial 4.0 International), as described at http://creativecommons.org/licenses/by-nc/4.0/.

    Previous Section
     

    References

    1. ↵
      Altemose N, Logsdon GA, Bzikadze AV, Sidhwani P, Langley SA, Caldas GV, Hoyt SJ, Uralsky L, Ryabov FD, Shew CJ, et al. 2022. Complete genomic and epigenetic maps of human centromeres. Science 376: eabl4178. doi:10.1126/science.abl4178
      CrossRefMedlineGoogle Scholar
    2. ↵
      Black EM, Giunta S. 2018. Repetitive fragile sites: centromere satellite DNA as a source of genome instability in human diseases. Genes (Basel) 9: 615. doi:10.3390/genes9120615
      CrossRefGoogle Scholar
    3. ↵
      Bzikadze AV, Pevzner PA. 2020. Automated assembly of centromeres from ultra-long error-prone reads. Nat Biotechnol 38: 1309–1316. doi:10.1038/s41587-020-0582-4
      CrossRefMedlineGoogle Scholar
    4. ↵
      Bzikadze AV, Pevzner PA. 2023. UniAligner: a parameter-free framework for fast sequence alignment. Nat Methods 20: 1346–1354. doi:10.1038/s41592-023-01970-4
      CrossRefMedlineGoogle Scholar
    5. ↵
      Cechova M, Harris RS, Tomaszkiewicz M, Arbeithuber B, Chiaromonte F, Makova KD. 2019. High satellite repeat turnover in great apes studied with short- and long-read technologies. Mol Biol Evol 36: 2415–2431. doi:10.1093/molbev/msz156
      CrossRefMedlineGoogle Scholar
    6. ↵
      Gao S, Yang X, Guo H, Zhao X, Wang B, Ye K. 2023. HiCAT: a tool for automatic annotation of centromere structure. Genome Biol 24: 58. doi:10.1186/s13059-023-02900-5
      CrossRefMedlineGoogle Scholar
    7. ↵
      Giunta S, Funabiki H. 2017. Integrity of the human centromere DNA repeats is protected by CENP-A, CENP-C, and CENP-T. Proc Natl Acad Sci 114: 1928–1933. doi:10.1073/pnas.1615133114
      Abstract/FREE Full Text
    8. ↵
      Gotoh O. 1990. Optimal sequence alignment allowing for long gaps. Bull Math Biol 52: 359–373. doi:10.1007/BF02458577
      CrossRefMedlineGoogle Scholar
    9. ↵
      Henikoff S, Ahmad K, Malik HS. 2001. The centromere paradox: stable inheritance with rapidly evolving DNA. Science 293: 1098–1102. doi:10.1126/science.1062939
      Abstract/FREE Full Text
    10. ↵
      Jarvis ED, Formenti G, Rhie A, Guarracino A, Yang C, Wood J, Tracey A, Thibaud-Nissen F, Vollger MR, Porubsky D, et al. 2022. Semi-automated assembly of high-quality diploid human reference genomes. Nature 611: 519–531. doi:10.1038/s41586-022-05325-5
      CrossRefMedlineGoogle Scholar
    11. ↵
      Li H. 2018. Minimap2: pairwise alignment for nucleotide sequences. Bioinformatics 34: 3094–3100. doi:10.1093/bioinformatics/bty191
      CrossRefMedlineGoogle Scholar
    12. ↵
      Liao W-W, Asri M, Ebler J, Doerr D, Haukness M, Hickey G, Lu S, Lucas JK, Monlong J, Abel HJ, et al. 2023. A draft human pangenome reference. Nature 617: 312–324. doi:10.1038/s41586-023-05896-x
      CrossRefMedlineGoogle Scholar
    13. ↵
      Logsdon GA, Eichler EE. 2023. The dynamic structure and rapid evolution of human centromeric satellite DNA. Genes (Basel) 14: 92. doi:10.3390/genes14010092
      CrossRefGoogle Scholar
    14. ↵
      Logsdon GA, Rozanski AN, Ryabov F, Potapova T, Shepelev VA, Catacchio CR, Porubsky D, Mao Y, Yoo D, Rautiainen M, et al. 2024. The variation and evolution of complete human centromeres. Nature 629: 36–145. doi:10.1038/s41586-024-07278-3
      CrossRefGoogle Scholar
    15. ↵
      Louza FA, Telles GP, Gog S, Prezza N, Rosone G. 2020. gsufsort: constructing suffix arrays, LCP arrays and BWTs for string collections. Algorithms Mol Biol 15: 18. doi:10.1186/s13015-020-00177-y
      CrossRefMedlineGoogle Scholar
    16. ↵
      Manuelidis L, Wu JC. 1978. Homology between human and simian repeated DNA. Nature 276: 92–94. https://pubmed.ncbi.nlm.nih.gov/105293. doi:10.1038/276092a0
      CrossRefMedlineGoogle Scholar
    17. ↵
      Marco-Sola S, Moure JC, Moreto M, Espinosa A. 2021. Fast gap-affine pairwise alignment using the wavefront algorithm. Bioinformatics 37: 456–463. doi:10.1093/bioinformatics/btaa777
      CrossRefMedlineGoogle Scholar
    18. ↵
      McKinley KL, Cheeseman IM. 2016. The molecular basis for centromere identity and function. Nat Rev Mol Cell Biol 17: 16–29. doi:10.1038/nrm.2015.5
      CrossRefMedlineGoogle Scholar
    19. ↵
      Miga KH, Alexandrov IA. 2021. Variation and evolution of human centromeres: a field guide and perspective. Annu Rev Genet 55: 583–602. doi:10.1146/annurev-genet-071719-020519
      CrossRefMedlineGoogle Scholar
    20. ↵
      Miga KH, Koren S, Rhie A, Vollger MR, Gershman A, Bzikadze A, Brooks S, Howe E, Porubsky D, Logsdon GA, et al. 2020. Telomere-to-telomere assembly of a complete human X chromosome. Nature 585: 79–84. doi:10.1038/s41586-020-2547-7
      CrossRefMedlineGoogle Scholar
    21. ↵
      Nurk S, Koren S, Rhie A, Rautiainen M, Bzikadze AV, Mikheenko A, Vollger MR, Altemose N, Uralsky L, Gershman A, et al. 2022. The complete sequence of a human genome. Science 376: 44–53. doi:10.1126/science.abj6987
      CrossRefMedlineGoogle Scholar
    22. ↵
      Rhie A, Nurk S, Cechova M, Hoyt SJ, Taylor DJ, Altemose N, Hook PW, Koren S, Rautiainen M, Alexandrov IA, et al. 2023. The complete sequence of a human Y chromosome. Nature 621: 344–354. doi:10.1038/s41586-023-06457-y
      CrossRefMedlineGoogle Scholar
    23. ↵
      Schueler MG, Higgins AW, Rudd MK, Gustashaw K, Willard HF. 2001. Genomic and genetic definition of a functional human centromere. Science 294: 109–115. doi:10.1126/science.1065042
      Abstract/FREE Full Text
    24. ↵
      Shepelev VA, Alexandrov AA, Yurov YB, Alexandrov IA. 2009. The evolutionary origin of man can be traced in the layers of defunct ancestral alpha satellites flanking the active centromeres of human chromosomes. PLoS Genet 5: e1000641. doi:10.1371/journal.pgen.1000641
      CrossRefMedlineGoogle Scholar
    25. ↵
      Smith GP. 1976. Evolution of repeated DNA sequences by unequal crossover: DNA whose sequence is not maintained by selection will develop periodicities as a result of random crossover. Science 191: 528–535. doi:10.1126/science.1251186
      Abstract/FREE Full Text
    26. ↵
      Song JH, Lowe CB, Kingsley DM. 2018. Characterization of a human-specific tandem repeat associated with bipolar disorder and schizophrenia. Am J Hum Genet 103: 421–430. doi:10.1016/j.ajhg.2018.07.011
      CrossRefMedlineGoogle Scholar
    27. ↵
      Tian Q, Zhang P, Zhai Y, Wang Y, Zou Q. 2024. Application and comparison of machine learning and database-based methods in taxonomic classification of high-throughput sequencing data. Genome Biol Evol 16: evae102. doi:10.1093/gbe/evae102
      CrossRefMedlineGoogle Scholar
    28. ↵
      Zhang P, Liu H, Wei Y, Zhai Y, Tian Q, Zou Q. 2024. FMAlign2: a novel fast multiple nucleotide sequence alignment method for ultralong datasets. Bioinformatics 40: btae014. doi:10.1093/bioinformatics/btae014
      CrossRefMedlineGoogle Scholar
    29. ↵
      Zhou T, Zhang P, Zou Q, Han W. 2024. HAlign 4: a new strategy for rapidly aligning millions of sequences. Bioinformatics 40: btae718. doi:10.1093/bioinformatics/btae718
      CrossRefMedlineGoogle Scholar
    | Table of Contents

    This Article

    1. Published in Advance February 12, 2025, doi: 10.1101/gr.279763.124 Genome Res. 35: 1209-1218 © 2025 Zhang et al.; Published by Cold Spring Harbor Laboratory Press

    Article Category

    Share

    Preprint Server



    Navigate This Article

    Current Issue

    1. January 2026, 36 (1)
    1. Current Issue
    1. Alert me to new issues of Genome Research