Delineating yeast cleavage and polyadenylation signals using deep learning
Abstract
3′-end cleavage and polyadenylation is an essential process for eukaryotic mRNA maturation. In yeast species, the polyadenylation signals that recruit the processing machinery are degenerate and remain poorly characterized compared with the well-defined regulatory elements in mammals. Here we address this issue by developing deep learning models to deconvolute degenerate cis-regulatory elements and quantify their positional importance in mediating yeast poly(A) site formation, cleavage heterogeneity, and strength. In S. cerevisiae, cleavage heterogeneity is promoted by the depletion of U-rich elements around poly(A) sites as well as multiple occurrences of upstream UA-rich elements. Sites with high cleavage heterogeneity show overall lower strength. The site strength and tandem site distances modulate alternative polyadenylation (APA) under the diauxic stress. Finally, we develop a deep learning model to reveal the distinct motif configuration of S. pombe poly(A) sites, which show more precise cleavage than S. cerevisiae. Altogether, our deep learning models provide unprecedented insights into poly(A) site formation of yeast species, and our results highlight divergent poly(A) signals across distantly related species.
In eukaryotes, the 3′-ends of mRNAs are cotranscriptionally generated by a two-step catalytic process: endonucleolytic cleavage followed by poly(A) tail synthesis (Richard and Manley 2009). Cleavage and polyadenylation happens through the recruitment of processing factors to sequence motifs around poly(A) sites. Although poly(A) signals in mammals are well defined, the sequence composition of yeast poly(A) sites remains poorly understood despite some processing factors demonstrating homology across the species (Mandel et al. 2008; Tian and Graber 2012). In mammals, the essential motifs include the CPSF binding site (AAUAAA or close variants) typically located ∼20 nt upstream of the cleavage sites; the CSTF binding site (U/GU-rich motifs), ∼20 nt downstream. Additional motifs can play auxiliary regulatory roles. However, the poly(A) signals in Saccharomyces cerevisiae are highly degenerate and variable across genes.
Previous experimental and computational characterization of yeast poly(A) sites identified cis-elements promoting site formation: the UA-rich elements located 40 nt upstream (designated as the efficiency element) bound by the cleavage and polyadenylation factor 1B (CF1B), the A-rich motif 20 nt upstream (named as the positioning element) bound by CF1A, and the U-rich elements surrounding the cleavage site bound by the polyadenylation factor complex CPF (Guo and Sherman 1996; Graber et al. 1999a,b). The composition of the poly(A) site sequence itself can also influence cleavage site selection (Guo and Sherman 1996; Graber et al. 1999a,b; Dichtl and Keller 2001). However, some binding motifs (e.g., UA-rich and A-rich elements) can be highly degenerate (Guo and Sherman 1996). Currently, there are no quantitative comparisons of the relative importance of near-cognate poly(A) signals.
Recent advances in mapping 3′-ends of RNA isoforms in S. cerevisiae using deep sequencing showed that the cleavage heterogeneity is quite extensive for some mRNAs (Moqtaderi et al. 2013). A cleavage zone can span dozens of nucleotides in a yeast mRNA, which rarely happens for mammalian genes. It remains unknown if the polyadenylation events occurring across a cleavage zone represent poly(A) site microheterogeneity or the utilization of separate alternative poly(A) sites. Both heterogeneous cleavage and alternative polyadenylation (APA) can generate mRNAs with different 3′ UTRs, thereby regulating subcellular RNA localization, translation efficiency, and stability (Tian and Manley 2017; Gruber and Zavolan 2019; Mitschka and Mayr 2022). mRNA isoforms with only a few nucleotide differences in 3′-ends can show drastic variability in RNA secondary structure and stability (Geisberg et al. 2014; Moqtaderi et al. 2018). Extensive APA regulation occurs during the stress response (Graber et al. 2013; Geisberg et al. 2020, 2022). Studies have shown a compensatory link between RNA isoform generation and their transcript half-lives, which serves to regulate steady-state mRNA levels under stress conditions (Geisberg et al. 2023). Moreover, the poly(A) sites from another yeast species Schizosaccharomyces pombe show different sequence composition versus S. cerevisiae (Liu et al. 2017). Currently, the polyadenylation complexes in S. pombe remain uncharacterized. It remains an open question how the poly(A) sites are determined across yeast species, although experiments showed that 3′ UTRs are modular entities that can determine the cleavage and polyadenylation profiles independent of the coding sequences (Lui et al. 2022).
A challenge to characterizing yeast poly(A) signals is that conventional motif enrichment analysis is hardly applicable to deconvoluting the degenerate motifs and examining the signal differences among genes. The deep learning modeling is well suited to address this question. Specifically, convolutional recurrent neural networks can quantitatively capture dynamic interactions among cis-regulatory motifs and resolve the sequence complexity. Although a few models have been developed to study human poly(A) sites (Leung et al. 2018; Arefeen et al. 2019; Bogard et al. 2019; Vainberg Slutskin et al. 2019; Xia et al. 2019; Stroup and Ji 2023), they have not been applied to study yeast polyadenylation. Here, we aimed to develop deep learning models to characterize the motif grammar mediating polyadenylation site formation, strength, and cleavage profiles in S. cerevisiae, as well as to examine the differences in S. pombe.
Results
Developing a deep learning model to characterize poly(A) sites in S. cerevisiae
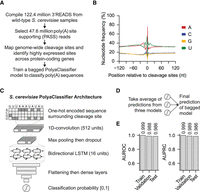
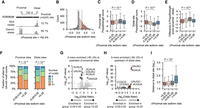
To identify genome-wide cleavage and polyadenylation sites in S. cerevisiae, we analyzed published 3′ region extraction and deep sequencing (3′READS) data (Supplemental Table S1; Hoque et al. 2013; Blair et al. 2016; Liu et al. 2017; Geisberg et al. 2020). After mapping the sequencing reads to reference genome and transcriptome, we selected 47.6 million poly(A) site supporting (PASS) reads with at least two nongenomic template As to map cleavage sites at the nucleotide resolution and quantify their expression (Fig. 1A). As extensive cleavage heterogeneity happens at the yeast 3′-ends (Moqtaderi et al. 2013), we used an iterative approach and selected 40,453 top-expressed cleavage sites across 5491 genes as representatives to develop the deep learning model (for details, see Methods). The nucleotide profiles of these sites correspond to the known features: overall enriched for A/U, with an A-rich peak located 10–30 nt upstream, and U-richness around the cleavage sites (Fig. 1B; Supplemental Fig. S1A).
Developing the S. cerevisiae PolyaClassifier model. (A) Overview of 3′READS data processing and the model training steps. (B) Distribution of nucleotide frequency surrounding the cleavage sites in S. cerevisiae. (C) Architecture of the S. cerevisiae PolyaClassifier model, which is described in more detail in Supplemental Table S2. (D) Schematic illustrating how the final bagged S. cerevisiae PolyaClassifier model predictions are calculated from the average predictions from three individual models trained on resampled data. (E) The AUROC and AUPRC values showing the classification performance of the PolyaClassifier constituent models on the training, testing, and validation sets. The AUROC and AUPRC values are shown.
We next sought to develop a deep neural network model, named PolyaClassifier, to classify the positive poly(A) sequences versus other nucleotides. The sequences surrounding the cleavage sites defined above were used as positive examples for the model training. Meanwhile, we used an equal number of random genome sequences or shuffled nucleotides as negative examples (for details, see Methods). The model takes the one-hot embedded sequences as input, includes one convolutional layer and one bidirectional long short-term memory (LSTM) layer to capture the motif interactions, and performs cleavage site classification (Fig. 1C).
Using a grid search, we optimized the hyperparameters for the PolyaClassifier model, including the lengths and number of input sequences for the model training, the numbers of dense layers and layer units, convolutional filter sizes, and dropout rate (for details, see Methods) (Supplemental Fig. S1B–H; Supplemental Table S2). In our final model, we used 500 nt sequences surrounding cleavage sites (–250–+250 nt) as the input. To account for many possible negative sequences, we used the bagging approach by taking the averaged predicted probabilities from three parallel trained models (Fig. 1D).
Our final model achieved high accuracy in classifying positive and negative sequences. The area under the receiver operating characteristic curve (AUROC) and the area under the precision-recall curve (AUPRC) for the holdout test data set were both 0.986 for the three constituent models included in the final bagged model (Fig. 1E). The bagging approach further improved the AUROC to 0.989 and AUPRC to 0.990 for the holdout test data (Supplemental Fig. S1I). The standard deviation of AUROC values for 10 randomly sampled positive and negative testing sets was 0.0005, indicating the robustness of our bagged model. The prediction accuracy of the model was also demonstrated by poly(A) sites defined by other 3′-end sequencing methods, including 3P-Seq (AUROC = 0.994 and AUPRC = 0.994) (Subtelny et al. 2014) and Helicos single-molecule sequencing (AUROC = 0.994 and AUPRC = 0.995) (Supplemental Fig. S1J; Ozsolak et al. 2010; Roy et al. 2016).
Identifying cis-regulatory motifs and their positional importance in S. cerevisiae poly(A) site formation
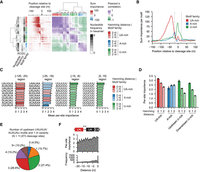
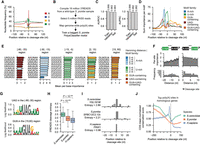
Leveraging the PolyaClassifier model, we used a hexamer disruption approach (Stroup and Ji 2023) to unbiasedly identify cis-regulatory motifs contributing to genome-wide poly(A) site formation. For a given poly(A) site sequence, we replaced each hexamer 100 times with random nucleotides and calculated the median log-odds changes (Δlog-odds) in the predicted classification probability. If a hexamer is important for the poly(A) site formation, we expect that its disruption would cause a decrease in predicted probability. We applied this approach to 11,673 well-expressed cleavage sites in S. cerevisiae (with 100 or more reads and usage level ≥5%). Then, we calculated the importance score for each hexamer as the sum(Δlog-odds) for each position from –250 to +250 nt around the cleavage sites. Using a scanning window, we identified motifs showing higher sum importance scores than expected and their position-specific importance (for details, see Methods) (Fig. 2A). Identified motifs belong to known families promoting poly(A) site formation in S. cerevisiae, including the UA-rich motifs (25–100 nt upstream), A-rich motifs (∼20 nt upstream), and U-rich motifs (around cleavage sites) (Fig. 2A,B; Supplemental Table S3). UA-rich motifs showed slightly higher per-site importance compared with A-rich and U-rich motifs (Fig. 2C; Supplemental Fig. S2A).
Identifying cis-regulatory elements mediating poly(A) site formation in S. cerevisiae. (A) Heatmaps showing the sum classification importance (left) and Pearson's correlation between motif importance profiles (right) for cis-regulatory elements significantly contributing to poly(A) site definition (N = 137). Each row represents a hexamer motif and is annotated with the nucleotide content and motif family. Motif families were defined by the Hamming distance between the hexamer and the archetypical motifs UAUAUA/AUAUAU (UA-rich), AAAAAA (A-rich), or UUUUUU (U-rich). (B) The per-motif sum classification importance profiles centered at the cleavage site for the cis-regulatory element families. Significant motifs with a Hamming distance ≤2 nt were included for each family (N = 40 UA-rich, 31 A-rich, and 51 U-rich motifs). (C) Bar plots showing the per-site importance score of the top 10 motifs in each region surrounding the cleavage site. Bars are colored by the family to which the motif belongs. Data are presented as the mean and the 95% confidence interval (error bar). (D) Bar plot summarizing the mean per-site importance for cis-regulatory elements grouped by their motif family and Hamming distance in their region of peak activity. UA-rich motifs occur in the [–120,–25] region (N = 2 for Hamming distance 0 nt, 29 for 1 nt, 9 for 2 nt), A-rich (N = 1 for Hamming distance 0 nt, 12 for 1 nt, 18 for 2 nt) in the [–5,–15] region, and U-rich in the [–15,–5] and [2,15] regions (N = 1 for Hamming distance 0 nt, 18 for 1 nt, 32 for 2 nt). Data are presented as the mean and the 95% confidence interval (error bar). (E) The fraction of poly(A) sites (100 or more PASS reads and 5% expression relative to the max site) with nonoverlapping upstream efficiency elements, indicated by the presence of AUAUAU/UAUAUA and 1 nt variants (N = 11,673 sites). (F) The per-site importance (top) and frequency (bottom) of upstream UA-rich motifs are grouped by the distance to the last UA-rich motif closest to the cleavage site. Only the two UA-rich motifs located closest to the cleavage sites were included in the analyses (N = 9306 sites). Data are presented as the mean and the 95% confidence interval (error bar).
Our model quantifies the relative importance of near-cognate motifs. The upstream UA-rich motifs representing the binding of CF1B showed the maximum per-site importance and occurrence at ∼40 nt upstream of the cleavage site (Fig. 2B; Supplemental Fig. S2A,B). The UA-rich motif can be quite degenerate, and motifs such as UAUAUA, AUAUAG, UAUGUA, UACGUA, AUAUAA, and UACAUA showed comparable per-site importance scores (Fig. 2C). The variants demonstrate similar location enrichments in the upstream regions (Supplemental Fig. S2A,C,D). Overall, the 1 nt variants of UAUAUA or AUAUAU showed an average of 14.8% lower importance, and the 2 nt variants averaged 28.6% lower scores (Fig. 2D).
The majority of poly(A) sites (79.7%) have multiple upstream UA-rich elements, with 27.4% containing two and 52.3% having three or more (Fig. 2E). Then, we examined the optimal distance between the two UA-rich elements closest to the cleavage site. We calculated the per-site importance of the upstream UA-rich element as a function of the distance to the downstream one. The upstream UA-rich elements showed higher importance when the two elements were located within 5 nt (Fig. 2F). It is possible that multiple UA-rich elements located close by can increase the efficiency of the CF1B complex binding.
The A-rich motifs located ∼20 nt upstream of the cleavage sites represent the binding sites of CF1A (Fig. 2B). Previous studies examined a few poly(A) sites and identified the representative motifs AAAAAA or AAUAAA (Mónica et al. 2011). Here based on our genome-wide analyses, UAAUAA, AAUAAU, AUAAUA, and UAUAAU show the highest per-site importance score in the region (Fig. 2C). In fact, the presence of one or two Us in AAAAAA increases the motif importance by 14.0% and 15.3%, respectively (Fig. 2D). Some motif variants, such as AUAUAA or UAAAUA, are likely to function as the binding sites of both CF1B (UA-rich variants) and CF1A (A-rich variants), considering the distribution of their occurrences and per-site importance scores (Supplemental Fig. S2B).
The U-rich elements bound by the CPF complex are located within 20 nt both upstream of and downstream from the cleavage site (Fig. 2A,B; Supplemental Fig. S2A). On average, 1 nt variants of UUUUUU decreased the per-site importance score by 27%, whereas 2 nt variants decreased the score by 49% (Fig. 2C,D). Altogether, we used the PolyaClassifier model to quantitatively reveal the relative importance of degenerate motifs in promoting S. cerevisiae poly(A) site formation.
Examining molecular mechanisms mediating the cleavage heterogeneity in S. cerevisiae
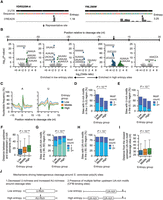
Poly(A) sites in S. cerevisiae show different levels of cleavage heterogeneity. Some sites show high cleavage heterogeneity spanning >30 nt, whereas for others, the cleavage sites are relatively precise (Fig. 3A; Supplemental Fig. S3A). We developed an entropy score to quantify the extent of cleavage heterogeneity of a poly(A) site. For each cleavage site region, we selected the representative site showing the highest number of PASS reads and measured the uniformness of the read distribution in the surrounding ±25 nt region (for details, see Methods). A higher entropy value indicates a higher number of unique 3′-ends generated during mRNA processing (Fig. 3A; Supplemental Fig. S3A).
Poly(A) site heterogeneity is driven by cleavage site composition and upstream efficiency elements. (A) Examples of the PASS read distribution surrounding a low entropy site (left) and a high entropy site (right). The entropy values are shown. (B) Motif enrichment analysis comparing the low (bottom 20%) versus high (top 20%) entropy poly(A) site groups. Five different poly(A) site regions were analyzed as indicated in the figure. The x-axis indicates the degree of enrichment as measured by log2(odds ratio). Positive values indicate enrichment in the high entropy sites, and negative values indicate enrichment in the low entropy sites. The y-axis shows the −log10(chi-squared test P-value) for the motifs enriched in the high entropy group and log10(chi-squared test P-value) for ones enriched in the low entropy sites. (C) The nucleotide distribution flanking the maximum cleavage sites showing the fraction of As (left) and Us (right). (D) The fraction of sites in each entropy group containing one or more U-rich motifs in the [–15,0] region immediately upstream of the maximum cleavage site. U-rich motifs with up to 2 nt mismatches from UUUUUU were included. The P-value from the chi-squared test for independence across entropy groups is shown. (E) Similar to D, except showing the analyses in the [0,15] region immediately downstream from the maximum cleavage site. (F) Box plots showing the distance between the closest upstream and downstream flanking U-rich elements. The P-value is the result of a Wilcoxon rank-sum test comparing the low versus high group. (G) The fraction of sites in each entropy group containing one or more UA-rich motifs in the [–90,–50] region upstream of the maximum cleavage site. UA-rich motifs with up to 2 nt mismatches from AUAUAU or UAUAUA were included. The P-value from the chi-squared test for independence across entropy groups is shown. (H) Similar to G, except showing the fraction of sites with UA-rich motifs in the [–50,–30] region upstream of the maximum cleavage site. (I) Box plots showing the distance from the closest UA-rich motif in the [–90,–30] region to the cleavage site. (J) Schematic depicting the mechanisms identified from this analysis that may lead to heterogeneous cleavage in S. cerevisiae.
We performed cis-element enrichment analyses comparing poly(A) site sequences showing high versus low cleavage heterogeneity (comparing the sites with top 20% vs. low 20% entropy scores) (Fig. 3B). The most significant difference was found in the –15–+15 nt region around the poly(A) sites. Although the precise cleavage sites showed enrichment of U-rich elements (e.g., UUUUUU, UUCUUU, and UCUUUU) in the region (chi-squared test P-value < 10−50), the highly heterogeneous sites were enriched with AU-rich elements (e.g., AUAAUA, UAAUAA, AAAAAU, and AAUAAU; chi-squared test P-value < 10−15) (Fig. 3B). Considering the frequency of individual nucleotides, the highly heterogeneous cleavage sites show lower U-richness and higher A-richness in the sequence surrounding the maximum cleavage site (Fig. 3C; Supplemental Fig. S3B–D). Next, we examined the occurrence of U-rich hexamers (binding sites of the CPF complex). High heterogeneity sites are less likely to have U-rich hexamers flanking the cleavage site versus the low heterogeneity group (Δfraction of sites = 31.2% upstream and 20.6% downstream) (Fig. 3D,E). Some sites in the high heterogeneity group have both upstream and downstream U-rich elements, but the two elements tend to be located farther apart than in the low heterogeneity group (Fig. 3F). Altogether, the data indicated that poly(A) sites showing high heterogeneous cleavage are devoid of U-rich elements around cleavage sites, which can lead to the weaker binding of the CPF complex.
Another major difference between high and low heterogeneity cleavage sites was the frequency of UA-rich elements located 30–90 nt upstream (the binding sites of CF1B). The motif enrichment analyses showed the UA-rich motifs occur more frequently in the upstream 50 to 90 nt region but are found with lower frequency in the 30 to 50 nt region in the high heterogeneity sites (Fig. 3B,G,H). Considering the closest upstream UA-rich element, these motifs were farther away from the cleavage site in the high heterogeneity group (Fig. 3I). Taken together, our above analyses showed that the heterogeneous cleavage sites in S. cerevisiae tend to be depleted of U-rich elements around the cleavage site and have a higher occurrence of farther upstream UA-rich motifs (Fig. 3J).
Developing a deep learning model named PolyaCleavage to capture the cleavage heterogeneity of poly(A) sites based on primary sequences
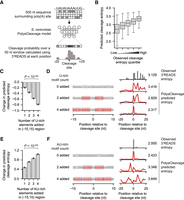
We reasoned that if the poly(A) site sequences determine the extent of cleavage heterogeneity, we should be able to capture that regulation by deep learning modeling. To this end, using the 500 nt sequences centered at the maximum cleavage sites as the input, we developed another deep learning model, named PolyaCleavage, to predict the cleavage probability distribution in the middle 50 nt region (for details, see Methods) (Fig. 4A; for the model architecture, see Supplemental Table S2). The optimal model parameters were selected using a grid search with fivefold cross-validation (Supplemental Fig. S4A). To evaluate the performance of our algorithm, we calculated the entropy values measuring the cleavage heterogeneity based on the PolyaCleavage prediction. The predicted entropy values were correlated with those calculated using the observed 3′READS data (Pearson correlation coefficient = 0.593 for the holdout testing set) (Fig. 4B; Supplemental Fig. S4B). Additionally, the weighted mean cleavage positions were well correlated between the prediction and observed values (Pearson correlation coefficient = 0.763 for the testing set) (Supplemental Fig. S4C). The performance of our PolyaCleavage model also generalized to other 3′-end sequencing data types, such as 3P-Seq and Helicos single-molecule sequencing (Supplemental Fig. S4D,E). These data indicated that our PolyaCleavage model quantitatively captured the cleavage heterogeneity based on the primary sequences.
Cleavage heterogeneity can be modulated by changing the poly(A) site surrounding cis-regulatory elements. (A) Workflow describing our design of the S. cerevisiae PolyaCleavage model. (B) Box plots showing the increase in predicted cleavage entropy as the observed cleavage entropy measured by 3′READS increases. Cleavage sites from the holdout testing set were split into five evenly sized groups (N ∼ 809 sites per group). (C) The change in predicted cleavage entropy as nonoverlapping U-rich elements are sequentially introduced in the [–15,+15] region surrounding the maximum cleavage site. The data are presented as the mean and the 95% confidence interval (error bar). The P-value from the Wilcoxon signed-rank paired test comparing the addition of one U-rich element to four U-rich elements is shown. Consensus high entropy sites with flanking UA-rich motifs and no surrounding U-rich elements were included (N = 182 actual cleavage sites, 29,056 altered sequences). (D) An example showing the effect of introducing U-rich elements around the cleavage site in a high entropy cleavage site from YIL156W-B. The predicted entropy values are shown. (E) The change in predicted cleavage entropy as nonoverlapping AU-rich elements are sequentially introduced in the [–15,+15] region immediately surrounding the maximum cleavage site. The data are presented as the mean and the 95% confidence interval (error bar). The P-value from the Wilcoxon signed-rank paired test comparing the addition of one AU-rich element to four AU-rich elements is shown. Consensus low entropy sites with flanking U-rich motifs were included (N = 222 actual cleavage sites, 35,012 altered sequences). (F) Similar to D, showing the effect of introducing AU-rich elements around the cleavage site in a low entropy poly(A) site from YPR154W.
Next, we leveraged the PolyaCleavage model to study the genomic parameters we identified above in regulating cleavage heterogeneity. We first examined the roles of U-rich motifs around the cleavage sites. Adding U-rich motifs to the ±15 nt region around highly heterogeneous poly(A) sites induced more precise cleavage as predicted by the PolyaCleavage model (Fig. 4C,D; Supplemental Fig. S4F). On the other hand, introducing AU-rich elements around the sites was predicted to increase cleavage heterogeneity (Fig. 4E,F; Supplemental Fig. S4G). The predicted change in entropy was correlated with the number of U-rich or AU-rich elements introduced. We also examined the effects of upstream CF1B binding sites by reducing the number of UA-rich elements in –90 nt to –30 nt regions. We observed more precise cleavage as we reduced the number of upstream UA-rich elements (Supplemental Fig. S4H,I). Altogether, by developing the PolyaCleavage model, we showed that the sequence surrounding poly(A) sites determines the degree of cleavage heterogeneity in S. cerevisiae and confirmed the regulatory roles of identified factors.
Developing a deep learning model named PolyaStrength to quantify S. cerevisiae poly(A) site strength
To quantify the poly(A) site expression levels, we used an iterative approach and grouped nearby cleavage sites (within 20 nt) into clusters to account for cleavage microheterogeneity (for details, see Methods) (Supplemental Table S4). We used the 20 nt window because we showed that an A-rich motif located 20 nt upstream was important for downstream polyadenylation (Fig. 2B). The expression level of a poly(A) site (defined by the cluster boundaries) was calculated using the summed PASS read count in the cluster region. For genes with multiple poly(A) sites in the 3′ UTR, we calculated the relative isoform abundance of each site as the ratio between the number of supporting PASS reads versus the sum of reads supporting the top two expressed sites.
A major regulator of poly(A) site isoform abundance ratio is the efficiency of cis-regulatory elements in recruiting the polyadenylation factors. Next, we developed a deep learning model, named PolyaStrength, using the 500 nt sequences centered at the maximum cleavage sites as the input to predict the site isoform ratios on the log-odds scale (Fig. 5A). A grid search and fivefold cross-validation were used to obtain the optimal model parameters (for details, see Methods) (Supplemental Fig. S5A–D; for the model architecture, see Supplemental Table S2).
Development of the S. cerevisiae PolyaStrength model. (A) Diagram depicting how the S. cerevisiae PolyaStrength model was trained on the relative isoform abundance for APA sites in the 3′ UTR. (B) Box plot showing the predicted PolyaStrength scores grouped by observed site isoform abundance (N = 2392 sites with usage <0.2, 798 with usage 0.2–0.5, 584 with usage 0.5–0.8, and 375 with usage >0.8). (C) The AUROC and AUPRC values showing the performance of the S. cerevisiae PolyaStrength model to distinguish lowly versus highly used 3′-UTR-APA sites (more than eightfold) from the training, validation, and testing sets. The mean and standard deviation (error bar) from 10 sets of sampled poly(A) site pairs are shown for each data split, with the mean noted above each bar. (D) The per-motif sum importance scores around the max cleavage sites for indicated cis-regulatory element families. Significant motifs with a Hamming distance ≤2 nt from the archetypical motifs UAUAUA/AUAUAU, AAAAAA, and UUUUUU were included. (E) Scatter plot showing the correlation between the motif importance scores for the S. cerevisiae PolyaClassifier and PolyaStrength models. The peak sum importance score in any 20 nt window is used, and the Pearson's correlation is shown. The important poly(A) motifs are colored. (F) The predicted PolyaStrength scores for poly(A) site types based on their relative position. The P-value from the Wilcoxon rank-sum test comparing the first versus last 3′-UTR-APA sites is shown. (G) The observed isoform ratios of coding region and 3′-UTR-APA sites. For details about how the isoform ratio is calculated, see Methods. The P-value from the Wilcoxon rank-sum test comparing first versus last 3′-UTR-APA sites is shown. Single 3′-UTR sites are not included. (H) The predicted PolyaStrength scores for low, middle, and high entropy poly(A) sites from Figure 3. The P-value using the Wilcoxon rank-sum test comparing the low versus high entropy groups is shown.
Our PolyaStrength score is correlated with 3′-UTR poly(A) site isoform ratios (Fig. 5B) and effectively classified the highly versus lowly used paired poly(A) sites from a gene (more than eightfold expression level differences) with the AUROC and AUPRC values >0.94 for the training, validation, and testing sets (Fig. 5C). The model performance was also confirmed by data from 3P-Seq and Helicos single-molecule sequencing with AUROC and AUPRC values >0.90 for classifying paired sites (Supplemental Fig. S5E,F). A previous study used the massively parallel reporter assay (MPRA) and introduced 590,024 random 3′-UTR sequences to a reporter gene (Supplemental Fig. S5G; Savinov et al. 2021). Polyadenylation activity is a major regulator of the reporter gene expression. Our PolyaStrength scores are correlated with reporter expression levels and can classify the top 5% expressed (29,502 sequences) versus the bottom 5% (29,529 sequences) with an AUROC = 0.83 (Supplemental Fig. S5H,I).
Using the PolyaStrength model, we used the hexamer disruption approach as described above to identify cis-regulatory elements contributing to site strength. Similar motifs were identified compared with those from the PolyaClassifier model, including the UA-rich elements (∼30–90 nt upstream), A-rich elements (∼20 nt upstream), and U-rich elements around the cleavage site (Fig. 5D; Supplemental Table S5). The motif importance scores were highly correlated between the PolyaStrength and PolyaClassifer models, indicating that similar motifs promote poly(A) site formation and strength (Fig. 5E).
We grouped the poly(A) sites based on their relative genomic locations in 3′ UTRs: single sites in non-APA genes, as well as first, middle, or last sites in APA genes (Supplemental Table S4). The single poly(A) sites were stronger than other types, and the first poly(A) sites were generally stronger and showed higher usage levels than other APA sites (Fig. 5F,G). The sites located in coding regions tended to be weaker and have lower usage levels than those in 3′ UTRs (Fig. 5F,G). Poly(A) sites showing high cleavage heterogeneity were also weaker than those with precise cleavage (Fig. 5H).
The poly(A) site strengths and tandem site distances contribute to the APA regulation during diauxic stress
Next, we examined APA regulation under diauxic stress. A previous study showed a global increase in proximal site usage under stress conditions owing to slower elongation of RNA polymerase II (Fig. 6A; Geisberg et al. 2020). However, this global regulation pattern does not apply to every gene, and the proximal sites of different genes showed variable degrees of isoform ratio changes; 32.1% of genes showed >25% of isoform expression shifted toward the upstream proximal site, 20.6% of genes had isoform changes <5%, and 8.5% showed the opposite regulation with a decrease in proximal site isoform expression >5% (Fig. 6A,B; Supplemental Fig. S6A,B). The underlying reasons remain uncharacterized.
APA regulation under diauxic stress in S. cerevisiae. (A) An example gene YGR060W shows increased usage of proximal poly(A) site under diauxic stress. The proximal and distal poly(A) site clusters are shown above in gray with the maximum cleavage site in each cluster marked with a black line. The distance between representative sites is noted. The proximal poly(A) site isoform abundance ratios in different conditions are shown. (B) The distribution of delta isoform ratios for proximal sites showing different usage under diauxic stress compared with rich media conditions (N = 2976). The vertical dashed lines show the groups of differentially used sites based on their isoform ratio changes. (C) The PolyaStrength scores of the proximal sites grouped by the Δisoform abundance ratios. The P-value from the Wilcoxon rank-sum test comparing the group with a high proximal site shift (Δratio > 0.25) and low Δratio group (–0.05 to 0.05) is shown. (D) Similar to C, except showing the PolyaStrength scores of the paired distal sites. (E) Similar to C, except showing the PolyaStrength score differences between the paired proximal and distal sites. (F) Stacked bar chart showing the number of UA-rich elements present in the [–90,–25] region upstream of proximal (left) and distal (right) sites grouped by Δproximal site isoform ratio. The P-values from the chi-squared test for independence are shown. (G,H) Motif enrichment analysis comparing poly(A) sites in the low Δratio group (–0.05 to 0.05) versus high Δratio group (>0.25). We examined the region [–90,–25] nt upstream of proximal (G) and distal (H) sites. The x-axis indicates the degree of enrichment as measured by log2(odds ratio). Positive values indicate enrichment in the high Δratio group, and negative values indicate enrichment in the low Δratio group. The y-axis shows the −log10(chi-squared test P-value) for the motifs enriched in the high Δratio group and log10(chi-squared test P-value) for ones enriched in the low Δratio group. (I) Similar to C, except showing the distance between the paired proximal and distal sites.
We grouped the poly(A) sites based on their changes in isoform abundance ratios (Fig. 6B) and observed a correlation between site strength and APA regulation. The proximal poly(A) sites that showed higher isoform abundance increase under diauxic stress were weaker considering their absolute and relative strengths to the distal sites (Fig. 6C–E). The motif enrichment analyses showed that these weaker poly(A) sites tend to have fewer upstream UA-rich motifs (Fig. 6F–H) but no significant differences in the frequency of A-rich or U-rich motifs (Supplemental Fig. S6C,D). For the minor fraction of proximal sites showing decreased usage, they were weaker and located further away from the corresponding distal sites (Fig. 6C–E,I). Altogether, we developed the PolyaStrength model to quantify poly(A) site strength, which can be useful for dissecting the molecular mechanisms underlying APA regulation during biological processes.
Examining the motif composition of poly(A) sites in S. pombe using deep learning
S. pombe is another commonly used yeast model species. Unlike S. cerevisiae, the configuration of the polyadenylation machinery in S. pombe remains mostly uncharacterized. Previous 3′READS profiling and analyses showed that nucleotide profiles surrounding S. pombe poly(A) sites differ from S. cerevisiae and mammals (Liu et al. 2017). Overall, the poly(A) region is highly AU-rich, with an A-rich peak located at 20 nt upstream and U-richness around the cleavage sites and >30 nt upstream (Fig. 7A; Supplemental Fig. S7A; Supplemental Table S6). Using a similar approach to our analysis of S. cerevisiae, we built a PolyaClassifer model to distinguish S. pombe poly(A) sequences versus negative sequences (Fig. 7B; Supplemental Fig. S7B–H). Our S. pombe model classified the sites with high accuracy, with AUROC and AUPRC values ≥0.98 for the training, validation, and testing sets for the three constituent models (Fig. 7C). The final bagged model achieved an AUROC = 0.988 and AUPRC = 0.989.
The S. pombe PolyaClassifier model reveals divergent motifs mediating poly(A) site definition. (A) Distribution of nucleotide frequency surrounding the representative cleavage sites in S. pombe. (B) Overview of the data processing workflow to train the S. pombe PolyaClassifier model. (C) The AUROC and AUPRC values showing the constituent model performance for the training, validation, and testing sets. (D) The per-motif sum classification importance profiles centered at the maximum cleavage site (N = 63 A-rich, 87 U-rich, 23 GUA-containing, 19 UAG-containing, and 11 GUA + UAG-containing motifs). (E) Bar plots showing the per-site importance of the top 10 motifs in each region surrounding the maximum cleavage site. Bars are colored by the family to which the motif belongs. Data are presented as the mean and the 95% confidence interval (error bar). Only motifs present in ≥1% of well-expressed sites used in the analysis were included. (F) The per-site importance (top) and frequency (bottom) for U-rich motifs grouped by their distance upstream of (left) or downstream from (right) the A-rich motif. Data are presented as the mean and the 95% confidence interval (error bar). (G) The position-weight matrices showing the log-likelihood of the importance of nucleotides surrounding UAG and GUA 3-mers. For the detailed calculation, see Methods. (H) The distribution of 3′READS cleavage entropy values for the top poly(A) site in each gene homologous across S. cerevisiae, S. pombe, and H. sapiens (N = 3296, 2720, and 3777, respectively). The P-values from the Wilcoxon rank-sum tests comparing S. cerevisiae to S. pombe and H. sapiens are shown. (I) An example of the PASS read distribution ±25 nt surrounding the top-expressed poly(A) site in homologous genes: S. cerevisiae gene YGL191W, S. pombe gene SPBC12C2.12c, and H. sapiens gene PINX1. The cleavage entropy value calculated from the 3′READS for each species is shown. (J) A metaplot showing the conservation score for the [–250,150] nt surrounding the top-expressed poly(A) site in all homologous genes across the three species. The conservation score was normalized to the mean score in coding regions. The data are shown as the mean with the shaded region indicating the 95% confidence interval.
The hexamer disruption analyses revealed the motifs that contributed to poly(A) site formation, including the A-rich motifs located –20 nt upstream, U-rich motifs surrounding the cleavage sites, UAG-containing motifs –80 to –30 nt upstream, and GUA-containing motifs +15–+60 nt downstream (Fig. 7D,E; Supplemental Fig. S7I,J; Supplemental Table S7). The upstream A-rich motifs can be quite degenerate, and the ones with the highest importance tend to contain Us, such as AAUAAA, UUAAUA, UAAUAU, and AUUAAU (Fig. 7E). Considering the per-site importance, the top A-rich motifs showed an overall approximately twofold higher scores than other elements (Fig. 7E). The U-rich motifs were found across a broad region from upstream of to 20 nt downstream from the cleavage sites (Fig. 7D; Supplemental Fig. S7J). When we group upstream U-rich motifs by their distance to the anchoring A-rich motif, the U-rich motifs showed maximum importance when they were immediately downstream from the A-rich motif (<6 nt) (Fig. 7F). The UAG-containing motifs were most important in the context of upstream “U(G/U)(U/A)” and downstream Us, whereas GUA-containing motifs were more important in the context of upstream Us and a downstream G/A (Fig. 7G). Our results revealed the motif configuration of S. pombe poly(A) sites, which is distinct from S. cerevisiae.
Using our entropy calculation method, we quantified the cleavage heterogeneity of S. pombe poly(A) sites. Overall, the cleavage heterogeneity was much lower than in S. cerevisiae and we did not observe large cleavage “zones,” although the overall heterogeneity was larger than in homologous human genes (Fig. 7H,I; Supplemental Fig. S8A). Next, we examined the evolution of poly(A) site sequences across model species using the phastCons conservation scores calculated based on multiple genome alignments (Siepel et al. 2005; Rhind et al. 2011). We examined the conservation of S. pombe poly(A) sequences using the alignments across four Schizosaccharomyces yeasts, the conservation of S. cerevisiae sites across seven Saccharomyces yeasts, and the human site conservation across 100 vertebrates. For all species, the conservation scores were normalized to the mean conservation of coding regions. For human poly(A) sites, we observed high sequence conservation upstream of the cleavage site, which peaked at the PAS region (overall conservation level is nearly comparable to coding regions) (Fig. 7J; Supplemental Fig. S8B,C). However, the poly(A) regions show much lower conservation levels in S. cerevisiae (∼50% of coding regions) and S. pombe (∼35% of coding regions) (Fig. 7J; Supplemental Fig. S8B,C).
For S. cerevisiae, we observed a modest conservation peak around the upstream 40 nt region (Fig. 7J; Supplemental Fig. S8B,C). The motifs contributing to poly(A) formation (UA-rich, A-rich, and U-rich elements defined in Fig. 2) show higher conservation rates than other motifs in the region (Supplemental Fig. S8D). We further analyzed the genetic variants across 1011 S. cerevisiae isolates (Peter et al. 2018). Using the ±1 kb region around poly(A) sites as the background, the UA-rich motifs (–90 to −25 nt upstream of poly(A) sites) were depleted of disruptive variants (Supplemental Fig. S8E). However, the trend was not significant for A-rich and U-rich motifs, suggesting that mutations in these motifs can be tolerated (Supplemental Fig. S8E). For S. pombe, the conservation levels gradually decreased toward the poly(A) sites, and the signal motifs did not show higher conservation than others (Supplemental Fig. S8F). The general low conservation levels of poly(A) sequences across yeast species can be partly owing to the degenerate nature of the regulatory motifs but also indicated that their poly(A) regions are under positive selection.
Discussion
The yeast species have been valuable model systems to dissect basic molecular mechanisms mediating steps of gene expression. Although the transcription initiation and elongation have been well characterized using these model organisms, the regulation of cleavage and polyadenylation has been understudied. Only recently, studies used deep sequencing approaches to map genome-wide poly(A) sites and examine the functional roles of different 3′-end RNA isoforms in S. cerevisiae. An unexpected finding was the extensive heterogeneous cleavage for some mRNA genes. Although the conventional model showed important motifs contributing to poly(A) site formation, it is not sufficient to explain the cleavage heterogeneity and signal differences among genes. It has been puzzling how the 3′-ends of mRNAs are determined in S. cerevisiae. Here, we developed the first deep learning models to examine the motif grammars mediating poly(A) site formation, heterogeneity, and strength in S. cerevisiae.
Previous molecular experiments of several poly(A) sites indicated that the cis-regulatory elements mediating S. cerevisiae polyadenylation can be quite degenerate. However, no study has been carried out to systematically examine the relative importance of signal variants. Our deep learning models PolyaClassifer and PolyaStrength provided unprecedented insights into the degenerate nature of the cis-regulatory motifs in S. cerevisiae. Using a hexamer disruption approach, we unbiasedly identified the positional importance of motifs mediating S. cerevisiae poly(A) site formation and strength. The significant motifs belong to the previously defined families: the CF1B binding sites (the upstream UA-rich elements), the CF1A binding sites (A-rich motifs), and the CPF binding sites (the U-rich elements around cleavage sites).
Our analyses provided quantitative measurements of the near-cognate motif strengths. For the CF1B binding site, replacing 1 nt of the consensus motif UAUAUA or AUAUAU sometimes does not change their strengths. An unexpected finding is that most poly(A) sites contain multiple upstream UA-rich elements, suggesting that the CF1B complex or some subunit protein(s) could form dimers like the mammalian CstF complex. And for the CF1A binding, adding one or two Us in AAAAAA does not change the motif strength and sometimes can even make the motif stronger. The location of the A-rich element is like the PAS motif in mammals (AAUAAA or variants), which is 20 nt upstream of the poly(A) site. However, the CF1A binding site can be much more degenerate than mammalian PAS, in which AAUAAA is much stronger than other variants. This degenerate nature of motifs in S. cerevisiae can create many possible poly(A) site combinations.
We used an entropy score to quantify the cleavage heterogeneity of poly(A) sites. Our comparative analyses revealed sequence differences between sites showing high versus low cleavage heterogeneity. First, the depletion of U-rich elements and enrichment of AU-rich motifs surrounding poly(A) sites promoted heterogeneous cleavage. This could reduce the binding affinity of the CPF complex. A previous study showed that the C-terminal domain of Yth1p tethers Fip1p and poly(A) polymerase to the U-rich elements (Barabino et al. 2000). A possible model is that for the high heterogeneity cleavage sites, the upstream binding sites of CF1A and CF1B are sufficient to recruit the cleavage and polyadenylation machinery, including the CPF complex. However, CPF binding is not stable because of the lack of U-rich elements, causing cleavage to occur across multiple sites. In fact, previous experiments showed that the required polyadenylation signals in S. cerevisiae include only the CF1A and CF1B binding sites and the poly(A) sequence itself (i.e., AU-rich sequence at the cleavage site) (Guo and Sherman 1996). Later studies showed that the U-rich elements flanking poly(A) sites are bound by the CPF complex and enhance the polyadenylation activities (Dichtl and Keller 2001). These experimental results are in line with our findings. Second, the increased numbers of CF1B binding sites (upstream UA-rich elements) can lead to different conformation positions of the polyadenylation machinery and increased cleavage heterogeneity downstream.
By developing the PolyaCleavage model, we confirmed that the primary poly(A) sequences encode the cleavage heterogeneity. We could capture the dynamic changes of cleavage heterogeneity by mutating key motifs. Adding U-rich motifs surrounding poly(A) sites led to more precise cleavage, whereas adding AU-rich motifs increased heterogeneity. We also confirmed the effects of the number of upstream CF1B binding sites. These mechanisms, in combination with the degenerate nature of yeast cis-elements, drive the high number of cleavage and polyadenylation sites utilized in S. cerevisiae genes.
We also developed a PolyaStrength model to measure the poly(A) site strength, which is determined by similar motifs as described above for site formation. The single poly(A) sites showed the highest strength. For APA genes, the proximal poly(A) site tends to be stronger than the downstream ones. This differs from mammalian genes, in which the distal poly(A) sites are generally stronger (Hoque et al. 2013; Wang et al. 2018). The finding emphasizes the species-specific regulation of poly(A) site distribution across the genome. The sites showing highly heterogeneous cleavage tend to be weaker, which is in line with that they are generally depleted of U-rich motifs around the poly(A) site. Our PolyaStrength model is useful for future studies of APA regulation during biological processes. Here, we showed that under diauxic stress, the differential usage levels of poly(A) sites are correlated with the site strength, especially the occurrence of upstream UA-rich motifs, and tandem site distances.
We examined the poly(A) site composition in S. pombe. For both S. pombe and S. cerevisiae, their poly(A) sites contain degenerate A-rich motifs located at 20 nt upstream, as well as the U-rich motifs surrounding the cleavage sites. However, the S. cerevisiae sites use unique upstream UA-rich motifs, whereas the S. pombe sites contain upstream UAG-containing and downstream GUA-containing motifs. The GUA motif in S. pombe was suggested to be the binding site of Seb1 (Lemay et al. 2016). In S. pombe, the A-rich motifs located 20 nt upstream show higher importance scores than other motifs, whereas in S. cerevisiae, the farther upstream UA-rich motifs are more important than others. For the cleavage patterns, S. pombe sites more resemble mammalian sites. The cleavage activity is more precise than in S. cerevisiae, and we rarely observe a large heterogeneous cleavage zone. These results highlighted the unique configuration of cleavage and polyadenylation complexes in S. pombe, and their associated trans-factors remain to be characterized.
Our study emphasizes the power of the deep learning approach to study the motif grammar mediating 3′-end cleavage and polyadenylation. To further illustrate this, we applied our method and characterized the poly(A) signals of Arabidopsis thaliana by analyzing the 3′READS data (Supplemental Fig. S9A–D; Supplemental Tables S1, S8; Guillermina Kubaczka et al. 2024). The contributing signals include the UGUA motifs located at –150 to –30 upstream of poly(A) sites, the degenerate A-rich motifs around –20 nt, and the U-rich motifs located upstream of cleavage sites and 20 nt downstream (Supplemental Fig. S9E–G; Supplemental Table S9). The site configuration is distinct from those of S. cerevisiae, S. pombe, and humans (Supplemental Fig. S9H,I). These results demonstrated the poly(A) signal differences among animal, fungi, and plant species. It will be interesting to examine the poly(A) signals across more model species from these kingdoms, which will reveal the basic evolutionary principles driving the 3′-end formation of RNAs.
Methods
Identifying genomic poly(A) sites from 3′READS data
We used 3′READS data to comprehensively identify poly(A) sites across the S. cerevisiae and S. pombe genomes (Hoque et al. 2013; Blair et al. 2016; Liu et al. 2017; Geisberg et al. 2020). We compiled data from seven S. cerevisiae samples and one S. pombe sample for wild-type yeast cultured under rich media conditions (Supplemental Table S1). We analyzed the 3′READS data as follows. The leading Ts were trimmed from each read, and we logged the number of Ts for downstream use. The trimmed reads were aligned to the transcriptome and then the genome using TopHat2 (v2.1.0) (Kim et al. 2013). For S. cerevisiae, we used the Ensembl reference genome version R64-1-1 and the gene annotation curated by the Struhl laboratory. For S. pombe, we used the Ensembl reference genome assembly ASM294v2 and the corresponding gene annotation from release 53.
The uniquely mapped reads with two or more nongenomic As named the PASS reads were used for the downstream analyses identifying poly(A) sites. Our last alignment site is located at a non-A position. However, cleavage tends to happen in A-rich regions (Dichtl and Keller 2001). For some sites, there are genomic As after the non-A site, and we cannot distinguish where the cleavage happens among the positions. We evenly distributed the PASS reads from the first non-A to the last As. To assign cleavage sites to their respective genes, we extended 3′-ends of annotated genes up to 500 nt or until the transcription start site of the downstream gene on the same strand without overlap.
Developing the PolyaClassifier model to classify poly(A) site sequences in S. cerevisiae and S. pombe
Input data set
To train the model, we identified high-confidence cleavage sites. For S. cerevisiae, we required that a cleavage site be supported by 10 or more PASS reads and ≥2% of reads from the maximum expressed site of a gene. We had much fewer reads for S. pombe and required that a cleavage site should contain five or more PASS reads. In total, we identified 161,080 individual cleavage sites in S. cerevisiae and 42,192 in S. pombe. We used an iterative approach to sample a subset of cleavage sites as representatives to train the model. We first sampled the highest expressed cleavage site from each gene. Next, we selected the positive sites located ≥5 nt away from the previously sampled sites and picked the next highest expressed site. Using this iterative method, we sampled 40,453 representative cleavage sites in S. cerevisiae and 12,678 sites in S. pombe. The sequences around these cleavage sites were used as positives to train the model. The negative sequences included the random genome sequences without PASS reads in the middle 50 nt regions, as well as shuffled transcript sequences keeping the single-nucleotide content the same. Details of the analysis of A. thaliana poly(A) sites are included in the Supplemental Methods.
For the model training, we tried different lengths of sequences around poly(A) sites and finally picked 500 nt as the input because longer sequences did not enhance model performance (for further information, see Supplemental Methods). Each sequence was one-hot-encoded to a 4 × 500 matrix in which the rows represent the nucleotides A, C, G, and U and the columns represent the position along the sequence. At each position, the row corresponding to the nucleotide present in the genomic sequence is marked with a one, and all others are marked with a zero. This numerical encoding was fed into the model as input, paired with the binary classification label of one if the site was positive and zero if it was negative.
General model architecture and training schema
The PolyaClassifier model is constructed using a 1D convolutional layer followed by max pooling and dropout layers. It then contains a bidirectional LSTM layer followed by a dropout layer. The output of these layers is then flattened and fed into a series of dense layers. The final dense layer uses a sigmoid activation to predict the classification probability of each site. The 1D convolutional layer used a species-specific filter size and a stride of one. This combination of layers extracts informative sequence motifs and their spatial position within the sequence.
We partitioned the input data sets (positive and negative sequences) into 80% training, 10% validation, and 10% holdout testing
sets. The positive sequences were split at the gene level so that all sites associated with the same gene were kept together
during splitting. We then trained the PolyaClassifier models using a batch size of 100 with an initial learning rate of 0.001
and the Adam optimizer with Nesterov momentum. After five epochs, we used a decaying learning rate, in which the learning
rate was reduced by a factor of e–0.1 after each subsequent training epoch. The model was trained to minimize the binary-cross entropy loss function, implemented
out-of-box in TensorFlow2:
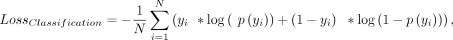where yi is the classification label for the sequence i (one for positive site and zero for negative sequence), and p(yi) is the predicted probability of a sequence i being a positive poly(A) site. After each training epoch, the loss and accuracy were tracked for the training and validation
splits. Model training was stopped after reaching a minimum loss for the validation data.
Performance evaluation
To evaluate the performance of a PolyaClassifier model, we calculated the AUROC and AUPRC for the training, validation, and holdout test set using the Python library scikit-learn. We validated the performance of our deep learning models using non-3′READS data from 3P-Seq, Helicos single-molecule sequencing, and a MPRA, which is described in the Supplemental Methods.
Parameter grid search and model selection
We used a grid search to identify optimal model parameters. Parameters such as the input sequence lengths, the dense layer kernel initializer, the number and shape of dense layers, the number of convolutional and LSTM units, the shape of convolutional filters, and the dropout rate were varied one at a time, whereas all other parameters were held constant. As many possible negative poly(A) sequences exist in the genome, the bagging approach was used to ensure the robust performance of our algorithm. The details are described in the Supplemental Methods, and the final model architecture is shown in Figure 1, C and D, and described in Supplemental Table S2.
Characterizing cis-regulatory elements modulating poly(A) site formation
We used a systematic hexamer disruption approach to identify the cis-regulatory elements that contribute to the PolyaClassifier predictions and therefore are important in defining poly(A) sites. We replaced each hexamer in the sequence surrounding a poly(A) site with randomized nucleotides 100 times without altering the rest of the sequence. We then calculated the median change in model predictions for each hexamer occurrence using the logit-transformed PolyaClassifier probability (log-odds).
We employed this technique to discover the motifs defining poly(A) sites genome-wide in S. cerevisiae and S. pombe. We carried out motif disruption for 11,673 well-expressed cleavage sites in S. cerevisiae (100 or more reads, ≥5% isoform abundance ratio, and ≥5 nt distance from the adjacent sites) and 2492 in S. pombe (50 or more reads, ≥5% isoform abundance ratio, and ≥5 nt distance from the adjacent sites). For each position from –250 nt to +250 nt surrounding the cleavage site, we quantified the sum importance score for each hexamer by taking the sum of the disruption effect. We also calculated the per-site importance by dividing the sum importance score by the motif frequency. Doing this for each position surrounding the maximum cleavage site created an importance profile showing the position-specific effects of each hexamer.
Next, we characterized the cis-regulatory elements that significantly contributed to site definition using a two-step filtering procedure. Previous work has shown that yeast polyadenylation cis-regulatory elements are optimally located within 80 nt upstream of and 30 nt downstream from the cleavage site (Tian and Graber 2012). First, we shuffled the sum importance scores from the regions outside [–80,30] and constructed a background distribution of 20 nt window scores. We used the 99.9th percentile score from the distribution as the false-discovery rate (FDR) threshold to identify motifs showing motif importance significantly above the background level. Next, we split the region around the maximum cleavage site into eight bins ([–250,–120], [–120,–80], [–80,–40], [–40,0], [0,40], [40,80], [80,120], [120,250]) and compared the 20 nt sum importance window score of each motif to the distribution of scores for other motifs in that same region. We retained those motifs with scores that exceeded the 99th percentile in a region. This process identified 137 motifs that significantly contributed to PolyaClassifier predictions in S. cerevisiae and 230 motifs in S. pombe.
The significant motifs we identified in S. cerevisiae belong to three families: (1) the UA-rich family that contained motifs similar to UAUAUA or AUAUAU, (2) the A-rich family that are near-cognates of AAAAAA, and (3) the U-rich family that was represented by UUUUUU. We measured the motif similarity to each of the archetypical motifs using the Hamming distance, which is equal to the number of mismatches in the sequence (i.e., AUUAAA compared with AAAAAA has a Hamming distance of two). Motifs were included in a family if they had a Hamming distance ≤2 nt. We then calculated the mean per-site and sum importance profiles for families of motifs. To further support the functional significance of these motif families, we analyzed the enrichment of genetic variants around top S. cerevisiae poly(A) sites and found that variants were generally depleted within UA-rich motifs (Supplemental Fig. S8E; for details, see Supplemental Methods).
S. pombe is distantly related to S. cerevisiae on an evolutionary timescale and is known to show divergent patterns of polyadenylation regulation (Liu et al. 2017). The contributing motifs we identified above belong to four unique families: (1) the A-rich family containing motifs with three or fewer mismatches compared with AAAAAA, (2) the U-rich family containing motifs with two or fewer mismatches compared with UUUUUU, (3) the GUA-containing motif family, and (4) the UAG-containing motif family. We also separate those motifs that contain both a GUA and UAG, although they demonstrate activity similar to other GUA-containing and UAG-containing motifs. We calculated the mean per-site and sum importance profiles for these families of motifs, as described above. We also leveraged the motif disruption approach to investigate the sequence context surrounding the GUA and UAG elements (for details, see Supplemental Methods).
Identifying the regulators of poly(A) site cleavage heterogeneity
Some genes in S. cerevisiae undergo extensive heterogeneous cleavage, whereas others show more precise cleavage (Ozsolak et al. 2010; Moqtaderi et al. 2013). We measured the degree of heterogeneity at a cleavage site using the entropy value. Using the PASS reads, we compiled the
cleavage probability vector for the 50 nt window centered at the maximum cleavage site. Supposing the total read number from
the poly(A) region is n and the read count in position i is mi, we calculated the fraction of reads pi = mi/n. We then calculated the entropy value E using the cleavage vector distribution as follows:
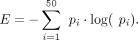
The entropy values were used to partition well-expressed cleavage sites (100 or more reads, ≥5% isoform ratio, ≥5 nt distance from the adjacent sites, PolyaClassifier probability ≥0.9) into three groups: low entropy sites that exhibited very defined cleavage sites (bottom 20% of entropy values, N = 2280), middle entropy sites (middle 60%, N = 6840), and high entropy sites that demonstrated high cleavage heterogeneity (top 20%, N = 2280).
To determine the motifs contributing to low versus high cleavage entropy, we split the sequences around each maximum cleavage site into five regions ([–90,–50], [–50,–30], [–30,–15], [–15,15], [15,30]). For each region, we conducted a chi-squared test to identify motifs enriched in the sequences from either high or low entropy group. We further confirmed these findings by comparing the motif counts across entropy groups. We also used the same approach to quantify the cleavage heterogeneity for poly(A) sites in S. pombe and humans.
Developing the PolyaCleavage model
Input data set
To determine whether primary poly(A) site sequences determine the cleavage heterogeneity, we sought to train a model that uses the 500 nt sequence surrounding a cleavage site as the input to predict the cleavage profile. The sequence centered at the cleavage site was one-hot-encoded as described above. The PolyaCleavage model architecture is similar to PolyaClassifier, but the parameters vary slightly. The model selection process is described in detail in the Supplemental Methods. We calculated the cleavage probabilities for the region ±25 nt around the maximum cleavage sites, using the PASS reads, as the ratio between the read number at each position and the total read count in the region. The 50 nt long vector represented the cleavage probability at each site, and the sum is one.
PolyaCleavage training and evaluation
The model was trained using the Adam optimizer with Nesterov momentum to minimize the Kullback–Leibler divergence loss function:
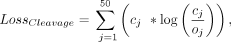where cj and oj are the predicted and observed cleavage probabilities, respectively, for each position j across the 50 nt window vector. The loss function was implemented out-of-box in TensorFlow2.
To evaluate the performance of a PolyaCleavage model, we compared the observed and predicted cleavage heterogeneity as well
as mean cleavage position (MCP), which were calculated from the 3′READS cleavage probability vector and the predicted cleavage
vector, respectively. The cleavage heterogeneity was quantified by the entropy score described above. The MCP is the dot product
between the position indices and the cleavage probability vector, which must sum to one. For position i from a vector of length 50 with a cleavage probability of pi, the MCP m was calculated as follows:
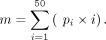
The resulting MCP measures the weighted mean and indicates the most likely cleavage position. The correlation between the observed and predicted entropy scores and MCP values quantifies the similarity between the 3′READS distribution and our model predictions surrounding a given poly(A) site.
We then applied the PolyaCleavage model to investigate the genomic parameters regulating cleavage heterogeneity. To this end, we performed in silico experiments altering the sequences surrounding low and high entropy cleavage sites to validate the mechanisms contributing to cleavage heterogeneity. This process is described in detail in the Supplemental Methods.
Developing the PolyaStrength model
Input data set
As some nearby cleavage sites can result from the heterogeneous cleavage of the same poly(A) site, we clustered these closely located sites to quantify their expression levels. To this end, we grouped adjacent cleavage sites through an iterative clustering approach. We started by selecting the highest expressed site not yet assigned to a cluster. We searched 20 nt upstream and 20 nt downstream and added all cleavage sites within this region to the cluster. We repeated this process until all sites were clustered. We picked the 20 nt window because the A-rich motif (recognized by CF1A) located 20 nt upstream is important for the downstream cleavage. We considered that the sites located within 20 nt of a maximum cleavage site are likely caused by heterogeneous cleavage. If the boundaries of the two clusters were within 10 nt of each other, we adjusted the cluster boundaries to evenly split the area between the maximum cleavage site of each cluster. For example, if the maximum sites of two neighboring clusters were 8 nt apart, the edges of the cluster would be adjusted so that each cluster covered 4 nt of that region. We filtered out clusters supported by fewer than 10 3′READS or with an expression <2% of the maximum number in each gene. This process yielded 30,932 poly(A) site clusters in S. cerevisiae.
We selected clustered poly(A) sites within the 3′ UTR or extended downstream region of genes undergoing APA and therefore contained at least two expressed poly(A) sites supported by 3′READS (N = 20,691 sites). These sites formed the data set for the PolyaStrength model. For genes containing multiple poly(A) sites, we calculated the isoform ratio of each site as measured by the ratio of PASS read number assigned to the site to the sum of reads supporting the top two sites in a gene. Supposing the supporting read number for site i is ni, its isoform ratio ui and the logit-transformed value oi were calculated as follows:
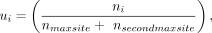
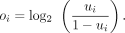
The maximum cleavage site within each clustered poly(A) site served as the representative site for subsequent model training and analysis.
PolyaStrength training and evaluation
The PolyaStrength model architecture is similar to PolyaClassifier, but the parameters vary slightly. The model selection
process is described in detail in the Supplemental Methods. We used the 500 nt sequence surrounding the representative cleavage site of each cluster as the input for model training.
The sequences were one-hot-encoded as described above. The output layer uses a linear activation to predict the logit-transformed
isoform ratio levels. All PolyaStrength models were trained using the Adam optimizer with Nesterov momentum to minimize the
mean-squared error:
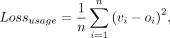where oi and vi are the observed and predicted logit-transformed usage levels for the poly(A) site i. The loss function was implemented out-of-box in TensorFlow2. The data flowed into the model using a batch size of 100 and
an initial learning rate of 0.001. After five epochs, we used a decaying learning rate, in which the learning rate was reduced
by a factor of e–0.1 after each subsequent training epoch. Model training was stopped after reaching a minimum loss for the validation data.
To evaluate the performance of a PolyaStrength model, we created pairs of poly(A) sites from either the validation or holdout test sets located in the same 3′ UTR. We required that the paired sites have a more than eightfold difference in supporting reads. We then calculated the AUROC and AUPRC using the difference in predicted PolyaStrength scores to classify the highly versus lowly expressed sites of a pair. Because paired sites are selected using random sampling, we calculated the mean AUROC and AUPRC from 10 sets of pairs.
Identifying motifs important to poly(A) site strength
To examine the motifs mediating poly(A) site strength, we used a similar hexamer disruption approach as described for the PolyaClassifier model. This is described in further detail in the Supplemental Methods.
Investigating the regulation of APA under diauxic stress
We applied the PolyaStrength model to understand the factors driving APA under diauxic stress. This analysis is described in detail in the Supplemental Methods.
Poly(A) site sequence conservation
We utilized phastCons conservation tracks to study the sequence conservation surrounding poly(A) sites across species (Siepel et al. 2005). This analysis is described in detail in the Supplemental Methods.
Software availability
The source codes are included in the Supplemental Code document and were deposited in GitHub (https://github.com/zhejilab/PolyaModelsYeast).
Competing interest statement
The authors declare no competing interests.
Acknowledgments
This work was supported by grants to Z.J.: the National Institutes of Health (National Institute of General Medical Sciences: R35GM138192; National Heart, Lung, and Blood Institute: R01HL161389) and the Lynn Sage Scholar fund. E.K.S. was supported by the predoctoral training program in Biomedical Data Driven Discovery (National Library of Medicine: T32LM012203). We thank the members of the Ji laboratory for helpful discussions.
Author contributions: E.K.S. and Z.J. conceived and designed the study. E.K.S. performed the data analysis. E.K.S. and Z.J. wrote the manuscript. Z.J. supervised the research.
Footnotes
-
[Supplemental material is available for this article.]
-
Article published online before print. Article, supplemental material, and publication date are at https://www.genome.org/cgi/doi/10.1101/gr.278606.123.
- Received October 10, 2023.
- Accepted June 17, 2024.
This article is distributed exclusively by Cold Spring Harbor Laboratory Press for the first six months after the full-issue publication date (see https://genome.cshlp.org/site/misc/terms.xhtml). After six months, it is available under a Creative Commons License (Attribution-NonCommercial 4.0 International), as described at http://creativecommons.org/licenses/by-nc/4.0/.
