A general calculus of fitness landscapes finds genes under selection in cancers
- Teng-Kuei Hsu1,12,
- Jennifer Asmussen2,12,
- Amanda Koire3,
- Byung-Kwon Choi2,
- Mayur A. Gadhikar4,
- Eunna Huh5,
- Chih-Hsu Lin3,
- Daniel M. Konecki3,
- Young Won Kim6,
- Curtis R. Pickering4,
- Marek Kimmel7,8,
- Lawrence A. Donehower9,
- Mitchell J. Frederick10,
- Jeffrey N. Myers4,
- Panagiotis Katsonis2 and
- Olivier Lichtarge1,2,3,5,6,11
- 1Department of Biochemistry and Molecular Biology, Baylor College of Medicine, Houston, Texas 77030, USA;
- 2Department of Molecular and Human Genetics, Baylor College of Medicine, Houston, Texas 77030, USA;
- 3Program in Quantitative and Computational Biosciences, Baylor College of Medicine, Houston, Texas 77030, USA;
- 4Department of Head and Neck Surgery, The University of Texas M.D. Anderson Cancer Center, Houston, Texas 77030, USA;
- 5Department of Pharmacology and Chemical Biology, Baylor College of Medicine, Houston, Texas 77030, USA;
- 6Program in Integrative Molecular and Biomedical Sciences, Baylor College of Medicine, Houston, Texas 77030, USA;
- 7Departments of Statistics and Bioengineering, Rice University, Houston, Texas 77005, USA;
- 8Department of Systems Engineering and Biology, Silesian University of Technology, 44-100 Gliwice, Poland;
- 9Department of Molecular Virology and Microbiology, Baylor College of Medicine, Houston, Texas 77030, USA;
- 10Department of Otolaryngology–Head and Neck Surgery, Baylor College of Medicine, Houston, Texas 77030, USA;
- 11Computational and Integrative Biomedical Research Center, Baylor College of Medicine, Houston, Texas 77030, USA
-
↵12 These authors contributed equally to this work.
Abstract
Genetic variants drive the evolution of traits and diseases. We previously modeled these variants as small displacements in fitness landscapes and estimated their functional impact by differentiating the evolutionary relationship between genotype and phenotype. Conversely, here we integrate these derivatives to identify genes steering specific traits. Over cancer cohorts, integration identified 460 likely tumor-driving genes. Many have literature and experimental support but had eluded prior genomic searches for positive selection in tumors. Beyond providing cancer insights, these results introduce a general calculus of evolution to quantify the genotype–phenotype relationship and discover genes associated with complex traits and diseases.
From short-term disease risk to long term species evolution, the genotype–phenotype relationship describes how genetic variations induce biological change (Manolio et al. 2009). Experimental screens tracking the effect of these variations include RNA interference (RNAi) (Boutros and Ahringer 2008), CRISPR-Cas9 knockouts (Mali et al. 2013; Koike-Yusa et al. 2014; Wang et al. 2014b; Hart et al. 2015), and deep mutational scans (Fowler et al. 2014) within the limitations of achievable perturbations and assays (Mak and Justman 2017). Alternately, statistical analyses of genome-wide association identify overrepresented variants in case-control studies. These presumably influence the phenotype common to case subjects (Hirschhorn and Daly 2005; Hardy and Singleton 2009), although sample size, signal quality (McCarthy et al. 2008), and rate biases (Korte and Farlow 2013) may limit accuracy.
Here, we propose a different approach to recover the genotype–phenotype relationship, which is based on representing genetic variations as moves in the fitness landscape (Wright 1932). Prior theory suggests that these moves should generally be small and nearly neutral (Nei 2005). Against this background, we hypothesize that gene mutations driving new phenotypes are the result of abnormally large moves in the fitness landscape. Testing this hypothesis requires a metric for motions in the fitness landscape. We propose to use the evolutionary action (EA) of mutations on fitness described in prior work as the derivative of the genotype–phenotype relationship (Katsonis and Lichtarge 2014). In practice, the EA score correlates with the experimental effects of mutations (Katsonis and Lichtarge 2014) and consistently performs well in blinded assessments of predictions of deleterious mutations against state-of-the-art statistical and machine learning methods (Katsonis and Lichtarge 2017, 2019). A limitation of EA, however, is that it describes only the impact of single mutations, or individual moves in the fitness landscape. This is not sufficient to interpret complex polygenic phenotypes owing to multiple causal variants. To identify groups of gene variations that in aggregate drive patients to a disease region of the fitness landscape, we therefore propose a new operation, called Cohort Integration (CI), which sums the individual effects of variants measured with EA over all genes and over all patients. Calculus suggests that this summation will reverse the differential operation that led to EA in the first place and thus recover the genotype–phenotype relationship, meaning it will uncover genes that drive cohort-specific traits.
Here, we test this model in cancer. Tumor genomes evolve (Greaves and Maley 2012) by acquiring advantageous somatic mutations that, when considered collectively across a cohort of cancer patients, should be associated with a large displacement in the fitness landscape. The average number of coding mutations per tumor can be as small as about eight in leukemia but is more often confoundingly large, such as about 1600 in colorectal cancers (Vogelstein et al. 2013). Among these, however, the number of cancer-driving somatic mutations are relatively few, three to five by some estimates (Tomasetti et al. 2015), and finding these cancer drivers remains difficult, as well as critical for personalized therapy (Chin et al. 2011). To search for cancer genes that harbor these driver mutations, state-of-the-art methods (Dees et al. 2012; Davoli et al. 2013; Vogelstein et al. 2013; Lawrence et al. 2014; Tokheim et al. 2016; Martincorena et al. 2017; Bailey et al. 2018; Dietlein et al. 2020; Martínez-Jiménez et al. 2020) pool statistics and machine learning to search for signs of positive selection in cancer genes, including mutation frequency (Dees et al. 2012; Lawrence et al. 2014), surrounding nucleotide context (Dietlein et al. 2020), inactivation bias (Greenman et al. 2007; Van den Eynden et al. 2015; Martincorena et al. 2017), functional impact (Gonzalez-Perez and Lopez-Bigas 2012; Davoli et al. 2013), and structural or functional clustering (Tamborero et al. 2013; Porta-Pardo and Godzik 2014). Some of the challenges to identify driver genes include inaccurate background mutation rates (Lawrence et al. 2013), too few mutations per gene (Van den Eynden et al. 2015), and unbalanced distributions of passenger mutations (Bignell et al. 2010) that lead to a repertoire of mutational signatures (Alexandrov et al. 2013, 2020). Notably, as much as 60% to 80% of genes identified by one method are not found by others (Tokheim et al. 2016), and a large number of rare cancer drivers in individual patients remains hidden for lack of a population-wide role (Garraway and Lander 2013; Chang et al. 2016). The sequencing of diverse types of somatic tumor tissue from a large number of patients by The Cancer Genome Atlas (TCGA) (The Cancer Genome Atlas Research Network 2008; The Cancer Genome Atlas Research Network et al. 2013; Tomczak et al. 2015; The ICGC/TCGA Pan-Cancer Analysis of Whole Genomes Consortium 2020) yields a rich data set for discovering new cancer genes. Here, we used CI to prioritize the collective fitness impact of variants across all genes and all patients in a cohort in order to discover candidate cancer-driver genes and compare this approach to other cancer gene identification techniques (Greenman et al. 2007; Dees et al. 2012; Gonzalez-Perez and Lopez-Bigas 2012; Davoli et al. 2013; Tamborero et al. 2013; Lawrence et al. 2014; Porta-Pardo and Godzik 2014; Van den Eynden et al. 2015; Tokheim et al. 2016; Martincorena et al. 2017; Bailey et al. 2018).
Results
CI of the fitness effects detects selection on a variant set
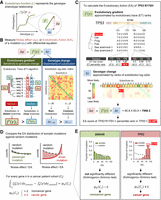
As detailed in the Supplemental Information, our evolutionary calculus model hypothesizes a formal genotype–phenotype relationship. Differentiating this relationship yields the EA equation for the fitness effects of genetic variants. Integrating the numerical values of the gene fitness effects given by EA over a patient cohort should measure the relationship of each gene with the phenotype, as illustrated in the visual summary of the evolutionary calculus theory (Fig. 1A–E). As a basic test of EA in cancer, the experimental and clinical effects of TP53 (Kato et al. 2003), MLH1 (Raevaara et al. 2005), BRCA1, and BRCA2 (Spurdle et al. 2012) mutations agree with EA fitness scores better than alternative methods (Supplemental Fig. S1).
Evolutionary calculus of the genotype–phenotype relationship. (A) Our hypothesis is that the genotype (γ) is linked to phenotype (φ) through a continuous evolutionary function (f). (B) The fitness effect (Δφ), or evolutionary action (EA), of each mutation is the product of evolutionary gradient (f′) and genotypic change (Δγ). Evolutionary gradient is the sensitivity of the mutated position to substitution approximated by evolutionary trace (ET), which accounts for the phylogenetic distances between homologous sequences (Δφ) that vary at a residue position (Δγ); the size of genotypic change can be approximated by substitution odds. (C) EA score calculation for the R175H variant of TP53. The evolutionary gradient (f′) of position 175 was measured by ET ranks of importance, and the genotypic change (Δγ) of R-to-H substitution was measured by ranks of context-dependent substitution log-odds. These two terms were then multiplied and normalized to yield the EA score. (D) To identify genes under positive selection in a trait-associated cohort, for every gene k, we compared the cohort integral, represented by the distribution of EA scores, of its cancer somatic mutations in the patient cohort (Cj) with the cohort integral of random mutations. A nonrandom cohort integral indicates the gene k harbors cancer-driver mutations and therefore is a cancer-driver gene. (E) Cancer-driver genes are identified by nonrandom cohort integrals. Cohort integral of somatic mutations was significantly different from random (one-tailed two-sample Kolmogorov–Smirnov test) for the cancer gene TP53, in contrast to the noncancer gene DNAH5.
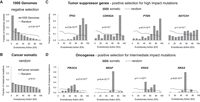
For proof of concept of the CI approach, we used mutation data from distinct populations and from random simulations. The cohort integral of nearly 24 million germline missense variants from more than 2500 diverse, healthy individuals in The 1000 Genomes Project (The 1000 Genomes Project Consortium 2015) showed an exponentially decreasing distribution as a function of EA, biased toward lower EA values than simulated random nucleotide substitutions (P = 3.8 × 10−29; see Methods) (Fig. 2A). This EA distribution bias is consistent with negative selection against germline variants with large fitness effects among healthy-born individuals. In contrast, the cohort integral of 645,359 cancer somatic missense mutations from 5996 patient tumor genomes across 20 cancers from TCGA (Tomczak et al. 2015) was exponentially decreasing at a slower rate that was indistinguishable from computer-simulated random substitutions of nucleotides in protein-coding regions (P = 0.41) (Fig. 2B). This is consistent with most cancer somatic missense mutations being random and under little selection (Greenman et al. 2007). A single-gene illustration is the TCGA-wide cohort integral of DNAH5, a large and frequently mutated gene that has not, to the best of our knowledge, been associated with cancer and that appears free of any selection pressure (P = 0.84) (Supplemental Fig. S2A). The distribution of EA values was also indistinguishable between random nucleotide substitutions and computer-simulated variants generated according to mutational signatures of mono- and trinucleotide substitution ratios observed in somatic mutations from 20 different cancer types (Supplemental Table S1; Supplemental Fig. S2B,C). These observations suggest that the distribution of EA values is insensitive to biases related to the mechanism that generates the mutations and is specific to fitness selection forces.
Coding variants under selection have nonrandom cohort integrals. The cohort integrals for all germline variants in the 1000 Genomes Project (A) and all somatic mutations from The Cancer Genome Atlas (TCGA; B). The somatic TCGA mutations were also shown for the tumor-suppressor genes TP53, CDKN2A, PTEN, and NOTCH1 (C) and for the oncogenes PIK3CA, BRAF, KRAS, and NRAS (D). The dashed lines correspond to simulated random amino acid changes in all human genes (A,B) or the respective single gene (C,D). The P-values of cohort integral differences between the observed and simulated random mutations were calculated by the one-tailed two-sample Kolmogorov–Smirnov test.
In contrast, cohort integrals of representative well-established tumor suppressors, such as TP53, CDKN2A, PTEN, and NOTCH1, computed over all TCGA somatic missense mutations found in any cancer type, were all strongly biased toward high EA scores, usually above 70 and consistent with complete loss of function (P-value = 2.8 × 10−303, 2 × 10−7, 9.7 × 10−50, and 1.4 × 10−11, respectively) (Fig. 2C). This difference indicates positive selection and fits the expectation that cancer-causing mutations often weaken tumor suppression. Likewise, the cohort integrals of representative oncogenes, such as PIK3CA, BRAF, KRAS, and NRAS, were all also highly significant (P-value = 2.2 × 10−57, 9.4 × 10−179, 1.1 × 10−63, and 9.6 × 10−45, respectively) (Fig. 2D). Their peak EA scores, however, fell between 30 and 70, consistent with gain-of-function variants that repurpose rather than destroy a protein. We may also apply CI on individual cancer types. For example, CDH1 is known to drive breast and stomach cancers (Corso et al. 2020). This gene has a significant, nonneutral cohort integral in these cancer types (P-value = 0.002 and 0.03, respectively) (Supplemental Fig. S2D) but not in any other cancer type individually or collectively (P-value = 0.9) (Supplemental Fig. S2E). These data show that CI identifies populations and genes under different selection pressures. Typically, inherited coding variants in healthy individuals are under negative selection, passenger coding variants in cancer populations are under random (or no) selection pressure, and well-known cancer-driver genes are under positive selection, with intermediate EA values in oncogenes and larger EA values in tumor suppressors. These differences suggest that CI provides a new method to identify genes under positive selection.
CI recovery of cancer-driving genes performs on par with or better than existing state-of-the-art methods
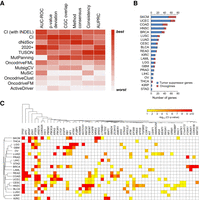
To assess performance on recovering cancer-driver genes, we compared CI to 10 state-of-the-art algorithms using multiple criteria of success. All algorithms were evaluated over the same test population of 7916 exomes from 34 cancer types, collected by another study (Tokheim et al. 2016). Nevertheless, the result should be cautiously interpreted because the included methods may rely on different variant types and engage external complementary information. We adapted and enriched previously used benchmark measures (Tokheim et al. 2016) to evaluate each method for precision measured by the overlap of the discovered genes with a gold-standard gene set (CGC Overlap, Supplemental Table S2) and with the consensus of genes discovered by the other algorithms (Method Consensus); the combined true- and false-positive rates measured by area under the receiver operating characteristic (AUC-ROC) and precision-recall (AUPRC) curves; the overlap of the discovered genes when using each half of the test population (Consistency); and the discrepancy between observed and theoretical P-value distributions (P-value deviation). Using only the missense mutations as input to the CI approach resulted in 61 significantly nonrandom genes after multiple testing correction (Q-value < 0.1), with a CGC Overlap of 0.64, AUPRC of 0.32, and AUC-ROC of 0.73. Although this CGC Overlap was the best compared with the other methods, the small number of discovered genes resulted in intermediate AUC-ROC and AUPRC performance (Supplemental Fig. S3). This likely stems from the fact that other methods used additional mutations, such as nonsense variants and frame-shift insertions and deletions (fs-indels). However, accounting for nonsense variants in the CI framework is straight forward because random nucleotide changes provide the expected rate of nonsense mutations, and we can score them with the highest impact for a loss-of-function variant (EA = 100). CI of missense plus nonsense mutations thus discovered 98 genes after multiple testing correction (Q-value < 0.1), which increased AUC-ROC (0.79) and AUPRC (0.39) values compared with using missense variants only, and precision (CGC Overlap of 0.56) remained better than the state-of-the-art methods (Fig. 3A; Supplemental Fig. S3; Supplemental Table S3, “CI”). To also account for fs-indels in our approach, we further combined the CI P-value of each gene with the probability that fs-indels appear in that gene by chance (see Methods). This modified CI approach prevents the discovery of genes owing to fs-indel variants only and results in the inclusion of borderline CI analysis genes (P-value < 0.05, but Q-value > 0.1) when these genes have sufficient support from the fs-indel variants analysis. This raised the number of discovered genes to 159 and further improved the AUC-ROC (0.81) and AUPRC (0.43) values [Fig. 3A; Supplemental Fig. S3; Supplemental Table S3, “CI (with INDEL)”]. Using fs-indels variants alone recovers 349 candidate cancer genes with a 0.28 AUPRC and 0.19 CGC Overlap. Additionally, we assessed the performance of CI with fs-indels across 13 cancer types within test population. As expected, the robustness of the CI with fs-indels method, as measured by AUC-ROC, AUPRC, and Consistency, decreases with cancer cohort size (Supplemental Fig. S4). A comparable performance reduction is observed for other state-of-the-art methods. This benchmark analysis establishes that the calculus-based CI methods have robust performance compared with state-of-the-art methods for identifying candidate cancer genes. Additionally, CI P-values for missense and nonsense mutations can be combined with P-values based on an independent test for fs-indels with no appreciable loss of performance; therefore, CI with fs-indels is used hereafter.
CI recovers cancer-driving genes in benchmarking and prospective analyses. (A) The performance of CI against 10 state-of-the-art methods over the same input samples. The heatmap represents the relative performance of the methods (red means the best, and white means the worst performance) for six evaluation metrics: area under the receiver operating characteristic curve, deviation from the expected P-value distribution, overlap with the COSMIC Cancer Gene Census, overlap with the consensus of all the other methods, the consistency among cohort subsamples, and the area under the precision-recall curve. (B) CI identified 460 genes under positive selection in TCGA tumors. The number of tumor suppressors (blue) and oncogenes (red) identified by CI in each cancer type. (C) Heatmap representation of CI Q-value of the 56 candidate genes that were identified in two or more cancer types. The significance level is represented by a color scale from red (more significant) to yellow (less significant). The cancer types were ordered according to a dendrogram of pairwise distances based on the overlap of predicted driver genes (see Methods).
To examine the power of CI, we tested the robustness of its results as we reduced the number of test population exomes by down-sampling. First, we defined a target set of 58 genes, as those identified by CI using all 7916 test exomes and also reported as cancer associated by at least four of five reference sources (see Supplemental Table S4; Davoli et al. 2013; Kandoth et al. 2013; Vogelstein et al. 2013; Lawrence et al. 2014; Forbes et al. 2017). Then, for increments of 100 tumor exomes, we calculated the percentage overlap of the genes identified by the subset and the target genes. For each increment, we generated 10 subsets by resampling exomes and calculated the average and standard deviation of the overlap (Supplemental Fig. S5). Using half of the 7916 exomes was sufficient to detect 86% of the target genes, whereas 1150 exomes (14%) were sufficient to detect half of the target genes. These results show that CI is robust and powerful, producing reliable results even with a fraction of the input data and suggesting that it may also be capable of identifying driver genes in specific cancer types.
CI detects genes under positive selection across cancer mutational landscapes
Next, to discover new candidate cancer-driving genes, we applied CI prospectively and separately over the genomic sequencing data from 5996 TCGA tumor genomes across 20 cancers from TCGA (see Methods). CI detected 326 candidates that were implicated in at least one TCGA cancer type (Fig. 3B). Moreover, 134 additional candidate pan-cancer genes were found by analyzing all cancer genomes together (Q-value < 0.1) (Supplemental Table S5). CI was also applied to an updated release of TCGA tumor exomes (Supplemental Table S6) with significantly overlapping findings (Supplemental Table S7). The 460 genes identified in any and all of the 20 cancer types included 116 transcription regulators, 65 enzymes, and 33 kinases (Supplemental Fig. S6A). Gene set enrichment analysis (GSEA) using hallmark gene sets (see Methods) (Liberzon et al. 2015) found nine significant associations (Supplemental Fig. S6B), including PI3K-AKT-MTOR signaling (Q-value = 3 × 10−4), apical junction (Q-value = 3 × 10−4), and p53 pathway (Q-value = 6 × 10−4). An ingenuity pathway analysis (see Methods) (Kramer et al. 2014) found significant overlap with 261 overlapping canonical pathways (Q-value < 0.1) (Supplemental Table S8), most of which are cancer-signaling pathways. The top molecular and cellular functions (Supplemental Table S9) included gene expression (Q-value = 4 × 10−15 to 4 × 10−38), cell death and survival (Q-value = 9 × 10−11 to 6 × 10−25), cell cycle (Q-value = 3 × 10−11 to 7 × 10−23), cell growth and proliferation (Q-value = 6 × 10−11 to 3 × 10−22), and cellular development (Q-value = 8 × 10−11 to 4 × 10−18).
We hypothesized that if CI robustly identified cancer-driver genes, then it could point out which patient cohorts shared tumors of similar genetic etiology. This was tested with a similarity tree of cancer types based on the candidate drivers that were predicted independently in each type (see Methods) (Fig. 3C). As expected, patients with renal papillary carcinoma (KIRP) clustered together with those suffering from renal clear cell carcinoma (KIRC), rectal adenocarcinoma (READ) with colon adenocarcinoma (COAD), and lower grade glioma (LGG) with glioblastoma multiforme (GBM). Head–neck (HNSC), cervical (CESC), bladder (BLCA), and lung squamous cell carcinoma (LUSC) clustered in one branch, in agreement with a study proposing LUSC, HNSC, and BLCA as a squamous-like subtype (Hoadley et al. 2014). Together these data suggest that across distinct patient cohorts, CI robustly identifies biologically reasonable candidate cancer-drivers in specific cancers and can indicate which genes associate more broadly with the tissue-of-origin.
To assess novelty, we compared the 460 genes to a gold-standard control list of genes already associated with cancer in established sources (Supplemental Table S4): the COSMIC Cancer Gene Census (Forbes et al. 2017) and candidate genes suggested by 20/20 (Vogelstein et al. 2013), MutSigCV (Lawrence et al. 2014), TUSON (Davoli et al. 2013), and MuSiC (Kandoth et al. 2013). Of the 465 genes from these combined sources, CI recovered 147 (P-value = 1 × 10−124, hypergeometric test), with mutual agreement coverage rising from 13% (37 of 285, P-value = 3 × 10−16) for genes imputed by a single source only to 95% (39 of 41, P-value = 8 × 10−61) for genes agreed upon by all five (Supplemental Fig. S6C). For the 313 candidates identified by CI but not part of this gold-standard list, cancer was the top disease or function annotation according to ingenuity pathway analysis (Supplemental Table S10). Moreover, 215 genes had independent cancer associations from three lines of evidence: appearance in at least 10 cancer papers (n = 118, P-value = 0.0001) (Supplemental Fig. S6D), significant diffusion to known cancer drivers in the STRING protein–protein interaction network (n = 55, P-value = 2 × 10−5) (Supplemental Fig. S6E; Shin et al. 2007; Lisewski et al. 2014; Szklarczyk et al. 2015), and a nonsynonymous-to-synonymous mutation ratio, dN/dS, greater than one and consistent with positive selection (n = 159, P-value = 2 × 10−14) (Supplemental Fig. S6F). Overall, 27 genes had support from all three types of evidence, 58 from two, and 130 from one, leaving 98 genes (21%) with no prior support from any of these sources (Supplemental Fig. S6G). Moreover, when we quantified a confidence score for cancer association by weighing the support sources (see Methods), the CI significance Q-value correlated strongly with the cancer-association confidence scores (P-value < 0.0001) (Supplemental Fig. S6H).
CI profiles distinguish tumor-suppressor genes from oncogenes
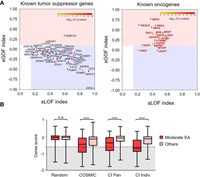
Because tumor suppressors and oncogenes have distinct peaks in their EA distributions (Fig. 2C,D), we could measure the selection pressure for complete loss of function (sLOF) with the skew of the distribution toward the maximum EA of 100, expected for tumor suppressors, and the selection pressure for gain of function (sGOF) by the skew toward the intermediate EA of 50, expected for oncogenes. For example, known tumor-suppressor genes and oncogenes (Supplemental Table S11) had significantly greater sLOF or sGOF scores, respectively, than other genes (Supplemental Fig. S7A), enabling a separation of tumor-suppressor genes from oncogenes (Supplemental Fig. S7B) that was measurable with an area under the receiver-operator characteristic curve of 0.96 (Supplemental Fig. S7C). At a binary separation threshold of 0.1, the accuracy was 90% (Supplemental Fig. S7D), classifying correctly 93% (50 out of 54) of tumor suppressors and 83% (15 out of 18) of oncogenes (Fig. 4A). These data show that CI may sort oncogenes from tumor suppressors based on distinct selection profiles in the cancer mutational landscape. We could then classify the 460 candidate cancer genes identified by CI into 357 likely tumor-suppressor genes and 103 likely oncogenes (Supplemental Table S5). Among the 98 (21%) of new genes identified by CI, 18 were likely oncogenes and 80 were tumor suppressors.
CI distinguished tumor-suppressor genes from oncogenes. (A) The selection for gain-of-function (sGOF) and loss-of-function (sLOF) indices for 54 known tumor-suppressor genes (left) and 18 known oncogenes (right). Genes were plotted according to the sLOF index (x-axis) and sGOF index (y-axis) for the cancer type with the most significant Q-value, and the circle color indicates the CI Q-value for the most significant cancer type, which is represented by a color scale from red (more significant) to yellow (less significant). Genes located in the red rectangular area are classified as oncogenes, and genes located in the blue rectangular area are tumor-suppressor genes. (B) Genome-scale CRISPR gene-dependency screen–validated CI oncogenes. Oncogenes from the COSMIC database (COSMIC), oncogenes identified by the CI method across all cancers (CI PAN), or oncogenes from individual cancer types (CI Indiv.) show a statistically significant shift toward essentiality (Ceres score ≤ −0.6) when harboring variants of moderate EA range (30 ≤ EA score < 70) as opposed to other mutations, including low EA variants (0 ≤ EA < 30), high EA variants (70 ≤ EA < 100), nonsense variants, and other uncategorized variants. No difference was observed for random genes. Statistical significance was calculated with a Mann–Whitney U test.
Experimental support for oncogenes and tumor suppressors
Next, we verified these genes against the CRISPR essentiality screen from the Cancer Dependency Map (DepMap) database (Tsherniak et al. 2017), which used Cas9-mediated DNA cleavage to observe the effects of gene inactivation on cell proliferation. Because certain cancer cell lines are dependent on activated oncogenes to maintain their malignant properties, known as oncogene addiction (Weinstein and Joe 2008), this screen should be a good test system to independently validate the role of the 103 putative oncogenes. As expected, cancer cell lines are dependent on CI oncogenes when they harbor mutations with EA scores between 30 and 70, which is the range for gain-of-function mutations, and a similar dependency was observed in the known oncogenes from COSMIC but not in random genes (Fig. 4B; Supplemental Table S12). Moreover, CI oncogenes identified in individual cancers had significantly stronger essentiality responses in their corresponding cancer types, suggesting tissue specificity (Supplemental Fig. S8). These results together show that CI is able to classify oncogenes and tumor-suppressor genes and can also identify oncogenic gain-of-function variants in the context of specific cancer types.
CI provides insight into the biology of specific cancers
Head and neck squamous carcinoma
For illustration, we initially focus our attention on head and neck squamous carcinoma (HNSC). Based on the somatic mutations from 508 HNSC tumors, CI identified 45 candidate genes (Fig. 5A; Supplemental Table S13), and the majority (39 out of 45) were predicted to be tumor suppressors, consistent with the genomic landscape of this cancer reported by others (Agrawal et al. 2011; Stransky et al. 2011; The Cancer Genome Atlas Research Network 2015). CI identified the major candidate tumor suppressors previously published for HNSC, including TP53, FAT1, NOTCH1, CDKN2A, CASP8, PTEN, RB1, FBXW7, AJUBA, and NSD1. CI also identified two well-known oncogenes for HNSC (PIK3CA and HRAS), as well as known oncogenes in other cancers but new in HNSC (NEF2L2, RAC1, and MAPK1) (Supplemental Table S5). Of the 45 candidates, 28 have already been associated with cancer (though not necessarily HNSC) in COSMIC or by other state-of-the-art methods, and 17 genes were predictions unique to CI, nine of which were associated with cancer in literature (Supplemental Table S13).
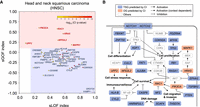
CI identified 45 genes under positive selection in head and neck squamous carcinoma (HNSC). (A) The 45 HNSC candidate genes were plotted according to their sLOF index (x-axis) and sGOF index (y-axis) as circles. The color of each circle indicates the CI Q-value in HNSC in a color scale of red (more significant) to yellow (less significant). Genes located in the red rectangular area were classified as oncogenes (names shown in red), and genes located in the blue rectangle area were classified as tumor-suppressor genes (names shown in blue). (B) Pathways associated with CI-identified candidates in HNSC.
HNSC candidate genes were involved in pathways associated with oncogenesis (Fig. 5B). Cell differentiation is a key pathogenic pathway in HNSC that includes the well-known HNSC drivers NOTCH1, TP63, FAT1, and ZNF750 (Agrawal et al. 2011; Pickering et al. 2013; The Cancer Genome Atlas Research Network 2015). CI recovered three of these known drivers and predicted three more candidates from the same pathway, NOTCH2, PDZRN4, and KDF1. We have previously detected NOTCH2 as a driver in aggressive cutaneous squamous cell carcinoma (Pickering et al. 2014), and its homology with the known tumor-suppressor gene NOTCH1 lends further support to the notion that NOTCH2 is also a HNSC driver gene. PDZRN4 belongs to the LNX gene family of homologous RING type E3 ubiquitin ligases (Katoh and Katoh 2004), and two related LNX family members have been shown to bind NUMB, a negative NOTCH regulator (Rice et al. 2001). Exogenous expression of PDZRN4 has been shown to inhibit growth of hepatocellular carcinoma cell lines (Hu et al. 2015a), suggesting a tumor-suppressor function consistent with the CI classification. KDF1 regulates TP63 and has been identified as a regulator of squamous differentiation through both human and mouse genetic studies (Lee et al. 2013). Another key pathway in HNSC is epigenetic regulation. CREBBP, EP300, KMT2D, and NSD1 have previously been identified as frequently mutated epigenetic regulators in HNSC (The Cancer Genome Atlas Research Network 2015), and we have identified ARID2 and KMT2B as additional HNSC cancer-related epigenetic regulators. Other important pathways are the DNA damage and cell stress processes, and CI identified the DNA-damage-response gene HNRNPUL1 and the nonsense-mediated RNA decay (NMD) factor UPF2, the latter can be targeted by Pateamine A (Dang et al. 2009). Last, we identified NF2, which is a proven tumor-suppressor gene and is responsible for hereditary neurofibromatosis type II but has not been previously linked to HNSC. These results suggest that CI can identify new candidate driver genes in individual cancer types, although further experimental studies are required to validate them as true drivers.
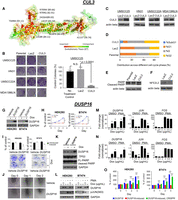
We validated experimentally the CUL3 gene, which was neither in our gold-standard list nor an established HNSC gene but was identified by CI as a tumor suppressor in this cancer type (CI Q-value = 0.07; sGOF = −0.13; sLOF = 0.66). CUL3 is the core component of E3 ubiquitin-protein ligase complexes that down-regulates NFE2L2, a known driver of HNSC. Previous work shows that the disruption of such adaptor–substrate recognition promotes malignancy (Ohta et al. 2008) and has been associated with poor prognosis in HNSC (Martinez et al. 2015). CUL3 somatic mutations in TCGA HNSC samples are located at functionally and structurally important sites (Fig. 6A), as predicted by the evolutionary trace (ET) algorithm (Lichtarge et al. 1996; Mihalek et al. 2004). To assess how CUL3 activity impacts cell growth and survival, four HNSC cell lines were engineered to ectopically express wild-type protein. Of the four cell lines, clonogenic potential was diminished by wild-type CUL3 ectopic expression in UMSCC25 cells (P-value < 0.0001) (Fig. 6B) compared with expression of the control gene LacZ. UMSCC25 was the only cell line to show a prominent higher-molecular-weight CUL3 band following ectopic expression (Fig. 6C), which is suggestive of the post-translational neddylation (Hori et al. 1999) that is required for CUL3 ligase activity (Pintard et al. 2004). Further investigation revealed that ectopic expression of CUL3 in UMSCC25 cells substantially reduced the percentage of G1 cells and produced a concomitant increase in the subG1 fraction (Fig. 6D), indicating cell death. There was also an increase in cleaved PARP (Fig. 6E), consistent with apoptosis, and, as expected, decreased levels of NFE2L2 (also known as NRF2), the known HNSC driver (Fig. 6F). Collectively, these data show the ability of CI to discern cancer-driving genes in the HNSC TCGA population, even if the mutation is uncommon. The rarity of actual CUL3 mutations in HNSC could be explained by the cancer cells simply preventing CUL3 neddylation instead, which would still disable the protein.
Overexpressing CUL3 in HNSC cell lines suppresses tumor growth. (A) Somatic missense mutations in CUL3 are shown as spheres in the structure of a homologous protein (chain C of PDB: 2HYE, sequence identity = 39.82%), and the EA score of the given mutation is shown in parentheses. The importance of position was evaluated by ET and is represented by a color scale from red (more important) to green (less important). (B) Clonogenic assay following infection of the cell lines UMSCC25, HN31, UMSCC22A, and MDA1386LN with lentivirus to express wild-type CUL3 or the control gene LacZ. (C) Western blot shows the ectopic expression of wild-type CUL3 after lentivirus infection. (D) Cell cycle distribution for the UMSCC25 cell line following expression of CUL3. (E) PARP levels, a marker of apoptotic death, increase in UMSCC25 cells expressing CUL3; (F) levels of NFE2L2 (NRF2), the HNSC-driving protein, are reduced. Overexpression of DUSP16 inhibited cell proliferation, colony formation, migration, and induced apoptosis by inhibition of JNK pathway. (G) DUSP16 overexpression was assessed by induction with doxycycline (1 µg/mL) to stable HEK293 and BT474 cells containing inducible DUSP16 construct. (H) Overexpression of DUSP16 inhibited cell proliferation of established cells. (I) Clonogenic assay: Overexpression of DUSP16 inhibited colony formation of HEK293 and BT474 cells. The experiment was performed in triplicates, and the density of the stained cells was measured at 630 nm after extraction with 10% acetic acid. (J) In vitro scratch assay. Cells were plated and incubated until confluent and then scratched with pipette tip and further incubated to compare recovery of scratched area. (K) Overexpression of DUSP16 induced apoptosis in stable BT474 cells. (L) Overexpression of DUSP16 inhibited JUN phosphorylation in stable HEK293 and BT474 cells. Overexpression of DUSP16 induced down-regulation of JUN and FOS transcription in HEK293 cells (M) and BT474 cells (N). (O) Depletion of DUSP16 by CRISPR antagonized cell growth inhibition by overexpression of DUSP16. (*) P-value < 0.05, (**) P-value < 0.005, and (***) P-value < 0.001.
Breast cancer
Similar observations are made when CI is applied to 977 breast cancer (BRCA) tumor samples. Of the 40 candidate genes identified in BRCA, 32 are predicted to be tumor suppressors, and six of these have not been identified by other studies (Supplemental Table S5). One of these six genes is a dual specificity protein phosphatase, a family of genes known to both positively and negatively regulate cellular pathways associated with tumorigenesis (Patterson et al. 2009; Meeusen and Janssens 2018). Based on these observations, we elected to focus additional in vitro experimental analyses on dual specificity protein phosphatase 16 (DUSP16).
DUSP16 (CI Q-value = 0.09; sGOF = −0.53; sLOF = 0.62) has been implicated as a candidate negative growth regulator and potential tumor suppressor, at least in part through negative regulation of JNK signaling (Domotor 1989; Hoornaert et al. 2003; Keyse 2008). To confirm the role of DUSP16 as a negative growth regulator, we generated clonal lines of HEK293 and BT474 human cells containing transduced doxycycline-inducible DUSP16 (Fig. 6G). Addition of doxycycline to both cell lines resulted in significant reduction (P-value < 0.001) in cell division relative to the same clones in the absence of doxycycline (Fig. 6H). The ability of doxycycline-induced HEK293 and BT474 cells to form colonies after plating individual cells at low density was also significantly reduced (HEK293, ∼40%, n = 5, P-value = 0.014; BT474, ∼50%, n = 3, P-value = 0.036) (Fig. 6I). Additionally, cell migratory activity was shown to be reduced in cells with elevated DUSP16 (Fig. 6J; Supplemental Fig. S9A). Elevation of DUSP16 was associated with increased cellular apoptotic markers in BT474 cells (Fig. 6K) and enhanced dephosphorylation of JNK (Supplemental Fig. S9B), as well as JUN at Ser63, a major proliferative transcription factor in AP-1 signaling (Fig. 6L; Supplemental Fig. S9C). This effect on JUN and potentially AP-1 signaling was shown in the reduction of AP-1 transcription targets JUN and FOS in the presence and absence of phorbol ester (an AP-1 signaling activator) stimulation (Fig. 6M,N). Finally, we also showed that the DUSP16-induced inhibition of cell division in HEK293 and BT474 cells can be reversed when DUSP16 protein expression is down-regulated by CRISPR (Fig. 6O). These results provide evidence that DUSP16 is a potent tumor suppressor and provides additional support for the ability of CI to identify novel cancer-driver genes.
Potential therapeutic applications
With a view to personalized therapy, we noted that 70 CI oncogenes were not found in the gold-standard list (Supplemental Table S14), of which 13 may be druggable, including nine that can be directly targeted by drugs and four that belong to a targetable gene family. For example, the candidate PDE10A, a phosphodiesterase involved in PKG and PKA signaling (Soderling et al. 1999), is unique to CI in skin cutaneous melanoma (SKCM) and is predicted to be an oncogene. Consistent with a possible oncogenic role, its increased expression stimulates cell growth by activating the Wnt/β-catenin pathway (Li et al. 2015). Selective PDE10A inhibitors, such as papaverine, PQ-10, and Pf-2545920, have already been shown to suppress colon tumor cell growth (Lee et al. 2016). Another unique candidate with an oncogenic CI profile is DYRK1A in endometrial cancer (UCEC). This dual-specificity protein kinase regulates cell cycle progression (Fernández-Martínez et al. 2015), and its drug-induced inhibition decreases proliferation and colony formation in vitro and suppresses tumor growth in vivo (Radhakrishnan et al. 2016). These examples show that CI oncogenes could suggest potential therapeutic targets.
Discussion
The genotype-to-phenotype relationship is central to biology (Fisher 1930; Wright 1932). It hinges on the fitness effect of mutations, namely, their molecular, cellular, and physiological impact on the population
structure (Orr 2009) and location in the fitness landscape (Wright 1932). Mutational scan experiments explore these fitness landscapes to a resolution limited by mutations, assays, and epistasis
(Cunningham and Wells 1989; Pal et al. 2003, 2006; Datta et al. 2008). Alternately, we show here that evolutionary comparative sequence analysis across species can probe a vastly greater set
of mutational trials coupled to evolutionary fitness via phylogenetic divergences (Lichtarge et al. 1996; Mihalek et al. 2004; Wilkins et al. 2010). EA first tapped these evolutionary data through differential analysis of fitness landscapes (Katsonis and Lichtarge 2014) to compute the effect of single mutations relatively accurately (Katsonis and Lichtarge 2017,2019) and usefully (Neskey et al. 2015; Osman et al. 2015a,b; Chun et al. 2019; Clarke et al. 2019). The hypothesis is that genotype (γ) and phenotype (φ) are linked through a continuous and differentiable evolutionary fitness
function f, such that f(γ) = φ. EA exploited the computation of the gradient (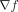
), although f itself remained unknown. Now, we show how to integrate 
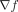in the fitness landscape to compute the path-determining genes driving a population to phenotype regions of interest. In
effect, CI solves f numerically for each gene, in line with the antiderivative property stemming from the fundamental theorem of calculus. Integration
thus completes the calculus model introduced with EA. This calculus has two consequences: It reveals evolutionary constraints
and the genetic determinants of complex phenotypes (Kim et al. 2020; Koire et al. 2021).
The completion of the EA calculus points to a physics-based description of evolution. Although interpretations may differ
(Doebeli et al. 2017), one possibility is to view f as a potential function describing the ability of a genotype to perform the evolutionary work required for reproduction in the fitness landscape. The gradient of such a potential,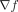 
, would then define a field describing the evolutionary force at each point of the genome space acting against a substitution in the direction of each of the 19 alternate amino acids.
Together, this space and its field are akin to the “fitness landscape” and its slope proposed by Wright (1932). The EA equation can now be interpreted as the product of a force times a displacement, namely, the evolutionary work of a mutation pulling a genotype across the landscape against the evolutionary force field. CI, by summing the work of all mutations minus random background fluctuations, is the energy of driver gene mutations propelling
the patient cohort along paths to phenotypic traits. This physical interpretation makes testable predictions: The random background
mutational energy of populations at steady state should follow the Boltzmann exponential distribution of energy (Landau and Lifshitz 1980). This model fits observations (Fig. 2; Supplemental Fig. S2) and matches the distribution of fitness effect Fisher anticipated (Fisher 1930) and expanded more recently by others (Sella and Hirsh 2005). In cancer, this equilibrium distribution of mutational energy is illustrated by the background EA distribution of unconstrained
random passenger mutations in a gene such as DNAH5. In contrast, TP53, PIK3CA, and other cancer drivers are under selection rather than fluctuating randomly around an equilibrium, and their mutational
distributions differ drastically from a decaying exponential form.
In practice, our data show that in cancer this approach complements others to identify driver genes (Tokheim et al. 2016). It finds 460 genes under positive selection across 20 different types of cancer cohorts sequenced by TCGA. Almost one third of these drivers are well-known driver genes (32%). Nearly half (47%) are known in other types of cancers or supported by publications, interactions with cancer-associated genes, or other evidence of positive selection. The remainder are less-studied genes (21%). Among the most implicated pathways were chromatin remodeling, nuclear receptor signaling, apoptosis, protein elongation, transcription, and G-protein signaling. This is consistent with cancer biology and progression, but it also includes many genes that were not previously reported by other large genetic studies (Dees et al. 2012; Davoli et al. 2013; Kandoth et al. 2013; Vogelstein et al. 2013; Bailey et al. 2018). For example, we identified SNF/SWI members SMARCA2 (pan-cancer), SMARCA1 (colon and pan-cancer), SMARCC2 (pan-cancer), and BRD7 (skin and pan-cancer), which are unreported in other large cancer sequencing studies. Among the latter, SMARCA1 and SMARCC2 have been shown to function as tumor suppressors in gastric cancers (Takeshima et al. 2015). Transcription factors belonging to the Forkhead (i.e., FOXP1), Homeobox (MSX2, HOXB7, HOXB9, TGIF1, and POU4F1), and Kruppel-like (i.e., KLF5 and KLF3) families were found in the pan-cancer analysis (TGIF1 and KLF5 were also found in colon and bladder cancer, respectively), and members from each of these classes of transcription factors have been extensively linked to cancer previously (Tetreault et al. 2013; Joo et al. 2016; Miller et al. 2016). Two protein elongation factors, EEF1A1 and EIF1AX, were predicted to be oncogenes in the pan-cancer analysis, consistent with many reports that elongation factors as a class are overexpressed in multiple tumor types and control proliferation and cell death (Abbas et al. 2015). Three genes are involved in G-protein signaling: RGS22 (pan-cancer) encodes a GTPase activating protein previously found to function as a tumor suppressor in pancreatic and esophageal cancers (Hu et al. 2011, 2015b); ARHGAP5 (colon and pan-cancer) encodes a Rho GTPase activating protein shown to increase invasiveness of lung cancer cell lines (Wang et al. 2014a); and RGL2 (pan-cancer) encodes a guanine nucleotide exchange factor that positively regulates growth of lung cancer cell lines (Santos et al. 2016).
CI also captures the distinct selection profiles of tumor suppressors and oncogenes. The former have complete loss-of-function mutations with EA scores above 70, and the latter have gain of function mutations with EA scores between 30 and 70. During validation of two predicted tumor suppressors, intact versions of CUL3 in head and neck cancer and DUSP16 in breast cancer, each inhibited cancer cell growth in their corresponding cell lines. For CUL3, these data are consistent with a large-scale cancer gene identification study that pooled multiple predictive algorithms (Bailey et al. 2018). For oncogenes, we found strong agreement between our predicted oncogenes and a large-scale tumor dependency screen (DepMap data) (Fig. 4B; Supplemental Table S12). Of note, of the 70 candidate oncogenes we find, a third are currently categorized as druggable targets.
EA calculus has several limitations. It does not currently account for common and important noncoding cancer mutations, such
as genomic rearrangements (Mitelman et al. 2007; Mertens et al. 2015) or epigenetic (Esteller 2008) or gene copy number variations (Shlien and Malkin 2009; Yu and Shao 2009). Also, our approach does not account for the fact that oncogenic drivers are often seen at hot spot residues (Chang et al. 2018) or near each other in protein sequence and structure (Tamborero et al. 2013). Together, with the fact that oncogenic drivers have milder EA scores than tumor-suppressor drivers, this may lead to lower
sensitivity in identifying oncogenes. However, P-values that account for mutation clustering and recurrence, suggested by existing methods, could be integrated through Fisher's
combined probability test (Fisher 1948), as illustrated here for frameshift indels (see Methods; Supplemental Fig. S10). Other integrative approaches using machine learning are of interest and could reflect even broader types of data (Guan et al. 2012; Hu et al. 2015b; Yu et al. 2016, 2017). Additionally, the number of available homologous sequences for some genes may be insufficient to produce EA scores of high
accuracy. For these genes, somatic mutations may mimic a random distribution, and the genes will not be identified as cancer-driver
candidates. Although this limitation may reduce sensitivity, it should not affect the precision of our approach. The sensitivity
of the approach depends logarithmically on the sample size. Therefore, small sample sizes are sufficient for finding prominent
cancer genes, whereas the discovery of very rare drivers remains a challenge. Differential mutation probabilities across sites
might be an important confounder of the substitution odds that approximate Δγ, because this calculation involves aligned sequences of various pair identities that correspond to different branching lengths.
Finally, epistasis is implicit in estimates of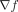 
with ET, but its explicit modeling would require the fitness cross-effect of dual genome positions x and y, namely, ∂2f/∂x∂y, a second-order mixed derivative term beyond the scope of this first-order analytic theory. Formal questions of differentiability
and integrability in fitness landscapes are also not trivial (Carneiro and Hartl 2010). Here, differentiability of f is consistent with evolvability (Wagner and Altenberg 1996) through smooth mutational steps and, more strictly, with Schwartz distributions (Schwartz 1963). The discrete domain of integration, which consists of many somatic variants, in many genes and over many patients cannot
support Riemann integration but is consistent with Lebesgue–Stieltjes integration (Carter and Brunt 2012) and, more strictly, a stochastic integral of Ito or Stratonovich type (LeGall 2016).
In summary, we propose a general analytic and evolutionary framework for the genotype–phenotype relationship. The approach
uses differential and integral calculus to interpret the mutational burden in patient cohorts in light of the couplings between
mutations, selection, and divergence throughout evolution. This method sidesteps the difficulty of measuring mutational effects
from incomplete and complex descriptions of protein structures and their dynamics, interactions, and pathways in and across
cells. Instead, it only requires three quantities: f, Δγ, and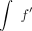 
. We showed previously how to compute f′ and Δγ (Katsonis and Lichtarge 2014), and now by computing 
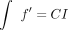, we complete this calculus of fitness landscape. The result may appear surprising but is consistent with the ability of calculus
to routinely solve otherwise seemingly intractable problems (Penrose 2007) and is also consistent with the view that biology is likely to follow statistical thermodynamic rules for the large-scale
behavior of complex systems that eschews details of internal structures and forces (Sella and Hirsh 2005; Koonin 2011). Indeed, we find that mutations in genes that are under no specific selective force follow a random distribution. In contrast,
genes under selection such as those that drive a group of individuals to a specific location of the fitness landscape will
be typified by a nonrandom distribution. In principle, this is a general approach to identify the genotype determinants of
the phenotype specific to a population (Kim et al. 2020; Koire et al. 2021), as we show here for cancer.
Methods
Calculation of the EA score of coding missense variants
The EA is an untrained and formal model to measure the fitness effect of missense variants analytically, using protein evolution data from homologous sequences. Thus, EA predictions of fitness effects are not based on or adjusted according to experimental values. As described in detail elsewhere (see Supplemental Material; Katsonis and Lichtarge 2014), in order to estimate the fitness effect of variants, EA considers the fitness landscape to be a mapping from genotype (γ) to phenotype fitness values (φ) via the evolutionary function f: f(γ) = φ (Equation 1). In essence, Equation 1 describes the genotype–phenotype relationship. Assuming genotypes are evolvable, f should be differentiable, such that to first order a sufficiently small genotype variant (Δγ) owing to a mutation would lead to a fitness perturbation (Δφ) given by f′(γ) · Δγ ≈ Δφ = EA (Equation 2), where EA is the evolutionary action of the mutation Δγ on fitness, and f′(γ) is the functional sensitivity of the mutated site to genotype variants. Although the function f in Equation 1 is unknown, we may still compute Equation 2 in the special context of amino acid substitution variants by approximating its two terms. First, f′(γ) is approximated with ET ranks of importance (Lichtarge et al. 1996). ET measures the functional importance of protein residues by accounting for the phylogenetic distances (Δφ) between homologous sequences given a variation (Δγ) at a given residue position. Thus, positions that tend to vary mostly between phylogenetically distant homologous sequences are ranked as more important. Second, Δγ is approximated for coding variants from amino acid substitution odds. These substitution odds reflect the differences in various physicochemical properties of amino acids and are calculated from numerous homologous sequence pairs for the specific functional importance of the mutated positions. Thus, alanine to serine has greater substitution odds, as well as lesser contribution to EA than alanine to tryptophan, in keeping the greater similarities between the former pair than the latter. These are first-order approximations, and local functional and structural features of proteins will impact their accuracy. But these local effects are treated as second-order effects and, for now, ignored. In practice, this is justified because EA performs well in objective tests against state-of-the-art methods to assess the deleterious impact of mutations (Katsonis and Lichtarge 2017,2019). EA scores for human gene variants are available for nonprofit use at http://eaction.lichtargelab.org/.
Cohort integration
The methodological innovation in this work is to integrate Equation 2 in order to recover the genotype–phenotype relationship from Equation 1. In all generality, integrals are sums of terms, called integrands, each one evaluated from a function of a variable over a range, called domain. Here, the variable is the genotype variation, the function is Equation 2, the integrands are the EA scores, and the domain is all mutations in a patient cohort compared with control mutations (for details, see Supplemental Materials). Therefore, the integral will be a sum of EA scores for patient variants compared with the sum of random variants. Considering gene-specific distributions of EA scores, we may calculate integrals gene by gene, and with a one-tailed, two-sample Kolmogorov–Smirnov test, we may find whether these integrals differ significantly from zero. Insignificant differences indicate genes with coding variants in the cancer cohort that are consistent with random mutational events, not under selection. However, significant Kolmogorov–Smirnov tests indicate genes with variants that experienced selection in the cancer cohort, namely, genes with genotype perturbations linked to the phenotype of the cohort. To eliminate genes with EA distributions that are not biased to high or intermediate EA scores (different than those seen in Fig. 2C,D), we asked that either the sLOF index is greater than 0.15 or the sGOF index is greater than 0.1. This integral analysis only used missense and nonsense mutations compared with random nucleotide changes. Frameshift insertions and deletions (fs-indels) were treated separately because they require different control variants. For fs-indels, we used the binomial probability test to compare their frequency in each gene to their frequency in the genome, assuming that most tumor mutations do not contribute to cancer (passengers) and that the rate of passenger mutations is constant throughout the genome. As such, the fs-indel mutation rate was calculated in the context of each cancer type by dividing the total number of fs-indel mutations by the combined size of the genes with at least one mutation. We combined for each gene the CI P-value (missense and nonsense mutations) with the P-value for fs-indels according to Fisher's combined probability (Fisher 1948) and then corrected for multiple-hypothesis testing (Q-value < 0.1) (Storey and Tibshirani 2003). Because the fs-indels analysis is very sensitive to sequencing quality and in order to avoid potentially false-positive findings, we further filtered out genes with missense and nonsense CI P-value less than 0.05. In practice, this filtering prevented discoveries based on fs-indel variants only and acted to lower the stringent threshold of the missense and nonsense variant CI analysis. A flowchart of the CI approach is provided in Supplemental Fig. S10.
Tumor-suppressor and oncogene classification with sLOF and sGOF index
We defined the sLOF index and sGOF index to quantify the bias of coding variants toward high and intermediate EA scores, respectively. To do so, we considered the distribution of EA scores that corresponds to variants obtained from all possible nucleotide changes in each gene. Then, we calculated a reference curve of how the average of the distribution changes when we exclude any fractions of the variants with the lowest (positive selection) or the highest (negative selection) EA scores. A positive sLOF index equal to x indicates that the average EA score of the given coding variants is equal to the averaged EA score of all possible nucleotide substitutions in a gene minus fraction x of the substitutions with the lowest EA scores, whereas a negative sLOF index −x indicates that the given coding variants have an average EA equal to that of all possible nucleotide substitutions minus fraction x of the substitutions with the highest EA. To account for bias to intermediate EA scores, we considered the minimum difference of each EA score from zero or from 100 (DEA values). The DEA values for all possible nucleotide changes in a gene created a new distribution scaled from zero to 50. We calculated a reference curve of how the average of the distribution changes when we excluded any fractions of the variants with the lowest (positive selection) or the highest (negative selection) DEA values. The positive sGOF index equal to y indicates that the average DEA value of given coding variants is equal to the average DEA value of all possible nucleotide substitutions minus the fraction y of the substitutions with the lowest DEA values (most distant from an EA of 50), and a negative sGOF index −y indicates that the given coding variants have average EA equal to that of all possible nucleotide substitutions minus the fraction y of the substitutions with the highest DEA values (closest to 50). In sum, a positive sLOF indicates the selection characteristic of a mutated tumor-suppressor gene, whereas a positive sGOF indicates the selection characteristic of a mutated oncogene. We then annotate genes as tumor suppressors when their sLOF index >0.15 and as oncogenes when the sGOF index >0.1. Genes that satisfy both the tumor-suppressor and oncogene criteria are annotated as oncogenes, because oncogenes typically also have positive sLOF indices (owing to biases of the genetic code to conservative substitutions), whereas tumor suppressors typically have negative sGOF indices.
Software availability
The CI software is available as Supplemental Code together with a README.txt file that contains the instructions for installation and execution. The method is also available through the web server at http://cohort.lichtargelab.org/.
Competing interest statement
The authors declare no competing interests.
Acknowledgments
This work was supported by the National Institutes of Health (GM066099, AG074009, AG061105, AG068214 to O.L., R01 DE14613 to M.K., and DE025181 to J.N.M.). M.K. was also supported by the National Science Center of Poland (2018/29/B/ST7/02550). J.A. was supported by a training fellowship from the Gulf Coast Consortia, on the NLM Training Program in Biomedical Informatics & Data Science (T15LM007093). A.K. was supported by RP160283–Baylor College of Medicine Comprehensive Cancer Training Program and the Baylor Research Advocates for Student Scientists (BRASS).
Author contributions: T.-K.H., P.K., and O.L. designed the study and interpreted the results. T.-K.H., P.K., M.K., and O.L. developed the methodology. T.-K.H., J.A., P.K., C.-H.L., E.H., Y.W.K., and D.M.K. analyzed the data. B.-K.C. and M.A.G. performed the experiments. T.-K.H., P.K., J.A., C.-H.L., D.M.K., B.-K.C., C.R.P., M.J.F., and O.L. wrote the manuscript. T.-K.H., P.K., J.A., A.K., C.R.P., M.J.F., L.A.D., M.K., J.N.M., and O.L. reviewed and edited the manuscript. P.K. and O.L. supervised the research.
Footnotes
-
[Supplemental material is available for this article.]
-
Article published online before print. Article, supplemental material, and publication date are at https://www.genome.org/cgi/doi/10.1101/gr.275811.121.
-
Freely available online through the Genome Research Open Access option.
- Received May 25, 2021.
- Accepted March 14, 2022.
This article, published in Genome Research, is available under a Creative Commons License (Attribution-NonCommercial 4.0 International), as described at http://creativecommons.org/licenses/by-nc/4.0/.
