A statistical physics approach for disease module detection
Abstract
Extensive evidence indicates that the pathobiological processes of a complex disease are associated with perturbation in specific neighborhoods of the human protein–protein interaction (PPI) network (also known as the interactome), often referred to as the disease module. Many computational methods have been developed to integrate the interactome and omics profiles to extract context-dependent disease modules. Yet, existing methods all have fundamental limitations in terms of rigor and/or efficiency. Here, we developed a statistical physics approach based on the random-field Ising model (RFIM) for disease module detection, which is both mathematically rigorous and computationally efficient. We applied our RFIM approach to genome-wide association studies (GWAS) of ten complex diseases to examine its performance for disease module detection. We found that our RFIM approach outperforms existing methods in terms of computational efficiency, connectivity of disease modules, and robustness to the interactome incompleteness.
Complex diseases are believed to be caused, among other factors, by combinations of molecular alterations affecting cellular systems (Cho et al. 2012). Integration of disease-related genomics, epigenomics, transcriptomics, and other omics data with the human protein–protein interaction network (or interactome) could provide insight into the molecular mechanisms of complex diseases. A disease module represents a group of cellular components (e.g., dysfunctional pathways, complexes or cross-talk subgraphs between pathways in a molecular interaction network) that together contribute to cellular function that, when disrupted, may produce a particular disease phenotype (Cho et al. 2012). The concept of the disease module is based on the local hypothesis that if a gene or molecule is involved in a specific biochemical process or disease, its direct interactors might also be suspected to play some role in the same biochemical process or disease (Zanzoni et al. 2009; Barabási et al. 2011; Gustafsson et al. 2014). For example, proteins that are involved in the same disease show a high propensity to interact with each other (Oti et al. 2006; Goh et al. 2007), and proteins encoded by genes mutated in inherited genetic disorders have a significantly increased tendency to interact directly with proteins known to cause similar disorders (Gandhi et al. 2006; Xu and Li 2006). Hence, we expect that each disease can be linked to a well-defined neighborhood of the cellular molecular interactome, that is, its disease module, which is likely to include multiple disease-modifying genes [mutations, deletion, copy number variations, or expression changes can be linked to a particular disease phenotype (Suzuki et al. 2004)] that mediate various epigenetic, transcriptional, and posttranslational phenomena. Detection of the disease module for a pathophenotype of interest in turn can guide further experimental work toward uncovering the disease mechanism, predicting disease genes, and informing drug development (Chu and Chen 2008; Azmi et al. 2010; Zhao and Li 2010; Cheng et al. 2019; Morselli Gysi et al. 2021). For example, a previous study using the DIseAse MOdule Detection (DIAMOnD) algorithm found that the asthma module contains immune response mechanisms that are shared with other immune-related disease modules; and the GAB1 signaling pathway is a modulator in asthma (which has been experimentally validated) (Sharma et al. 2015).
Numerous computational methods have been developed to identify disease modules (Ulitsky et al. 2010; Bersanelli et al. 2016; de Weerd et al. 2020) by projecting the molecular profiles into the network and assigning scores/weights to nodes/edges. Those methods can be briefly classified into three categories: (1) Permutation-based methods (e.g., Hierarchical HotNet [Reyna et al. 2018] and DOMINO [Levi et al. 2021]), which involve a network randomization process to correct for typical protein–protein interaction (PPI) network biases. (2) Seed-genes-based methods (e.g., DIAMOnD [Ghiassian et al. 2015]), which “grow” the disease module from the seed genes in a local agglomerative process. (3) Heuristic-based methods, for example, ModuleDiscoverer (Vlaic et al. 2018), ROBUST (Bernett et al. 2022), attempt to find optimal subgraphs within the molecular interaction network. However, those methods all have fundamental limitations. For example, seed-gene based methods heavily rely on the initial selection of seed genes. As for heuristic-based methods that attempt to find optimal subgraphs within the molecular interaction network, they turn out to be computationally intractable in general as no universal definition of module structure exists (Fortunato and Hric 2016).
To address the limitations of previous methods, here we develop a novel method for disease module detection based on the random-field Ising model (RFIM) (Bray and Moore 1985; d'Auriac et al. 1985; Belanger and Young 1991), a classical model for random magnets in statistical physics, especially in the study of disordered magnets (Nattermann 1998). In its most general form, the RFIM applies to an ensemble of magnetic particles interacting with each other in the presence of an external magnetic field H. Each magnetic particle (also called spin) has two states σi = ±1 (i.e., UP or DOWN). hi’s are local magnetic fields (because of impurities) acting on each spin and hi > 0 (or <0) favors UP (or DOWN) state of spin i, respectively. The coupling constants Jij > 0 capture the ferromagnetic interactions between spins i and j such that two spins next to each other will tend to align to save the energy of the system. The control parameter H is just the external magnetic field, acting uniformly on all the spins to align them in the direction of H. The average state variable (or order parameter) M is the magnetization of the spin system.
In RFIM, we hypothesize that optimizing the “score” of the whole network rather than a particular subgraph or “growing” the disease module from the seed genes in a local agglomerative process will discover a biologically more meaningful disease module. Optimizing the score of the whole network (with appropriately assigned node weights and edge weights calculated from omics profiles) can be mapped to the ground state (i.e., the state with the lowest energy) problem of RFIM and then solved exactly by the max-flow algorithm with polynomial time complexity (Cherkassky and Goldberg 1997). The resulting disease module might not be a single connected component or a tree graph at all. Using this approach, all of the disease related subgraphs will emerge simultaneously.
To compare our RFIM approach with existing methods, we applied RFIM and five representative methods, DIAMOnD (Ghiassian et al. 2015), DOMINO (Levi et al. 2021), Hierarchical HotNet (Reyna et al. 2018), ModuleDiscoverer (Vlaic et al. 2018), and ROBUST (Bernett et al. 2022) (see Supplemental Material, Sec. 1 for details) to genome-wide association studies (GWAS) of ten different complex diseases: asthma (Ishigaki et al. 2020), breast cancer (Ishigaki et al. 2020), chronic obstructive pulmonary disease (Hobbs et al. 2017) (COPD), cardiovascular disease (Schunkert et al. 2011) (CVD), diabetes (Mehta 2012), colorectal cancer, gastric cancer, lung cancer, ovarian cancer, and prostate cancer (Ishigaki et al. 2020) (see Table 1).
Summary of GWAS studies used in the disease module detection
We want to point out that in this work we follow the original (or classical) formalization of the disease module detection problem. In other words, we project the omics data (collected from a large cohort of a specific disease) into the human interactome, and then identify a well-defined neighborhood of the human interactome, that is, the disease module for this particular disease, which is likely to include multiple disease-modifying genes (proteins) (Suzuki et al. 2004). This formalization is quite different from the recent one used in (Choobdar et al. 2019), in which the authors worked directly on the human molecular networks (of different types: protein interaction, signaling, co-expression, cancer dependency, and homology) to detect topological modules (i.e., locally dense neighborhoods of a network, such that the nodes of a module show a higher tendency to interact with each other than with nodes outside the module) in the human molecular networks. This topology-based module detection framework does not explicitly have any particular disease focus or specificity, which is fundamentally different from the original disease module detection formalization. Hence, in our opinion, methods developed for the two different formalizations of disease module detection are not directly comparable.
Results
Disease module detection using the random-field Ising model
We formalize the original disease module detection problem as a statistical physics problem as follows. We represent the state
of node (gene) i by a binary variable σi = ±1, where +1 (or −1) means gene i is “active” (or “inactive”), that is, belongs to the disease module (or not), respectively. The disease module is captured
by the state of all genes, denoted as {σi}. Given a graph G = (V, E), that is, the PPI network with a node set V (with node weights {hi}) and an edge set E (with edge weights {Jij}), we aim to find the optimal gene state {σi}, also called the ground state, that minimizes the following cost function:
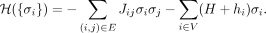(1)
The subgraph induced by the active nodes in the ground state is the disease module. We first assign a weight Jij to each of edge and hi to each node. Here, non-negative edge weights {Jij} favors positive correlations between the states of nodes i and j. The stronger the Jij value, the more likely nodes i and j have the same state. In the case of Jij = 0, the states of nodes i and j are totally independent (see Fig. 1A). hi represents the intrinsic preference of nodes belonging to the disease module regardless of the states of their neighboring
nodes (see Methods: Random-field Ising model [RFIM]). The parameter H is introduced to regulate the contributions of the two terms in Eq. (1). For any given H and a random initial gene state {σi}, a push-relabel algorithm for min-cut/max-flow problem in combinatorial optimization was used to find the optimal gene state
{σi} that minimizes the cost function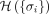 
. The genes whose states σi = 1 are those genes in the disease module. Note that the value of H effectively controls the average state variable 
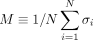of the system, or equivalently, the disease module size given by (1 + M)N/2 (see Fig. 1B). Hence, controlling the parameter H, we can obtain a disease module with any desired size between 0 and N (see Fig. 1C–E).
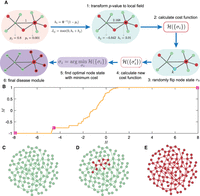
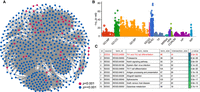
Disease module inference using statistical physics approach: a demonstration. (A) Schematic demonstration of the Random-field Ising model (RFIM) approach consisting of the following steps: (1) Given a graph
and gene-wise P-value associated with each node, we first transform P-value to node weight and assigned weight to each edge. (2) For any gene state {σi}, we calculated the cost function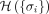 
. (3) An optimization method was used to find the optimal gene state {σi} that minimizes the cost function. (4) All genes with state σi = 1 are those genes in the disease module. (B) The magnetization curve M(H) of the random network system. A random network with N = 100 nodes (genes). Each gene is assigned a P-value, randomly chosen from a uniform distribution U(0, 1). The node weights hi are then computed using the inverse normal CDF. The edge weights Jij = max(0, hi + hj) if two genes are connected in the network. Otherwise, Jij = 0. The magnetization 
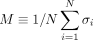is the average state of nodes in the system. As we increase the external field H, more nodes (genes) will be active, that is, M will monotonically increase and eventually approach 1. (C–E) disease module identified by RFIM at H = −8 (point b), H = −4 (point c) and H = 8 (point d), respectively. All the active components (highlighted in red) together can be considered as the disease module.
Our RFIM approach for the disease module detection has several advantages and novelties over existing approaches: (1) Because the ground state and the M(H) curve of the RFIM can be exactly calculated with polynomial time complexity (Cherkassky and Goldberg 1997; Liu and Dahmen 2007), we can run the calculation on very large data sets, for example, the human interactome, without any difficulty. (2) Both node weights and edge weights are naturally considered.
Computational complexity of disease module detection
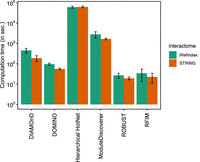
We assessed the computational complexity of different methods measured as the average computation time across all the ten diseases. We found that RFIM, ROBUST, DOMINO, and DIAMOnD are the four most efficient methods, which require significantly shorter running time than ModuleDiscoverer and Hierarchical HotNet (see Fig. 2). Moreover, we found that RFIM shows lower time complexity than other methods across different interactomes. For instance, the computation time of RFIM on a large interactome iRefIndex (Razick et al. 2008; Aranda et al. 2011) is close to that on a small interactome STRING (Franceschini et al. 2012). The computational efficiency of RFIM is because of the fact that the ground state of RFIM can be exactly solved with polynomial time complexity (see Methods: Calculation of the M(H) curve of RFIM).
Computational complexity of each disease module detection method. Each bar represents the average computation time (in seconds) overall all ten phenotypes. Error bar represents the standard derivation among 10 GWAS data sets. The computation time is measured as the running time on macOS machine with 2.4 GHz 8-Core Intel Core i9 processor. Hierarchical HotNet was paralleled using four cores.
Connectivity of the disease module
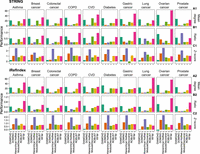
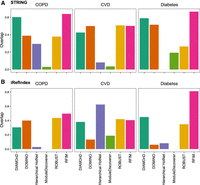
By definition, the disease module is a specific neighborhood within the interactome. Hence, the connectivity of the disease module should not be too low. We calculated the mean degree of the disease module detected by each method, finding that the disease module identified by RFIM shows the highest mean degree in seven of the ten diseases using either the STRING or iRefIndex interactome (see Fig. 3A1,A2). Yet, the mean degree of disease modules identified by other methods, that is, DOMINO and Hierarchical HotNet, is much lower for most diseases considered here. To compare the connectivity of the disease module and that of the genes surrounding it, we calculated the ratio between the average node degree of the disease module and that of its nearest neighbors in the interactome (i.e., the nodes that directly interact with the disease module genes). We found that the ratio of RFIM is generally much higher than that of other methods (see Fig. 3B1,B2). To evaluate the significance of the disease module's largest connected component (LCC), we compared it with a distribution of LCCs of randomly sampled genes of the same size as the disease module. We found that RFIM, DOMINO, ROBUST, and ModuleDiscoverer yield comparable Z-scores, and Hierarchical HotNet shows the highest Z-score (see Fig. 3C1,C2).
Connectivity comparison of the disease modules obtained by different methods and different phenotypes. We applied each disease module detection method in the genome-wide association studies (GWAS) of each disease separately and compared (A) the mean degree of genes in the disease module; (B) the ratio between the average degree of the disease module and that of the nodes that directly interact with the disease module nodes; (C) and statistical significance of the size of the disease module's largest connected component (LCC), with respect to LCCs of randomly sampled proteins of the same size as the disease module. Z-score is calculated from 1000 degree preserving randomizations.
Performance of disease-associated gene prediction
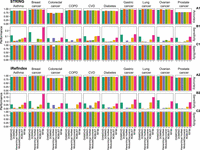
To examine whether those genes in the disease module are disease-associated, we used the disease-gene associations from the DisGeNET (Piñero et al. 2016) database as the gold standard. We treated the genes showing association with specific phenotype as positive instances and the remaining genes as negative instances. Then, the genes present (or absent) in the disease module are predicted as positive (or negative) instances, respectively. We compared the Accuracy, Sensitivity, and Specificity of each disease module identification method. We found that Accuracy (or Specificity) of different methods is similar to each other (see Fig. 4A1,A2; C1,C2), but the Sensitivity (ability to correctly classify genes as disease-associated) of RFIM is the highest among all the methods in eight phenotypes, regardless of interactome used in the calculation (see Fig. 4B1,B2).
Disease association for genes in disease module detected from integrating the genome-wide association studies (GWAS) with two interactomes for each phenotype and method. Accuracy (A), Sensitivity (B), and Specificity (C) between the genes in the disease module and the gold standard data set of disease-gene associations from DisGeNET. We treated the disease-associated genes of each phenotype in DisGeNET as positive instances and the remaining genes as the negative instances. Similarly, the genes in the disease module were considered as positive instances and the remaining genes were considered as negative instances.
Pathway enrichment analysis
To gain mechanistic insights into the list of genes in the disease module, we performed pathway enrichment analysis. In particular, we used the ReactomePA package (Yu and He 2016) to obtain the enriched pathways for genes in the disease module with P-values lower than 0.05 cutoff adjusted by False Discovery Rate. Then, for each disease considered in this study, we extracted the disease-associated genes using the DisGeNET (Piñero et al. 2016) database. We examined whether those enriched pathways include the disease-associated genes in DisGeNET, that is, with fraction of pathways with at least two disease-associated genes over all enriched pathways. We found that the disease module calculated by RFIM shows the highest number of enriched pathways for five (six) diseases integrated with STRING (iRefIndex) in the disease module detection (see Supplemental Fig. S1A) and this finding is valid if we counted the number of enriched pathways with at least four disease-associated genes (see Supplemental Fig. S1B). We also compared the P-values of gene set enrichment analysis (GSEA) between genes in the disease module and the KEGG pathways related to the phenotype of interest, finding that RFIM shows the highest P-value in three of the six phenotypes (see Supplemental Fig. S2A,B). Note that there are no KEGG pathways associated with COPD and ovarian cancer; and there are no significant KEGG pathways (with P < 0.05, based on GSEA) associated with breast cancer and gastric cancer. Hence, those four diseases were not considered here.
Robustness of disease module detection methods to the incompleteness of the interactome
The phenotype-specific disease module is apparently determined by both interactome and gene-wise P-values. Yet, the interactome is highly incomplete, covering a small fraction of known PPIs. To investigate the sensitivity of each disease module detection method to the incompleteness of interactome, we calculated the overlap between the disease modules for different levels of incompleteness of the underlying interactome. We firstly applied the disease module into the original interactome. Then, a fraction of PPIs randomly selected from the original interactome were removed. Finally, we performed the disease module detection algorithms again on the perturbed interactome and compared the fraction of overlapping genes in the union genes of the disease module identified from the original and perturbed interactome, respectively. Figure 5A,B shows that RFIM and ROBUST are more robust than other four methods, regardless of the fraction of PPIs have been removed.
Sensitivity of disease module detection to the interactome. For each interactome, STRING (A) or iRefIndex (B), we first applied each disease module into the original interactome. Then, a fraction of protein–protein interactions (PPIs) randomly selected from the original interactome were removed. Finally, we performed the disease module detection algorithms again using perturbed interactome and compared the fraction of overlapping genes in the union genes of the disease module identified from the original and perturbed interactome, respectively.
To examine the meaningfulness of the identified disease modules (Lazareva et al. 2021), we performed two meaningfulness tests: (1) KEGG gene set enrichment analysis (GSEA). We compared the P-value of gene set in the disease module identified from the original PPI network with that identified from 10 randomized PPI networks generated by each of the following five random network generators: degree preserving, expected degree preserving, topology preserving, and scale-free and uniform generators. (2) Overlap with DisGeNET disease genes. We compared the overlap genes with DisGeNET genes in the original PPI network with that in 10 randomized PPI networks generated by each of the above five random network generators. We found that those two meaningfulness tests display significant difference between modules on the original network and randomized networks (see Supplemental Fig. S3,A1,A2;B1,B2).
Disease module and enriched pathways
We visualized the structure of the disease module identified for asthma using our RFIM approach and the STRING interactome. We found that there are several sub-modules, each of which includes at least one gene that is significantly associated with disease (based on GWAS gene-wise P-value < 0.001; see Fig. 6A, red nodes). The disease module apparently contains many genes that are not significantly associated with the disease (i.e., with GWAS gene-wise P-value ≥ 0.001; see Fig. 6A, blue nodes). Those genes are “absorbed” into the disease module owing to their direct connection with those genes with very low GWAS P-values. We further performed the functional enrichment analysis of genes in the disease module using gprofiler2 (Kolberg et al. 2020). We found that these genes in the disease module are associated with many functional terms (see Fig. 6B). Finally, we showed the top-10 enriched KEGG pathways (with lowest P-values in Fig. 6B) enriched with genes in the disease module (see Fig. 6C). For example, in asthma, we found proteasome inhibition, Spliceosome and Notch signaling, all of which have been reported in asthma literature (Elliott et al. 1999; Hussain et al. 2017; Chen et al. 2019). In particular, Th2 cells and their cytokines play a role in the pathophysiology of allergic and nonallergic asthma (Truyen 2006). See Supplemental Figures S4A1–C10 and S5A1–C10 for the disease modules and functional terns of other disease phenotypes.
Submodules in the asthma disease module and the enriched functional terms. (A) Genes in the asthma disease module form several sub-modules. Genes with P-values lower (or higher) than 0.001 are colored with red (or blue), respectively. (B) Enriched functional terms of genes in disease module of asthma using gprofiler2 (Kolberg et al. 2020). (C) Top-10 enriched KEGG pathways of genes in the asthma disease module using STRING.
We also examined the biological relevance of these genes belonging to the disease module. To narrow down the validation space, we focused on the common genes simultaneously identified by at least four methods (see Supplemental Fig. S6A,B for the pairwise overlap of disease modules identified by any two methods). We anticipate that those common genes are more important than genes identified by a single method. We found that those common genes were typically not significantly associated with the disease (based on the GWAS gene-wise P-values ≥ 0.001 (see Table 2). Yet, almost all these genes have been shown to be relevant for the particular disease. For example, for COPD, POFUT2 is a Notch signaling pathway gene associated with smoking and COPD (Tilley et al. 2009). For asthma, the gene IL6 has shown active role in pathogenies of asthma and COPD (Rincon and Irvin 2012). For lung cancer, loss of CDH1 up-regulated epidermal growth factor receptor in non-small-cell lung cancer cells (Liu et al. 2013). And HLA-DPA1 has been shown to be associated with lung cancer (Heo et al. 2021). For CVD, JAK2 is involved in the pathogenesis and has potential to mediate CVD (Kirabo and Sayeski 2010). For diabetes, SMURF1 is promising strategies to block cardiac fibrosis in the early stage of diabetes (Bai et al. 2016). GRB2-mediated HER2 signing plays a critical role in gastric cancer development (Yu et al. 2009). PABPC1 was up-regulated in ovarian cancer samples and higher expression of PABPC1 relates to a shorter survival for patients with ovarian cancer (Feng et al. 2021). PRKACB was implicated in the progression of colon and prostate cancers (Merkle and Hoffmann 2011). These results imply that the genes in the disease module can be potentially associated with specific diseases despite their nonsignificance based on the current GWAS.
Biological relevance of genes simultaneously identified by at least four disease module detection methods
Validation of disease module genes via GWAS of different sample sizes
To further validate the genes in disease modules, we applied the five disease module detection methods to additional GWAS of smaller sizes for COPD, CVD, and diabetes. For each disease, we examined whether those genes in the disease module identified from the small GWAS can still be found in the large GWAS. For our RFIM method, we found that over 40% of the genes in the disease module identified from the small GWAS can still be identified in the disease module identified from the large GWAS, regardless of the disease or the interactome (see Fig. 7A,B). Moreover, this overlap between the disease modules detected by RFIM is much higher than that of the other five methods, regardless of disease and interactome.
Overlap of disease modules detected from small and large genome-wide association studies (GWAS) of the same disease. For each
interactome, STRING (A) or iRefIndex (B), we applied each disease module detection method into the two GWAS of the same disease, separately. Denote the disease modules
identified from the small and big GWAS as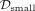 
and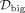 
, respectively. Then, the overlap is defined as 
.
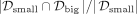Discussion
A complex disease can be linked to a well-defined neighborhood of the cellular molecular interactome, referred to as the disease module. Detecting the disease module allows us to identify genes most likely to involved in the disease. These genes do not necessarily have significant P-values in GWAS or other omics data, and hence cannot be easily identified without leveraging the human interactome. Here, we developed a novel disease module detection method based on a statistical physics model RFIM, which is both mathematically rigorous and computationally efficient. We applied our method to analyze six GWAS data sets, covering well-defined complex disease phenotypes. We found that the disease modules identified by RFIM display higher connectivity and more enriched pathways than the other existing methods. Furthermore, we found literature evidence that those genes in the disease module (especially those common genes identified by different methods) have significant associations with the specific disease.
Our RFIM approach can be naturally used to integrate other omics data, for example, gene expression and DNA methylation, with the interactome. We admit that applying a disease module detection method via integrating omics data and the human interactome sometimes requires an annotation, which might lead to inaccuracy. For example, GWAS signals (Regan et al. 2010; Pedroso and Breen 2011; Pedroso et al. 2012; Cho et al. 2014) do not provide precise localization to a gene and the affected gene could be located at great genomic distance. Yet, we expect that using nearby genes is accurate enough to create meaningful disease modules.
Our RFIM framework does have limitations. First, the score of each gene is calculated from the gene-wise P-value; thus, the final disease module heavily relies on the quality of the GWAS, that is, the sample size and other covariates that can impact the P-value associated with each gene. Second, the disease module identified by RFIM can be constituted by multiple disconnected submodules. This is because RFIM identifies the disease module by solving a global optimization problem over the entire interactome, and it does not require that the disease module is a single connected component in the human interactome. In addition, evaluation of modules using phenotype-specific methods were not performed in the current analysis.
Methods
Random-field Ising model (RFIM)
We formalized the disease module detection into finding the optimal gene state {σi}, also called the ground state, that minimizes the cost function of Eq. (1) (see Supplemental Material, Sec. 2 for other optimal subgraphs identification methods). The first term in the right-hand side of Eq. (1) represents the influence of nodes (genes) on their neighbors’ states. By defining non-negative edge weights {Jij}, we implicitly assume that neighboring nodes (genes) in the interactome tend to have the same state; that is, they tend to belong to the disease module (or not) together. In other words, Jij > 0 favors positive correlations between the states of nodes i and j. The stronger the Jij value, the more likely nodes i and j have the same state. In the case of Jij = 0, the states of nodes i and j are totally independent. The second term on the right-hand side of Eq. (1) stands for the intrinsic preference of nodes belonging to the disease module regardless of the states of their neighboring nodes. The intrinsic preference of node i can be quantified as hi = Φ−1(1 − pi), where Φ−1 is the inverse normal cumulative distribution function and pi is the P-value of node (gene) i calculated from the omics profile. Note that hi is a monotonically decreasing function of pi with hi → +∞ as pi → 0 and hi → −∞ as pi → 1. Nodes with very positive hi (or equivalently, very small pi) tend to belong to the disease module.
The parameter H is introduced to regulate the contributions of the two terms in Eq. (1). Note that the value of H effectively controls the average state variable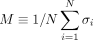 
of the system, or equivalently, the disease module size given by (1 + M)N/2. For example, if H is extremely low such that (H + hi) < 0 for all the nodes, then the ground state is simply {σi = −1}; that is, all nodes will be inactive (M = −1 and there is no disease module, which is a trivial solution. With gradually increasing H, more nodes will be active. Eventually, if H is high enough such that (H + hi) > 0 for all the nodes, then the ground state is {σi = +1}; that is, all nodes will be active (M = +1), and the whole interactome is the disease module, which is also a trivial solution. Hence, by controlling the parameter H, we can obtain a disease module with any desired size between 0 and N.
In our calculation, we define the edge weight Jij = max(0, hi + hj) if nodes i and j are connected in the interactome, and Jij = 0 otherwise. This definition of Jij is to ensure that (1) the two terms in the right-hand side of Eq. (1) are numerically comparable and (2) Jij is non-negative even in case the intrinsic preference of nodes i (or j) belonging to the disease module is extremely low (i.e., with hi or hj → −∞). Note that the disease module calculated from the active nodes in the ground state of the RFIM is not necessarily a
single-connected component. In fact, it might contain multiple-connected components in the network G. To ensure the connectivity of the disease module is not too low, we modify the intrinsic preference of node i belonging to the disease module as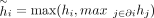 
, where ∂i represents the neighborhood (i.e., the set of neighboring nodes) of node i.
Calculation of the M(H) curve of RFIM
To calculate the M(H) curve of RFIM, we first need to calculate the exact ground state of the system at an arbitrary applied external field H. This is the basic step of calculating the M(H) curve, that is, the ground-state evolution for varying H. There is a well-known mapping of the ground-state problem of RFIM to a min-cut/max-flow problem in combinatorial optimization. The mapping and the so-called push-relabel algorithm for the min-cut/max-flow problem has been well described in the literature (Cherkassky and Goldberg 1997). The run time of the push-relabel algorithm (Cherkassky and Goldberg 1997) scales as O(N4/3) with N the system size (number of nodes). The M(H) curve can be calculated with the method reported in Hartmann (1998) and Frontera et al. (2000). It is essentially based on the fact that the ground state energy is convex up in H, which allows for estimates of the fields H where the magnetization jumps (called “avalanches”) occur. This algorithm finds steps by narrowing down ranges where the magnetization jumps with an efficient linear interpolation scheme (Frontera et al. 2000). Applying the no-passing rule (i.e., flipped spins can never flip back with increasing H) can further speed up the calculation of the RFIM M(H) curve (Liu and Dahmen 2007). It has been shown that for RFIM, the continuous distribution of external field (e.g., Gaussian distribution) can exclude the ground-state degeneracies (Alava and Rieger 1998; Hartmann 1998). As the P-values in our model were transformed using an inverse normal cumulative distribution, the external field of each gene/node is also continuous. Therefore, the optimal solution is unique. For our RFIM approach, we calculated the M(H) curve of the RFIM by systematically tuning H. The disease module is detected from the ground state of the RFIM at H = Hc. We chose Hc to ensure the disease module reaches a desired size. We found that M(H) curve can display abrupt increasing with H, thus we chose module size consisting of <5% of the total genes in the GWAS for all phenotypes. Otherwise, the module size over different phenotypes can vary significantly.
Data sets
Interactome
For each disease, we overlaid the GWAS gene-wise P-values onto the human interactome. For the human interactome, we used the STRING (Franceschini et al. 2012) (9606.protein.links.v11.5.txt) database (http://string-db.org), which aims to provide a critical assessment and integration of PPIs, including both direct (physical) and indirect (functional) associations. We removed the PPIs whose normalized scores are lower than 0.7. The STRING Ensemble protein id (ENSP) is transformed into preferred gene name (e.g., Entrez Gene ID) using the protein information (9606.protein.info.v11.5.txt) downloaded from the STRING database. To examine the impact of different interactomes on the disease module detection methods, we also used another interactome iRefIndex (Razick et al. 2008; Aranda et al. 2011) from the data set extracted using R (R Core Team 2013) package cisPath (Wang et al. 2015) (version 1.28.0).
GWAS
We used MAGMA (de Leeuw et al. 2015) (Multi-marker Analysis of GenoMic Annotation) to analyze the GWAS data. In MAGMA, SNPs were annotated to the genes based on dbSNP version 135 SNP location and NCBI 37.3. Two gene annotations were used in MAGMA. Only SNPs located between a gene's transcription start and stop sites were annotated to that gene for the main analyses and a 10 kilobase window around each gene was made in additional annotation (de Leeuw et al. 2015). The GWAS data of CVD were downloaded from http://www.cardiogramplusc4d.org/data-downloads/ (version 2015). The GWAS data of diabetes were downloaded from http://diagram-consortium.org/downloads.html (Version 2016). The GWAS data of COPD were collected in Hobbs et al. (2017), which combines 26 cohorts containing 63,192 individuals (15,256 COPD cases and 47,936 controls). The P-values and annotations of SNPs for CVD, diabetes, and COPD were obtained using MAGMA. For the asthma, breast cancer, lung cancer, colorectal cancer, gastric cancer, ovarian cancer (Ishigaki et al. 2020), and prostate cancer data sets, the P-values of SNPs were directly downloaded from http://jenger.riken.jp/en/result and SNPs have been annotated to the genes in the summary results. The P-value of each gene in all data sets was obtained using mean χ2 statistic of SNPs included in the gene and a known approximation of the sampling distribution of the mean χ2 statistic (Brown 1975; Hou 2005) using MAGMA.
Software availability
All data and scripts are available at GitHub (https://github.com/spxuw/RFIM) and as Supplemental Code.
Competing interest statement
In the past three years, M.H.C. and E.K.S. received grant support from GlaxoSmithKline and Bayer. M.H.C. has received consulting or speaking fees from Genentech, AstraZeneca, and Illumina. The other authors declare no competing interests.
Acknowledgments
We thank all three reviewers for their very constructive comments and suggestions.
Author contributions: Y.-Y.L. conceived and designed the project. X.-W.W. and D.Q. prepared the GWAS data. X.-W.W. did all the further calculations and data analysis. X.-W.W. and Y.-Y.L. wrote the manuscript. All authors contributed to result interpretation and revised the manuscript.
Footnotes
-
[Supplemental material is available for this article.]
-
Article published online before print. Article, supplemental material, and publication date are at https://www.genome.org/cgi/doi/10.1101/gr.276690.122.
- Received February 18, 2022.
- Accepted August 23, 2022.
This article is distributed exclusively by Cold Spring Harbor Laboratory Press for the first six months after the full-issue publication date (see https://genome.cshlp.org/site/misc/terms.xhtml). After six months, it is available under a Creative Commons License (Attribution-NonCommercial 4.0 International), as described at http://creativecommons.org/licenses/by-nc/4.0.
