A statistical physics approach for disease module detection

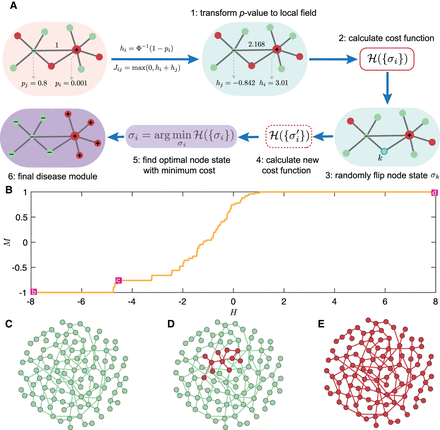
Disease module inference using statistical physics approach: a demonstration. (A) Schematic demonstration of the Random-field Ising model (RFIM) approach consisting of the following steps: (1) Given a graph and gene-wise P-value associated with each node, we first transform P-value to node weight and assigned weight to each edge. (2) For any gene state {σ_i}, we calculated the cost function 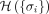. (3) An optimization method was used to find the optimal gene state {σ_i} that minimizes the cost function. (4) All genes with state σ_i = 1 are those genes in the disease module. (B) The magnetization curve M(H) of the random network system. A random network with N = 100 nodes (genes). Each gene is assigned a P-value, randomly chosen from a uniform distribution U(0, 1). The node weights h_i are then computed using the inverse normal CDF. The edge weights J_ij = max(0, h_i + h_j) if two genes are connected in the network. Otherwise, J_ij = 0. The magnetization 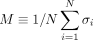is the average state of nodes in the system. As we increase the external field H, more nodes (genes) will be active, that is, M will monotonically increase and eventually approach 1. (C–E) disease module identified by RFIM at H = −8 (point b), H = −4 (point c) and H = 8 (point d), respectively. All the active components (highlighted in red) together can be considered as the disease module.