Modeling expression ranks for noise-tolerant differential expression analysis of scRNA-seq data

  1. Debarka Sengupta1,7,9,10
  1. 1Department of Computer Science and Engineering, Indraprastha Institute of Information Technology, Delhi 110020, India;
  2. 2Max Planck Institute of Molecular Cell Biology and Genetics, Dresden 01307, Germany;
  3. 3Microsoft India Private Limited, Hyderabad, Telangana 500032, India;
  4. 4Fluidigm Corporation, South San Francisco, California 94080, USA;
  5. 5Department of Computer Science, Jadavpur University, Kolkata, West Bengal 700032, India;
  6. 6Machine Intelligence Unit, Indian Statistical Institute, Kolkata 700108, India;
  7. 7Department of Computational Biology, Indraprastha Institute of Information Technology, Delhi 110020, India;
  8. 8Interdisciplinary Statistical Research Unit, Indian Statistical Institute, Kolkata 700108, India;
  9. 9Centre for Artificial Intelligence, Indraprastha Institute of Information Technology, Delhi 110020, India;
  10. 10Institute of Health and Biomedical Innovation, Queensland University of Technology, Brisbane, QLD 4000, Australia
  • Corresponding authors: debarka{at}iiitd.ac.in, debarka.sengupta{at}qut.edu.au, abhik.ghosh{at}isical.ac.in
    •  
    Next Section

    Abstract

    Systematic delineation of complex biological systems is an ever-challenging and resource-intensive process. Single-cell transcriptomics allows us to study cell-to-cell variability in complex tissues at an unprecedented resolution. Accurate modeling of gene expression plays a critical role in the statistical determination of tissue-specific gene expression patterns. In the past few years, considerable efforts have been made to identify appropriate parametric models for single-cell expression data. The zero-inflated version of Poisson/negative binomial and log-normal distributions have emerged as the most popular alternatives owing to their ability to accommodate high dropout rates, as commonly observed in single-cell data. Although the majority of the parametric approaches directly model expression estimates, we explore the potential of modeling expression ranks, as robust surrogates for transcript abundance. Here we examined the performance of the discrete generalized beta distribution (DGBD) on real data and devised a Wald-type test for comparing gene expression across two phenotypically divergent groups of single cells. We performed a comprehensive assessment of the proposed method to understand its advantages compared with some of the existing best-practice approaches. We concluded that besides striking a reasonable balance between Type I and Type II errors, ROSeq, the proposed differential expression test, is exceptionally robust to expression noise and scales rapidly with increasing sample size. For wider dissemination and adoption of the method, we created an R package called ROSeq and made it available on the Bioconductor platform.

    In the past few years, single-cell RNA-sequencing (scRNA-seq) has significantly accelerated the characterization of molecular heterogeneity in healthy and diseased tissue samples (Tanay and Regev 2017). The declining costs of library preparation and sequencing have fostered the adoption of single-cell transcriptomics as a routine assay in studies arising from diverse domains, including stem cell research, oncology, and developmental biology (Kumar et al. 2017; Zhu et al. 2017). Advanced droplet-based scRNA-seq technologies can profile several thousands of cells in a single experiment (Macosko et al. 2015; Zheng et al. 2017). Despite considerable progress in technology development, expression readouts obtained from these high-throughput platforms suffer from various technical and trivial biological distortions (Sengupta et al. 2016; Vallejos et al. 2017). These include single-cell library size differences, cell cycle effects, amplification bias, low RNA capture rate, and high levels of dropout events (Kharchenko et al. 2014). Different from bulk RNA sequencing, gene expression modeling in single cells requires special statistical considerations (Grün et al. 2014). A number of parametric and nonparametric methods have already been proposed for modeling single-cell expression data and finding differentially expressed genes (DEGs). SCDE (Kharchenko et al. 2014), MAST (Finak et al. 2015), and BPSC (Vu et al. 2016) are notable among these. SCDE and MAST model gene expression using well-known probability density functions and mixture models involving some of those. BPSC, on the other hand, handles single-cell expression bimodality by using a beta-Poisson mixture. Different from these, we hypothesize that considering expression ranks instead of absolute expression estimates would make a model less susceptible to the noise and the technical bias, as commonly observed in single-cell data. To realize the same, here we investigate the suitability of discrete generalized beta distribution (DGBD) (Martínez-Mekler et al. 2009) in modeling the distribution of expression ranks instead of the raw count. The consideration of rank-ordering distribution is inspired by the seminal work by Martínez-Mekler and colleagues, in which they showed the universal applicability of the same in linking frequency estimates and their ranks (Martínez-Mekler et al. 2009). In this article, we report ROSeq, a Wald-type test to determine differential expression from scRNA-seq data, by using DGBD-based modeling of gene expression.

    Previous SectionNext Section

    Results

    Overview of ROSeq

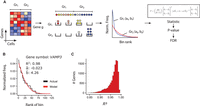
    Since the introduction of the single-cell technologies, numerous parametric models have been proposed, primarily accounting for dropout events. The majority of these are mixture models of distinct probability density functions. We conjecture that a limitation of such approaches could be that they disregard the other noise sources as enumerated in the Introduction section. Ranks are commonly known to be more robust compared with the corresponding expression estimates. In fact, with the increase in sample size, single-cell studies are now seen embracing the traditional Wilcoxon's rank-sum test to identify DEGs. Although nonparametric methods are assumption free (Sengupta et al. 2016), they often lack statistical power. In this work, we explored the utility of discretizing an expression vector into bins and ordering them (meaning ordering ranks corresponding to bins) based on bin-wise cellular frequencies, thereby making it modelable by DGBD (also known as rank-ordered distribution) (Fig. 1A; Martínez-Mekler et al. 2009). Fitting DGBD on expression readouts involves maximum likelihood estimates (MLEs) of two shape parameters, denoted by a and b. Figure 1B depicts an example of DGBD-based modeling of VAMP3 expression across 288 single cells from the biological replicate NA19098 of the Tung data (Tung et al. 2017). (For data set description and naming convention refer to Methods.) For a comprehensive assessment of the quality of fit, we estimated R2 for all the 11,513 genes that qualified the filtering criteria. DGBD fits yielded R2 > 0.9 for a vast majority of the genes (Fig. 1C), thereby underscoring its appropriateness in modeling expression ranks. Leveraging DGBD-based modeling of expression, we devised ROSeq, a Wald-type test to determine differential expression in single-cell data (Fig. 1A). We inspected the gene expression marginals (empirical distribution approximated using the density function by R) and the corresponding DGBD fits for some example DE/non-DE genes (called using ROSeq). We noticed that DGBD significantly stabilizes the shape diversity, as otherwise observed in the case of the gene expression marginals (Supplemental Figs. S1, S2). This highlights the strength of rank-ordered distribution, which homogenizes diversely shaped marginals and enables reliable estimation of the distribution parameters.

    Figure 1.
    View larger version:
    Figure 1.

    Modeling single-cell gene expression using ROSeq. (A) As part of the ROSeq differential expression analysis workflow, cells are first binned depending on expression values associated with a particular gene. For each cell-group, bins are ranked depending on cell frequency. The discrete generalized beta distribution (DGBD) is used as a probability mass function to express a normalized bin-wise cell frequency as a function of its corresponding rank using two real parameters a and b. A Wald-type test is used on the MLE of these parameters across the cell-groups to find differentially expressed genes. (B) DGBD-based modeling of VAMP3 expression (source: Tung data) (Tung et al. 2017). Discretized expression bins are ranked based on normalized bin-wise cellular frequencies. (C) Distribution of R2 values obtained from DGBD-based modeling of 11,513 expressed genes (source: Tung data) (Tung et al. 2017).

    Comparative benchmarking based on matched bulk RNA sequencing data

    Tissue-level measurement of gene expression is considered more robust compared with single-cell-based estimates. As such, it is a common practice to benchmark single-cell-based DEG calls against DEGs obtained from matched bulk expression profiles. We accessed scRNA-seq data from three previous studies that also performed bulk RNA-seq on the same samples. Description of the data sets can be found in the Methods section. A total of eight contrasting cell-group pairs were constructed as follows: myoblasts before and 24 h after differentiation (source: Trapnell data) (Trapnell et al. 2014), all three pairs of biological replicates of induced pluripotent stem cells (iPSCs) (source: Tung data) (Tung et al. 2017), and all three pairs of undifferentiated H1, H9 human embryonic stem cells (ESCs) and neuronal progenitor cells (NPCs; source: Chu data) (Chu et al. 2016). We also profiled single expression of foreskin BJ fibroblasts and K562 cells, with matching bulk replicates (referred to as Gupta data) (Supplemental Table S1). We used the standard Seurat pipeline (without batch correction) (Butler et al. 2018) to visualize the single cells in the presence of batch information and obtained perfect segregation between the two cell types (Supplemental Fig. S3), strengthening the case for straightforward differential expression analysis. Bulk replicates were used for confident DEG calls. In addition to ROSeq, single-cell DEG calls were made using five best-practice methods, namely, BPSC, SCDE, Wilcoxon's rank-sum test, MAST, and DESeq2 (Love et al. 2014). A single-cell DEG call was considered true positive if the gene was also present in the list of DEGs detected by analyzing the matching bulk transcriptomes. If not, it was counted as a false positive (Supplemental Tables S2–S9). In six out of the eight cases, ROSeq topped in terms of the estimated area under the ROC curve (AUC-ROC) values (Fig. 2A–C; Supplemental Fig. S4A,B,E). SCDE performed best in the remaining two cases, with a negligible margin over ROSeq (Supplemental Fig. S4C,D). Although DESeq2 is not specialized for single cells, we used it as a control to ensure single-cell-focused methods yield overall better performance.

    Figure 2.
    View larger version:
    Figure 2.

    Benchmarking of single-cell DE call accuracy against DE genes detected at tissue levels. (A) ROC and the associated AUC values obtained by bulk-based benchmarking of single-cell DEG calls between BJ and K562 cells (Gupta data). (B) ROC plot for H1 and H9 cells (source: Chu data) (Chu et al. 2016). (C) ROC plot for NA19098 and NA19239 cells (source: Tung data) (Tung et al. 2017).

    Besides AUC, we also tracked other popular measurements of classification accuracy, including F1, Matthews correlation coefficient (MCC) (Sing et al. 2005), and Cohen's kappa (k) (Kvålseth 1989). Among these, MCC factors in the performance of a binary classification system in all four confusion matrix categories, whereas k corrects the accuracy measurement by the expected performance. Of note, F1, MCC, and k were calculated on confusion matrices determined using a cutoff on the differential expression probabilities computed on the scRNA-seq data sets. Such a cutoff maximizes the sum of sensitivity and specificity (Robin et al. 2011). In the majority of the cases, ROSeq maximized these scores, with striking margins in the case of MCC and k. Based on the overall performance, the methods can be rank-ordered as follows: ROSeq, SCDE, MAST, Wilcoxon, BPSC, DESeq2 (Supplemental Table S10).

    ROSeq uses a constant k, which is multiplied with σ, that is, the standard deviation of the pooled expression estimates across the cell-groups (Methods). We observed that the choice of k impacts ROSeq's performance. On the Gupta data set comprising BJ fibroblasts and K562 cells, we assessed five different values of k: 0.01, 0.05, 0.1, 0.2, and 0.5. k = 0.05 stood out clearly, thereby strengthening its choice as a default (Supplemental Table S11). It should be noted that benchmarking with regard to bulk DE calls only helps show the robustness of single-cell DE analysis methods. However, in practice, single-cell expression studies are indispensable to decipher tissue heterogeneity, which is otherwise masked in bulk-based expression readouts. As a standard practice, one should first cluster the single-cell expression profiles based on gene expression similarity and perform DE analysis across the identified clusters.

    Type I errors

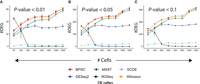
    To evaluate the Type I error control associated with ROSeq, we constructed several null data sets by segregating cells of the same type into two groups for varied group sizes (Soneson and Robinson 2018). For each of the methods, we tracked the fraction of the tested genes that were assigned a nominal P-value. Three different cutoffs—namely, 0.01, 0.05, 0.1—were considered for the P-values. We iterated this simulation experiment for varied cell-group sizes: 50, 100, 200, 300, 400, 500, 1000, and 1500. For each cell-group size, 20 null data sets were constructed and subjected to the DEG callers. For this experiment, we used Jurkat transcriptomes from the Zheng data (Zheng et al. 2017). In addition to ROSeq, five other methods, namely, BPSC, SCDE, Wilcoxon's rank-sum test, MAST, and DESeq2, were considered for performance comparison. Among all the six methods, ROSeq offered the overall best performance in all cases except for the cell-groups having 100 or a smaller number of cells (Fig. 3A–C). With 50/100 cells in each group, SCDE outperformed ROSeq. With more cells, the structure of the rank-frequency distributions is comprehended more precisely, because it helps in modeling the distribution spectrum in a finer grid. Additionally, the testing procedure in ROSeq uses the asymptotic critical values (obtained through the large-sample theory), which yields better inference for larger sample sizes. ROSeq discretizes the observed expression by binning before fitting DGBD. As a result, as opposed to other methods, ROSeq needs to approximate gene expression marginals with smaller effective sample sizes. This negatively influences the parameter estimation process and can explain ROSeq's suboptimal performance on smaller groups of cells. The rest of the methods, including the successors of SCDE, made a significant number of DEG calls. ROSeq was found to be the only method that neared zero DEG calls with increased sample size. We tracked standard error (SE) scores across the various cases, which showed least variability to shuffling of the data.

    Figure 3.
    View larger version:
    Figure 3.

    Type I error rates. (A) Line chart showing Type I error rates with SE (depicted by error bars), obtained by applying different DEG callers on 20 randomly sampled null data sets, for varied cell-group sizes. We applied a P-value cutoff of 0.01. These experiments were performed using Jurkat transcriptomes (approximately 3200 cells and approximately 32,000 transcripts) (Zheng et al. 2017). (B,C) Similar plots with P-value cutoff of 0.05 and 0.1, respectively.

    Tolerance to noise owing to excessive dropout events

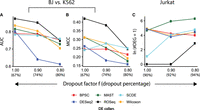
    As stated earlier, single-cell gene expression readouts are distorted by technical biases such as RNA degradation during cell isolation and processing, variable reagent amounts, the presence of cellular debris, and PCR amplification bias. Further, because of the small number of detected molecules, single-cell expression estimates are inherently noisy, even in the absence of technical variability (Sengupta et al. 2016). The majority of the state-of-the-art dropout induction methods simulate scRNA-seq data with variable concentration of dropouts. This approach often involves making strong assumptions about gene expression marginals. We developed a strategy to inject dropouts in a real scRNA-seq data set by exploiting the linear relationship between average read count and log-odds of dropout rate, as described elsewhere (Zappia et al. 2017). This allowed us to introduce varied levels of dropouts by the means of controlling average read counts (Methods). We introduced various levels of dropouts (67%–80%) in BJ fibroblasts and K562 cells. DEGs detected by analyzing matching bulk RNA-seq data sets were used to compute AUC and MCC values. ROSeq clearly dominated the rest of the methods in calling the correct DEGs (Fig. 4A,B). We also evaluated the Type I errors by constructing null data by sampling Jurkat transcriptomes (source: Zheng data set) (Zheng et al. 2017). As expected, ROSeq made the least number of DEG calls as we increased the dropout levels from 90% to 94% (Fig. 4C). As an independent approach, we used the Splatter R package (Zappia et al. 2017) to generate null data sets with variable dropout concentrations, which helped us to track the Type I error rates. ROSeq's performance remained consistent (Supplemental Fig. S5). Collectively, these experiments reinforce the tolerance of ROSeq to noise caused by dropouts.

    Figure 4.
    View larger version:
    Figure 4.

    Tolerance against expression dropouts. (A) Line chart showing decline in AUC with the increase in dropout levels. Performance was recorded on the Gupta data set comprising BJ fibroblasts and K562 cells. (B) Line chart showing MCC values that largely mirror AUC values in subfigure A. (C) Line chart showing the trend of increased false DEG calls with the increase in dropout levels. Null data sets were created using Jurkat cell transcriptomes from the Zheng data set. Each of the contrasting groups contains 1000 cells.

    Runtime efficiency

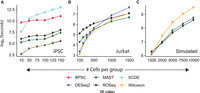
    The advent of droplet-based commercial platforms that has enabled profiling of tens of thousands of cells in a single experiment has become a common affair. Unsupervised clustering of large-scale scRNA-seq data produces numerous clusters, each of which typically harbors a large number of cells. As such, besides accuracy, the scalability has become a desirable feature for the DEG callers. We benchmarked time consumption by the methods for variable sizes of input scRNA-seq data sets. For the construction of the data sets, we performed the same steps as we did for estimating the Type I error rates. SCDE and BPSC are considerably slow compared with the rest of the methods (Fig. 5A). As such, we used a small data set constituting 288 iPSCs (replicate id: NA19098) for tracking the execution time for all six methods (sampled scRNA-seq profiles with replacement owing to lack of cells). These data consist of 19,027 transcripts. ROSeq secured fourth place, following Wilcoxon, DESeq2, and MAST. SCDE was the slowest among them all, followed by BPSC (Fig. 5A). To test on larger sample sizes, we made use of the Jurkat transcriptomes (source: Zheng data) (Zheng et al. 2017), which allowed us to split the cells randomly into two equal-sized groups (without replacement) with a maximum 1500 cells in each group. These data consist of 32,738 transcripts. We dropped SCDE and BPSC from the comparison owing to their slower turnaround time. Cell-group sizes varied between 100 and 1500. Although all the methods took similar amounts of time, ROSeq showed a downward turn as the cell numbers increased (Fig. 5B). This inspired us to speed-test the methods further on even larger sample sizes. To this end, we used the Splatter R package to simulate cells in up to 10,000-sized groups (6000 genes). In this case, ROSeq turned out to be the fastest (Fig. 5C). MAST showed a similar performance, whereas Wilcoxon diverged significantly, thus suggesting some computing bottleneck. All experiments reported in this article were performed on a workstation configured with AMD Ryzen 7 3700X eight-core processor with a clock speed of 4249.648 MHz, 64GB DDR4 RAM, and an Ubuntu 18.04.4 LTS operating system with 5.3.0-40-generic kernel. For the iPSC data, we used a single core; for the remaining larger data sets, we used four cores. We observed that ROSeq speeds up significantly as the number of cores are increased.

    Figure 5.
    View larger version:
    Figure 5.

    Tracking execution time on scRNA-seq data of varied sizes. (A) Line chart showing median time taken by each algorithm on 100 randomly sampled null data sets containing iPSC transcriptomes (replicate id: NA19098). (B) Line chart showing median time taken by each algorithm on 20 randomly sampled null data sets containing Jurkat transcriptomes. (C) Line chart showing median time taken by each algorithm on 20 randomly sampled null data sets using the Splatter R package (Zappia et al. 2017). Note that for the iPSC data, we used a single CPU core; for the remaining larger data sets, we used four cores of the workstation.

    Previous SectionNext Section

    Discussion

    Martínez-Mekler and colleagues showed that two-parameter DGBD (rank-ordered distribution) gives excellent fits to diverse phenomena, arising from the arts and the social and natural sciences (Martínez-Mekler et al. 2009). We evaluated the applicability of DGBD to gene expression data. We found DGBD to fit well to the entire spectrum of expressed genes of varying expression levels. We further developed ROSeq, a DGBD-based Wald-type test, for differential expression analysis of scRNA-seq data. Most of the statistical models for single-cell expression data use mixed models to accommodate high dropout rates. ROSeq discretizes the data, thereby stabilizing local distortions in the shape of the distribution, owing to noise and technical bias. This conclusion is strengthened by our experimentation with dropouts. ROSeq showed the best performance with the increase in artificially injected dropout levels. Most of the methods that rely on negative binomial or Poisson distributions enforce raw count data as input. ROSeq works on real values and does not impose such constraints. This is particularly beneficial because integrative single-cell omics studies are very common these days, which typically involve batch correction that inevitably transform the read counts into real values. In this regard, it should be noted that ROSeq is not inbuilt with any batch correction method. As such, it expects the user to input an scRNA-seq data set that is not only library size normalized but also free of other covariates as applicable.

    We systematically compared the performance of ROSeq with some of the existing best-practice methods such as SCDE, MAST, and BPSC, which are largely tailored for single-cell expression data. Among various critical observations, our systematic tracking of Type I errors revealed that a relatively higher number of cells (at least 100 in each contrasting group) is required for ROSeq to attain optimal performance comparable with SCDE. Current studies report hundreds to thousands of cells per unsupervised cell cluster with the advent of droplet-based single-cell profiling platforms. As such, we do not foresee any hindrance to ROSeq's applicability owing to cell paucity. However, ROSeq might produce suboptimal DEG calls if a cluster contains a small number of cells. Diverse types of progenitor cells, circulating tumor cells, etc., are examples of such rare cell types (Jindal et al. 2018). This shortcoming can be attributed to ROSeq's use of asymptotic distribution.

    Statistical test of differential expression involves comparing the marginal distribution of a gene's expression across two cell-groups. Gene expression marginals in single cells vary widely across platforms and chemistry and cellular conditions. As such, it is difficult to rely on any specific parametric distribution function for modeling gene expression in single cells. Conversely, ROSeq analyzes the distribution of rank-ordered discretized expression bins across two cell-populations. We showed that rank-ordered distribution stabilizes diversely shaped gene expression marginals (Supplemental Figs. S1, S2) while capturing necessary information about lineage/condition-specific expression patterns. Although ranks are considered to be lossy, they provide a means to bypass expression modeling. The results presented in this work suggest that it could be beneficial to model gene expression ranks compared with gene expression.

    Benchmarking bulk tissue-based DEG calls underscored competitive performance by the methods, tailored for single-cell expression data. However, SCDE and ROSeq maximized the DEG call accuracy. ROSeq is particularly powerful when the single-cell-based expression estimates are inherently noisy. In such cases, ROSeq by far outwits the other tested methods. Further, with an increased number of input cells, ROSeq offers better turnaround time than most DEG callers.

    The current implementation of ROSeq allows comparison between two groups of cells for differential expression. The Wald's statistic we used to formulate the differential expression test can be extended with the help of statistical inference theory to test the equality of the parameter values across more than two independent groups. In this case, additional statistical tests would be required to pinpoint the parent cell lineage associated with a DE gene. An immediate future extension of ROSeq therefore would be enabling multigroup (≥2) comparisons.

    Previous SectionNext Section

    Methods

    Description of data sets

    We used four publicly available scRNA-seq data sets for the various analyses. For better readability, we name the data sets after the first investigators’ surnames. Among these, the Trapnell data contain scRNA-seq profiles of 77/99 primary myoblasts sampled before/24 h after differentiation (Trapnell et al. 2014). Tung data consist of single-cell transcriptomes of iPSCs generated from three different individuals, marked as NA19098, NA19101, and NA19239, respectively (Tung et al. 2017). A total of 288 cells were profiled for each of the three individuals. For both the Trapnell and the Tung data sets, three bulk RNA-seq replicates were available from the respective studies for each condition/individual. The Chu data set consists of undifferentiated H1 (n = 212) and H9 (n = 162) human ES cells and NPCs (n = 173), with a total of nine matched bulk replicates (H1 = 4, H9 = 3, and NPCs = 2) (Chu et al. 2016). To diversify our experiments, we used the Zheng data set containing 3258 single-cell transcriptomes of Jurkat cells, processed using the GemCode technology (Zheng et al. 2017). Single-cell data sets with a good number of matched bulk replicates are scarce, which constrains the validation of DEG callers. We produced scRNA-seq data and matching bulk replicates of human foreskin BJ fibroblast (150 single cells and three bulk replicates) and K562 (352 single cells and four bulk replicates) to facilitate extensive benchmarking. The following section describes the details pertaining to the laboratory methodologies. Bioinformatic processing, including read alignment and expression quantification, mirrors our previous report (Iyer et al. 2020). Collectively, the BJ/K562 scRNA-seq data are referred to as the Gupta data set.

    Cell culture, CD staining, and scRNA-seq

    BJs (ATCC CRL-2522) are cultured in T75 flasks that are 90% confluent in an incubator (37°C, 5% CO2). The culture medium contains minimum essential medium (MEM) with GlutaMAX (Gibco 41090101) and is supplemented with 10% FBS and 10 mM HEPES. The BJ cells are stained with CellTracker orange (CTO) CMRA Dye (Thermo Fisher Scientific C34551) as a universal marker and Alexa Fluor 647 conjugated CD44 antibody. The cell-staining solution is prepared by adding 2.4 µL of 1 mM CTO to 8 mL of HBSS without calcium or magnesium (−/−) at a final concentration of 0.3 µM. The cell-staining solution is protected from light until use within 30 min. The entire volume of medium from the T75 flask that is 90% confluent is removed. Ten milliliters of HBSS (−/−) is dispensed onto the side wall of the flask without perturbing the cells. The flask is then swirled to rinse the cell layer, and all traces of cell medium and HBSS-rinse volume were removed. The entire volume of freshly prepared CTO staining medium (8 mL) is added to the cells, and the flask is placed in the dark for 20 min at 37°C in a 5% CO2 incubator. Following incubation, the staining solution is removed. Subsequently, 2.1 mL of TrypLE Express reagent (Thermo Fisher Scientific PN 12604013) is added to the cells, and the flask is swirled so that the entire surface of cells is covered. The flask is then incubated in the dark for 20 min at 37°C in a 5% CO2 incubator. During incubation, cell detaching from the surface is monitored every 3 min. The incubation is complete when 90% of the cells are detached. Following this, 2.1 mL of culture medium is added to the cells to quench the TrypLE Express reagent. The entire volume of the cell suspension is transferred from the flask to a 15-mL nonpyrogenic conical tube. The cells are then counted, and the volume of cell suspension containing 1–1.5 million cells is transferred to a new 15-mL nonpyrogenic conical tube. The cells are rinsed with HBSS. The cell suspension is then centrifuged at 300g for 5 min, supernatant is removed without disturbing the pellet, and finally, the pellet is resuspended in 200 µL volume. An aliquot of 100 µL cell suspension is used for surface-marker staining. The remaining 100 µL is used as the negative surface-stained control. To the 100 µL cell suspension, 2 µL of CD44 antibody preconjugated to Alexa Fluor 647 (BioLegend PN 103018, anti-mouse/human, clone IM7, 0.5 mg/mL) is added for the positive-stain tube. For “no stain” control, 2 µL of HBSS (−/−) is added. Both the tubes are incubated for 20 min at room temperature with occasional inverting and flicking. Subsequently, 13 mL of HBSS is added to each tube and centrifuged at 300g for 5 min. The supernatant is removed, and the pellet is resuspended in 100–150 µL culture medium with FBS, but without phenol red, to prevent high background fluorescence during cell selection on the Polaris system. The resuspension volume of culture medium accounts for cell losses during the staining procedure and is chosen to yield a cell concentration greater than the target concentration of 550 cells per microliter. Typically, 10 µL of cell mix is loaded into a C Chip disposable hemocytometer (INCYTO DHC-N01) and imaged on the Polaris system to estimate the staining intensity and purity. To achieve optimal buoyancy, cells in the range of 333–550 cells per microliter are mixed with a suspension reagent (Fluidigm 101-0434) at 3:2 (ratio of cells to cell suspension reagent). The K562 cell staining, cell selection and sample processing on a Fluidigm Polaris system, and sequencing are described elsewhere (Ramalingam et al. 2017; Sanada and Ooi 2019).

    Data preprocessing

    For each data set, we first filtered out cells having fewer than 2000 detected (nonzero read count) genes. Gene filtering followed the cell filtering step. We retained the genes having a read count of greater than three in at least three cells (Iyer et al. 2020). Next, the pruned count matrix was subjected to different normalization techniques depending on the target differential expression method. For Wilcoxon's rank-sum test, BPSC, and MAST, count per million (CPM) normalization (calculated using edgeR) (Robinson et al. 2010) was used, following the recommendation by Soneson and Robinson (2018). SCDE and DESeq2 (Love et al. 2014) were supplied with the processed raw count data as input. For ROSeq, we first subjected the processed raw count matrices to the trimmed mean of M-values (TMM) normalization (Robinson et al. 2010), followed by Voom transformation (Law et al. 2014).

    Mapping expression estimates to ranks

    For gene expression modeling, ROSeq accepts normalized read count data as input. For each gene, ROSeq first defines its range by identifying the minimum and the maximum values by pooling the normalized expression estimates across both cell-groups under study. Next, the range is split into k × σ-sized bins, where k is a scalar with a default value of 0.05, and σ is the standard deviation of the pooled expression estimates across the cell-groups. Each of these bins is assigned a rank based on the sequential order of its expression range. At the level of a cell-group, this leads to mapping of bin-wise cell frequencies to ranks, such that the bin with the highest cellular frequency is assigned the least rank (i.e., one). The DGBD is used as a probability mass function to express a normalized bin-wise cell-frequency yr as a function of its corresponding rank r using two real parameters, a and b. In other words, the DGBD formulation can be thought of as a discrete distribution of the rank frequencies. 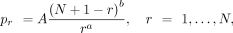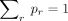If N is the total number of bins for a given gene, then the DGBD specifies the probability pr for the rth rank to have a (relative) size of yr, which can be expressed as Formula (1) where A is the normalizing constant ensuring Formula. 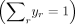Note that the sum of the normalized frequencies also equals one Formula.

    Estimation of the DGBD parameters

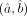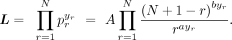    For a given gene and a specific cell-group, the best-fitting parameter values Formula are determined by maximizing, with respect to (a, b), the log-likelihood corresponding to the model given by Equation 1. 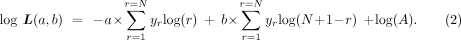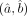Considering the discrete probability distribution structure of the DGBD formulation of (relative) rank sizes, the resulting likelihood function is given by Formula Now, taking logarithm, the required log-likelihood function, log L, can be computed as Formula (2) The resulting estimates Formula correspond to the DGBD under which the observed data are most likely to be generated. Such maximum likelihood estimates (MLEs) are the most efficient (least SE) and enjoy several optimum properties on large sample sizes (Casella and Berger 2002).

    To test differential expression of a gene between two cell-groups, based on the above MLEs 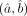Formula, we additionally need estimates of their SEs (equivalently their variance). From the theory of maximum likelihood (Myung 2003), the asymptotic variance of 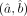Formula is given by the inverse of the associated Fisher information matrix I(a, b), which can be consistently estimated by 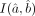Formula. 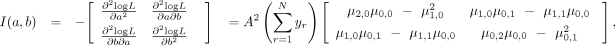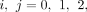For the log-likelihood function of the DGBD model given in Equation 2, the form of the Fisher information matrix I may be simplified in a more succinct form as follows: Formula (3) where, for each Formulawe define 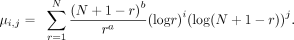Formula Note that μ0,0 = 1/A. See the Supplemental Note (Supplemental Methods) for the derivation of I(a, b).

    Testing for differential expression: two-sample Wald test

    Further, to statistically test if a gene is differentially expressed between two subpopulations, ROSeq uses the (asymptotically) optimum two-sample Wald test based on the MLE of the parameters and their asymptotic variances, given by the inverse of the Fisher information matrix.

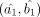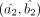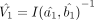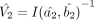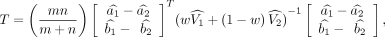    Let us assume that the DGBD parameters corresponding to the contrasting cell-groups 1 and 2 are denoted by (a1, b1) and (a2, b2), respectively, and their MLEs based on the available normalized expression data are given by Formula and Formula with the respective number of bins being m and n. We can estimate the asymptotic variance matrices for these MLEs, using Equation 3, as FormulaandFormula, respectively. Under the DGBD model, the desired testing for differential gene expressions is equivalent to the test for the null hypothesis H0: a1 = a2, b1 = b2 against the omnibus alternative. The Wald test statistic T for testing H0 can be written as follows: Formula where w = n/(m + n). If the null hypothesis H0 is correct, that is, the genes in the two subpopulations are not differentially expressed, the above test statistics T asymptotically follows a central chi-square distribution, 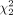Formula, with two degrees of freedom. Therefore, we conclude that the genes are differentially expressed (i.e., reject H0) at 95% level of significance if the observed value of the test statistics T exceeds the 95% quantile of the 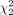Formula distribution (which is approximately six). The corresponding P-value is given by the probability that a 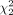Formula random variable exceeds the observed value of T.

    Benchmarking of single-cell DEG calls

    To benchmark single-cell DEG calls, we used matched bulk RNA-seq data from the same studies. DESeq was used for making DEG calls based on bulk RNA-seq data (Anders and Huber 2010). DESeq's standard pipeline uses the median of ratios method of normalization. DEGs were selected at an FDR cutoff of 0.05. To ensure the trustworthiness of the bulk-based DEG calls, we imposed a strict fold change criterion (i.e., log2 fold change cutoff of three) as recommended elsewhere (Hart et al. 2013; Giustacchini et al. 2017).

    Dropout induction in real scRNA-seq data

    Given a count matrix, to simulate dropouts, we computed Eg = log2(Rg + 1), where Rg denotes the average read count of gene g across the input transcriptomes. We also computed log-odds of the dropout probability Dg for a gene g, where Dg = log(pg/1 − pg). Here pg denotes the observed probability of dropouts for g.

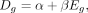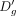    We modeled Dg with regard to Eg using linear regression as indicated below: Formula (4) which simply describes a line with slope β and y-intercept α. As dropout rate increases with decrease in expression, one would expect β < 0. We confirmed this by visualizing the relationship between Formula and Eg. Of note, Splatter, a popular dropout induction method, makes similar assumptions about the relationship between average expression and dropout rate (Zappia et al. 2017). Given a matrix, the introduction of additional dropouts reduces average read count for each gene. 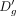On the flip side, by using the above linear model, one can estimate Formula associated with 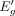Formula, where 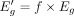Formula. Here, 0 < f < 1 is a factor that determines the decrease in average read count, and is constant across all genes. By using Equation 4, one can compute the expected increase Δg in Dg owing to change in Eg as follows:

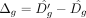
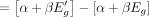
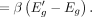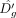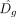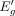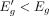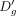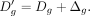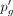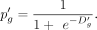
    Formula Formula Formula Here, Formula and Formula are estimated log-odds associated with Eg and Formula, respectively. Also, Δg > 0, because β < 0 and Formula. We can use Δg to compute Formula as follows: Formula Finally, the new dropout probability Formula can be computed as follows: Formula

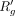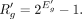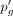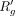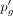    We can also retrieve the updated average read count Formula using the below equation: Formula Now, Formula and Formula are used to introduce additional dropouts and adjust average read count, respectively. New dropouts are created by muting the expression of g in randomly chosen cells in which it was earlier expressed. The number of additional dropouts can be easily calculated by tracking the difference between Formula and pg. After introducing the dropouts, we calculate the interim average read count 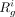Formula. 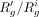Further, we scale the cell-specific read counts of g by multiplying the values by Formula.

    Software availability

    The ROSeq R package (R Core Team 2020) is available at the Bioconductor portal (http://www.bioconductor.org/packages/release/bioc/html/ROSeq.html). A more frequently updated version of the software can be accessed at the GitHub (https://github.com/krishan57gupta/ROSeq). The ROSeq source code is also available for download as Supplemental Code.

    Previous SectionNext Section

    Data access

    All raw and processed sequencing data generated in this study have been submitted to the NCBI Gene Expression Omnibus (GEO; https://www.ncbi.nlm.nih.gov/geo/) under accession number GSE160910.

    Previous SectionNext Section

    Competing interest statement

    N.R. and K.H. are employees and stockholders of Fluidigm Corporation.

    Previous SectionNext Section

    Acknowledgments

    This work is partially supported by the INSPIRE faculty grant DST/INSPIRE/04/2015/003068 awarded to D.S. by the Department of Science and Technology, Government of India. G.A. is supported by a Ramalingaswami Re-entry Fellowship by the Department of Biotechnology, Government of India.

    Author contributions: D.S. conceived the study. D.S. and A.G. supervised K.G. and M.L. for developing the theory. K.G., M.L., and A.B. developed the R package. K.G. and M.L. performed the majority of the experiments. G.A., S.B., and U.M. provided specific inputs to designing of the experiments, and interpretation of the findings. N.R. supervised the wet laboratory experiments with assistance from C.D.S., C.G., and K.H. K.G., M.L., A.G., and D.S. wrote the manuscript. All the authors read and approved the manuscript.

    Previous SectionNext Section

    Footnotes

    • Received June 9, 2020.
    • Accepted February 22, 2021.

    This article is distributed exclusively by Cold Spring Harbor Laboratory Press for the first six months after the full-issue publication date (see https://genome.cshlp.org/site/misc/terms.xhtml). After six months, it is available under a Creative Commons License (Attribution-NonCommercial 4.0 International), as described at http://creativecommons.org/licenses/by-nc/4.0/.

    Previous Section
     

    References

    1. ↵
      Anders S, Huber W. 2010. Differential expression analysis for sequence count data. Genome Biol 11: R106. doi:10.1186/gb-2010-11-10-r106
      CrossRefUnknownMedlineGoogle Scholar
    2. ↵
      Butler A, Hoffman P, Smibert P, Papalexi E, Satija R. 2018. Integrating single-cell transcriptomic data across different conditions, technologies, and species. Nat Biotechnol 36: 411–420. doi:10.1038/nbt.4096
      CrossRefMedlineGoogle Scholar
    3. ↵
      Casella G, Berger RL. 2002. Statistical inference. Thomson Learning, Pacific Grove, CA.
      Google Scholar
    4. ↵
      Chu LF, Leng N, Zhang J, Hou Z, Mamott D, Vereide DT, Choi J, Kendziorski C, Stewart R, Thomson JA. 2016. Single-cell RNA-seq reveals novel regulators of human embryonic stem cell differentiation to definitive endoderm. Genome Biol 17: 173. doi:10.1186/s13059-016-1033-x
      CrossRefMedlineGoogle Scholar
    5. ↵
      Finak G, McDavid A, Yajima M, Deng J, Gersuk V, Shalek AK, Slichter CK, Miller HW, McElrath MJ, Prlic M, et al. 2015. MAST: a flexible statistical framework for assessing transcriptional changes and characterizing heterogeneity in single-cell RNA sequencing data. Genome Biol 16: 278. doi:10.1186/s13059-015-0844-5
      CrossRefMedlineGoogle Scholar
    6. ↵
      Giustacchini A, Thongjuea S, Barkas N, Woll PS, Povinelli BJ, Booth CA, Sopp P, Norfo R, Rodriguez-Meira A, Ashley N, et al. 2017. Single-cell transcriptomics uncovers distinct molecular signatures of stem cells in chronic myeloid leukemia. Nat Med 23: 692–702. doi:10.1038/nm.4336
      CrossRefGoogle Scholar
    7. ↵
      Grün D, Kester L, Van Oudenaarden A. 2014. Validation of noise models for single-cell transcriptomics. Nat Methods 11: 637–640. doi:10.1038/nmeth.2930
      CrossRefMedlineGoogle Scholar
    8. ↵
      Hart SN, Therneau TM, Zhang Y, Poland GA, Kocher JP. 2013. Calculating sample size estimates for RNA sequencing data. J Comput Biol 20: 970–978. doi:10.1089/cmb.2012.0283
      CrossRefMedlineGoogle Scholar
    9. ↵
      Iyer A, Gupta K, Sharma S, Hari K, Lee YF, Ramalingam N, Yap YS, West J, Bhagat AA, Subramani BV, et al. 2020. Integrative analysis and machine learning based characterization of single circulating tumor cells. J Clin Med 9: 1206. doi:10.3390/jcm9041206
      CrossRefGoogle Scholar
    10. ↵
      Jindal A, Gupta P, Jayadeva, Sengupta D. 2018. Discovery of rare cells from voluminous single cell expression data. Nat Commun 9: 4719. doi:10.1038/s41467-018-07234-6
      CrossRefGoogle Scholar
    11. ↵
      Kharchenko PV, Silberstein L, Scadden DT. 2014. Bayesian approach to single-cell differential expression analysis. Nat Methods 11: 740–742. doi:10.1038/nmeth.2967
      CrossRefMedlineGoogle Scholar
    12. ↵
      Kumar P, Tan Y, Cahan P. 2017. Understanding development and stem cells using single cell-based analyses of gene expression. Development 144: 17–32. doi:10.1242/dev.133058
      Abstract/FREE Full Text
    13. ↵
      Kvålseth TO. 1989. Note on Cohen's kappa. Psychol Rep 65: 223–226. doi:10.2466/pr0.1989.65.1.223
      CrossRefGoogle Scholar
    14. ↵
      Law CW, Chen Y, Shi W, Smyth GK. 2014. voom: precision weights unlock linear model analysis tools for RNA-seq read counts. Genome Biol 15: R29. doi:10.1186/gb-2014-15-2-r29
      CrossRefMedlineGoogle Scholar
    15. ↵
      Love MI, Huber W, Anders S. 2014. Moderated estimation of fold change and dispersion for RNA-seq data with DESeq2. Genome Biol 15: 550. doi:10.1186/s13059-014-0550-8
      CrossRefMedlineGoogle Scholar
    16. ↵
      Macosko EZ, Basu A, Satija R, Nemesh J, Shekhar K, Goldman M, Tirosh I, Bialas AR, Kamitaki N, Martersteck EM, et al. 2015. Highly parallel genome-wide expression profiling of individual cells using nanoliter droplets. Cell 161: 1202–1214. doi:10.1016/j.cell.2015.05.002
      CrossRefMedlineGoogle Scholar
    17. ↵
      Martínez-Mekler G, Martínez RA, del Río MB, Mansilla R, Miramontes P, Cocho G. 2009. Universality of rank-ordering distributions in the arts and sciences. PLoS One 4: e4791. doi:10.1371/journal.pone.0004791
      CrossRefMedlineGoogle Scholar
    18. ↵
      Myung IJ. 2003. Tutorial on maximum likelihood estimation. J Math Psychol 47: 90–100. doi:10.1016/S0022-2496(02)00028-7
      CrossRefGoogle Scholar
    19. ↵
      Ramalingam N, Fowler B, Szpankowski L, Leyrat AA, Hukari K, Maung MT, Yorza W, Norris M, Cesar C, Shuga J, et al. 2017. Fluidic logic used in a systems approach to enable integrated single-cell functional analysis. Front Bioeng Biotechnol 4: 70. doi:10.3389/fbioe.2016.00070
      CrossRefGoogle Scholar
    20. ↵
      R Core Team. 2020. R: a language and environment for statistical computing. R Foundation for Statistical Computing, Vienna. https://www.R-project.org/.
      Google Scholar
    21. ↵
      Robin X, Turck N, Hainard A, Tiberti N, Lisacek F, Sanchez JC, Müller M. 2011. pROC: an open-source package for R and S+ to analyze and compare ROC curves. BMC Bioinformatics 12: 77. doi:10.1186/1471-2105-12-77
      CrossRefMedlineGoogle Scholar
    22. ↵
      Robinson MD, McCarthy DJ, Smyth GK. 2010. edgeR: a Bioconductor package for differential expression analysis of digital gene expression data. Bioinformatics 26: 139–140. doi:10.1093/bioinformatics/btp616
      CrossRefMedlineGoogle Scholar
    23. ↵
      Sanada CD, Ooi AT. 2019. Single cell dosing and mRNA sequencing of suspension and adherent cells using the PolarisTM system. Methods Mol Biol 1979: 185–195. doi:10.1007/978-1-4939-9240-9_12
      CrossRefGoogle Scholar
    24. ↵
      Sengupta D, Rayan NA, Lim M, Lim B, Prabhakar S. 2016. Fast, scalable and accurate differential expression analysis for single cells. bioRxiv doi:10.1101/049734
      Abstract/FREE Full Text
    25. ↵
      Sing T, Sander O, Beerenwinkel N, Lengauer T. 2005. ROCR: visualizing classifier performance in R. Bioinformatics 21: 3940–3941. doi:10.1093/bioinformatics/bti623
      CrossRefMedlineGoogle Scholar
    26. ↵
      Soneson C, Robinson MD. 2018. Bias, robustness and scalability in single-cell differential expression analysis. Nat Methods 15: 255–261. doi:10.1038/nmeth.4612
      CrossRefMedlineGoogle Scholar
    27. ↵
      Tanay A, Regev A. 2017. Scaling single-cell genomics from phenomenology to mechanism. Nature 541: 331–338. doi:10.1038/nature21350
      CrossRefMedlineGoogle Scholar
    28. ↵
      Trapnell C, Cacchiarelli D, Grimsby J, Pokharel P, Li S, Morse M, Lennon NJ, Livak KJ, Mikkelsen TS, Rinn JL. 2014. The dynamics and regulators of cell fate decisions are revealed by pseudotemporal ordering of single cells. Nat Biotechnol 32: 381–386. doi:10.1038/nbt.2859
      CrossRefMedlineGoogle Scholar
    29. ↵
      Tung PY, Blischak JD, Hsiao CJ, Knowles DA, Burnett JE, Pritchard JK, Gilad Y. 2017. Batch effects and the effective design of single-cell gene expression studies. Sci Rep 7: 39921. doi:10.1038/srep39921
      CrossRefMedlineGoogle Scholar
    30. ↵
      Vallejos CA, Risso D, Scialdone A, Dudoit S, Marioni JC. 2017. Normalizing single-cell RNA sequencing data: challenges and opportunities. Nat Methods 14: 565–571. doi:10.1038/nmeth.4292
      CrossRefGoogle Scholar
    31. ↵
      Vu TN, Wills QF, Kalari KR, Niu N, Wang L, Rantalainen M, Pawitan Y. 2016. β-Poisson model for single-cell RNA-seq data analyses. Bioinformatics 32: 2128–2135. doi:10.1093/bioinformatics/btw202
      CrossRefMedlineGoogle Scholar
    32. ↵
      Zappia L, Phipson B, Oshlack A. 2017. Splatter: simulation of single-cell RNA sequencing data. Genome Biol 18: 174. doi:10.1186/s13059-017-1305-0
      CrossRefGoogle Scholar
    33. ↵
      Zheng GX, Terry JM, Belgrader P, Ryvkin P, Bent ZW, Wilson R, Ziraldo SB, Wheeler TD, McDermott GP, Zhu J, et al. 2017. Massively parallel digital transcriptional profiling of single cells. Nat Commun 8: 14049. doi:10.1038/ncomms14049
      CrossRefMedlineGoogle Scholar
    34. ↵
      Zhu S, Qing T, Zheng Y, Jin L, Shi L. 2017. Advances in single-cell RNA sequencing and its applications in cancer research. Oncotarget 8: 53763–53779. doi:10.18632/oncotarget.17893
      CrossRefGoogle Scholar
    | Table of Contents

    This Article

    1. Published in Advance March 5, 2021, doi: 10.1101/gr.267070.120 Genome Res. 31: 689-697 © 2021 Gupta et al.; Published by Cold Spring Harbor Laboratory Press

    Article Category

    Share

    Preprint Server



    Navigate This Article

    Current Issue

    1. January 2026, 36 (1)
    1. Current Issue
    1. Alert me to new issues of Genome Research