The origin, global distribution, and functional impact of the human 8p23 inversion polymorphism
- Maximilian P.A. Salm1,8,9,
- Stuart D. Horswell2,
- Claire E. Hutchison1,
- Helen E. Speedy1,
- Xia Yang3,
- Liming Liang4,
- Eric E. Schadt3,
- William O. Cookson5,
- Anthony S. Wierzbicki6,
- Rossi P. Naoumova7 and
- Carol C. Shoulders1,9
- 1Centre for Endocrinology, Barts & the London School of Medicine & Dentistry, Queen Mary University of London, London EC1M 6BQ, United Kingdom;
- 2Bioinformatics & Biostatistics Group, Cancer Research UK London Research Institute, London WC2A 3LY, United Kingdom;
- 3Department of Systems Biology, Sage Bionetworks, Seattle, Washington 98109, USA;
- 4Department of Epidemiology, Department of Biostatistics, Harvard School of Public Health, Boston, Massachusetts 02115, USA;
- 5National Heart & Lung Institute, Imperial College London, London SW3 6LY, United Kingdom;
- 6Guys & St. Thomas Hospital, King's College London, London SE1 2PR, United Kingdom;
- 7Institute of Clinical Science, Imperial College London, London W12 0NN, United Kingdom
Abstract
Genomic inversions are an increasingly recognized source of genetic variation. However, a lack of reliable high-throughput genotyping assays for these structures has precluded a full understanding of an inversion's phylogenetic, phenotypic, and population genetic properties. We characterize these properties for one of the largest polymorphic inversions in man (the ∼4.5-Mb 8p23.1 inversion), a structure that encompasses numerous signals of natural selection and disease association. We developed and validated a flexible bioinformatics tool that utilizes SNP data to enable accurate, high-throughput genotyping of the 8p23.1 inversion. This tool was applied retrospectively to diverse genome-wide data sets, revealing significant population stratification that largely follows a clinal “serial founder effect” distribution model. Phylogenetic analyses establish the inversion's ancestral origin within the Homo lineage, indicating that 8p23.1 inversion has occurred independently in the Pan lineage. The human inversion breakpoint was localized to an inverted pair of human endogenous retrovirus elements within the large, flanking low-copy repeats; experimental validation of this breakpoint confirmed these elements as the likely intermediary substrates that sponsored inversion formation. In five data sets, mRNA levels of disease-associated genes were robustly associated with inversion genotype. Moreover, a haplotype associated with systemic lupus erythematosus was restricted to the derived inversion state. We conclude that the 8p23.1 inversion is an evolutionarily dynamic structure that can now be accommodated into the understanding of human genetic and phenotypic diversity.
Genomic inversions are a ubiquitous class of structural variation, implicated in speciation (Lowry and Willis 2010), adaptation (Hoffmann and Rieseberg 2008), and human disease (Girirajan and Eichler 2010). In addition to dislocating coding sequences (Feuk 2010), inversions can influence gene expression (Weiler and Wakimoto 1995) and facilitate aberrant recombination events that cause genomic disorders (Feuk 2010). Moreover, inversions suppress local recombination, which can preserve beneficial or deleterious haplotypic configurations (Hoffmann and Rieseberg 2008; Joron et al. 2011). These characteristics are largely exemplified by the 17q21.31 inversion, which is associated with decreased microtubule-associated protein tau (MAPT) expression, predisposes carriers to the 17q21.31 micro-deletion syndrome, and exhibits perfect linkage disequilibrium (LD) across its ∼970-kb interval (Donnelly et al. 2010). However, aside from this inversion, human inversions remain largely uncharacterized, which is partly attributable to the difficulty in assaying these structures at the population level (Feuk 2010; Alkan et al. 2011a).
The 8p23.1 inversion (8p23-inv) is one of the largest polymorphic inversions found in man, encompassing ∼4.5 Mb (Giglio et al. 2001; Sayers et al. 2011). Conventionally 8p23-inv is genotyped using fluorescent in situ hybridization (FISH) (Giglio et al. 2001), which is not amenable to high-throughput analyses and requires viable cells. Moreover, the size of the inversion's single copy region (∼3.5 Mb) approaches the practical resolution of metaphase FISH (Raap 1998). In the small samples studied to date, the inversion has estimated frequencies of ∼59% in the Yoruba, ∼20%–50% in Europeans, and ∼12%–27% in Asians (Broman et al. 2003; Sugawara et al. 2003; Antonacci et al. 2009), while its frequency in other ethnicities remains unspecified. At the species level, 8p23-inv has only been observed in humans, chimpanzees, and bonobos (Antonacci et al. 2009), but whether this shared feature reflects homology or homoplasy is unresolved.
Multiple loci within the inversion are putative targets of natural selection (Barreiro et al. 2008; Deng et al. 2008; Lopez Herraez et al. 2009; Pickrell et al. 2009; Browning and Weir 2010). Furthermore, 8p23-inv not only increases the risk of producing offspring with unbalanced chromosomal rearrangements (Hollox et al. 2008) but also encompasses numerous loci associated with autoimmune (e.g., Gregersen et al. 2009; Deng and Tsao 2010; Nordmark et al. 2011) and cardiovascular (e.g., Levy et al. 2009; Teslovich et al. 2010; Dehghan et al. 2011) disease phenotypes. The precise molecular mechanisms underlying these associations are poorly defined. Given the profound effect of inversions on local genetic structure (Hoffmann and Rieseberg 2008), future studies should benefit from detailed characterization of 8p23-inv (Harley et al. 2009).
Inversions are often associated with elevated LD within their boundaries due to recombination inhibition between noncollinear regions in inversion heterozygotes (Hoffmann and Rieseberg 2008). This makes high-throughput inversion-typing via genetic markers that perfectly correlate with the structure tenable (Donnelly et al. 2010). This approach was applied to 8p23-inv, identifying candidate inversion proxy single-nucleotide polymorphisms (SNPs) in small (n ≤ 13), ancestrally diverse HapMap samples (Antonacci et al. 2009). Furthermore, two potential inversion-associated SNP homozygosity tracts were identified in six Europeans (Bosch et al. 2009). However, these two studies generally do not concur, in either the predictive SNPs identified or the inversion-type predictions made, which may be attributable to inflated LD estimates stemming from the small sample sizes analyzed (Iles 2008). In a related approach, principal components analysis of phased SNP genotypes was used to predict inversion-type (Deng et al. 2008), but as discussed by Antonacci et al. (2009), these predictions differed considerably from FISH genotype data.
Herein we present a novel, robust high-throughput method to genotype 8p23-inv. By use of this tool, we define population, evolutionary, and functional attributes of the inversion.
Results
Development of a novel 8p23 inversion detection method
To develop a high-throughput assay for 8p23-inv, we typed the inversion by FISH in 68 CEU samples representing 13 CEU trios and 42 HapMap phase II founders (Supplemental Table S1; Supplemental Fig. S1). For clarity, N (noninverted) refers to the orientation represented in the human genome reference (hg19) and I to the inverted state. The inversion was transmitted according to Mendelian inheritance patterns as expected, and published inversion genotypes were confirmed (Supplemental Table S1).
No HapMap SNPs or 1000 Genome Project variants were in complete LD with 8p23-inv (data not shown). Thus no known SNP acts as a perfect proxy for the inversion. However, 20 SNPs with a strong correlation to the inversion (i.e., r2 > 0.8) (Supplemental Table S2) were identified. To evaluate their combined efficacy in predicting inversion-type, a leave-n-out cross-validation imputation analysis was performed. While the concordance between known and imputed inversion-type using this SNP set was 86.5 ± 9.2% (mean ± SD), the full range was 45%–100%. Such uncertainty precludes reliable inversion genotyping, and we therefore developed an alternative inversion-typing method based on local genetic substructure.
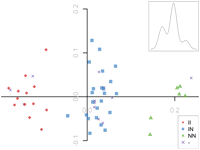
To explore the relationship between genetic substructure and inversions in the 8p23 region in Europeans, SNP genotypes restricted to the inversion interval in CEU founders were examined using multidimensional scaling (MDS). Individuals stratified into three groups along the first axis, in perfect correlation with their inversion-type (Fig. 1). Moreover, a tri-modal Gaussian mixture model fit to the positions along the first axis allowed effectively unsupervised clustering of this data set into their concomitant inversion-types with associated confidence values. The clustering solution is independently corroborated by three measures: connectivity, the Dunn index, and silhouette width. These concatenated processes constitute the “PFIDO” algorithm (Supplemental Fig. S2), which perfectly classified all empirically determined inversion-types (P = 8.25 × 10−17).
Genetic substructure in the 8p23 inversion region correlates perfectly with inversion status in CEU HapMap II samples. A multidimensional scaling (MDS) analysis based on 5494 SNPs typed in 54 CEU founder members (that satisfied the inclusion criteria; see Methods). The x- and y-axis correspond to the first and second “axes” derived by MDS, and each point represents an individual, labeled by inversion-type (as defined by FISH). (Inset) Tri-modal point distribution found in the first dimension.
To assess the algorithm's accuracy, inversion-type was predicted in a cohort of 1402 related British Caucasians, using 49 SNPs from a SNP set optimized for PFIDO (Supplemental Note; Supplemental Tables S2, S3; Supplemental Fig. S3). At a clustering threshold of P < 0.05, inversion-types were called for 1338 individuals (call rate > 95%). No violations of Mendelian inheritance patterns were detected, nor was Hardy-Weinberg equilibrium (HWE) breached in unrelated individuals (P = 0.19, n = 233), suggesting that the inversion-type predictions are robust. The predictions were verified by FISH in seven unrelated samples: At the designated clustering cut-off of P < 0.05, all were correct (P = 9.52 × 10−3).
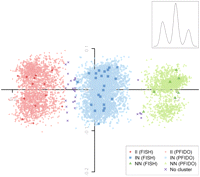
The PFIDO algorithm does not rely on any specific SNP enabling retrospective analyses of existing GWAS data sets. For example, inversion-type classification of CEU reference samples was without error when restricting the input SNPs to those represented on three popular genotyping arrays, even though their SNP content overlap is ∼7% (Supplemental Fig. S4). Four data sets representing ancestrally European samples (Wellcome Trust Case Control Consortium 2007) further illustrate retrospective inversion-typing (Fig. 2): the frequency of the N allele in the CEU sample is similar in the combined WTCCC control (42.9%), WTCCC coronary artery disease (44.4%), and WTCCC type 2 diabetes cohorts (45.6%).
8p23 inversion prediction in WTCCC cohorts. PFIDO output (based on 1043 SNPs) is shown overlaying the corresponding MDS plot, for four data sets combined. Predicted inversion-type frequencies are in HWE in all cohorts and CEU FISH-derived inversion-types served as an internal control. For further details, see Figure 1 legend.
Population stratification of the 8p23 inversion
To explore the relationship between the 8p23 inversion and genetic substructure in non-European populations, 8p23-inv was typed by FISH in 17 JPT and 15 YRI HapMap II samples (Supplemental Table S1). The frequencies of I alleles were 21% (JPT) and 52% (YRI), concurring with previous observations (Sugawara et al. 2003; Antonacci et al. 2009), while the correlation between experimentally determined inversion-type and genetic substructure was less distinct than in Europeans, with less pronounced clustering of each inversion-type along the first MDS-derived axis (Supplemental Note). Nevertheless, PFIDO correctly categorized 2 and 3 clusters in the JPT and YRI samples, respectively (Supplemental Fig. S5). Moreover, at a PFIDO clustering threshold of P < 0.05, experimentally determined JPT and YRI inversion-types were all predicted correctly (P = 1.40 × 10−3 and P = 3.61 × 10−5, respectively).
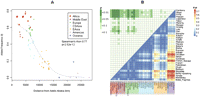
To establish the worldwide distribution of 8p23-inv, PFIDO was applied to a combined data set representing 1894 individuals sampled from 56 globally distributed populations (Supplemental Table S4). The 8p23 inversion exhibits a striking clinal distribution, strongly correlating with geographic distance from Addis Ababa (Fig. 3A), a conceivable origin of modern humans (Handley et al. 2007). The I allele is frequent in sub-Saharan Africa (mean = 69.7 ± 5.6%) and progressively diminishes in frequency across the Eurasian continent, effectively disappearing in the Americas (mean = 1.3 ± 2.5%). This population stratification is reflected in a global Fst of 0.213, suggesting greater partitioning of 8p23-inv frequency variance between populations than within populations (Holsinger and Weir 2009). Pairwise Fst values (estimated in the Human Genome Diversity Project [HGDP]) also strongly correlate with the geographic distance between sampled populations (Mantel test, r = 0.7, P = 1 × 10−4), and there is empirically significant pairwise genetic differentiation between African and Oceanic/American samples (P < 0.01) (Fig. 3B).
Population stratification of 8p23-inv. (A) The worldwide frequency distribution of 8p23-inv. The frequency of the inverted allele (I) in each population (Supplemental Table S4) is plotted against geographical distance from Addis Ababa (Ethiopia). Populations are color-coded according to continental origin, and larger symbols correspond to larger samples (n > 60). The dashed LOESS fitted line highlights the significant negative correlation between the two variables, as assessed by the Spearman's rank correlation test. Although one Oceanic sample (Tongan/Samoan) appears as an outlier, its allele frequency (19%) is consistent with this sample's previously reported genetic relationship to East Asians (Xing et al. 2010). (B) Pairwise Fst between HGDP populations, based on 8p23-inv. The bottom right triangle shows pairwise Fst values: Each shaded box represents a pairwise population comparison, with higher values in red. The top left triangle (green) shows the corresponding significance of the Fst values relative to an empirical distribution of 1000 SNPs (Supplemental Fig. S6C). (Dark green) Fst values in the top 1% of the distribution (i.e., P < 0.01); (lighter green) Fst values in the top 5% (i.e., P < 0.05). Populations are grouped by continent of origin (as in A).
To examine whether the inversion's distribution is explicable by nondemographic factors (e.g., positive selection), the 8p23-inv distribution in the HGDP data set was compared with that of 19,969 autosomal SNPs, selected to represent loci of similar allele frequency under putatively neutral selection. Relative to these SNPs, the inversion's geographical correlation differs marginally (P < 0.049) (Supplemental Fig. S6A). Similarly, the 8p23-inv global Fst (0.218) is marginally significant compared with the null distribution (P < 0.022) (Supplemental Fig. S6B). Thus the inversion's distribution is largely consistent with demographic models of the human expansion out of Africa, with a potential weak contribution from positive/negative selection. Nevertheless, given this distribution, population stratification must be accounted for in 8p23-inv case-control association analyses
Inversion-specific haplotypes and their phenotypic influence
We examined the influence of 8p23-inv on local gene expression in five data sets (Supplemental Note). 8p23-inv was robustly associated with BLK, PPP1R3B, XKR6, FAM167A, and CTSB mRNA levels (Supplemental Table S5A). The association between 8p23-inv and PPP1R3B expression is particularly noteworthy as the trend is consistent across populations (Supplemental Fig. S7) and PPP1R3B mRNA levels have been associated with serum lipid levels (Teslovich et al. 2010).
Although inversions can directly influence gene expression (Weiler and Wakimoto 1995), they also exert indirect effects by maintaining allelic configurations (Myers et al. 2007). To explore the latter, the contribution of SNPs in cis with inversion alleles to the expression quantitative trait loci (eQTLs) was explored using an allele-specific expression data set (Ge et al. 2009). 8p23-inv was less significantly associated with the 14 reported “expression windows” than the originally reported SNP associations (Ge et al. 2009: supplemental table S1). Moreover, including these SNPs as covariates in the 8p23-inv analysis left only one significant association: that between 8p23-inv and primary transcripts from the BLK-FAM167A intergenic region (Supplemental Table S5B). However, another SNP identified by re-sequencing (rs1382567) (Ge et al. 2009) is more significantly associated with the BLK-FAM167A intergenic region expression than 8p23-inv (Supplemental Table S5B). These data suggest that the inversion-eQTLs are primarily mediated via SNP alleles common to a specific inversion background.
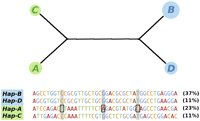
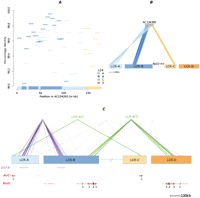
Allelic expression associations with BLK-FAM167A have been refined to four 16-kb haplotypes (A–D); the A-haplotype accounts for differential BLK and FAM167A expression, while the A- and C-haplotypes account for differential expression from the BLK-FAM167A intergenic region (Ge et al. 2009). In Europeans these haplotypes are completely restricted to specific inversion backgrounds; the B- and D-haplotypes reside on an I background, while the A- and C-haplotypes are found on an N background (Fig. 4). It is therefore likely that associations between 8p23-inv and BLK/FAM167A expression are mediated by the major A-haplotype found only on the N background. Moreover, the efficacy of 8p23-inv as a predictor of BLK-FAM167A intergenic expression is probably attributable to the N background harboring both the A- and C-haplotypes. Regarding disease, risk alleles for systemic lupus erythematosus (SLE) and rheumatoid arthritis (RA) are transmitted solely on the A-haplotype (Fig. 4), and their functional effect is putatively mediated via BLK expression (Hom et al. 2008; Gregersen et al. 2009). Thus, variants specific to the noninverted configuration contribute to the etiology of these autoimmune disorders.
Median-joining network representing phased HapMap CEU haplotypes influencing BLK-FAM167A mRNA levels. The network was constructed using 42 SNPs (Supplemental Table S5C) mapping to chr8:11,376,782–11,393,411 phased in 45 samples; 8p23-inv heterozygotes were omitted to minimize phasing-induced errors, as were haplotypes with frequencies ≤2%. Haplotype groups are denoted by circles (with circle size proportional to haplotype frequency) and colored by whether the haplotypes derive from II (blue) or NN (green) samples. Haplotype groups are named “A–D,” corresponding with previous nomenclature (Ge et al. 2009). Distances between nodes are proportional to the number of differences distinguishing each haplotype; actual haplotypes (and their frequencies in CEU founders) are provided below the network. Risk alleles for systemic lupus erythematosus and rheumatoid arthritis identified in four GWAS are highlighted (rs2736340, rs13277113, rs2618476) (Graham et al. 2008; Hom et al. 2008; Gregersen et al. 2009; Chung et al. 2011).
In summary, recombination suppression induced by the inversion appears to have maintained allelic combinations that collectively influence levels of at least five transcripts, leading to distinct expression patterns associated with inversion-type. This suppression of recombination may also have contributed to preservation of a risk haplotype on the N allele for SLE and RA.
Defining the origin of 8p23-inv
To investigate whether 8p23-inv predates the speciation event between humans and chimpanzees, we estimated the “time to most recent common ancestor” (TMRCA) between inversion alleles (Zody et al. 2008). Overlapping allelic RPCI-11 BAC sequences (totaling 178 kb) derived from a likely African-American inversion heterozygote (Supplemental Note) were aligned to a chimpanzee genome assembly (Supplemental Table S6). Assuming the chimpanzee and human lineages diverged 4.5–6 million years ago (mya) (Locke et al. 2011), the I- and N-sequences diverged on average between 390 ± 70 and 520 ± 90 thousand years ago (kya). Including the orangutan sequence (and dating the orangutan-human lineage split at 12–16 mya) (Locke et al. 2011) yielded similar divergence dates whether comparing the RPCI-11 sequence to the chimpanzee (390 ± 100 to 520 ± 130 kya) or orangutan (420 ± 100 to 560 ± 130 kya). Similarly, aligning 2.1 Mb of the chimpanzee genome to HuRef haplotypes (a predicted inversion-heterozygote of European descent) generated comparable 8p23-inv divergence dates of 250 ± 60 to 340 ± 80 kya.
Gene flow potentially confounds these divergence estimates by homogenizing genetic diversity over time, resulting in a seemingly recent TMRCA (Supplemental Note and Fig. S8). We therefore estimated the TMRCA between HuRef haplotypes for a ∼22-kb interval with no evidence of gene flow (chr8:10848492–10870275; CEU N and I haplotypes share no polymorphic sites according to HapMap and 1000 Genome Project data), which yielded divergence dates of 315 ± 58 and 420 ± 78 kya. An alternative method designed to estimate the minimum TMRCA between inversion alleles (Andolfatto et al. 1999) indicated that N and I alleles diverged ∼364–389 kya (based on HapMap CEU and YRI data). Collectively these data indicate that 8p23-inv occurred at least 3.5 million years after the human–chimpanzee lineage split, suggesting that 8p23-inv arose independently in the Homo and Pan lineages and is thus a recurrent event within primate lineages.
Evolution of the genomic architecture facilitating 8p23-inv
FISH and genetic mapping have narrowed the 8p23-inv breakpoints to two highly homologous low-copy repeat (LCR) regions known as “distal repeat” (REPD; ∼1.14 Mb) and “proximal repeat” (REPP; ∼635 kb) (Hollox et al. 2008). As these structures plausibly enabled inversion formation via nonallelic homologous recombination (NAHR) (Feuk 2010), we investigated their origin by analyzing the syntenic primate sequence in these locations. This identified two orangutan-derived bacterial artificial chromosomes (BACs) that span the syntenic REPP completely, each mapping to two single-copy regions within and outside the human inversion and supporting the inverted orientation as the ancestral state (AC207782 & AC212986) (Supplemental Fig. S9). Remarkably, only 1.5 kb of these BACs shows homology with human LCR sequences (Jiang et al. 2008), indicating an effective absence of LCRs at the syntenic orangutan REPP. Conversely, the orangutan REPD position contains extensive LCRs; for example, a clone that unambiguously maps to the syntenic REPD contains 26.8 kb of LCRs (AC206098) (Supplemental Fig. S9). In gorillas, however, BAC-end sequence analysis identified 11 clones with one end anchored in unique sequence and the other end mapping to REPD/REPP LCRs (Supplemental Fig. S9). These data suggest the paired REPD/REPP arrangement evolved after the emergence of orangutans in the primate lineage.
The timing of REPP formation is also reflected in the genetic divergence between LCR subunits. TMRCA analysis of a nonduplicated LCR section in orangutans that is duplicated in humans and chimpanzees dates the divergence of human REPP/REPD to ∼9.5 mya (Supplemental Fig. S10A,B), suggesting REPP was formed prior to the emergence of gorillas during primate speciation. Moreover, pairwise TMRCA analyses of seven ancestral LCR subunits (Jiang et al. 2008) common to REPP/REPD exhibit two peaks in age distribution (Supplemental Fig. S10C): one at ∼9 mya and another at ∼800 kya (approaching the TMRCA of the I and N alleles).
Collectively, the data suggest that LCR segments were duplicatively transposed (Johnson et al. 2006) from the REPD to the REPP locus in the common ancestor of gorillas, chimpanzees, and humans, resulting in a 27-kb deletion (Supplemental Fig. S11) and the paralogous LCR loci that now bracket the human 8p23-inv, the substrates for inversion-formation. Such a model accounts for the restriction of 8p23-inv to the human and chimpanzee lineages and supports the inverted orientation as the ancestral state.
A breakpoint mapping to a HERV-K element is associated with 8p23-inv
To map the inversion breakpoints at the nucleotide level, REPD and REPP were stringently reassembled into tiling paths using only finished RPCI-11 8p23 BACs (Supplemental Note). This produced two assemblies mapping to REPD (named LCR-A and -B) and two assemblies mapping to REPP (LCR-C and -D), which broadly mirror the existing reference genome assembly, except for the exclusion of non–RPCI-11 data (Supplemental Figs. S12-14). Six RPCI-11 BACs with significant homology with LCRs-A–D were identified that represent putative structural variants. These exhibited mosaic homology patterns, in which subsections of each BAC optimally aligned to different LCR haplotypes (Fig. 5A,B; Supplemental Fig. S15). Similar haplotype junction patterns were found in several clones (Supplemental Fig. S15), indicating that these are not cloning artifacts (Osoegawa et al. 2007).
LCR structural diversity captured by sequenced RPCI-11 clones. (A) Pairwise alignments (PID > 99%) between LCRs A–D and 10-kb windows of a specified BAC. Each alignment is colored by LCR haplotype, and the dashed line represents PID > 99.9%. A “consensus” is represented on the x-axis, in which each 10-kb window is assigned to its most homologous LCR haplotype. In this example, an interleaved mosaic pattern between LCR-A and -B is found in the first 100 kb of the clone, followed by a transition into LCR-C toward the clone's end. (B) For the specified BAC, the top pairwise alignment for each 10-kb BAC window (i.e., the consensus) is mapped to its corresponding LCR haplotype (joining lines). The inversion's single-copy region (interrupted gray line) links the LCR-B and -C haplotypes. This example includes a junction between LCR-A and -C. (C) LCR haplotype junctions discovered in six finished RPCI-11 BACs. Each transition from one haplotype to another is represented by a joining line. (Purple/green) Those that cluster together and are observed in more than one BAC. The first group (purple, represented by AC134683, AC134395, and AC148106) covers the DEFB locus. The second group (green, represented by AC134683 and AC134395) constitutes a junction between LCR-A and LCR-C. The third group (green, involving AC087342, AC092766, AC105214, and AC148106) represents junctions between LCR-B and LCR-D. Notably, AC087342 is anchored by 46 kb of uniquely mapping sequence in the distal end of the inversion. The first annotation track represents the copy-number variant DEFB locus (purple); the second and third annotation tracks (red) indicate inverted repeats between LCR-A and -C (“AvC”) or LCR-B and -D (“BvD”). Statistically significant recombinant sites (numbered 1–5) (Table 1) are marked by vertical breaks in the inverted repeats. The inversion's single-copy region is represented as in (B).
Statistically significant recombination events in LCR-A/C and LCR-B/D haplotype groups
The haplotype junctions fall into three broad categories (Fig. 5C): The first covers the DEFB locus, a site of extensive copy-number variation (Hollox et al. 2008); the second constitutes a junction between LCR-A and LCR-C; and the third represents junctions between LCR-B and LCR-D. The latter two groups map to large inverted repeats between haplotypes (Fig. 5C). Based on the premise that the inversion was created by NAHR between inverted repeats, the junctions represented in the second and third groups are reasonable candidates for inversion breakpoints.
To explore the potential breakpoints further (see also Supplemental Fig. S16 & Supplemental Note: Fosmid-End Sequences Support the LCR–Haplotype Junctions), multiple sequence alignments of the LCR-A/C and LCR-B/D BAC groups were constructed and analyzed for historical recombination events. At a Bonferroni corrected P < 0.01, five recombination events were detected by all seven detection methods employed (Table 1). In all cases, phylogenetic analysis of the sequences flanking the breakpoint revealed clear migration of one clade between two divergent clades (e.g., Supplemental Fig. S17A), consistent with a recombination product having formed from sequences represented by the two divergent clades. Four recombinant events were detected in multiple BAC libraries (Table 1), suggestive of common breakpoints.
To establish whether recombinant haplotypes co-segregated with inversion-type, 34 CEU founders (15x II, 14x NN, 5x IN) were typed for breakpoint-spanning haplotypes using the double “amplification refractory mutation system” (Lo et al. 1991), followed by PCR-product sequencing to verify haplotype specificity (Supplemental Fig. S17B). After multiple-testing correction, a single haplotype exhibited significant association with inversion-type (P = 3.22 × 10−5, rϕ = 0.8) (Table 1, event 5): The “parental” LCR-B related haplotype-group was more common in II samples (14/15) than NN samples (2/14), while the reciprocal “recombinant” LCR-D–related haplotype-group was present in all NN samples and five II samples (P = 0.05) (Supplemental Fig. S18).
In summary, a recombination event was identified that strongly correlates with inversion-type. The data also suggest the N allele derives from an ancestral I allele, consistent with the clinal geographic distribution of 8p23-inv and the orientation of the region in orangutans. Moreover, the recombination event maps to an inverted pair of 9.5-kb human endogenous retrovirus elements (HERV-K27 and HERV-KOLD130352) (Romano et al. 2006), members of an ancient retrovirus family frequently implicated in promoting NAHR (Jern and Coffin 2008).
Discussion
At 8p23-inv, inversion-type and genetic substructure correlate perfectly in ancestrally diverse populations, providing a further example of inversion-mediated recombination suppression (Hoffmann and Rieseberg 2008). This feature acts as an effective surrogate for the inversion, enabling high-throughput 8p23-inv genotyping: Crucially, our predictions perfectly correlated with all FISH-determined inversion-types (n = 110). The efficacy of our genotyping method (PFIDO) implicitly suggests that 8p23 inversion events were infrequent and relatively ancient. Nevertheless, given that no genetic markers were found that perfectly correlate with inversion-type, 8p23-inv may not be an absolute recombination barrier, which corresponds with theoretical predictions for larger inversions (Andolfatto et al. 2001).
Although 8p23-inv encompasses ∼4.5 Mb, its worldwide distribution broadly reflects that of simpler genetic markers (Supplemental Fig. S6). Conceptually, the serial founder model of migration from Africa (Novembre and Di Rienzo 2009) accounts for its distribution. This implies that the inversion is not responsible for any highly penetrant adaptive/nonadaptive phenotypes and appears to be under neutral (or very weak) selection pressure. However, numerous signals of natural selection reside within 8p23-inv (e.g., Barreiro et al. 2008; Pickrell et al. 2009; Browning and Weir 2010). Whether detection of selection was confounded by 8p23-inv remains to be determined; for example, estimates of interpopulation differentiation (Novembre and Di Rienzo 2009) may be influenced by random fluctuations of alleles “hitch-hiking” on the stratified inversion, whereas long-range LD-based neutrality tests (Barreiro and Quintana-Murci 2010) may be affected by the inversion's pronounced effect on local LD patterns (O'Reilly et al. 2008). Therefore reassessment of selection at 8p23 loci (controlled for inversion-type) is warranted.
Marked population stratification of 8p23-inv may explain the ethnic genetic map length differences observed in the region (Wegmann et al. 2011); for example, there is an inverse correlation between African-American and Asian genetic distance for the breakpoint spanning intervals (Jorgenson et al. 2005; He et al. 2011). Given that the I allele is ∼4.5× more frequent in Africans than in Asians (Fig. 3A), breakpoint-flanking markers that are physically close on the (noninverted) genome reference map will frequently be separated by a considerable distance in Africans due to the inversion, resulting in (unexpectedly) long genetic map distances. In Asians, the physical distance between the same markers would generally be concordant with the reference map (with correspondingly “normal” genetic distances). Comparison of the intermarker genetic distances between Africans and Asians consequently gives an impression of increased local recombination in Africans (Jorgenson et al. 2005), whereas the converse would be expected for markers distantly separated on the genome reference map.
Like the 17q21.31 inversion (Zody et al. 2008), the Homo and Pan 8p23 inversions appear to have occurred independently as the divergence time between these lineages significantly predates that estimated for the human I and N alleles (∼200–600 kya); therefore, the Pan paniscus inversion allele (Antonacci et al. 2009) is likely to represent an independent inversion event. Although the TMRCA analyses suffice to date 8p23-inv relative to primate speciation events, the actual age estimates are necessarily imprecise. Not only do TMRCA estimates depend on numerous model assumptions (e.g., minimal gene flow), the construction of deep genealogies for inversions is theoretically restricted by their effective population size (Garrigan and Hammer 2006). The difficulty in precisely estimating TMRCA for inversions is exemplified by the 17q21.31 inversion, for which estimates differ greatly, from 1.9–2.7 mya (Zody et al. 2008) to ∼14–108 kya (Donnelly et al. 2010); nevertheless, these estimates suffice to place the 17q21.31 inversion event in the Homo lineage.
The timing of REPP formation (Supplemental Fig. S10) coincides with a burst of LCR activity that occurred after the divergence of African great apes and orangutans (Marques-Bonet et al. 2009). This could explain the restriction of 8p23-inv to the African great ape lineage; once accelerated LCR formation had generated the paired REPP/REPD arrangement, the region was susceptible to NAHR-mediated structural instability. Although a derived inversion allele was not observed in gorillas (Antonacci et al. 2009), this may be attributable to limited sampling (n = 3); alternatively, further REPP/REPD rearrangements may have been required prior to inversion formation (e.g., LCR expansion beyond a certain size) (Liu et al. 2011).
In humans, it is unlikely that inversion at 8p23 was a highly recurrent event; this would have eroded the gene-flow barrier between inversion haplotypes, abolishing the observed correlation between inversion-type and genetic substructure. However, a single universal inversion breakpoint was not identified (Supplemental Fig. S18) suggesting some inversion recurrence. Indeed, this might account for the unexpected number of shared polymorphisms observed between I and N alleles (Supplemental Note). Alternatively, given the structural diversity of the surrounding LCRs (Hollox et al. 2008), successive waves of gene conversion and duplication/deletion may have obscured breakpoint signals beyond reasonable recognition. In this regard, the candidate breakpoint may mark a haplotype strongly correlated with inversion status. Finally, in the absence of uninterrupted haplotype-specific LCR assemblies bridging flanking single-copy sequence, the amount of uncharacterized REPD/REPP sequence remains unclear. Therefore, to reliably resolve additional 8p23-inv breakpoints, further positionally anchored REPP/REPD assemblies will be invaluable, a task suited to “third-generation” sequencing techniques (Schadt et al. 2010; Alkan et al. 2011b).
The single LCR–haplotype junction associated with 8p23-inv maps to inverted HERV-K elements, which refines and validates a previously proposed 8p23-inv breakpoint (Antonacci et al. 2009). Transposable elements such as HERV-K are common NAHR substrates (Jern and Coffin 2008); for example, ∼20% of the fixed inversions distinguishing human and chimpanzee genomes are products of NAHR between Alu or LINE-1 elements (Lee et al. 2008). Similarly, >16% of human HERV-K elements may have mediated large-scale genome rearrangements during primate evolution (Hughes and Coffin 2001). Retrotransposons promote genomic instability through replication-fork stalling (Zaratiegui et al. 2011), and such a mechanism (mediated by paralogous HERV-K elements) may have generated a common 8p23-inv allele.
8p23-inv exerts an indirect functional impact by inhibiting meiotic recombination, leading to the preservation of deleterious haplotypes. Indeed, SLE risk alleles were restricted to a haplotype on the derived N chromosome (Fig. 4), a haplotype that plausibly accounts for the strong association between 8p23-inv and BLK expression (Ge et al. 2009). Again, a parallel situation exists on the 17q21.31 inversion, in which the “MAPT H1c” haplotype (associated with neurodegenerative disorders and MAPT expression) (Pittman et al. 2006) is restricted to the derived noninverted chromosome (Zody et al. 2008).
The inversion is also robustly associated with mRNA levels of other transcripts, particularly PPP1R3B whose expression levels influence serum lipid levels in rodents and humans (Gasa et al. 2002; Teslovich et al. 2010). Intriguingly, BLK is also involved in pancreatic β-cell insulin metabolism (Borowiec et al. 2009) and insulin is a key regulator of lipid metabolism (Guilherme et al. 2008), suggesting 8p23-inv may influence lipid phenotypes via its joint association with PPP1R3B and BLK expression. Such propositions can now be formally tested using PFIDO.
Methods
All samples were collected with informed consent and approval from relevant institutional review boards. Statistical analyses were performed in R (R Development Core Team 2011) unless otherwise stated. Full descriptions of the enhanced FISH protocol and of SNP genotype data sets are provided in the Supplemental Note.
The PFIDO
The PFIDO (phase free inversion detection operator) algorithm predicts 8p23 inversion-type from diploid SNP genotype data without the need for phase inference (Supplemental Fig. S2). PFIDO first excludes SNPs missing >30% genotype data and then individuals missing >10% data. A pairwise identity-by-state distance matrix is calculated across individuals, using the snpMatrix package (Clayton and Leung 2007), followed by transformation with MDS. Outlier samples are identified in each dimension using the extremevalues package and are optionally excluded. The derived “axis” (i.e., dimension) displaying the most evidence of substructure is identified using the Shapiro-Wilk test, and the mclust package clusters individuals along this axis using a model-based approach (Fraley and Raftery 2006). Specifically, 18 parameterized Gaussian mixture models (1–9 component Gaussian distributions with equal or nonequal variance) are fit by maximum likelihood estimates to the univariate point distribution. The most parsimonious model is selected using the Bayesian information criterion (BIC), and the number of component Gaussian distributions in the chosen model reflects the number of estimated clusters. The conditional probability of an individual belonging to each cluster, given the mixture model parameters, is calculated for each cluster using a z-score. Model selection is further assessed by three clustering metrics (connectivity, the Dunn index and silhouette width) via the clValid package (Brock et al. 2008); the clustering solution that optimizes these measures is expected to match that selected by BIC. These features allow the user to flexibly define acceptance thresholds for the final clustering result; by selecting a P-value threshold, all inversion-type calls in the outcome surpass the chosen level of confidence. PFIDO functions on any R compatible platform and is freely available from http://www.whri.qmul.ac.uk/staff/Shoulders.html.
8p23-inv imputation based on tagging SNPs
Leave-n-out cross-validation analysis was performed using PLINK to impute inversion status based on “tagging” SNPs (r2 > 0.8) (Supplemental Table S2). Each iteration (n = 1000) randomly masked one-fourth of the CEU data set for 8p23-inv status and compared the subset's imputed inversion-types against the experimental data.
Global 8p23 inversion distribution
All populations were seeded with HapMap genotypes from an appropriate reference panel (Supplemental Table S4; Huang et al. 2009; Teo et al. 2009; International HapMap 3 Consortium 2010), serving as internal positive controls and concomitantly supporting correct cluster assignment. Following PFIDO, samples were regrouped as recommended (Donnelly et al. 2010; Xing et al. 2010) to mitigate sampling error. Six populations with sample sizes less than 10 and two populations in which inversion-allele frequency breached HWE (exact test; P < 0.05) were excluded.
Geographic coordinates were retrieved from the HGDP-CEPH Database (Li et al. 2008), using the mean where a range was given. Populations in the study by Xing et al. (2010) and in HapMap were geographically assigned to their sampling location, apart from CEU and CHD samples (assigned to Northern Europe and Eastern China, respectively) (Lao et al. 2008; International HapMap 3 Consortium 2010). Chinese SGVP samples were assigned to Southern China (Teo et al. 2009), whereas SGVP Malay and Indian populations were placed in their country of origin's center. Geographic distances from Addis Ababa were calculated as recommended (Handley et al. 2007) using the geosphere package. The correlation between geographic distance from Addis Ababa and allele frequency was calculated using the Spearman's rank correlation coefficient. Fst values were calculated using the Hierfstat package (de Meeus and Goudet 2007). Although negative Fst values are possible, they are biologically ill-defined (Barreiro et al. 2008), and so were set to zero.
To construct the empirical null distributions (Hancock et al. 2008), SNPs with similar allele frequency to the inversion (MAF > 0.4) in the HGDP-H952 data set were filtered to produce a set in linkage equilibrium (r2 < 0.2) using PLINK. SNPs were removed within the inversion interval and gene coding regions (i.e., not defined as functionally “unknown” in the UCSC dbSNP130 Table). Rank correlation coefficients and global Fst values were calculated for the remaining 19,969 SNPs. Pairwise Fst values were calculated for a random subsample of these SNPs (n = 1000). Major/minor alleles were designated relative to the ancestral allele.
TMRCA analyses
The minimum TMRCA was estimated using the formula E[Tmrca] = 4Nef(1 − ni−1) as derived for inversions according to the method of Andolfatto et al. (1999), where Ne is the effective population size (CEU = 11,418; YRI = 17,469), ni is the number of inverted chromosomes, and f is approximated using the number of segregating sites specific to inverted and noninverted alleles, which partially accommodates minimal gene flow. A generation time of 25 yr was assumed. In a complementary analysis, sequence overlaps between finished RPCI-11 BACs were extracted. Those corresponding to alternate haplotypes (PID < 99.999%) (Supplemental Table S6) were aligned to whole-genome shotgun assemblies representing a chimpanzee (“Clint”/CH251, contig NW_001240294.1) and a Sumatran orangutan (“Susie”/ISIS no. 71, contigs NW_002882464.1, NW_002882460.1, NW_002882451.1) using MUSCLE. Assembled HuRef haplotypes (Levy et al. 2007) were similarly aligned to NW_001240294.1. Alignments <10 kb or covering LCRs were excluded. Genetic distances were calculated in MEGA4 (Tamura et al. 2007) using the Kimura 2-parameter method (complete deletion option) (Kimura 1980), and evolutionary rate equality assessed with Tajima's relative rate test (alignments with P < 0.05 were discarded) (Tajima 1993). Divergence times between RPCI-11 haplotypes were calculated according to the method describe by Zody et al. (2008) with the formula T = K/2R (where T is time, K the Kimura 2-parameter estimate, and R the average between taxa substitution rate). Either chimpanzee or orangutan were used as an outgroup, and average divergence times were weighted by alignment length.
Analysis of primate REPD/REPP
REPD/REPP (±200 kb) were downloaded from the UCSC database (hg19) and aligned to the nr database using MegaBLAST. All nonhuman primate sequence was retained and remapped back onto the human genome assembly to confirm their mapping to REPP/REPD. Gorilla BAC end sequence data was downloaded from the Trace Archive (ftp://ftp.ncbi.nih.gov/pub/TraceDB/; download date November 26, 2011).
Identifying recombinant sequences
“Finished” BAC sequences were fragmented into overlapping 10-kb segments and aligned to RPCI-11–specific LCR haplotypes using MegaBLAST (parameters: -p 90 -s 90 -q -3 -r 1 -W 28). Each BAC fragment's optimal alignment against each LCR haplotype was retrieved. Alignments with <99% identity were discarded, which diminished the risk of mistakenly analyzing paralogous LCRs from other cytogenetic intervals, as confirmed by 17 negative control BACs that map to paralogous LCRs on chromosomes 3, 4, 7, 11, and 12.
RPCI-11 clones with evidence of LCR mosaicism were screened for recombination events using seven algorithms implemented in the RDP3 suite (Supplemental Note; Martin et al. 2010). A Bonferroni correction was applied to the P-values, and P < 0.01 was deemed significant. Recombination events with a defined breakpoint identified by all methods and supported by phylogenetic evidence are reported.
Haplotype-specific PCR
Primers flanking putative breakpoints were designed using Primer3, positioning sequence variants that distinguish BAC haplotype groups at the primer's 3′ end (Supplemental Table S7). PCR was performed in quadruplicate with CEU DNA (Coriell Institute) using AmpliTaq Gold (Applied Biosystems; PCR parameters optimized empirically). To verify product specificity, PCR products were purified with Exonuclease I and SAP and sequenced on an ABI 3730xl using BigDye v3.1 (Applied Biosystems). Association between haplotype presence/absence and inversion-type was tested using an Fisher's exact test, followed by Bonferonni correction for the 12 haplotypes tested.
Acknowledgments
This research was supported by the Medical Research Council and a British Heart Foundation grant. We thank Emma Jones, Margaret Town, Matthew Hurles, and Panos Deloukas for helpful discussions.
Footnotes
-
↵9 Corresponding authors.
E-mail max.salm05{at}imperial.ac.uk.
E-mail c.shoulders{at}qmul.ac.uk.
-
[Supplemental material is available for this article.]
-
Article published online before print. Article, supplemental material, and publication date are at http://www.genome.org/cgi/doi/10.1101/gr.126037.111.
- Received May 9, 2011.
- Accepted March 6, 2012.
This article is distributed exclusively by Cold Spring Harbor Laboratory Press for the first six months after the full-issue publication date (see http://genome.cshlp.org/site/misc/terms.xhtml). After six months, it is available under a Creative Commons License (Attribution-NonCommercial 3.0 Unported License), as described at http://creativecommons.org/licenses/by-nc/3.0/.