Extraction of Functional Binding Sites from Unique Regulatory Regions: The Drosophila Early Developmental Enhancers
- Dmitri A. Papatsenko1,5,
- Vsevolod J. Makeev2,
- Alex P. Lifanov3,
- Mireille Régnier4,
- Anna G. Nazina1, and
- Claude Desplan1
- 1Department of Biology, New York University, New York, New York, 10003-6688, USA; 2State Scientific Center Genetika, Moscow 113545, Russia; 3Institute of Chemical Physics, Moscow 117421, Russia; 4 Institut National de Recherche en Informatique et en Automatique Rocquencourt, 78153, Le Chesnay Cedex, France
Abstract
The early developmental enhancers of Drosophila melanogaster comprise one of the most sophisticated regulatory systems in higher eukaryotes. An elaborate code in their DNA sequence translates both maternal and early embryonic regulatory signals into spatial distribution of transcription factors. One of the most striking features of this code is the redundancy of binding sites for these transcription factors (BSTF). Using this redundancy, we explored the possibility of predicting functional binding sites in a single enhancer region without any prior consensus/matrix description or evolutionary sequence comparisons. We developed a conceptually simple algorithm,Scanseq, that employs an original statistical evaluation for identifying the most redundant motifs and locates the position of potential BSTF in a given regulatory region. To estimate the biological relevance of our predictions, we built thorough literature-based annotations for the best-known Drosophiladevelopmental enhancers and we generated detailed distribution maps for the most robust binding sites. The high statistical correlation between the location of BSTF in these experiment-based maps and the location predicted in silico by Scanseqconfirmed the relevance of our approach. We also discuss the definition of true binding sites and the possible biological principles that govern patterning of regulatory regions and the distribution of transcriptional signals.
In contrast to coding sequences, where each base pair can be placed in the informational context of protein structure, regulatory DNA of promoters and enhancers has no obvious uniform language, no universal code. However, it is clear that a significant fraction of this regulatory DNA code represents sequences recognized by transcription factors.
Most of the current strategies for identifying binding sites for transcription factors (BSTF) rely on the extraction of binding sites by comparing a set of functionally related regulatory sequences. Algorithms such as MEME (Bailey and Elkan 1995),YEBIS (Yada et al. 1998), CONSENSUS (Hertz et al. 1990), and ANN-Spec (Workman and Stormo 2000) employ various methods based on expectation maximization (EM; Bailey and Elkan 1994) and Gibbs sampling (Lawrence et al. 1993). In addition, several word-counting algorithms have been developed to approach the problem. For instance, the recent Moby Dick program (Bussemaker et al. 2000b) employs a suffix-tree strategy (Apostolico et al. 2000;Marsan and Sagot 2000) to build word dictionaries and then deduce the most significant motifs. Strategies based on extraction from a set often use as an important criterion that a majority of sequences contain the same motif (MEME). For instance, in a typical case in which an unaligned set was represented by a large number (521) of relatively short proximal promoter sequences (−100 to +5; Pesole et al. 1992), this extraction method allowed reliable prediction, mainly of proximal promoter elements (TATA-box) and of ubiquitous binding sites (Bussemaker et al. 2000a). Specific binding motifs that are present in only one or a few members of the set, however, are likely to be lost using this approach.
Until now very few attempts have been made to approach BSTF prediction from another angle, relying for instance on the observation that functional binding sites are often found in clusters within regulatory regions and thus cause a biased word distribution within a given sequence. This bias makes it feasible to extract BSTFs from just a single region. This could be an important achievement as it could identify the transcriptional information specific only to this particular regulatory sequence. The significance of such an extraction from a single sequence is especially important for the analysis of extended and complex regulatory regions found in higher eukaryotes. A promising attempt to predict binding sites in a single wide region was based on measuring hexamer frequencies within the Drosophila Ubx-C region (Lewis et al. 1995).
The fact that many experimentally found BSTF of higher eukaryotes are repeated within a narrow regulatory region allows one to use the same basic principle for the extraction from a single sequence as for the extraction from a set of unaligned sequences, (i.e., by exploring motif redundancy). This redundancy is also affected by the presence of accessory (weak, or shadow) sites, which are often found in a regulatory region nearby the experimentally confirmed strong sites (Kassis et al. 1989; Stanojevic et al. 1991; Small et al. 1992). Although the meaning of these sites is unclear, they have been observed in a wide array of regulatory sequences. Thus, families of related words (motifs) would reliably describe specific BSTF patterns found in a single regulatory region.
One of the differences between extraction from a single sequence and extraction from a set is the higher statistical ambiguity caused by an insufficient length of sequence, by small numbers of repeats, and by the presence of related and overlapping motifs in the same sequence. Moreover, along with multiple BSTF, regulatory regions often contain other statistically significant patterns such as long simple repeats (…CACACA…) or poly(N) tracts (…TTTTT…). The exact function of these sequences is generally not known, but they often interfere with attempts to reveal binding sites. Therefore, special statistics accounting for word overlaps is important when using extraction from a single sequence.
Another known problem related to BSTF extraction without a consensus/matrix description is the lack of biological confirmation for the prediction relevance. Because, in most cases, a typical algorithm requires an estimated BSTF length and number of expected motifs (MEME;Bailey and Elkan 1995), at least some training procedures which are based on a reliable training set appear to be necessary for a given biological system. During the last few years, such training sets have become available for unicellular organisms like Escherichia coli and yeast in the form of annotated promoter databases (van Helden et al. 1998, 2000; Zhu and Zhang 1999). However, the situation evolves much more slowly for higher eukaryotes (Cavin Perier et al. 1998).
To overcome biological ambiguity of such predictions, we focused on a particularly well-known system: the early developmental enhancers fromDrosophila. For this system, we developed experimentally based definitions for the most robust binding sites and we built precise maps of their distribution in these enhancer regions. The enhancers of the Drosophila developmental genes have several advantages for our study—(1) Functional similarity: Typically a stripe of expression at the blastoderm stage of embryonic development; (2) Similar regulation: Most enhancers respond to a relatively small number of known maternal or gap genes (Bicoid, Hunchback, Krüppel, etc.) or pair-rule genes (Eve, Ftz, Hairy, etc.); (3) Structural homogeneity: The enhancers typically have a defined length (∼1000 bp) and are not located near unique proximal promoter elements such as TATA, DPE, and INR (Weis and Reinberg 1992; Burke et al. 1998; Pedersen et al. 1998); and (4) Level of characterization: The large amount of biochemical, genetic, and evolutionary (comparisons between species) data accumulated in the literature for these enhancers makes them an extremely valuable resource.
Based on the principles described above for the extraction from a single region, we developed a new algorithm, Scanseq, that requires no consensus/matrix description and locates the position of potential binding sites in one given sequence. We then investigated the correlation between the Scanseq predictions and the experimentally verified distribution of binding sites in a set ofDrosophila developmental enhancers. We found a high correlation for all enhancers used in our set, using a wide range of algorithm parameters. With the help of a special training procedure, we defined the most effective parameter ranges that can be used in a search for unknown BSTF in this type of complex regulatory regions inDrosophila and likely in other multicellular organisms. We also analyzed the distribution of weak shadow sites and revealed their specific arrangements in several developmental enhancers from our collection.
RESULTS
Developmental Enhancers: Maps of Binding-Site Distribution
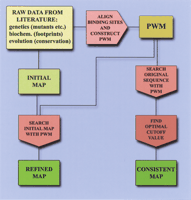
We thoroughly annotated a number of Drosophiladevelopmental enhancers and generated maps of BSTF distribution to measure the efficiency/accuracy of the Scanseqpredictions. Building such maps required accurate processing of a thorough literature compilation, as well as establishing definitions for BSTF. We designed two strategies for the treatment of the compiled literature data (Fig. 1). The first strategy solved the frequent disagreements in the length and the exact location of BSTF reported by different sources. The second strategy implemented a uniform criterion for the minimal strength of a true binding site. As an indirect measure of this strength, we used the positional weight matrix (PWM) score for this site (Berg and von Hippel 1987).
Strategies for BSTF map construction. Two strategies for constructing maps of binding sites rely on a matrix search for experimentally defined binding sites for transcription factors (BSTF). The first strategy (refined map path) is used to verify the exact location and size of the experimental sites. A second strategy (consistent map path) takes into account both the presence of the experimentally verified sites and the matrix score of found matches. The initial map is the raw footprint data from a literature source.
Our compilation contained footprints and other data for 20 of the best-known early Drosophila developmental enhancers (see appendix 1.3 on the New York University Web site:http://homepages.nyu.edu/∼dap5/PSS/appendix1.html). To minimize interference of possible experimental errors, we only included sites for a given transcription factor found in at least two different enhancers (reported by two different research groups) from our collection. We also required that a site be verified by at least two independent methods, including biochemical (footprints), genetic (mutant), or evolutionary (highly conserved blocks) analyses and not simply by a search for a consensus. After such filtering, our set contained binding sites for seven transcription factors: Bicoid (34 sites total), Caudal (15), Ftz (25), Hunchback (43), Knirps (47), Krüppel (21), and Tramtrak (7). We also narrowed down the number of regulatory regions to 10, each containing at least two of the seven types of sites: engrailed intron (enint; Kassis et al. 1989; Florence et al. 1997), even-skipped stripe 2 (eve2; Stanojevic et al. 1991; Small et al. 1992; Arnosti et al. 1996), even-skipped stripe 3+7 (eve3+7; Small et al. 1996), fushi-tarazu proximal enhancer (ftzprox;Han et al. 1993, 1998; Yu et al. 1999), hairy stripe 6 enhancer (hairy6; Langeland et al. 1994), hairystripe 7 enhancer (hairy7; La Rosee et al. 1997, 1999),abdominal-A enhancer (iab2; Shimell et al. 2000), Krüppel region 730 (kr730; Hoch et al. 1991), spaltearly enhancer (sal; Kuhnlein et al. 1997; Barrio et al. 1999;de Celis et al. 1999), and tailless enhancer (tll;Hoch et al. 1992; Liaw et al. 1995).
In the next stage, we built alignments (CLUSTALW, LaserGene) for each type of selected BSTF and outlined a well-defined core made of positions with a high information content (see appendix 1.1 on the Web site). For each type of site, a PWM was built from the core alignment. We used PWMs that were not normalized for the average nucleotide composition (setp α = 0.25 into formula 6 below) to avoid any possible bias for base composition in a particular sequence.
Searches with these PWMs revealed not only the presence of the experimentally verified BSTF, but also multiple high-scoring matches. Therefore, we generated two alternative types of BSTF maps for each regulatory region. The first map, refined, contained only high-scoring PWM hits that coincided with the experimentally identified sites (footprints). This map served to fix the length and the location of the already-known binding sites. However, it is known that in vitro analyses often reveal only the strongest binding sites (Tronche et al. 1997). Therefore, we also developed a second map, consistent, that was based on the relative PWM scores of the found matches.
To determine the relevant PWM score cutoff, we calculated at each cutoff value the number of hits (H, number of experimentally confirmed sites), the number of false-positive sites (FP), and the number of false-negatives (FN, missing but experimentally confirmed sites) between the refined and the resulting consistent map. This procedure was performed
independently for each type of BSTF considered. To give more weight to the experimentally verified BSTFs in the consistent
map, we added more penalties to FN than toFP. We built our penalty function by modifying the likelihood ratio criterion (see appendix 1.2 on the Web site)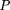
We considered the PWM cutoff to be optimal at the maximum of the given function (see appendix 1.2, Krüppel).
Possible experimental errors, as well as the specificity of our descriptions (alignments, PWM), probably cause the disagreements found between the refined and the consistent maps built. An example of comparison between these maps is shown in Table1. We consider our consistent maps (see appendix 1.3 on the Web site) as the closest approximation to the distribution of true BSTF. However, it is unlikely that one should expect a better agreement between the Scanseq prediction and one of the two maps than between the two maps themselves.
Comparison between the Refined and Consistent Maps
Formulation of the Scanseq Algorithm
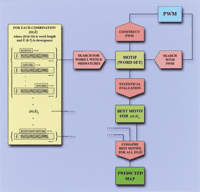
We based our Scanseq algorithm on the assumption that each word recognized by a given transcription factor (BSTF) belongs to its own family of similar words (binding-site motif) found in the same enhancer sequence. Scanseq (Fig.2) extracts statistically significant motifs from a single sequence and generates a map of potential binding sites for this sequence. The algorithm features special statistics for accounting for word overlaps in the same DNA strand and for correlating word overlaps in the complementary strands of DNA (see Methods and appendix 2.2 on the Web site).
Scanseq algorithm. Initial search is performed with words of length m with 0-k mismatches. For each word found in the sequence, the corresponding motif (word set), is refined by positional weight matrix (PWM), and is statistically evaluated through Z score. In the final stage, Z scores for motifs within a range ofm and k are compared and a predicted map is generated. Note that the PWM in the Scanseq algorithm is not the same as in the strategy of BSTF map construction, and it does not include any a priori information about binding motifs.
The Scanseq algorithm includes the following basic stages. In the first step, a search is performed with each m-letter word in the sequence (the seed word) for all similar words with no more than k mismatches. The resulting word family forms the initial motif for each seeded word. In the second step, the search is performed with the PWM constructed for each of the initial motifs. This matrix is normalized for the average sequence composition and uses pseudocounts to cope with small-sampling problem. In the third step, the algorithm calculates the expectation and the variance for the number of occurrences in the random sequence for the double-stranded DNA. The Z score of the refined motif is assigned to each corresponding initial seed word. In most cases, the characteristic length of the potential recognition motif and its divergence level is not known. Therefore, the algorithm performs several calculation rounds with different mand k and finds motif with the highest Z score for a given initial seed word. Selected optional range for the parametersm, k (mmax ,mmin , and kmax ), and Z-score cutoff value defines the predicted map.
Parameters and Predictions
Depending on the amount of available information, regulatory regions in general can be divided into three categories: unidentified, identified in the genome but with no further annotation, and well-known regions with at least some maps for BSTF distribution. Typically, the first category requires an independent preliminary analysis (recognition in the genome) before predicting BSTF. The second category requires some a priori (default) parameter settings deduced from an appropriate training set. Individual training of parameters on one sequence might be applied to the third category of sequences to reveal yet unknown BSTF. Most currently available motif-extracting programs usually require custom settings for the number of expected motifs and their approximate length. We introduced a relatively simple parameter, coverage (c), instead of the widely used number of expected motifs.
The distribution of known BSTFs within the developmental enhancers (consistent maps) showed that on average they represent about a quarter of the sequence length (0.24; see Table 2). Therefore, we took this value as the default coverage expectation. Generally, this important parameter must be approached with care as we observed that in several cases significant deviations from this default coverage occur. The extreme examples were the abdominal Aenhancer (iab2) and the hairy stripe 6 region, whose coverage of the consistent maps were 7% and 65%, respectively (see Table 2). For the length of the BSTFs, we used a range from 7 bp to 15 bp, which is the size observed for the most robust binding motifs found in the developmental enhancers (see appendix 1.2 on the Web site). We also allowed the maximal divergence of the initial search (which represents the number of mismatches, kmax ) to vary in the range of 0%–40% (see also Z-score profiles in Fig.3).
Results of Individual Trainings
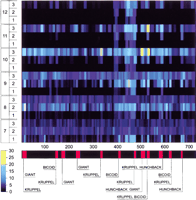
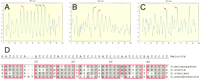
Sensitivity of Scanseq to the parameters of the initial search. Z-score profile plot (X-axis is the position in the sequence) is shown for the even-skipped stripe 2 enhancer using a range of length (m) and divergence (k). Each horizontal line corresponds to a combination of m (7 bp–10 bp) and k (1–3 mismatches) that are shown on the left side. Z-score values are represented by the color scale (bottom left). The bottom bar shows the distribution of binding sites for transcription factors (BSTF; consistent map) in theeven-skipped stripe 2 enhancer. The best statistical correlation with the consistent map for eve stripe 2 was observed at the following parameters: {m = 7; k = 1}, {m = 8; k = 1}, and {m = 9; k = 2}.
To estimate the accuracy of the prediction with no prior consensus/matrix description, we measured the correlation between
the experiment-based consistent maps and the maps of predicted sites generated by the Scanseq algorithm. Three statistical values were monitored: (1) The Matthews correlation coefficient (CC; Matthews 1975),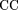
where TP is the number of positions covered by both the predicted and the experimental maps, TN is the number of positions covered by neither of the maps, FP is the number of positions covered only by the predicted map, and FN is the number of positions covered only by the experimental map; (2) The overlap quality (OQ; Gelfand et al. 1996)
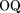and (3) the logarithmic gain in the prediction quality:
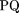Where OQ
exp is the expectation of OQfor random prediction with a given coverage:
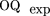The values for OQ and PQ vary in the range of 0 (no correlation) to 1 (complete coincidence); the correlation coefficient CC varies from −1 to 1.
Training Parameters on an Individual Region
To assess the sequence-to sequence variations of the best parameters, we first trained Scanseq on each individual enhancer sequence. For each considered combination of parameters, defining minimal and maximal length of the binding motif and its divergence (m min , mmax , andkmax ), we found the optimal coverage c (the fraction of the total sequence length covered with the predicted sites) that produced the highest CC and OQ values (see appendix 3 on the Web site). The optimal individual parameters found for the 10 developmental enhancers are shown in Table 2.
Despite the fact that the optimal length/divergence parameter combination differed in most cases, the correlation between the predicted and the consistent maps was positive for virtually all combinations tested (see appendix 3 on the Web site and Fig. 3). In the worst case (hairy stripe 6 enhancer), 65% of which was covered with BSTF, the PQ was still positive. In many cases the optimized coverage c was very close to the observed coverage (c-MAP) for the consistent experiment-based map.
The practical advantage of individual training is clear from the example of eve stripe 2 region (Fig.4). At the best parameter values found for the consistent map (only Bicoid, Hunchback, and Krüppel sites were included), we also managed to predict another distinct motif at position 510: CATAATAAT. This sequence exactly coincides with the most conserved half of the first Giant site in theeve stripe 2 region: TAAAAACACATAATAAT. The best individual parameter combination, which is often specific for a particular sequence, typically produces minimal statistical noise there (see the difference in Z scores in Table 2).
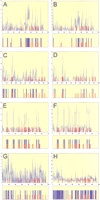
(see figure on preceding page) Scanseqpredictions. Z-score profile plots and maps of predictions are shown for even-skipped stripe 2 (panels A, B),hairy stripe 7 (panels C, D),even-skipped stripe 4+6 (panels E, F), andrunt stripe 5 (panels G, H). The plots show the maximum observed Z scores (Y-axis) for each position in the sequence (X-axis) using a selected parameter range (mmin, mmax ,kmax , and c). Panels A,C, E, and G (see parameters and statistics in Table 3) show the results after training on the group-of-10 enhancers. The results of individual trainings (see Table 4) are shown in panels B, D, F, and H. The predicted map is shown below each Z-score profile plot. The blue bars represent the most redundant segments (predicted byScanseq); the red bars represent the established distribution for binding sites for transcription factors (BSTF): Consistent maps for even-skipped stripe 2 (Giant sites were not used in the training), hairy stripe 6, and the virtual maps for even-skipped stripe 4+6 and runt stripe 5 are shown.
Training Parameters on the Group-of-10 Regions
To assess the best default parameters for sequence-independent predictions, we trained Scanseq on the entire group-of-10 consistent maps from our enhancer collection. To find the optimal ranges for length and divergence (mmax ,mmin , and kmax ), we calculated the average CC and PQ values for our 10 enhancers for each tested parameter combination (at the optimal coverage c; see above). Then we sorted the parameter combinations in a descending order of average CC orPQ values (see appendix 3 on the Web site). The combination of 7 bp–9 bp with 0–1 mismatches provided the best scores for both selected measures of statistical correlation. We set the coverage expectation according to the average value we observed in the 10 consistent maps (cav = 0.24). The results summarized in Table 3 indicate that these default parameters still worked well for most examples from the training set.
Statistics for Prediction with the Default Parameters
The greatest decrease in the prediction quality for sequence-independent training (as compared to individual training) was mainly caused by the difference between the selected default coverage (0.24) and the observed coverage. A striking example of the negative effect of the default coverage on prediction quality was with theiab2 region, where the consistent map covered only 7% of the long (1.7 Kb) sequence. At the default coverage of 24%, individually trained predictions (which are rather selective, PQ = 0.89,c = 10%; see Table 2) decreased (PQ = 0.47), mainly due to the unavoidable appearance of false-positives (compare 7% to 24%). In contrast, the Scanseq predictions were much less sensitive to the motif length and its divergence. The observed sensitivity of the algorithm to the coverage expectation value apparently reflects the natural variation of BSTF density in a defined regulatory region. In some enhancers (hairy6), true binding sites seem to cover most of the region; whereas, in others (eve2, iab2), they show relatively sparse distribution. Clearly, observed densities of BSTF will also depend on selection of regulatory region borders, definition of true binding site, etc. This important problem of coverage expectation has its own biological importance and will require independent analysis. A detailed comparison between the individually trained predictions and the predictions at the found default parameters is given for evestripe 2 region in Figure 5.
Detailed map of predictions for even-skipped stripe 2. The comparison between the Scanseq predictions (in red) and the consistent map (in green) shows the efficiency of individual training (panel B) versus training on a group of 10 (panelA). In both cases, periodic sequences (ATCCC)ngenerated very high statistical scores.
Testing the Default Parameters on the eve stripe 4+6 and runt stripe 5
For two enhancers from our initial collection, even-skippedstripe 4+6 (Fujioka et al. 1999) and runt stripe 5 (Klingler and Gergen 1993), the distribution of BSTF was unknown. We used these two poorly characterized regions to test the agreement between two independent methods of BSTF predictions: Scanning with PWM, which uses available description of consensus/matrix for known sites, andScanseq, which is based on motif redundancy.
The pair-rule genes eve and runt are expected to be regulated by at least some of the same upstream maternal and gap genes that regulate the other enhancers used in our training set:bcd, hb, kr, kni, and gt. In fact, mutants for most of these genes alter the expression of theeve4+6 and runt stripe 5 enhancers significantly. We scanned each of the two regions with our PWM matrices built for Bicoid, Hunchback, Krüppel, Knirps, and Giant at the cutoff values defined above. The resulting maps for eve4+6 andrunt5 were called virtual maps because they reflect the distribution of expected but not experimentally verified BSTF. We then extracted potential binding sites from these regions withScanseq at the default parameter values, described in the previous section (mmin = 7,mmax = 9, kmax = 1, andc = 0.24).
Comparison between the virtual maps and the predictions byScanseq showed striking statistical correlation. The statistical significance values for eve stripe 4+6 were among the highest (CC = 0.61, PQ = 0.64; see Table 3) and the predicted map (Fig. 4) showed an astonishing correlation with its virtual map. The virtual map for the eve stripe 4+6 region contained only Hunchback and Knirps sites but not Bicoid, Krüppel, and Giant sites (see appendix 1.3 on the Web site). Scanseqalso efficiently recognized the same two types of binding motifs. This exclusively in silico analysis strongly supports the involvement of Hunchback and Knirps in the regulation of the eve4+6 region, as suggested from genetic experiments (Fujioka et al. 1999). The predicted map for runt5 also showed positive, though significantly lower (CC = 0.15; PQ = 0.20), correlation with its virtual map at the default parameters. Comparison between the results of prediction at the default versus individually trained parameter values for eve4+6 and runt5 confirmed once again the importance of the correct coverage expectation for the Scanseq algorithm. Thus, in the case of individual training, all putative sites in runt5 with one exception fell into the predicted regions that covered 55% of the sequence length.
DISCUSSION
Definition of True Binding Site
The efficiency of the Scanseq program indirectly confirms that the multiple binding motifs in Drosophiladevelopmental enhancers are statistically significant. In these regions, weak and strong sites together form powerful word families. To independently confirm the abundance of weak shadow sites in these enhancers, we searched the even-skipped stripe 2 region (728 bp) with our PWMs for Bicoid, Krüppel, Hunchback, and Giant and built a distribution of PWM scores for all positive matches. Table4 shows the comparison of such distribution with the expectation in random sequences having the same length and base content.
Distribution of Binding-Site Matches in the eve2 Region by PWM Score
Most of the experimentally verified true sites generated the highest scores (>6) and their presence in such numbers was statistically unexpected in eve stripe 2. The second score zone (4–6) contained the weak sites with mismatches in the core. Surprisingly, for this score zone, the observed number of sites still exceeded the expected number for all four types of binding motifs. The strong agreement of data for all four binding motifs suggest that theeve stripe 2 enhancer has at least twice as many sequences related to known BSTF than reported experimentally.
This simple test not only confirms the specific presence of accessory shadow sites (not revealed by footprint) around the strong sites, but also provides new grounds for the definition of BSTF. In fact, some of the poorly scoring shadow sites might be considered as true sites, thus changing the initial alignments, as well as the critical cutoff values. Apparently the procedure for the definition of BSTF must be iterative and include likelihood criteria (see equation 1) at the first stage, followed by statistical refinement of the motif at the second stage (Table 4).
BSTF Arrangements and Role of Tandem Clusters
It is still unclear whether the detected weak shadow sites have functional significance and how much they contribute to transcriptional regulation of the enhancers. To shed some light on this problem, we analyzed the distribution of weak sites from the score zone 4–6 (Table4) and found striking features in their arrangement: The weak sites often formed tandem clusters in the enhancers from our training set (Table 5).
Periodic Sequences in Drosophila Developmental Enhancers
Equally spaced sets of 5–10 repeats of an imperfect site form a highly unusual periodic sequence, with a small period of repeat, often causing overlap of neighboring matches (compare RATCCC to CTAATCCC—Bicoid). The fine structure of the most impressive examples and the evolutionary conservation of one of the sequences are presented in Figure6. The arrangement of the shadow sites in tandem clusters and the striking conservation of these tandems in evolution strongly support their biological significance.
Structure and conservation of tandem repeats. Periodic structures of ∼100-bp region from even-skipped stripe 2 (A,D), even-skipped stripe 4+6 (B), andfushi-tarazu proximal enhancer (C) are revealed by matrix search for Bicoid, Knirps, and Tramtrack, respectively (see also Table 5). The red arrows indicate sites that produce a positional weight matrix score in the 4–6 range (shadow sites). Evolutionary conservation in four species of Drosophila is shown foreve stripe 2 (ATCCC)n (D).
We see two possible roles for the tandem repeats in enhancers. One, they might be directly involved in the tight binding of transcription factors; in this case the multiplication of weak sites into tandem clusters could make such binding highly cooperative and strong (Burz et al. 1998). Two, the tandem clusters may participate in a variety of recruitment mechanisms. In the simplest case, long repetitive sequences may effectively serve to trap a protein from solution and recruit the transcription factor to its strong binding site within the enhancer. This hypothesis assumes that the initial binding to a repeat of shadow sites is weak and that the transcription factor quickly slides or jumps to stronger neighboring sites. The possibility of such lateral diffusion for transcription factors on DNA has been widely discussed in the literature (Berg et al. 1981; Berg and von Hippel 1985; Khory et al. 1990).
Although the exact role of the tandem repeats of shadow sites in enhancers, as well as their precise structure, remain to be explored, they represent a unique opportunity for unveiling the regulatory code of promoters. The unusual structures of periodic sequences might not only assist in identifying true binding sites in promoter and enhancer regions, but they may also serve for the efficient recognition of regulatory sequences. This, however, will require further analysis and classification to distinguish true regulatory tandems from satellite, telomeric, and other repeated sequences.
Strategies for BSTF Prediction
The prediction of Knirps and Hunchback sites in the eve4+6region shows that several methods can be successfully combined for the mapping of BSTF in defined regulatory regions. Each method, however, has its limitations. For instance, the analysis of the evolutionary conservation of regulatory regions usually does not reveal the binding sites themselves, but only conserved blocks within a regulatory sequence. Due to the possible presence of conserved transcriptional signals other than BSTFs and to the extreme flexibility of the regulatory code, the interpretation of such conserved blocks as candidate binding sites might be incorrect. Another widely used approach requires a prior description of BSTF in the form of a matrix (PWM, hidden Markov model) or consensus. This method is much more reliable, but the description is not always available. The currently existing databases, such as TRANSFAC and TRDD (Heinemeyer et al. 1998), contain only a limited fraction of all transcriptional factors, many of which represent fairly pleiotropic regulators, found in a vast number of regulatory regions. Moreover, as was shown in the current work, the definition of BSTFs must also include a relevant cutoff for the search to distinguish between true sites and false-positives. However even such consistent cutoff values do not prevent the detection of chance matches at irrelevant places of genome (Berg and von Hippel 1987).
Methods of the third class use no a priori information and extract sites from the set of unaligned sequences, each of which is believed to contain somewhere the same BSTF, for instance, from regulation experiments. The most powerful techniques in this case are expectation maximization (Bailey and Elkan 1994) and Gibbs sampling (Lawrence et al. 1993). This approach became popular for analysis of microarray experimental data. These methods extract common motifs from a set of sequence data, which might not be sufficient, especially in the case of unique tissue-specific signals, often presented only in one sequence of the set. In this context, the extraction of BSTF from a single region with no assumption of matrix/consensus/conservation takes an important place in the unveiling of the regulatory DNA code. Although this method is currently less precise than the more conventional extraction with the PWM, we have shown that it can be adopted for virtually any regulatory sequence and deliver biologically relevant predictions.
The possibility of BSTF extraction from a single sequence makes application of the technique especially important for genome computational studies and genome annotation projects. However, the meaningful predictions can be generated only if clustered BSTFs are presented in a promoter region and correct parameter settings are found for a particular biological system. Currently, available information about the organization of eukaryotic promoter cannot provide us with the answer of how common binding-site clustering is. However, in many known cases (B.P. Berman et al., in prep.), this clustering is frequent enough to make our prediction strategy successful.
To investigate the possible application range of our algorithm, we performed similar calculations for rhodopsin promoters ofDrosophilla, the system, which has been studied experimentally by the authors of this paper (see appendix, rhodopsin promoters, on the Web site). The minimal rhodopsin promoters are much shorter than the developmental enhancers are (∼300 bp versus ∼1000 bp); they contain nonredundant elements such as the TATA box, and, in opposite to the developmental enhancers, they activated at the very end of the developmental cascade. Extraction of known recognition motifs from theDrosophila rhodopsin promoters at the default parameter settings, established for the developmental enhancers, have shown similar performance (maximum observed CC = 0.59). The training of Scanseq on the group of six most knownDrosophila rhodopsin promoters delivered exactly the same optimal parameter settings (7 bp–9 bp, 1 mismatch). Identical behavior of the Scanseq program in two biologically distinct systems supports its wide application range.
We believe that our algorithm can still be improved by a better definition of the borders of regulatory regions (see appendix, imperfect sequence data, on the Web site), independent estimation of the coverage expectation, and a better comparison of the extracted motifs.
METHODS
Scanseq Algorithm
Search for Redundant Motifs
For each m-letter seed word located in position lof S, all words in S were found that differ from the seed word by no more than k substitutions. This set ofql
words found comprised the initial motifHl
for position l. Because the initial motif, Hl
, is an alignment, one can build a PWM, Wl
, from this alignment using equation 6 (Berg and von Hippel 1987; Tatusov et al. 1994) with pseudocounts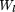
where q
α(i) is the number of occurrences of letters of type α in thei
th column of the alignment. For the null statistical hypothesis, we considered the Bernoulli sequenceR, with letter probabilities estimated from S:pα
= Nα
/Nfor each letter type α. We scanned the sequence with matrix Wl
and selected the PWM threshold in a way such that for each seed word, the total number of high-scoring words is equal to
the previously found number ql
.
Statistical Evaluation
This ql
was our observation for the number of similar words found in the sequenceO = ql
. To test whether this number was significantly greater than the number of similar words counted in a random sequence of the
same length and composition, we constructed Z score:Z = (O − E)/V
1/2. In this formula, E is the expected number of words found in a random sequence, and V is its variation. In our case, E was the expectation of the motif H̃
1, which includes all possible m-words scoring withWl
higher then the selected threshold. We built this motif explicitly by generating all m words and testing their Wl
scores. Counting in two strands, we reformulated as weighted counting on one strand. In this case, the motif must also contain
all mutually complementary words, which we added when necessary (see appendix 2.2 on the Web site;Régnier 2000). During this addition, any word ω that already had its own inverse complement, notably any palindrome, obtained the weight ω = 2; whereas, all other words obtained the weight ω = 1. Then for double-stranded counting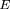
With the sum taken over all words ω belonging to the motifH̃
1, each of which has probabilityP(ω), the variance V takes the form
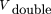where the sum over f is taken over all words belonging to motif H, the matrix A
ω,freflects possible overlaps with different shifts between wordsω and f, c
1 is the linearity constant, the value of which is small as compared toVdouble
for our length range of hundreds of base pairs (Régnier 2000; Régnier et al. 2000). This constant also can be calculated analytically, but it makes sense only whenm ∼ n, which is not our case. ForO < E, we put Z = 0 by definition. Our previous calculations (Régnier et al. 2000) showed that correlations between words overlapping in the same or at complementary strands forO ∼ 10, result in changes of Z with factors of the order of 2, as compared to the Poisson's approximation.
Evaluation of Motif Length and Divergence
A regulatory region usually contains binding motifs with different characteristics involving site length and divergence. In this case, fixing of any particular m and k could result in extraction of only particular types of signals. To bring more flexibility into the procedure, we first ran Scanseq with different m and k values and then compared the Z scores assigned to words seeded with these different parameters (Fig.3). We considered that word w 1(m 1, k 1, Z 1) dominates word w 2 (m 2,k 2, Z 2) ifm 1 ≥ m 2,Z 1 > Z 2 andw 1 covers no less than m 2 − 1 letters of w 2. Then for each position lthere will be a dominant word wl seeded at this position. The Z score of this dominant word was assigned to position l. We scanned over all realistic ranges of signal lengths and maximal mismatch numbers. However, since the irrelevantm and k introduce undesirable noise, it is more practical to train the algorithm for the best minimalmmin and maximal mmax length of the word, as well as for the maximal number of mismatches kmax .
Construction of Predicted Maps
To generate the predicted maps of BSTF distribution, we selected positions with Z scores higher than a custom cutoff valueZmin . Depending on the chosenZmin , the dominant selected words cover a certain fraction of the DNA sequence. Due to the dramatic difference in Z-score values generated in different sequences for the samemmax, mmin , andkmax , we found it practical to consider the overall length of sequence covered with the predicted map, or coveragec, as a custom parameter, instead of Z score. Note that for each c, there is a corresponding Zmin . The specification of four parameters—mmax ,mmin , kmax , and c—is sufficient to generate a predicted map. To find the best values for these parameters, we applied explicit training on our set of enhancer sequences.
Acknowledgments
We thank Steven Small, Bud Mishra, Michael Gelfand, and Tiffany Cook for helpful discussion and critical reading of manuscript. This work was supported by grants from National Science Foundation (IBN 0002958) and National Institutes of Health/National Eye Institute (EY13010) to C.D. V.M. and A.L. were also supported in part by grants from Ludwig Institute for Cancer Research and Howard Hughes Medical Institute East Europe. Web appendix is available athttp://homepages.nyu.edu/∼dap5/PSS/appendix1.html.
The publication costs of this article were defrayed in part by payment of page charges. This article must therefore be hereby marked “advertisement” in accordance with 18 USC section 1734 solely to indicate this fact.
Footnotes
-
↵5 Corresponding author.
-
E-MAIL dap5{at}nyu.edu; FAX (212) 995-4710.
-
Article and publication are at http://www.genome.org/cgi/doi/10.1101/gr.212502.
-
- Received August 27, 2001.
- Accepted December 14, 2001.
- Cold Spring Harbor Laboratory Press
