How to Interpret an Anonymous Bacterial Genome: Machine Learning Approach to Gene Identification

  1. William S. Hayes and
  2. Mark Borodovsky1
  1. School of Biology, Georgia Institute of Technology, Atlanta, Georgia 30332-0230 USA
 
Next Section

Abstract

In this report we address the problem of accurate statistical modeling of DNA sequences, either coding or noncoding, for a bacterial species whose genome (or a large portion) was sequenced but not yet characterized experimentally. Availability of these models is critical for successful solution of the genome annotation task by statistical methods of gene finding. We present the method, GeneMark-Genesis, which learns the parameters of Markov models of protein-coding and noncoding regions from anonymous bacterial genomic sequence. These models are subsequently used in the GeneMark and GeneMark.hmm gene-finding programs. Although there is basically one model of a noncoding region for a given genome, several models of protein-coding region are automatically obtained by GeneMark-Genesis. The diversity of protein-coding models reflects the diversity of oligonucleotide compositions, particularly the diversity of codon usage strategies observed in genes from one and the same genome. In the simplest and the most important case, there are just two gene models—typical and atypical ones. We show that the atypical model allows one to predict genes that escape identification by the typical model. Many genes predicted by the atypical model appear to be horizontally transferred genes. The early versions of GeneMark-Genesis were used for annotating the genomes of Methanoccocus jannaschii and Helicobacter pylori. We report the results of accuracy testing of the full-scale version of GeneMark-Genesis on 10 completely sequenced bacterial genomes. Interestingly, the GeneMark.hmm program that employed the typical and atypical models defined by GeneMark-Genesis was able to predict 683 new atypical genes with 176 of them confirmed by similarity search.

Pioneer methods for statistical identification of protein-coding regions in DNA sequence were developed in the early 1980s (Fickett 1982; Gribskov 1984; Staden 1984). These methods exploited the statistically significant differences in compositional features of continuous protein-coding and noncoding DNA sequences. The search for formal mathematical tools that would express these differences in the most efficient way led to the introduction of inhomogeneous, three-periodic Markov chain models of protein-coding regions (Borodovsky et al. 1986a). These models, along with ordinary Markov models of noncoding DNA sequence, were incorporated into a Bayesian algorithm, GeneMark, analyzing DNA sequence locally within a sliding window (Borodovsky et al. 1986b, Borodovsky and McIninch 1993). Later on these models were used in a global maximum likelihood algorithm, GeneMark.hmm, analyzing the whole DNA sequence at once (Lukashin and Borodovsky 1998). The combination of parameters of three-periodic Markov models of different orders, the interpolated model, was used in the GLIMMER program for gene finding in bacterial genomes (Salzberg et al. 1998). Three-periodic Markov models have been also used in the programs most often used for eukaryotic gene finding, such as GENSCAN (Burge and Karlin 1997), GRAIL (Xu et al. 1994), and HMMgene (Krogh 1997). Sound application of the Markov model-based approach to gene finding have been performed recently in annotating the first complete bacterial genomes Haemophilus influenzae, Mycoplasma genitalium, and others (see Methods). Difficulties soon surfaced. Unlike the pioneer genome sequencing project of H. influenzae, many genomes completed later were swiftly sequenced starting from the zero point. Therefore, there was an absence of previously experimentally annotated DNA sequence necessary to determine the parameters of Markov models. This difficulty was aggravated by the fact that protein-coding sequences in a given bacterial genome were not homogeneous in their compositional features (Medigue et al. 1991). Therefore, the program using models trained on the bulk set of protein-coding sequences happened to be insensitive in finding genes of minor inhomogeneity classes. In cases when preliminary information on gene classes is available, class-specific models of protein-coding regions could improve the performance of the gene-finding method (Borodovsky et al. 1995). Therefore, the problem was to derive accurate models of coding and noncoding regions, including specific models for several gene classes, from the anonymous sequence.

The GeneMark-Genesis method described below addressed this problem. The method worked in two main steps. A set of “long” open reading frames (ORFs) identified in bacterial genomic sequence was used to start a process of obtaining parameters of Markov models of protein-coding and noncoding regions. The initial models were used in the GeneMark program to score the putative gene sequences and to form the cluster seeds for the class-specific training sets. Then the clusterization procedure using relative entropy (Cover and Thomas 1991) as a distance function was run until convergence and several sets of presumably coding sequences with more homogeneous compositional features were obtained. In the simplest and the most important case, there were just two clusters that gave rise to so-called typical and atypical models of protein-coding region.

The early versions of the GeneMark-Genesis program were used in genome sequencing projects of M. jannaschii (Bult et al. 1996) andH. pylori (Tomb et al. 1997); however, complete publication of the method was delayed until comprehensive data on the accuracy of various algorithm options were obtained.

We tested the GeneMark-Genesis program on 10 complete bacterial genomes (see Methods). The results of the tests were presented in terms of local “short fragment prediction accuracy” characterized by false-negative and false-positive error rates and in terms of global “whole gene prediction accuracy” characterized by sensitivity and specificity parameters. The intriguing possibility to predict genes of different evolutionary origins at an early stage of anonymous genome analysis did not escape our attention. For the Escherichia coli genome, we have analyzed the relationship between compositionally atypical genes and horizontally transferred genes as identified in previous studies (Medigue et al. 1991; Lawrence and Ochman 1997). We showed that using the atypical gene models in the GeneMark.hmm program led to prediction of >400 new genes in the 10 genomes. From these predictions, 176 were corroborated by protein sequence similarity search by gapped BLAST (Altschul et al. 1997).

Previous SectionNext Section

RESULTS AND DISCUSSION

Root Models

The Root models, of orders zero to five, were generated, as described in Methods, for the 10 complete bacterial genomic sequences. For each genome, the predictive accuracy of the Root model was evaluated by the “short DNA fragment identification” procedure with cross-validation. The accuracy of the Root model was compared with the predictive accuracy of the GenBank model. A summary of these comparisons is given in Table 1. The “optimal” order of the Root (GenBank) model was defined as the order of the model that produced the lowest false-negative error rate. The error rates produced by the Root (GenBank) models of the optimal order are shown in Table 1. The slightly higher false-negative error rates produced by the Root models are within 2% of the error rates generated by the GenBank models.

View this table:
Table 1.

False-Negative Prediction Error Rates for Optimal Orders of the Root and GenBank Models for 10 Species

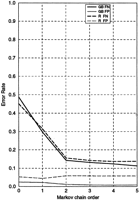
More detailed comparison of the Root and GenBank models performance is presented in Figure 1 for the E. coli case. The observed relatively high false-positive error rate of the Root model (Fig. 1) is partly attributable to the higher contamination of the noncoding test set for the Root model with true protein-coding regions as compared with the noncoding test set for GenBank model. Note that although the Root model prediction accuracy in terms of the false-negative error rate is close to the GenBank model for each given order (Fig. 1), there is still room for improvement for both the Root and GenBank model performance. For each genome, the accuracy of the Root model and the GenBank model was also characterized in terms of sensitivity (Sn) and specificity (Sp) values (see Methods). The GenBank model performed slightly better than the Root model, for instance, the Sn and Sp average for B. subtilis was 0.941 for the GenBank model and 0.921 for the Root model. For the more homogeneous genome ofH. pylori, the Sn and Sp average was 0.952 and 0.946 for the GenBank model and the Root model, respectively. For all of the species studied in this paper, the difference in predictive accuracy between the two models, measured by the average of Sn and Sp, was less than three percentage points. The upper limit of averaged Sn and Sp was 0.943 for the GenBank model and 0.919 for the Root model.

Figure 1.
View larger version:
Figure 1.

False-negative (FN) and false-positive (FP) prediction error rates observed in the short fragment identification procedure implemented theE. coli genome. The Root and GenBank models were employed in the GeneMark program making the predictions. Similar graphs are called accuracy graphs (see Figs. 2 and 3, below).

Clustering

We used the clustering procedures described in the Methods section to reduce the level of inhomogeneity in the sets of coding regions used for training models of several gene classes. The results of ORF clusterization and the characteristics of the performance of these cluster-specific models are presented and discussed in this section.

It was argued that the GeneMark-type algorithm reliably identifies the protein-coding regions whose oligonucleotide composition conforms to the Markov model that GeneMark is using. The Markov model, however, derived from a large enough set of genes represents the composition features common to the majority of genes in this set. Therefore, even using this model in the GeneMark program to analyze the same set of genes, some coding regions with atypical composition could be misidentified as noncoding. Our attempt to divide the initial set of long ORFs into several homogeneous subsets (clusters) pursued the goal of forming at least, and preferably at most, two clusters that would be used as training sets for typical and atypical models. As shown below, for all bacterial genomes in the current study, the two-cluster division was indeed possible and worked sufficiently well for gene-finding purposes. To follow the previous studies of E. coli genome (Medigue et al. 1991), however, we also considered the three-cluster case with the third cluster called the highly typical cluster.

The two-means clustering algorithm, which produced the type A clusters, was initially tested on a “toy” sequence, the hybrid DNA sequence combining E. coli and H. influenzae genomic sequences. The long ORF clusters, typical and atypical, obtained by the clustering procedure were named as EC and HI clusters after the name of the species representing a majority of the ORFs in a particular cluster. The typical cluster turned out to be theEC cluster, as there are almost three times as many E. coli ORFs as H. influenzae ORFs. Table 2shows the sizes of the overlaps between the sets of true E. coli and H. influenzae ORFs and the resulting ECand HI clusters obtained from the hybrid sequence.

View this table:
Table 2.

Composition of Typical and Atypical ORF clusters Obtained for Combined Sequence in Terms of Native E. coli and H. influenzaeORFs

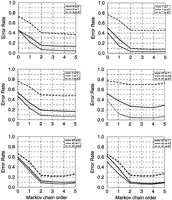
The models derived from the EC and HI clusters of long ORFs were evaluated using the “short DNA fragment identification” procedure. In Figure 2, the top panel shows the false-negative error rate produced by the Combined (Root) model of different orders. This model was used to identify coding function in short fragments of long ORFs from the Combined set (solid line), from the EC cluster (dotted line), and from theHI cluster (dashed line). Obviously, the Combined model more reliably recognized as coding the sequences from the larger ECcluster than the sequences from the smaller HI cluster (the majority of the training set effect). The EC cluster derived model, the middle panel, identified quite well the coding property of short sequences from the EC cluster, was less precise, on average, in identifying sequences from the Combined set, and was a poor coding function predictor for the sequences from the HIcluster. The HI cluster model, the bottom panel, predicted the coding property of sequences from the HI cluster quite well, moderately well for those from the Combined set and rather poorly for the sequences from EC cluster. As is seen in Table 2 and Figure 2, the toy example demonstrated the ability of the algorithm to detect the presence of two types of protein-coding sequences in one anonymous DNA sequence.

Figure 2.
View larger version:
Figure 2.

Accuracy graph of the analysis of the combined sequence of E. coli and H. influenzae (see text and Fig. 3 legend).

The two-means clusterization procedure was applied to the 10 complete bacterial genomes, assuming no annotation was known, to obtain the typical and atypical clusters of long ORFs (A, B, and C types of clusters). The cluster-specific models of protein-coding sequences obtained from these clusters were designated as 2A-, 2B-, and 2C-type models. The three-means (k = 3) clustering procedure was also applied to the 10 genomes and produced the typical, atypical, and highly typical ORF clusters (of types A, B, and C). The cluster-specific models obtained from these clusters were designated as 3A-, 3B-, and 3C-type models. The sizes of all clusters are given in Table 3. Interestingly, the largest atypical clusters of type A were found in the two Mycoplasma genomes.

View this table:
Table 3.

Numbers of Long ORFs in the Clusters of Type A, B, and C Obtained byk-Means Clustering Procedure (k = 2, 3)

Long ORFs from the atypical cluster defined either by the two- or three-means clustering possessed an atypical oligonucleotide composition. Many of these ORFs could be descendants of genes horizontally transferred into the bacterial genome in the course of evolution. For a given genome, one might expect to see two types of horizontally transferred genes, the ones with GC content lower than average and ones with GC content higher than average. Therefore, one may assume that the atypical cluster should contain two subsets, one with higher-than-average GC content and another one with lower than average GC content. The clustering results, however, did not quite meet this expectation. Atypical long ORFs in all bacterial genomes, besides the two genomes of M. genitalium and M. pneumonia, yielded bell-shaped unimodal GC content distributions. Also, as shown in Table 4, in all but the two Mycoplasmagenomes, the GC content of the atypical cluster was 3%–5% lower than the typical cluster.

View this table:
Table 4.

GC Content for the Typical and Atypical Clusters of Types A, B, and C

As an exception to the rule, among the M. genitalium long ORFs assigned to type A or C atypical clusters by two-means clustering procedure there were nine ORFs highly deviant in GC content. Only one of the nine ORFs, the one encoding a cell envelope protein of unknown function, was annotated in GenBank. Among the M. pneumoniaORFs assigned to type A or C atypical clusters there were 22 ORFs with deviated GC content. Of these 22 ORFs, 20 were annotated in GenBank. These annotated genes were either adhesin genes or genes of hypothetical proteins. Two M. jannaschii ORFs with highly deviant GC content were assigned to type A or C atypical clusters.

Incidentally, those of the GC-deviant ORFs observed in these three species that were annotated in GenBank were encoding cell-envelope or surface-structure proteins. The other atypical ORFs, predicted as genes but not annotated, were also likely to belong to the same family. Interestingly, for the three species mentioned above, all GC deviants did not belong to the atypical clusters of type B.

The cross-validation tests have shown (Table 5), that the models derived from atypical clusters were sufficient to identify, almost all ORFs in these clusters as protein-coding sequences.Therefore, typical and atypical models together covered an overwhelming majority of long ORFs in a given bacterial genome. Therefore, assuming no compositional difference between sets of longer and shorter genes there was no practical need, from the gene finding standpoint, to continue sub-clustering any of the atypical clusters.

View this table:
Table 5.

Fraction of Atypical Long ORFs Predicted by the GeneMark Program using the Atypical Model

Note that the outcome of the clustering procedure could vary depending on the procedure parameters. Because clustering is essentially an optimization process, the final division of the initial set into clusters corresponds to a local minimum of the distance function. To prove that the minimum is the global one is rarely computationally feasible. Nevertheless, it was observed that significant variations of the ORF cluster seeds did not influence the result of the clustering. For instance, for a genome such as E. coli a random assignment of long ORFs into “seed” clusters for two- or three-means clustering still resulted in essentially the same set of clusters.

For each genome, the accuracy of models derived from ORF clusters was assessed by the “short fragment identification method”. This analysis is illustrated in Figure 5, below for the E. coligenome case. The three left panels of Figure 3 show the false-negative error rates observed in application of the Root model (top), the typical model (middle), and the atypical model (bottom) obtained by two-means clustering. The three curves in each panel correspond to the three control sets of short protein-coding fragments derived from the Root cluster (solid line), typical cluster (dotted line), and atypical cluster (broken line), respectively. The error rates observed in application of the models derived by three-means clustering are shown in the right panels (Fig. 3) devoted to typical (top), highly typical (middle), and atypical model (bottom). The three curves in each panel correspond to the control sets of short sequences derived from typical cluster (solid line), highly typical cluster (dotted line), and atypical cluster (broken line). A lighter gray curve is seen in all panels except for the top left one. This curve, which is attributable to the graphical design might occlude the solid line underneath it, represents the cross-validation error rate obtained for the model derived from the preclustering procedure. This curve appears only in the tests where the test set could overlap with the training set and where cross-validation was used, such as the typical model versus typical ORF cluster test, etc. It was observed that in most instances the preclustering cross-validation false-negative error rates are practically the same as the postclustering cross-validation error rates.

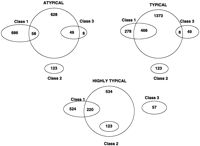
Figure 5.
View larger version:
Figure 5.

Venn diagrams representing overlaps between the E. coli gene classes (Medingue et al. 1991) and ORF clusters obtained by three-means clustering.

Figure 3.
View larger version:
Figure 3.

The accuracy graphs for the E. coli genome analysis(see text). Average false-positive error rates were 0.055 for the Root model; 0.43 for the typical and 0.060 for the atypical models, respectively, obtained by two-means clustering; 0.055 for the typical, 0.036 for the highly typical, and 0.071 for the atypical model obtained by three-means clustering.

The graphs of the error rates produced by the models obtained by the three-means clustering (Fig. 3) well resemble the results of the previous work (Fig. 1 in Borodovsky et al. 1995). In that study, the protein-coding sequence models were derived from the three classes ofE. coli genes described by Medigue et al. (1991). Classification presented in that study was based on the clustering of 61 dimensional vectors of codon frequencies by correspondence analysis. Genes assigned to class I included the majority of the E. coligenes with neither an optimal codon usage pattern nor an unusual one. Class II included genes highly expressed under exponential growth conditions. DNA sequences of class II genes show a strong bias toward the “optimal” E. coli codons. Class III genes mainly included genes horizontally transferred into the E. coligenome during the course of evolution. These gene sequences might keep remnants of the codon usage strategies of their prehistoric hosts. In the current study, we observed clear correlations (Figs. 4 and5) between typical, highly typical, and atypical clusters of long ORFs and the updated sets of class I, class II, and class III sets of genes (A. Danchin, pers. comm.). Correlation was also observed between codon usage patterns of the class I, class II, and class III genes and the ones of typical, highly typical, and atypical ORFs (data not shown). These observations gave the motivation to name the ORF clusters as typical, atypical, and highly typical.

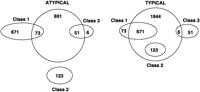
Figure 4.
View larger version:
Figure 4.

Venn diagrams representing overlaps between the E. coli gene classes (Medigue et al. 1991) and ORF clusters obtained by two-means clustering.

The atypical gene clusters derived for the E. coli genome were also compared with the set of 756 E. coli horizontally transferred genes classified as such in the earlier work (Lawrence and Ochman 1997) and kindly provided by J.G. Lawrence. Only 410 of 756 genes were longer than 500 nucleotides. These 410 genes were compared with the A-, B-, and C-type clusters of ORFs obtained by two- or three-means clustering procedure applied to the E. coli set of ORFs longer than 500 nucleotides. It is seen (Table 5) that the type-A cluster is more than twice as large as the designated set of 410 genes and includes either 324 or 321 of them, clusters 2A and 3A, respectively. Cluster C with 470 ORFs demonstrated a much stronger relative overlap with the set of 410 genes, 257 to 260 genes in 2C and 3C clusters, respectively. Cluster B with 470 ORFs had only 132 and 152 overlapping items for 2C and 3C, respectively. Interestingly, the cluster B-type construction rule somehow discriminated against longer ORFs. The vast majority of the discussed above E. coli A- and C-type clusters, from 92% to 99%, were the ORFs >700 nucleotides (Table 6), whereas in cluster C the ORFs >700 nucleotides constituted only ∼78%.

View this table:
Table 6.

Compositional Features of Atypical Clusters 2A and 3A of E. coli Long (⩾500 Nucleotide) ORFs

The relatively small overlap of >500 nucleotides, genes of class III with clusters A, B, and C (Table 6) is explained by the fact that the class III list, updated as of 1995, did not include full information on the E. coli genome completed in 1997. Classification of genes in genomes other than E. coli was not available in terms of the names horizontally transferred genes. It seems plausible, however, that many long ORFs assigned to the atypical gene clusters obtained for the other nine genomes, particularly to the clusters of type C, are the genes horizontally transferred into these genomes in the course of evolution. Application of the GeneMark.hmm program has demonstrated that some of these genes are still absent in the 10 publicly available genome annotations (see below).

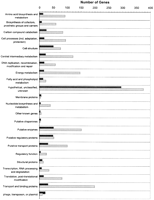
Many long ORFs used as initial material in GeneMark-Genesis have been annotated as genes in GenBank and their properties were indicated. This allowed us to analyze the features of the typical and atypical ORFs as follows. Figure 4 shows distribution of the E. coli typical and atypical long ORFs with regard to the functional categories defined by Monica Riley (1993) and annotated in the GenBank record (Blattner et al. 1997). The Atypical ORFs have a majority among “phage, transposon, or plasmid” category and constitute a significant fraction of cell structure genes, genes of putative regulatory proteins, and genes of hypothetical proteins and genes of proteins with unknown function.

In Figure 3 that when the E. coli typical model was used, protein-coding function was easily identified in the highly typical protein-coding sequences (dotted line in the top right panel showing low error rate) but not in the atypical protein-coding sequences (dashed line in the same panel). Actually, the typical model recognized the highly typical segments even better than the typical ones. This is the reason why the highly typical gene model appeared to be redundant for gene-finding purposes as far as the E. coli genome is concerned. On the other hand, the E. coli atypical gene model, which worked fairly well for all types of genes, seems to be a necessary tool for identifying atypical genes. The similar pattern of error rate dependence on the model type and the model order was observed for the other nine genomes (data not shown). These results support the idea that three gene classes exist in the other nine bacterial genomes. This possibility had already been proven true in the case of the B. subtilis genome (Kunst et al. 1997).

Sn and Sp Characteristics

The Sn and Sp values, as defined in Methods, indicate both the ability of GeneMark employing a particular model to predict true (annotated) genes and to avoid false-positive predictions. Predictions that do not match the GenBank annotation reduce the value of specificity. Some newly predicted genes, however, might be correct. There have been many instances where genes predicted by a computer method in presumably noncoding sequence, as determined from the GenBank annotation, were experimentally confirmed at a later time (Robison et al. 1994; Borodovsky et al. 1995; McIninch et al. 1996).

In terms of Sn and Sp, none of the cluster types, A, B, or C, was found to be superior in terms of producing better models. For the 10 genomes, the performance of GeneMark, measured by Sn and Sp, was studied for various combinations of the models. For the E. coli case, the comparison of predictive accuracy of single models and combinations of models is presented in Table 7. It is seen that the combination of typical and atypical cluster models generally performed very well. A concise list of the averaged Sn and Sp values obtained in similar experiments for all 10 genomes is given in Table8. Here, the averaged Sn and Sp values for pre-clustering cross validation are displayed in italics and parentheses. Karlin et al. (1998) reported differences in codon usage pattern between short (100–300 codons) and long genes (>500 codons). It was indicated that up to 5% increase in G+C content of codon site 3 was observed for long genes of the E. coligenome, whereas in the H. influenzae genome this increase was <1%. Would the observed difference in codon usage between long and short genes affect the prediction accuray? The results of the accuray assessment (Table 8) showed that Avg(Sn,Sp) values for E. coliand H. influenzae were as close as 0.1%. This result provides indirect evidence that the difference in codon usage for long versus short genes, changing G+C content of codon site 3, should not contribute significantly to prediction error rate.

View this table:
Table 7.

Characteristics of Gene Prediction Accuracy for the E. coliGenome with 4289 Annotated Genes

View this table:
Table 8.

Gene Prediction Accuracy in Terms of Avg(Sn,Sp) Observed for the 10 Genomes

Gene Clusters in the Kullback–Liebler Distance Space—Accuracy of the Gene Prediction

The observation (Fig. 3, top right) that the typical gene model was able to correctly identify function of a highly typical gene fragment more reliably than the function of a typical gene fragment is intriguing. The quantitative nature of this observation could be explained in terms of the Kullback–Liebler (KL) distance that measures the “contrast” between two competing statistical models involved in the pattern recognition procedure. KL distance, or relative entropy, is a convenient distance measure for clustering procedure dealing with sequence objects that are targets of some pattern recognition process. In such a case, it is desirable that the distance measure is proportional to the “ease” to discriminate between two objects. Classical determination procedure is based on likelihood ratio. Relative entropy is an expected logarithm of the likelihood ratio (Cover and Thomas 1991). On the intuitive level, the larger the contrast between models, the KL distance, the easier the task to classify an object, a sequence fragment, into one of two classes, coding or noncoding. For ordinary first-order Markov models Pand Q with initial and transitional probabilities designated as pi and pij ,qi , and qij , respectively, the KL distance is defined as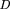Formula This definition is applied under the assumption that model Pactually fits the real sequence of events. This assumption, however, may not always be a true one. For instance, let us consider the short DNA fragment identification procedure where competing models of coding and noncoding regions are invloved. In this case, the KL distance is defined by the slightly different equation (Borodovsky et al. 1986a):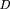Formula Here P and Q represent coding and noncoding models, respectively. Index k defines the phase (frame) of the three-periodic model, indices i and j define nucleotides in adjacent positions, p k i andp kij are initial and transitional probabilities of the three-periodic model, qij are transitional probabilities for the ordinary first order Markov model of noncoding region.

It was observed for several genomes (Table 9), that when the model P fits the tested sequence, such as a true gene sequence, the likelihood of misidentification of a protein-coding fragment correlates negatively with the KL distance between the modelsP and Q as determined by equation 2.

View this table:
Table 9.

Negative Correlation of KL distances and False-Negative Prediction Error Rates Produced by GeneMark in Short Fragment Identification

It may happen, however, that the model P does not fit the sequence data. Under the assumption that the input sequence fits another model, P*, it was shown (M. Borodovsky, unpubl.), that the misidentification error rate should correlate negatively with the value of the “efficient” KL distance determined by the formula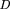Formula Here D(P*∥P) is defined as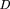Formula  Particularly, if the typical model P is used to identify a highly typical gene segment that actually fits the highly typical modelP*, the “efficient” KL distance, computed by equation 3 is larger than the KL distance between the models P andQ determined by equation 2. This leads to the expectation that the typical model will identify the function of a highly typical segment with a misidentification rate lower than one produced by the same model for a typical gene segment. This effect has indeed been observed.

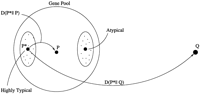
The geometry of the KL distance space of long ORF sequences and noncoding sequences is illustrated in Figure 6. This figure emphasizes the idea that the set of long ORFs is inhomogeneous and should be represented rather by a cloud of points, contrary to the set of noncoding sequences that should be represented by one point. The noncoding point also represents the model of the noncoding region. The sequences from the atypical cluster, located within the cloud (big circle), are shown to be closer to the point representing the noncoding region than the sequences from highly typical cluster. The centers of the clusters (circles) represent the typical, atypical, and highly typical models. Note that the points are connected by curves reminding one that the KL distance is not a regular Euclidean distance and does not satisfy the triangle inequality.

Figure 6.
View larger version:
Figure 6.

Schematic representation of the genomic sequence space with the KL distance metrics. The elements of the space are protein-coding and noncoding sequences.

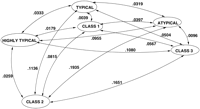
A more elaborate picture, Figure 7, shows the cluster relationships in terms of KL distances for the typical, highly typical, and atypical clusters, type A, and class I, class II, and class III gene sets. The B-type atypical cluster was slightly closer to the other clusters and classes, with the exception of class III. The C-type atypical cluster was located further away from the other sets with the exception of class III.

Figure 7.
View larger version:
Figure 7.

Schematic representation of actual KL distances, as defined by the order 3 Markov models, between the E. coli gene classes (Medigue et al. 1991) and ORF clusters obtained by three-means clustering.

New Gene Predictions by Atypical Models

The GeneMark.hmm analysis of the 10 genomes using 2A cluster derived typical and atypical models allowed the identification of 683 new putative genes, each longer than 96 nucleotides. These genes were identified as atypical model predictions, therefore, indicating the atypical model fits better to the composition of these sequences than the typical model. These findings deserve special attention because the genes with atypical composition are harder to detect and therefore thus predicted genes are good candidates for being horizontally transferred genes delivering special adaptive advantages for microorganisms that carry these genes. For 176 predictions, the gapped BLAST analysis (Altschul et al. 1997) corroborated the predictions with statistically significant similarity to known proteins in the NCBI nonredundant sequence database (Table 10). In a majority of cases, the similarity was with hypothetical proteins whereas in 11 cases the similarity was detected with proteins related to insertion elements. Full lists of the results can be found atftp://genmark.biology.gatech.edu/pub/gmgen.ghmAT.blast ftp://genmark.biology.gatech.edu/pub/gmgen.ghmAT.best.

View this table:
Table 10.

New Atypical Gene Predictions for the 10 Genomes Made by the GeneMark.hmm program

The differences in distribution of proteins tranlated from typical and atypical long ORFs into functional categories (Riley 1993) can be seen in Figure 8. The proteins translated from atypical ORFs were represented more strongly than the transposon, or plasmid categories. The relative abundance of atypical ORF-derived proteins was observed among hypothetical and unknown proteins as well as in cell structure proteins, putative enzymes, and putative regulatory proteins.

Figure 8.
View larger version:
Figure 8.

Distribution of functional categories of the E. coli genes in the typical and atypical (type A) ORF clusters obtained by two-means clustering. (solid bars) Atypical; (shaded bars) typical.

Previous SectionNext Section

METHODS

Materials

To test the GeneMark-Genesis program, we used the complete genomic sequences of the following bacterial species: Archaeoglobus fulgidus (Klenk et al. 1997; GenBank accession no. AE000782),B. subtilis (Kunst et al. 1997; AL009126), E. coli(Blattner et al. 1997; U00096), H. influenzae (Fleischmann et al. 1995; L42023), H. pylori (Tomb et al. 1997; AE000511),M. genitalium (Fraser et al. 1995; L43967), M. jannacshii (Bult et al. 1996; L77117), M. pneumoniae(Himmelreich et al. 1996; U00089), M. thermoautotrophicum(Smith et al. 1997; AE000782), and Synechocystis PCC6803 (Kaneko et al. 1996; SYNECO). The size of each sequence, the number of annotated genes, and the average GC content are given in Table11. The GeneMark-Genesis clustering results were compared with the results of earlier studies by Medigue et al. (1991)and by Lawrence and Ochman (1997). The updated versions of the threeE. coli gene classes were kindly provided by A. Danchin (Institute Pasteur, Paris, France). Dr. J. Lawrence (University of Pittsburgh, PA) provided us with the DNA sequences of 756 E. coli genes, classified as horizontally transferred genes.

View this table:
Table 11.

Information on Genomic Sequences Used in this Study

Generating the Root Model

The GeneMark-Genesis algorithm presented here makes substantial use of the GeneMark algorithm (Borodovsky and McIninch 1993) and can be viewed as an extension of GeneMark. GeneMark-Genesis does not require experimentally validated sets of training sequences to obtain the crucial set of parameters used in GeneMark, initial and transition probabilities of Markov models of coding and noncoding regions. The Markov model of DNA gene sequence is a machine-learned model that reflects the pattern of correlation between adjacent nucleotides, the pattern evolutionary developed under restrictions intrinsic to coding region (amino acid composition, codon usage pattern, etc.) or noncoding region (dinucleotide composition, etc.).

Given an anonymous bacterial sequence, the parameters of the initial model of protein-coding region were obtained from the set of ORFs identified in the sequence, such as one of the 10 complete genomic sequences with annotation assumed unknown. An ORF starts with a start codon and ends with the in frame stop codon. Whereas the ORF’s 3′ end is unique, there is an ambiguity in the position of its 5′ end. This ambiguity is eliminated by specifying an ORF as the longest possible ORF (with the start codon being the furthest possible from the given stop codon).

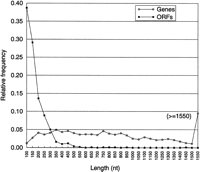
As Figure 9 shows that an ORF >500 nucleotides found in the B. subtilis genome is unlikely to be a noncoding random ORF. This is also true for the nine other bacterial genomes. Therefore, by selecting ORFs >500 nucleotides in anonymous bacterial DNA sequence one has a high likelihood of selecting only true coding regions.

Figure 9.
View larger version:
Figure 9.

Length distribution for B. subtilis annotated genes and random ORFs. Data from the University of Wisconsin, Madison (http://www.genetics.wisc.edu).

A note of caution should be made concerning the initial part of a long ORF. If the true start codon is located inside the ORF, the sequence upstream to the start codon is noncoding. The average length of this noncoding sequence is small, however. For instance, according to the GenBank annotation of the B. subtilis genome this length is equal to 18 nucleotides. Therefore, if the selected ORFs are long enough, the bias in estimated model parameters should be negligibly small. In this work, a threshold of 700 nucleotides was used. This choice made the relative amount of erroneously included noncoding region even smaller than the choice of a 500-nucleotide threshold. If two long ORFs overlapped by >30 nucleotides, the longer ORF was kept in the training set. By combining a number of long ORFs detected in bacterial genomic DNA one could obtain an amount of presumably protein-coding sequence sufficient to derive Markov models of high order. For instance, it was estimated that 1029 Mb of combined protein-coding sequence is generally sufficient to derive accurately enough parameters for the three-periodic Markov model of order five (M. Borodovsky, unpubl.).

The set of long ORFs identified in a given complete genomic sequence was used to determine parameters of the Markov model of the protein-coding region, the “pre-Root” model of orders zero to five. For a pre-Root Markov model of a noncoding sequence, we used the zero order model with four probability parameters estimated by genome specific frequencies of mononucleotides. The pre-Root models were employed in the GeneMark program for predicting coding regions in the original genomic sequence. Predicted protein-coding regions were combined into a new training sequence. The rest of the sequence, considered noncoding, was included into the noncoding training set. The Markov models, coding and noncoding, whose parameters were defined using these training sets, were called the Root models. For comparison purposes, the GenBank annotation of a given genome was used to compile training sets of coding/noncoding sequence. The models defined by training on these sets were called the GenBank models.

Note that the Root models were generated as described above for complete genomic sequences of M. jannaschii and H. pylori and used in the GeneMark program to identify protein-coding regions in these genomes (Bult et al. 1996; Tomb et al. 1997). RecentlySalzberg et al. (1998) have used sets of ORFs >500 nucleotides to derive the interpolated Markov models of bacterial protein-coding regions that were used in the GLIMMER gene-finding program.

Generating ORF Clusters

The general goal of clustering was to obtain several compositionally homogeneous training sets for class-specific gene models that would enhance the gene-finding ability of the GeneMark program. This goal dictated the choice of seed clusters as well as the choice of the distance definition in the space of ORF sequences. Thek-means clustering algorithm, with k equal to two or three (see below), was employed:

1.
Sort n objects (ORFs) into c clusters.
2.
Compute m 1 … m c cluster centers.
3.
Classify the n objects by assigning them to the cluster with the closest center cluster.
4.
If any object was assigned to a new cluster, go to 2; otherwise stop.

The initial step of the algorithm was to prepare the ORF cluster “seeds”. The GeneMark program employing the Root models was used to score all long ORFs identified in a given genomic sequence. The long ORFs with a GeneMark score of <0.5 were assigned to the atypical seed cluster. All other long ORFs, in the two-means clustering procedure, were assigned to the typical seed cluster. In the case of the three-means clustering, the atypical seed cluster was selected as described above, then 15% of the long ORFs with the highest scores were assigned to the highly typical seed cluster, and all other ORFs were assigned to the typical seed cluster.

Each ORF was characterized by a vector of 61 codon frequencies. The ORF cluster center was defined by the vector of cumulative codon frequencies observed in all ORFs in the cluster. The distance between codon frequency vectors could be defined by a symmetrical Kullback–Liebler-type formula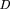Formula Here x is an ORF’s codon frequency vector, and cis a cluster’s cumulative codon frequency vector.fi , represents the frequency of the ith codon in the ORF, and qi represents the frequency of the ith codon in the ORF cluster. 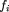In the actual formula used in the clustering procedure, the codon frequency valuesfi (qi ) were normalized by the frequency of the encoded amino acid and multiplied by the size of the group of synonymous codonsFormula Here, T codons is the count of all codons for a particular ORF or cluster. N i-syn is the number of synonymous codons for the ith codon. faa-i is the frequency of the amino acid in an ORF, or ORF cluster, corresponding to the ith codon. Ci is the count of all codons of the ith type. To ward off the zero frequency numerical problem, the codon counts were initialized to one. 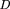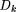Substitution of defined frequencies into formula (5) transformed it into a weighted sum of symmetricized KL-distancesDk (x‖‖c) defined for each group of synonymous codons.Formula The weights N i-syn were equal to the size of each synonymous group, andDk (x‖‖c) was defined asFormula where u ki and v kiare relative codon usage frequencies in the kth group of synonymous codons. Note, that in formula 7 the terms relating to the methionine and tryptophan amino acids have disappeared.

The final clusters of ORFs to which the k-means clustering algorithm converged were used as training sets for the specific Markov models of protein-coding regions. The regions that were predicted as coding by at least one cluster specific model were eliminated from the set of noncoding sequences used for training the Root model. The sequence left was used for training the Markov model of noncoding sequence. The differences in noncoding models obtained by slightly different clustering processes were not found to be critical for the gene prediction results. Therefore, in what follows, we do not discuss the minor differences between the models of noncoding sequence.

The training set for the atypical gene model could be obtained in several ways. As was indicated earlier, the set of horizontally transferred E. coli genes constitutes about 15% of the whole gene pool (Medigue et al. 1991; Lawrence and Ochman 1997). The clustering method described above, however, when applied to a complete bacterial genomic sequence produced the atypical gene cluster, cluster A as it is called below, which usually consisted of ∼30% of the total number of genes. We modified the atypical gene cluster content to make its size closer to the size of the horizontally transferred gene set as was estimated in previous studies. For instance, only 15% of all long ORFs that were closest to the center of the cluster produced by method A, were included into another version of the atypical cluster, cluster B. All other ORFs were included into the typical cluster. In yet another modification, only 15% of all of the long ORFs, those produced by method A that were furthest from the typical cluster center were assigned to the atypical cluster, cluster C.

Note that a different approach to obtain homogeneous sets of protein coding regions and eventually to derive class-specific GeneMark models for anonymous bacterial genomic sequences was suggested by Hirosawa et al. (1997). In this approach, tested on the SynechocystisPCC6803 genome, iterative runs of GeneMark were used instead of iterative k-means clustering. Recently, clustering ofArabidopsis thaliana genes was performed (Peresetsky et al. 1998). In this project, several types of gene sequence characterization were used—by parameters of the Markov models of zero and first order as well as by codon usage vector. The variant of k-means clusterization procedure employed as a distance function the Euclidean distance between parameter vectors.

Prediction Accuracy Evaluation using Sets of Short DNA Fragments

The GeneMark program prediction accuracy was characterized by the false-negative and false-positive error rates observed in identification of short DNA fragments, either coding or noncoding. To obtain the test set of presumably coding short sequences, the long ORFs from a designated set were cut into a number, Nc , of nonoverlapping 96-nucleotide sequences. Each individual fragment was then identified as coding or noncoding. If the output GeneMark score was lower than the threshold, 0.5, the fragment was interpreted as noncoding and, therefore, misidentified. The total number of false-negative predictions, FN, was recorded and the ratioFN/Nc defined the observed false-negative error rate. Note that the uncertainty in the position of the true start codon in a long ORF might slightly elevate the false-negative error rate as a few true noncoding fragments could be generated by chopping a long ORF. To define the false-positive error rate, presumably noncoding sequences were cut into a number, Nn , of short 96-nucleotide sequences. Now if the output GeneMark score for a given fragment was higher than the threshold, 0.5, the fragment was interpreted as protein-coding, therefore misidentified. The observed false-positive error rate was defined as the ratio FP/Nn , where FP was the total number of false-positive predictions. When a Markov model of protein-coding regions was tested on protein-coding DNA sequence from the same gene class as one the model was derived from, the above accuracy evaluation procedure was used in cross-validation mode.

Sensitivity and Specificity

The sensitivity, Sn, and specificity, Sp, parameters, formulas 9 and 10, were used to characterize the accuracy of the models and the algorithm in terms of whole gene prediction. Here, as a control, we used the GenBank annotation, assuming it is correct on the whole gene location but might be off in terms of the start codon position. Sn is defined as the ratio of the number of correctly located genes to the number of genes annotated in the GenBank record for this sequence. Sp is the ratio of the number of correctly located genes to the total number of genes predicted by the algorithm in the given sequence.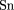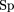Formula Formula  When the performance of a combination of models was evaluated, the GeneMark program was used to analyze a given sequence once for each model being considered. An ORF was counted as a predicted gene if the ORF was predicted as a coding one by at least one model. If the same ORF was predicted as protein-coding one by several models, however, these coinciding predictions were considered as one item for counting the total numbers of predictions.

Postclustering and Preclustering Accuracy Evaluation Procedures

When the basic cross validation procedure was used for an accuracy evaluation of the Markov model of a protein-coding region, this model was derived from 6/7 of a particular long ORF cluster and the other 1/7 of the ORF cluster was used as a test set. Such an evaluation was done 7 times by testing each 1/7 of the ORF cluster with the model trained on the other 6/7 part of the cluster. The resulting false-negative rate was an average of the seven observed rates. Notably, the accuracy evaluation using the whole set of long ORFs was performed posterior to the clustering of long ORFs identified in a given sequence. This procedure was called postclustering cross-validation.

Additional accuracy evaluation was made to make sure that clustering does not introduce a systematic bias into the model derivation. To perform this preclustering cross-validation procedure, the initial sequence was divided into seven parts. The 6/7 of the whole sequence was used for the k-means clustering (see above) and deriving models. The 1/7 of the sequence was used to test the models on the long ORFs assigned to specific, typical or atypical, ORF clusters by the initial k-means clustering (with the same parameter k) that had been performed initially with the whole sequence. The resulting false negative error rate was obtained as an average of the seven observed outcomes. Both the postclustering and the preclustering cross-validation procedures were performed only for testing the particular model on the sequence cluster with the same name (i.e., typical model vs. typical ORFs, etc.). The postclustering and the preclustering Markov models were also assessed using the Sn and Sp parameters.

Gene Prediction by Atypical Model

Contrary to using different models in GeneMark in a consecutive manner, the GeneMark.hmm program uses the models, particularly typical and atypical, in parallel; therefore, for each identified gene the program indicated the model that fits best in terms of maximum likelihood to the gene sequence (Lukashin and Borodovsky 1998). Genes predicted by the atypical model were of special interest since these genes were potentially horizontally transferred genes as well as genes that are difficult to spot by the typical model. We analyzed all 10 bacterial genomes using the GeneMark.hmm program, with the models derived from A-type clusters obtained by k-means (k = 2) clustering. The regions predicted as genes by the atypical model, >96 nucleotides, were selected, translated, and searched against the nonredundant protein sequence database supported by NCBI using the gapped BLAST program (Altschul et al. 1997). The BLAST hits with P values smaller than 1e −5 were considered as statistically significant evidence for nonrandom similarity to an earlier discovered protein. These findings indicated that the current predictions are most likely functional genes rather than the false positives.

Previous SectionNext Section

Acknowledgments

We thank Antoine Danchin, Ashok Kolaskar, Owen White, Jean-Francois Tomb, and Jefferey Lawrence for helpful discussions. We are grateful to James McIninch and John Besemer for discussions and valuable software programming assistance. This work has been supported in part by the National Institutes of Health.

The publication costs of this article were defrayed in part by payment of page charges. This article must therefore be hereby marked “advertisement” in accordance with 18 USC section 1734 solely to indicate this fact.

Previous SectionNext Section

Footnotes

  • ↵1 Corresponding author.

  • E-MAIL mark{at}amber.gatech.edu; FAX (404) 894-0519.

    • Received August 17, 1998.
    • Accepted October 23, 1998.
Previous Section
 

REFERENCES

  1. ↵
    1. Altschul S.F.,
    2. Madden T.L.,
    3. Schdffer A.A.,
    4. Zhang J.,
    5. Zhang Z.,
    6. Miller W.,
    7. Lipman D.J.
    (1997) Gapped BLAST and PSI-BLAST: A new generation of protein database search programs. Nucleic Acids Res. 25:3389–3402.
    Abstract/FREE Full Text
  2. ↵
    1. Blattner F.R.,
    2. Plunkett G., III,
    3. Bloch C.A.,
    4. Perna N.T.,
    5. Burland V.,
    6. Riley M.,
    7. Collado-Vides J.,
    8. Glassner J.D.,
    9. Rode C.K.,
    10. Mayhew G.F.,
    11. et al.
    (1997) The complete genome sequence of Escherichia coli K-12. Science 277:1453–1462.
    Abstract/FREE Full Text
  3. ↵
    1. Borodovsky M.,
    2. McIninch J.D.
    (1993) GeneMark: Parallel gene recognition for both DNA strands. Comp. Chem. 17:123–133.
    Google Scholar
  4. ↵
    1. Borodovsky M.Yu.,
    2. Sprizhitsky A.,
    3. Golovanov E.I.,
    4. Alexandrov A.A.
    (1986a) Statistical features in the Escherichia coli genome functional primary structure. II. Non-homogeneous Markov chains. Mol. Biol. 20:833–840.
    Google Scholar
  5. ↵
    (1986b) Statistical features in the E. coli genome functional primary structure. III. Computer recognition of protein coding regions. Mol. Biol. 20:1140–1150, ibid.
    Google Scholar
  6. ↵
    1. Borodovsky M. Yu.,
    2. McIninch J.,
    3. Koonin E.,
    4. Rudd K.,
    5. Medigue C.,
    6. Danchin A.
    (1995) Detection of new genes in the bacterial genome using Markov models for three gene classes. Nucleic Acids Res. 23:3554–3562.
    Abstract/FREE Full Text
  7. ↵
    1. Bult C.J.,
    2. White O.,
    3. Olsen G.J.,
    4. Zhou L.,
    5. Fleischmann R.D.,
    6. Sutton G.G.,
    7. Blake J.A.
    (1996) Complete genome sequence of the methanogenic archeon, Methanococcus jannaschii. Science 273:1058–1073.
    Abstract
  8. ↵
    1. Burge C.,
    2. Karlin S.
    (1997) Prediction of complete gene structures in human genomic DNA. J. Mol. Biol. 268:78–94.
    CrossRefMedlineGoogle Scholar
  9. ↵
    1. Cover T.M.,
    2. Thomas J.A.
    (1991) Elements of information theory. (John Wiley & Sons, Inc. New York, NY).
    Google Scholar
  10. ↵
    1. Fickett J.
    (1982) Recognition of protein-coding regions in DNA sequences. Nucleic Acids Res. 10:5303–5318.
    Abstract/FREE Full Text
  11. ↵
    1. Fleischmann R.D.,
    2. Adams M.D.,
    3. White O.,
    4. Clayton R.A.,
    5. Kirkness E.F.,
    6. Kerlavage A.R.,
    7. Bult C.J.,
    8. Tomb J.,
    9. Dougherty B.A.,
    10. Merrick J.M.,
    11. et al.
    (1995) Whole-genome random sequencing and assembly of Haemophilus influenzae Rd. Science 269:496–512.
    Abstract/FREE Full Text
  12. ↵
    1. Fraser C.M.,
    2. Gocayne J.D.,
    3. White O.,
    4. Adams M.D.,
    5. Clayton R.A.,
    6. Fleischmann R.D.,
    7. Bult C.J.,
    8. Kerlavage A.R.,
    9. Sutton G.,
    10. Kelly J.M.,
    11. et al.
    (1995) The minimal gene complement of Mycoplasma genitalium. Science 270:397–403.
    Abstract/FREE Full Text
  13. ↵
    1. Gribskov M.,
    2. Devereux J.,
    3. Burgess R.R.
    (1984) The codon preference plot: Graphic analysis of protein coding sequences and prediction of gene expression. Nucleic Acids Res. 12:539–549.
    Google Scholar
  14. ↵
    1. Himmelreich R.,
    2. Hilbert H.,
    3. Plagens H.,
    4. Pirkl E.,
    5. Li B.-C.,
    6. Herrmann R.
    (1996) Complete sequence analysis of the genome of the bacterium Mycomplasma pneumoniae. Nucleic Acids Res. 24:4420–4449.
    Abstract/FREE Full Text
  15. ↵
    1. Hirosawa M.,
    2. Isono K.,
    3. Hayes W.,
    4. Borodovsky M.
    (1997) Gene identification and classification in the Synechocystis genomic sequence by recursive GeneMark analysis. DNA Sequence 8:17–29.
    MedlineGoogle Scholar
  16. ↵
    1. Kaneko K.,
    2. Sato S.,
    3. Kotani H.,
    4. Tanaka A.,
    5. Asamizu E.,
    6. Nakamura Y.,
    7. Miyajima N.,
    8. Hirosawa M.,
    9. Sigiura M.,
    10. Sasamoto S.,
    11. et al.
    (1996) Sequence analysis of the genome of the unicellular cyanobacterium Synechosistis sp. strain PCC6803. II. Sequence determination of the entire genome and assignment of potential protein-coding regions. DNA Res. 3:109–136.
    Abstract/FREE Full Text
  17. ↵
    1. Karlin S.,
    2. Mrazek J.,
    3. Campbell A.M.
    (1998) Codon usages in different gene classes of the Escherichia coli genome. Mol. Microbiol. 29:1341–1355.
    CrossRefMedlineGoogle Scholar
  18. ↵
    1. Klenk H.P.,
    2. Clayton R.A.,
    3. Tomb J.F.,
    4. White O.,
    5. Nelson K.E.,
    6. Ketchum K.A.,
    7. Dodson R.J.,
    8. Gwinn M.,
    9. Hickey E.K.,
    10. Peterson J.D.,
    11. et al.
    (1997) The complete genome sequence of the hyperthermophilic, sulphate-reducing archaeon Archaeglobus fulgidus. Nature 390:364–370.
    CrossRefMedlineGoogle Scholar
  19. ↵
    1. Krogh A.
    (1997) Two methods of improving performance of an HMM and their application for gene finding. Proc. ISMB-1997 5:179–186.
    Google Scholar
  20. ↵
    1. Kunst F.,
    2. Ogasawara N.,
    3. Moszer I.,
    4. Albertini A.M.,
    5. Alloni G.,
    6. Azevedo V.,
    7. Berteron M.G.,
    8. Bessieres P.,
    9. Bolofin A.,
    10. Borchert S.,
    11. et al.
    (1997) The complete genome sequence of the Gram-positive bacterium Bacillus subtilis. Science 390:249–256.
    Google Scholar
  21. ↵
    1. Lawrence J.G.,
    2. Ochman H.
    (1997) Amelioration of bacterial genomes: Rates of change and exchange. J. Mol. Evol. 44:383–397.
    CrossRefMedlineGoogle Scholar
  22. ↵
    ———. 1998. Molecular archaeology of the Escherichia coligenome. Proc. Natl. Acad. Sci. (in press)..
    Google Scholar
  23. ↵
    1. Lukashin A.V.,
    2. Borodovsky M.
    (1998) GeneMark.hmm: New solutions for gene finding. Nucleic Acids Res. 26:1107–1115.
    Abstract/FREE Full Text
  24. ↵
    1. McIninch J.D.,
    2. Hayes W.S.,
    3. Borodovsky M.
    (1996) Applications of GeneMark in multispecies environment. Proc. ISMB-1996 4:165–175.
    Google Scholar
  25. ↵
    1. Medigue C.,
    2. Rouxel T.,
    3. Vigier A.,
    4. Henaut A.,
    5. Danchin A.
    (1991) Evidence for horizontal gene transfer in Escherichia coli speciation. J. Mol. Biol. 222:851–856.
    CrossRefMedlineGoogle Scholar
  26. ↵
    Peresetsky, A., C. Mathe, P. Dehais, M. Van Montagu, and P. Rouze. 1998. Classification of Arabidopsis thaliana gene sequences: Coding sequences clustering into two groups according to codon usage.J. Mol. Biol. (in press)..
    Google Scholar
  27. ↵
    1. Riley M.
    (1993) Functions of the gene products of Escherichia coli. Microbiol. Rev. 57:862–952.
    Abstract/FREE Full Text
  28. ↵
    1. Robison K.,
    2. Gilbert W.,
    3. Church G.
    (1994) Large-scale bacterial gene discovery by similarity search. Nature Genet. 7:205–214.
    CrossRefMedlineGoogle Scholar
  29. ↵
    1. Salzberg S.L.,
    2. Delcher A.L.,
    3. Kasif S.,
    4. White O.
    (1998) Microbial gene identification using interpolated Markov models. Nucleic Acids Res. 26:544–548.
    Abstract/FREE Full Text
  30. ↵
    1. Smith D.R.,
    2. Doucette-Stamm L.A.,
    3. Deloughery C.,
    4. Lee H.-M.,
    5. Dubois J.,
    6. Aldredge T.,
    7. Bashirzadeh R.,
    8. Blakely D.,
    9. Cook R.,
    10. Gilbert K.,
    11. et al.
    (1997) Complete genome sequence of Methanobacterium thermoautotrophicum delta H: Functional analysis. Comparative genomics. J. Bacteriol. 179:7135–7155.
    Abstract/FREE Full Text
  31. ↵
    1. Staden R.
    (1984) Measurements of the effect that coding for a protein has on DNA sequence and their use for finding genes. Nucleic Acids Res. 12:551–567.
    Google Scholar
  32. ↵
    1. Tomb J-F.,
    2. White O.,
    3. Kerlavage A.R.,
    4. Clayton R.A.,
    5. Sutton G.G.,
    6. Fleischmann R.D.,
    7. Ketchum K.A.,
    8. Klenk H.P.,
    9. Gill S.,
    10. Dougherty B.A.,
    11. et al.
    (1997) The complete genome sequence of the gastric pathogen Helicobacter pylori. Nature 388:539–547.
    CrossRefMedlineGoogle Scholar
  33. ↵
    1. Xu Y.,
    2. Einstein J.R.,
    3. Mural R.J.,
    4. Shah M.,
    5. Uberbacher E.C.
    (1994) Constructing gene models from accurately predicted exons: An application of dynamic programming. Comp. Appl. Biosci. 10:613–623.
    Abstract/FREE Full Text
| Table of Contents

This Article

  1. doi: 10.1101/gr.8.11.1154 Genome Res. 8: 1154-1171 Cold Spring Harbor Laboratory Press

Article Category

Share

Preprint Server



Navigate This Article

Current Issue

  1. January 2026, 36 (1)
  1. Current Issue
  1. Alert me to new issues of Genome Research