TFcomb identifies transcription factor combinations for cellular reprogramming based on single-cell multiomics data

  1. Xuegong Zhang1,2
  1. 1MOE Key Laboratory of Bioinformatics and Bioinformatics Division of BNRIST, Department of Automation, Tsinghua University, Beijing 100084, China;
  2. 2Center for Synthetic and Systems Biology, School of Life Sciences and School of Medicine, Tsinghua University, Beijing 100084, China
  • Corresponding author: weilei92{at}tsinghua.edu.cn
    •  
    Next Section

    Abstract

    Reprogramming cell state transitions provides the potential for cell engineering and regenerative therapy. Finding the reprogramming transcription factors (TFs) and their combinations that can direct the desired state transition is crucial for the task. Computational methods have been developed to identify such reprogramming TFs. However, most of them can only generate a ranked list of individual TFs and ignore the identification of TF combinations. Even for individual reprogramming TF identification, current methods often fail to put the real effective reprogramming TFs at the top. To address these challenges, we developed TFcomb, a computational method that leverages single-cell multiomics data to identify reprogramming TFs and TF combinations. We modeled the task of finding reprogramming TFs and their combinations as an inverse problem, and used Tikhonov regularization to guarantee the generalization ability of solutions. For the coefficient matrix of the model, we designed a graph attention network to augment gene regulatory networks built with single-cell RNA-seq and ATAC-seq data. Benchmarking experiments on data of human embryonic stem cells demonstrate superior performance of TFcomb against existing methods for identifying individual TFs. We curate data sets of multiple cell reprogramming cases and demonstrate that TFcomb can efficiently identify reprogramming TF combinations from vast potential combinations. We apply TFcomb on a data set of mouse hair follicle development and find key TFs in cell differentiation. All experiments show that TFcomb is powerful in identifying reprogramming TFs and TF combinations from single-cell data sets to empower future cell engineering.

    A major aspect of cell engineering is to artificially direct transitions of different cellular states, including reprogramming of somatic cells to pluripotent stem cells, directional differentiation of pluripotent stem cells to somatic cells, and directional conversions between somatic cells (Wichterle et al. 2002; Takahashi and Yamanaka 2006, 2016; Marson et al. 2008). These artificial transitions are collectively referred to as cellular reprogramming. It has been demonstrated that a small number of transcription factors (TFs), referred to as reprogramming TFs, are essential to redirect cell state transitions (Graf and Enver 2009; Buganim et al. 2013; Morris and Daley 2013). Given the complex biological mechanisms underlying cellular reprogramming, utilizing a combination of TFs is typically more effective than relying on a single TF (Takahashi and Yamanaka 2006; Guerrero‐Ramirez et al. 2018; Wang et al. 2021). However, there are roughly 2000 different TFs in humans (Fulton et al. 2009; Vaquerizas et al. 2009); it is impractical to experimentally identify all the reprogramming TF combinations. Therefore, computational methods for effectively identifying reprogramming TFs and TF combinations are needed to reduce experimental burden.

    Most of existing methods (Cahan et al. 2014; D'Alessio et al. 2015; Rackham et al. 2016; Qin et al. 2020; Xu et al. 2021; Qiu et al. 2022; Rukhlenko et al. 2022) can only give a ranked list of individual TFs and ignore the identification of TF combinations. A few methods have previously explored the identification of reprogramming TF combinations. Ronquist et al. (2017) tried to identify TF combinations directing fibroblasts to other cell states by solving the difference equation constructed by time-series Hi-C and RNA-seq data, but the algorithm can hardly be extended to other cell types or states owing to the high data requirements. NETISCE (Marazzi et al. 2022) employed signal flow analysis and feedback vertex set control to identify TF combinations. Although for a specific conversion of cell states, NETISCE only gives a single TF combination as the output, lacking the quantitative comparison to all the remaining possible TF combinations. Overall, there still lacks a flexible and effective computational method that can identify reprogramming TF combinations.

    Even for the identification of individual reprogramming TFs, there are inherent limitations of existing methods that prevent these TFs from being consistently ranked at the top. These methods can be generally categorized into three types: dynamic model based, gene regulatory network (GRN) based, and differential analysis based. The dynamic model–based methods (Ronquist et al. 2017; Marazzi et al. 2022; Rukhlenko et al. 2022) construct the difference equations to model the temporal dynamics of cell states. These models describe how cell states change over time in response to various internal and external factors. By solving the equations, the reprogramming TFs can be predicted. However, these equations are difficult to solve on high-dimensional data containing thousands of genes, which limits the range of identified TFs. As for the GRN-based methods (Cahan et al. 2014; Rackham et al. 2016; Qin et al. 2020; Xu et al. 2021), they usually inferred GRNs for both source states and target states and then utilized the GRNs to calculate the importance score for each TF during the cell state transitions. Because of the intuitive parameter settings in the calculation of importance scores, this kind of method lacks generalization performance on new data sets. The differential analysis–based methods (D'Alessio et al. 2015; Hammelman et al. 2022; Qiu et al. 2022) can also be a solution to identify the reprogramming TFs. For example, the differentially expressed TFs between target states and source states can be a candidate list of reprograming TFs. Although these TFs may be important during the transitions, they do not necessarily direct one cell state to another and thus can hardly meet the needs to identify reprogramming TFs. All the above limitations highlight the need for improved capabilities in the identification of individual reprogramming TFs.

    Here, we developed a computational method, TFcomb, to identify reprogramming TFs and TF combinations using single-cell multiomics data. TFcomb models the TF identification task as an inverse problem, and by solving the inverse problem, TFcomb assigns each TF or TF combination a directing score for quantitative identification of reprogramming TFs and TF combinations. By incorporating Tikhonov regularization, TFcomb guarantees the generalization ability of solutions and effectively focuses on key TFs that truly drive state transitions. TFcomb utilizes GRNs inferred from single-cell RNA-seq and ATAC-seq data, ensuring the inclusion of causal regulatory relationships. Additionally, TFcomb employs a graph attention network (GAT) to recover missing regulatory links in GRNs, enabling the identification of reprogramming TFs from a broad spectrum of candidate TFs. TFcomb may serve as an efficient tool for identifying reprogramming TFs and TF combinations that direct cell state transitions at the single-cell level.

    Previous SectionNext Section

    Results

    Overview of the TFcomb framework

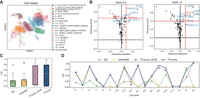
    We developed TFcomb as a computational method for identifying reprogramming TF combinations directing cell state transitions from the source state to the target state (Fig. 1A). TFcomb takes both scRNA-seq data and scATAC-seq data as inputs. The scRNA-seq data should contain cells of both the source and target states. The scATAC-seq data are not required to be simultaneously sequenced in the same cells of the scRNA-seq data but are best derived from similar tissues to guarantee the reliability. These data are first employed to construct a primary GRN with CellOracle (Kamimoto et al. 2023) by using scATAC-seq data to infer regulatory directions from TFs to target genes and using scRNA-seq data to calculate the corresponding regulatory coefficients (Methods).

    Figure 1.
    View larger version:
    Figure 1.

    A graphical illustration of TFcomb. (A) Overview of TFcomb. TFcomb can identify the TFs and TF combinations that reprogram the source-cell state to the target-cell state. (B) TFcomb first constructs a primary GRN with scRNA data and scATAC data, and then it enhances the primary GRN with GAT. The normalized gene expression and the primary regulatory network comprise the input graph, and each node represents a gene. The whole model consists of the GAT encoder and the multilayer perceptron predictor. A multihead attention mechanism is applied in the GAT layer to stabilize the learning process. (C) The TF identification task is modeled as an inverse problem and solved with Tikhonov regularization. TFcomb uses the calculated expected alteration to get the directing score of each TF.

    The dropout events of scATAC-seq data and the incomplete TF binding motif knowledge may lead to missing important TF–target links. Following the idea that graph neural networks can predict the interactions of genes (Chen and Liu 2022; Li et al. 2022), TFcomb employs a GAT model to enhance the primary GRN by recovering missing TF–target links (Fig. 1B). Taking the primary GRN as the input training data, TFcomb trains a GAT model and then applies the model to obtain additional putative TF–target pairs with high confidence (Methods). After GAT enhancement, TFcomb acquires an enhanced GRN, which has more comprehensive regulatory relations and can better describe the whole transition process (Supplemental Note 1; Supplemental Figs. S1, S2).

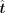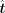    TFcomb models the TF identification task as an inverse problem (Fig. 1C). With the GRN matrix A and the cell state transition vector Δy, TFcomb solves the expected alteration vector Formula of TFs with Tikhonov regularization (Methods). Then, for each single TF or TF combination, the corresponding expected alterations are fixed to get a specific alteration vector Formula. TFcomb calculates the Pearson correlation coefficient (PCC) between 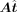Formula and Δy as the directing score, which assesses the importance of a single TF or a TF combination in directing the cell state transition. The final TF set is selected based on both expected alterations and directing scores with a same quantile threshold and is ranked by directing scores.

    TFcomb outperforms baseline methods in identifying individual reprogramming TFs

    To the best of our knowledge, there is not a quantitative benchmark of individual reprogramming TF identification for single-cell data sets. To address this, we adopted a single-cell atlas built by Joung et al. (2023) to construct the benchmark for reprogramming TF identification. This atlas profiled human embryonic stem cells (hESCs) infected with a lentivirus library to perform overexpression of a single-TF-encoding gene in each cell. With TF overexpression directing hESCs to differentiate into different cell states, this atlas can be an experimentally validated ground truth to evaluate the reprogramming TF identification in cell state transitions. We selected cells of one source state and 15 target states to construct the benchmark data set (Methods). Each target state contains a set of ground-truth reprogramming TFs, and the number of the ground-truth TFs ranges from one to eight (Fig. 2A). For the benchmarking metric, we defined a TF identification score (TIS) to evaluate the identified reprogramming TFs based on the rankings and amounts (Methods).

    Figure 2.
    View larger version:
    Figure 2.

    TF identification benchmarking on a single-cell human embryonic stem cell (hESC) atlas. TFs here refer to genes that encode the corresponding transcription factors (TFs). (A) UMAP visualization of the single-cell hESC atlas. (B) TFcomb TF identification plot on target states 8-0 and 14. Red lines are the quantile thresholds to filter 10 TFs. Key TFs are annotated in red. (C) TF identification score (TIS) comparison across 18 target states. The box plots indicate the medians (c), means (triangles), and first and third quartiles (bounds of boxes). (D) Line plots of TIS comparison across 18 target states.

    We compared TFcomb with several baseline methods. Because of the high data requirements, such as the need for time-series data (Ronquist et al. 2017), we did not include dynamic model–based methods. GRN-based methods typically require epigenomic data such as chromatin immunoprecipitation followed by sequencing (ChIP–seq) data (Xu et al. 2021) of specific cell types for inferring GRNs, but these data are not available for the induced hESC data set as the induced cells cannot be labeled as specific cell types. To overcome the limitation, we replaced the GRN inference part of ANANSE with CellOracle and used ANANSE to calculate the importance score of each TF. For differential analysis methods, we performed differential expression (DE) analysis between the source state and the target state by the Wilcoxon rank-sum test. We also evaluated TFcomb without the GAT enhancement (TFcomb_WOE) to assess the effect of the GAT module. For each method, a list of ranked top 10 TFs was generated to perform the benchmark.

    As shown in Figure 2C, TFcomb significantly outperformed DE and ANANSE and achieved higher TISs. TFcomb achieved comparable or better performance than DE in 16 of 18 target states, except for target states 9-0 and 14 (Fig. 2D). In most target states, such as the target states 8-1 and 16, the ground-truth reprogramming TFs ranked high in the TFcomb-identified TF list, whereas they did not appear in the DE-identified list. ANANSE achieved best performance in target states 1 and 7-2, whereas in most of remaining states, it showed poor performance. This is reasonable because of the instability of ANANSE which ignores part of the information of TFs whose difference between target state and source state is not statistically significant. Compared with TFcomb_WOE, TFcomb obtained better performance in five target states (8-0, 9-1, 9-2, 11-0, and 14), comparable performance in 11 target states, and poorer performance in two target states (3 and 9-0). Taking state 8-0 as an example (Fig. 2B), TFcomb identified NR5A2 and NR5A1 with the fifth and the sixth ranking, respectively, whereas TFcomb_WOE only identified NA5R2 and NR5A1 with the eighth and 11th ranking, respectively (Supplemental Fig. S3). Besides, TFcomb raised the rankings of key TF-encoding genes like GRHL1, KLF4, EOMES, and KLF17 (Supplemental Fig. S3). We also illustrated the relationship between the recovered links and the original links for each cell state, suggesting that the improvement may be attributed to that the GAT model learned the broader regulatory relations of key TFs (Supplemental Fig. S4).

    Focusing on the TFcomb-identified TF list for each target state, each TF is given two biologically meaningful scores of the expected alteration and the directing score (Fig. 2B; Supplemental Fig. S5). The expected alteration represents the expression variation that the TF is supposed to change to direct the source state to the target state, and the directing score indicates similarity of the perturbed cell state and the target-cell state after changing the TF with expected alteration, which is used to rank the TFs. The identified reprogramming TFs generally exhibited significantly higher directing scores than the remaining TFs (Fig. 2B; Supplemental Fig. S5), which indicates their importance in directing cell state transitions. We also conducted a one-side t-statistic test to determine whether the directing score of the key TF is significantly higher across all states. The results indicate that in most cases, TFcomb infers the key TFs with significantly higher directing scores (Supplemental Fig. S6). For instance, TFcomb identified the reprogramming TF LHX6 in target state 16 with the highest expected alteration and directing score (Supplemental Fig. S5), and LHX6 in state 16 showed significantly higher direction scores across all the states (P-value = 9.6 × 10–4) (Supplemental Fig. S6).

    We further examined the target states in which TFcomb exhibited unsatisfactory performance. In some target states, both TFcomb and baseline methods could not identify any ground-truth TFs in the top 10 TF list, such as the states 11-1 and 13. We noticed that the ground-truth TF expression in these cases either is consistent between the source state and target state (Supplemental Fig. S7A) or is especially low in the whole data set (Supplemental Fig. S7B), and these gene expression patterns make it challenging to identify reprogramming TFs. In state 3, TFcomb performed slightly worse than TFcomb_WOE. We further compared the identification result of state 3 between TFcomb and TFcomb_WOE and found that, with the GAT enhancement, TFcomb raised the ranking of KLF1 from 14th to 11th and diminished the ranking of KLF2 from 10th to 12th (Supplemental Fig. S3). Most cells of state 3 expressed KLF1 and KLF5 with high values, whereas few cells expressed KLF2 (Supplemental Fig. S8), which indicates that the GAT enhancement may ignore the key TFs with low expression in target states. Beyond the aforementioned cases, because some TFs lack the binding motif in the databases, we missed it at the beginning of GRN inference. For example, in state 9-0 the reprogramming TF GRHL3 is not included in the alternative TF list. To overcome such a limitation, we supplemented these TFs from existing knowledge databases of TFs regulating targets, such as NicheNet (Methods). We observed that with the modification, TFcomb could identified GRHL3 with the 24th ranking (Supplemental Fig. S9).

    TFcomb identifies reprogramming TF combinations of various cell reprogramming cases

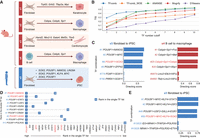
    We then evaluated the performance of TFcomb on identifying reprogramming TF combinations. We collected single-cell data sets for five different cell reprogramming scenarios of human and mouse (Supplemental Fig. S10). For the mouse, we investigated fibroblasts to keratinocytes (Kurita et al. 2018), fibroblasts to macrophages (Feng et al. 2008), fibroblasts to cardiomyocytes (Addis et al. 2013), and B cells to macrophages (Xie et al. 2004). For humans, we investigated fibroblasts to induced pluripotent stem cells (iPSCs) (Takahashi and Yamanaka 2006; Yu et al. 2007; Huangfu et al. 2008). Each reprogramming case has been extensively investigated with several reported reprogramming TFs (Fig. 3A). We denoted these cases from s1 to s5 for brevity (Fig. 3A).

    Figure 3.
    View larger version:
    Figure 3.

    TFcomb identifies the TFs directing cell reprogramming across different scenarios. TFs here refer to genes that encode the corresponding TFs. (A) Five reprogramming scenarios (s1–s5) with experimentally validated reprogramming TF combinations. (B) The line plots show the comparison of different methods based on the TIS calculated between identified TFs and ground-truth reprogramming TFs. (C) Ranked TF combinations with TFcomb-predicted directing scores. The ground-truth combinations of case s4 (Cebpa, Cebpb, and Spi1) and s5 (POU5F1 and SOX2) are marked in red. (D) Comparison between the single-TF list and double-TF list of TFcomb in case s5. The single ground-truth reprogramming TFs in the rows and the double ground-truth reprogramming TFs in the columns are both marked in red. (E) Ranked TF combinations with TFcomb predicted directing scores. The Yamanaka factors are marked in red.

    In these cases, the source- and target-cell states are specified cell types, and most of the GRN-based methods (D'Alessio et al. 2015; Rackham et al. 2016; Xu et al. 2021) have been applied to identify the reprogramming TF lists of these cases. Although different types of data were used by these methods, the consistency of the reprogramming cases allows for a direct comparison of the identified TF lists reported in the literature. We thus compared TFcomb and TFcomb_WOE with the D'Alessio method (D'Alessio et al. 2015), Mogrify (Rackham et al. 2016), and ANANSE (Xu et al. 2021). The Mogrify prediction results are downloaded at https://mogrify.net/, and the results of D'Alessio et al. (2015) and ANANSE are obtained from the original paper (D'Alessio et al. 2015; Xu et al. 2021). The methods that did not report TF lists of these reprogramming scenarios were excluded in this comparison.

    To comprehensively analyze the performance of these methods, we calculated the average TIS across different scenarios for each method and illustrated results with a ranking cutoff of the identified TF list from one to 10. With a TF ranking cutoff from one to three, TFcomb outperformed other methods with significantly higher TISs. With a TF ranking cutoff from four to 10, TFcomb and ANANSE achieved a higher TIS than the Mogrify and D'Alessio methods, and the performance of TFcomb and ANANSE is comparable. Moreover, TFcomb significantly outperformed TFcomb_WOE, which indicates that the GAT enhancement module effectively improves the identification result of reprogramming TFs (Fig. 3B). We provided a detailed example of the reprogramming case of human fibroblasts to iPSCs to show how the enhanced GRN improves the performance (Supplemental Fig. S11). Besides, TFcomb identifies reprogramming TFs with the highest ranking in four of five reprogramming cases (Supplemental Fig. S12). These results demonstrate that TFcomb outperforms baselines and identifies key reprogramming TFs with high ranking.

    In addition to the better performance on single reprogramming TF identification compared with existing methods, to the best of our knowledge, TFcomb is the only method capable of quantitatively identifying possible TF combinations at single-cell level. TFcomb can calculate a directing score for each combination of TFs (Methods). We took reprogramming cases s4 and s5 as examples. We applied TFcomb to acquire a ranked list of the 40 top TFs for each case and then calculated and ranked all the possible combinations of triple TFs and double TFs for cases s4 and s5, respectively. As shown in Figure 3C, the ground-truth combination of case s4 (Cebpa, Cebpb, and Spi1) ranks the 25th in the total of 9880 combinations, and the ground-truth combination of case s5 (POU5F1 and SOX2) ranks the eighth in the total of 780 combinations. To further demonstrate that the TF combinations that TFcomb identified are not simple combinations of identified single TFs, we compared the ranking of single TF and double TFs identified by TFcomb in case s5. As shown in Figure 3D, the top 10 double-TF combinations are all in the format of POU5F1 with another TF. NANOG, MYC, and SOX2, which are part of known reprogramming TF combinations, ranked 10th, fourth, and 12th, respectively, in the single-TF list, but their rankings rose significantly to first, second, and eighth in the double-TF list. This result indicates that TFcomb captures and identifies the interactions between these known reprogramming TFs and POU5F1. This comparison shows that TFcomb can identify reliable TF combinations instead of simply combining single TFs based on their rankings. The above results demonstrate that TFcomb can assist and accelerate cell reprogramming experiments without any prior selection.

    In wet laboratory experiments, candidate TFs for directing cell programming are sometimes hand-picked by prior knowledge or experimental feasibility. To further explore the potential of TFcomb with hand-picked candidate TFs, we try to identify Yamanaka factors (Takahashi and Yamanaka 2006) that reprogramed fibroblasts to pluripotent stem cells with a combination of four TFs (POU5F1, SOX2, KLF4, and MYC). We added the 24 candidate TFs that Takahashi and Yamanaka (2006) chose in their experiment to our processed single-cell data set. There are 10,626 candidate combinations of selecting four TFs in the top 24 TF list, and TFcomb identified the Yamanaka factor combination with the 50th ranking (Fig. 3E), which suggests that if Takahashi and Yamanaka applied TFcomb before conducting experiments, they would find the best combination in the 50th experiment, which leads to a substantial decrease in both cost and time.

    Although we demonstrated the effectiveness of TFcomb through the ground-truth TFs in reprogramming scenarios, there are some novel TFs identified by TFcomb with high directing scores. Although this approach effectively prioritizes potential TF drivers, we acknowledge the possibility of false positives among the combinations ranked above the ground-truth ones. Nonetheless, we believe that some novel TFs identified by TFcomb could be effective in reprogramming scenarios. For example, in the reprogramming case of human fibroblasts to iPSCs, ID3 is not one of the ground-truth TFs but is identified as the second TF by TFcomb (Supplemental Fig. S13). It has been demonstrated that ID3 overexpression significantly increased stemness markers in endothelial cells (Das et al. 2015). Besides, in the reprogramming case of mouse fibroblasts to cardiomyocytes, Ppargc1a is not ground-truth TFs but is ranked highly by TFcomb (Supplemental Fig. S13). A previous study (Murphy et al. 2021) identified PPARGC1 as a key regulator of cardiac maturation. We recommend users critically evaluate the results inferred by TFcomb in combination with existing literature. By cross-referencing our predictions with established studies, users can gain a deeper understanding of the identified TFs and their potential biological significance.

    TFcomb identifies key TFs directing mouse hair follicle development

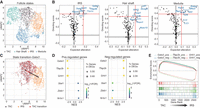
    We then investigated whether TFcomb can identify key TFs directing cell differentiation. We collected a SHARE-seq data set profiling mouse skin with paired scRNA-seq data and scATAC-seq data (Ma et al. 2020). This data set comprises cells of the mouse hair follicle development system. In this system, transit-amplifying cells (TACs) differentiate into different lineages: inner root sheath (IRS), hair shaft, or medulla. These lineages have been utilized to evaluate various computational methods (Lynch et al. 2022; Tran et al. 2022). Because of a large imbalance in cell types of original data set, we subsampled an equal number of each cell type in the hair follicle development system and obtained a data set of 2688 cells (Fig. 4A); 2748 genes were retained after gene filtering. We applied TFcomb on each lineage and selected top 10 TFs as the candidate TFs (Fig. 4B).

    Figure 4.
    View larger version:
    Figure 4.

    TFcomb identifies key TFs in mouse hair follicle development. TFs here refer to genes that encode the corresponding TFs. (A) UMAP visualization of down-sampled mouse hair follicle scRNA-seq data. (B) TFcomb TF identification plot on mouse hair developing lineages of IRS, hair shaft, and medulla. Red lines are the quantile thresholds to filter 10 TFs. DEGs are annotated in bold. (C) UMAP visualization of TAC transiting towards IRS with Gata3 changing the expected variation. (D) Dot plots of gene set enrichment analysis (GSEA) results, showing enrichment of the positively and negatively regulated target sets of TFcomb-identified TFs within DEGs between TAC and IRS. TFs that rank top three and bottom three are selected. (NES) normalized enrichment scores, (FDR) false-discovery rate. (E) GSEA plot of TF positively and negatively regulated gene sets within DEGs between TAC and IRS.

    In the IRS lineage, Gata3 is the top one identified TF with an expected alteration of 0.422 and a directing score of 0.691. It has been reported that Gata3 plays a direct role in differentially regulating cell lineages of hair follicle (Kurek et al. 2007), and loss of Gata3 negatively impacts the formation of IRS (Kaufman et al. 2003). Our identification result is consistent with these existing findings, indicating that Gata3 is a key TF directing the IRS lineage (Fig. 4C). Among other identified TFs in the IRS lineage, Tfap2a is considered to be upregulated in IRS during early hair follicle morphogenesis (Panteleyev et al. 2003), and MAF is known to be involved in hair morphogenesis of IRS layers (Miyai et al. 2010).

    As for the hair shaft lineage, TFcomb identified Lef1 as the top TF. LEF1 is demonstrated as a key regulator of Wnt/β-catenin signaling in hair shaft differentiation (Närhi et al. 2008). Besides, in the identified TFs, RUNX1 is colocalized with LEF1 and is a specific marker of hair shaft (Raveh et al. 2006), and Hoxc13 affects hair shaft differentiation with various alternative mechanisms (for review, see Awgulewitsch 2003).

    Although medulla lineage has been less explored compared with the other two lineages, we can still find some existing literatures to support our identified TFs. For instance, the deletion of Prdm1 can result in aberrant medulla cell organization (Telerman et al. 2017), which indicates the important role of Prdm1 in medulla formation. Additionally, Foxq1 is discovered to control medulla differentiation through a common mechanism as the regulatory pathway of Hoxc13 (Potter et al. 2006). Even if Foxq1 is not a differentially expressed gene (DEG), it can still be identified by TFcomb, which suggests TFcomb can identify key TFs even when the difference between target state and source state is relatively small.

    We compared the identified TFs of different lineages and found an interesting TF, Grhl1, identified in all the lineages. Grhl1 is known to be dynamically expressed in the interfollicular epidermis (IFE) differentiation (Joost et al. 2016) and is reported to associated with all the three lineages (Joost et al. 2020), which is in agreement with our findings. We hypothesized that GRHL1 may be an important regulator in hair follicle development. With considerable and reliable support of existing literature, we verified that TFcomb can identify the key TFs in mouse hair follicle development.

    We further characterized the identified TFs in detail, taking the IRS lineage as a case. We explored the relationship between the targets regulated by these TFs and DEGs between the IRS and TAC lineages. Specifically, we examined the top three identified TFs (Gata3, Grhl1, and Tfap2b) and the bottom three identified TFs (Nr3c1, Zbtb1, and Brf1). For each TF, we categorized its regulated targets into positively regulated and negatively regulated groups according to the regulatory values in our inferred GRN. We then conducted gene set enrichment analysis (GSEA) on these target sets using ranked fold changes in DE analysis (Fang et al. 2023). As shown in Figure 4D, the average normalized enrichment score (NES) of the top three TFs’ positive target sets is –3.05, whereas the bottom three TFs had an average NES of 1.67. Conversely, the average NES for the negative target sets was 2.72 for the top TFs and –2.16 for the bottom TFs. The positively regulated target sets of the top TFs were significantly enriched in genes characteristic of the IRS state, whereas their negatively regulated targets were enriched in genes associated with the TAC state (Fig. 4E). The results suggested that TFcomb effectively identifies TFs whose target genes play crucial roles throughout the transition process.

    Previous SectionNext Section

    Discussion

    In this paper, we presented TFcomb, a computational framework to identify reprogramming TFs and TF combinations directing state transitions. As far as we know, TFcomb is the first method specially designed for quantitatively identifying reprogramming TF combinations and can be directly applied on single-cell data sets with either annotated cell types or unnamed clusters. The reliance of TFcomb on single-cell data ensures its flexible scalability, and we demonstrated that TFcomb exhibits superior performance in cellular reprogramming under various scenarios. We anticipate that TFcomb will serve as an effective computational tool to complement existing experimental methods, particularly in situations in which candidate combinations are too numerous to be exhaustively tested, situations in which prior knowledge is limited and needs to be supplemented by algorithmic approaches to narrow the experimental search space, and situations in which high-throughput experimental validation is impractical.

    We established a comprehensive benchmark framework for validating computational methods on reprogramming TF identification. Besides, we collected multiple single-cell data sets of experimentally validated reprogramming cases to confirm the applicability of TFcomb in cellular reprogramming. The benchmark framework and the single-cell data sets may benefit further studies on the development of related algorithms.

    We utilized a GAT module to enhance the GRN and achieved better performance, especially in real reprogramming scenarios. The GAT model was trained on a base GRN generated by CellOracle. CellOracle incorporates scATAC-seq data to establish regulatory relationships between TFs and their targets, and its regression method primarily captures correlations among genes. The additional links recovered by GAT can enhance and complement these correlations. Therefore, GAT recovers missing links to enhance the model's ability to capture the importance of key TFs, rather than attributing a specific biological meaning to every recovered link. We claim that if a GRN can perfectly captured correlations among genes, the improvement of the GAT module may be slight.

    There are also several avenues for improving TFcomb. Cell state transition is a continuous biological process, and thus, the framework of TFcomb can be extended to model TF variations as a changing tendency during the whole transition. Besides, not only TFs but also some other regulation components, such chromatin regulators, splicing factors, and microRNAs (Badia-i-Mompel et al. 2023), can be incorporated into TFcomb. In addition, although the linear model of TFcomb has been proved to be efficient in this study, it is supposed to be valuable to incorporate with nonlinear regulatory relations when dealing with more complex cell state transitions.

    Previous SectionNext Section

    Methods

    Notations

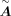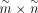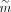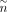    Formula is the base GRN inferred from scATAC-seq data, with dimensions Formula, where Formula and Formula denote number of targets and number of TFs, respectively.

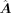    Formula is the primary GRN inferred from scRNA-seq data using CellOracle, with dimensions m × n, where m and n denote number of total genes and number of TFs, respectively.

    A is the enhanced GRN by enhancing 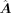Formula with the GAT module. The dimensions are m × n.

    X is the node feature matrix input to GAT, with dimensions c × m, where c is the total number of source and target cells.

    M is the adjacent matrix input to GAT, with dimensions m × m.

    L is the binary label matrix indicating the regulatory relations between TFs and targets, with dimensions m × n.

    S is the notation of source-cell state.

    T is the notation of target-cell state.

    X0 is the processed gene expression data of source-cell state, with dimensions c0 × m, where c0 is the cell number of source-cell state.

    X1 is the processed gene expression data of target-cell state, with dimensions c1 × m, where c1 is the cell number of target-cell state.

    Δy is the state transition vector calculated by the difference between averaged X1 and X0, with dimensions of m × 1.

    t is the variations of TFs, with dimensions n × 1.

    K is the ground-truth key TF list.

    C is the identified candidate ranked TF list.

    Data preprocessing

    We processed scRNA-seq data following the standard pipeline of SCANPY (Wolf et al. 2018). We selected highly variable genes (HVGs) between source and target state cells with a fixed dispersion threshold. As the feature selection with HVGs would miss some important TFs, we further selected TFs to supplement the gene set of interest. We calculated three sets of TFs: (1) top 400 TFs highly variable in source and target cells, (2) top 100 TFs differentially expressed between source and target cells, and (3) top 100 TFs highly expressed in target cells. We took the intersection of these sets as supplemental TFs and append them into the gene set of interest. The final gene set of interest usually includes 2000 to 3000 genes.

    Primary GRN construction with CellOracle

    As we model cell state transition as a linear process, we expect a GRN maintaining linear relations between TFs and target genes. Here we used CellOracle (Kamimoto et al. 2023) to construct linear GRNs, and it has proved to be more accurate than tree-based ensemble methods, such as SCENIC (Aibar et al. 2017) and GENIE3 (Huynh-Thu et al. 2010). CellOracle takes both scRNA-seq data and scATAC-seq data as input.

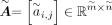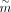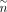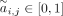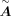    Following CellOracle workflow, we first used the whole cells of scATAC data to construct a base GRN matrix Formula, where Formula and Formula denote number of targets and number of TFs, respectively. Note that target here means a gene that is regulated by a specific TF, and may also be a TF itself. Formula represents whether TF j has a regulatory relation with gene i, and one means yes. CellOracle locates transcriptional start sites (TSSs) within the accessible chromatin regions, which are also called peaks, and then applies Cicero (Pliner et al. 2018) to identify the correlated peaks to the TSS for each gene. Then the DNA sequence of each correlated peak is used to scan TFs with the gimmemotifs v.5 vertebrate motif data set (https://gimmemotifs.readthedocs.io/en/master/). For the TFs that are not included in the gimmemotifs database, we searched the corresponding motifs in JASPAR database (Rauluseviciute et al. 2024). In this way, the TFs and targets can be linked, and after regulatory score filtering, we acquired the base GRN matrix Formula. The calculation of 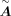Formula follows the default parameters of CellOracle. 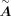If a TF misses the motif sequence in the motif databases and it is required as a candidate TF, we linked it with the targets based on the existing knowledge database NicheNet to supplement Formula.

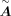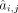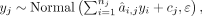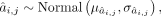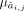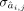    Then a bagging ridge model is applied to predict the expression of a target gene based on regulatory TFs identified in Formula, and the output is a posterior distribution of coefficient value Formula:Formula (1) Formula (2) where yj is the single target gene expression, yi is candidate TF expression, nj is the number of candidate TFs regulating jth gene, and cj is the intercept. ε, Formula, and Formula are parameters of normal distributions. Then we got the primary GRN matrix 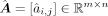Formula, where m and n denote number of total genes and number of TFs, respectively, and 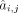Formula represents the regulatory coefficient of the jth TF to the ith target. Note that 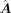Formula is acquired from scRNA-seq data based on the positive links in 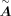Formula, so the size of 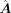Formula is generally less than 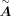Formula. For each transition from a source-cell state to a target-cell state, we calculated a primary GRN matrix 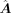Formula, and the calculation of 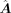Formula follows the default parameters of CellOracle.

    GRN enhancement with GATs

    As shown in Figure 1B, the GAT prediction model consists of two parts, the GAT encoder and the multilayer perceptron (MLP) predictor. The input of the encoder is the node feature matrix X ∈ ℝc×m and the adjacent matrix M ∈ ℝm×m, where c is the total number of source and target cells. X is the processed log-normalized scRNA-seq expression matrix, and M is transformed from 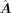Formula by connecting each TF–target pair whose value is not zero in 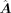Formula. X and M comprise the input graph. In the input graph, each node is a gene represented by a vector x·, j ∈ ℝc, a column of X. The encoder consists of three graph attentional layers, each layer learns a shared weight matrix, 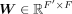Formula, and takes a set of node features as input, G = {g1, g2, …, gm}, gi ∈ ℝF′, and produces a new set of node features, 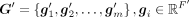Formula, where F and 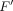Formula are feature numbers. In the first layer, F is equal to c. 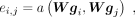The attention coefficient of gene j to gene i is calculated byFormula (3) where the attention mechanism a is a single layer feedforward network. 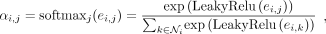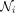Only neighbors of gene i are used to calculate the attention coefficients, and then, the coefficient is normalized by the Softmax function:Formula (4) where Formula is the first-order neighbors of gene i, including i, and Leaky ReLU is a nonlinear activation function. 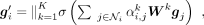Multihead attention mechanism is then applied to stabilize the learning process, and the output of gene i isFormula (5) where ∥ is concatenation operation, and σ is the ELU activation function. 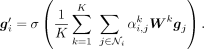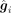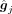For the last graph attention layer, the concatenation is replaced by averagingFormula (6) After the GAT encoder, the gene i and gene j are encoded to Formula and Formula, respectively. 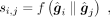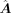The predicted score of gene i regulating gene j is calculated byFormula (7) where f is a three-layer MLP. Here, we denote L = [li,j] ∈ ℝm×n as a binary label matrix indicating the regulatory relations between TFs and targets, and L is transformed from Formula by converting all the nonzero values in 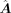Formula to one. Here, we use the binary cross entropy loss to optimize the model: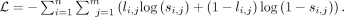Formula (8) After adding the recovered links, we acquired an enhanced GRN matrix A ∈ ℝm×n.

    Model training of GATs

    The label matrix L is generally class-imbalanced, and the negative links are significantly more than positive links. To handle the problem, we followed the data split strategy of DeepTFni (Li et al. 2022) using a 10-fold scheme. We split the positive links into 10 subsets of equal size. One subset and a same number set of randomly sampled negative links form the test set, and all the remaining links form the train set. The splitting repeats 10 times, and each set of the positive links is used for one time as a test set.

    The model is built by the PyTorch library and DGL library. The initial learning rate is 0.01, and Adam optimizer is used to optimize the model. The maximum epoch number is 1500, and an early stopping strategy is adopted. The head numbers of the GAT layers are fixed to four, four, and six, respectively. The hidden GAT layer dimension is set to 16, and the output GAT layer dimension is set to seven.

    After the model is trained, for each fold we set the median predicted value of the test set as the classification threshold. We used the trained model to predict each TF–target link and assign a value; these values are classified to zero to one based on the threshold; and one represents the link is predicted as positive. The links predicted as positive more than eightfold are retained as candidate recovering links. Among these candidate links, tine top 5% links are further selected to be the final recovering links based on the predicted scores to discard the false-positive samples. We conducted experiments to explore how the number of recovered links and identification performance vary with different recovery ratios, and we selected a recovery ratio of 5% as the default value (Supplemental Note 2; Supplemental Fig. S14).

    Then we set the final recovering links as positive in 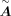Formula and repeat the CellOracle (Kamimoto et al. 2023) GRN calculation process of getting 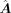Formula to acquire an enhanced GRN matrix, A ∈ ℝm×n.

    Modeling TF identification as a linear inverse problem

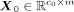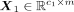    Suppose the transition is from source-cell state S to target-cell state T. The processed gene expression data of S is Formula, and processed gene expression data of T is Formula, where c0 and c1 are the cell number of S and T, respectively. We then averaged the expression across all the cells of S and T, respectively, to acquire mean expression vectors y0 ∈ ℝm×1 and y1 ∈ ℝm×1. 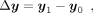The state transition vector can be calculated byFormula (9) where Δy indicates the direction that governs the cell state transition. We assume the alteration of TFs will direct cells to deviate from the original state by influencing the regulated target genes. 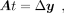With a linear GRN matrix, A, we can model the transition process by the regulating relations of TFs to targets:Formula (10) where t ∈ ℝn×1 represents the variations of TFs. The solving of t with known A and Δy is commonly referred to as a linear inverse problem (Bai et al. 2020). This equation describes the state transition that TFs only transmit one-step signals to the regulated targets, whereas in the GRN the TFs can propagate regulatory signals with multiple iterations. 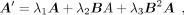Following the setting of CellOracle, we set the propagation iterations to three, and the GRN matrix is modified asFormula (11) where B = [bi,j] ∈ ℝm×m is the GRN matrix transformed from A; for gene j that regulates gene i, the bi,j is set as the value in A and otherwise is set to zero. λ1, λ2, and λ3 denote the weights of TF propagation of one step, two steps, and three steps, respectively. Considering the one-step propagation of TFs predominantly influences the regulatory process, in this paper we empirically fixed λ1, λ2, and λ3 to 0.6, 0.2, and 0.2, respectively (Supplementary Note 2; Supplemental Fig. S15). 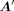In our case, the row number m of Formula is larger than the column number n, which leads to an overdetermined problem and may not have a solution. Consequently, we aim to find a 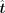Formula that ensures 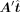Formula closely resembles Δy. 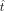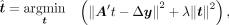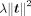Additionally, we added the Tikhonov regularization to restrict the range of Formula, and it can be solved byFormula (12) where Formula is a Tikhonov regularization, also called L2 regularization, and λ controls the degree of the regularization. We apply the ridge regression function in the scikit-learn library (Pedregosa et al. 2011) to solve the problem, and λ is set to one. The solved 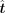Formula represents the expected alterations of TFs.

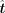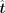    After acquiring the expected alteration vector Formula, for each TF we calculated a directing score to measure the importance in the transition procedure. For each TF, keep the corresponding value and set other values to zero in Formula to get a new 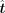Formula, and the PCC between 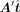Formula and Δy is calculated as the directing score. The final TF set is selected based on both expected alterations and directing scores with a same quantile threshold, and is ranked by directing scores. To acquire a candidate TF list with a specific number, the quantile threshold is calculated with iterative searching. The directing score of a TF combination could be calculated in a same way.

    Benchmark construction on a TF-overexpression hESC atlas

    Joung et al. created a barcoded open reading frame (ORF) library of 3548 TF splice isoforms (Joung et al. 2023). The barcoded TF ORFs were packaged into lentivirus and then transduced into hESCs at low multiplicity of infection (MOI) to perform single-TF overexpression across cells. These hESCs were then profiled by scRNA-seq to get a TF overexpression single-cell atlas. After down sampling, the atlas retains 671,453 cells covering 3266 TFs. The original atlas is clustered to nine major clusters. Clusters 6–8 are confirmed to be differentiated cells and were further subclustered to 25 minor clusters (Joung et al. 2023). Cluster 5 was suggested as the precursor population for clusters 6–8, based on trajectory analysis provided in the original paper, and cells in cluster 5 were shown to retain pluripotency based on gene signature analysis in the original paper. Therefore, we consider cells of major cluster 5 to be an appropriate representation of the source state. Then we randomly sampled 2000 cells in major cluster 5 and combined them to the 25 minor clusters to form the benchmarking data set. The 2000 sampled cells are regarded as the source-cell state that possibly transits to the 25 target-cell states (Supplemental Fig. S16).

    In the original paper of the benchmarking data, the overexpression of TFs in cells was detected using unique barcodes. Each target-cell state comprises distinct groups of overexpressed TFs, and these TFs are considered as ground-truth reprogramming TFs directing differentiation from the source-cell state to the target-cell state. For each TF in each target-cell state, we divided the number of cells that indicate the TF ORF in the state by number of cells that indicate this TF ORF in the whole atlas to calculate the percentage. Then we filtered out the TFs of percentage <5% and counting cells less than five in each target-cell state, and 15 target-cell states are retained, with key TFs counting from one to eight (Fig. 2A).

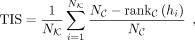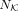    Then for each target-cell state we defined a TIS between the ground-truth key TF list K and identified candidate ranked TF list C:Formula (13) where Formula is length of K, 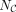Formula is the length of C, and hi is the ith TF in K. If hi is in C, 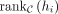Formula means the ranking of hi in C, and the ranking starts from zero. If hi is not in C, 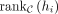Formula is set to 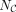Formula. We provided an illustration of TIS calculation in Supplemental Figure S17. TIS can be a comprehensive metric ranging from one to zero and considering both the rankings and numbers of identified TFs.

    Data sets

    The scRNA-seq data of hESCs with TF overexpression were downloaded from the NCBI Gene Expression Omnibus (GEO; https://www.ncbi.mlm.nih.gov/geo/) under accession number GSE217215, whereas the scATAC-seq data providing the base GRN were obtained from GSE174367. For reprogramming cases s1 and s2, the scRNA-seq data were retrieved from GSM5696148 and the scATAC-seq data from GSM5696149. The data for reprogramming case s3 were sourced from GSM5795776 (scRNA-seq) and GSM4644946 (scATAC-seq), whereas case s4 data were obtained from GSM4644956 (scRNA-seq) and GSM4644948 (scATAC-seq). For reprogramming case s5, the scRNA-seq data were downloaded from https://www.hipimmuneatlas.org/, and the scATAC-seq data were obtained from ArrayExpress (https://www.ebi.ac.uk/biostudies/arrayexpress) under accession number E-MTAB-11616. The data of mouse hair follicle development were downloaded from GSE140203.

    Software availability

    The code of TFcomb is available at GitHub (https://github.com/Chen-Li-17/TFcomb) and as Supplemental Code. We also provided detailed documentation and tutorials for using TFcomb at the Read the Docs website (https://tfcomb.readthedocs.io/en/latest/).

    Previous SectionNext Section

    Competing interest statement

    Tsinghua University has filed patent applications related to the work described here. The title of the patent application is “Method, device, and equipment for identifying driving factors in the process of cell state transition.” The China Provisional Application was filed on January 5, 2024, with the application number 202410023244.5.

    Previous SectionNext Section

    Acknowledgments

    The work is supported in part by the National Natural Science Foundation of China (grants 62373210, 62433001, 62250005, and 92470105) and the National Key R&D Program of China (grant 2021YFF1200900). Figure 3 was created with BioRender (https://www.biorender.com).

    Author contributions: C.L. and L.W. conceived the main idea of the study. C.L. designed and developed the method. C.L. performed the data analysis and method benchmarking. S.C., Y.C., and M.H. contributed to the discussion of results. H.B. helped with the construction of the method framework. L.W. supervised the study. C.L., L.W., and X.Z. wrote the manuscript with the help from other authors.

    Previous SectionNext Section

    Footnotes

    • Received August 23, 2024.
    • Accepted March 14, 2025.

    This article is distributed exclusively by Cold Spring Harbor Laboratory Press for the first six months after the full-issue publication date (see https://genome.cshlp.org/site/misc/terms.xhtml). After six months, it is available under a Creative Commons License (Attribution-NonCommercial 4.0 International), as described at http://creativecommons.org/licenses/by-nc/4.0/.

    Previous Section
     

    References

    1. ↵
      Addis RC, Ifkovits JL, Pinto F, Kellam LD, Esteso P, Rentschler S, Christoforou N, Epstein JA, Gearhart JD. 2013. Optimization of direct fibroblast reprogramming to cardiomyocytes using calcium activity as a functional measure of success. J Mol Cell Cardiol 60: 97–106. doi:10.1016/j.yjmcc.2013.04.004
      CrossRefMedlineGoogle Scholar
    2. ↵
      Aibar S, Gonzalez-Blas CB, Moerman T, Van Anh H-T, Imrichova H, Hulselmans G, Rambow F, Marine J-C, Geurts P, Aerts J, et al. 2017. SCENIC: single-cell regulatory network inference and clustering. Nat Methods 14: 1083–1086. doi:10.1038/nmeth.4463
      CrossRefMedlineGoogle Scholar
    3. ↵
      Awgulewitsch A. 2003. Hox in hair growth and development. Naturwissenschaften 90: 193–211. doi:10.1007/s00114-003-0417-4
      CrossRefMedlineGoogle Scholar
    4. ↵
      Badia-i-Mompel P, Wessels L, Müeller-Dott S, Trimbour R, Ramirez Flores RO, Argelaguet R, Saez-Rodriguez J. 2023. Gene regulatory network inference in the era of single-cell multi-omics. Nat Rev Genet 24: 739–754. doi:10.1038/s41576-023-00618-5
      CrossRefMedlineGoogle Scholar
    5. ↵
      Bai Y, Chen W, Chen J, Guo W. 2020. Deep learning methods for solving linear inverse problems: research directions and paradigms. Signal Processing 177: 107729. doi:10.1016/j.sigpro.2020.107729
      CrossRefGoogle Scholar
    6. ↵
      Buganim Y, Faddah DA, Jaenisch R. 2013. Mechanisms and models of somatic cell reprogramming. Nat Rev Genet 14: 427–439. doi:10.1038/nrg3473
      CrossRefMedlineGoogle Scholar
    7. ↵
      Cahan P, Li H, Morris SA, da Rocha EL, Daley GQ, Collins JJ. 2014. CellNet: network biology applied to stem cell engineering. Cell 158: 903–915. doi:10.1016/j.cell.2014.07.020
      CrossRefMedlineGoogle Scholar
    8. ↵
      Chen G, Liu Z-P. 2022. Graph attention network for link prediction of gene regulations from single-cell RNA-sequencing data. Bioinformatics 38: 4522–4529. doi:10.1093/bioinformatics/btac559
      CrossRefMedlineGoogle Scholar
    9. ↵
      D'Alessio AC, Fan ZP, Wert KJ, Baranov P, Cohen MA, Saini JS, Cohick E, Charniga C, Dadon D, Hannett NM, et al. 2015. A systematic approach to identify candidate transcription factors that control cell identity. Stem Cell Reports 5: 763–775. doi:10.1016/j.stemcr.2015.09.016
      CrossRefMedlineGoogle Scholar
    10. ↵
      Das JK, Voelkel NF, Felty Q. 2015. ID3 contributes to the acquisition of molecular stem cell-like signature in microvascular endothelial cells: its implication for understanding microvascular diseases. Microvasc Res 98: 126–138. doi:10.1016/j.mvr.2015.01.006
      CrossRefMedlineGoogle Scholar
    11. ↵
      Fang Z, Liu X, Peltz G. 2023. GSEApy: a comprehensive package for performing gene set enrichment analysis in Python. Bioinformatics 39: btac757. doi:10.1093/bioinformatics/btac757
      CrossRefMedlineGoogle Scholar
    12. ↵
      Feng R, Desbordes SC, Xie H, Tillo ES, Pixley F, Stanley ER, Graf T. 2008. PU.1 and C/EBPα/β convert fibroblasts into macrophage-like cells. Proc Natl Acad Sci 105: 6057–6062. doi:10.1073/pnas.0711961105
      Abstract/FREE Full Text
    13. ↵
      Fulton DL, Sundararajan S, Badis G, Hughes TR, Wasserman WW, Roach JC, Sladek R. 2009. TFCat: the curated catalog of mouse and human transcription factors. Genome Biol 10: R29. doi:10.1186/gb-2009-10-3-r29
      CrossRefMedlineGoogle Scholar
    14. ↵
      Graf T, Enver T. 2009. Forcing cells to change lineages. Nature 462: 587–594. doi:10.1038/nature08533
      CrossRefMedlineGoogle Scholar
    15. ↵
      Guerrero-Ramirez GI, Valdez-Cordoba CM, Islas-Cisneros JF, Trevino V. 2018. Computational approaches for predicting key transcription factors in targeted cell reprogramming. Mol Med Rep 18: 1225–1237. doi:10.3892/mmr.2018.9092
      CrossRefMedlineGoogle Scholar
    16. ↵
      Hammelman J, Patel T, Closser M, Wichterle H, Gifford D. 2022. Ranking reprogramming factors for cell differentiation. Nat Methods 19: 812–822. doi:10.1038/s41592-022-01522-2
      CrossRefMedlineGoogle Scholar
    17. ↵
      Huangfu D, Maehr R, Guo W, Eijkelenboom A, Snitow M, Chen AE, Melton DA. 2008. Induction of pluripotent stem cells by defined factors is greatly improved by small-molecule compounds. Nat Biotechnol 26: 795–797. doi:10.1038/nbt1418
      CrossRefMedlineGoogle Scholar
    18. ↵
      Huynh-Thu VA, Irrthum A, Wehenkel L, Geurts P. 2010. Inferring regulatory networks from expression data using tree-based methods. PLoS One 5: e12776. doi:10.1371/journal.pone.0012776
      CrossRefMedlineGoogle Scholar
    19. ↵
      Joost S, Zeisel A, Jacob T, Sun XY, La Manno G, Lönnerberg P, Linnarsson S, Kasper M. 2016. Single-cell transcriptomics reveals that differentiation and spatial signatures shape epidermal and hair follicle heterogeneity. Cell Syst 3: 221–237.e9. doi:10.1016/j.cels.2016.08.010
      CrossRefMedlineGoogle Scholar
    20. ↵
      Joost S, Annusver K, Jacob T, Sun XY, Dalessandri T, Sivan U, Sequeira I, Sandberg R, Kasper M. 2020. The molecular anatomy of mouse skin during hair growth and rest. Cell Stem Cell 26: 441–457.e7. doi:10.1016/j.stem.2020.01.012
      CrossRefMedlineGoogle Scholar
    21. ↵
      Joung J, Ma S, Tay T, Geiger-Schuller KR, Kirchgatterer PC, Verdine VK, Guo BL, Arias-Garcia MA, Allen WE, Singh A, et al. 2023. A transcription factor atlas of directed differentiation. Cell 186: 209–229.e26. doi:10.1016/j.cell.2022.11.026
      CrossRefMedlineGoogle Scholar
    22. ↵
      Kamimoto K, Stringa B, Hoffmann CM, Jindal K, Solnica-Krezel L, Morris SA. 2023. Dissecting cell identity via network inference and in silico gene perturbation. Nature 614: 742–751. doi:10.1038/s41586-022-05688-9
      CrossRefMedlineGoogle Scholar
    23. ↵
      Kaufman CK, Zhou P, Pasolli HA, Rendl M, Bolotin D, Lim KC, Dai X, Alegre ML, Fuchs E. 2003. GATA-3: an unexpected regulator of cell lineage determination in skin. Genes Dev 17: 2108–2122. doi:10.1101/gad.1115203
      Abstract/FREE Full Text
    24. ↵
      Kurek D, Garinis GA, van Doorninck JH, van der Wees J, Grosveld FG. 2007. Transcriptome and phenotypic analysis reveals Gata3-dependent signalling pathways in murine hair follicles. Development 134: 261–272. doi:10.1242/dev.02721
      Abstract/FREE Full Text
    25. ↵
      Kurita M, Araoka T, Hishida T, O'Keefe DD, Takahashi Y, Sakamoto A, Sakurai M, Suzuki K, Wu J, Yamamoto M, et al. 2018. In vivo reprogramming of wound-resident cells generates skin epithelial tissue. Nature 561: 243–247. doi:10.1038/s41586-018-0477-4
      CrossRefMedlineGoogle Scholar
    26. ↵
      Li H, Sun Y, Hong H, Huang X, Tao H, Huang Q, Wang L, Xu K, Gan J, Chen H, et al. 2022. Inferring transcription factor regulatory networks from single-cell ATAC-seq data based on graph neural networks. Nat Mach Intell 4: 389–400. doi:10.1038/s42256-022-00469-5
      CrossRefGoogle Scholar
    27. ↵
      Lynch AW, Theodoris CV, Long H, Brown M, Liu XS, Meyer CA. 2022. MIRA: joint regulatory modeling of multimodal expression and chromatin accessibility in single cells. Nat Methods 19: 1097–1108. doi:10.1038/s41592-022-01595-z
      CrossRefMedlineGoogle Scholar
    28. ↵
      Ma S, Zhang B, LaFave LM, Earl AS, Chiang Z, Hu Y, Ding JR, Brack A, Kartha VK, Tay T, et al. 2020. Chromatin potential identified by shared single-cell profiling of RNA and chromatin. Cell 183: 1103–1116.e20. doi:10.1016/j.cell.2020.09.056
      CrossRefMedlineGoogle Scholar
    29. ↵
      Marazzi L, Shah M, Balakrishnan S, Patil A, Vera-Licona P. 2022. NETISCE: a network-based tool for cell fate reprogramming. NPJ Syst Biol Appl 8: 21. doi:10.1038/s41540-022-00231-y
      CrossRefGoogle Scholar
    30. ↵
      Marson A, Foreman R, Chevalier B, Bilodeau S, Kahn M, Young RA, Jaenisch R. 2008. Wnt signaling promotes reprogramming of somatic cells to pluripotency. Cell Stem Cell 3: 132–135. doi:10.1016/j.stem.2008.06.019
      CrossRefMedlineGoogle Scholar
    31. ↵
      Miyai M, Tanaka YG, Kamitani A, Hamada M, Takahashi S, Kataoka K. 2010. c-Maf and MafB transcription factors are differentially expressed in Huxley's and Henle's layers of the inner root sheath of the hair follicle and regulate cuticle formation. J Dermatol Sci 57: 178–182. doi:10.1016/j.jdermsci.2009.12.011
      CrossRefMedlineGoogle Scholar
    32. ↵
      Morris SA, Daley GQ. 2013. A blueprint for engineering cell fate: current technologies to reprogram cell identity. Cell Res 23: 33–48. doi:10.1038/cr.2013.1
      CrossRefMedlineGoogle Scholar
    33. ↵
      Murphy SA, Miyamoto M, Kervadec A, Kannan S, Tampakakis E, Kambhampati S, Lin BL, Paek S, Andersen P, Lee DI, et al. 2021. PGC1/PPAR drive cardiomyocyte maturation at single cell level via YAP1 and SF3B2. Nat Commun 12: 1648. doi:10.1038/s41467-021-21957-z
      CrossRefMedlineGoogle Scholar
    34. ↵
      Närhi K, Järvinen E, Birchmeier W, Taketo MM, Mikkola ML, Thesleff I. 2008. Sustained epithelial β-catenin activity induces precocious hair development but disrupts hair follicle down-growth and hair shaft formation. Development 135: 1019–1028. doi:10.1242/dev.016550
      Abstract/FREE Full Text
    35. ↵
      Panteleyev AA, Mitchell PJ, Paus R, Christiano AM. 2003. Expression patterns of the transcription factor AP-2α during hair follicle morphogenesis and cycling. J Invest Dermatol 121: 13–19. doi:10.1046/j.1523-1747.2003.12319.x
      CrossRefMedlineGoogle Scholar
    36. ↵
      Pedregosa F, Varoquaux G, Gramfort A, Michel V, Thirion B, Grisel O, Blondel M, Prettenhofer P, Weiss R, Dubourg V, et al. 2011. Scikit-learn: machine learning in Python. J Mach Learn Res 12: 2825–2830.
      CrossRefMedlineGoogle Scholar
    37. ↵
      Pliner HA, Packer JS, McFaline-Figueroa JL, Cusanovich DA, Daza RM, Aghamirzaie D, Srivatsan S, Qiu X, Jackson D, Minkina A, et al. 2018. Cicero predicts cis-regulatory DNA interactions from single-cell chromatin accessibility data. Mol Cell 71: 858–871.e8. doi:10.1016/j.molcel.2018.06.044
      CrossRefMedlineGoogle Scholar
    38. ↵
      Potter CS, Peterson RL, Barth JL, Pruett ND, Jacobs DF, Kern MJ, Argraves WS, Sundberg JP, Awgulewitsch A. 2006. Evidence that the satin hair mutant gene Foxq1 is among multiple and functionally diverse regulatory targets for Hoxc13 during hair follicle differentiation. J Biol Chem 281: 29245–29255. doi:10.1074/jbc.M603646200
      Abstract/FREE Full Text
    39. ↵
      Qin Q, Fan JY, Zheng RB, Wan CX, Mei SL, Wu Q, Sun HF, Brown M, Zhang J, Meyer CA, et al. 2020. Lisa: inferring transcriptional regulators through integrative modeling of public chromatin accessibility and ChIP-seq data. Genome Biol 21: 32. doi:10.1186/s13059-020-1934-6
      CrossRefMedlineGoogle Scholar
    40. ↵
      Qiu X, Zhang Y, Martin-Rufino JD, Weng C, Hosseinzadeh S, Yang D, Pogson AN, Hein MY, Min KH, Wang L, et al. 2022. Mapping transcriptomic vector fields of single cells. Cell 185: 690–711.e45. doi:10.1016/j.cell.2021.12.045
      CrossRefMedlineGoogle Scholar
    41. ↵
      Rackham OJL, Firas J, Fang H, Oates ME, Holmes ML, Knaupp AS, Suzuki H, Nefzger CM, Daub CO, Shin JW, et al. 2016. A predictive computational framework for direct reprogramming between human cell types. Nat Genet 48: 331–335. doi:10.1038/ng.3487
      CrossRefMedlineGoogle Scholar
    42. ↵
      Rauluseviciute I, Riudavets-Puig R, Blanc-Mathieu R, Castro-Mondragon JA, Ferenc K, Kumar V, Lemma RB, Lucas J, Chèneby J, Baranasic D, et al. 2024. JASPAR 2024: 20th anniversary of the open-access database of transcription factor binding profiles. Nucleic Acids Res 52: D174–D182. doi:10.1093/nar/gkad1059
      CrossRefMedlineGoogle Scholar
    43. ↵
      Raveh E, Cohen S, Levanon D, Negreanu V, Groner Y, Gat U. 2006. Dynamic expression of Runx1 in skin affects hair structure. Mech Dev 123: 842–850. doi:10.1016/j.mod.2006.08.002
      CrossRefMedlineGoogle Scholar
    44. ↵
      Ronquist S, Patterson G, Muir LA, Lindsly S, Chen H, Brown M, Wicha MS, Bloch A, Brockett R, Rajapakse I. 2017. Algorithm for cellular reprogramming. Proc Natl Acad Sci 114: 11832–11837. doi:10.1073/pnas.1712350114
      Abstract/FREE Full Text
    45. ↵
      Rukhlenko OS, Halasz M, Rauch N, Zhernovkov V, Prince T, Wynne K, Maher S, Kashdan E, MacLeod K, Carragher NO, et al. 2022. Control of cell state transitions. Nature 609: 975–985. doi:10.1038/s41586-022-05194-y
      CrossRefMedlineGoogle Scholar
    46. ↵
      Takahashi K, Yamanaka S. 2006. Induction of pluripotent stem cells from mouse embryonic and adult fibroblast cultures by defined factors. Cell 126: 663–676. doi:10.1016/j.cell.2006.07.024
      CrossRefMedlineGoogle Scholar
    47. ↵
      Takahashi K, Yamanaka S. 2016. A decade of transcription factor-mediated reprogramming to pluripotency. Nat Rev Mol Cell Biol 17: 183–193. doi:10.1038/nrm.2016.8
      CrossRefMedlineGoogle Scholar
    48. ↵
      Telerman SB, Rognoni E, Sequeira I, Pisco AO, Lichtenberger BM, Culley OJ, Viswanathan P, Driskell RR, Watt FM. 2017. Dermal Blimp1 acts downstream of epidermal TGFβ and Wnt/β-catenin to regulate hair follicle formation and growth. J Invest Dermatol 137: 2270–2281. doi:10.1016/j.jid.2017.06.015
      CrossRefMedlineGoogle Scholar
    49. ↵
      Tran A, Yang P, Yang JYH, Ormerod JT. 2022. scREMOTE: using multimodal single cell data to predict regulatory gene relationships and to build a computational cell reprogramming model. NAR Genom Bioinform 4: lqac023. doi:10.1093/nargab/lqac023
      CrossRefGoogle Scholar
    50. ↵
      Vaquerizas JM, Kummerfeld SK, Teichmann SA, Luscombe NM. 2009. A census of human transcription factors: function, expression and evolution. Nat Rev Genet 10: 252–263. doi:10.1038/nrg2538
      CrossRefMedlineGoogle Scholar
    51. ↵
      Wang HF, Yang YC, Liu JD, Qian L. 2021. Direct cell reprogramming: approaches, mechanisms and progress. Nat Rev Mol Cell Biol 22: 410–424. doi:10.1038/s41580-021-00335-z
      CrossRefGoogle Scholar
    52. ↵
      Wichterle H, Lieberam I, Porter JA, Jessell TM. 2002. Directed differentiation of embryonic stem cells into motor neurons. Cell 110: 385–397. doi:10.1016/S0092-8674(02)00835-8
      CrossRefMedlineGoogle Scholar
    53. ↵
      Wolf FA, Angerer P, Theis FJ. 2018. SCANPY: large-scale single-cell gene expression data analysis. Genome Biol 19: 15. doi:10.1186/s13059-017-1382-0
      CrossRefMedlineGoogle Scholar
    54. ↵
      Xie HF, Ye M, Feng R, Graf T. 2004. Stepwise reprogramming of B cells into macrophages. Cell 117: 663–676. doi:10.1016/S0092-8674(04)00419-2
      CrossRefMedlineGoogle Scholar
    55. ↵
      Xu Q, Georgiou G, Frölich S, van der Sande M, Veenstra GJC, Zhou HQ, van Heeringen SJ. 2021. ANANSE: an enhancer network-based computational approach for predicting key transcription factors in cell fate determination. Nucleic Acids Res 49: 7966–7985. doi:10.1093/nar/gkab598
      CrossRefMedlineGoogle Scholar
    56. ↵
      Yu J, Vodyanik MA, Smuga-Otto K, Antosiewicz-Bourget J, Frane JL, Tian S, Nie J, Jonsdottir GA, Ruotti V, Stewart R, et al. 2007. Induced pluripotent stem cell lines derived from human somatic cells. Science 318: 1917–1920. doi:10.1126/science.1151526
      Abstract/FREE Full Text

    Articles citing this article

    • Unified multimodal learning enables generalized cellular response prediction to diverse perturbations bioRxiv January 28, 2026 0: 2025.11.13.688367v2-2025.11.13.688367
    | Table of Contents

    This Article

    1. Published in Advance April 10, 2025, doi: 10.1101/gr.279955.124 Genome Res. 35: 1429-1439 © 2025 Li et al.; Published by Cold Spring Harbor Laboratory Press

    Article Category

    Share

    Preprint Server



    Navigate This Article

    Current Issue

    1. January 2026, 36 (1)
    1. Current Issue
    1. Alert me to new issues of Genome Research