Size-based expectation maximization for characterizing nucleosome positions and subtypes

  1. Shaun Mahony1
  1. 1Center for Eukaryotic Gene Regulation, Department of Biochemistry and Molecular Biology, Pennsylvania State University, University Park, Pennsylvania 16802, USA;
  2. 2State Key Laboratory of Experimental Hematology, National Clinical Research Center for Blood Diseases, Haihe Laboratory of Cell Ecosystem, Institute of Hematology & Blood Diseases Hospital, Chinese Academy of Medical Sciences & Peking Union Medical College, Tianjin 300020, China;
  3. 3Department of Developmental Biology, School of Basic Medical Sciences, Southern Medical University, Guangzhou 510515, China
  • Corresponding authors: kuangyuyen{at}ihcams.ac.cn, mahony{at}psu.edu
    •  
    Next Section

    Abstract

    Genome-wide nucleosome profiles are predominantly characterized using MNase-seq, which involves extensive MNase digestion and size selection to enrich for mononucleosome-sized fragments. Most available MNase-seq analysis packages assume that nucleosomes uniformly protect 147 bp DNA fragments. However, some nucleosomes with atypical histone or chemical compositions protect shorter lengths of DNA. The rigid assumptions imposed by current nucleosome analysis packages potentially prevent investigators from understanding the regulatory roles played by atypical nucleosomes. To enable the characterization of different nucleosome types from MNase-seq data, we introduce the size-based expectation maximization (SEM) nucleosome-calling package. SEM employs a hierarchical Gaussian mixture model to estimate nucleosome positions and subtypes. Nucleosome subtypes are automatically identified based on the distribution of protected DNA fragments. Benchmark analysis indicates that SEM is on par with existing packages in terms of standard nucleosome-calling accuracy metrics, while uniquely providing the ability to characterize nucleosome subtype identities. Applying SEM to a low-dose MNase-H2B-ChIP-seq data set from mouse embryonic stem cells, we identified three nucleosome types: short-fragment nucleosomes, canonical nucleosomes, and di-nucleosomes. Short-fragment nucleosomes can be divided further into two subtypes based on their chromatin accessibility. Short-fragment nucleosomes in accessible regions exhibit high MNase sensitivity and are enriched at transcription start sites (TSSs) and CTCF peaks, similar to previously reported “fragile nucleosomes.” These SEM-defined accessible short-fragment nucleosomes are found not just in promoters but also in distal regulatory regions. Additional analyses reveal their colocalization with the chromatin remodelers CHD6, CHD8, and EP400. In summary, SEM provides an effective platform for exploration of nonstandard nucleosome subtypes.

    The nucleosome is the basic packaging unit of chromatin, typically comprising ∼147 bp DNA wrapped around the histone octamer (Luger et al. 1997). Nucleosomes participate in gene regulation both by physically impeding access to DNA and by serving as a substrate for interactions with regulatory proteins (Klemm et al. 2019). Chemical modifications on histone tails, including methylation, acetylation, and ubiquitination, can alter DNA affinity to the octamer and can be engaged by regulatory proteins (Kouzarides 2007; Torres and Fujimori 2015). Several histone tail chemical modifications are well correlated with transcriptional activity or repression (Kim et al. 2005; Papp and Müller 2006; Wang et al. 2008). Histone variants, such as H2A.Z and H3.3, have also been reported to play roles in many important biological events, such as DNA replication and enhancer activity (Chen et al. 2013b; Zentner and Henikoff 2013).

    The most common technique for studying nucleosome landscapes across the genome is micrococcal nuclease sequencing (MNase-seq). MNase is an endo-exonuclease that preferentially digests accessible DNA between nucleosomes. After size selection, mononucleosome-sized DNA fragments are retained for high-throughput sequencing (Mavrich et al. 2008; Jiang and Pugh 2009). However, depending on the composition of the nucleosome and the factors engaging the nucleosome, not all nucleosomes protect the canonical 147 bp of DNA. For example, nucleosomes engaged by Pol II lose one H2A-H2B dimer and transiently become hexamers (Ramachandran et al. 2017). Nucleosomes containing the histone variant H2A.Z can exhibit a distinct unwrapping state from the canonical nucleosome (Wen et al. 2020). Some studies employing alternative nucleosome mapping methods, including low-dose MNase-seq, methidiumpropyl-EDTA sequencing (MPE-seq) (Ishii et al. 2015), cleavage under targets and release using nuclease (CUT&RUN) (Brahma and Henikoff 2019), and chemical mapping (Voong et al. 2016), found MNase-sensitive nucleosome subtypes in yeast and mouse that protect shorter DNA fragments than canonical nucleosomes (Ishii et al. 2015; Voong et al. 2016; Brahma and Henikoff 2019). These studies have begun revealing variations in nucleosome composition across the genome.

    Despite experimental results that have characterized a wider diversity of nucleosome composition, most nucleosome-calling software packages still assume that nucleosomes uniformly protect ∼147 bp of DNA (Becker et al. 2013; Chen et al. 2013a; Zhou et al. 2016). Current approaches use this rigid assumption when estimating the locations and occupancy properties of nucleosomes, making their performance suboptimal when characterizing nucleosomes of noncanonical DNA length. Although some packages have begun incorporating the ability to detect nucleosome positioning dynamics (Chen et al. 2013a; Zhou et al. 2016), none are yet able to distinguish various nucleosome subtypes from MNase-seq data.

    To resolve the lack of an effective method for characterizing nucleosome subtypes, we introduce a new nucleosome-calling package called size-based expectation maximization (SEM). We evaluate the performance of SEM by comparing it to existing nucleosome-calling packages. We then apply SEM to analyze a low-dose MNase-ChIP-H2B data set from mouse embryonic stem cells (mESCs) (Ishii et al. 2015), thereby demonstrating SEM's ability to characterize various nucleosome subtypes genome-wide.

    Previous SectionNext Section

    Results

    A hierarchical Gaussian mixture model for characterizing nucleosome types

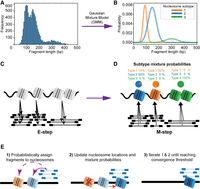
    SEM is a hierarchical Gaussian mixture model (GMM), which probabilistically models the positions, occupancy, fuzziness, and subtype identities of nucleosomes from MNase-seq data (Fig. 1). The components of the mixture model represent individual nucleosomes; the properties of each nucleosome are modeled based on the mapped locations and lengths of MNase-seq fragments. Specifically, each nucleosome component is defined by its dyad location, occupancy, fuzziness, and the probability of belonging to each nucleosome subtype.

    Figure 1.
    View larger version:
    Figure 1.

    Overview of the SEM algorithm. (A) SEM first calculates the global fragment size distribution from the MNase-seq data. (B) A Gaussian mixture model (GMM) is used to deconvolve the fragment size distribution into a set of nucleosome subtypes. (C) In the expectation step of the algorithm, each MNase-seq fragment is probabilistically assigned to nucleosome components according to the current locations, strengths, and subtype identities of the components. (D) In the maximization step of the algorithm, the various nucleosome properties are updated based on the current fragment assignments. (E) Detailed illustration of how nucleosome properties are updated during EM iterations.

    SEM runs in two major phases: nucleosome subtype discovery and nucleosome finding. During the first phase, SEM fits a GMM onto the fragment size distribution of the entire MNase-seq data set to determine the Gaussian distribution parameters of each nucleosome subtype (Fig. 1A,B). The number of clusters, corresponding to the number of nucleosome subtypes, is an essential parameter of the model. It can be specified by the user according to prior knowledge of the biological sample, or SEM can automatically determine the best fit value using a Dirichlet process mixture model (DPMM).

    In the second phase, SEM uses a hierarchical GMM to compute the likelihood that each specific nucleosome is responsible for generating each MNase-seq fragment in the data set. A generalized expectation maximization (GEM) framework is used to calculate the latent assignment of MNase-seq fragments to nucleosomes and to estimate the various properties associated with each nucleosome (see Methods). Briefly, the expectation step in the algorithm probabilistically assigns MNase-seq fragments to the nucleosome components that are most likely to have generated them based on their current locations and properties (Fig. 1C). Then the maximization step updates the properties of the nucleosome components based on the best fit to the current fragment assignments (Fig. 1D). For example, a nucleosome component's dyad location, occupancy, and fuzziness properties are re-estimated based on the mean midpoint location, weights, and variance of currently assigned MNase-seq fragments. Subtype identity is updated based on the size distribution of assigned fragments. The algorithm iterates through expectation and maximization steps until convergence (Fig. 1E).

    To better reflect the known biological properties of nucleosomes, several priors are integrated into the model. First, a sparse prior on nucleosome occupancy eliminates components that do not have enough fragments assigned, thereby encouraging solutions in which each nucleosome is supported by MNase-seq data. Another sparse prior on subtype probability encourages each component to be a member of individual subtypes, which improves the interpretability of nucleosome subtype assignments. The physical exclusion of adjacent nucleosomes is also taken into consideration to ensure that neighboring nucleosomes do not overlap in the model.

    SEM accurately predicts conventional nucleosome properties

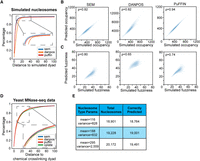
    We first evaluated the performance of SEM in predicting conventional nucleosome properties, including nucleosome dyad location, nucleosome occupancy, and fuzziness, on both simulated and real MNase-seq data sets. To generate the simulated data set, we took reference nucleosome dyad locations from yeast (Jiang and Pugh 2009), based on a collection of nucleosome dyad locations compiled from six data sets. The occupancy and fuzziness of each nucleosome were then computed using a H4 MNase-ChIP-seq data set against the reference nucleosome dyads (see Methods). Background “noise” reads following a Poisson distribution were added globally to the simulated data set to test the robustness of each algorithm.

    SEM's performance in this simulated data set was evaluated against two other nucleosome-calling packages: DANPOS and PuFFIN (Chen et al. 2013a; Polishko et al. 2014). All three packages were executed using their default settings (see Methods). The numbers of nucleosomes predicted by each package was similar to the number in the reference set (i.e., about 60,000 nucleosomes). SEM and PuFFIN outperform DANPOS in predicting simulated nucleosome dyad locations (Fig. 2A). PuFFIN achieves the best estimates of simulated nucleosome occupancy, as evaluated by the Pearson correlation coefficient (Fig. 2B). Although SEM and DANPOS have similar correlations with the simulated occupancy, DANPOS has a general tendency to overestimate nucleosome occupancy (Fig. 2B, middle panel). SEM outperforms PuFFIN and DANPOS in estimating the simulated fuzziness levels, again evaluated by Pearson correlation coefficient (Fig. 2C).

    Figure 2.
    View larger version:
    Figure 2.

    Comparison of SEM to existing nucleosome-calling packages on common metrics. (A) Cumulative percentage of distances between predicted nucleosome dyads and simulated nucleosome dyads in simulated MNase-seq data. (B) Correlation between predicted occupancy and simulated occupancy. Each simulated nucleosome is assigned to the closest predicted nucleosome for the purposes of comparison. (C) Correlation between predicted fuzziness and simulated fuzziness. Each simulated nucleosome is assigned to the closest predicted nucleosome for the purposes of comparison. (D) Cumulative percentage of distances between predicted nucleosome dyads and chemical cross-linking dyads in real MNase-seq data (Voong et al. 2016). (E) Numbers of total simulated nucleosomes and correctly predicted nucleosomes of each nucleosome subtype.

    We further evaluated the performance of SEM using real MNase-seq data (Zhou et al. 2016). Because no ground truth of nucleosome occupancy or fuzziness is available, our evaluation solely focused on predictions of nucleosome dyad locations. The nucleosome dyad locations obtained from the chemical cross-linking experiment were used as the “gold standard” owing to its ability to specifically break DNA nucleotides near the dyad location. We included a fourth nucleosome-calling package, Cplate, in this comparison, as predicted nucleosome dyad locations in the same data set were available in the original Cplate publication (Zhou et al. 2016). Notably, although SEM, DANPOS, and PuFFIN exhibited significant performance disparities in simulated data sets, all four software packages exhibited comparable performance when evaluated on the real MNase-seq data set (Fig. 2D).

    Additionally, we evaluated SEM's ability to distinguish various nucleosome subtypes. A simulated MNase-seq data set, in which reads are sampled from three distinct nucleosome subtypes, was generated. SEM achieved high accuracy in correctly identifying the subtypes from which each simulated nucleosome was sampled (Fig. 2E).

    To summarize, our results indicate that SEM performs comparably with existing nucleosome-calling packages in predicting nucleosome dyad locations. Although PuFFIN displays greater accuracy in predicting nucleosome occupancy, SEM outperforms it in predicting nucleosome fuzziness. Overall, SEM yields comparable performance to other nucleosome-calling packages when it comes to conventional nucleosome metrics. In addition, SEM can precisely predict nucleosome subtypes in simulated data.

    Genome-wide detection of nucleosome subtypes in mESCs

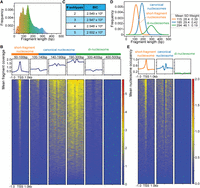
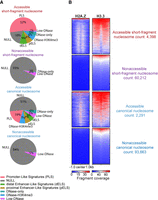
    To assess whether SEM can distinguish different types of nucleosomes from MNase-seq data, we applied it to a low-dose MNase-H2B-ChIP-seq data set from mESCs (Ishii et al. 2015). The original study focused on characterizing the locations of so-called fragile, or MNase-sensitive, nucleosomes, which protect shorter DNA fragments than canonical nucleosomes under low-dose MNase digestion (Ishii et al. 2015; Chereji et al. 2017). Although the study found evidence for MNase-sensitive nucleosomes at TSSs and CTCF binding sites, the overlapping fragment size distributions of canonical nucleosomes and fragile nucleosomes make it difficult to distinguish between these nucleosome subtypes at individual sites. The original study applied hard fragment-length cut-offs (50–100 bp, 101–140 bp, 140–190 bp) to define different nucleosome subtypes. However, the application of these thresholds does not adequately distinguish between nucleosome subtypes at TSSs or CTCF binding sites, given the variations observed in the overall fragment size distribution (Fig. 3A,B; Supplemental Fig. S1A). Our goal here is to assess whether SEM can more clearly discriminate nucleosome subtypes and add additional insights into the nature of the MNase-sensitive nucleosomes characterized in the original study.

    Figure 3.
    View larger version:
    Figure 3.

    SEM characterizes three nucleosome subtypes in a low-dose MNase-ChIP-seq data set from mESCs. (A) Fragment size distribution of the low-dose MNase-ChIP-seq data set. (B) Heatmap and profile plot of MNase-seq fragments split by fragment size (50–100 bp, 100–140 bp, 140–190 bp, 190–300 bp, 300–400 bp, 400–500 bp) around TSSs. (C) Bayesian information criterion (BIC) computed across varying numbers of nucleosome subtypes. (D) Fragment size distribution of each nucleosome subtype as determined by SEM. (E) Heatmap and profile plot of each SEM-defined nucleosome subtype around TSSs.

    Visual inspection of the DNA fragment size distribution suggests that there are three main modes of MNase-protected fragments in the MNase-H2B-ChIP data set and, thus, three distinct nucleosome subtypes (Fig. 3A). We confirmed that including three nucleosome subtypes in the SEM model provided the best fit to the data by evaluating the Bayesian information criterion (BIC) metric over varying numbers of subtypes (Fig. 3C). Based on their mean fragment sizes, we refer here to each SEM-defined nucleosome subtype as short-fragment nucleosomes (∼115 bp mean size), canonical nucleosomes (∼185 bp mean size), and di-nucleosomes (∼295 bp mean size) (Fig. 3A,D). Here, the larger mean size of DNA fragments protected by the canonical nucleosome, compared with the typically reported 147 bp, likely results from incompletely digested linker DNA at a subset of nucleosomes under the light MNase digestion conditions used in the MNase-H2B-ChIP experiment. SEM discovered a total of 6,200,234 nucleosomes along the mouse genome (Supplemental Data D1). More than half exhibit mixed nucleosome subtype identity, indicating the highly dynamic nature of nucleosomes across the whole genome (Supplemental Fig. S1C,D). In comparison with hard fragment-length cut-offs, SEM's detection of nucleosome subtypes more clearly separates nucleosomes belonging to each subtype at TSSs and CTCF sites (Fig. 3E; Supplemental Fig. S1B). Specifically, short-fragment nucleosomes are enriched at the centers of TSSs and CTCF sites, whereas canonical nucleosomes are well positioned in the flanking regions (Fig. 3E; Supplemental Fig. S1B).

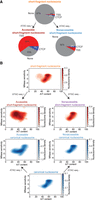
    The enrichment of SEM-defined short-fragment nucleosomes at TSSs and CTCF sites mirrors that of the MNase-sensitive nucleosomes defined in the original study. However, only a small proportion of all SEM-defined short-fragment nucleosomes overlap TSSs or CTCF sites (Fig. 4A). We therefore asked whether SEM's short-fragment nucleosome category consists of a homogenous class of MNase-sensitive nucleosomes or whether it encompasses multiple short-fragment nucleosome subtypes. To more clearly delineate the properties of each nucleosome subtype, we focus only on SEM-defined nucleosomes with occupancy greater than five reads and unambiguous subtype assignments (i.e., one of the nucleosome subtype probabilities >0.9).

    Figure 4.
    View larger version:
    Figure 4.

    Subcategorization of SEM nucleosome subtypes reveals a population of accessible short-fragment nucleosomes. (A) Percentages of short-fragment nucleosome subtype and subcategories located at TSS regions (±500 bp) and CTCF binding sites. (B) 2D density plots show the relationships between A/T content and MNase sensitivity of each nucleosome subtype and subcategory; color bars indicate the log density of nucleosomes. Nucleosome subcategories were obtained by examining if the nucleosome is fully overlapped by ATAC-seq peak (ATAC-seq +) or not (ATAC-seq –).

    We first subcategorized SEM's nucleosome subtypes according to their association with potential regulatory regions by overlapping with mESC ATAC-seq peaks (Ostapcuk et al. 2018). Two-thirds of the SEM-defined accessible short-fragment nucleosomes overlap with TSSs or CTCF binding sites, whereas the nonaccessible short-fragment nucleosomes are primarily located in distal regions (Fig. 4A). We then calculated the MNase sensitivity of each nucleosome subcategory by comparing the number of MNase-seq fragments from the low-dose MNase-H2B-ChIP-seq data set with the number of fragments from a high-dose MNase-seq data set (Ishii et al. 2015) in the ±50 bp region surrounding each nucleosome dyad (Supplemental Fig. S2A). Accessible short-fragment nucleosomes display high MNase sensitivity, consistent with the MNase-sensitive short-fragment nucleosomes found in the original study. However, the nonaccessible short-fragment nucleosomes do not display significantly higher MNase sensitivity than the nonaccessible canonical nucleosomes (Supplemental Fig. S2A).

    Because the nonaccessible short-fragment nucleosomes do not display higher MNase sensitivity, we asked whether their shorter fragment lengths could be accounted for by MNase digestion biases toward A/T-rich sequences (Dingwall et al. 1981). We therefore compared the MNase sensitivity index for each nucleosome to the A/T content in the ±50 bp region surrounding each nucleosome dyad (Fig. 4B). Although higher A/T content appears to correlate with higher MNase sensitivity at nonaccessible nucleosome categories, the A/T content properties of nonaccessible short-fragment nucleosomes are again similar to those of nonaccessible canonical nucleosomes. However, nonaccessible short-fragment nucleosomes display significantly higher A/T content at entry and exit sites compared with nonaccessible canonical nucleosomes (t-test statistic = 45.78, P-value < 2 × 10–308) (Supplemental Fig. S2B). This suggests that the MNase bias toward digesting A/T-rich sequences at nucleosome flanks could be responsible for the shorter fragment distributions at this subset of short-fragment nucleosomes. In other words, there may not be any substantial difference between the nonaccessible short-fragment nucleosomes and canonical nucleosomes as defined by SEM, other than a greater susceptibility to MNase biases at entry and exit sites.

    In contrast to the nonaccessible short-fragment nucleosomes, the accessible short-fragment nucleosomes display high MNase sensitivity despite being generally G/C-rich (Fig. 4B). We confirmed the levels of MNase sensitivity using the MNase accessibility (MACC) score (Mieczkowski et al. 2016). The MACC score is the slope of the fitted line between fragment counts and logarithmic-scaled MNase concentration in titrated MNase-seq experiments, in which a high MACC score represents a highly MNase sensitive region. The MACC score is substantially higher at accessible short-fragment nucleosomes compared with random nucleosome positions (Supplemental Fig. S3A). This indicates that SEM-defined accessible short-fragment nucleosomes represent a subpopulation of G/C-rich, MNase-sensitive short-fragment nucleosomes that is distinctly separated from the broader pool of short-fragment nucleosomes.

    Although the analyzed MNase-ChIP-seq experiment incorporated a H2B ChIP pulldown, it is possible that our detected short-fragment nucleosome subcategories result from MNase protection by nonnucleosomal regulatory proteins that artifactually cross-link with neighboring nucleosomes. To assess this potential concern, we examined nucleosome centering positioning (NCP) scores derived from a H4S47C-mediated chemical cross-linking approach (Voong et al. 2016). The accessible short-fragment nucleosomes display a clear peak in NCP scores, as well as nucleosome array phasing similar to canonical nucleosomes, providing orthogonal evidence for the presence of nucleosomes at the short-fragment nucleosome loci (Supplemental Fig. S3B).

    In summary, SEM identified three distinct nucleosome subtypes in mESCs from the low-dose MNase H2B ChIP-seq data set. By integrating chromatin accessibility data, the SEM-defined short-fragment nucleosomes were further subdivided into two subcategories. Accessible short-fragment nucleosomes display several properties corresponding to the previously proposed fragile nucleosomes, including high MNase sensitivity and enrichment at TSSs and CTCF binding sites.

    Accessible short-fragment nucleosomes associate with distinct regulatory activities

    Most previous studies of fragile or MNase-sensitive nucleosomes have focused on their occurrence at TSSs and CTCF binding sites (Ishii et al. 2015; Voong et al. 2016). As shown above, SEM-defined accessible short-fragment nucleosomes are highly enriched at these regions (Fig. 4A). However, a substantial portion (33%) of SEM's accessible short-fragment nucleosomes do not overlap either TSSs or CTCF binding sites (Fig. 4A). To investigate the types of locations occupied by non-TSS/CTCF accessible short-fragment nucleosomes, we overlapped these nucleosomes with candidate cis-regulatory elements (cCREs) from the ENCODE SCREEN database (Fig. 5A; The ENCODE Project Consortium et al. 2020). Notably, 17% of the accessible short-fragment nucleosomes overlap with either proximal or distal enhancer-like signatures (pELSs or dELSs, respectively).

    Figure 5.
    View larger version:
    Figure 5.

    Accessible short-fragment nucleosomes are associated with regulatory elements and histone variants. (A) Pie chart summarizing the overlap between SEM-defined nucleosome subcategories and ENCODE SCREEN cCRE types. (B) Heatmap displaying the enrichment of histone variants H2A.Z and H3.3 around nucleosome dyad locations.

    The association between accessible short-fragment nucleosomes and cis-regulatory elements suggests a possible role in transcriptional regulation. Therefore, we investigated whether accessible short-fragment nucleosomes overlap the occupancy of factors involved in nucleosome composition or histone modifications associated with regulatory activities in mESCs. A previous report in Drosophila suggested that H3.3/H2A.Z-containing nucleosomes are enriched at regulatory regions and are unstable under high-salt conditions (Jin et al. 2009). Thus, we examined the enrichment of both histone variants around nucleosome subcategories. We found that H3.3 is highly enriched at regions flanking the accessible short-fragment nucleosomes, albeit locally depleted at dyad locations (Fig. 5B). H2A.Z also displays higher levels of enrichment flanking accessible short-fragment nucleosomes compared with nonaccessible nucleosome subtypes (Fig. 5B). Active histone modifications, including H3K27ac, H3K4me3, H3K9ac, and H4ac, were enriched at sites adjacent to accessible short-fragment nucleosomes (Supplemental Fig. S4), whereas repressive marks, including H3K27me3 and H2AK119ub, do not show enrichment at accessible short-fragment nucleosome sites. Finally, several chromatin remodelers are enriched at accessible short-fragment nucleosome dyad locations, including SMARCA4, CHD4, CHD6, CHD8, and EP400. EP400 is more prominently enriched at accessible short-fragment nucleosomes relative to other remodelers and is centrally enriched at accessible short-fragment nucleosome dyad locations (Supplemental Fig. S5). These chromatin remodelers are known to influence the contact between DNA and the nucleosome (Clapier et al. 2017). EP400 has also been reported to deposit H3.3 at promoter and enhancer regions (Pradhan et al. 2016), which may correspond to the H3.3 enrichment observed at accessible short-fragment nucleosome sites. Therefore, the enrichment of chromatin remodelers at accessible short-fragment nucleosomes suggests a mechanism for their destabilization.

    Finally, we interrogated whether short-fragment nucleosomes are related to distinct transcription factor (TF) binding activities. Specifically, we performed enrichment analysis to investigate which TFs’ binding sites (sourced through ChIP-Atlas) (Oki et al. 2018; Zou et al. 2022) significantly overlap with each nucleosome subcategory. The ChIP-seq peaks of many TFs are heavily enriched around accessible nucleosomes subtypes, including peaks for the pluripotency factors POU5F1 (also known as OCT4), SOX2, NANOG, and KLF4 (Supplemental Table S1). This observation is not necessarily surprising given the general enrichment of TF binding sites in accessible regions. TFs generally show lower fold-enrichment levels at nonaccessible short-fragment nucleosomes, aligning with the expectation that nucleosomes located in less accessible regions would naturally attract fewer binding factors (Supplemental Table S1).

    In summary, accessible short-fragment nucleosomes defined by SEM are not restricted to TSSs and CTCF binding sites and correspond to sites of specific chromatin remodeler enrichment. Although the regulatory roles played by these atypical nucleosomes require further investigation, our analyses demonstrate the efficacy of SEM in characterizing diverse nucleosome types.

    Previous SectionNext Section

    Discussion

    In recent years, there has been growing interest in nucleosome subtypes and compositional variants beyond canonical nucleosomes (Ramachandran et al. 2017; Brahma and Henikoff 2019; Wen et al. 2020; Hsieh et al. 2022). Here, we introduced SEM, a new nucleosome-calling framework capable of distinguishing various nucleosome subtypes from a single MNase-digested sequencing experiment. When compared with other nucleosome-calling packages, SEM exhibits comparable performance on conventional nucleosome-calling metrics while uniquely providing an automatic annotation of nucleosome subtype identity.

    Using SEM on a low-dose MNase-H2B-ChIP-seq data set from mESCs, we identified a nucleosome subtype that protects shorter DNA fragments compared with canonical nucleosomes. A further integration of ATAC-seq data classified the short-fragment nucleosomes into two subcategories, which we labeled accessible short-fragment nucleosomes and nonaccessible short-fragment nucleosomes. Although SEM-defined nonaccessible short-fragment nucleosomes may result from MNase digestion bias at entry and exit sites, it is worth noting that this nucleosome subcategory could be overlooked in traditional MNase-seq experiments conducting mononucleosome size selection. Thus, MNase-seq experiments that omit mononucleosome size selection, in combination with SEM analysis, could more accurately characterize nucleosome positions across the genome. Future versions of SEM could resolve the issues associated with MNase bias by incorporating the relationship between sequence content and DNA fragment size into the probabilistic model.

    SEM-defined accessible short-fragment nucleosomes share a similar distribution to previously reported fragile nucleosomes at TSSs and CTCF sites. However, SEM's ability to identify short-fragment nucleosomes genome-wide shows that accessible short-fragment nucleosomes are not restricted to TSSs and CTCF sites but are also present in distal regulatory regions. Previous studies have suggested that histone variants H3.3 and H2A.Z regulate nucleosome stability or lead to nucleosome fragility (Jin and Felsenfeld 2007; Jin et al. 2009; Wen et al. 2020). We find an enrichment of H3.3, and to a lesser extent H2A.Z, at accessible short-fragment nucleosome sites. Accessible short-fragment nucleosomes are also associated with active histone marks but not repressive marks. Accessible short-fragment nucleosomes in mESCs are coenriched with the chromatin remodelers SMARCA4, CHD4, CHD6, CHD8, and EP400, suggesting that this nucleosome subcategory represents hotspots of chromatin remodeler activity. Assessing whether these chromatin remodelers play an active role in establishing short-fragment nucleosomes will require further experimental investigation (e.g., via knockdown perturbations followed by MNase-seq experiments). Further work also remains to investigate whether SEM-defined accessible short-fragment nucleosomes play distinct regulatory roles in mESCs. However, our analyses demonstrate that SEM's genome-wide probabilistic approach to nucleosome subtype calling provides clear advantages over the typically employed fragment-length threshold approaches.

    Previous SectionNext Section

    Methods

    Nucleosome subtype characterization

    To model different nucleosome subtypes present in an MNase-seq data set, we first apply a GMM to the overall fragment size distribution. This step can be processed with or without a user-defined number of subtypes. If the number of types has been defined, a finite GMM is used on the fragment size distribution to find the parameters of each type. GMM initialization is achieved using k-means clustering on the fragment sizes. Briefly, fragments are sorted by size and divided into percentile-based groups. The mean sizes of each group are used as initial centroids for k-means clustering. The final assignments from k-means serve as the starting point for the GMM. Alternatively, if the number of subtypes has not been defined, a value can be automatically determined from the fragment size distribution by a DPMM.

    SEM probabilistic model

    SEM is based on a hierarchical GMM that describes the likelihood of observing a set of MNase-seq fragments from a set of nucleosomes. Each nucleosome contributes a distribution of reads surrounding its genomic position to the overall mixture of reads. We assume that fragment locations are independently conditioned on the dyad location, fuzziness, and subtype mixture probabilities of their underlying nucleosomes.

    SEM performs nucleosome discovery by finding the set of nucleosomes that maximizes the penalized likelihood of the observed MNase-seq fragments. First, we assume there are K nucleosome fragment size subtypes, where each subtype is a Gaussian distribution with mean Ψ = ψ1, …, ψK, variance Φ = ϕ1, …, ϕK, and weight Ω = ω1, …, ωK. Thus, the expected size distribution of fragments from each nucleosome follows a mixture of the subtype distributions, conditioned on their subtype probabilities. Throughout the whole genome, we consider N MNase-seq fragments that have been mapped to genomic locations 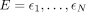Formula with size H = η1, …, ηN and with M potential nucleosomes at genomic locations U = μ1, …, μM with fuzziness Θ = θ1, …, θM and subtype mixture probabilities T = τ1, …, τM = [τ1,1, …, τ1,K, ], …, [τM,1, …, τM,K,]. The locations of fragments from nucleosome m follow a Gaussian distribution, in which the Gaussian mean equals the nucleosome dyad location μm, and the variance equals the fuzziness parameter θm. We represent the latent assignment of fragments to nucleosomes that caused them as Z = z1, …, zN, where zi = j, where j is the index of the nucleosome whose dyad is at position μj that generates fragment i.

    The conditional probability of fragment ri being generated from nucleosome j located in μj with mixture probability ρj and fuzziness θj is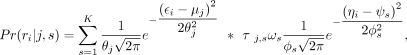Formula (1) where τj,s represents the probability of nucleosome j belonging to fragment size type s.

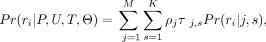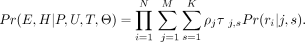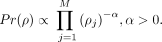    The probability of a fragment is a convex combination of possible nucleosomes:Formula (2) where ρ represents the weighted occupancy of a nucleosome. The overall likelihood of the observed set of fragments is thenFormula (3) We incorporate several biological assumptions in the form of priors on the parameters. 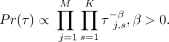We place a sparseness-promoting negative Dirichlet prior α on the nucleosome-weighted occupancy π, based on the assumption that each nucleosome should have sufficient numbers of assigned fragments to support its existence in the modelFormula (4) We also incorporate an additional prior to encourage nucleosomes to choose less ambiguous subtype identities. 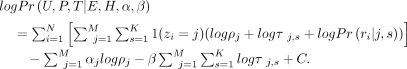To do so, we place a Dirichlet prior β on the nucleosome type mixture probability τ:Formula (5) In summary, the complete-data log posterior is as follows:Formula (6)

    Expectation maximization

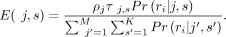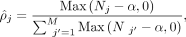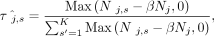    We initialize mixing probabilities ρ with uniform probabilities, ρj = 1/M, j = 1, …, M. At the E step, we calculate the relative responsibility of each nucleosome subtype per nucleosome in generating each fragment as follows:Formula (7) The maximum posterior probability (MAP) estimation of ρ, τ is as follows:Formula (8) Formula (9) where Nj represents the number of fragments assigned to nucleosome j, and Nj,s represents the number of fragments assigned to nucleosome j of type s. The value of α is the minimum number of MNase-seq fragments required to support a nucleosome surviving in this round. In the first five rounds of expectation maximization, sparse priors are set to their minimum value (one for α and zero for β) to avoid elimination of true nucleosomes owing to poor initialization. Then sparse priors are gradually increased in the following five rounds until reaching the default or user-defined values. The default values of α and β are one and 0.05, respectively.

    MAP values of μj,s are determined by finding the location with the maximized probability in ±50 bp flanking sites of the current nucleosome dyad. If the maximization step results in two components sharing the same weighted positions, they are combined in the next iteration of the algorithm.

    Considering the efficiency of the algorithm, the fuzziness and the subtype mixture probabilities of each nucleosome are updated every two rounds. In the first several rounds, prior α and β is multiplied by an annealing factor according to the number of completed rounds to avoid too early elimination of nucleosomes. As expectation maximization proceeds, the log likelihood increases after each iteration, and convergence is defined when log likelihood increases <1% compared with the previous iteration.

    Exclusion zone

    Each nucleosome protects DNA and should sterically exclude other nucleosomes at the same position. For example, canonical nucleosomes protect 147 bp DNA, which means the minimum distance between two canonical nucleosomes should be >147 bp. Thus, when there is no nucleosome eliminated during an iteration after a sparse prior is fully incorporated, an extra step will be taken to remove nucleosomes that are too close to adjacent nucleosomes. Each time the overlapped nucleosome with the lowest responsibility (i.e., occupancy) will be removed, until all nucleosomes have a large enough spacing to each other. The exclusion zone is currently set to 127 bp to avoid false removal of nucleosomes owing to the inaccurate prediction of nucleosome dyads.

    MNase-seq data simulation

    To simulate the MNase-seq data set on the sacCer3 reference genome, we first took the nucleosome dyad location maps from Jiang and Pugh (2009) as a reference. MNase H4 ChIP-seq data sets obtained from the NCBI Sequence Read Archive (SRA; https://www.ncbi.nlm.nih.gov/sra) under accession numbers SRR3649286, SRR3649291 (Chereji et al. 2017) were used to infer the nucleosome occupancy and fuzziness for simulation. Specifically, we used the MNase-seq fragments within ±73 bp around each nucleosome dyad to compute the occupancy and fuzziness. Simulated MNase-seq fragments were then generated given the computed nucleosome metrics, distributed following a Gaussian with mean (nucleosome dyad), variance (nucleosome fuzziness), and weight (nucleosome occupancy) parameters set from the above data. Background noise fragments following a Poisson distribution were added to the simulated data set to test the robustness of each algorithm. We used a background noise ratio of 0.05 in this study. The Poisson mean λ is determined by the ratio of background noise among the whole data set using the formulaFormula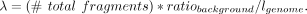

    Nucleosome calling on MNase-seq data sets

    On both simulated and real data sets, SEM, DANPOS, and PuFFIN were run under default settings. Cplate predictions on real MNase-seq data set were taken from Zhou et al. (2016).

    Determining nucleosome subcategories in mESCs

    SEM was run on a low-dose MNase H2B ChIP-seq data set (SRA; SRR2034510, SRR2034511) from Ishii et al. (2015) under default settings with the number of nucleosome subtypes set to three. Nucleosomes are then filtered such that occupancy is greater than five reads and one of the nucleosome subtype probabilities >0.9. The nucleosome subcategories were determined by overlapping the filtered nucleosomes with ATAC-seq peaks. To ensure the whole nucleosome is located within an accessible region, we required that the dyad location of accessible nucleosome has to be at least 100 bp away from the boundary of the ATAC-seq peak. The remaining nucleosomes are deemed nonaccessible.

    Data processing

    All FASTQ files were first trimmed by Trimmomatic (Bolger et al. 2014) with the options “LEADING:3 TRAILING:3 SLIDINGWINDOW:4:15 MINLEN:36 {adapter_file}:2:30:10” using the corresponding adapters, and then trimmed FASTQ files were mapped to the mm10 reference genome by Bowtie 2 (Langmead and Salzberg 2012). Mapped BAM files were filtered by the criteria that MAPQ scores of both reads in a pair be greater than or equal to 10. ATAC-seq peak calling was performed by using Genrich (https://github.com/jsh58/Genrich) with the ATAC-seq mode enabled by the “-j” option.

    ChIP-Atlas enrichment analysis

    ChIP-seq peak enrichment analysis was performed through the ChIP-Atlas website. Specifically, each nucleosome subcategory was overlapped with peaks from ChIP experiments targeting “TFs and others” in “Pluripotent stem cell.” The threshold for significance was set to 50.

    Bayesian information criterion

    BIC scores were computed on GMM models fitted with numbers of the components set to two, three, four, and five. The formula is 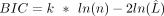Formula, where 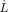Formula is the likelihood of the fitted model, k is the number of the parameters, and n is the number of data points.

    Statistical test on A/T content

    The ratio of A/T nucleotides at the nucleosome entry and exit sites was computed by calculating A/T nucleotide percentages in the regions bounded by [–100 bp, –50 bp] and [+50 bp, +100 bp] relative to the nucleosome dyad. Then, an independent t-test was performed to compare the percentages at nonaccessible short-fragment nucleosomes to those at nonaccessible canonical nucleosomes.

    Software availability

    The SEM software package is available on GitHub (https://github.com/YenLab/SEM) and Bioconda (https://anaconda.org/bioconda/sem). The version of the SEM code used in this paper is archived as Supplemental Code.

    Previous SectionNext Section

    Competing interest statement

    The authors declare no competing interests.

    Previous SectionNext Section

    Acknowledgments

    We thank the members of the Center for Eukaryotic Gene Regulation at Penn State for helpful feedback and discussions. This work was supported by National Institutes of Health R35-GM144135 and National Science Foundation DBI CAREER 2045500 (to S.M.). Any opinions, findings and conclusions, or recommendations expressed in this material are those of the authors and do not necessarily reflect the views of the funders. This work was initiated by J.Y. as a masters student in K.Y.’s laboratory at the Department of Developmental Biology, School of Basic Medical Sciences, Southern Medical University, Guangzhou, China. Work by the Yen laboratory is supported by the National Natural Science Foundation of China (grants 31522031 and 31571526).

    Previous SectionNext Section

    Footnotes

    • Received February 15, 2024.
    • Accepted May 13, 2024.

    This article is distributed exclusively by Cold Spring Harbor Laboratory Press for the first six months after the full-issue publication date (see https://genome.cshlp.org/site/misc/terms.xhtml). After six months, it is available under a Creative Commons License (Attribution-NonCommercial 4.0 International), as described at http://creativecommons.org/licenses/by-nc/4.0/.

    Previous Section
     

    References

    1. ↵
      Becker J, Yau C, Hancock JM, Holmes CC. 2013. NucleoFinder: a statistical approach for the detection of nucleosome positions. Bioinformatics 29: 711–716. doi:10.1093/bioinformatics/bts719
      CrossRefMedlineGoogle Scholar
    2. ↵
      Bolger AM, Lohse M, Usadel B. 2014. Trimmomatic: a flexible trimmer for Illumina sequence data. Bioinformatics 30: 2114–2120. doi:10.1093/bioinformatics/btu170
      CrossRefMedlineGoogle Scholar
    3. ↵
      Brahma S, Henikoff S. 2019. RSC-associated subnucleosomes define MNase-sensitive promoters in yeast. Mol Cell 73: 238–249.e3. doi:10.1016/j.molcel.2018.10.046
      CrossRefGoogle Scholar
    4. ↵
      Chen K, Xi Y, Pan X, Li Z, Kaestner K, Tyler J, Dent S, He X, Li W. 2013a. DANPOS: dynamic analysis of nucleosome position and occupancy by sequencing. Genome Res 23: 341–351. doi:10.1101/gr.142067.112
      Abstract/FREE Full Text
    5. ↵
      Chen P, Zhao J, Wang Y, Wang M, Long H, Liang D, Huang L, Wen Z, Li W, Li X, et al. 2013b. H3.3 actively marks enhancers and primes gene transcription via opening higher-ordered chromatin. Genes Dev 27: 2109–2124. doi:10.1101/gad.222174.113
      Abstract/FREE Full Text
    6. ↵
      Chereji RV, Ocampo J, Clark DJ. 2017. MNase-sensitive complexes in yeast: nucleosomes and non-histone barriers. Mol Cell 65: 565–577.e3. doi:10.1016/j.molcel.2016.12.009
      CrossRefMedlineGoogle Scholar
    7. ↵
      Clapier CR, Iwasa J, Cairns BR, Peterson CL. 2017. Mechanisms of action and regulation of ATP-dependent chromatin-remodelling complexes. Nat Rev Mol Cell Biol 18: 407–422. doi:10.1038/nrm.2017.26
      CrossRefMedlineGoogle Scholar
    8. ↵
      Dingwall C, Lomonossoff GP, Laskey RA. 1981. High sequence specificity of micrococcal nuclease. Nucleic Acids Res 9: 2659–2673. doi:10.1093/nar/9.12.2659
      CrossRefMedlineGoogle Scholar
    9. ↵
      The ENCODE Project Consortium, Moore JE, Purcaro MJ, Pratt HE, Epstein CB, Shoresh N, Adrian J, Kawli T, Davis CA, Dobin A, et al. 2020. Expanded encyclopaedias of DNA elements in the human and mouse genomes. Nature 583: 699–710. doi:10.1038/s41586-020-2493-4
      CrossRefMedlineGoogle Scholar
    10. ↵
      Hsieh LJ, Gourdet MA, Moore CM, Muñoz EN, Gamarra N, Ramani V, Narlikar GJ. 2022. A hexasome is the preferred substrate for the INO80 chromatin remodeling complex, allowing versatility of function. Mol Cell 82: 2098–2112.e4. doi:10.1016/j.molcel.2022.04.026
      CrossRefGoogle Scholar
    11. ↵
      Ishii H, Kadonaga JT, Ren B. 2015. MPE-seq, a new method for the genome-wide analysis of chromatin structure. Proc Natl Acad Sci 112: E3457–E3465. doi:10.1073/pnas.1424804112
      Abstract/FREE Full Text
    12. ↵
      Jiang C, Pugh BF. 2009. A compiled and systematic reference map of nucleosome positions across the Saccharomyces cerevisiae genome. Genome Biol 10: R109. doi:10.1186/gb-2009-10-10-r109
      CrossRefMedlineGoogle Scholar
    13. ↵
      Jin C, Felsenfeld G. 2007. Nucleosome stability mediated by histone variants H3.3 and H2A.Z. Genes Dev 21: 1519–1529. doi:10.1101/gad.1547707
      Abstract/FREE Full Text
    14. ↵
      Jin C, Zang C, Wei G, Cui K, Peng W, Zhao K, Felsenfeld G. 2009. H3.3/H2A.Z double variant-containing nucleosomes mark “nucleosome-free regions” of active promoters and other regulatory regions. Nat Genet 41: 941–945. doi:10.1038/ng.409
      CrossRefMedlineGoogle Scholar
    15. ↵
      Kim TH, Barrera LO, Zheng M, Qu C, Singer MA, Richmond TA, Wu Y, Green RD, Ren B. 2005. A high-resolution map of active promoters in the human genome. Nature 436: 876–880. doi:10.1038/nature03877
      CrossRefMedlineGoogle Scholar
    16. ↵
      Klemm SL, Shipony Z, Greenleaf WJ. 2019. Chromatin accessibility and the regulatory epigenome. Nat Rev Genet 20: 207–220. doi:10.1038/s41576-018-0089-8
      CrossRefMedlineGoogle Scholar
    17. ↵
      Kouzarides T. 2007. Chromatin modifications and their function. Cell 128: 693–705. doi:10.1016/j.cell.2007.02.005
      CrossRefMedlineGoogle Scholar
    18. ↵
      Langmead B, Salzberg SL. 2012. Fast gapped-read alignment with Bowtie 2. Nat Methods 9: 357–359. doi:10.1038/nmeth.1923
      CrossRefMedlineGoogle Scholar
    19. ↵
      Luger K, Mäder AW, Richmond RK, Sargent DF, Richmond TJ. 1997. Crystal structure of the nucleosome core particle at 2.8 Å resolution. Nature 389: 251–260. doi:10.1038/38444
      CrossRefMedlineGoogle Scholar
    20. ↵
      Mavrich TN, Jiang C, Ioshikhes IP, Li X, Venters BJ, Zanton SJ, Tomsho LP, Qi J, Glaser RL, Schuster SC, et al. 2008. Nucleosome organization in the Drosophila genome. Nature 453: 358–362. doi:10.1038/nature06929
      CrossRefMedlineGoogle Scholar
    21. ↵
      Mieczkowski J, Cook A, Bowman SK, Mueller B, Alver BH, Kundu S, Deaton AM, Urban JA, Larschan E, Park PJ, et al. 2016. MNase titration reveals differences between nucleosome occupancy and chromatin accessibility. Nat Commun 7: 11485. doi:10.1038/ncomms11485
      CrossRefMedlineGoogle Scholar
    22. ↵
      Oki S, Ohta T, Shioi G, Hatanaka H, Ogasawara O, Okuda Y, Kawaji H, Nakaki R, Sese J, Meno C. 2018. ChIP-atlas: a data-mining suite powered by full integration of public ChIP-seq data. EMBO Rep 19: e46255. doi:10.15252/embr.201846255
      Abstract/FREE Full Text
    23. ↵
      Ostapcuk V, Mohn F, Carl SH, Basters A, Hess D, Iesmantavicius V, Lampersberger L, Flemr M, Pandey A, Thomä NH, et al. 2018. Activity-dependent neuroprotective protein recruits HP1 and CHD4 to control lineage-specifying genes. Nature 557: 739–743. doi:10.1038/s41586-018-0153-8
      CrossRefMedlineGoogle Scholar
    24. ↵
      Papp B, Müller J. 2006. Histone trimethylation and the maintenance of transcriptional ON and OFF states by trxG and PcG proteins. Genes Dev 20: 2041–2054. doi:10.1101/gad.388706
      Abstract/FREE Full Text
    25. ↵
      Polishko A, Bunnik EM, Le Roch KG, Lonardi S. 2014. PuFFIN: a parameter-free method to build nucleosome maps from paired-end reads. BMC Bioinformatics 15: S11. doi:10.1186/1471-2105-15-S9-S11
      CrossRefGoogle Scholar
    26. ↵
      Pradhan SK, Su T, Yen L, Jacquet K, Huang C, Côté J, Kurdistani SK, Carey MF. 2016. EP400 deposits H3.3 into promoters and enhancers during gene activation. Mol Cell 61: 27–38. doi:10.1016/j.molcel.2015.10.039
      CrossRefGoogle Scholar
    27. ↵
      Ramachandran S, Ahmad K, Henikoff S. 2017. Transcription and remodeling produce asymmetrically unwrapped nucleosomal intermediates. Mol Cell 68: 1038–1053.e4. doi:10.1016/j.molcel.2017.11.015
      CrossRefGoogle Scholar
    28. ↵
      Torres IO, Fujimori DG. 2015. Functional coupling between writers, erasers and readers of histone and DNA methylation. Curr Opin Struct Biol 35: 68–75. doi:10.1016/j.sbi.2015.09.007
      CrossRefMedlineGoogle Scholar
    29. ↵
      Voong LN, Xi L, Sebeson AC, Xiong B, Wang J-P, Wang X. 2016. Insights into nucleosome organization in mouse embryonic stem cells through chemical mapping. Cell 167: 1555–1570.e15. doi:10.1016/j.cell.2016.10.049
      CrossRefMedlineGoogle Scholar
    30. ↵
      Wang Z, Zang C, Rosenfeld JA, Schones DE, Barski A, Cuddapah S, Cui K, Roh T-Y, Peng W, Zhang MQ, et al. 2008. Combinatorial patterns of histone acetylations and methylations in the human genome. Nat Genet 40: 897–903. doi:10.1038/ng.154
      CrossRefMedlineGoogle Scholar
    31. ↵
      Wen Z, Zhang L, Ruan H, Li G. 2020. Histone variant H2A.Z regulates nucleosome unwrapping and CTCF binding in mouse ES cells. Nucleic Acids Res 48: 5939–5952. doi:10.1093/nar/gkaa360
      CrossRefGoogle Scholar
    32. ↵
      Zentner GE, Henikoff S. 2013. Regulation of nucleosome dynamics by histone modifications. Nat Struct Mol Biol 20: 259–266. doi:10.1038/nsmb.2470
      CrossRefMedlineGoogle Scholar
    33. ↵
      Zhou X, Blocker AW, Airoldi EM, O'Shea EK. 2016. A computational approach to map nucleosome positions and alternative chromatin states with base pair resolution. eLife 5: e16970. doi:10.7554/eLife.16970
      CrossRefGoogle Scholar
    34. ↵
      Zou Z, Ohta T, Miura F, Oki S. 2022. ChIP-Atlas 2021 update: a data-mining suite for exploring epigenomic landscapes by fully integrating ChIP-seq, ATAC-seq and Bisulfite-seq data. Nucleic Acids Res 50: W175–W182. doi:10.1093/nar/gkac199
      CrossRefMedlineGoogle Scholar

    Articles citing this article

    • Structural Characterization of Native RNA Polymerase II Transcription Complexes and Nucleosomes in Drosophila melanogaster bioRxiv February 6, 2025 0: 2025.02.03.636274v2-2025.02.03.636274
    • Innovations in computational biology: RECOMB 2024 Special Issue Genome Res September 1, 2024 34: vii-viii
    | Table of Contents

    This Article

    1. Published in Advance June 17, 2024, doi: 10.1101/gr.279138.124 Genome Res. 34: 1334-1343 © 2024 Yang et al.; Published by Cold Spring Harbor Laboratory Press

    Article Category

    Share

    Preprint Server



    Navigate This Article

    Current Issue

    1. February 2026, 36 (2)
    1. Current Issue
    1. Alert me to new issues of Genome Research