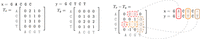Aligning distant sequences to graphs using long seed sketches
- Amir Joudaki1,2,5,
- Alexandru Meterez1,5,
- Harun Mustafa1,2,3,
- Ragnar Groot Koerkamp1,
- André Kahles1,2,3 and
- Gunnar Rätsch1,2,3,4
- 1Department of Computer Science, ETH Zurich, Zurich 8092, Switzerland;
- 2University Hospital Zurich, Biomedical Informatics Research, Zurich 8091, Switzerland;
- 3Swiss Institute of Bioinformatics, Lausanne 1015, Switzerland;
- 4ETH AI Center, 8092 Zurich, Switzerland
-
↵5 These authors contributed equally to this work.
Abstract
Sequence-to-graph alignment is crucial for applications such as variant genotyping, read error correction, and genome assembly.
We propose a novel seeding approach that relies on long inexact matches rather than short exact matches, and show that it
yields a better time-accuracy trade-off in settings with up to a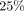 
mutation rate. We use sketches of a subset of graph nodes, which are more robust to indels, and store them in a k-nearest
neighbor index to avoid the curse of dimensionality. Our approach contrasts with existing methods and highlights the important
role that sketching into vector space can play in bioinformatics applications. We show that our method scales to graphs with
1 billion nodes and has quasi-logarithmic query time for queries with an edit distance of 
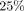. For such queries, longer sketch-based seeds yield a 
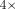increase in recall compared with exact seeds. Our approach can be incorporated into other aligners, providing a novel direction
for sequence-to-graph alignment.
Our work focuses on sequence-to-graph alignment, defined as aligning a query sequence to a sequence graph (Garrison et al. 2018; Ghaffaari and Marschall 2019; Rautiainen and Marschall 2020). Sequence-to-graph alignment involves finding the minimal number of editing operations to transform the query to a reference sequence encoded in the graph. Although there are various cost schemes for penalizing edits, edit distance assigns a cost of one to substitution, insertion, and deletion on the query.
Because the time complexity of optimal sequence-to-graph alignment grows linearly with the number of edges in the graph (Jain et al. 2020; Gibney et al. 2022), many approaches instead follow an approximate seed-and-extend strategy (Altschul et al. 1990), which operates in four main steps: (1) seed extraction, which in its simplest form involves finding all substrings with a certain length; (2) seed anchoring, finding matching nodes in the graph, (3) seed filtration, often involving clustering (Chang et al. 2020; Rautiainen and Marschall 2020) or colinear chaining (Almodaresi et al. 2021; Karasikov et al. 2022; Chandra and Jain 2023; Ma et al. 2023) of seeds, and (4) seed extension, involving performing semiglobal pairwise sequence alignment forward and backward from each anchored seed (Li 2013). We will review the usage of exact seeds used in tools such as vg (Garrison et al. 2018) and GraphAligner (GA) (Rautiainen and Marschall 2020) and discuss their limitations in a high mutation-rate setting.
The following example highlights the limitations of k-mers, defined as substrings with length k, as candidates for seeding:
(limitations of k-mer seeds). We have a reference sequence, denoted as S, that is uniformly drawn from the set of DNA nucleotides {A, C, G, T}. We create a query sequence q by copying a substring of S at some offset Δ and substituting each nucleotide independently with probability r. To retrieve the offset Δ using k-mer matches, at least one k-mer in the query must be copied without mutations. The probability of having at least one intact k-mer in the query is bounded by (|q| − k + 1)(1 − r)k by union bound. We also expect to have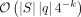 
matches between all pairs of reference and query k-mers owing to chance (for the formal analysis, see Supplemental Material A). Informally, we have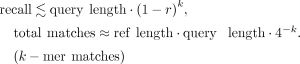
The simple setting in Example 1 illustrates the challenge many alignment methods face in trading off recall with time complexity. Because using a large k for seed length reduces the number of spurious matches, methods such as BWA-MEM (Li 2013), E-MEM (Khiste and Ilie 2015), deBGA (Liu et al. 2016), and PuffAligner (Almodaresi et al. 2021) find maximal exact matches (MEMs) between the read and the reference genome. However, the higher precision comes at the expense of fewer seeds and lower recall. For example, for k = 31, mutation rate r = 0.25, and query length 100 in Example 1, the expected recall is only (100)(1 − 0.25)31 ≈ 0.01.
The alternative is to use shorter seeds to increase the likelihood of finding accurate alignments. Methods that use de Bruijn graphs (DBGs) as a graph model (Bowe et al. 2012) or use an auxiliary index (Sirén 2017) are restricted to finding seeds of minimum length k. To find seeds when the query has a high edit distance relative to the reference sequences, sequence-to-graph alignment tools will either set k to a small value (Limasset et al. 2016; Garrison et al. 2018; Rautiainen and Marschall 2020) or use a variable-order DBG model (Boucher et al. 2015; Belazzougui and Cunial 2019; Karasikov et al. 2020, 2022) to also allow for anchoring seeds of length less than k (Karasikov et al. 2020, 2022). However, shorter seeds generally lead to a more complex and connected graph topology, which can lead to a combinatorial explosion of the search space. In the same setting as Example 1, with |S| = 109, |q| = 100 and k = 12, there will be approximately 109 · 100 · 4−12 ≈ 5960 matches owing to chance.
Because of the inherent shortcomings of short and long exact matches, Břinda et al. (2015) propose spaced seeds (Califano and Rigoutsos 1993; Pevzner and Waterman 1995; Ma et al. 2002; Burkhardt and Kärkkäinen 2003) to incorporate long seeds at higher mutation rates by masking out some positions in the seed. For example, using 0101 as a mask, “ACGT” will match with “GCAT.” Although spaced seeds were shown to be more sensitive than contiguous seeds without increasing the number of spurious matches, they assume that only mismatches occur in the alignment with no insertions or deletions (indels) (Mak et al. 2006). Another alternative to k-mers for sequence comparison is the use of strobemers (Sahlin 2021), which provide improved performance in terms of evenly distributed sequence matches and sensitivity to different mutation rates and match coverage across sequences.
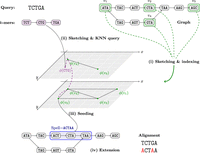
In this work, we propose using long inexact seeds based on tensor sketching (Joudaki et al. 2021). We use a succinct de Bruijn graph (DBG) (Bowe et al. 2012) as the graph model and preprocess it in two main stages: First, a subset of nodes in the DBG is sketched into a vector space, whereas insertions, deletions, and substitutions are approximately embedded into the ℓ2 metric. Second, to be able to efficiently retrieve similar sketch vectors, the sketches of nodes are stored in a hierarchical navigable small world (HNSW) (Malkov and Yashunin 2018) index. Aligning a query sequence involves three main stages: (1) Compute sketch vectors for all k-mers in the query; (2) use the HNSW index to find the nearest vectors as candidate seeds; and (3) extend these seeds backward and forward to find the best possible alignment. Figure 1 gives an overview of our sketch-based scheme.
Illustrating the four main stages of MG-Sketch for a sequence graph with k = 3 node lengths. (i) Preprocessing involves sampling a subset of nodes (highlighted in green) to ensure that every walk of length 3 contains at least one sampled node. Each sampled node is sketched using ϕ:Σk → R2, which approximates the edit distance. The sketches are stored in a hierarchical structure with multiple levels, and connections between nodes are navigated to refine nearest neighbor queries. (ii) Sketch every k-mer in the query (magenta) and find the nearest neighbors stored in the index. (iii) Seed an alignment at the node returned in the previous step. (iv) Extend forward and backward from each seed, finding the path in the graph that maximizes the alignment score of the query.
The main contributions of this work are showing that the tensor sketching method can be incorporated into a seed-and-extend sequence-to-graph alignment approach, which is a new direction for applying sketching methods in bioinformatics, and showing experimental results that show the effectiveness of our method in improving accuracy for high mutation rates, using both simulated and real meta-genome graphs.
Results
We implemented the MetaGraph Sketch (MG-Sketch) algorithm, which uses our novel sketch-based seeder, in the MetaGraph (Karasikov et al. 2020) framework. We primarily compare against MetaGraph Align (MG-Align) which is also implemented in MetaGraph but uses an exact seeding scheme. We compare MG-Sketch against GraphAligner (GA) (Rautiainen and Marschall 2020), vg map (Hickey et al. 2020), and VG MPMAP (Sibbesen et al. 2023) on both synthetic and real data sets (for more details, see Supplemental Material B).
Synthetic data generation
We generate a synthetic data set by initializing the sequence pool with 
, where s0 is a random sequence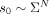 
, for some fixed length N ∈ N+. At each level i ∈ N+, we randomly mutate all sequences in the pool by independently substituting every character with 1% probability. We add the
mutated sequences to the pool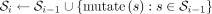 
, doubling the pool size. We repeat this process up to ℓ levels.
We build a DBG G using MetaGraph (Karasikov et al. 2020), on the synthetic sequences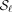 
with N = 1000 and k = 80. Recall that all sequences in Sℓ are of size N, resulting in O(2ℓN) nodes in the graph. Construction of Sℓ ensures that ∼1% of the nodes in G are “branching”; that is, they have at least one incoming or outgoing connection, thereby increasing the difficulty of the
sequence-to-graph alignment.
To create the ground truth sequences for alignment, we start with a random walk wi in the graph consisting of 250 edges. The reference sequences si are obtained by projecting the walk onto the graph, resulting in a spelled sequence of length |π(wi)| = 80 + 250 = 330. Because of the size of the graphs and number of branches in our experiments, it is highly unlikely that
the same path will be sampled multiple times. The query sequences qi are obtained by applying mutations with rates of 5%, 10%, 15%, 20%, and 25% to the reference sequences si, where each mutation is i.i.d. and with probability 
is a substitution, insertion, or deletion. Conceptually, the alignment method f takes the query qi and graph G as input and returns a candidate spell f(qi, G) as output. We quantify the optimality of f by measuring the edit distance between the reference and the candidate spell: ed(si, f(qi)). We define recall as ed(si, f(qi)) ≤ |si|λ, where λ ∈ [0, 1] controls the accuracy of the alignment (lower is more accurate). For all experiments, we set λ = 0.1.
Finally, we average the recall and alignment time per query over 500 samples at each mutation rate: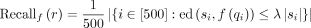 
.
Sketch-based alignment achieves high recall in high mutation settings
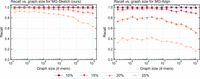
We show that MG-Sketch achieves a uniformly higher recall than MG-Align. Figure 2 shows that MG-Sketch outperforms MG-Align across all graph sizes, particularly in high mutation regimes. MG-Sketch reaches 3 × and 1.8 × higher recall than MG-Align on 25% and 20% mutation rates, respectively, while getting a comparable or better recall in all other cases. If MG-Align does not find exact 80-mer matches, it falls back to shorter seeds, until a minimum seed length of 15 is reached. If we compute the expected number of hits analogous to Example 1, we get (330/15)(1 − 0.25)15 ≈ 0.29. This is comparable to the empirical value for 25% mutation in Figure 2. Our results show that MG-Sketch exceeds this recall by a significant margin, highlighting the importance of long inexact seeds.
Recall achieved across different mutation rates with increasing graph sizes for MG-Sketch (left) and MG-Align (right). We run MG-Sketch with t = 6, w = 16, s = 8, D = 14, and K = 40 neighbors. Query generation follows the same approach as explained in the section “Synthetic data generation.” We omit the 0% and 5% mutation rates, as both methods achieve almost perfect recall.
Sketch-based aligner scales quasi-linearly with graph size
We show that the high accuracy of MG-Sketch does not compromise scalability. To compare the scalability of our approach, we measured peak memory usage and average alignment time per query for graphs with ℓ ∈ {4, …, 20}, as outlined in the section “Synthetic data generation.” This generates graphs with 16,000 up to approximately 1 billion k-mers, posing a challenge to the scalability of each method. We use the MetaGraph base graph for evaluating MG-Sketch and MG-Align (for more details, see Supplemental Material B).
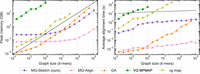
Peak memory usage scales linearly with graph size
Peak memory usage imposes a hard limit on the size of graphs that a method can preprocess. In Figure 3, we observe that peak memory usage in MG-Sketch scales linearly with the graph size. In particular, for graphs with more than 10 million nodes, MG-Sketch requires less memory than all other methods except MG-Align. For MG-Align, lower memory usage comes at the cost of lower recall compared with MG-Sketch. In contrast, VG MPMAP peak memory usage grows rapidly above 80 GB. Therefore, we only evaluate VG MPMAP for graphs with up to 1 million nodes. Although vg map requires less memory than VG MPMAP, the runtime exceeded 24 h for graphs with more than 60 million nodes. It is evident in Figure 3 that the peak memory usage of GA grows faster than linear, making MG-Sketch and MG-Align the only methods with linear memory complexity.
Peak RAM usage and query time versus graph size. Graphs are generated with k = 80 according to the section “Synthetic data generation.” We run MG-Sketch with t = 6, D = 14, w = 16, s = 8, and K = 10 neighbors, using query sequences with a mutation rate of 25%. Traces for VG MPMAP and vg map are incomplete as they exceed time or memory limit. (Left) Peak RAM usage versus graph size, with the black dashed line indicating linear memory complexity. (Right) Average alignment time versus graph size, with the black dashed line indicating logarithmic time complexity. For recall comparisons, see Figure 4.
Query alignment time grows quasi-logarithmically with graph size
Given that sequence graphs have billions of nodes, it is crucial for the alignment time to avoid growing linearly with the graph size. Figure 3 shows that MG-Sketch achieves an almost logarithmic scale with the graph size. In contrast, the average time for vg map and VG MPMAP grows much faster than logarithmic. The alignment time for GA also grows faster than linearly; however, this includes the preprocessing time for building the minimizer seeder from the graph.
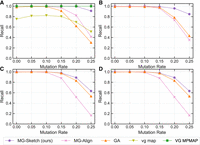
Notably, the scalability of MG-Sketch does not compromise the recall. Figure 4 shows that for all graph sizes and mutation rates, MG-Sketch achieves a higher or equal recall compared with that of the other tools, with the exception of VG MPMAP. Although VG MPMAP has higher recall at 25%, for graphs with over 1 million, it exceeds our memory limit of 80 GB.
Recall achieved across different mutation rates with increasing graph sizes for each baseline. The number of nodes in the graph for each plot is 100,000 (A), 10 million (B), 100 million (C), and 1 billion (D). Values are measured on the de Bruijn graph generated by MetaGraph. We run MG-Sketch with K = 40 neighbors and D = 14, w = 16, s = 8, t = 6. Query generation follows the same approach as explained in the section “Synthetic data generation,” with the mutation rates 0%, 5%, 10%, 15%, 20%, and 25%.
In scenarios with low mutation rates, as evident in Figure 2, both MG-Align and MG-Sketch achieve nearly perfect recall. However, MG-Align shows faster runtimes in these cases. The relatively slower performance of MG-Sketch in low mutation cases is owing to the extension from inexact sketch-based seeds. The relatively slower performance of MG-Sketch in low mutation cases is not unexpected, considering our primary focus is on high mutation scenarios in which most methods face challenges in achieving high recall.
Good scalability and recall translate into real-world applications
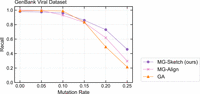
To show our approach in a more practical setting, we generated a pan-genome DBG containing 51,283 assembled virus genome sequences collected from the NCBI GenBank database (https://www.ncbi.nlm.nih.gov/genbank/) (Mustafa et al. 2018). Graph construction was performed using the MetaGraph framework, using a k of 80. The resulting graph contained 337,480,265 nodes. Similar to previous evaluations, we generated 500 query sequences by sampling random walks of length 330 from the graph, subsequently applying random mutations at rates ranging from 5% to 25%. Confirming our previous observations on scalability, the sketching-based approach was able to outperform both the MG-Align and GA approaches, starting from mutation rates of 10% and 15%, respectively (Fig. 5). Notably, for the highest mutation rate, MG-Sketch almost doubles the recall compared with the next best approach.
Seeding recall for the GenBank viral graph. Recall is shown for MG-Sketch, MG-Align, and GA as purple, pink, and orange lines, respectively, for query sets of increasing distance, simulated with a random mutation rate ranging from 0% to 25%.
Sketches linearly preserve mutation rate
Tensor sketching can be described as a dimensionality reduction technique for the tensor embedding of a sequence, which is defined as the number of occurrences of fixed-length t subsequences in the sequence (for details, see Methods). Unlike k-mers, subsequences can appear with an arbitrary number of gaps in between, making them more robust to local changes in the sequence. If we assume a constant subsequence length t = O(1), a single insertion, deletion, or substitution approximately affects O(1/n) fraction of subsequences, where n is the length of the sequence.
We can formalize this intuition under a random sampling and substitution-only mutation regime, by proving that the expected tensor embedding distance scales linearly with the mutation rate. Because tensor sketching approximates the tensor embedding distance, it approximately preserves the mutation rate while keeping the time complexity linear as a function of the sequence length and t. Define (normalized) tensor embedding distance dte between two sequences a and b as
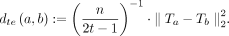(1)
The following lemma shows that tensor embedding approximates edit distance.
Tensor embedding preserves mutation rate (substitution only) under ℓ2 norm :: Let a be a uniform random sequence of length n in Σn, and for a given mutation rate r ∈ [0, 1], let b be a sequence where ai is substituted by a new character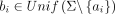 
with probability r and bi = ai otherwise. Then
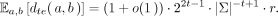(2)
Note that the 22t−1 factor does not depend on the sequences. Therefore, Lemma 1 provides a guarantee that the average distance of mutated pairs
remains within a linear estimate of the mutation rate. Observe that the edit distance in this setting will be approximately
nr. Therefore, we can, alternatively, refer to r as edit distance normalized by length. The proof of Lemma 1 is given in Supplemental Material C. For numerical validation of this bound, see Figure 6. Although Lemma 1 is stated for substitution-only mutations, tensor embedding and sketching linearly preserve general mutation
rates, including indels, up to a constant distortion factor (see Fig. 7).
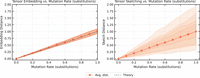
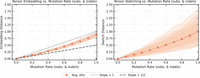
Comparison of expected distances for tensor embedding (left) and tensor sketching (right) as a function of the substitution mutation rate, for sequences of length n = 1000. Each data point is computed using 100 independent sequence pairs, and the process is repeated 100 times to compute the mean shown as the solid trace and the confidence interval shown as the shaded region, which covers the 5% − 95% range of the results. (Left) The solid trace shows the mean tensor embedding distance with t = 3, and the dashed trace shows the theoretical lower bound from Lemma 1. (Right) The solid trace shows the mean tensor sketch distance with t = 3 and D = 8, 16, 32, 64. The shaded regions correspond to increasing values of D, with the lightest shade corresponding to D = 8 and the darkest to D = 64.
Comparison of expected distances for tensor embedding (left) and tensor sketching (right) as a function of the substitution, insertion, and deletion mutation rate, with each mutation type having probability 
. The solid trace and shaded region show the mean and confidence interval, respectively, computed similarly to Figure 6, for sequences of length n = 1000. (Left) The solid trace shows the mean tensor embedding distance with t = 3, and the two dashed traces show the mean is between 1 and 1/2 slopes. (Right) The solid trace shows the mean tensor sketch distance with t = 3 and D = 8, 16, 32, 64. The shaded regions correspond to increasing values of D, with the lightest shade corresponding to D = 8 and the darkest to D = 64.
Discussion
In this work, we present a novel approach to sequence alignment called MG-Sketch that is resistant to mutations. Our method uses sketch-based seeds, and we show through theoretical analysis and empirical results that it scales to graphs with up to 109 nodes. Although MG-Align and MG-Sketch share the same extension algorithm, our sketch-based seeds significantly improve alignment recall in high mutation-rate regimes of >15%. Conversely, in scenarios in which exact matches can be constrained, such as low mutation-rate cases, MG-Align shows faster runtimes while producing recall results that are comparable to those of MG-Sketch. This is because MG-Align avoids the overhead associated with extending from inexact sketch-based seeds. We believe that sketching schemes that preserve edit distance, such as tensor sketching, offer a promising direction for pushing the boundaries of sequence analysis to higher variation settings.
In the following, we will compare and contrast our method with existing approaches, including discussing the strengths and weaknesses of each. Finally, we will explore potential avenues for future research in this exciting and rapidly evolving field.
Suffix array data structures
Applications of suffix array data structures, such as Burrows–Wheeler transform (BWT) (Burrows 1994) and FM-index (Ferragina and Manzini 2000), have improved the efficiency of sequence alignment and similarity searches by enabling the retrieval of matching substrings between a query and a sequence up to a fixed length k. The development of generalized suffix trees has extended this concept to sequence-to-graph alignment tools (Sović et al. 2016; Sirén 2017; Garrison et al. 2018; Minkin and Medvedev 2020), allowing them to construct an index of graph nodes to identify candidate matches for seed-and-extend. However, our work focuses on the high mutation regime, where these substring matching methods are inherently ill-suited, as we show in Example 1 and in our empirical evaluation presented in Results. In other words, although BWT and suffix array data structures have been transformative in sequence analysis, they struggle to handle highly mutated sequences. Our work presents a new approach that is optimized for these challenging scenarios.
Minimizers
Minimizers are a powerful technique for compressing sequence data without sacrificing crucial information. This approach has been used in many popular bioinformatics tools (Li 2013, 2016, 2018). Another concept that builds on the idea of minimizers is the notion of syncmers (Edgar 2021), but they modify the sampling criteria to ensure selection only depends on the k-mer content.
Although we have not explored minimizers or syncmers in this work, using minimizers in MG-Sketch can balance the trade-off between query processing time and accuracy by replacing the k-cover in MG-Sketch with minimizer-based sampling criteria and, consequently, fewer KNN queries and fewer attempted extensions. One natural minimizer criterion can be selecting a random orientation v in Rd and choosing the node with the minimum inner product value in a local neighborhood of the graph. This approach shows promise as a potential avenue for future research.
Spaced seeds
Spaced seeds are a powerful tool for improving sensitivity in homology search and alignment, defined as a pattern of relevant
and irrelevant positions (Ma et al. 2002; Langmead and Salzberg 2012; Břinda et al. 2015). However, spaced seeds have two main limitations. First, they are not sensitive to indels. In our mutation model, in which
edit operations are equally likely, we expect to see approximately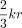 
indels in every k-mer, which limits the effectiveness of spaced seeds when 
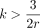. The second shortcoming of spaced seeds is that using a single seed may increase the risk of no matches. To mitigate this
risk, Pattern Hunter II proposed using a set of spaced seed patterns (Li et al. 2004). However, finding an optimal set of spaced seeds is an NP-hard problem, and even finding a set of “good” spaced seeds is
challenging (Choi and Zhang 2004; Choi et al. 2004). In the sequel, we discuss how sketching into a vector space can help circumvent this problem.
Indel-tolerant sketching
Sketching the edit distance remains a fundamental challenge for sequence analysis. To address this, several sketching methods have been developed, including Order Min Hash (OMH) (Marçais et al. 2019), strobemers (Sahlin 2021), and tensor sketching (Joudaki et al. 2021), all of which sketch noncontiguous parts of the string. In this context, it is informative to compare these methods and contrast their differences. In Strobemers of order t, the ℓ-mers of a sequence are considered in a series of nonoverlapping windows, and t ℓ-mers that minimize a hash value are subsampled and concatenated. In OMH of order t, ℓ-mers of a sequence are sampled according to a total order and concatenated to produce the hash. The total order ensures that the t-tuple of ℓ-mers is uniformly drawn from the set of all ordered tuples.
It is worth noting that when ℓ = 1, tensor sketch is highly similar to OMH and Strobemers, as all methods approximate the distance of ordered tuples between two strings. However, when ℓ > 1, OMH and Strobemers become insensitive to higher mutation rates, as a single mutation can affect 2ℓ − 1 different ℓ-mers.
One advantage of Strobemers is that the distance between consecutive selected substrings has a uniform distribution under random sequence distribution, a property not guaranteed by OMH and tensor sketch. However, the fixed definition of windows in Strobemers relative to the starting position makes it more sensitive to frame-shifts compared with OMH and tensor sketch.
Future study of MG-Sketch
Sketching into Rd
Our work shows the promising potential of sketching genomic data into vector spaces, a finding that has been supported by recent work in this area (Zhao et al. 2022). In light of these results, it may be helpful to broadly group sketching methods into “hash-based” and “vector-based” sketching schemes. Although hashes provide a binary hit-or-miss result, vector spaces offer a more nuanced representation of genomic data.
Consider hash-based sketch ϕh(x): = (xi)i∈h, where h is randomly drawn from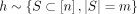 
, and vector-based sketch 
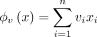, where 
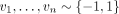are random sign hashes. If we randomly draw 
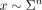and mutate y by substituting each position with a probability of r, the expected hash-based similarity is Eh[ϕh(x) = ϕh(y)] = (1 − r)m, whereas the expected vector-based sketch distance is Ev[(ϕv(x) − ϕv(y))2] = r.
We can see that (1 − r)m is not sensitive to higher mutation rates when r > 1/m. Therefore, our work highlights the potential of vector-based sketches as a promising direction for future research in the genomics field. The benefits of vector sketches come at the expense of additional complexity in similarity searches in high dimensions, known as curse of dimensionality, which will be discussed next.
Hardware optimization
Despite the curse of dimensionality, recent developments in search indices, such as HNSW (Malkov and Yashunin 2018), have made it possible to apply vector space searching to billions of samples in high dimensions. Vector representations are also more amenable to hardware-optimized operations, which is a potential advantage. Our approach uses Facebook AI Similarity Search (FAISS) (Johnson et al. 2019) and tensor sketching, both of which are optimized for GPUs, enabling efficient data parallelism. In fact, our CUDA-optimized tensor sketching implementation is 200 × faster than the single-threaded CPU implementation (https://curiouscoding.nl/posts/numba-cuda-speedup/). By leveraging the CUDA-optimized implementations of FAISS and tensor sketching, we can take advantage of data parallelism on GPUs, resulting in improved performance and efficiency. Thus, hardware optimizations have become increasingly important in genomics research, and our approach takes advantage of the latest hardware innovations to deliver more efficient and effective results.
Seed filtering and chaining
There are also several areas for improvement that are beyond the scope of this work. For instance, we have not implemented any seed filtering techniques such as colinear chaining (Li et al. 2020; Almodaresi et al. 2021; Karasikov et al. 2022; Chandra and Jain 2023; Ma et al. 2023). These approaches use a cut-off threshold rather than the number of neighbors for anchoring, which can reduce the number of anchors in sparse areas of the sketch space and decrease the number of false matches. Additionally, other subsampling methods such as spaced-minimized subsampling (Roberts et al. 2004; Vaddadi et al. 2019; Ekim et al. 2021) may provide additional benefits.
Theoretical guarantees
One desirable aspect of sketch-based methods is that they are randomized algorithms. Thus, one can improve recall through multiple independent runs and ensure theoretical guarantees such as those in Lemma 1. Further investigation of the guarantees of MG-Sketch may reveal additional insights, such as a probabilistic bound on deviations for tensor sketching and the inclusion of indels in the analysis.
Methods
Preliminaries
Terminology and notation
We use [N]: = {1, …, N}. Σ denotes the alphabet, for example, the nucleotides {A, C, G, T}, or amino acids. For k ∈ N+,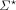 
denotes the set of all strings over Σ, and Σk denotes the subset of all strings with length k. Throughout the text, we use the terms string and sequence interchangeably to refer to members of 
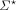. q[i] and qi denote the ith character of the sequence, and q[i:j]: = qiqi+1…qj denotes the sliced substring from i, up to j. k-mers(s) denote the substrings of length k in string s:k-mers(s): = {s[i:i + k − 1]:1 ≤ i ≤ |s| − k + 1}. p° q denotes the concatenation of p and q. The edit distance ed(p, q), also referred to as the Levenshtein distance (Levenshtein et al. 1966), is defined as the minimum number of insertion, deletion, and substitution operations needed to transform one sequence into
the other. The normalized edit distance is defined as edit distance divided by maximum length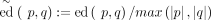 
. Throughout the paper, the term “mutation” refers to the normalized edit distance, serving as an abstraction for the combined
biological sources of variation and errors in sequencing.
Succinct DBG
The reference DBG is a directed graph over the reference sequences that encodes all substrings of length k as vertices and all substrings of length k + 1 as directed edges. Formally, let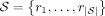 
be the input sequences. The reference graph is a directed graph G = (V, E), with vertices 
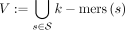and edges E: = {(u, v, v[k]) ∈ V × V × Σ:u[2:k] = v[1:k − 1]}. The label of edge e = (u, v, v[k]) ∈ E is denoted by le: = v[k] ∈ Σ.
Sequence-to-graph alignment
Define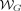 
as the set of all walks, where each walk 
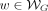is defined as a list of adjacent edges w = ((v0, v1, l1), …, (v|w|−1, v|w|, l|w|)) ∈ E|w|. Define the spelling of a walk as the concatenation of the first k-mer on the walk, with the labels of the rest of the edges on the same walk 
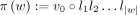. Thus, given the query sequence 
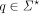and the reference graph G, an optimal alignment belong to the set of walks that achieve the minimum edit distance between the query sequence and the spelling of the walk
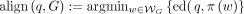. Note that align(q, G) is defined as a set, rather than a single walk, because multiple walks can achieve the minimum value.
Estimating edit distance using tensor sketch
Our approach to the seed extraction and anchoring steps of seed-and-extend (see Introduction) is based on an index of k-mer sketches rather than k-mers. Briefly, we compute tensor sketches (Joudaki et al. 2021) of the graph nodes and store them in a nearest-neighbor search index (Johnson et al. 2019) that maps each sketch to its corresponding graph node.
Tensor sketching maps sequences to a vector space that embeds the edit distance into the ℓ2 metric. Conceptually, tensor sketching can be described in two steps: (1) tensor embedding, which counts how many times each subsequence appears in the sequence, and (2) implicit tensor sketching, which lowers the dimension without constructing the larger tensor embedding space.
Tensor embedding
Given sequence a ∈ Σn, define I as set of increasing subsequences of length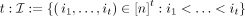 
, and for all s ∈ Σt, define tensor embedding Ta[s] as the number of occurrences of s as a subsequence in a:
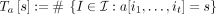. We can view Ta as a |Σ|t-dimensional tensor, with the alphabet as its indices. Given sequences a, b, we approximate the edit distance by 
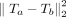up to a constant factor. Figure 8 illustrates how the embedding distance approximates edit operations.
Tensor embedding illustration for t = 2. Observe that the substitution, insertion, and deletion correspond to blocks of nonzero elements in the difference tensor.
Tensor sketching
Tensor sketching is an implicit, Euclidean-norm-preserving dimensionality reduction scheme. Crucially, it projects |Σ|t-dimensional tensors onto constant D ∈ N+ dimensions and linearly preserves ℓ2 distances. We define the tensor sketching function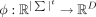 
, which embeds an |Σ|t-dimensional tensor into RD. Given pairwise independent hash functions hi:Σ → [D] and si:Σ → { − 1, 1}, define the tuple hash 
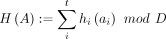and tuple sign hash 
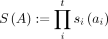, where A = (ai)i≤t ∈ Σt. Finally, the tensor sketch ϕ for a tensor 
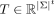is defined as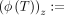 
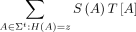for all z ∈ [D].
Crucially, we have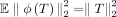 
and bounded second moments 
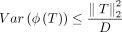(see lemma 7 of the work by Pham and Pagh 2013). Figures 6 and 7 show that sketch distance approximations of embedding distances improve with respect to the sketch dimension D.
It is important to note that although computing ϕ(T) for a general tensor T takes |Σ|t time, when T is the tensor embedding of a string T: = Tx, computing ϕ(Tx) can be performed without ever constructing the tensor Tx. Figure 9 illustrates the main ideas behind “implicitly sketching” when H is a rank-1 tensor. This illustrates that the embedding of x, which is constructed by appending a character to x′, can be written as sum of the embedding of x′, implying that we can compute the sketch recursively (for details, see implicit sketching in section 2.2 of the work by Joudaki et al. 2021). Figures 6 and 7 show that the sketch distance approximation of embedding distance improves with respect to the sketch dimension D.
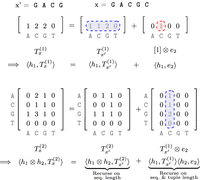
Implicit sketching when the sketch tensor is rank-1.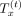 
denotes the tensor embedding of order t:
, and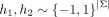 
denote sign hashes. e2 = [0, 1, 0, 0] is the indicator corresponding to the appended character “C.”
Finally, Joudaki et al. (2021) report that tensor slide sketch (TSS), which concatenates tensor sketches of windows w, using a stride Δ within a given k-mer, improves the sensitivity to smaller edit distances. Therefore, we used TSS for our seeding scheme (for more details, see Supplemental Material D).
Anchoring seeds with a hierarchical search index
The final preprocessing step is to build a k-nearest neighbor index of sketches. Conceptually, we can represent the search index as a function from vector space RD to a list of graph nodes K-NN(v) = (v1, …, vK), for some predetermined number of neighbors K ∈ N+. During the alignment, we anchor every seed in the query s ∈ k-mers(q) to the vertices returned by the index K-NN(ϕ(s)).
Note that if v and u are within s steps on the graph, they share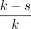 
of their sequence content. To avoid indexing redundant information, we only store a k-cover of the graph, defined as a subset of vertices such that any walk on the graph with more than k nodes contains at least one node in the k-cover. For any walk 
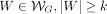, it holds that 
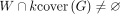. Observe that if the optimal alignment walk for a query has more than k nodes, it suffices to sketch the k-cover to anchor at least one of its seeds.
Although sketch vectors are more robust to mutations than exact seeds, retrieving nearest neighbors in a high-dimensional space faces the curse of dimensionality (Köppen 2000). Locality sensitive hashing (Indyk and Motwani 1998; Datar et al. 2004) is the first method to get a constant approximation for the nearest neighbors problem, with a theoretically proven sublinear time with respect to data set size. However, to scale to billions of nodes in the genome graphs, it is crucial to store sketch vectors in a HNSW index (Malkov and Yashunin 2018). We use the efficient implementation of HNSW from FAISS (Johnson et al. 2019). The pseudocode for the anchoring is presented in Algorithm 1.
Anchoring
Input: De Bruijn graph G(V,E)
Query q∈Σ*
Output: Anchors A⊆k-mers(q) × VK
Parameter: Neighbors K∈N+
H ← HNSW()
for v in k-cover(G) do
Φ ← Sketch(v)
H.add(Φ)
end
A ← {}
for s in k-mers(q) do
Φ ← Sketch(s)
A ← A∪ {(a,H.KNN(Φ))}
end
Return: A
Adjusting extension for misaligned anchors
MG-Align follows a seed-and-extend approach, with a dynamic program to determine which path to take in the graph, producing a semiglobal alignment. We made a few modifications to adjust for misaligned anchors in the MG-Sketch seeder. To show this issue, let v1, v2, …, vM denote a list of adjacent k-mers on the graph, and let s1, …, s|q|−k+1 denote seeds in the query si: = q[i:i + k − 1]. Let us assume that if si is anchored to vj, the alignment will be optimal. Observe that ed(si, si+δ) ≤ 2δ, obtained by deleting the initial δ characters from si and inserting the last δ characters of vi+δ. By the triangle inequality, if ed(si, vj) ≤ d, it holds that ed(si+δ, vj) ≤ d + 2δ. Although tensor sketching preserves the edit distance, owing to inherent stochasticity in sketching and retrieval, si+δ may be anchored to vj instead of si to vj. This may produce an additional cost of 2δ during the forward and backward extension. To avoid this unnecessary cost, during the forward extension, indels occurring in the beginning of the query are free. If the forward extension completes, we initiate the backward extension from the position of the first matching positions.
Software availability
The implementation of our method is available as open source software at GitHub (https://github.com/ratschlab/tensor-sketch-alignment/). The code required to reproduce the experiments is available on the main repository, and as Supplemental Code.
Data access
The raw data used in this manuscript have been synthetically generated and are available at Zenodo (https://doi.org/10.5281/zenodo.7769367). The code to generate the synthetic data is available as Supplemental Code. The data used in Figure 5 are an assembly of 51,283 virus genomes. The assembly and the individual accession number of each viral genome in the assembly are available at https://public.bmi.inf.ethz.ch/projects/2018/graph-anno/fasta/virus50000/.
Competing interest statement
The authors declare no competing interests.
Acknowledgments
A.J. is funded through Swiss National Science Foundation Project grant no. 200550 to A.K. H.M. is funded as part of Swiss National Research Programme (NRP) 75 “Big Data” by the SNSF grant no. 407540_167331. A.J., H.M., and A.K. are also partially funded by ETH core funding (to G.R.). R.G.K. was funded through an ETH Research grant (ETH-17 21-1) to G.R.
Author contributions: A.J. and A.M. came up with the conceptual and experimental design with help from H.M.; A.M. implemented the method advised by H.M. and A.J.; A.J. and R.G.K. proved Lemma 1; and A.J. and A.M. drafted the manuscript with help from A.K., G.R., H.M., and R.G.K.
Footnotes
-
[Supplemental material is available for this article.]
-
Article published online before print. Article, supplemental material, and publication date are at https://www.genome.org/cgi/doi/10.1101/gr.277659.123.
- Received January 5, 2023.
- Accepted April 16, 2023.
This article is distributed exclusively by Cold Spring Harbor Laboratory Press for the first six months after the full-issue publication date (see https://genome.cshlp.org/site/misc/terms.xhtml). After six months, it is available under a Creative Commons License (Attribution-NonCommercial 4.0 International), as described at http://creativecommons.org/licenses/by-nc/4.0/.
