Fast inference of genetic recombination rates in biobank scale data
Abstract
Although rates of recombination events across the genome (genetic maps) are fundamental to genetic research, the majority of current studies only use one standard map. There is evidence suggesting population differences in genetic maps, and thus estimating population-specific maps, are of interest. Although the recent availability of biobank-scale data offers such opportunities, current methods are not efficient at leveraging very large sample sizes. The most accurate methods are still linkage disequilibrium (LD)–based methods that are only tractable for a few hundred samples. In this work, we propose a fast and memory-efficient method for estimating genetic maps from population genotyping data. Our method, FastRecomb, leverages the efficient positional Burrows–Wheeler transform (PBWT) data structure for counting IBD segment boundaries as potential recombination events. We used PBWT blocks to avoid redundant counting of pairwise matches. Moreover, we used a panel-smoothing technique to reduce the noise from errors and recent mutations. Using simulation, we found that FastRecomb achieves state-of-the-art performance at 10-kb resolution, in terms of correlation coefficients between the estimated map and the ground truth. This is mainly because FastRecomb can effectively take advantage of large panels comprising more than hundreds of thousands of haplotypes. At the same time, other methods lack the efficiency to handle such data. We believe further refinement of FastRecomb would deliver more accurate genetic maps for the genetics community.
A genetic map for a population or a species contains the locations of genetic markers or variant sites in relation to one another based on the probability of recombination, rather than a physical location along each chromosome. An accurate genetic map, which is an estimation of the recombination rates along a chromosome, serves as the foundation for genetic studies like gene mapping, population genetics, and genealogical studies. Given that recombination rates differ between populations, the estimation of population-specific genetic maps is crucial for advancing genetic research, particularly in diverse populations.
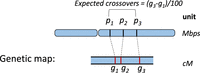
The genetic map is measured in centimorgans (cM), where a 1-cM genetic distance between two loci represents a 1% chance of recombination occurring between two loci during each meiosis. In the human genome, 1 cM roughly equates to 1 Mbp. The recombination rates may considerably vary within 1 Mbp, and the average of 1 cM equal to 1 Mbp may not hold at fine-scale (high) resolutions (see Fig. 1). Some regions may also have significantly different recombination rates than the average.
An example of a genetic map for a chromosome. The expected average number of intervening crossovers in a generation within (p1, p2) and (p1, p3) are (g2 − g1)/100 and (g3 − g1)/100, respectively.
The traditional approach to infer the recombination rates is to use genotype data from a large number of parent–offspring pairs to capture an adequate number of meiotic crossover events (Kong et al. 2010; Halldorsson et al. 2019). Fine-scale pedigree-based recombination rates from deCODE (Halldorsson et al. 2019) are widely used. However, it is increasingly recognized that recombination rates vary from population to population (Spence and Song 2019). Collecting a large number of parent–offspring pairs can be a practical bottleneck for most populations. An alternative approach is to use a single human sperm cell referred to as sperm-typing (Jeffreys et al. 1998; Jeffreys et al. 2001). A semen sample represents a significant portion of the meiotic crossover events because it contains hundreds of millions of sperm. Sperm-typing can predict a person's unique recombination rate. However, at high resolution, the rates may not always remain consistent with other individuals within the population. The sperm-typing is also a time-intensive and money-consuming process.
Another approach involves using population samples (Fearnhead and Donnelly 2001; Li and Stephens 2003; McVean et al. 2004; Kuhner 2006; Chan et al. 2012; Barroso et al. 2019). Recombination event signals in population samples are dispersed among the individuals. Not all recombination event signals, however, are correlated with the current genetic map because crossovers could have introduced them in the distant past. An early method based on population samples, LDhat, uses linkage disequilibrium (LD) patterns for fitting a Bayesian model via MCMC (McVean et al. 2004). Although the results of LDhat are noteworthy, the limitations related to the computational tractability issues are significant as its capacity is restrained to a maximum of several hundred haplotypes. It is anticipated that the methods that can leverage large samples may achieve superior performance.
Recently, IBDrecomb (Zhou et al. 2020) was developed to leverage the recent development of fast identity-by-descent (IBD) segment calling methods. IBD segments are identical DNA fragments that are inherited from a common ancestor. Under the assumption that the IBD segment boundaries were caused by recombination events, IBDrecomb counts the IBD segment boundaries and generates a map iteratively using the normalized counts of the IBD segments. However, IBDrecomb is not adequately efficient as it requires outputting all pairwise IBD segments, which is not conducive for biobank-scale cohorts. Here, we introduce a novel approach that efficiently identifies potential recombination breakpoints in very large cohorts using the positional Burrows–Wheeler transform (PBWT). Our method is the first to directly use PBWT to estimate recombination rate. To enable accurate recombination rate estimation, we have the following methodological innovations and contributions: (1) Our method bypasses calling pairwise IBDs (e.g., IBDrecomb) to achieve the needed efficiency crucial for large cohorts; (2) the crossovers are counted by minor allele counts within individual PBWT blocks, which is efficient while avoiding overcounting; and (3) to avoid fragmenting PBWT blocks owing to genotyping errors and recent mutations, we leveraged P-smoother. Our results confirmed the effectiveness of P-smoother.
Methods
Preliminaries
Positional Burrows–Wheeler transform
The PBWT (Durbin 2014) facilitates an efficient approach for finding haplotype matches and also compression of haplotypes in large biobank-scale cohorts. The underlying idea of PBWT is to store the haplotype sequences based on their reversed prefix order. Following Durbin's notation (Durbin 2014), we define a panel of haplotype sequences X, where X is a two-dimensional matrix. Xk represents the values of haplotypes at the site k and X = [X0, X1, …XN−1], where N denotes the number of sites. Xk is an array with M entries, where M denotes the number of haplotype sequences. We also assume the entries of the array Xk are binary.
Prefix array and PBWT matrix
The sequence indices sorted at each site k are referred to as the positional prefix array ak. PBWT matrix y stores the values of haplotype sequences in the reversed prefix order at each site. If divergence values and the haplotype sequences X are stored, there will be no need to store the PBWT matrix, and the values at a site k for each haplotype i can be queries (yk[i] = Xk[ak[i]]).
Divergence array
Divergence array dk at each variant site k for every haplotype stores the starting position of the match between the haplotype with its preceding haplotype sequence in the reversed sorted order up to the site k − 1. The divergence value keeps track of the starting site index of the longest match for each haplotype. We refer to the value of the divergence array for each haplotype as its divergence value. dk is used to both identify a long match with a length ≥L and determine the starting position of the match.
Haplotype matching blocks for efficient identification of long matches
PBWT facilitates an efficient approach to enumerate all pairwise haplotype matches longer than a given length. Although Durbin's
algorithm outputs all pairwise matches in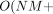 
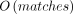, a block-based approach (Alanko et al. 2020; Naseri et al. 2020; Williams and Mumey 2020) can enumerate all matching blocks without explicitly outputting all pairs in O(NM). By sorting the haplotype sequences based on their reversed prefix order, the longest match for each haplotype sequence
is placed in the adjacent position. Moreover, all pairwise haplotype sequences at the site k that are identical for at least L sites from k are separated by a haplotype sequence j with the condition dk[j] > k − L (Durbin 2014). We define a L-block at a site k as a set of haplotype indices that share long matches with each other ending at site k with a minimum length of L. All L-blocks at any site k may be efficiently scanned by consensus PBWT algorithms (Alanko et al. 2020; Naseri et al. 2020; Williams and Mumey 2020).
PBWT smoothing for reducing mismatches owing to errors and mutations
The original PBWT scans the haplotype sequences starting from the first site. The divergence and positional prefix arrays are calculated at each site, and the matches starting from the previous sites can be enumerated at each site. PBWT cannot tolerate mismatches in long matches. As a result, the long matches harboring mismatches will be discarded or reported partially depending on the minimum cutoff length. The bidirectional PBWT data structures (Naseri et al. 2021b), on the other hand, provide an efficient approach to tolerate possible mismatches in the middle of long matching blocks.
To tolerate genotyping errors, the haplotype panel is smoothed using bidirectional PBWT. The preprocessing step alternates the alleles that are different in the middle of matching blocks of haplotypes. The smoothing procedure (P-smoother) only alternates the minor alleles if the minor allele frequency is below a certain threshold (with the minor allele frequency threshold equal to 5% by default) in the matching blocks. This allows our method to be highly error-tolerant and to maintain accuracy even when subjected to genotyping errors.
Inferring recombination rates
Similar to pedigree-based (Halldorsson et al. 2019) and population-based inference (Zhou et al. 2020) methods, we use an iterative approach to count crossover events of a certain type at each bin (or window) across the genome. To estimate the recombination rates efficiently, crossover events should be counted efficiently and unbiased across the genome. Instead of counting all IBD segment boundaries, we count the boundaries of diverging haplotypes across all matching blocks in each bin. Haplotypes diverging at site k are defined as the haplotypes that are matching with at least one other haplotype until the site k − 1, and the match between the haplotype and other haplotypes in the block terminates at the site k. We consider that haplotypes in a block are split into two clusters, one having the major allele and the other the minor allele at site k. We can call the haplotypes carrying the minor allele as diverging from the block with haplotypes carrying the major alleles.
Given a haplotype panel comprising N sites, the recombination rates are calculated for each window in terms of physical distances (default, w = 5000). We assume that the total genetic length in centimorgans is known or specified by the user. This assumption is commonly
held for indirect inference of recombination rates (Zhou et al. 2020). If the total genetic length is not correctly specified, the estimated rates will be biased toward the total genetic length
bias. The bias should be proportional to the misspecified total genetic length. We iterate over the sites, and the number
of minor alleles for haplotypes within any L-block are counted. The number of total recombination events in each window is simply the sum of all minor allele counts from
the sites in the window i. Our approach avoids enumerating all pairwise haplotype matches at each site. Please note that the time complexity of enumeration
of all pairwise matches, especially for very short segments could be theoretically quadratic. Theoretically, the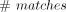 
could be O(M2) for very short matches. Our method only iterates over the haplotypes at each site and computes the number of minor alleles
in each block. In addition, the divergence values for the haplotypes with the minor alleles are then considered to update
the value for the preceding windows containing their divergence values. The overall time complexity of our method is O(NM), where N denotes the number of sites and M denotes the number of haplotypes.
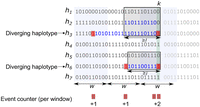
Figure 2 shows an example of a haplotype panel sorted by their reversed prefix order at the site k. The haplotypes marked with a red cross at the site k are being considered in the calculation of recombination events. For each L-block, the haplotypes with minor alleles are considered, and the allele count for the window overlapping with their divergence value is updated. Each block is likely derived from a different genealogical branch. The ancestral accumulation of recombination events is therefore controlled by considering L-haplotype blocks. Algorithm 1 describes the procedure of counting possible recombination events at each window using PBWT arrays. The array g[i] contains the genetic location of the site i. L denotes the minimum genetic length for a match. As we iterate over the haplotypes in the reversed prefix order, the condition g[dk[j]] > g[k] − L triggers the enumeration of possible recombination events. The array count stores the total count of recombination events (minor allele counts) for each window. The array pos contains the genomic (physical) position of the sites.
A snapshot of the FastRecomb algorithm for counting potential recombination events at the variant site k. When sweeping through the PBWT panel, haplotypes are sorted by their reverse suffix ending at site k. FastRecomb identifies diverging haplotypes, that is, haplotypes carrying minor alleles at site k in all l-blocks (boxes) ending at site k. Then, both ends (red shading) of the current match (blue) of a diverging haplotype with other haplotypes of the block will trigger a potential crossover event. All events are captured by “event counter” ϕi and ρi for each window i of length w.
countAltAlleles
for k = 1 to N do
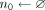
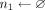
for j = 1 to M do
if g[k] − g[dk[i] < L than
if |n0|>0 and |n1| > 0 then
count[pos[k]/w] ← count[pos[k]/w] + min(|n0|, |n1|)
if min(|n0|, |n1|) == |n0| then
for i in n0 do
count[pos[dk[i]]/w] ← count[pos[dk[i]]/w] + 1
else
for i in n1 then
count[pos[dk[i]]/w] ← count[pos[dk[i]]/w] + 1
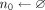
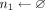
if Xk[ak[j]] == 0 then
n0.add(j)
else
n1.add(j)
The recombination rate for each window i is calculated by the formula
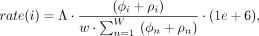where Λ denotes the total chromosome length in centimorgans, and w is the window size in terms of physical distance (in base pairs). ϕi represents the sum of minor allele counts in matching blocks across all sites in the ith window. ρi denotes the sum of diverging haplotypes with their diverging values located within the ith window. We start with a simple assumption of a constant recombination rate across the chromosome (1 cM ≈ 1 Mbp). In the
first iteration, the matches are considered by assuming the minimum length is in mega-base pairs. In each iteration, for each
window, the average between the current calculated rate from the previous iteration is considered.
Results
Simulation
We simulated 1 million haplotypes of European and African ancestry using the deCODE genetic map (Kong et al. 2010). The OutOfAfrica_2T12 model in stdpopsim (Adrion et al. 2020) was used to simulate haplotypes of Chromosome 20 with the following command line:
-
stdpopsim HomSap -c chr20 -d OutOfAfrica_2T12 -g DeCodeSexAveraged_GRCh36 500000 500000
stdpopsim uses the coalescent simulator msprime (Kelleher et al. 2016) as its simulator engine. The variant sites with an allele frequency of less than 0.05 were filtered out. The total number of variant sites after the MAF filter was 66,546. We also inserted different genotyping errors into the simulated panel.
Evaluation of estimated rates
To evaluate the performance of our method, FastRecomb (for source code, see Software availability), the Pearson correlation coefficients for different base (b) resolutions were calculated. The highest resolution was set to 10-kb, which was the resolution of the genetic map in deCODE (GRCh36). We compared the performance of FastRecomb with IBDrecomb and LDhat. The current implementation of FastRecomb does not treat the end-regions differently as was performed in IBDrecomb. As a result, the values for the end-regions may not be optimal. Here, we focus on the inferred recombination rates in the mid-region (excluding 5 Mbp from both sides of the chromosome). For FastRecomb, we first ran P-smoother (Yue et al. 2022) with the parameters L′ = 20, W′ = 20, g = 1, MAF = 5% and then ran FastRecomb with the parameters L = 66.3, d = 0.5, w = 5000, r = 5. r denotes the number of iterations, and d denotes the minimum target length in centimorgans. For LDhat, we ran the interval method with a block penalty of five and for 22.5 million iterations with a sample being taken every 15,000 iterations. For IBDrecomb, we ran refined-ibd (Browning and Browning 2013) with a minimum LOD score of one and a minimum IBD segment length of 0.3 cM. We then ran merge-ibd-segments with a gap of 0.6 cM and discord of one. Because of the resource-intensive and run time requirements of LDhat and IBDrecomb, we used only 192 and 5000 haplotypes, respectively. For LDhat, 192 haplotypes were the largest number of haplotypes for which a pre-omputed likelihood lookup table was available. For IBDrecomb, 5000 haplotypes were the size of the simulated data in their study. We also tried running refined-ibd on 100,000 haplotypes, and the program had not terminated after a month of running.
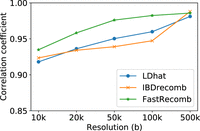
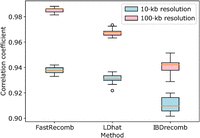
Figure 3 shows the correlation coefficients of the three methods for the mid-region (excluding 5 Mbp from both ends of the chromosome). No genotyping errors were added to the haplotype panel. FastRecomb performs better than other methods for the mid-region in different resolutions. For 500-kb resolution, all the methods achieve a high correlation coefficient close to one. We also analyzed the five highest recombination rate locations in deCODE (Chr 20) to examine how the hotspots are replicated. We compared the top five recombination rates inferred by different tools to deCODE using different distance cutoffs. Two from FastRecomb and IBDrecomb and one from LDhat regions were within 10,000 of the five deCODE hotspots. FastRecomb, IBDrecomb, and LDhat scored three, two, and two for a distance cutoff of 400,000, respectively. Running on an eight-core 2.10-GHz Intel Xeon E5-2620 v4, LDhat (interval + stat) took 2.39 CPU h, IBDrecomb (refined-ibd + IBDrecomb) took 83.6 CPU h (∼3.25 wall-clock h), and FastRecomb (P-smoother + FastRecomb) took 13.2 CPU h. Please note that only 192 haplotypes were used for LDhat and 5000 for IBDrecomb. FastRecomb's time complexity is linear to the sample size; hence, it is possible to run the program with 1 million haplotypes without using extensive resources. The maximum resident set size (peak memory) for FastRecomb was only ∼77 MB. The peak memory values for LDhat and IBDrecomb were ∼781 MB and ∼810 MB, respectively.
Pearson correlation coefficients between the inferred recombination rates and the ground truth.
Robustness against genotyping errors
Genotyping errors in real data sets are more dominant than mutations. It is almost impossible to ignore the genotyping error rates in practice. We evaluated the performance of FastRecomb, IBDrecomb, and LDhat using different genotyping error rates. We implanted error rates of 0.05%, 0.1%, and 0.2%. The errors were randomly inserted for each haplotype. For example, to simulate an error rate of 0.1%, we randomly selected 0.1% of the variant sites for each haplotype and altered the alleles. Figure 4 shows the correlation coefficients for the three methods in mid-region using 0.05% (A), 0.1% (B), and 0.2% (C) error rates. The correlation coefficients of FastRecomb are not affected by increasing the error rates (see Fig 4). For IBDrecomb, however, additional genotyping errors decrease the correlation coefficient values. LDhat, similar to FastRecomb, appears to be robust against error rates up to 0.2% for each haplotype. We repeated the experiment with the genotyping error of 0.1% for 10 different panels generated using varying seed values s = {1, …10} (see Fig. 5).
Pearson correlation coefficients in panels containing different error rates; 0.05% (A), 0.1% (B), and 0.2% (C).
Performance of recombination rate estimation tools at 10-kb and 100-kb resolution using 10 different panels with a genotyping error rate of 0.1%.
Performance growth with increasing sample size
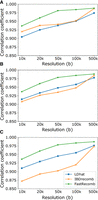
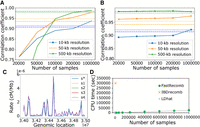
FastRecomb's performance depends on the number of samples from a population. Principally, FastRecomb facilitates the use of information that large-scale genetic data entail. To evaluate the performance of FastRecomb with increasing sample size, we extracted subpanels with 20,000, 50,000, 100,000, and 200,000 from the simulated 1 million haplotypes. Figure 6 illustrates the correlation coefficients for the mid-region using different sample sizes (from 20,000 to 1 million haplotypes with a genotyping error rate of 0.1%). The results of LDhat and IBDrecomb have been included as dotted and dashed lines, respectively. The sample sizes for LDhat and IBDrecomb were 192 and 5000. As shown in Figure 6 (panels A and B), the correlation coefficients for FastRecomb increase with the increasing number of haplotypes in general. Although the performance of FastRecomb grows faster with minimum cutoff length l = 0.5 cM (panel A), the best performance is achieved at 1 million samples. The minimum cutoff length l = 0.1 cM (panel B) for FastRecomb delivers competitive results with smaller sample sizes. In fact, for the 50-kb and 500-kb resolutions, FastRecomb with l = 0.1 cM already outperforms IBDrecomb and LDhat starting with a sample size of 20,000.
Effect of sample size on the performance of FastRecomb. (A) Pearson correlation coefficient of FastRecomb improves with the increasing number of haplotypes. (B) Smaller cutoff length will result in better performance with smaller number of samples. The minimum cutoff for A is l = 0.5 cM and for B is l = 0.1 cM. Estimated rates for four different 50,000 subsets (s1, s2, s3, and s4) out of the 200,000 sample in the 34- to 35-MB genomic region at 10-kb resolution are depicted in C. The minimum cutoff was set to l = 0.5 cM. s* denotes the recombination rates in the simulated data. (D) The running time increases linearly with the sample size. The error rates for all runs were set to 0.1%. Dashed and dotted lines represent the IBDrecomb and LDhat results, respectively.
Admittedly, the performance growth with increasing sample sizes is slow for FastRecomb, especially for l = 0.1 cM. We investigated the recombination rate estimates for a 1-Mb region and found the rate estimates across randomly selected subsamples are reasonably stable (Fig. 6C). FastRecomb shows a proficient ability to identify peaks while adding some small bumps in some zero-rate regions.
The run time of FastRecomb in the simulated data verifies the linear time complexity with the sample size (Fig. 6D). Running for 1 million samples took FastRecomb <50 k sec, making it the only method scalable to biobank scale data.
Performance of FastRecomb without smoothing
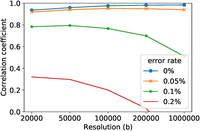
The smoothing preprocessing step is crucial for panels with a high number of genotyping errors. We calculated the correlation coefficients of FastRecomb without the smoothing steps for different error rates (see Fig. 7). As shown in Figure 7, a low error rate (e.g., 0.05%) may not affect the results significantly. Higher error rates, however, could lead to a significant performance reduction.
Pearson correlation coefficients of FastRecomb without smoothing the haplotype panel using different error rates.
Table 1 contains the correlation coefficients for the mid-region with smoothing and without smoothing. The genotyping error rate was set to 0%. The results show that the smoothing would not lower the correlation coefficients even if no genotyping error was expected.
Correlation coefficients for mid-regions in a panel without genotyping errors
Performance of FastRecomb in end-regions
The coefficient values for end-regions in 10-kb and 500-kb resolutions from the panel with 0.1% error rates have been included in Table 2. LDhat shows a better performance in the end-regions. For the end-region of 2–5 Mbp, the difference between LDhat and FastRecomb is less noticeable in 10,000 resolution. The current implementation of FastRecomb does not treat the end-region differently. Hence, the correlation coefficients for the end-regions are not as high as those of the mid-region. IBDrecomb treats end-regions differently from the mid-region by a special procedure to compensate for the lower IBD boundary counts owing to chromosomal ends. The special treatment by IBDrecomb improves the accuracy of the rates in the end-region, but for LDhat, the correlation coefficients in the end-region are still higher.
Pearson correlation coefficients for end-regions and mid-region for different recombination rate inference methods
Recombination rate estimation in real data
The objective of this experiment is to show the scalability and to verify the population-specific recombination rates in real large-scale data. The phased haplotypes were extracted and converted to VCF format from the UK Biobank release (version 2). Phasing was performed by the UK Biobank team using SHAPEIT3, as previously described (Bycroft et al. 2018). We only used the phased haplotypes and also did not include imputed data. Our method presupposes a satisfactory phasing quality. Our prior investigation has shown that the UK Biobank shows high phasing quality (Naseri et al. 2021a), with a switch error rate below 0.3%, which translates to one error per 20 Mb per haplotype. At this degree of phasing quality, we anticipate that FastRecomb will be minimally affected. When the input panels are sufficiently large, their phasing quality is also expected to be favorable. However, if the input data are not well phased, we would not recommend our method.
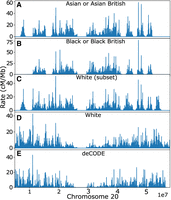
We applied FastRecomb on four different subsets of UK Biobank data: (1) Asian or Asian British individuals, (2) Black or Black British individuals, (3) White individuals, and (4) White (subset) individuals containing 7816 randomly selected samples. The ethnic background (data-field, 21,000) of only 8034 individuals was Black or Black British individuals. Therefore, we selected a subset of White individuals similar to that of Black or Black British individuals. The number of White (subset) individuals with available genotype data was slightly less than 8034. Approximately 1 CPU h and 55 MB memory were used to estimate the recombination rates for the largest panel containing all White individuals within the UK Biobank data. Figure 8 illustrates the estimated rates for each subset in Chromosome 20. Table 3 contains the correlation coefficients and the number of individuals for different subsets of UK Biobank samples.
Estimated rates using different subsets of UK Biobank across Chromosome 20: (A) Asian or Asian British, (B) Black or Black British, (C) subset of White individuals, and (D) all White individuals. The rates from deCODE (sex averaged) are presented for comparison (E).
Correlations between inferred rates in UK Biobank and deCODE map at 100-kb resolution
Correlation with White (subset) individuals was lower than White (all) individuals, confirming the higher power of a larger sample size. Also, among populations with comparable sample sizes, the similar population has higher correlation, suggesting FastRecomb captured population-specific recombination maps. Note that even the highest correlation (0.79) between the estimated map from 458,677 (British) White individuals and the deCODE map is not as high as that from simulation (e.g., Table 1). This may be because the genetic map between the Icelandic population (deCODE) may be different from the UK population, among other factors.
Discussion
In this work, we presented a new method to estimate the recombination rates in biobank-scale cohorts. A unique hallmark of the proposed method, FastRecomb, is its scalability. FastRecomb implicitly considers all matches between pairs of haplotypes while avoiding enumerating all possible pairs using PBWT blocks. As a result, the run time of FastRecomb grows linearly with the number of variant sites and the number of individuals. Also, FastRecomb avoids the explicit outputting of IBD segments, a potential I/O bottleneck. These innovations enable FastRecomb to be easily applicable to panels with hundreds of thousands or even millions of haplotypes without requiring extensive resources. The wall time of our method can be further improved using multithreading. Currently, FastRecomb only supports a single CPU, but by parallelizing it, for example, using parallel PBWT (Wertenbroek et al. 2023), we can reduce the run time of processing a million haplotypes from several hours to less than an hour. This performance improvement can be incorporated into future versions of our method, allowing us to process larger data sets more efficiently.
The recombination rates inferred by FastRecomb can achieve the highest correlation coefficients given a large number of samples. The most important factor contributing to the improved performance outcome is FastRecomb's scalability, which allows the use of data from large biobanks. Additionally, the preprocessing step and the use of a shorter IBD length cutoff ensure robustness against genotyping errors, which would otherwise reduce the accuracy of IBD-based approaches like IBDrecomb. In our simulated data, panels with 100,000 individuals achieve comparable or slightly better performance compared with LDhat and IBDrecomb in the mid-region of the chromosome. With 500,000 individuals, the recombination rates inferred by FastRecomb are more accurate in the mid-region. In our experiments, we set the minimum length l for counting minor alleles in blocks of matching haplotypes to 0.5 cM. For smaller panels, the IBD coverage for 0.5 cM may not be sufficient for certain regions. As a result, the inferred recombination rates may not be representative of the underlying population. Smaller cutoff lengths (e.g., 0.1 or 0.2 cM) may result in more accurate correlation coefficients for small panels comprising only a few thousand haplotypes, but the correlation coefficients may not be necessarily better than the longer cutoff in large panels. This is because of the high probability of a match between two haplotypes for small cutoffs (e.g., 1 cM), especially if the marker density is not very high.
FastRecomb has a number of limitations. FastRecomb assumes that mismatches after a long match are owing to recombination events where some mismatches could be caused by recent mutations or genotyping errors. This problem can be addressed by smoothing the panel. On the validity of using IBD end points to estimate recombination rates, we followed that of IBDrecomb. Our main contribution is not to improve the estimation bias but rather to provide an efficient solution to count recombination events that is alternative to the calling of IBD segments. We admit that using IBD end points could have estimation bias caused by inaccurate estimation of IBD end points or an unknown total genetic map. Detailed investigation and correcting such biases will be future work. Moreover, in our experiments, we focused on the mid-region of the chromosome, which entailed ∼82% of the entire chromosome. In fact, the widely distributed deCODE genetic map, which we used for our simulation, lacks the rate for a few million base pairs at the end-regions: The genetic map of Chr 20 starts from position 5,016,799, and the last non-zero genetic recombination rate is 56,476,799, whereas all the sites until the end (57,006,899) are assumed to be zero. According to the investigators of the deCODE map (Kong et al. 2010), the end-regions were excluded as the determination of recombinations is less reliable for these regions. In future work, we will experiment with special treatment for the end-regions similar to IBDrecomb while counting the IBD boundaries. Moreover, we limited evaluation of our method to array data. Error rates in sequencing data might be higher, especially for rare variants. As a result, the accuracy of FastRecomb will rely on the performance of the smoothing step. Thinning the data using minor allele frequencies is also a possible solution for panels with high error rates in rare variants.
Based on our experiments, FastRecomb has the potential of outperforming the current state-of-the-art methods when the haplotype panel is large enough. Moreover, our method is robust against genotyping errors as the performance of FastRecomb was not affected by increasing the error rates from 0% to 0.2%. In summary, FastRecomb unleashes the power of biobank-scale haplotype panels for estimating population-specific genetic maps. Given the fact that some human populations may have unique recombination hot spots and their genetic map may differ, it is essential to estimate their unique genetic map for downstream analysis. As the access to biobanks housing hundreds of thousands to millions of individuals increases, efficient methods such as FastRecomb may become critical for population-specific genetic map estimation.
Software availability
Source code is available at GitHub (https://github.com/ZhiGroup/FastRecomb) and as Supplemental Code.
Competing interest statement
The authors declare no competing interests.
Acknowledgments
This research has been conducted using the UK Biobank Resource under Application Number 24247. This work was supported by the National Institutes of Health under grants R01HG010086, R56HG011509, and OT2OD002751.
Author contributions: A.N., S.Z., and D.Z. performed the conceptualization. A.N., W.Y., and D.Z. performed the methodology. A.N. was responsible for software. A.N. and W.Y. performed data curation, investigation, and validation. S.Z. and D.Z. performed funding acquisition and supervision. A.N. and D.Z. wrote the original draft. A.N., W.Y., S.Z., and D.Z. reviewed and edited.
Footnotes
-
[Supplemental material is available for this article.]
-
Article published online before print. Article, supplemental material, and publication date are at https://www.genome.org/cgi/doi/10.1101/gr.277676.123.
- Received January 6, 2023.
- Accepted June 9, 2023.
This article is distributed exclusively by Cold Spring Harbor Laboratory Press for the first six months after the full-issue publication date (see https://genome.cshlp.org/site/misc/terms.xhtml). After six months, it is available under a Creative Commons License (Attribution-NonCommercial 4.0 International), as described at http://creativecommons.org/licenses/by-nc/4.0/.
