Defining the separation landscape of topological domains for decoding consensus domain organization of the 3D genome

  1. Shihua Zhang3,4,5,6
  1. 1Key Laboratory of Information Fusion Technology of Ministry of Education, School of Automation, Northwestern Polytechnical University, Xi'an 710072, China;
  2. 2Department of Software Engineering, Yunnan University, Kunming 650500, China;
  3. 3NCMIS, CEMS, RCSDS, Academy of Mathematics and Systems Science, Chinese Academy of Sciences, Beijing 100190, China;
  4. 4School of Mathematical Sciences, University of Chinese Academy of Sciences, Beijing 100049, China;
  5. 5Center for Excellence in Animal Evolution and Genetics, Chinese Academy of Sciences, Kunming 650223, China;
  6. 6Key Laboratory of Systems Health Science of Zhejiang Province, School of Life Science, Hangzhou Institute for Advanced Study, University of Chinese Academy of Sciences, Hangzhou 310024, China
  • Corresponding author: zhangsw{at}nwpu.edu.cn, zsh{at}amss.ac.cn
    •  
    Next Section

    Abstract

    Topologically associating domains (TADs) have emerged as basic structural and functional units of genome organization and have been determined by many computational methods from Hi-C contact maps. However, the TADs obtained by different methods vary greatly, which makes the accurate determination of TADs a challenging issue and hinders subsequent biological analyses about their organization and functions. Obvious inconsistencies among the TADs identified by different methods indeed make the statistical and biological properties of TADs overly depend on the chosen method rather than on the data. To this end, we use the consensus structural information captured by these methods to define the TAD separation landscape for decoding the consensus domain organization of the 3D genome. We show that the TAD separation landscape could be used to compare domain boundaries across multiple cell types for discovering conserved and divergent topological structures, decipher three types of boundary regions with diverse biological features, and identify consensus TADs (ConsTADs). We illustrate that these analyses could deepen our understanding of the relationships between the topological domains and chromatin states, gene expression, and DNA replication timing.

    Recent advances in imaging technologies (Bintu et al. 2018; Su et al. 2020) and chromosome conformation capture (3C)–based technologies such as Hi-C (Dekker et al. 2002; Dostie et al. 2006; Simonis et al. 2006; Lieberman-Aiden et al. 2009; Rao et al. 2014) provide unprecedented opportunities to decipher the mysteries of three-dimensional (3D) genomic organizations in the nucleus of eukaryotes. The genome folds into a hierarchical configuration consisting of multiscale chromatin structures such as chromosomal territories (Cremer and Cremer 2001; Lieberman-Aiden et al. 2009; Dixon et al. 2012), A/B compartments (Lieberman-Aiden et al. 2009; Rao et al. 2014), topologically associating domains (TADs) (Dixon et al. 2012; Crane et al. 2015), and chromatin loops (Rao et al. 2014; Tang et al. 2015). TADs, manifested as squares of increased intensity in the Hi-C contact maps, are structural domains with intensive self-interactions. They are demarcated by TAD boundaries (start and end regions of a domain), which serve as insulators to prevent inter-TAD interactions and favor intra-TAD interactions (Dixon et al. 2012; Crane et al. 2015). TADs are often considered stable neighborhoods for gene regulation (Rao et al. 2014; Spielmann et al. 2018; Eres and Gilad 2021) and are reported to be highly conserved across multiple cell types and different species (Rao et al. 2014; Vietri Rudan et al. 2015; Schmitt et al. 2016; Luo et al. 2021; McArthur and Capra 2021). In addition, the disorder of TADs is closely related to some severe diseases (Lupiáñez et al. 2015; Spielmann et al. 2018), even cancer (Taberlay et al. 2016; Dixon et al. 2018). Therefore, TADs are the basic structural and functional units of chromatin organization, and the accurate determination of TADs is of vital importance for the 3D genome study.

    Researchers have developed a variety of methods to define TADs based on diverse computational strategies (Dali and Blanchette 2017; Forcato et al. 2017; Zufferey et al. 2018). For example, some one-dimensional (1D) topological indicators, including the directionality index (DI) (Dixon et al. 2012), insulation score (IS) (Crane et al. 2015), and contrast index (CI) (Zhan et al. 2017), were developed to capture the boundaries between adjacent TADs. TopDom (Shin et al. 2016), HiTAD (Wang et al. 2017), HiCDB (Chen et al. 2018), and OnTAD (An et al. 2019) were further designed based on some modified 1D indicators. Moreover, MSTD (Ye et al. 2019), IC-Finder (Haddad et al. 2017), ClusterTAD (Oluwadare and Cheng 2017), and CHDF (Wang et al. 2015) were designed to extract the interaction signals in the Hi-C contact map and then conduct clustering on them to achieve this task. Probabilistic models (e.g., GMAP [Yu et al. 2017] and HiCseg [Lévy-Leduc et al. 2014]) with certain assumptions have also been developed. In addition, some methods like 3DNetMod (Norton et al. 2018), Spectral (Chen et al. 2016), and deDoc (Li et al. 2018) treated the Hi-C contact map as an adjacency matrix of chromatin interaction network and used community detection or graph segmentation algorithms for this task.

    However, different TAD-calling methods have identified inconsistent and diverse TADs (Dali and Blanchette 2017; Forcato et al. 2017; Zufferey et al. 2018). Zufferey et al. (2018) systematically evaluated and compared several TAD-calling methods by designing a series of application scenarios. They reported distinct differences in the TADs found by different methods and provided helpful guidelines for choosing a suitable approach for users. But, the selected method cannot consider all aspects and may still suffer from certain limitations. It is also difficult to interpret the inconsistencies among results from different approaches owing to the lack of a gold standard for TADs. Here, we apply 16 TAD-calling methods to Hi-C data generated for seven human cell lines (Rao et al. 2014). We aim to explore the inconsistencies among different TAD-calling methods and provide an alternative solution to deal with them by integrating the results from different approaches to obtain more consensus and reliable TADs, which will facilitate the biological analysis for both TADs and their boundaries.

    Previous SectionNext Section

    Results

    TADs identified by different methods show nonnegligible inconsistency

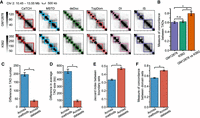
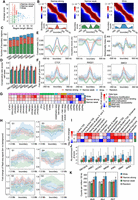
    We exemplify the diverse TADs identified by 16 TAD-calling methods with the Hi-C contact matrices of GM12878 and K562 (Fig. 1A; Supplemental Fig. S1B). TADs identified by different methods were quite inconsistent, but each method yielded more similar results between GM12878 and K562. Correspondingly, the measure of concordance (MoC), which reflects the similarity between TADs, was smaller among TADs found by different methods on GM12878 or K562 than that between TADs from the same method on two cell lines (Fig. 1B). We further confirmed that TADs found by different methods on the same data were more diverse in number and average size than those found by the same method across seven cell lines (Fig. 1C,D; Supplemental Fig. S1C,D). Moreover, the TADs identified by the same method across cell lines were more consistent than those obtained by different methods on the same data in terms of the location of boundaries and overlap of TAD domains (measured by the Jaccard index between boundary sets and the MoC between domain sets) (Fig. 1E,F). We observed similar results for all TAD-calling methods (Supplemental Fig. S1E–H), which suggested that the existing methods could identify very inconsistent TADs. Thus, the TADs we get heavily depend on the method rather than the Hi-C data, which may obscure the characterization of real topological domains. For example, the cohesin complex (RAD21 and SMC3) and the chromatin insulator protein CTCF are frequently reported to be enriched in TAD boundaries, and they appear to be required for boundary formation, maintenance, and remodeling (Rao et al. 2014; Dixon et al. 2016; Hansen et al. 2017; Szabo et al. 2019). However, even on the same data, TADs identified by different methods may show different levels of enrichment for CTCF, RAD21, and SMC3 (Supplemental Fig. S2A,B). Therefore, performing biological analysis based on TADs derived from different methods may result in quite diverse observations.

    Figure 1.
    View larger version:
    Figure 1.

    Comparison of TADs identified by 16 TAD-calling methods on Hi-C data from diverse cell lines. (A) TADs identified by different methods on the same chromatin region of GM12878 and K562. The results of six methods are shown, and the remaining ones are shown in Supplemental Figure S1B. (B) Comparison of measure of concordance (MoC) between TADs identified by different methods in GM12878 or K562 and between TADs identified by the same method in two cell lines, for the region in A. (C–F) Comparison of the difference in TAD number (C), TAD size (D), the Jaccard index between boundary sets (E), and the MoC between domain sets (F) across TADs identified by different methods on the same data set or across TADs identified by the same method on different data sets for seven human cell lines. The error bars represent the 95% confidence intervals. Mann–Whitney U tests are performed. (*) P-value < 0.0001.

    Boundary voting reveals the unreliability of TADs of individual methods

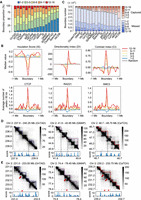
    Here, we evaluate TADs from different methods based on a boundary voting strategy (Supplemental Fig. S2C) and assign a boundary score to each bin along the chromosome by counting the number of methods that define it as a TAD boundary. Thus, the boundary scores are integers ranging from zero to 16. The distribution of boundary scores for bins on Chromosome 2 of GM12878 indicates the presence of many low-scoring boundaries (Supplemental Fig. S2D). By dividing the boundary scores into five intervals, we found that each method could return some low-scoring boundaries with a score of one or two, but the proportions varied across methods (Fig. 2A). For example, OnTAD and DI possess significantly fewer low-scoring boundaries, whereas Spectral and HiCDB have a much higher proportion of them. Moreover, boundaries belonging to different score intervals show diverse profiles for DI, IS, and CI and have different enrichment patterns for three structural proteins (Fig. 2B). We observe that the higher-scoring boundaries show stronger insulation strength of chromatin interactions, as well as higher-level enrichment of CTCF and the cohesin complex. On the contrary, boundaries belonging to the score interval of one to two show completely counterintuitive patterns for both 1D indicators and structural proteins, indicating these boundaries are not reliable. In addition, after collecting all candidate boundaries (bins with non-zero scores) found by the 16 methods, we find that some methods return more potential boundaries but also bring in more low-scoring ones, such as HiCDB and deDoc, whereas some methods like DI and OnTAD tend to capture boundaries with higher scores to ensure their reliability, but they may miss more candidate ones with moderate scores (Fig. 2C). For example, we observe that more high-scoring bins are located far away from the boundaries captured by methods like DI and OnTAD (Supplemental Fig. S2E). The overall distribution of the boundary scores for TADs found by each method can be seen in Supplemental Figure S3B. More specifically, based on the boundary scores, we discover some unreliable domains and missed boundaries for each method (Fig. 2D,E; Supplemental Fig. S4). The unreliable TADs with low-scoring boundaries are visually inconsistent with the domain patterns shown in the Hi-C contact maps (Fig. 2D), and the missed boundaries match well with some peaks in the boundary score profile (Fig. 2E). All these results indicate that the existing TAD-calling methods suffer from distinct limitations, but the consensus among them can lead us to find more reliable and comprehensive TADs.

    Figure 2.
    View larger version:
    Figure 2.

    Systematic evaluation of 16 TAD-calling methods based on the boundary voting strategy. (A) Proportion of boundaries with different levels of boundary score for all 16 methods. These methods are sorted in ascending order by the proportion of boundaries belonging to the first level (ranging from one to two). (B) Profiles of three topological indicators (insulation score [IS], directionality index [DI], contrast index [CI]) and profiles of three structural proteins (CTCF, RAD21, SMC3) within 2-Mb regions centered on boundaries with different boundary score levels or randomly selected regions. (C) Number of boundaries with different boundary scores captured or missed by each method. These methods are sorted in ascending order by the number of captured boundaries. (D) Hi-C contact maps around the unreliable TADs with low boundary scores for three methods, including OnTAD, GMAP, and CaTCH. The unreliable TADs are indicated by white frames, and the low-scoring boundaries are indicated by dashed lines. (E) Hi-C contact maps around the high-scoring boundaries that are missed by a certain method. The examples for three methods including OnTAD, GMAP, and CaTCH are shown. The missed boundaries are indicated by red arrows, and the corresponding boundary scores are indicated by red triangles.

    Defining the TAD separation landscape based on the consensus of all TAD-calling methods

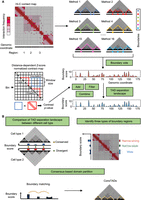
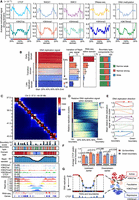
    To overcome the drawbacks and make good use of the consensus structural information of individual TAD-calling methods, we propose a computational strategy to dissect and integrate the TADs identified by existing methods. First, we apply all TAD-calling methods to the same Hi-C contact map and collect their TAD boundaries. Second, we construct the boundary score profile of all bins along the genome based on a boundary voting strategy. Third, we refine the boundary score profile through three kinds of operations to get the TAD separation landscape (Fig. 3A).

    Figure 3.
    View larger version:
    Figure 3.

    Overview of the construction of the TAD separation landscape and its three applications. (A) The representative Hi-C contact map contains several candidate boundary regions, and different TAD-calling methods identify diverse TADs with variable boundaries. Based on the boundary voting strategy, each bin on the genome will get a score to indicate how many methods consider it to be a TAD boundary. The TAD separation landscape is constructed from the original boundary score profile using three additional operations, including add, filter, and combine, which are calculated based on the contrast P-value, an indicator to reflect the insulation effect of chromatin interactions for each bin. (B) Three applications of the TAD separation landscape, including domain boundary comparison, boundary type identification, and consensus domain detection.

    The consecutive bins with non-zero scores represent the potential boundary regions. However, the original boundary score profile contains numerous low-scoring bins, which are unreliable and noisy, making the adjacent boundary regions too close (Supplemental Fig. S5D–F). Therefore, we introduced an additional 1D indicator, called contrast P-value, to refine the boundary score profile. For each bin, the contrast P-value reflects the degree of difference between the contact frequency within the upstream and downstream regions versus that across them (Fig. 3A). Next, three kinds of operations are performed to modify the boundary score profile and construct the TAD separation landscape based on the contrast P-value (Methods). Through these refinements, we can filter out some unreliable bins with low scores (Supplemental Fig. S5E) and adjust the distance between adjacent boundary regions (Supplemental Fig. S5F). We further show that the refined profiles possess boundary regions with higher scores, and the distances between adjacent regions become larger and more consistent with the lengths of topological domains identified by general TAD-calling methods (Supplemental Fig. S5G–J). We refer to the refined boundary score profile as the TAD separation landscape, which integrates the results of a set of TAD-calling methods and can precisely and comprehensively depict the locations of potential boundary regions between adjacent TADs (Fig. 3A).

    The TAD separation landscape can serve as an effective indicator for comparing topological domains across cell types to reveal the conserved and cell type–specific boundaries between different cell lines. It indicates the presence of three different types of boundary regions with distinct chromatin insulation patterns and biological functions. It also contributes to the detection of consensus TADs (ConsTADs) (Fig. 3B).

    Comparing TAD boundaries across cell types based on the TAD separation landscape

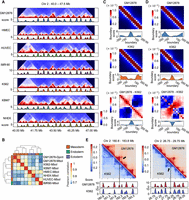
    We construct the TAD separation landscapes for the Hi-C contact maps of Chromosome 2 in seven human cell lines, respectively. The boundary regions indicated by the TAD separation landscapes match well with the domain borders in the Hi-C contact maps (Fig. 4A). Then we divide all bins along the chromosome into six levels according to their average boundary scores across seven cell lines. The higher the level, the larger the boundary score, and the first level only contains bins with a score of zero. We find that bins with higher boundary score levels are more conserved across cell types and are enriched for more housekeeping genes as well as CTCF binding peaks, and the regions bounded by CTCF show a higher level of cross-species sequence conservation (Supplemental Fig. S6A). Furthermore, based on the TAD separation landscapes, the clustering results of multiple Hi-C samples are very consistent with the organogenesis process, in which the cell lines from the same germ layer are grouped together (Fig. 4B). However, other 1D indicators such as DI, IS, and CI cannot depict the relationship between different cell lines as well as the TAD separation landscape (Supplemental Fig. S6B). Therefore, these results suggest that the TAD separation landscape can precisely characterize the locations of TAD boundaries and reflect their biological significance and cell type specificity.

    Figure 4.
    View larger version:
    Figure 4.

    Comparison of TAD boundaries across different cell lines. (A) Hi-C contact maps and the corresponding TAD separation landscapes of a chromatin region in seven cell lines. (B) Clustering of multiple Hi-C samples from different cell lines based on their TAD separation landscapes. (C,D) The aggregated Hi-C contact maps around the GM12878-specific boundary regions (C) and K562-specific boundary regions (D) between comparison of the GM12878 and K562 cell lines, combined with the average boundary score profiles of the corresponding regions. The differences between these aggregated maps and the average boundary scores are also shown. (E) The contrastive Hi-C contact maps around a GM12878-specific boundary region (left) and a K562-specific boundary region (right). The Hi-C contact maps and corresponding boundary score profiles in GM12878 (marked in red) and K562 (marked in blue) are shown. The dashed lines and arrows indicate the location of the cell type–specific boundary regions.

    Taking the comparison of GM12878 and K562 as an example, we showed that the TAD separation landscapes could serve as effective indicators to facilitate the identification of conserved and cell type–specific TAD boundaries between different cell lines. The aggregated Hi-C contact maps around the conserved boundary regions between GM12878 and K562 show significant insulation of chromatin contacts, coupled with the peaks of average boundary scores in both cell lines, whereas the cell type–specific boundary regions are accompanied by specific contact insulation and a boundary score peak only in one cell line (Fig. 4C,D; Supplemental Fig. S7A). Moreover, two examples show that the TAD separation landscapes can indeed capture the changes between the topological domains in these cell lines (Fig. 4E). In addition, we find that CTCF and CTCFL are the most enriched transcription factors (TFs) for both conserved and cell type–specific boundaries. The conserved boundary regions show similar enrichment for CTCF binding in GM12878 and K562, but for cell type–specific boundaries, the CTCF enrichment is indeed different (Supplemental Fig. S8D–F). Moreover, the pairwise comparisons between the seven cell lines based on their TAD separation landscapes also reveal the conserved, cell type–gained, and cell type–lost boundaries (Supplemental Fig. S7C,D). The cell type–specific boundaries only occupied a relatively small part, and nearly half of the boundaries were conserved between two cell lines, confirming that TADs are highly conserved among cell types (Dixon et al. 2012; Rao et al. 2014).

    Apart from the pairwise comparisons between cell lines, the TAD separation landscapes could also facilitate the boundary comparison among multiple cell types. We identify the conserved boundaries shared by all seven cell lines and the specific boundaries unique to each cell line (Supplemental Fig. S7E). The conserved boundaries show strong insulation of chromatin interactions and boundary score peaks in all cell lines, whereas the cell type–specific boundaries only show these patterns in the corresponding cell line (Supplemental Fig. S9A,B). In addition to the most conserved and specific boundaries, the TAD separation landscapes can also reveal boundaries shared by part of the cell lines, which match well with the domain borders in the corresponding Hi-C contact maps (Supplemental Fig. S10). These results suggest that the TAD separation landscapes could capture both the commonalities and differences in the topological organizations between different cell types.

    TAD separation landscape divides boundary regions into three different types with strong biological relevance

    The boundary regions revealed by the TAD separation landscape are variable in length and boundary scores. Based on the number of bins contained in each region and their average boundary score, we divided the boundary regions into three different types: narrow-strong boundary regions (NSBs), narrow-weak boundary regions (NWBs), and wide boundary regions (WBs) (Fig. 5A). The NSBs and NWBs typically cover few bins with high or low boundary scores, respectively, whereas the WBs can occupy many bins with moderate scores. The aggregated Hi-C contact maps around three different types of boundary regions indicate that they have distinct insulation patterns of chromatin contacts. The NSBs show strong insulation against chromatin contacts, whereas the NWBs show local insulation with weaker strength, and the WBs are larger fragments separating two adjacent domains. The insulation patterns of these boundary regions can be well captured by the boundary score profiles (Fig. 5B). We identified all three types of boundary regions in the seven cell lines (Supplemental Fig. S11). In each cell line, the NWBs always accounted for the largest proportion, whereas the NSBs and WBs were slightly fewer (Fig. 5C). However, the cross–cell type comparison reveals that the NWBs are less conserved among different cell lines, whereas the NSBs show a high degree of conservation, implying that different cell lines possess similar strong insulation patterns near these regions (Fig. 5D). Coherently, the WBs show wide-range insulation patterns and broad distributions of protein binding peaks, and the NSBs show sharp insulation patterns and concentrated protein binding profiles, whereas the NWBs have moderate and localized insulation effect and are less dependent on the structural proteins (Fig. 5E,F).

    Figure 5.
    View larger version:
    Figure 5.

    Three types of boundary regions defined based on the TAD separation landscape. (A) Scatter plot of boundary regions based on their lengths and average boundary scores. (B) Aggregated Hi-C contact maps around the NSBs (left), NWBs (middle), and WBs (right), combined with the average boundary score profiles in GM12878. (C) Number of three types of boundary regions identified in seven cell lines. (D) Conservation of three types of boundary regions among the seven cell lines. (E) Profiles of 1D indicators including CI (left), IS (middle), and DI (right) around different types of boundaries and random control in GM12878. The shaded areas represent the 95% confidence intervals in 1000 bootstraps. (F) Profiles of peaks fold change of TFs including CTCF (left), RAD21 (middle), and SMC3 (right) around different types of boundaries and randomly selected regions in GM12878. The fold changes are calculated by dividing the peak numbers in each bin by the average peak numbers across the chromosome. (G) Fold change profiles of multiple types of biological data constructed for three types of boundary regions in GM12878. Fold change of a biological marker in each type is defined as the median signal in boundary regions divided by the median signal across the chromosome. (H) Fold change profiles of Repli-seq signal around three types of boundaries and randomly selected regions in six different phases of the cell cycle: G1, S1, S2, S3, S4, and G2. (I) Fold change profiles of ChromHMM states constructed for three types of boundary regions in GM12878. The fold change of a chromatin state in each type is defined as the total length of the state in boundary regions divided by the expected state length in chromosome background. (J) Enrichment of Alu elements in three types of boundaries for seven cell lines. (K) Density of the Alu subfamilies in three types of boundaries and randomly selected regions in GM12878. Mann–Whitney U tests were performed between boundary regions and random regions, respectively. (*) P-value < 0.01.

    Moreover, the WBs are enriched with active histone modifications such as H3K27ac, H3K36me3, and H3K79me2, and they also have stronger RNA polymerase II (Pol II) signals and chromatin openness, showing significantly strong transcription activity, whereas the NSBs showed similar enrichment patterns but with weaker intensity. The NWBs do not show significant enrichment in most biological data but possess distinct patterns for Repli-seq signals that are entirely different from the WBs and NSBs (Fig. 5G). Based on the enrichment profiles of Repli-seq signals around the three types of boundary regions during six phases of the cell cycle, we observe a gradual shift of the replication patterns, in which the WBs and NSBs show signal enrichments in some early stages, like G1, S1, and S2, but decrease in later stages, such as S3, S4, and G2. In contrast, the NWBs show opposite trends, and the nascent DNA replication strands remain at a low level in the early phases but tend to be enriched in the later phases (Fig. 5H). In addition, based on the enrichment analysis of 15 chromatin states annotated by ChromHMM (Ernst and Kellis 2012) in three types of boundary regions, we observe that the WBs are enriched with active TSS, strong transcription, and other chromatin states associated with active gene transcription, and NSBs show stronger enrichment of bivalent chromatin regions, such as bivalent TSS and bivalent enhancer as well as the Polycomb group of proteins (Fig. 5I). We observed similar patterns in different cell lines (Supplemental Fig. S12A). Bivalent chromatin segments have been found to play vital roles in the developmental regulation of pluripotent embryonic stems cells, as well as in gene imprinting and some diseases (Bernstein et al. 2006; Sanz et al. 2008; Vastenhouw and Schier 2012; Blanco et al. 2020; Kumar et al. 2021). Recalling the strong conservation of NSBs across cell types (Fig. 5D) and the general enrichment of bivalent chromatin segments on these boundary regions in multiple cell lines, we suspect that the NSBs may be crucial for stem cell differentiation and cell fate decision, which deserve further exploration. We also explored the relationships between these boundary regions and the chromatin states annotated by Segway-GBR (Libbrecht et al. 2015), as well as another chromatin structure termed as subcompartment (Supplemental Fig. S12B,C; Rao et al. 2014; Xiong and Ma 2019). The WBs are highly related to both broad and cell type–specific gene expression, and the NSBs are associated with broad gene expression and the facultative heterochromatin, whereas the NWBs typically belong to the constitutive heterochromatin or quiescent chromatin regions. These results are consistent with the assignment of subcompartments to these boundary regions. The WBs mainly belong to the A1 subcompartments that have been reported as transcriptionally active regions, and the NSBs are enriched with A2 subcompartments, which were considered as active regions resembling the A1 type, but in a recent study, they were indicated to be intermediate subcompartments containing some poised promoters (Liu et al. 2021). The NWBs are mainly divided into B-type subcompartments, which usually serve as transcriptionally repressed regions.

    Moreover, we observe a gradually increasing enrichment from two types of narrow boundary regions to the WBs for two kinds of repeat elements, Alu and TcMar-Tigger, and the WBs show stronger enrichment of both repeat elements relative to the random control in multiple cell lines (Fig. 5J; Supplemental Fig. S13). More specifically, the NSBs are enriched with AluS and AluJ compared with the randomly selected regions, and the WBs show significant enrichment for all Alu subfamilies (Fig. 5K). Our results are consistent with some previous studies reporting the enrichment of Alu elements in TAD boundaries (Dixon et al. 2012; Luo et al. 2021), and further suggest that different types of boundary regions may be enriched with certain subfamilies of Alu. As for TcMar-Tigger, it was rarely reported to be associated with TAD boundary, and its function needs to be further investigated. Furthermore, we also explore the TFs that are enriched in three types of boundary regions (Supplemental Fig. S14C,D). We find that for three types of boundary regions, most of the enriched TFs are shared, such as CTCF and CTCFL, and there are also some special TFs for each type, such as TCF12 for NSBs, SPIB for NWBs, and NEUROD1 for WBs in GM12878, which might promote the study of the formation and maintenance mechanisms of these boundary regions in certain cell types (Supplemental Fig. S14C).

    ConsTADs facilitate the understanding of biological modifications and DNA replication patterns within topological domains

    Based on the TAD separation landscape, we design a boundary-matching strategy to identify the ConsTADs that represent the topological domains under the consensus of the 16 TAD-calling methods (Methods). We explore the profiles of some TFs and epigenomic modifications within these ConsTADs and find two kinds of distribution patterns. First, some TFs like CTCF, SMC3, and RAD21, as well as the chromatin accessibility, are more enriched or stronger in boundary regions than domain interiors, which is consistent with the conventional observation that CTCF and cohesin contribute to the formation and maintenance of the topological domain through binding at the boundary regions (Rao et al. 2014; Dixon et al. 2016; Hansen et al. 2017; Szabo et al. 2019). Second, some histone modifications such as H3K27ac, H3K4me3, and H3K79me2 are more abundant inside the domains, probably because more regulatory events are involved in domain interiors, and therefore, the modifications associated with the activity of regulatory elements such as enhancers and promoters are stronger within domains (Fig. 6A; Supplemental Fig. S15B).

    Figure 6.
    View larger version:
    Figure 6.

    Biological relevance of ConsTADs. (A) Relative profiles of several biological features within ConsTADs and adjacent regions in GM12878. (B) Five clusters of topological domains with distinct DNA replication signals accompanied by the variances of the Repli-seq signal, the average RNA-seq signal, and the boundary type components within each type of domains. (C) Hi-C contact maps of a region on Chromosome 2 of GM12878 accompanied by the ConsTADs (black frames in contact map), the corresponding boundary types and domain types, and ChIP-seq and Repli-seq profiles. (D) Five clusters of topological domains with distinct relative DNA replication models, which indicate the relative early or late replication timing of chromatin regions within each domain. (E) Mean profiles of the relative DNA replication signals for five clusters of domains in D. Arrows indicate the direction of DNA replication from early to late. (F) Average number of CTCF binding peaks around the upstream and downstream boundary for each domain in five clusters. Mann–Whitney U tests were performed to get the P-values. (G) The replication domain model. (Left) DNA replication timing across TADs belonging to early, transition, and late replication domains accompanied with the CTCF profiles at TAD boundaries. (Right) The corresponding chromatin arrangement of replication domains and their chromatin states and prominent modifications.

    Pope et al. (2014) found that the human genome could be divided into some constant timing regions (CTRs) with relatively uniform replication timing, whereas the early and late CTRs were interrupted by some timing transition regions (TTRs). Based on the TADs identified by DI, they concluded that TAD boundaries usually isolated the early CTRs from TTRs, whereas the TTRs and neighboring late CTRs predominantly belonged to the same TADs. However, we find that DI tends to identify a small number of TADs with relatively large scales and may lack a fine depiction of the topological domains (Supplemental Fig. S1C,D). According to the Repli-seq data, we divide ConsTADs into five clusters containing two clusters of early and late replication domains, as well as three clusters of transition domains (Fig. 6B; Supplemental Fig. S15E). We observe relatively uniform replication signals within the early and late replication domains, whereas the transition domains show larger variances, indicating a gradual DNA replication timing within them. The early and late replication domains perhaps correspond to the early and late CTRs that Pope et al. found, and benefiting from the intensive depiction of topological domains by ConsTADs, we found the TTRs also correspond to independent TADs rather than being contained in the same TADs with late CTRs (Fig. 6B).

    In addition, the five clusters of replication domains obtained from ConsTADs show different epigenomic patterns and gene expression levels (Fig. 6B; Supplemental Fig. S16A). The early replication domains have the strongest signal for some active markers, such as H3K4me3, H3K27ac, and H3K36me3, as well as gene expression. As the replication timing changes from early to late, these epigenomic and transcriptional signals become sequentially weaker in the three types of transition domains and reach their weakest in the late replication domains. The repressive marker H3K9me3 shows an opposite pattern with a progressively stronger signal from early replication domains to the late ones, whereas the facultative marker H3K27me3 is stronger in three types of transition domains (Supplemental Fig. S16A). It is known that both H3K9me3 and H3K27me3 are markers associated with gene repression, but unlike H3K9me3, which keeps genes silenced all the time and prevents binding of multiple TFs, H3K27me3 still allows genes to be activated through TF binding in different cell states (Bernstein et al. 2006; Soufi et al. 2012). These results suggest that the topological domains not only have different DNA replication timings but also correspond to different chromatin states with certain biological properties. For instance, we find that the early replication domains are typically enriched in active subcompartments like A1 and A2 and belong to regions with strong transcriptional activity, whereas the late replication ones mainly fall in the quiescent regions and repressive subcompartment like B2, and the transition domains are correlated with some intermediate subcompartments such as A2, B1, and B3 and usually locate in bivalent chromatin regions (Supplemental Fig. S16B). Moreover, the components of the boundary types for different replication domains are shown in Figure 6B. As the replication timing changes from early to late, the proportion of the WBs and NSBs in domain boundaries gradually decreases, whereas the proportion of the NWBs significantly increases. This is consistent with our conclusion that the DNA sequences near the WBs and NSBs replicate earlier, whereas sequences around the NWBs replicate late (Supplemental Fig. S14B). Lastly, the major activities of DNA replication within the five types of replication domains occur in different phases of the cell cycle: For example, the early replication domains mainly focus on G1 and S1 phases; the three types of transition domains correspond to S2, S3, and S4 phases; and the replication of DNA sequences in the late replication domains concentrate in the G2 phase (Supplemental Fig. S16C). Taken together, we give an example to show the strong relationship between replication domains, boundary types, epigenomic modifications, DNA replication timing, and gene expression (Fig. 6C). Hence, the topological domains, as well as their replication types, may serve as a bridge to understand some cell type–specific gene expression patterns. For example, we observe a significant change in replication domain types between GM12878 and K562 around the genes ITGA4 and NCKAP1 (Supplemental Fig. S16D,E). ITGA4 encodes a homing receptor for lymphocytes, and it locates in an early replication domain accompanied by active modifications in GM12878 but resides in a late replication domain in K562 and shows a lower expression level. In contrast, NCKAP1 resides near the boundary of two earlier replication domains in K562 and stays in a boundary region near late replication domains and possesses lower expression in GM12878.

    Based on the normalized Repli-seq signals, we can also divide the ConsTADs into five clusters with different relative replication patterns (Fig. 6D). We defined the direction of replication for each domain cluster according to the average signal profiles (Fig. 6E). For most domains, replication starts from the boundary at one side and then extends to the other one. Some domains replicate inward from both boundaries, but one side replicates earlier, and only a small part of domains replicate from inside to the boundaries on both sides. These results are consistent with a previous study in which Petryk et al. (2016) found that replication origins in the human genome typically overlapped with TAD boundaries, whereas replication could terminate dispersedly between initiation zones. Moreover, the boundaries with earlier replication have stronger CTCF binding strength (Fig. 6F). We also observe a positive correlation between the CTCF signal and the DNA replication signal, as well as a negative correlation between the CTCF signal and the distance to replication origins for TAD boundaries (Supplemental Fig. S17F,G). These results suggest that the topological domains are the basic units of DNA replication and that the direction of replication within the domain is closely related to the CTCF binding strength around the boundary regions.

    And, last, we propose a novel model of replication domains (Fig. 6G). The topological domains serve as the basic units of DNA replication. We can divide them into early and late replication domains, as well as transition domains, which have stable and variable replication patterns, respectively. The direction of DNA replication within each domain is related to the CTCF profiles, and the boundary with a stronger CTCF binding strength tends to replicate earlier. Furthermore, each type of replication domain has a dominant epigenomic modification, such as H3K27ac for early replication domains, H3K27me3 for transition domains, and H3K9me3 for late replication domains, corresponding to active, facultative, and repressive chromatin states, respectively.

    Previous SectionNext Section

    Discussion

    In this study, we proposed a computational framework to integrate the TADs from 16 methods and constructed the TAD separation landscape based on their consensus. We showed that the TAD separation landscape not only could accurately depict the locations of boundaries but also served as an indicator to facilitate the comparison of topological structures across multiple cell lines. Moreover, we revealed three types of domain boundaries with different transcriptional activity, DNA replication timing, and enrichment patterns of repeat elements like Alu and TcMar-Tigger. And, last, we define the ConsTADs to represent the topological domains captured by the consensus of the 16 methods, which enhance our understanding of epigenomic patterns, chromatin state organization, and DNA replication model within topological domains.

    However, it should be noted that this study is a proof of principle of the ConsTADs by integrating 16 methods based on the Hi-C contact maps of Chromosome 2 at 50-kb resolution. We also performed the same process for the boundary voting, boundary type classification, and subsequent analyses on the whole genome (Supplemental Figs. S8, S17–S21). The boundary score can be used for genome-wide comparison of boundaries between different cell lines (Supplemental Fig. S8). The biological properties of ConsTADs from the whole genome remained the same as those from Chromosome 2 (Supplemental Figs. S17, S18). We indeed observed positive correlations between boundary score and boundary insulation strength, as well as the TF enrichment (Supplemental Fig. S19). All chromosomes can produce three types of boundary regions with similar properties to those found on Chromosome 2, indicating the conclusions are not chromosome specific (Supplemental Figs. S20, S21).

    We also performed the experiments on the Hi-C contact map of Chromosome 2 for K562 at a 10-kb resolution and still found such three types of boundary regions with similar properties (Supplemental Fig. S22A,B). Moreover, the new technique Micro-C can produce ultra-high-resolution contact maps (up to nucleosome resolution) and reveal the existence of some fine-scale domains (Hsieh et al. 2020). Similarly, we observed that different methods identified very inconsistent domains on the Micro-C contact maps, and we can define consensus domains and corresponding boundary regions by integrating the results of different methods (Supplemental Fig. S22C,D). However, many traditional TAD-calling methods were not designed to handle Micro-C data. The high-dimensional Micro-C contact maps contain many fine-scale topological domains with more obscure boundaries. Therefore, the reliability and properties of these consensus domains obtained from Micro-C data still need to be further explored.

    In addition, the proposed strategy for defining the TAD separation landscape and ConsTADs can be easily extended to more TAD-calling methods or can flexibly exclude some of them. We evaluated the similarity between ConsTADs and the TADs detected by 16 TAD-calling methods and suggested a light version of ConsTADs by integrating 10 pivotal methods to reduce the difficulty of running multiple methods while ensuring that the results are consistent with those obtained by using all methods (Supplemental Fig. S23). We hope more researchers can benefit from it.

    There are several directions for future studies. First, the TAD separation landscape can contribute to exploring the dynamics of chromatin organization across a series of time points or developmental stages in some biological processes such as the cell cycle or embryonic development. Second, the three types of boundaries can be used to explore the topological organization in the bulk Hi-C contact maps and those for individual cells. For example, Su et al. (2020) presented a high-throughput imaging platform to assay the 3D organization of chromatin at the genome scale in thousands of cells, and they defined the probability for each genomic region serving as the TAD boundary in a population of IMR-90 single cells. We found that the genome regions corresponding to the three types of boundary regions also show higher boundary probabilities than those labeled as nonboundaries (Supplemental Fig. S22E). The regions labeled as WBs and NSBs could serve as domain boundaries in more cells and correspond to some apparent boundary structures in the proximity frequency matrix built from all single cells, whereas the regions belonging to NWBs might act as dynamic boundaries among single cells and correspond to some weaker boundaries in the proximity frequency matrix (Supplemental Fig. S22F). These results reflected the high heterogeneity of topological domains at the single-cell level, and the boundary regions we defined may be able to reflect the conservation and the dynamics of domain boundaries among single cells.

    Previous SectionNext Section

    Methods

    Data sets

    We used in situ Hi-C contact maps for seven human cell lines, including GM12878, HMEC, HUVEC, IMR-90, K562, KBM7, and NHEK (obtained from the NCBI Gene Expression Omnibus [GEO; https://www.ncbi.nlm.nih.gov/geo/] accession number GSE63525) and find TADs at 50-kb resolution. We collected corresponding ChIP-seq, DNase-seq, Repli-seq, and RNA-seq data for these cell lines. We also got the chromatin states annotated by ChromHMM (Ernst and Kellis 2012) and Segway (Libbrecht et al. 2015), as well as the subcompartment annotated by SNIPER (Xiong and Ma 2019) for these cell lines. The details of the data used in this study are reported in Supplemental Table S1.

    TAD-calling methods

    We collected 16 TAD-calling methods for comparison and integration, including some classical ones, such as DI (Dixon et al. 2012) and IS (Crane et al. 2015), as well as methods like TopDom (Shin et al. 2016), which was considered to perform well in the tests of Zufferey et al. (2018). But methods like TADtree (Weinreb and Raphael 2016), TADbit (Serra et al. 2017), and matryoshka (Malik and Patro 2019) run too slow, and some methods like Arrowhead (Rao et al. 2014) with rare requirements on the input data format were excluded from this study. In addition, we also introduced some newly developed methods such as deDoc (Li et al. 2018) and MSTD (Ye et al. 2019).

    We used the iterative correction and eigenvector decomposition method (ICE) (Imakaev et al. 2012) for Hi-C data normalization and then tried to use these TAD-calling methods with default parameters or set the parameters according to the investigators’ recommendations (Supplemental Table S2). We also recorded the computation time and memory used by these methods (Supplemental Table S3). Moreover, among the 16 methods we adopted, three methods including HiTAD, OnTAD, and 3DNetMod claimed that they could reveal hierarchical TADs. For these methods, we extracted domains with the lowest level to preserve both high- and low-level boundaries (Supplemental Fig. S1A).

    Boundary voting strategy

    We integrated the results of different TAD-calling methods with a strategy of boundary voting. In this process, we first extract the boundary sets of each method and divide them into start boundaries and end boundaries. The bin identified as a boundary can get one score. Thus, we can get two boundary score profiles for start and end boundaries, respectively. Then, we take the profile of maximum value between these two boundary score profiles to ensure that a method contributes, at most, one score to a bin. Finally, the profiles of boundary scores obtained by all these methods are summed; thus, a boundary score is assigned to each bin along the genome, representing the number of methods that define it as the boundary of a TAD (Fig. 3A; Supplemental Fig. S2C).

    Assessment of the reliability of boundaries with different scores

    Bins with non-zero boundary scores formed the collection of candidate boundary sets. These boundaries were divided into five intervals with different scores. We then adopted three kinds of 1D topological indicators, including the directionality index (DI), insulation score (IS), and contrast index (CI), as well as three kinds of structural biological markers, including CTCF, RAD21, and SMC3, to assess the reliability of boundaries in different score intervals. These three 1D topological indicators are computed according to Supplemental Figure S3A. Here, we showed the profiles of three 1D topological indicators and three structural proteins for boundaries in each score interval (Fig. 2B).

    Construction of the TAD separation landscape

    Based on the boundary voting strategy, we got the original boundary score profile for bins along the genome. We then introduced the contrast P-value to refine the original boundary score profile.

    First, we applied a distance-dependent Z-score normalization to the Hi-C contact map to alleviate the effect of genomic distance on the strength of the contact frequency. The normalization was performed by calculating the Z-score for the chromatin interactions at each distance (Supplemental Fig. S5A). Then we used a single-side Mann–Whitney U test to check whether the insulation region showed weaker contacts compared with the upstream and downstream regions and to get the contrast P-value. A small contrast P-value reflects strong insulation of chromatin contact at the current bin. We presented different window sizes for the calculation of the contrast P-value and selected the most suitable one according to the Pearson's correlation between the original boundary score profile and the contrast P-value profiles with different windows (Supplemental Fig. S5B). We then used the profile of the contrast P-value as a reference and refined the original boundary score profile by three kinds of operations, including add, filter, and combine. The add operation will add one score to bins with zero boundary scores but with contrast P-values below a preset cutoff. The filter operation will turn the boundary scores to zero for bins with P-values greater than the cutoff, but the boundary scores are kept for bins in the valleys of P-value profiles. The combine operation will combine two adjacent boundary regions separated by one bin gap, and the gap will be filled with the average boundary score of the upper and lower bins (Supplemental Fig. S5C). In this study, we set a cutoff of 0.05 for the contrast P-value. We termed the refined boundary score profile as the TAD separation landscape, which could accurately depict the regions of the TAD boundary and was highly consistent with the domain patterns in Hi-C contact maps (Supplemental Fig. S5D).

    Analyses of TAD separation landscapes of multiple cell lines

    We built the TAD separation landscapes for seven human cell lines, including GM12878, HMEC, HUVEC, IMR-90, K562, KBM7, and NHEK; combined them with other data to explore their biological significance; and used them as references for deciphering conserved and cell type–specific boundary regions among multiple cell lines.

    We performed the comparison of TAD separation landscapes constructed for different cell lines. For the pairwise comparison of two cell lines, we first identified the core boundary regions between them. We added up the TAD separation landscapes of the two cell lines and used a cutoff to filter out bins with scores below two, which meant that the scores of these bins were converted to zero in the added score profile. We defined the consecutive bins with non-zero scores in the added score profile as core boundary regions. For each core boundary region, we examined the maximum score of the corresponding region in the TAD separation landscapes of the two cell lines. If the maximum scores of core regions in the two cell lines are both above five, we defined them as conserved boundary regions. For a core boundary region, if the maximum score exceeds five only in one cell line whereas the maximum score does not exceed two in the other one and if the difference between these two maximum scores is equal to or greater than five, then we consider it as a cell type–specific boundary region. For multiple comparisons of cell lines, we also added up the TAD separation landscapes and filtered bins with a cutoff of five to identify the core boundary regions. If the maximum score of the corresponding region was larger than five in the TAD separation landscape of a certain cell line, we consider this cell line to possess this core boundary region. Thus, we can identify the boundary regions that are conserved in all seven cell lines, that specifically occurred in a certain cell line (Supplemental Fig. S9), or that are shared by several cell lines (Supplemental Fig. S10).

    Identification of three types of boundary regions

    The continuous bins with non-zero boundary scores in the TAD separation landscape form the boundary regions. For each boundary region, the region length and average boundary score form a two-dimensional feature vector. We then performed the k-means clustering for all boundary regions. According to the sum of squared error and silhouette coefficient, we found that the number of clusters should be set to three. We used k-means to initially divide the boundary regions into three types, and for the one with the longest region lengths, we selected the 10% quantile of their region lengths as the threshold to separate out the wide boundary regions (WBs). For the remaining two types of narrower boundaries, one type had a larger boundary score, and we selected the 10% quantile of their boundary score as the threshold and divided the two clusters into narrow-strong boundary regions (NSBs) and narrow-weak boundary regions (NWBs) (Supplemental Fig. S11).

    Boundary region conservation across cell lines

    If one boundary region shows up in two cell lines and the boundary type remains the same, we consider it to be conserved between these two cell lines. Hence, for boundary regions from each cell line, we computed and displayed the ratio of cell lines in which it was considered as conserved (Fig. 5D).

    Enrichment analysis of epigenomic modifications and DNA replication timing

    We collected the track signals in bigWig format for multiple biological features including histone modifications, TF binding, DNA methylation, chromatin accessibility, gene expression, and DNA replication timing to explore their enrichment in three types of boundary regions. For each kind of data, we first computed the average signal in each 50-kb bin along the chromosome and selected the median values of these average signals as the background. We then calculated the average signal in each boundary region and extracted the median values for each boundary type. And, last, the fold change was obtained by dividing the boundary values by the background across the chromosome (Fig. 5G).

    As for the Repli-seq data for six phases of the cell cycle, we got the average values in all 50-kb bins along the chromosome and used the mean value of them as the background. Then the values in each bin were divided by the background to get the fold change. Finally, the profile of these fold changes around three types of boundary regions was displayed according to the order of the phases in the cell cycle (Fig. 5H; Supplemental Fig. S20G).

    Enrichment analysis of chromatin states and subcompartments in boundary regions or domains

    For each type of boundary regions or domains, we calculated the fold change (FC) of the enrichment for chromatin states or subcompartments by dividing the observed state or subcompartment lengths into boundaries or domains by the expected lengths across the chromosome (Fig. 5I).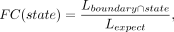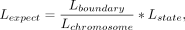Formula Formula where the 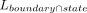Formula denotes the length of overlap between a region and a chromatin state or subcompartment, and Lboundary, Lstate, and Lchromosome represent the total lengths of regions, chromatin state, and chromosome, respectively.

    Enrichment analysis of repeat elements in boundary regions

    We collected repeat elements of the human genome (GRCh37). For each boundary region, we randomly selected 500 regions with an equal length to it and counted the number of repeat elements located in the boundary region and these random regions, respectively. We then calculated the enrichment Z-score of repeat elements in the boundary region based on the mean and variance of the elements in random regions. Hence, a Z-score above one indicates the repeat element is enriched in the boundary region (Fig. 5J; Supplemental Fig. S13). For subfamilies of Alu element and TcMar-Tigger, we also compared the counts per million (CPM) in boundary regions and randomly selected regions (Fig. 5K; Supplemental Fig. S21D), and the results of this analysis remained the same when using more recent reference genome GRCh38 (Supplemental Fig. S21E).

    Enrichment analysis of TFs in boundary regions

    First, we collected the accessible loci located in boundary regions based on DNase-seq data and extracted their DNA sequences. Then we used HOMER (Heinz et al. 2010) to find the TF motifs in these DNA sequences and calculated the significance of their enrichment with the hypergeometric test. TFs were then ranked according to their P-values, and the top 25 or 20 TFs for each type of boundary region were selected for comparison (Supplemental Figs. S8E,F, S14C,D).

    Analysis of the epigenomic patterns within ConsTADs

    For each domain, we extended 20% of the domain length upstream and downstream, respectively. Then, the domains together with their flanking areas were divided into 700 intervals with equal length, and the mean epigenomic signal in each interval was calculated. For each domain, the 700-dimensional epigenomic signal vector was scaled by min-max normalization. We then calculated the average signal profile across all ConsTADs and applied the function scipy.signal.savgol_filter in a Python package called SciPy (Virtanen et al. 2020), to smooth the profiles for visualization (Fig. 6A; Supplemental Fig. S18A).

    Clustering topological domains based on DNA replication signals

    The wavelet-smoothed signals are a weighted average of Repli-seq signals from six phases of the cell cycle, in which higher values correspond to earlier replication. Each domain was divided into 500 equal-length intervals, and the average wavelet-smoothed signals of Repli-seq for each interval were calculated. Then, an agglomerative clustering using Ward linkage with Euclidean distance was used to get five kinds of replication domain clusters (Supplemental Fig. S15E).

    We also obtained the relative DNA replication signal within each domain by using the min-max normalization to show the relative early or late of DNA replication among regions inside the domain. We then applied the agglomerative clustering to these normalized signals of ConsTADs and got five clusters with distinct relative replication modes (Fig. 6E).

    Computation time and RAM used by 16 methods and ConsTADs

    We tested the 16 TAD-calling methods on Hi-C contact maps at 50-kb resolution for all GM12878 chromosomes and recorded the total and maximum computational time and RAM. The detailed information was listed in Supplemental Table S3. We also recorded the runtime and memory consumption of the ConsTADs procedure. The results are shown in Supplemental Figure S19, A and B. All these tests were performed on a computer with Intel Core i9-10920X CPU at 3.50 GHz.

    Software availability

    The ConsTADs source code is available as Supplemental Code and at GitHub (https://github.com/zhanglabtools/ConsTADs).

    Previous SectionNext Section

    Competing interest statement

    The authors declare no competing interests.

    Previous SectionNext Section

    Acknowledgments

    This work has been supported by the National Key Research and Development Program of China (2021YFA1302500 and 2019YFA0709501), the National Natural Science Foundation of China (62173271, 61873202, 61621003), the Strategic Priority Research Program of the Chinese Academy of Sciences (CAS; XDPB17), and the Key-Area Research and Development of Guangdong Province (2020B1111190001).

    Previous SectionNext Section

    Footnotes

    • Received August 8, 2022.
    • Accepted February 23, 2023.

    This article is distributed exclusively by Cold Spring Harbor Laboratory Press for the first six months after the full-issue publication date (see https://genome.cshlp.org/site/misc/terms.xhtml). After six months, it is available under a Creative Commons License (Attribution-NonCommercial 4.0 International), as described at http://creativecommons.org/licenses/by-nc/4.0/.

    Previous Section
     

    References

    1. ↵
      An L, Yang T, Yang J, Nuebler J, Xiang G, Hardison RC, Li Q, Zhang Y. 2019. OnTAD: hierarchical domain structure reveals the divergence of activity among TADs and boundaries. Genome Biol 20: 282. doi:10.1186/s13059-019-1893-y
      CrossRefGoogle Scholar
    2. ↵
      Bernstein BE, Mikkelsen TS, Xie X, Kamal M, Huebert DJ, Cuff J, Fry B, Meissner A, Wernig M, Plath K, et al. 2006. A bivalent chromatin structure marks key developmental genes in embryonic stem cells. Cell 125: 315–326. doi:10.1016/j.cell.2006.02.041
      CrossRefMedlineGoogle Scholar
    3. ↵
      Bintu B, Mateo LJ, Su JH, Sinnott-Armstrong NA, Parker M, Kinrot S, Yamaya K, Boettiger AN, Zhuang X. 2018. Super-resolution chromatin tracing reveals domains and cooperative interactions in single cells. Science 362: eaau1783. doi:10.1126/science.aau1783
      Abstract/FREE Full Text
    4. ↵
      Blanco E, González-Ramirez M, Alcaine-Colet A, Aranda S, Di Croce L. 2020. The bivalent genome: characterization, structure, and regulation. Trends Genet 36: 118–131. doi:10.1016/j.tig.2019.11.004
      CrossRefMedlineGoogle Scholar
    5. ↵
      Chen J, Hero AO 3rd., Rajapakse I. 2016. Spectral identification of topological domains. Bioinformatics 32: 2151–2158. doi:10.1093/bioinformatics/btw221
      CrossRefMedlineGoogle Scholar
    6. ↵
      Chen F, Li G, Zhang MQ, Chen Y. 2018. HiCDB: a sensitive and robust method for detecting contact domain boundaries. Nucleic Acids Res 46: 11239–11250. doi:10.1093/nar/gky789
      CrossRefGoogle Scholar
    7. ↵
      Crane E, Bian Q, McCord RP, Lajoie BR, Wheeler BS, Ralston EJ, Uzawa S, Dekker J, Meyer BJ. 2015. Condensin-driven remodelling of X chromosome topology during dosage compensation. Nature 523: 240–244. doi:10.1038/nature14450
      CrossRefMedlineGoogle Scholar
    8. ↵
      Cremer T, Cremer C. 2001. Chromosome territories, nuclear architecture and gene regulation in mammalian cells. Nat Rev Genet 2: 292–301. doi:10.1038/35066075
      CrossRefMedlineGoogle Scholar
    9. ↵
      Dali R, Blanchette M. 2017. A critical assessment of topologically associating domain prediction tools. Nucleic Acids Res 45: 2994–3005. doi:10.1093/nar/gkx145
      CrossRefGoogle Scholar
    10. ↵
      Dekker J, Rippe K, Dekker M, Kleckner N. 2002. Capturing chromosome conformation. Science 295: 1306–1311. doi:10.1126/science.1067799
      Abstract/FREE Full Text
    11. ↵
      Dixon JR, Selvaraj S, Yue F, Kim A, Li Y, Shen Y, Hu M, Liu JS, Ren B. 2012. Topological domains in mammalian genomes identified by analysis of chromatin interactions. Nature 485: 376–380. doi:10.1038/nature11082
      CrossRefMedlineGoogle Scholar
    12. ↵
      Dixon JR, Gorkin DU, Ren B. 2016. Chromatin domains: the unit of chromosome organization. Mol Cell 62: 668–680. doi:10.1016/j.molcel.2016.05.018
      CrossRefMedlineGoogle Scholar
    13. ↵
      Dixon JR, Xu J, Dileep V, Zhan Y, Song F, Le VT, Yardimci GG, Chakraborty A, Bann DV, Wang Y, et al. 2018. Integrative detection and analysis of structural variation in cancer genomes. Nat Genet 50: 1388–1398. doi:10.1038/s41588-018-0195-8
      CrossRefMedlineGoogle Scholar
    14. ↵
      Dostie J, Richmond TA, Arnaout RA, Selzer RR, Lee WL, Honan TA, Rubio ED, Krumm A, Lamb J, Nusbaum C, et al. 2006. Chromosome Conformation Capture Carbon Copy (5C): a massively parallel solution for mapping interactions between genomic elements. Genome Res 16: 1299–1309. doi:10.1101/gr.5571506
      Abstract/FREE Full Text
    15. ↵
      Eres IE, Gilad Y. 2021. A TAD skeptic: Is 3D genome topology conserved? Trends Genet 37: 216–223. doi:10.1016/j.tig.2020.10.009
      CrossRefGoogle Scholar
    16. ↵
      Ernst J, Kellis M. 2012. ChromHMM: automating chromatin-state discovery and characterization. Nat Methods 9: 215–216. doi:10.1038/nmeth.1906
      CrossRefMedlineGoogle Scholar
    17. ↵
      Forcato M, Nicoletti C, Pal K, Livi CM, Ferrari F, Bicciato S. 2017. Comparison of computational methods for Hi-C data analysis. Nat Methods 14: 679–685. doi:10.1038/nmeth.4325
      CrossRefMedlineGoogle Scholar
    18. ↵
      Haddad N, Vaillant C, Jost D. 2017. IC-Finder: inferring robustly the hierarchical organization of chromatin folding. Nucleic Acids Res 45: e81. doi:10.1093/nar/gkx036
      CrossRefMedlineGoogle Scholar
    19. ↵
      Hansen AS, Pustova I, Cattoglio C, Tjian R, Darzacq X. 2017. CTCF and cohesin regulate chromatin loop stability with distinct dynamics. eLife 6: e25776. doi:10.7554/eLife.25776
      CrossRefMedlineGoogle Scholar
    20. ↵
      Heinz S, Benner C, Spann N, Bertolino E, Lin YC, Laslo P, Cheng JX, Murre C, Singh H, Glass CK. 2010. Simple combinations of lineage-determining transcription factors prime cis-regulatory elements required for macrophage and B cell identities. Mol Cell 38: 576–589. doi:10.1016/j.molcel.2010.05.004
      CrossRefMedlineGoogle Scholar
    21. ↵
      Hsieh TS, Cattoglio C, Slobodyanyuk E, Hansen AS, Rando OJ, Tjian R, Darzacq X. 2020. Resolving the 3D landscape of transcription-linked mammalian chromatin folding. Mol Cell 78: 539–553.e8. doi:10.1016/j.molcel.2020.03.002
      CrossRefMedlineGoogle Scholar
    22. ↵
      Imakaev M, Fudenberg G, McCord RP, Naumova N, Goloborodko A, Lajoie BR, Dekker J, Mirny LA. 2012. Iterative correction of Hi-C data reveals hallmarks of chromosome organization. Nat Methods 9: 999–1003. doi:10.1038/nmeth.2148
      CrossRefMedlineGoogle Scholar
    23. ↵
      Kumar D, Cinghu S, Oldfield AJ, Yang P, Jothi R. 2021. Decoding the function of bivalent chromatin in development and cancer. Genome Res 31: 2170–2184. doi:10.1101/gr.275736.121
      Abstract/FREE Full Text
    24. ↵
      Lévy-Leduc C, Delattre M, Mary-Huard T, Robin S. 2014. Two-dimensional segmentation for analyzing Hi-C data. Bioinformatics 30: i386–i392. doi:10.1093/bioinformatics/btu443
      CrossRefMedlineGoogle Scholar
    25. ↵
      Li A, Yin X, Xu B, Wang D, Han J, Wei Y, Deng Y, Xiong Y, Zhang Z. 2018. Decoding topologically associating domains with ultra-low resolution Hi-C data by graph structural entropy. Nat Commun 9: 3265. doi:10.1038/s41467-018-05691-7
      CrossRefGoogle Scholar
    26. ↵
      Libbrecht MW, Ay F, Hoffman MM, Gilbert DM, Bilmes JA, Noble WS. 2015. Joint annotation of chromatin state and chromatin conformation reveals relationships among domain types and identifies domains of cell-type-specific expression. Genome Res 25: 544–557. doi:10.1101/gr.184341.114
      Abstract/FREE Full Text
    27. ↵
      Lieberman-Aiden E, van Berkum NL, Williams L, Imakaev M, Ragoczy T, Telling A, Amit I, Lajoie BR, Sabo PJ, Dorschner MO, et al. 2009. Comprehensive mapping of long-range interactions reveals folding principles of the human genome. Science 326: 289–293. doi:10.1126/science.1181369
      Abstract/FREE Full Text
    28. ↵
      Liu Y, Nanni L, Sungalee S, Zufferey M, Tavernari D, Mina M, Ceri S, Oricchio E, Ciriello G. 2021. Systematic inference and comparison of multi-scale chromatin sub-compartments connects spatial organization to cell phenotypes. Nat Commun 12: 2439. doi:10.1038/s41467-021-22666-3
      CrossRefGoogle Scholar
    29. ↵
      Luo X, Liu Y, Dang D, Hu T, Hou Y, Meng X, Zhang F, Li T, Wang C, Li M, et al. 2021. 3D genome of macaque fetal brain reveals evolutionary innovations during primate corticogenesis. Cell 184: 723–740.e21. doi:10.1016/j.cell.2021.01.001
      CrossRefGoogle Scholar
    30. ↵
      Lupiáñez Darío G, Kraft K, Heinrich V, Krawitz P, Brancati F, Klopocki E, Horn D, Kayserili H, Opitz John M, Laxova R, et al. 2015. Disruptions of topological chromatin domains cause pathogenic rewiring of gene-enhancer interactions. Cell 161: 1012–1025. doi:10.1016/j.cell.2015.04.004
      CrossRefMedlineGoogle Scholar
    31. ↵
      Malik L, Patro R. 2019. Rich chromatin structure prediction from Hi-C data. IEEE/ACM Trans Comput Biol Bioinform 16: 1448–1458. doi:10.1109/TCBB.2018.2851200
      CrossRefGoogle Scholar
    32. ↵
      McArthur E, Capra JA. 2021. Topologically associating domain boundaries that are stable across diverse cell types are evolutionarily constrained and enriched for heritability. Am J Hum Genet 108: 269–283. doi:10.1016/j.ajhg.2021.01.001
      CrossRefMedlineGoogle Scholar
    33. ↵
      Norton HK, Emerson DJ, Huang H, Kim J, Titus KR, Gu S, Bassett DS, Phillips-Cremins JE. 2018. Detecting hierarchical genome folding with network modularity. Nat Methods 15: 119–122. doi:10.1038/nmeth.4560
      CrossRefGoogle Scholar
    34. ↵
      Oluwadare O, Cheng J. 2017. ClusterTAD: an unsupervised machine learning approach to detecting topologically associated domains of chromosomes from Hi-C data. BMC Bioinformatics 18: 480. doi:10.1186/s12859-017-1931-2
      CrossRefGoogle Scholar
    35. ↵
      Petryk N, Kahli M, d'Aubenton-Carafa Y, Jaszczyszyn Y, Shen Y, Silvain M, Thermes C, Chen CL, Hyrien O. 2016. Replication landscape of the human genome. Nat Commun 7: 10208. doi:10.1038/ncomms10208
      CrossRefMedlineGoogle Scholar
    36. ↵
      Pope BD, Ryba T, Dileep V, Yue F, Wu W, Denas O, Vera DL, Wang Y, Hansen RS, Canfield TK, et al. 2014. Topologically associating domains are stable units of replication-timing regulation. Nature 515: 402–405. doi:10.1038/nature13986
      CrossRefMedlineGoogle Scholar
    37. ↵
      Rao SS, Huntley MH, Durand NC, Stamenova EK, Bochkov ID, Robinson JT, Sanborn AL, Machol I, Omer AD, Lander ES, et al. 2014. A 3D map of the human genome at kilobase resolution reveals principles of chromatin looping. Cell 159: 1665–1680. doi:10.1016/j.cell.2014.11.021
      CrossRefMedlineGoogle Scholar
    38. ↵
      Sanz LA, Chamberlain S, Sabourin JC, Henckel A, Magnuson T, Hugnot JP, Feil R, Arnaud P. 2008. A mono-allelic bivalent chromatin domain controls tissue-specific imprinting at Grb10. EMBO J 27: 2523–2532. doi:10.1038/emboj.2008.142
      CrossRefMedlineGoogle Scholar
    39. ↵
      Schmitt AD, Hu M, Jung I, Xu Z, Qiu Y, Tan CL, Li Y, Lin S, Lin Y, Barr CL, et al. 2016. A compendium of chromatin contact maps reveals spatially active regions in the human genome. Cell Rep 17: 2042–2059. doi:10.1016/j.celrep.2016.10.061
      CrossRefMedlineGoogle Scholar
    40. ↵
      Serra F, Baù D, Goodstadt M, Castillo D, Filion GJ, Marti-Renom MA. 2017. Automatic analysis and 3D-modelling of Hi-C data using TADbit reveals structural features of the fly chromatin colors. PLoS Comput Biol 13: e1005665. doi:10.1371/journal.pcbi.1005665
      CrossRefGoogle Scholar
    41. ↵
      Shin H, Shi Y, Dai C, Tjong H, Gong K, Alber F, Zhou XJ. 2016. TopDom: an efficient and deterministic method for identifying topological domains in genomes. Nucleic Acids Res 44: e70–e70. doi:10.1093/nar/gkv1505
      CrossRefMedlineGoogle Scholar
    42. ↵
      Simonis M, Klous P, Splinter E, Moshkin Y, Willemsen R, de Wit E, van Steensel B, de Laat W. 2006. Nuclear organization of active and inactive chromatin domains uncovered by chromosome conformation capture–on-chip (4C). Nat Genet 38: 1348–1354. doi:10.1038/ng1896
      CrossRefMedlineGoogle Scholar
    43. ↵
      Soufi A, Donahue G, Zaret KS. 2012. Facilitators and impediments of the pluripotency reprogramming factors’ initial engagement with the genome. Cell 151: 994–1004. doi:10.1016/j.cell.2012.09.045
      CrossRefMedlineGoogle Scholar
    44. ↵
      Spielmann M, Lupiáñez DG, Mundlos S. 2018. Structural variation in the 3D genome. Nat Rev Genet 19: 453–467. doi:10.1038/s41576-018-0007-0
      CrossRefMedlineGoogle Scholar
    45. ↵
      Su JH, Zheng P, Kinrot SS, Bintu B, Zhuang X. 2020. Genome-scale imaging of the 3D organization and transcriptional activity of chromatin. Cell 182: 1641–1659 e1626. doi:10.1016/j.cell.2020.07.032
      CrossRefMedlineGoogle Scholar
    46. ↵
      Szabo Q, Bantignies F, Cavalli G. 2019. Principles of genome folding into topologically associating domains. Sci Adv 5: eaaw1668. doi:10.1126/sciadv.aaw1668
      FREE Full Text
    47. ↵
      Taberlay PC, Achinger-Kawecka J, Lun AT, Buske FA, Sabir K, Gould CM, Zotenko E, Bert SA, Giles KA, Bauer DC, et al. 2016. Three-dimensional disorganization of the cancer genome occurs coincident with long-range genetic and epigenetic alterations. Genome Res 26: 719–731. doi:10.1101/gr.201517.115
      Abstract/FREE Full Text
    48. ↵
      Tang Z, Luo OJ, Li X, Zheng M, Zhu JJ, Szalaj P, Trzaskoma P, Magalska A, Wlodarczyk J, Ruszczycki B, et al. 2015. CTCF-mediated human 3D genome architecture reveals chromatin topology for transcription. Cell 163: 1611–1627. doi:10.1016/j.cell.2015.11.024
      CrossRefMedlineGoogle Scholar
    49. ↵
      Vastenhouw NL, Schier AF. 2012. Bivalent histone modifications in early embryogenesis. Curr Opin Cell Biol 24: 374–386. doi:10.1016/j.ceb.2012.03.009
      CrossRefMedlineGoogle Scholar
    50. ↵
      Vietri Rudan M, Barrington C, Henderson S, Ernst C, Odom DT, Tanay A, Hadjur S. 2015. Comparative Hi-C reveals that CTCF underlies evolution of chromosomal domain architecture. Cell Rep 10: 1297–1309. doi:10.1016/j.celrep.2015.02.004
      CrossRefMedlineGoogle Scholar
    51. ↵
      Virtanen P, Gommers R, Oliphant TE, Haberland M, Reddy T, Cournapeau D, Burovski E, Peterson P, Weckesser W, Bright J, et al. 2020. SciPy 1.0: fundamental algorithms for scientific computing in Python. Nat Methods 17: 261–272. doi:10.1038/s41592-019-0686-2
      CrossRefMedlineGoogle Scholar
    52. ↵
      Wang Y, Li Y, Gao J, Zhang MQ. 2015. A novel method to identify topological domains using Hi-C data. Quant Biol 3: 81–89. doi:10.1007/s40484-015-0047-9
      CrossRefGoogle Scholar
    53. ↵
      Wang XT, Cui W, Peng C. 2017. HiTAD: detecting the structural and functional hierarchies of topologically associating domains from chromatin interactions. Nucleic Acids Res 45: e163. doi:10.1093/nar/gkx735
      CrossRefGoogle Scholar
    54. ↵
      Weinreb C, Raphael BJ. 2016. Identification of hierarchical chromatin domains. Bioinformatics 32: 1601–1609. doi:10.1093/bioinformatics/btv485
      CrossRefMedlineGoogle Scholar
    55. ↵
      Xiong K, Ma J. 2019. Revealing Hi-C subcompartments by imputing inter-chromosomal chromatin interactions. Nat Commun 10: 5069. doi:10.1038/s41467-019-12954-4
      CrossRefGoogle Scholar
    56. ↵
      Ye Y, Gao L, Zhang S. 2019. MSTD: an efficient method for detecting multi-scale topological domains from symmetric and asymmetric 3D genomic maps. Nucleic Acids Res 47: e65. doi:10.1093/nar/gkz201
      CrossRefGoogle Scholar
    57. ↵
      Yu W, He B, Tan K. 2017. Identifying topologically associating domains and subdomains by Gaussian mixture model and proportion test. Nat Commun 8: 535. doi:10.1038/s41467-017-00478-8
      CrossRefGoogle Scholar
    58. ↵
      Zhan Y, Mariani L, Barozzi I, Schulz EG, Blüthgen N, Stadler M, Tiana G, Giorgetti L. 2017. Reciprocal insulation analysis of Hi-C data shows that TADs represent a functionally but not structurally privileged scale in the hierarchical folding of chromosomes. Genome Res 27: 479–490. doi:10.1101/gr.212803.116
      Abstract/FREE Full Text
    59. ↵
      Zufferey M, Tavernari D, Oricchio E, Ciriello G. 2018. Comparison of computational methods for the identification of topologically associating domains. Genome Biol 19: 217. doi:10.1186/s13059-018-1596-9
      CrossRefGoogle Scholar

    Articles citing this article

    • An integrative TAD catalog in lymphoblastoid cell lines discloses the functional impact of deletions and insertions in human genomes Genome Res December 1, 2024 34: 2304-2318
    • Uncovering topologically associating domains from three-dimensional genome maps with TADGATE bioRxiv June 18, 2024 0: 2024.06.12.598668v1-2024.06.12.598668
    • A comprehensive catalog of 3D genome organization in diverse human genomes facilitates understanding of the impact of structural variation on chromatin structure bioRxiv May 18, 2023 0: 2023.05.15.540856v1-2023.05.15.540856
    | Table of Contents

    This Article

    1. Published in Advance March 9, 2023, doi: 10.1101/gr.277187.122 Genome Res. 33: 386-400 © 2023 Dang et al.; Published by Cold Spring Harbor Laboratory Press

    Article Category

    Share

    Preprint Server



    Navigate This Article

    Current Issue

    1. February 2026, 36 (2)
    1. Current Issue
    1. Alert me to new issues of Genome Research