Saturation mutagenesis reveals manifold determinants of exon definition

Saturation mutagenesis strategy

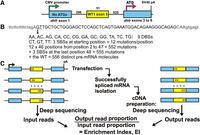
We constructed a three-exon minigene (Ke et al. 2011) comprised of a 51-nt central target exon WT1-5 (exon 5 of the human Wilms’ tumor gene 1) surrounded by terminal exons and intronic sequences derived from the Chinese hamster dhfr gene. Thousands of DNA exons were synthesized to specification by primer-extension of a custom DNA microarray. Minigene libraries that incorporated these oligomers into a central exon in a three-exon minigene were then prepared (Fig. 1A). Key features of the minigene framework were the provision of strong promoter (CMV) and polyadenylation (SV40) site and the removal of all start codons from the first exon (Arias et al. 2015) to minimize the chance of nonsense-mediated decay (NMD). The latter is already unlikely due to the modest size of the central exon (Maquat 2004). The splicing of this central exon in this framework requires exon definition, as mutations that compromise splicing have never been seen to yield intron-retained products (Zhang et al. 2005a,c). At each exonic position from 2 to 47, each dinucleotide in the WT1-5 exon was changed to every other possible dinucleotide (Fig. 1B). Positions 1 and 49 to 51 were left unmodified so as not to consider mutations affecting the splice site sequences themselves. The resulting mutant library comprised 555 mutations: 414 double base substitutions (DBSs) and 141 single base substitutions (SBSs) at each position from 2 to 47 and three SBSs mutations at position 48. Including the wild type, there were a total of 556 distinct molecules (Fig. 1B). Splicing of the WT exon takes place with an efficiency (percent spliced in, PSI; presented here as a proportion) of 0.065 (Ke et al. 2011); this low level is the result of depriving WT1-5 of its natural flanking intronic sequences (Zhang et al. 2005c). The modest splicing efficiency of the WT minigene was purposely engineered to allow detection of mutations that increase (up to 16-fold) as well as decrease (to 0) splicing efficiency.

View larger version:

• In this window
• In a new window

• Download as PowerPoint Slide

Figure 1.

Saturation mutagenesis scheme. (A) Minigene used for splicing studies. The central exon target was Wilms' tumor gene 1 exon 5. All ATG triplets were removed from dhfr exon 1 to minimize the chance of nonsense-mediated decay (NMD). A Kozak ATG sequence was added to dhfr exon 3 to allow mRNA to associate with polysomes. (B) Mutagenesis scheme. At each exon position from 2 to 47, all possible DBSs and SBSs were represented. (C) The input libraries as PCR products and the output libraries as amplified cDNA were deep-sequenced, and the ratio of the relative abundance of these output mutant molecules to the corresponding input abundance was designated the enrichment index (EI).

To pursue possible combinatorial effects of sequence changes, we additionally designed nine variations of the WT1-5 exon, substituting nine different hexamers for the WT stretch from positions 5 to 10, the effects of which we had previously documented (Ke et al. 2011). The final mutant library was thus comprised of a series of 10 “Hexmuts (HMs)” A to J, where HexmutA (HMA) is the true WT. These hexamers were chosen to match known splicing factor binding sites or to have other sequence characteristics as described in Table 1. The PSI values of the 10 relative WT HMs had previously been measured and ranged from 0.01 to 0.75 (Ke et al. 2011). The complete library thus consisted of 556 × 10 = 5560 molecules, including the 10 relative WT sequences.

The minigene library was constructed by incorporating these oligomers into ∼3-kb PCR product molecules using methods we have previously described (Ke et al. 2011). The minigene library (the input) was transfected into human HEK293 cells, and after 24 h of expression, the successfully spliced RNA molecules were isolated as size-selected RT-PCR products (the output). Both the input and the output exons from duplicate transfections were then sequenced on an Illumina platform (Fig. 1C). Output proportions between the biological duplicates were highly reproducible (R² > 0.99) (Supplemental Fig. S1), as were enrichment index (EI) values (R² > 0.97,). All 5550 mutant molecules were represented as input reads, with a median read number of 1611 for the two duplicate experiments summed. All but two molecules were represented by at least 50 reads, and 99% had more than 200 reads, allowing detection of phenotypes at 1% of WT levels. The ratio of the output reads to the input reads for each sequence was termed the enrichment index, which is proportional to the PSI (Ke et al. 2011). In quantifying successfully spliced molecules, we considered any that failed to include the full exon as being splicing-deficient. In particular, splicing to cryptic sites would be detected as missing from the size-selected molecules and accordingly classified as failures to correctly splice. However, the overwhelming majority of such failures were due to complete exon skipping, as evidenced in gel electrophoresis (Ke et al. 2011).

Mutant splicing phenotypes of the WT exon HMA

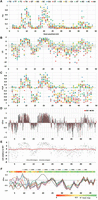
We have summarized the splicing phenotypes of the mutant populations in several ways to provide different perspectives. Figure 2 shows results for HMA, the true wild type. In Figure 2A, splicing is expressed as PSI, which was calculated from the EI values (Ke et al. 2011) and is a linear metric of splicing. In this plot, mutations with increased splicing are readily seen, some reaching the maximum PSI of 1, a 16-fold increase over the 0.065 PSI of WT HMA (gray dotted line in Fig. 2A). Mutations that substantially increase splicing of this exon were common and were clustered in several regions; 33% of all mutations led to an increase in splicing of twofold or more. Decreases in splicing are better visualized by plotting the log₂ of the EI (LEI) (Fig. 2B; see Table 2 for abbreviations).

View larger version:

• In this window
• In a new window

• Download as PowerPoint Slide

Figure 2.

Splicing phenotype maps of HMA. Terms used to express splicing efficiency can be found in Table 2. Different measures were used to quantify splicing: (A) PSI (proportion spliced in) exhibited by each molecule, calculated from EI (see Methods). This linear metric tends to hide the extent of decreases. The dotted gray line here and in B and C indicates the WT phenotype. (B) LEI, the log₂ of the EI, displaying a wide range of decreases at the expense of increases. The gray area encompasses changes that are less than twofold. (C) PUP, the proportion of the ultimate phenotype. The WT EI is set to zero and the EI of each mutant is normalized to the maximum change, treating increases and decreases separately and giving equal visual weight to both. In most HMs, the maximum splicing increase was to nearly 100% and the minimum was zero. (D) Landscape view: Each mutant is shown as a column; each starting position is comprised of 12 columns, one for each type of base change. Black columns, DBSs; red, SBSs. (E) Mutagenesis of intronless minigenes (red points). Splicing is expressed as the relative LEI: the log₂ of EI/WT EI. Increases in splicing are positive and decreases negative. Black points show the results with intron-containing minigenes for comparison. The other nine HMs yielded similar results (Supplemental Fig. S3). Thus, the vast majority of the mutations analyzed here are affecting splicing. (F) The same mutations produce similar relative phenotypes in the face of potent additional six-base substitutions. The map shows the median of scaled phenotypes (LEIsc) at each mutated exonic position for each of the HMs. Mutations distal to position 15 (beyond a 6-nt overlap of the 6-mer substitution region of 5 to 10) show parallel behavior across these HMs despite the fact that PSI values of WT HMs range from 0.025 to 0.75. HMA behaves exceptionally at positions 16 to 22, due to a secondary structure effect (vide infra). The heat map at the top shows the average R² values of LEIsc for all pairwise combinations of all HMs (except HMA and HMD), using the 12 mutations at each position.

Decreases were spread more widely across the exon and could drop essentially to zero, i.e., <2⁻⁸ = 1/256 that of the WT. Decreases greater than twofold, i.e., to EI values <0.5 of WT, were common—37%. Taken together, the frequency of mutations causing a twofold or greater splicing effect up or down was 70%, and single base substitutions rivaled the effects of double base substitutions in this regard: 65% vs. 72%. All positions but one (the edge position 48 with only three mutations) yielded at least one fourfold or greater difference (up or down) for at least one resident SBS or DBS. There was no apparent bias based on proximity to the splice sites (Supplemental Fig. S2). These numbers are reminiscent of the proportion of bases in a typical exon that can be placed into sequences that influence splicing as predicted by three computational algorithms (Chasin 2007) and argue against the idea that a large proportion of predicted ESRs are masked or otherwise inactive. These results contrast somewhat with the experiment of Mueller et al. (2015), who found that 16% of SBSs (5/32) at translationally silent positions in SMN1 exon 7 decreased splicing efficiency to one-half or less. This difference could be ascribed to the more robust splicing efficiency of their WT exon (75% to100%), our use of heterologous flanking exons, and/or their focus on the third position in codons (Mueller et al. 2015). High mutational vulnerabilities have also been seen in other recent high-throughput mutagenesis experiments (Findlay et al. 2014; Julien et al. 2016). The latter found that 26% of mutations in their test exon significantly altered the wild-type inclusion level of 49%, and 26% showed a twofold effect. For comparison, in the HMI exon, which has a similar level of inclusion (53%), 32% of the mutations produced a twofold or greater effect, in good agreement with the results of Julien et al. (2016). To give equal visual weight to increases and decreases, we devised a “proportion of the ultimate phenotype” (PUP) metric. Here, the highest increase in splicing (as EI, corresponding to a PSI of ∼1) relative to the WT was set to +1 and the lowest value (∼0) relative to the WT was set to −1. The WT is set to zero by this definition. As can be seen in Figure 2C, this sort of plot presents a more balanced map of positive and negative regions. In Figure 2D, each mutant molecule is present as a column, giving a less cluttered landscape. Here, splicing is presented as the LEIsc (log₂ of the EI, scaled), in which the LEI has been normalized so that the wild-type value is zero and the ranges from 0 to +1 and from 0 to −1 capture 97.5% of the positive and negative data, respectively, to avoid domination by outliers. All changes at a given position are represented by a set of 12 columns (overlaps allow all 16 dinucleotide combinations to be produced by 12 changes per starting position) (see Methods). In Figure 2D, the SBSs are colored red; it can be seen that their distribution and magnitude are similar to that of the DBSs, even if, on average, they are somewhat less effective (SBSs average absolute LEIsc scores = 88% that of DBSs). Consideration of sequences that overlap a mutation help explain this potency: For example, a SBS at position 39 virtually abolishes exon inclusion; this change disrupts several predicted ESEs and creates several predicted ESSs (Supplemental Table S1). If we can generalize from this model exon, ESRs are both numerous and fragile and so should represent a large target for mutation. This conclusion is in agreement with the increasing awareness of the role of ESR mutations in human disease (Sterne-Weiler et al. 2011; Xiong et al. 2015).

Although we have described these data as splicing phenotypes, we had to consider that many of these altered steady state mRNA levels were due to other causes. The design of these minigenes minimized the action of NMD, but there may be sequence changes that predispose a mRNA to other mechanisms of RNA degradation. In addition, it is possible that some mutated sequences are affecting the transcription rate. Indeed, these are interesting questions in their own right. To test these possibilities, we constructed an analogous library but created minigenes from which the introns had been removed, i.e., the mutant minigenes harbored the mature mRNA sequences. Unlike the minigenes with introns, saturation mutagenesis of the intronless minigenes produced much smaller or no effect on mRNA levels (see Fig. 2E for the HMA result: minigenes with introns [black points] versus without introns [red points]). Although we cannot rule out the possibility that some of these mutations may affect pre-mRNA stability, we think it more likely that almost all of the phenotypes measured here are due to effects on splicing.

Most cognate mutations in different HMs yield similar relative splicing phenotypes

The same saturation mutagenesis scheme was applied in parallel to the nine additional exon variants (HMB to HMJ) that exhibited a wide range of initial PSI values (Table 1). The mutant phenotypes for all 10 HMs are shown in Supplemental Figure S3. Here again, SBSs and DBSs generated a wide range of increased and decreased splicing efficiencies; overall, 49% of the mutants exhibited a twofold change (Table 1; Supplemental Fig. S4). Even in the case of the strongest splicer, HMH, with a WT PSI of 0.74, 18 mutations including two SBSs reduced splicing to <10% that of the relative WT. A list of the splicing phenotypes of all 5560 mutant molecules is presented in Supplemental Table S2. As was the case for HMA, mutagenesis of intronless versions of these exons had comparatively little or no effect on mRNA levels (Supplemental Fig. S3).

A principal reason for mutating the nine HM variants was to search for evidence of regulatory sequence interaction within exons as an important element of the splicing code. If this were the case, then introducing a sequence near the 5′ end of the exon (positions 5 to 10) could impact the phenotype of mutations located downstream; i.e., the very same SBSs and DBSs could lead to distinctive mutant phenotypes when comparing two HMs. Such interactions could be caused by specific contacts between different RNA binding proteins or by base pairing in RNA secondary structures. Mutational maps of the median splicing phenotype at each exonic position in the 10 HMs are compared in Figure 2F. The region from position 2 to ∼15 shows great variation among HMs as expected since this stretch overlaps the distinctive six-base substitutions they contain. That is, if two mutations are within about 6 nt, they may be creating an entirely new RBP binding sequence and so need not reflect an interaction between two RBP binding sequences. Once past this region of overlap, the shapes of the scaled mutational maps are remarkably similar despite the fact that the relative WT sequences that serve as the reference points for mutational change differ by almost four orders of magnitude in their splicing efficiency (Table 1). For example, HMB has a PSI of 0.20 and a WT EI value of 0.80; when mutated from GC to AT or to CG at position 21, the EI decreased to 29% or increased to 203% of the WT, respectively. HME has a PSI of 0.025 and an EI value of 0.074; when identically mutated at position 21, the EI decreased to 28% or increased to 267%, respectively. Thus, despite an order of magnitude difference in the initial EI values, the same mutations produce very similar results in terms of fold change. Such a simple multiplicative effect is expected from a model in which ESEs and ESSs act autonomously and additively by stabilizing or destabilizing splicing complexes (Ke et al. 2011; Arias et al. 2015). An exception is HMA, the true WT exon, which shows evidence of sequence interactions at positions 17 through 21, a region that is 7 to 11 nt downstream from the end of the hexamer substitution site. As will be seen below, this interaction can be attributed to a distinctive secondary structure in HMA that is not present in any other HM. R² values for all pairwise regressions of HMs for the region spanning positions 16 to 48 ranged from 0.63 to 0.95 and are shown in Supplemental Figure S5. We quantified this similar mutational vulnerability by calculating the correlation between median values for mutations at each position between Hexmuts in pairwise combinations. HMA and HMD were omitted because the former is subject to a strong secondary structural effect and because the latter gave rise to many mutations that could not be quantified as they yielded no measurable splicing (zero reads). The average R² values are shown as a heat map at the top of Figure 2F. Almost all positions distal to position 17 showed strong correlations between HMs, with R² values averaged across all HM pairs that ranged from 0.70 to 0.95. Thus, there was little evidence that sequence interaction was a major determinant of splicing outcome here. These results contrast with those of Julien et al. (2016), who found many combinations of SBSs that exhibited an epistatic effect in that their combined presence differed from a linear combination of their individual effects. About half their data could be explained by linear combinations (R² of 0.52 for observed vs. linearly predicted), leaving room for half to be subject to epistasis. Some of this epistasis could have been due to the formation of novel RBP binding sites when the two mutations are close together, a major location class they noted in their data. To focus more on combinatorial effects that involve interaction between different binding sites, we recalculated their data ignoring all mutations combinations that were >10 nt apart; the overall R² increased but only to 0.61. When we applied the same procedure to our own data, using the eight HMs as the second mutations, the R² of observed vs. linearly predicted was 0.94 (Supplemental Fig. S6). Thus, the discrepancy between our data remains. Unlike their experiment examining SBS combinations, in our experiments, one partner was always an extreme mutation, a 6-nt substitution. Epistasis that depends on specific protein–protein interactions may need to be honed over evolutionary time; the complete replacement of those proteins in our HM partner may have precluded our ability to see these subtle epistatic effects. That said, we find the ability of so many mutations to act autonomously to be equally interesting and it is a feature that must be taken into account in an understanding of the splicing code.

Di- and trinucleotides can act as gauges of splicing efficiency

Several genomic studies have reported that short sequence differences, even single nucleotide disparities, can aid in the identification of exons (Amit et al. 2012; Xiong et al. 2015). We therefore examined our genetic data for such biases. We started by comparing the effects of all 16 possible dinucleotides at all positions so as to minimize contextual effects imposed by neighboring sequences. To normalize the data, we subtracted the mean LEI at each position from each LEI value and then averaged across all positions in all HMs to get a single value for each 2-mer. The result was termed the LEI difference from mean, or LEIdm. LEIdm values ranged widely for different 2-mers, from −1.45 for TA to +1.26 for CG (Supplemental Fig. S7B). Even at the single nucleotide level, a substantial bias could be seen (C>A=G>T).

It has been noted previously based on genomic analysis (Majewski and Ott 2002; Lev Maor et al. 2015) and from functional selections (for review, see Chasin 2007) that CpG dinucleotides are preferentially associated with exon inclusion. Genomic results are subject to cross correlations to protein coding evolution; functional SELEX selections explore unnatural sequence space. The direct genetic evidence used here avoids these problems and so adds to the authenticity of the role of CpGs. CpGs here are probably acting intrinsically, as part of ESE sequences in the RNA, rather than as a substrate for a methylation mark (Gelfman and Ast 2013) since these minigenes are present only transiently (24 h) as a nonreplicating linear PCR product.

Trinucleotides were also distinctive. Among the top 10% (the six most stimulatory 3-mer creations) were five containing a CG (NCG and CGN) plus ACC (Supplemental Fig. S7C). The most deleterious 10% include the stop codon trinucleotides TAG and TAA, but not TGA, which was stimulatory. The LEIdm distributions for all 1-, 2-, and 3-mers are shown in Supplemental Figure S7. A genomic analysis corroborated this scoring: The abundance of trinucleotides in exons correlated positively with LEIdm scores (R² of 0.48, P < 10⁻⁶) and their abundance ratio with respect to introns showed an even stronger correlation (R² of 0.70, P < 10⁻⁵) (Supplemental Fig. S8A,B). We conclude that the mutational changes observed here reflect sequence information for splicing that is used generally rather than parochially. This high correlation of trinucleotides suggests that codon usage and splicing efficiency may have co-evolved. Since these genetic data are independent of translation, we were able to examine this question in an unbiased way. For codon usage, we excluded the three stop codons, the singular codons for methionine and tryptophan, and the eight codons that contain CG dinucleotides; the last exhibit low frequencies due to their mutational vulnerability. For the remaining 51 codons, the log₂ of the percent usage in humans (Nakamura et al. 2000) for the amino acid they specify showed a fair positive correlation with LEIdm, with an R² of 0.27 (P = 0.0003) (Supplemental Fig. S8C), considerably higher than the R² of 0.08 for a bacterial control (Supplemental Fig. S8D). This result is consistent with the idea that codon usage is under evolutionary pressure to provide sequences favorable for splicing and/or vice versa.

Pre-mRNA secondary structure plays a role in the WT exon HMA splicing

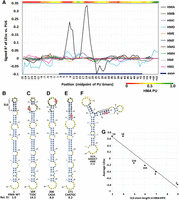
The mutations introduced here can affect the structure as well as the sequence of these pre–mRNA molecules. As an initial probe of a relationship between the stability of a secondary structure and splicing, we examined the mutants of each HM for a correlation between normalized changes in splicing (LEIsc) and the predicted folding free energies of mutant secondary structures. The latter (ΔG°) were calculated using the partition function option of RNAfold (Lorenz et al. 2011) on a 90-nt sequence that encompassed the 51-nt exon plus 23 nt of upstream and 16 nt of downstream sequence. The relative WT minimum free energy (MFE) structures of the 10 HMs are shown in Supplemental Figure S9. No strong correlations were found between ΔG° and LEIsc among the mutants in nine of the 10 HMs (B through J; Pearson's R values ranged from −0.08 to +0.07), but the true WT HMA stood out with a fairly strong R value of +0.47 (i.e., less stable structures correlated with more efficient splicing). HMA also stood out as having the most stable WT structure among HMs, with a ΔG° of −24.8 versus −20.2 to −16.1 kcal/mole for the nine others (Supplemental Fig. S9). Many splicing factors bind to single-stranded RNA (Buratti and Baralle 2004; Maris et al. 2005; Lunde et al. 2007) and ESRs tend to be single-stranded (Hiller et al. 2007; Ke et al. 2011). We therefore sought to identify regions in the HM sequences where single-strandedness correlated with splicing. Such a trend would have to be strong enough to be detectable over the background of direct effects of sequence changes on splicing. Toward this end, we correlated splicing efficiency with the average probability of the six bases in a 6-mer being unpaired (0 < PU < 1). PU values were extracted from the output of RNAfold that was run using the partition function, which weighs alternative structures dependent on their stability. A map of the signed R² values for correlations between LEIsc and the average PU of all stretches of six contiguous bases for the 555 mutants of HMA revealed a striking two-humped pattern across exonic positions 8 through 22 (Fig. 3A). The humps indicate that mutations that increase PU values tend to increase splicing efficiency. The heat map at the top of Figure 3A shows that the humps correspond to regions of strong base pairing (low PU) in the WT HMA. The minimum free energy structure of the WT HMA shows this region folded into a 5-5-5 stem–loop structure (stem–loop 6, or SL6) (Fig. 3B). Thus, splicing is positively correlated with the disruption of this stem. Three of the five bases of the upstream arm of SL6 overlap with the 6-mer HM sequence that is uniquely present in HMA, so none of the other HMs contains SL6. The SL6 stem is typically weakened when either arm of the stem is mutated (Fig. 3C,D). In contrast, some mutations strengthen SL6 by lengthening the 5-bp stem 3E. Accordingly, increases to 6, 7, and 9 bp progressively decrease splicing compared to the WT (Fig. 3G). This result could be explained by the existence of an ESE in an arm of SL6 that is being masked in the WT sequence. An alternative is that the stem of SL6 is being bound by a splicing repressor that recognizes the double-stranded structure. Consistent with the latter is the presence of a CUGG:CCGG duplex at the base of the loop, as is found in U2 snRNA, where it is bound by a U2B′′/U2A′ complex (Price et al. 1998). An MFE structure derived from another WT HM (HME) is shown in Figure 3F to illustrate the diversity of structures present in the mutant library. The MFE structures of all 5560 molecules can be accessed from Supplemental Table S2, columns J and L. Several conclusions can be drawn from this analysis: (1) Secondary structure wholly within an exon body can play a major role in splicing efficiency. (2) Single nucleotide changes can dramatically affect splicing efficiency by changing structure. (3) Once the WT SL6 was destroyed in creating HMB to HMJ, no other secondary structure of comparable importance for splicing emerged, suggesting that most predicted structures present little barrier to splicing. It is tempting to speculate that structures affecting splicing are not easily created but rather have been selected for in evolution. More subtle effects of secondary structure could be sought by designing mutations specifically designed to distinguish the effects of sequence vs. structure.

View larger version:

• In this window
• In a new window

• Download as PowerPoint Slide

Figure 3.

A stem–loop secondary structure in the HMA sequence inhibits splicing. (A) Map of the correlation (signed R²) of splicing with the probability of being unpaired (PU) in secondary structures. For each starting position of each HM, each mutant window of 6 nt was evaluated for its average PU. These PU values were then correlated to LEIsc scores. Note that the true WT HMA exhibits a strong region-specific correlation from exonic positions 8 to 22 but the other nine HMs show no such strong effect at any position. The heat map shows the PU values of WT HMA 6-mers. (B–F). The minimum free energy (MFE) structures of selected 90-nt folded sequences. Mutant serial numbers are indicated for reference to Supplemental Table S2.The 15-nt sequence of HMA stem–loop 6 is in bold. The base changes and the EI value relative to the WT are indicated. (B) Wild-type HMA. The location of stem–loop 6 (SL6), the structure that inhibits splicing, is indicated (bases 31 to 45); its coordinates in the exon are 8 to 22. (C) The MFE structure of an HMA mutation (circled) with a SBS in the upstream arm of SL6. (D) As in C, but the mutation is in the downstream arm of SL6. (E) An example of an HMA DBS that extends the stem length of SL6 from 5 to 9. This more stable stem produces a further reduction in splicing (panel G). (F) A contrasting example of a different HM, HME. The location of the hexamer difference from exon positions 5 to 10 is shown by the orange arc. The black bar indicates the sequence of what is the downstream arm of SL6 in HMA. Note the largely different MFE structure compared to HMA. (G) The double-strandedness of the SL6 stem of HMA correlates with splicing. The points show the average LEIsc values for MFE structures having the indicated number of paired bases in the SL6 stem. The points are labeled with the number of mutants having that stem length.

The mutations affect the exonic recruitment of spliceosome assembly proteins

In general, RBPs that bind to splicing enhancer sequences are thought to act by recruiting or stabilizing the binding of spliceosomal components to splice sites, with those binding to silencers acting in the opposite manner. It follows that most of these RBPs should be acting at an early step in splice site recognition. A required step in splice site recognition is exon definition, at least for exons bounded by long (>250 nt) introns, which is the usual case in humans (Fox-Walsh et al. 2005; De Conti et al. 2013; Chiou and Lynch 2014). To ask whether any of these mutations could affect exon definition, we measured the in vitro formation of a ribonucleoprotein complex on a library of RNA substrates consisting of an exon plus short intronic flanks, including the 3′ and 5′ splice sites and polypyrimidine tract but with no putative branch point. Such complexes, termed alpha complexes (Robberson et al. 1990) or cross-exon complexes (Schneider et al. 2010), have been previously described. If these ideas are correct, then many of the mutated exons should be influenced in the formation of a cross-exon complex to a degree similar to their splicing phenotype. We gauged the formation of an exon definition complex by the binding of proteins associated with U1 snRNP and U2AF, as these initiate assembly of the spliceosome across introns and probably across exons: U2AF by binding to the polypyrimidine tract and the 3′ splice site and U1 snRNP by binding to the 5′ splice site. We generated a library of these 5560 exonic RNA substrates using our pool of mutant minigene sequences to generate transcripts in vitro using T7 RNA polymerase. This pool was incubated with a splicing-competent HeLa cell nuclear extract and then immunoprecipitated (IP) to enrich for those molecules bound to either of the U2AF subunits U2AF65 (U2AF2) or U2AF35 (U2AF1) or to either of the U1 snRNP specific proteins U1A or U1–70K. The RNAs recovered from each of these four IPs were extracted and subjected to deep sequencing. Enrichment indices analogous to splicing EIs could be calculated for almost all of the mutant molecules (termed proportion pulled down, PPD) (see Methods). If enough of the mutations affected (1) splicing and (2) the ability to bind these splicing components to a similar degree, then we should see a significant correlation between the results of these two kinds of experiments.

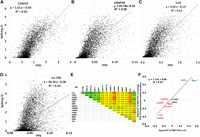
As can be seen in Figure 4, A through D, a substantial correlation was found between EI and PPD, with R² values of 0.63, 0.59, 0.61, and 0.24 for U2AF65, U2AF35, U1A, and U1-70K, respectively (all P-values < 10⁻¹⁴). To our knowledge, this is the first high-throughput analysis of sequences linking spliceosome-related exon complexes to splicing. U1-70K showed less of a correlation than U1A even though both are U1 snRNP subunits. U1-70K could be additionally associating with the exon via binding to other RBPs, such as HMGA1α or SRSF1 (Manabe et al. 2003; Ohe and Mayeda 2010; Cho et al. 2011), which could confound the correlation. On average, the correlation coefficients indicate that at least half of the mutations affect exon complex assembly to an extent similar to their effect on splicing. These correlations are likely to be an underestimate due to factors such as variation among IP efficiencies, corrections for nonspecific binding, and the loss of RBPs with modest binding affinities during isolation of the complexes. Although these four spliceosomal proteins themselves bind to sites close to one or the other ends of exons, mutations near the ends of the exon body had no greater effect on binding than internal mutations (Supplemental Fig. S10). Single antibodies were used for each IP, so there is no physical evidence that an immunoprecipitated molecule contains additional RBPs beyond the targeted protein, i.e., that they represent mature exon definition complexes. However, the genetic evidence that ties these complexes to splicing is compelling and leads us to conclude that (1) the exon complexes formed are valid indicators of an exon definition complex (since they correlate with splicing), (2) many if not most effective mutations in the body of an exon act through the early step of exon definition and cross-exon spliceosome formation, and (3) exon definition can be a highly mutable step in splicing, implying it is a large target for human genetic disease (Sterne-Weiler et al. 2011).

View larger version:

• In this window
• In a new window

• Download as PowerPoint Slide

Figure 4.

Correlation between splicing (EI) and RBP-exon binding in vitro. A library of the 5560 exon sequences plus short flanks was incubated with a HeLa nuclear extract and immunoprecipitated to pull down bound RNA molecules, which were quantified by deep-sequencing. PPD is the proportion of the library bound for each sequence, including correction for input proportion and the amount of RNA recovered. (A) U2AF65 (U2AF2); (B) U2AF35 (U2AF1); (C) U1A; (D) U1-70K. A and B are required for U2 snRNP binding, and C and D are components of the U1 snRNP. Both snRNPs are part of the initial spliceosome. (E) Correlation in binding among RBPs. Numbers shown are signed R² values. Positive, negative, and no correlations were found. Note that the four spliceosome-related proteins (U1A, U1-70K, U2AF65, U2AF35) positively correlated with SRSF1 and SRSF7 and negatively correlated with DAZAP1, hnRNP I (PTB), and TIA1 binding (see Supplemental Fig. S11 for additional scatter plots). Correlations with splicing (EI, last column) are also shown. (F) Individual RBPs may promote or prevent the formation of a functional exon definition complex. On the x-axis are plotted the correlations (as signed R² values) between the binding (PPDs) of individual RBPs to the mutant exons and splicing. On the y-axis are plotted the correlations between the binding (PPDs) of individual RBPs to the mutant exons and the average binding (PPDs) of the four spliceosome assembly proteins U2AF35, U2AF65, U1A, and U1-70K; these values were taken as an indicator of exon definition complex formation. This correlation of correlations plot allows a visualization of the positive relationship between the promotion (repression) of exon definition by an RBP and the promotion (repression) of splicing by that RBP. The correlations do not show causality but are consistent with that idea.

To search for additional exon-protein associations, we extended this IP/deep sequencing analysis to 10 additional RBPs. Six exhibited a negative correlation with splicing, two were positive, and two were neutral (R² values > 0.1, P < 10⁻¹⁰) (Fig. 4E, last column). Correlations between all pairs of RBPs were also carried out (Fig. 4E). As an example, the scatter plots comparing U2AF65 binding with each RBP are shown in Supplemental Fig. S11. Among the 91 pair-wise correlations using all 14 RBPs, 28 were positive (signed R² ≥ 0.1), 22 were negative (signed R² = <−0.1), and 41 were neither (Fig. 4E heat map). TIA-1 was a strong negative correlator, yet has been found to promote splicing of several exons. However, in those cases, it acted from a downstream intronic position (Zuccato et al. 2004; Izquierdo et al. 2005); opposing effects of RBPs depending on an intronic versus exonic position are not uncommon (Fu and Ares 2014). Surprisingly, binding of the much studied splicing inhibitor hnRNPA1 showed only a weak negative correlation with splicing (Fig. 4E, last column). The correlation between an RBP and splicing is itself proportional to its correlation to binding with the four spliceosome-related proteins (Fig. 4F). A clustering analysis of the binding specificities of SRSF7 and HNRNPI, the two splicing factors that correlated most strongly with spliceosomal protein binding (Fig. 4F), showed good agreement with those expected from the literature (Singh et al. 1995; Cavaloc et al. 1999; Xue et al. 2009; Llorian et al. 2010) and those generated from CISBP-RNA z-scores (Supplemental Fig. S12). These IP results are consistent with the idea that the RNPs brought down by these targeted IPs are multicomponent complexes, although this remains to be established. In any case, the fact that eight of 10 RBPs tested exhibited a correlation between exon binding and splicing as the sequences varied suggests that this small model exon can bind a variety of RBPs in a sequence-specific way and with functional splicing consequences.

The fate of a single exon is governed by a large number of RNA binding proteins

The availability of relative binding specificities of 200 RBP binding domains to essentially all ∼16,000 7-mer sequences (Ray et al. 2013) allowed us to ask whether any of these RBPs exhibited a correlation between binding affinity and splicing efficiency. We surveyed 91 RBP specificities designated as human from the CISBP-RNA database, where each 7-mer was assigned a normalized z-score as a measure of affinity relative to the mean of all 7-mers (http://CISBP-RNA.ccbr.utoronto.ca/). As a preliminary examination, we can consider some extreme examples where a SBS produces an extreme phenotypic change. A change from a wild-type A to T at position 39 in HMA drops the EI from 0.187 to 0.001; a 7-mer encompassing this change (AGAAGGG to AGTAGGG) greatly strengthens a binding site for the known silencer HNRNPA1, with a z-score change from 2.5 to 9.7. Several other 7-mers spanning this position have z-score changes consistent with this decrease in splicing: e.g., MSI1 and DAZAP1 as better binding silencers and SRSF1 and CNOT4 as poorer binding enhancers (Supplemental Table S3). A similar dramatic congruence of EI and z-score changes could be seen at positon 10, where an A or a C at position 10 resulted in an EI of 0.05 or 2.55, respectively. This positive splicing change was matched by a decrease in HNRNPA1 (a silencer) z-scores from 9.8 to 0.6 as well as an increase in RBM4 (an enhancer) z-scores from 0 to 4.0 (Supplemental Table S3).

We next systematically examined each of the 91 human RBPs from CISBP-RNA for evidence of a correlation between binding affinity and splicing. At each exon position from −3 to +46 (capturing 7-mers with as few as three mutated positions at the edges), we collected all molecules (usually 76) bearing a sequence change exclusively in the 7-mer starting at that position. Each HM was analyzed separately, with each generating 4459 regressions (91 proteins × 49 starting positions). The complete mutant set comprised 6639 unique 7-mers. To contend with this high number of tests, we set the false discovery rate (FDR) for correlations to 5% (Benjamini and Hochberg 1995). A priori, one would not expect to see many significant correlations in this search since (1) the 91 RBPs surveyed represent <10% of the total number of RBPs in the human proteome (Baltz et al. 2012; Castello et al. 2012; Gerstberger et al. 2014), and (2) the model exon is only 51 nt long and presents an intentionally limited range of sequence variations, small changes from a WT theme. Contrary to this expectation, we found that, on average, among the 10 HMs, 17% of the 4459 regressions were significant (range: 14% to 23%) (Supplemental Table S4). To confirm the validity of controlling for the FDR using the Benjamini and Hochberg algorithm, we estimated an empirical FDR by randomizing the 76 LEIs with respect to the 76 z-scores found at each protein/position and then repeated the correlation calculations applying the same Benjamini and Hochberg cutoff of P = 0.01. Any positive result from the randomized data could then be considered a false positive. Averaging 100 randomizations per Hexmut yielded a median empirical FDR of 5.8% (range of 5.3% to 9.2%) (Supplemental Table S5). Thus, among the significant correlations, ∼6% could be due to chance, close to the 5% target.

As one example, all significant correlations for HMB are shown in Supplemental Table S6. Of the 4459 regressions, 1046 were significant; about half were positive and half negative. Of the 91 RBPs, 87 were represented. Of the 49 exon positions surveyed, all were represented. The sign of the correlation of an RBP was almost always consistent across different positions (Supplemental Fig. S13). The average number of significant RBP correlations per position was 25. The R² values of these significant regressions ranged from 0.6 down to 0.1 (Supplemental Fig. S14); P-values ranged from 10⁻¹⁴ to 10⁻². Of the 1046 significant protein/positions, only 15 (1.4%) exhibited very high R² values (>0.5). More than half the R² values fell between 0.2 and 0.1. Low values such as these are not surprising: An R² of 0.1 means that 10% of the variation in splicing could be explained by the variation in binding of a particular RBP to a particular position in the exon, a meaningful positive result. The rest of the variation could be due to mutated 7-mers other than the one put in focus by the particular starting position and/or the binding of RBPs that were not examined. This logical picture should reflect the physical situation as well, as different RBPs compete for overlapping sequences.

Mutations in HMA present a picture of the natural wild-type exon. At an affinity z-score cutoff of >2, the entire exon would be covered using just the 91 RBPs considered here (Supplemental Fig. S15A). To minimize the complication of binding sites created by mutations, we can consider only those mutations that decreased RBP binding affinity. Using only these data, there were significant correlations for 58 RBPs encompassing 150 protein/positions; 106 were positive correlations and 44 negative (Supplemental Fig. S15B). These results suggest that the wild-type exon is interacting with a large number of proteins and that these interactions affect splicing efficiency. The binding properties of nearly all of the 91 human RBPs in this compendium correlated with splicing despite the fact that many are thought to function in aspects of RNA metabolism other than exon recognition, such as translation, mRNA stability or spliceosome structure, and/or have been designated as “cytoplasmic.” To the extent this sample of RBPs is representative, it follows that most of the >1000 RBPs in the cell have the potential to influence splicing.

Protein binding sequences combine to determine splicing outcomes

To test the idea that a smaller number of protein/positions can combine additively to determine splicing outcome, we used a stepwise regression to build a multiple linear regression model of the form: 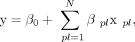where y is the response variable LEI, β₀ is a constant, β_pl is a weight, x_pl represents the z-score of protein p for the 7-mer at location l, and N is the total number of individual protein/positions found to yield a significant correlation with splicing, as described above. HMs were merged in this model, but HMD was omitted as it harbors many low values that were just estimated due to zero outputs. The final model was comprised of 48 proteins and 80 protein/positions. In 10-fold cross validations, the resulting equation predicted LEI scores with an average R² of 0.89, a slope near 1, and a y-intercept near zero (Fig. 5A). The success of the model is consistent with there being few important synergistic interactions between RBPs. Applying this model to individual HMs also yielded strong predictive ability (Supplemental Fig. S16).

View larger version:

• In this window
• In a new window

• Download as PowerPoint Slide

Figure 5.

Prediction of splicing efficiency. (A) An equation for multiple linear regression was derived using all splicing data except that of HMD. Eighty significant protein/positions were found and used. The results show the 5004 points (molecules) derived by merging all 10-fold cross-validations. (B) Prediction of splicing in all 5560 mutants based on the sum of exonic SMS scores. Note the strong correlation, the tendency toward saturation at high splicing efficiencies, and the outliers starting in the upstream and downstream stem arms of the functional stem–loop structure in HMA (open squares and circles, respectively). (C) ROC curve for the distinction between ∼100,000 human constitutive exons (average length 136 nt) and ∼100,000 pseudoexons (average length 128 nt). The maximum accuracy (true positives + true negatives)/(total combined sequences) was 0.81 for the experiment in which all 16,384 SMS scores were used.

Splicing scores for 7-mers predict splicing efficiency

The use of binding affinities of 7-mers provided in the CIS-BP database allowed us to assess the behavior of our model exon with considerable accuracy. In an effort to codify the mutant k-mer sequences as predictors of splicing in general, we therefore chose to use 7-mers. For this purpose, it was necessary to normalize the splicing phenotypes across all HMs and all positions. For each of the 76 mutant 7-mers found at a given internal position, we subtracted the average LEI from each LEI. If a 7-mer was present at more than one position, its values were averaged. For all the 7-mers derived from the same HM set, the values were then scaled from +1 to −1 around the median. These normalized and scaled values were then averaged across all HM sets and are termed “effective” LEI (eLEI) scores. Scores could be assigned to 6371 7-mers, almost all that are present in the population. Note that these eLEI scores are independent of RBP binding data. The average or sum of the eLEI scores of all 7-mers in an exon correlated well with the observed LEI of that molecule (R² = 0.77, N = 5560) (Supplemental Fig. S17). However, for general use, we were missing eLEI scores for the 10,013 7-mers not present among these molecules. To deduce these missing values, we took advantage of the correlations found between RBP binding and splicing. We used Random Forest (Pedregosa et al. 2011) to train regression trees on the affinities (z-scores) of the 6371 mutant 7-mers represented in our mutant sequences, using all 91 human proteins in the CISBP-RNA database and across all positions. Based on their z-scores, each of the missing 7-mers was then added to a tree individually and the value of the closest leaf bearing a known eLEI was noted. The average values of 100 such trees was assigned as the eLEI value for that missing 7-mer. In this way, splicing scores were generated for all the remaining 7-mers on the basis of their RBP binding characteristics. We term these 16,384 values saturation mutagenesis derived splicing scores (SMS scores) (listed in Supplemental Table S7). SMS scores predicted the splicing of mutant molecules well (R² = 0.84) (Fig. 5B). Interestingly, many of the mutants affected in the stem–loop structure seen to affect splicing in HMA showed up as outliers in this correlation, as might be expected if structure is confounding the prediction (Fig. 5B). That curve also showed signs of saturation at high SMS scores, again as might be expected as exon inclusion approaches 100%. As a genome-wide test of SMS scores, we asked how well they could be used to distinguish constitutive exons from pseudoexons. The latter are defined (Zhang et al. 2005b) as intronic stretches having splice site sequences similar to those of real exons but for which splicing has not been detected (see Methods for more details). As analyzed by a receiver operating characteristic (ROC) curve, average SMS scores achieved a very good AUC (area under the curve) of 0.88 (Fig. 5C). If only the 6371 SMS scores derived solely from the mutational data alone were used, the AUC was considerably lower, 0.72. This difference attests to the validity of using RBP binding affinities as a criterion to infer SMS scores for untested 7-mers. At the same time, it shows that consideration of all available human CISBP-RNA RBP affinities helps to distinguish real exons from pseudoexons. A composite map of SMS scores across >100,000 genomic exon and pseudoexon sequences showed the former to exhibit a sharp rise at the transitions between intronic flanks and exon bodies, whereas pseudoexons remain flat (Supplemental Fig. S18). Alternatively spliced cassette exons also exhibited the sharp distinction but attained somewhat lower scores compared to constitutive exons. The fact that, despite the presence of splice sites, pseudoexons showed no dip in scores suggests that a lack of ESEs by itself may be sufficient to disqualify a pseudoexon. Finally, we tested SMS scores for their ability to predict splicing phenotypes measured for four human exons carrying single nucleotide variations in disease-related genes (Soukarieh et al. 2016). An average R² value of 0.50 was attained, which was similar to those achieved by other recently developed algorithms applied to these data (Supplemental Table S8).