Ancient haplotypes of the HLA Class II region

Tens to hundreds of functionally distinct alleles have been described for the genes encoding the antigen-presenting molecules HLA-DQA1, -DQB1, and -DRB1 in the class II region of HLA (Bontrop et al. 1999; Marsh et al. 2000). Although there is detailed knowledge of coding-region variation in these genes, the data on haplotype evolution are fragmentary. Such information will be essential for understanding the molecular evolution of HLA and also for carrying out fine-structure mapping of associations between HLA haplotypes and the many human diseases that are influenced by an individual's HLA genotype (Price et al. 1999). Existing data on noncoding variation are either too anecdotal or too localized to particular gene segments to provide an overview of haplotype variation across any major segment of HLA. The few long-range studies that are available are limited to pairwise comparisons of arbitrarily chosen haplotypes (Guillaudeux et al. 1998; Horton et al. 1998; Gaudieri et al. 2000; Satta and Takahata 2000; Stewart et al. 2004); in contrast, short-range studies examine multiple haplotypes only in the immediate vicinity of particular polymorphic exons (McGinnis et al. 1994; Bergstrom et al. 1998; Kotsch and Blasczyk 2000). Despite their limited scope, these data clearly reveal patterns and levels of haplotype variation that have not been seen elsewhere in the human genome (International SNP Map Working Group 2001). At the high end, pairwise divergences reach 5%-10% across tens of thousands of base pairs, while at the low end they collapse to background levels of 0.1% or less.

The lack of systematic, long-range sequences of many haplotypes is largely due to the technical difficulty of acquiring haplotype-resolved sequences across tens of thousands of base pairs from the genomes of many individuals. For our analysis, we developed an efficient fosmid-based recloning system to obtain the sequences of 20 human haplotypes, as well as single sequences from a chimpanzee and a gorilla, across an average of 106 kbp of the class II region. Most of the human sequences, which were obtained from a geographically diverse panel of 10 individuals, include all of the DQB1, DQA1, and DRB1 genes. We believe that these data represent the first haplotype-resolved resequencing study of this breadth and depth for any locus in any organism.

Results

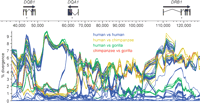
We based our analysis of the DQB1-DQA1-DRB1 region on a multiple alignment (Supplemental Table 1) of 23 sequences: one chimpanzee haplotype, one composite gorilla haplotype, and 21 human haplotypes (Fig. 1). Of the 21 human haplotypes, 20 were from our study and one was from the Human Genome Project. Multiple alignment of the 23 sequences led to 59,668 fully aligned sites, 5328 of which have at least two human alleles. Considering only the human-human comparisons, maximal pairwise divergences range from 2.1% to 9.3%, whereas minimal divergences are everywhere <0.1% (Fig. 2). Human-chimpanzee, human-gorilla, and chimpanzee-gorilla divergences have essentially the same upper limit as the human-human comparisons, but the lower limit for the inter-species comparisons is ∼1%. Indeed, over most of the region studied, there are examples of chimpanzee-human or gorilla-human comparisons that are in the 1%-2% range. Since this value is similar to genome-wide averages for interspecies comparisons among humans, chimpanzees, and gorillas (Chen and Li 2001), there is no indication of an unusually high mutation rate in the class II region.

We interpret the exceptionally high divergences between some pairs of haplotypes, regardless of the species from which they were sampled, as being due to a long history of independent haplotype evolution. This model, which requires extensive sequence variation to have flowed through many speciation bottle-necks, is well established for the coding-region polymorphisms of both Class I and Class II HLA genes (Lawlor et al. 1988; Mayer et al. 1988; Fan et al. 1989; Gyllensten and Erlich 1989; Gyllensten et al. 1990). Our data extend this evolutionary model to the entire class II region. Because there are no known functional elements interspersed among the HLA-DQB1, -DQA1, and -DRB1 genes (Beck and Trowsdale 1999; The MHC Sequencing Consortium 1999), we presume that most noncoding sequences have evolved neutrally, while balancing selection has acted on the functionally important variation within the three highly polymorphic genes (Hughes and Nei 1989; Begovich et al. 1992). Assuming normal mutation rates and neutrality at most noncoding sites, the most dissimilar haplotypes would have had to have evolved independently for ∼40 million years (Myr) to have diverged by as much as 9% (Satta et al. 1999).

View larger version:

• In this window
• In a new window

• Download as PowerPoint Slide

Figure 1.

A visual representation of the multi-aligned haplotypes. The arrows over the gene models indicate the direction of transcription. Haplotype designations are indicated on the left, including membership in haplotype groups A, B, C, D, or E, when appropriate. Haplotypes within a group are nearly identical across the entire region. The coordinate system, in base pairs, is based on haplotype RefSeq (see Methods). Physical distance in the figure corresponds to the longest path through the multi-alignment; deletions relative to the longest path are indicated by gaps in the appropriate haplotypes (and, if space allows, by a series of dots). However, the tick marks and coordinates on the horizontal axis refer to RefSeq coordinates. Coloring of the haplotypes clusters them locally according to the deep branches of the phylogenetic tree to which they belong. The local clusterings were achieved by constructing molecular phylogenies for nonoverlapping 5-kbp windows across the region. Sample phylogenetic trees are shown at the bottom of the figure. The bottoms of the horizontal gray bars across the trees, which correspond to a pairwise-sequence divergence of 4%, indicate the arbitrary threshold for assigning a group of haplotypes the same color in a local region. The gray bars visible at the ends of most haplotypes are segments that could not be assigned a color in that region because they ended within one of the 5-kbp windows used for tree construction. The gorilla sequence, although treated in most instances as a single composite haplotype, is shown here as two overlapping sequences, GORILLA_1 and GORILLA_2, because these two sequences, which are true haplotypes from a single individual, are of different parental origins.

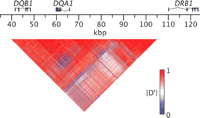
To produce the current pattern of haplotype divergence, recombination between highly divergent haplotypes must have been strongly suppressed relative to the genome-wide average recombination rate. Although “hitchhiking” of neutral variation on selected sites is a well established phenomenon (Smith and Haigh 1974; Kaplan et al. 1989), the level of recombinational suppression required to maintain long-range haplotype integrity over 40 Myr is extraordinary. In family studies, the sex-averaged recombination rate on chromosome 6 in the HLA region is ∼0.5 cM/Mbp (Martin et al. 1995; Kong et al. 2002), a value similar to the genome-wide average. At this recombination rate, the interval over which there is a probability of 0.5 that there will have been no recombination in 40 Myr is <100 bp. This estimate varies inversely with elapsed time and recombination rate and directly with the assumed generation time. Although none of these parameters is well established, any plausible set of values predicts that hitchhiking should be limited to a few hundred base pairs or less. In contrast to this prediction, we observe strong linkage disequilibrium across most of the multi-aligned region, a distance of tens of thousands of base pairs (Fig. 3). This result, which is consistent with previous studies based on limited sets of genetic markers (Begovich et al. 1992; Sanchez-Mazas et al. 2000; Stenzel et al. 2004), indicates that evolutionarily successful recombination events between deeply diverged haplotypes in most subintervals of the class II region have been rare relative to expectations based on genome-wide recombination rates.

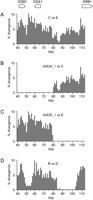
Nonetheless, a few clear instances of such events are evident when particular pairs of haplotypes are compared. We discovered these examples by examining all 210 distinct pairwise comparisons that can be made among the 21 human haplotypes we analyzed. This analysis was simplified by the observation that 13 of the 21 haplotypes fall into five groups, designated A-E, which are defined by near identity within each group (i.e., intragroup divergences, averaged across the DQB1-DQA1-DRB1 region, are <0.3%). We found one particularly dramatic example of what appears to have been a simple, recent reciprocal-recombination event: haplotype 04535_1 is nearly identical to the group E haplotypes over half the region and to the group C haplotypes over the remainder (Fig. 4B,C). In contrast, the group C and E haplotypes are deeply divergent across nearly the whole multi-aligned region (Fig. 4A). This pattern is suggestive of a reciprocal recombination between a C- and an E-group haplotype that occurred very recently compared to the time over which these two haplotypes have been diverging. Because this recent event affected the structure of only one of the 21 human haplotypes, it did not have a major influence on disequilibrium values for SNPs on opposite sides of the recombination junction. A more complex example is evident in pairwise comparisons between B- and D-group haplotypes, which are highly divergent except in two regions: one is between the DQB1 and DQA1 genes, and the other is in a 20-kbp interval between DQA1 and DRB1 (Fig. 4D). The latter feature appears to reflect either two successive recent recombination events or a very long gene-conversion track. Unlike the situation for haplotype 04535_1, we did not observe reciprocal divergence patterns at either of the apparent recombination sites. Two other recombinant haplotypes are evident in Figure 1 (e.g., 14661_2 appears to be a C/D recombinant and 01018_1 appears to be an A/E recombinant); however, neither of these examples is nearly as dramatic as those displayed in Figure 4, since there is substantial divergence between one or both segments in the recombinant haplotypes and the closest match in our data set.

The strong dip in the divergence of the B- and D-group haplotypes between the DQB1 and DQA1 genes (Fig. 4D) is of special interest. We explored the relationship between all the haplotypes in this region by constructing molecular phylogenies from the data in a series of 2-kbp windows that tiled the DQB1-DQA1 interval. The most striking feature of such phylogenies is the persistence of at least two deeply diverged branches throughout the12.3-kbp intergenic region (Fig. 5A-D). Additional deep splits occur in regions adjacent to the DQB1 and DQA1 genes. If recent recombination events had occurred between haplotypes belonging to the two deep intergenic branches, there would be sudden, major shifts in the topology of successive trees. We found no such examples in our data set. Even within each of the two major branches, tree topology is generally conserved, particularly in the branch of Figure 5, which includes the B-, C-, and D-group haplotypes. The only obvious example of a recent recombination event within this branch involves haplotype 14661_2, which appears to have been created by recent recombination between a C- and a D-group haplotype: haplotype 14661_2 clusters with the C-group haplotypes at the DQB1 end of the interval (Fig. 5A,B) and the D-group haplotypes at the DQA1 end (Fig. 5C,D).

View larger version:

• In this window
• In a new window

• Download as PowerPoint Slide

Figure 2.

Pairwise comparisons among the haplotypes. A separate line is plotted for each pairwise comparison, but only the different classes of interspecies comparison are assigned different colors. The coordinate system is the same as that in Figure 1. The vertical axis indicates percent divergence between the pairs of haplotype sequences. Pairwise divergences were calculated as averages for 2-kbp windows that slid 500 base pairs between points. The arrows over the gene models indicate the direction of transcription. The most variable exons of the three genes (in all cases, exon 2) are indicated by an asterisk.

The collapse in the depth of both major sublineages of the bifurcated tree in the DQB1-DQA1 interval (Fig. 5A-D) poses something of a dilemma. Low intrabranch divergence in this region relative to surrounding regions must be due to local changes in the mutation rate, recombination rate, or strength of selection. A regionally low mutation rate is implausible since interbranch divergence in this region is high and the divergences of human haplotypes from their closest chimpanzee and gorilla counterparts are unremarkable. Action of purifying selection within each branch is also implausible, since there are no known functional elements in the intergenic region, and, even if such elements exist, most SNPs are still likely to be evolving neutrally. We presume that the collapse of intrabranch diversity in the DQB1-DQA1 region is due to a subtle interplay between recombination and selection. In this model, recombination occurs at rates high enough to shorten intrabranch coalescence times—by decreasing hitchhiking of neutral alleles on sites within the DQB1 and DQA1 genes that are under balancing selection—but low enough to preserve key aspects of tree topology.

View larger version:

• In this window
• In a new window

• Download as PowerPoint Slide

Figure 3.

Pairwise linkage disequilibrium between SNPs in the DQB1-DQA1-DRB1 region. The matrix display shows linkage disequilibrium between pairs of SNPs, measured by the statistic |D′| (see Methods). The coordinates correspond to those defined in the Figure 1 legend.

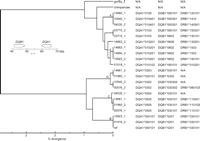
We found a simple correlation between noncoding haplotypes and coding-region alleles, particularly in the DQB1-DQA1 region. This correlation is evident in Figure 6, in which classical DQB1-DQA1-DRB1 allele designations are juxtaposed with a molecular phylogeny based on a typical segment of the DQB1-DQA1 intergenic region. This figure is easily interpreted because the allele designations, like the tree itself, are based on a hierarchical classification system (e.g., all classical ^*03 alleles have fewer sequence differences from one another than with any ^*02 alleles, and all ^*0301 alleles have fewer differences from each other than with any ^*0302 alleles). The nearly perfect correlation between the phylogenetic tree built from the complete haplotype sequences and the hierarchical clustering of the functional alleles of DQB1 and DQA1 reflects the nearly complete linkage disequilibrium between neutral and selected sites in this region. Indeed, the two deep branches of the intergenic trees (Fig. 5B,C) correlate absolutely with the DQ haplotypes observed in diverse human populations. In numerous large studies of multiple populations, DQB1 ^*02 and ^*03 alleles (bottom branch in Fig. 5B,C) are not found on the same haplotypes as DQA1 ^*01 alleles (top branch in Fig. 5B,C); similarly, DQB1 ^*05 and ^*06 alleles (top branch) are not found on the same haplotypes as DQA1 ^*03 and ^*05 alleles (bottom branch) (Imanishi et al. 1992; Charron 1997; Begovich et al. 2000). Hence, the absence of detectable historical recombination between the two deeply diverged branches simply reflects the rules governing “forbidden” combinations of DQB1 and DQA1 alleles, which encode the two subunits of the heterodimeric DQ protein. This result is particularly satisfying since there is a well established biochemical basis for this “gene-gene interaction:” the protein products of forbidden allele combinations have been shown to form unstable heterodimers in vitro (Kwok et al. 1993). Therefore, selection against recombinants—rather than an absence of recombination events—may account for the topology of the haplotype trees in the DQB1-DQA1 region. However, it should be noted that putative exceptions to the usual rules governing DQB1-DQA1 associations have been reported to exist at significant frequencies in some populations (Grahovac et al. 1998). If validated, we predict that the haplotypes that account for these exceptions will reflect relatively recent recombination between haplotypes associated with the two deep branches that characterize the DQB1-DQA1 intergenic region.

View larger version:

• In this window
• In a new window

• Download as PowerPoint Slide

Figure 4.

Histograms of the pairwise divergence among selected haplotypes. The coordinate system is the same as that employed in Figure 1. Divergences were calculated for 1-kbp bins, based on RefSeq coordinates, counting only discrepancies at nucleotide positions that could be fully aligned with all other haplotypes for which sequence was available in a given region. (A) Representative C-group haplotype compared to a representative E-group haplotype. (B) Recombinant haplotype 04535_1 compared to a representative C-group haplotype. (C) Recombinant haplotype 04535_1 compared to a representative E-group haplotype. (D) A representative B-group haplotype compared to a representative D-group haplotype. The actual haplotypes used to represent haplotype groups B, C, D, and E (see legend to Fig. 1) were 01018_2, 00576_1, 00576_2, and 10923_2, respectively.

The situation at the DRB1 end of the class II region is more complex. Substantial linkage disequilibrium exists between the strong haplotypes in the DQB1-DQA1 region and the classical DRB1 alleles. However, unlike the situation between DQB1 and DQA1, where “forbidden” combinations of alleles are on branches of the molecular phylogeny that remain deeply diverged across the whole DQB1-DQA1 interval, there is no consistent relationship between the extent of haplotype divergence between DQA1 and DRB1 and the extent to which the classical DQA1 and DRB1 alleles on these haplotypes are in linkage disequilibrium. Nonetheless, examples of this phenomenon do exist and are likely to reflect the effects of unusually longstanding or strong selection for maintenance of certain preferred combinations of DQB1, DQA1, and DRB1 alleles. The clearest example involves the C- and E-group haplotypes, which are deeply divergent across nearly the entire class II region (Fig. 4A). The C-group haplotypes carry DQB1-DQA1-DRB1 alleles ^*030-^*050^*-^*110, whereas the E-group haplotypes carry alleles ^*060-^*010-^*150. In one survey of over 2000 individuals from a worldwide sampling of 18 human populations, haplotypes with the C- and E-groups' combination of DQB1, DQA1, and DRB1 alleles were found in nearly all populations at frequencies ranging from a few percent to over 20% (Imanishi et al. 1992). In contrast, the allele combination ^*03-^*05-^*150 present on the C-E-recombinant haplotype, 04535_1 (Fig. 4B,C), was not found in this large study. Interestingly, the allele combination that would be associated with the reciprocal C-E recombinant, ^*060-^*010-^*110, was found at a frequency of 9% in a South African population, and at a lower frequency among American blacks (Imanishi et al. 1992).

Discussion

By analyzing 21 human haplotypes across the HLA class II region, the sequences of 20 of which were newly acquired for this study, we have demonstrated a dramatic pattern of haplotype divergence that appears to extend back ∼40 Myr. Although we found some examples of recent recombination events between deeply diverged haplotypes, the overall pattern of linkage disequilibrium across the region requires that such events be infrequent relative to predictions based on genome-wide recombination rates. There was no indication of scrambling of functional alleles at the class II genes, DQB1, DQA1, and DRB1, across highly divergent haplotypes by gene conversion or multiple-recombination events combined with selection. Overall, the data are largely consistent with a model in which deeply diverged haplotypes have evolved independently for tens of millions of years.

This model could either reflect infrequent recombination or selection against recombinant haplotypes. Despite longstanding interest in distinguishing between these two models (Cullen et al. 1997)—and evidence in an adjacent, much less polymorphic, segment of the HLA class II region that recombination hot spots can be the dominant influence on linkage disequilibrium patterns (Kauppi et al. 2003)—there is presently no basis for determining their relative contributions in the DQB1-DQA1-DRB1 region. The data presented here suggest a clear path forward for resolving this long-standing debate. High-resolution recombination studies, based on sperm typing, must be carried out on carefully selected men. The essential question is whether or not recombination rates are strongly suppressed in regions of heterozygosity for high haplotype divergence. Previous studies (Cullen et al. 2002), whether based on sperm typing or pedigree analysis, have not been able to control for this critical variable because of a lack of reference data on the common haplotype sequences present in the DQB1-DQA1-DRB1 region.

Recent long-range sequencing data for two HLA haplotypes (Stewart et al. 2004) allow us to put the extraordinary sequence polymorphism we observe in the class II region into a broader context. The two available sequences—from the COX and PGF cell lines, both of which are homozygous across the HLA locus due to identity-by-descent—fit cleanly into our B (COX) and E (PGF) haplotype groups. The region we analyzed captures most of the interval of extreme divergence (>2%) between the COX and PGF haplotypes. The overall pattern of divergence between the COX and PGF haplotypes across all of HLA is one of peaks of unusual divergence at sites of highly polymorphic genes (HLA-A, the HLA-B/-C region, the HLA-DQB1-DRB1-DQB1 region analyzed here, and HLA-DPB1), separated by normal or near-normal levels of variation; the typical extent of highly divergent (>0.5%) regions, of which the DQB1-DQA1-DRB1 gene cluster is the most dramatic example, is 100-300-kbp.

View larger version:

• In this window
• In a new window

• Download as PowerPoint Slide

Figure 5.

Molecular phylogenies for the 23 haplotypes in four 2-kbp windows sampled from the DQB1-DQA1 interval. The coordinate system is the same as that employed in Figure 1. Parts (A-D) differ only in the position of the 2-kbp window that was analyzed: horizontal bars below the coordinate axes indicate the position of the window that was the source of data for each tree. Branches leading to C- and D-group haplotypes (see Fig. 1 legend) are labeled.

We hypothesize that genomic regions of the type described here will occur commonly in biology even if extreme examples are rare in any given genome. The prerequisites are a cluster of genes that are individually under balancing selection and whose products interact. Under these circumstances, theory predicts precisely the type of long-range hitchhiking of neutral alleles on selected sites that we observe in the HLA class II region (Kelly and Wade 2000). Other gene clusters that are likely to exhibit similar effects include those that encode key components of the self-incompatibility systems present in many flowering plants (Charlesworth et al. 2003; Franklin-Tong and Franklin 2003; Hiscock and Tabah 2003).

Although new data will be needed to resolve the relative contributions of a low recombination rate and selection for preferred combinations of alleles to the evolution of the class II region, we hypothesize that both mechanisms are important. Certainly, it is plausible from data on model organisms that recombination rates might drop significantly when allelic segments have diverged by as much as 5%-10% (Shen and Huang 1989). However, we consider it likely that selection for preferred combinations of alleles is the decisive determinant of haplotype divergence in the class II region. This view suggests that haplotype divergence is predominantly the effect rather than the cause of the prevailing pattern of allelic association.

In addition to being important in its own right, the class II region provides a model for the types of genomic footprints that are left by the interplay of recombination, balancing selection, and gene-gene interaction. In the case of the HLA class II gene cluster, the footprint is uniquely strong and readily detectable without recourse to sophisticated statistical tests. However, it may prove possible to detect comparable, albeit weaker, footprints when similar processes have acted over shorter time intervals. The methods we employed provide a potentially general path toward the detailed analysis of genome segments with these properties.

Methods

DNA samples

DNA samples were obtained from the Coriell Cell Repositories. Self-descriptions of the nationality or geographic ancestry of the anonymous human donors are included here. Even though these descriptors do not conform to a consistent standard, they do indicate that the panel provides a diverse, worldwide sampling of human genetic variation: 04535 (Asian, Japanese), 10540 (Melanesian), 14660 (Black, African American), 01018 (Caucasian, Puerto Rican), 10923 (Caucasian, German), 00576 (Asian, Chinese), 14661 (Black, African American), 14663 (Black, African American), 01960 (Caucasian, Mexican), 03715 (Caucasian, European). Catalog numbers for chimpanzee and gorilla samples were 03646 and 05251, respectively.

Fosmid cloning

Fosmid libraries (Kim et al. 1992) were prepared by cloning 30-50-kbp fragments of genomic DNA, prepared by partial digestion with Sau3AI (New England Biolabs), and size-fractionated by preparative agarose gel electrophoresis into the BamH1 site of standard fosmid vectors (most commonly, pCC1FOS from Epicentre). Packaging into infectious bacteriophage lambda particles was carried out with Gigapack III XL lambda-packaging extract (Stratagene). The clones were propagated in XL1-Blue MR E. coli cells. After titering of the packaged ligation mixtures, pools of ∼3000-5000 clones were created by infection of an E. coli culture, which was then grown overnight under chloramphenicol selection (12 μg/mL). One aliquot of the cultures was stored for later clone isolation, and another aliquot was used to prepare DNA samples for PCR analysis with a set of PCR assays, spaced at intervals of ∼10 kbp across the region analyzed. A list of these assays is included in Supplemental Table 2. Because of the high polymorphism across the region, allelic variation was present in most amplicons for most individuals. The allelic variant present in a subset of the amplicons, as amplified from particular fosmid pools, was determined by sequencing the PCR products. Haplotype-specific-STS-content maps (Green and Olson 1990) of the target region were constructed from the PCR data. Individual fosmid clones spanning each haplotype were isolated from an appropriately chosen set of positive pools. The clone-isolation procedure involved one or two cycles of subpool creation followed by plating for single colonies.

View larger version:

• In this window
• In a new window

• Download as PowerPoint Slide

Figure 6.

Classical DQA1, DQB1, and DRB1 alleles present on the 21 human haplotypes juxtaposed to a molecular phylogeny from the middle of the DQB1-DQA1 intergenic region. The phylogenetic tree is redrawn from Figure 5C with branches leading to haplotype groups A-E, as defined in the Figure 1 legend, labeled. Entries are marked N/A (“not available”) either because there is not a match to an established human allele—as was true for the gorilla and chimpanzee alleles—or insufficient data were available to establish a match.

DNA sequencing

Isolated fosmids were sequenced by standard shotgun-sequencing procedures with data collection on ABI 3700 capillary sequencers. Assembly was with the phrap assembler (http://www.phrap.org/). Finishing relied on targeted data acquisition designed by the Autofinish program (Gordon et al. 2001), manual assessment of residual uncertainties with the aid of the Consed program (Gordon et al. 1998), and resolution of these problem regions through custom-designed experiments. Haplotype sequences were constructed by melding the overlapping set of fosmid sequences obtained from each haplotype.

Reference sequence

The reference sequence of the target region, RefSeq, was based on the July 2003 assembly of the human genome sequence; position 1 in RefSeq corresponds to chromosome 6 coordinate 32,722,342; RefSeq is on the opposite strand relative to the database entry (http://genome.ucsc.edu/).

Sequence alignments

Pairwise and multiple alignments of the haplotypes were carried out using a program developed during the present study. Pairwise alignments of each haplotype with RefSeq were constructed using an algorithm that finds a maximal chain of perfect matches of 20 or more nucleotides. The algorithm then fills in intervening regions by using a standard dynamic programming method (Durbin et al. 1998). The multiple alignment was based on the set of pairwise alignments with RefSeq. Nucleotide positions were only included in the multiple alignment when they could be uniquely aligned across all haplotypes. The entire multiple alignment is included in Supplemental Table 1.

Linkage disequilibrium analysis

The data displayed in Figure 3 are based on the statistic |D′|, which ranges from 0 (random association between two SNPs across the available haplotypes) to 1 (maximum possible positive or negative association, considering the allele frequencies of the two SNPs) (Lewontin 1964). The analysis was only carried out across the region for which we had data on all 21 human haplotypes, and it only included positions at which all 21 haplotypes could be aligned. Furthermore, we excluded SNPs in which the minor allele occurred two or fewer times, and we also excluded SNPs that are likely to have arisen by mutations at CG dinucleotides. Specifically, SNPs were excluded if they belonged to a dinucleotide in which two out of the three sequences CG, TG, and CA were represented among the 21 haplotypes. The filtering out of rare dinucleotides increases the sensitivity of |D′| to the effects of historical recombination events, and the elimination of most CG-related mutations decreases noise due to recurrent mutation. For the display in Figure 3, each of the 3468 SNPs that survived the filtering was assigned a range of coordinates that includes half the distance (in REFSEQ coordinates) to each of the SNPs that bracketed it. The details of this procedure, which produces a linear coordinate system at the expense of giving different SNPs different weights in the display, affect only the finest-scaled of the visible features of the figure.

Phylogenetic trees

The phylogenetic trees in Figures 1 and 5 were constructed using the Phylip package, version 3.5 (http://evolution.genetics.washington.edu/phylip.html), using the neighbor-joining/UPGMA (unweighted pair group methods with averages) method.

Allele assignments

Classical HLA alleles were assigned to the human haplotypes by comparing the HLA-DQB1, -DQA1, and -DRB1 coding regions with data tabulated in the April 2004 update of the Anthony Nolan database (http://www.anthonynolan.org.uk/HIG/data.html). In most instances, allele assignments were based on exact matches at all diagnostic nucleotide positions. Exceptions are enumerated in Supplemental Table 3.

Database submissions

The 20 human, the chimpanzee, and the two overlapping gorilla haplotypes sequenced for this study have been deposited in GenBank with accession nos. AY663393-AY663415.