From Complete Genomes to Measures of Substitution Rate Variability Within and Between Proteins
Abstract
Accumulation of complete genome sequences of diverse organisms creates new possibilities for evolutionary inferences from whole-genome comparisons. In the present study, we analyze the distributions of substitution rates among proteins encoded in 19 complete genomes (the interprotein rate distribution). To estimate these rates, it is necessary to employ another fundamental distribution, that of the substitution rates among sites in proteins (the intraprotein distribution). Using two independent approaches, we show that intraprotein substitution rate variability appears to be significantly greater than generally accepted. This yields more realistic estimates of evolutionary distances from amino-acid sequences, which is critical for evolutionary-tree construction. We demonstrate that the interprotein rate distributions inferred from the genome-to-genome comparisons are similar to each other and can be approximated by a single distribution with a long exponential shoulder. This suggests that a generalized version of the molecular clock hypothesis may be valid on genome scale. We also use the scaling parameter of the obtained interprotein rate distribution to construct a rooted whole-genome phylogeny. The topology of the resulting tree is largely compatible with those of global rRNA-based trees and trees produced by other approaches to genome-wide comparison.
Multiple, complete genome sequences from taxonomically diverse species create unprecedented opportunities for new phylogenetic approaches (Huynen and Bork 1998). Comparative genome analysis shows a striking complexity of evolutionary scenarios that involve, in addition to vertical descent, a number of horizontal gene transfer and lineage-specific gene loss events (Koonin et al. 1997;Doolittle 1999). With these “illicit” events being so prominent in the history of life (at least as far as prokaryotes are concerned), the question arises as to whether whole-genome comparisons are still capable of detecting a sufficiently strong signal to produce a coherent, large-scale phylogeny. One way to approach this problem is based on the presence or absence of representatives of different genomes in orthologous protein families (Fitz-Gibbon and House 1999;Snel et al. 1999; Tekaia et al. 1999). Another strategy involves the analysis of multiple protein families, with a subsequent attempt to derive a consensus that could reflect the “organismal” phylogeny (Teichmann and Mitchison 1999).
In the present study, we apply an alternative approach that, to our knowledge, has not been systematically explored before. The methodology is based on the analysis of the distributions of evolutionary rates among orthologous proteins (Fitch 1970), or the interprotein rate distribution. We hypothesized that the distribution of relative evolutionary rates does not change significantly in the course of evolution because all organisms possess similar repertoires of core protein functions that are primarily represented among orthologs (Tatusov et al. 1997). Below we describe a statistical test for this hypothesis. Under this assumption, the evolutionary distances, defined as the average number of substitutions per site between likely orthologs, linearly depend on substitution rates. Thus, the distribution of the rates can be determined from the distribution of the distances using a scaling factor proportional to the divergence time. To estimate these rates, it was necessary to use another fundamental distribution, that of the substitution rates among sites in individual proteins, or the intraprotein rate distribution. We show that intraprotein substitution rate variability appears to be significantly greater than generally accepted. We further demonstrate that the interprotein rate distributions inferred from the genome-to-genome comparisons are similar to each other and can be approximated by a single distribution with a long exponential shoulder. The scaling parameter of this distribution was used to construct a rooted whole-genome phylogenetic tree. The resulting topology is largely compatible with that of global rRNA-based trees and with those of the trees produced by other methods of genome-wide analysis.
RESULTS AND DISCUSSION
Estimating Evolutionary Distances Using the Intraprotein Rate Distribution
The evolutionary distances between likely orthologs, which were identified as statistically significant, symmetrical best hits, were obtained from the results of all-against-all comparisons of protein sequences from all pairs of genomes, as described in the Methods section. All genome-to-genome comparisons used at least 100 and, typically, >200 pairs of likely orthologs (Table1). The distribution functions of the fraction of unchanged sites show that, even for closely related species, such as the two Mycoplasmas or Escherichia coli andHaemophilus influenzae, there exists a considerable fraction of poorly conserved potential orthologs (Fig. 1a), in agreement with previous observations (Tatusov et al. 1996). We examined, case by case, the pairs with 30–40% identical residues, produced by the comparison of the two species of mycoplasmas, for structural and biological relevance and did not identify any apparent false-positive results. Such poorly conserved but apparently orthologous pairs of proteins include, for example, lipoproteins, adhesins, and other surface proteins. Distances were estimated from the identity fractions (Fig. 1a) by using the intraprotein rate distribution. This distribution traditionally had been estimated from multiple sequence alignments (Uzzell and Corbin 1971; Dayhoff et al. 1978; Holmquist et al. 1983; Gogarten et al. 1996; Zhang and Gu 1998). The existing methods rely on elaborate models of sequence change. They require knowledge of the tree topology for sequences in the multiple alignment and good estimates for the number of substitutions in each site. Usually, the tree topology is not easily recoverable, and some multiple substitutions at highly variable sites are always missed, leading to underestimates of the rate variability. The latter effect becomes particularly noticeable at larger evolutionary distances when highly variable sites approach saturation with substitutions. Furthermore, previously used methods are based on the assumption of independence of the site rates on the type of amino-acid replacements, which may result in a significant underestimate of the rate variability (Feng and Doolittle 1997). It is well known that amino acids are not equally interchangeable (Dayhoff et al. 1978), and it is erroneous to neglect this fact (Grishin 1995; Feng and Doolittle 1997). In addition, application of maximum likelihood for simultaneous estimation of rate variability and branch lengths of the tree employed by previous workers (Zhang and Gu 1998) results in a strong correlation between these parameters. The likely reason for such correlation is a highly curvilinear relationship between the average number of substitutions per site and identity fractions.
Number of Likely Orthologs Detected in Pairwise Genome Comparisons
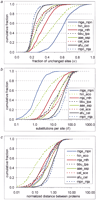
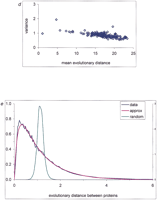
Interprotein rate variation. An empirical distribution function is shown for the fraction of unchanged sites (a), evolutionary distances (b), and normalized evolutionary distances (c) between likely orthologs for several genome pairs. For genome designations, see Methods. (d) Correlation between the variance of the distribution of normalized evolutionary distances and the mean distance between proteins in genome pairs. (e) Probability density function of interprotein substitution rate. The empirical density function of interprotein substitution rate estimated from distances obtained from genome comparisons (data), from approximation (approx) using formula (3), and from random sampling of the intraprotein rate distribution (random) are shown.
To avoid these limitations, we developed a method that involves only a few simple assumptions and does not require highly
accurate estimates of the number of substitutions. We express the intraprotein rate variation in terms of relative substitution
rates, which are normalized to keep the mean instantaneous rate over all sites in a sequence equal to 1: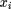 where xi
(t) is the relative instantaneous substitution rate for site i at time t, λi(t) is the absolute rate for sitei at time t, and n is the total number of sites in the given sequence. The assumptions are (1) sites evolve independently, (2) xi
(t) does not change if no substitutions occur in site i, (3) the probability that a site with a relative rate x remains unchanged after damino-acid substitutions per site occurred in the protein sequence ise
−xd, and (4) the distribution of relative substitution rates among sites does not change with time (Zuckerkandl and Pauling 1965; Tajima and Takezaki 1994; Grishin 1995, 1997). In our approach we use only these four assumptions, all of which have been explicitly or implicitly made in the previous
studies, but each of these studies has included some additional assumptions. It appears that our set of assumptions is the
least restrictive because it allows for individual site rates to change with time and for rates to differ between different
amino acids. Under the above assumptions:
where xi
(t) is the relative instantaneous substitution rate for site i at time t, λi(t) is the absolute rate for sitei at time t, and n is the total number of sites in the given sequence. The assumptions are (1) sites evolve independently, (2) xi
(t) does not change if no substitutions occur in site i, (3) the probability that a site with a relative rate x remains unchanged after damino-acid substitutions per site occurred in the protein sequence ise
−xd, and (4) the distribution of relative substitution rates among sites does not change with time (Zuckerkandl and Pauling 1965; Tajima and Takezaki 1994; Grishin 1995, 1997). In our approach we use only these four assumptions, all of which have been explicitly or implicitly made in the previous
studies, but each of these studies has included some additional assumptions. It appears that our set of assumptions is the
least restrictive because it allows for individual site rates to change with time and for rates to differ between different
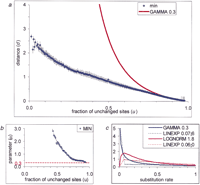
amino acids. Under the above assumptions: where u is the fraction of sites in which no substitutions occurred, d is the evolutionary distance (average number of substitutions per site), and ρ(x) is the probability density function of substitution rates. Thus, ρ(x) can be estimated using equation (1). We obtained the lower bound of d for a range of u values from multiple alignments of 15 protein families from the Pfam database (Bateman et al. 1999) (Fig.2a; and see Methods) and estimated the variation coefficient of the intraprotein rate distribution. The resulting value of
1.70 ± 0.08 is considerably greater than the previous estimates that have a mean of 1.09 (range = 0.43–2.02 for different
protein families; Zhang and Gu 1998). Because our approach involves only some of the assumptions used in other studies (see above) and also produces the lower
estimate for the variation coefficient due to the use of the lower bound for d(u) (Grishin 1999), the result is expected to be more accurate than those reported previously. The variance of this estimate between different
protein families was surprisingly small. This result could be explained by the use, for the estimation of the fraction of
unchanged sites in each family, of large samples of sequence pairs, each of which was highly conserved (see Methods), thus
virtually eliminating the possibility of incorrect alignments and minimizing the effect of unaccounted for multiple substitutions.
where u is the fraction of sites in which no substitutions occurred, d is the evolutionary distance (average number of substitutions per site), and ρ(x) is the probability density function of substitution rates. Thus, ρ(x) can be estimated using equation (1). We obtained the lower bound of d for a range of u values from multiple alignments of 15 protein families from the Pfam database (Bateman et al. 1999) (Fig.2a; and see Methods) and estimated the variation coefficient of the intraprotein rate distribution. The resulting value of
1.70 ± 0.08 is considerably greater than the previous estimates that have a mean of 1.09 (range = 0.43–2.02 for different
protein families; Zhang and Gu 1998). Because our approach involves only some of the assumptions used in other studies (see above) and also produces the lower
estimate for the variation coefficient due to the use of the lower bound for d(u) (Grishin 1999), the result is expected to be more accurate than those reported previously. The variance of this estimate between different
protein families was surprisingly small. This result could be explained by the use, for the estimation of the fraction of
unchanged sites in each family, of large samples of sequence pairs, each of which was highly conserved (see Methods), thus
virtually eliminating the possibility of incorrect alignments and minimizing the effect of unaccounted for multiple substitutions.
Intraprotein rate variation. (a) Dependence of the evolutionary distance d on the fraction of the unchanged sitesu estimated from multiple alignments. The curve designated “min” shows the lower bound of the estimated distances. The curve
“GAMMA 0.3” shows the d(u) dependency when the gamma distribution with α = 0.3 was used to describe intraprotein rate variation. (b) Estimation of the α parameter of the gamma distribution. The α values were extrapolated to u = 1. The obtained upper estimate for the α parameter is indicated by the red dotted line. (c) Probability density functions used to describe intraprotein rate variation. The figure illustrates two possible shapes of
the density function: the L-shaped gamma distribution (GAMMA 0.3) and the bell-shaped log-normal distribution (LOGNORM 1.8).
The parameter of the log-normal distribution was obtained by fitting the data from a in the same manner as for the gamma distribution. Dotted lines (LINEXP a;b) show two examples of the combination of linear and exponential densities given by the formula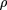 where A is a normalization constant andc is determined from the requirement of the mean xbeing equal to 1. The parameter a gives the point where the linear approximation ends; the parameter b determines the intercept.
where A is a normalization constant andc is determined from the requirement of the mean xbeing equal to 1. The parameter a gives the point where the linear approximation ends; the parameter b determines the intercept.
From our data, it is also possible to obtain the best-fit value of the parameter for any single-parameter density function
(Fig. 2b). Traditionally, the rate variation among sites has been described by gamma density (Nei et al. 1976; Ota and Nei 1994; Yang 1994; Li and Gu 1996; Grishin 1999):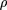 where Γ is the gamma function and α is the distribution parameter. We estimated α using our method. Consistent with the variation
coefficient analysis, the obtained value α = 0.31 is significantly lower than those generally used (on average, 0.7 – 0.8;
Gogarten et al. 1996; Zhang and Gu 1998), which corresponds to a higher site-rate heterogeneity. Analysis of individual protein families produced very similar values
of α, in the range of 0.27 ± 0.05 (Table2). This suggests that site-rate variation for different proteins is described by similar if not by identical distributions.
where Γ is the gamma function and α is the distribution parameter. We estimated α using our method. Consistent with the variation
coefficient analysis, the obtained value α = 0.31 is significantly lower than those generally used (on average, 0.7 – 0.8;
Gogarten et al. 1996; Zhang and Gu 1998), which corresponds to a higher site-rate heterogeneity. Analysis of individual protein families produced very similar values
of α, in the range of 0.27 ± 0.05 (Table2). This suggests that site-rate variation for different proteins is described by similar if not by identical distributions.
Gamma Distribution Parameter α Estimated from Multiple Alignments
The gamma density with α ≤ 1 is a decreasing, L-shaped function. In contrast, other distributions, for example, the bell-shaped log-normal distribution that also has been proposed to describe the site-rate variation (Olsen 1987), have a non-zero mode. To discriminate between an L-shaped and a bell-shaped distribution, we fitted our data to a two-parameter density function that is a combination of a linear segment near zero with an exponential tail (Fig. 2c). The negative slope of the best-fit linear segment obtained from the data strongly suggests an L-shaped density of substitution rates, with the single mode in zero. Thus the majority of the sites in a protein exhibit very low relative rates, whereas a small fraction of variable, selectively (almost) neutral sites absorb most of the substitutions through multiple mutations at the same site.
Based on the assumption of the evolutionary constancy of the interprotein rate distribution (see introduction), we proposed an independent way to estimate the parameter of the gamma density for the intraprotein rate distribution. The value of α was determined that minimized the differences between distributions of normalized evolutionary distances for all pairs of complete protein sets. The resulting value of α obtained by this approach (0.31 ± 0.03) is remarkably close to that derived from the multiple alignment comparison (0.31). Given the good agreement between these independent estimates, we believe that the gamma density with the parameter α = 0.3 provides an adequate description of the intraprotein rate variation.
Interprotein Distributions of Evolutionary Rates
The gamma distribution with the parameter α = 0.3 was used to calculate the distances for each pair of protein sets using equation (1) and to generate the respective distributions (Fig. 1b). Notably, even for genomes with high average identity between proteins, for example, the spirochaetes Borrelia burgdorferi andTreponema pallidum, the distances calculated as the average number of substitutions per site were large and significantly greater than those reported previously (Huynen and Bork 1998) (compare Fig. 1a and b). As expected, different genome pairs differed greatly in the median distance, which could be as low as one substitution per site between the two Mycoplasmas and as high as 50 substitutions per site between divergent organisms, such as Bacteria andArchaea (Fig. 1b). After normalization, these distributions were compared with each other to test our central hypothesis that the interprotein distribution is constant in evolution (Fig. 1c). It was found that 64% of genome pairs passed the chi-square test at the 0.01 level when compared with the rest of the data combined. Only a few genome pairs, in particular Escherichia coli andHaemophilus influenzae (χ2 ≈ 3700) andMethanococcus jannaschii and Methanobacterium thermoautotrophicum (χ2 ≈ 170), showed strong deviations from the distribution of the combined data (Fig. 1a–c). We suspect that these anomalies may be due to extensive loss of conserved genes, in particular those coding for metabolic enzymes, in H. influenzae (Tatusov et al. 1996) and massive horizontal gene transfer between the two archaeal methanogens, respectively. Figure 1c shows that most of the normalized distribution functions are much closer to each other than the non-normalized functions shown in Figure1b. The normalization brings all the distributions to the same variance, equalized to 1, but, in general, should not affect other parameters. However, the medians of the distributions show strong correlation with the variance and typically fall within the range between 0.5 and 1.0. In contrast, the medians of the normalized distributions (Fig. 1c) show little correlation with the medians of the not-normalized ones (Fig. 1b). For example, the median of the mge_mpn distribution is (as expected) much smaller than that of the mja_mth distribution shown in Figure 1b, but the reverse is true for these pairs after normalization (Fig. 1c). The shape of the hin_eco distribution after normalization significantly differs from that of the rest of the distributions (Fig. 1c; also see below).
A systematic bias in the obtained distributions of evolutionary distances might arise from the underestimate of the number of highly divergent orthologs (see Methods). Such fast-evolving pairs of orthologs could be missed because of the requirement of statistical significance of the observed sequence similarity (see Methods). The distributions of the fraction of unchanged sites level off at about 0.15 (Fig. 1a), which should be expected because alignments with <15% identity will typically fail the cutoff, even if the proteins involved are orthologs. This could lower the variance of the distributions, particularly for evolutionarily distant genomes. The fraction of weakly similar orthologs increases with the evolutionary distance between genomes. Therefore, if a large number of divergent orthologs is missed, the variance of the distribution of normalized distances will show an inverse correlation with the mean distance between proteins in genome pairs. Empirically, however, we found only a weak dependence between the variance and the mean (Fig. 1d).
Our assumption of time independence of the intraprotein rate distribution and of the notion of time-invariance of the interprotein rate distribution that was tested as described above are not equivalent to or dependent on the molecular-clock assumption. Molecular clock means that the substitution rate of a site or the average substitution rate of a protein does not change with time. We do not make such an assumption. Indeed, we allow rates of sites and proteins to depend on time as long as the distribution of relative rates remains time independent. There seem to be two principal scenarios whereby this distribution remains constant. Under the first scenario, the absolute substitution rates of sites may change with time, but in a correlated manner, so that the ratio of any two rates remains constant. In this case, the distribution of relative rates (each rate divided by the mean rate) will not change. However, this “relative molecular clock” is not necessary for the time invariance of the distribution, and we favor a different model. Under this second scenario, the rates of site (or protein) change may change freely, and the ratio of any two rates does not need to be fixed. However, we expect that if some sites (proteins) increase their relative rates, others take their place and decrease their relative rates so that there is no significant change in the overall rate distribution. This scenario can be viewed as a statistical interpretation of the covarion model of evolution (Miyamoto and Fitch 1995).
The two most deviant genome pairs were excluded from the combined data set, and the resulting distribution of normalized distances was used as an estimate of interprotein rate variation (Fig. 1e). The distribution of interprotein rates can be simulated by randomly sampling sites from the intraprotein rate distribution, given the distribution of protein lengths in each genome (Fig. 1e). The standard variance of the resulting distribution was about 10 times lower than that of the empirical distribution (Fig. 1e). This major difference between the simulated and observed interprotein rate distributions indicates that, for the purpose of describing the evolutionary process, a protein cannot be approximated by a random collection of sites from the intraprotein rate distribution. In other words, the interprotein rate distribution is not determined by the intraprotein rate variability but rather is dictated by the diversity of the functional constraints for different proteins. It is well known that some proteins (e.g., histones) evolve extremely slowly, whereas others (e.g., fibrinopeptides) are highly variable.
We attempted to fit the empirical interprotein rate distribution with different standard density functions, but none of the
fits was sufficiently close (not shown). We noticed, however, that the mean of the observed distribution is close to its variance,
which was set to 1. This is the case for the exponential distribution, and the following density gives the best fit to the
data with the parameters b = 1.01 and c = 5.88 (Fig. 1e). The resulting interprotein rate distribution described by equation (3) shows that most of the proteins change at a relatively
low rate, and there are very few proteins with a rate lower than this most probable one. The number of proteins with a rate
higher than the most probable rate decreases exponentially (Fig. 1e). The exponent is the distribution with the maximum entropy under the condition that the mean remains constant. According
to the maximum entropy principle (Miller and Horn 1998), at equilibrium, a broad class of distributions with a fixed mean (e.g., the Boltzmann distribution under the condition
of energy conservation) approaches exponential distribution (Grishin 1995). Thus, the presence of the exponential tail in the interprotein distribution is compatible with a constant mean rate of
protein change during evolution. In other words, on a genome scale (at least for most organisms with completely sequenced
genomes) and at large evolutionary intervals, the molecular-clock hypothesis might be a reasonable approximation. Individual
protein families may significantly deviate from the molecular-clock assumption, but the average rate of change for all proteins
combined does not seem to violate it (Doolittle et al. 1996; Feng et al. 1997).
with the parameters b = 1.01 and c = 5.88 (Fig. 1e). The resulting interprotein rate distribution described by equation (3) shows that most of the proteins change at a relatively
low rate, and there are very few proteins with a rate lower than this most probable one. The number of proteins with a rate
higher than the most probable rate decreases exponentially (Fig. 1e). The exponent is the distribution with the maximum entropy under the condition that the mean remains constant. According
to the maximum entropy principle (Miller and Horn 1998), at equilibrium, a broad class of distributions with a fixed mean (e.g., the Boltzmann distribution under the condition
of energy conservation) approaches exponential distribution (Grishin 1995). Thus, the presence of the exponential tail in the interprotein distribution is compatible with a constant mean rate of
protein change during evolution. In other words, on a genome scale (at least for most organisms with completely sequenced
genomes) and at large evolutionary intervals, the molecular-clock hypothesis might be a reasonable approximation. Individual
protein families may significantly deviate from the molecular-clock assumption, but the average rate of change for all proteins
combined does not seem to violate it (Doolittle et al. 1996; Feng et al. 1997).
Constructing a Global Phylogenetic Tree on the Basis of the Interprotein Rate Distribution
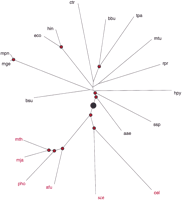
Distribution (3) can be used to find the maximum-likelihood scaling parameter for each genome pair; this parameter defines an additive evolutionary distance between the respective species. The matrix composed of these distances was used to construct a phylogenetic tree with the Fitch–Margoliash method (Fig. 3) and the neighbor-joining method (not shown). Both methods produced essentially the same tree topology. The tree clearly shows the separation of the three domains of life (bacteria, archaea, and eukaryotes), whereas the major bacterial lineages show a star phylogeny, which is generally compatible with the currently accepted gross evolutionary scenarios (Woese et al. 1990; Snel et al. 1999). Under the genome-scale molecular-clock assumption, the root is between archaea–eukaryotes and bacteria (Fig. 3), which agrees with the results of rooting by paralogy for several protein families (Gogarten et al. 1989; Iwabe et al. 1989;Brown and Doolittle 1997).
A phylogenetic tree for complete genomes. The nodes supported by bootstrap values >70% are marked by red dots. The inferred root position is indicated by a black circle. For genome designations, see Methods.
Some of the reported rRNA-based trees and trees based on gene content in complete genomes show a better resolution of the bacterial branches (Olsen et al. 1994; Fitz-Gibbon and House 1999; Snel et al. 1999). Heavy corrections for multiple substitutions that are inherent in our analysis inevitably lead to larger distances and thus to larger errors in the distance estimates, which may preclude the resolution of deep branching among bacteria. It has been shown under the molecular-clock hypothesis that tree reconstruction is consistent with simple proportions of different residues between sequences without correction (p distances; Rzhetsky and Sitnikova 1996). Thus, under the molecular-clock assumption, correct tree topology may be produced with underestimated distances when the adequate correction for multiple substitutions has not been made. Underestimated distances will display smaller standard errors and will allow for a better-resolved tree. The present analysis suggests that the molecular clock could be valid on the genome scale, and accordingly, undercorrection might not have led to incorrect tree topology in previous phylogenetic analyses. It appears likely that some of the unresolved bacterial branches in the tree shown in Figure 3 are indeed explained by a large error in distance estimates. For example, the grouping of R. prowazekiiwith Proteobacteria is convincingly supported by both rRNA-based phylogenetic analysis (Olsen et al. 1994) and detailed analysis of the genome (Andersson et al. 1998) but is missed in the tree produced by our approach (Fig. 3). Some other relationships reported in the previous analyses could be artifactual, however, such as, for example, the grouping of Synechocystis with Aquifex suggested by one of the genomewide analyses (Snel et al. 1999), but not others or the rRNA-based phylogeny (Olsen et al. 1994), or the grouping between gram-positive bacteria and Proteobacteria seen in another genomewide study (Fitz-Gibbon and House 1999). In these cases, the lack of resolution due to the extensive correction for multiple substitutions could provide the most realistic, if not the most informative, picture of the star phylogeny of the bacteria. Such a conclusion appears compatible with the results of phylogenetic analyses of multiple protein families (Teichmann and Mitchison 1999). To a large extent, the difficulties in resolving bacterial phylogeny could be due to massive horizontal transfer across bacteria.
Important as the effects of horizontal transfer seem to be, they are not sufficient to entirely wash out the phylogenetic signal in genomewide comparisons, at least the three primary domains of life are recovered reliably. Clearly, at this time, the final word on the best method(s) for genomewide comparison and its utility in phylogenetic reconstruction is not yet out. Experimentation with genome data on a much larger scale should help in finding the optimal solution and assessing the attainable level of resolution.
The results of this study indicate that using complementary information produced by whole-genome comparisons and by analysis of large protein families may significantly enhance our understanding of molecular evolution. Eventually, application of statistical methods to the rapidly growing amounts of such complementary data may result in the derivation of a compact set of “laws of evolutionary genomics.”
METHODS
Comparison of Protein Sequence Sets from Complete Genomes
The protein sets from complete genomes were retrieved from the genome division of the Entrez system (http://www.ncbi.nlm.nih.gov/Entrez/Genome/org.html) except for the nematode Caenorhabditis elegans proteins, which were retrieved from the Sanger Center FTP site (http://www.sanger.ac.uk/Projects/C_elegans/). The abbreviations for species names are: Bacteria—Aquifex aeolicus (aae), Bacillus subtilis (bsu), B. burgdorferi (bbu), Chlamydia trachomatis (ctr),Escherichia coli (eco), H. influenzae (hin),Helicobacter pylori (hpy), Mycobacterium tuberculosis(mtu), Mycoplasma genitalium (mge), Mycoplasma pneumoniae (mpn), Rickettsia prowazekii (rpr),Synechocystis sp. PCC6803 (ssp), T. pallidum (tpa); Archaea—Archaeoglobus fulgidus (afu), M. thermoautotrophicum (mth), M. jannaschii (mja),Pyrococcus horikoshii (pho); Eukaryota—Caenorhabditis elegans (cel), Saccharomyces cerevisiae (sce). The BLASTP program (Altschul et al. 1997) was used to perform an all-against-all similarity search for the set of proteins from 19 completely sequenced genomes. Only symmetrical best hits between genomes (Tatusov et al. 1997), supported by an e value <0.01 and fraction of low complexity regions (Wootton 1994) <50% in the aligned segment, were included in the analysis. These criteria maximize the likelihood that the sequence similarity reflects homology and that most of the proteins pairs identified using this approach are true orthologs. The fraction of unchanged sites u was estimated from the identity percentage q as u = (q −q∞ )/(1 − q∞ ), whereq∞ is the expected identity for random sequences (Feng et al. 1997; Grishin 1997).
Estimation of Intraprotein Rate Variation from Multiple Alignments
We used 14 large protein families from the Pfam database (Pfam IDs PF00016, PF00077, PF00078, PF00032, PF00509, PF00361, PF00129,
PF00559, PF00522, PF00393, PF01010, PF00042, PF00091, PF00075; see also Table2). The families were selected so that each contained more than 50 nonidentical sequences with >90% identity to a master sequence.
The sequence that had the maximal number of nonidentical family members with >90% identity was chosen as the master. These
criteria were adopted to minimize the effect of multiple and back substitutions. For each subaligment (a random subset of
more than four sequences from the alignment), the fraction of sites occupied by the same amino acid in all sequences (invariant
sites) was used as an estimate of the fraction of unchanged sites u (given that we analyzed only highly similar sequences, we assumed that such invariant sites have not been affected by back
substitutions). For each site in the subalignment, the number of different amino acids in this site minus one cannot exceed
(and for u➞1 approaches) the number of substitutions at this site. Averaged over the sites in the subalignment, this gives the lower
bound of d(u), which is the number of substitutions per site in the tree that relates all the sequences in the subalignment. Because the
lower bound approaches the true functiond(u) for u➞1 (d➞0), the standard deviation of ρ(x) is calculated from the second derivative of u(d) at d = 0, which is estimated numerically from the lower bound curve by extrapolation tod = 0. Conveniently, u(d), given by equation (1), is a moment-generating function for ρ(x) and the moments of the distribution can be found by recursive differentiation of u(d). Because the mean x is equal to 1, the standard deviation of x is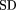 SD(x) is equal to the coefficient of variation that measures the degree of intraprotein rate heterogeneity. For each point (d,u), the α parameter of the gamma density function ρ(xα) that generates the curveu(d) (equation 1) passing through this point was calculated. The extrapolation of the obtained α values for each bin on the u axis to u = 1 for the lower bound of dgives an upper estimate of α under the conditions described previously (Grishin 1999).
SD(x) is equal to the coefficient of variation that measures the degree of intraprotein rate heterogeneity. For each point (d,u), the α parameter of the gamma density function ρ(xα) that generates the curveu(d) (equation 1) passing through this point was calculated. The extrapolation of the obtained α values for each bin on the u axis to u = 1 for the lower bound of dgives an upper estimate of α under the conditions described previously (Grishin 1999).
Estimation of Intra- and Interprotein Rate Variation from Genome Comparisons
For each pair of complete genomes, the u values obtained as described above were converted to the distances d by using equation (1) and the gamma distribution of intraprotein rates. The distances d were normalized by dividing each distance by the standard deviation of distances for a genome pair. The value of the parameter
α (equation 2) was found for which the differences between 171 normalized distributions of distances for all genomes pairs
(19 * 18/2) measured by the chi-square test were minimal. Specifically, normalized distances were binned into 20 intervals.
We minimized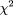 where nij
is the number of protein pairs from the genome pair i with the normalized distance in bin j,.
where nij
is the number of protein pairs from the genome pair i with the normalized distance in bin j,.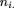 The resulting α = 0.3 was used to generate the final distribution of normalized distances for each pair of genomes. These
distributions were combined to obtain an estimate of interprotein rate density η(x) (equation 3). The normalized distance distribution for each genome pair was compared with the combined data using the chi-square
test.
The resulting α = 0.3 was used to generate the final distribution of normalized distances for each pair of genomes. These
distributions were combined to obtain an estimate of interprotein rate density η(x) (equation 3). The normalized distance distribution for each genome pair was compared with the combined data using the chi-square
test.
Phylogenetic Tree Analysis
The distance between genomes A and B was estimated as the scaling parameter DAB in the formula f(d) = η(d/DAB )/DAB , whered is the distance between orthologs from A and B,f(d) is the probability density function ofd, and η is given by equation (3). Bootstrap analysis was performed by resampling pairs of orthologs for each pair of genomes. The tree was constructed by using the method of Fitch and Margoliash (1967) implemented in the FITCH program of the PHYLIP package (Felsenstein 1996); the tree constructed by using the neighbor-joining method (Saitou and Nei 1987) implemented in the NEIGHBOR program of the PHYLIP package had the same topology. The root position was inferred by using a least-squares version of the midpoint rooting procedure (Wolf et al. 1999).
Acknowledgments
We thank Mikhail Gelfand, Alex Kondrashov, David Lipman, Andrei Mironov, John Spouge and John Wilbur for critical reading of the manuscript and helpful comments.
The publication costs of this article were defrayed in part by payment of page charges. This article must therefore be hereby marked “advertisement” in accordance with 18 USC section 1734 solely to indicate this fact.
Footnotes
-
↵1 Permanent address: Institute of Cytology and Genetics, Russian Academy of Sciences, Novosibirsk 630090, Russia.
-
↵2 Present address: University of Texas Southwestern Medical Center, Dallas, Texas 75235 USA.
-
↵3 Corresponding author.
-
E-MAIL grishin{at}chop.swmed.edu; FAX (214) 648-8856.
-
- Received October 14, 1999.
- Accepted May 2, 2000.
- Cold Spring Harbor Laboratory Press