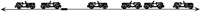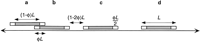Parking Strategies for Genome Sequencing
Abstract
The parking strategy is an iterative approach to DNA sequencing. Each iteration consists of sequencing a novel portion of target DNA that does not overlap any previously sequenced region. Subject to the constraint of no overlap, each new region is chosen randomly. A parking strategy is often ideal in the early stages of a project for rapidly generating unique data. As a project progresses, parking becomes progressively more expensive and eventually prohibitive. We present a mathematical model with a generalization to allow for overlaps. This model predicts multiple parameters, including progress, costs, and the distribution of gap sizes left by a parking strategy. The highly fragmented nature of the gaps left after an initial parking strategy may make it difficult to finish a project efficiently. Therefore, in addition to our parking model, we model gap closing by walking. Our gap-closing model is generalizable to many other strategies. Our discussion includes modified parking strategies and hybrids with other strategies. A hybrid parking strategy has been employed for portions of the Human Genome Project.
A large number and variety of strategies have been proposed and implemented for sequencing large genomes. Both mathematical and simulation models of these strategies are useful in conjunction with large-scale genome projects. These models serve three purposes. First, they allow projects to be planned efficiently, with appropriate allocation of resources, including estimates of project duration. Second, they allow the progress of projects to be monitored. Deviation of an observed parameter, such as target coverage, from its predicted value indicates a technical or biological problem, such as poor-quality data generation or the presence of unclonable regions on the target genome. Third, models allow for cost optimization. A mild increase in cost efficiency can result in tremendous absolute savings, given the overall high cost of large-scale genome sequencing. Costs can be optimized by choosing between alternative sequencing strategies, tuning controllable parameters such as clone-length distribution, and combing strategies to produce hybrid strategies.
In this paper, we present a mathematical model for the parking strategy for genome sequencing. This strategy, in combination with other strategies, has been used for portions of the Human Genome Project and may prove popular for future genome projects for organisms with large genomes (Roach et al. 1999; Batzoglou et al. 1999). The name of the parking strategy derives from a mathematically equivalent scenario that has interested mathematicians for over 50 years (Solomon and Weiner 1986). The scenario consists of cars arriving sequentially to park along an infinite unmarked curb. Each car selects a spot along the curb to park with no regard for subsequent cars. As time proceeds, the curb fills. Any gap greater than a car length will eventually be occupied by a car, but if a gap between two cars is created that is less than the length of a car, it will remain forever empty (Fig.1). The mathematical curiosity of this problem includes both the prediction of the jamming limit, which is the fraction of the curb occupied at infinite time, and the distribution of the length of the gaps between the cars at any given time.
Cartoon of the parking strategy. Cars arrive sequentially at an infinite curb and choose parking spots uniformly from all possible spots, subject to the constraint that they do not overlap any already-parked car. In the portion of the infinite curb illustrated here, only one additional car will fit. The left end of this car can be sited only within the darkened interval.
One may modify the problem in a manner that facilitates mathematical modeling without altering any of the results other than their relationship to the time scale. With this modification, as each car arrives, it picks one spot for its left edge uniformly from the entire curb. If parking at this spot is not possible due to the presence of already-parked cars, the arriving car drives off without parking. Otherwise, it parks.
The parking strategy for genome sequencing is exactly analogous to that of cars parking. One selects a clone, such as a BAC (bacterial artificial chromosome), at random from a target-genome clone library and sequences this BAC. Then one iterates: choosing an additional BAC at random from the library, screening it to see if it overlaps any previously sequenced BAC, discarding it if it does, and sequencing it if it does not. As time progresses, the known tracts of sequence on the target genome are distributed in exactly the same way that parked cars are distributed in the car-parking scenario.
Our analysis of the parking strategy for DNA sequencing is also applicable to certain DNA-mapping strategies. Palazzolo et al. (1991)described one such methodology, a double-end, clone-limited strategy.Zhang and Marr (1993) developed an approximate theoretical model for a similar strategy, nonrandom clone anchoring. These two strategies are derivatives of the parking strategy, and our analyses hold in these cases.
The following should be noted for this paper:
- 1.
- L is the length of each clone. The length of a typical BAC clone is approximately 150 kb. We assume L is constant. The complexity of calculation would increase if we modeled variation in clone length.
- 2.
- G is the length of the genomic target in base pairs. For our simulations, we set the length of the genome as 3 Gb. For our mathematical model, we assume G is infinite. This is reasonable when L << G and facilitates tractability. We also allow clone ends to occur at noninteger positions along the target.
- 3.
- ν is the number of clones screened per unit length of target; νε[0,∞). Screening might be done by partial sequencing but could conceivably utilize other characterization techniques, such as restriction digestion or mass spectrometry. As a project proceeds, ν increases. For a finite target, if clones are screened at a constant rate, ν is proportional to time. In the analogy of the car-parking problem, the rate of screening clones corresponds to the rate of cars arriving at a curb, seeking a parking space. For semantic convenience, we refer to ν as a form of time throughout this paper.
- 4.
- ρ is the proportion of the target covered by clones. IfL = 1, then for a strict parking protocol with no allowed clone overlap, ρ equals the number of clones sequenced per unit length of the target. In all cases, ρ ≤ Lν.
- 5.
- φ is the allowed fractional overlap of a clone with any previously sequenced clone; φε[0,1]. For the strict-parking strategy mentioned earlier, φ = 0.
Model
Strict Parking
Our model is derived using the approach of Krapivsky (1992). Clones are screened sequentially. If screening demonstrates that a clone does not overlap any previously sequenced clone, then that clone is sequenced. We let β(xν) represent the number of gaps of length x per unit length of the infinite target at time ν. More strictly, β(x,ν)dGdx is the expected number of gaps between length x and x + dx that have their left edges within the target interval, dG. If normalized, β(x,ν) becomes the probability distribution function for the length of a random gap chosen uniformly from all gaps.
As time progresses, gaps of length x may be split into two if a clone within that gap is sequenced. Also gaps of length xmay be created if a gap larger than x is split. The process of creation and elimination of gaps is described by the following equation: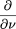 Note that gaps of length less than L cannot be destroyed, so for x < L we have:
Note that gaps of length less than L cannot be destroyed, so for x < L we have: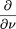 We can solve these equations with the aid of two initial conditions. These are derived, first, from the observation that the
number of gaps of any particular length before a project begins is zero, and second, that in the limit of a project just beginning,
none of the target is covered by clones so all of the target is covered by gaps. This gives us
We can solve these equations with the aid of two initial conditions. These are derived, first, from the observation that the
number of gaps of any particular length before a project begins is zero, and second, that in the limit of a project just beginning,
none of the target is covered by clones so all of the target is covered by gaps. This gives us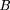
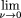 A reasonable guess for the form of the solution to equation (1) is
A reasonable guess for the form of the solution to equation (1) is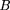 With some algebra, it follows from equations (1)–(5) that
With some algebra, it follows from equations (1)–(5) that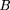 The top half of equation (6) follows from equations (1), (3), and (4). The bottom half of equation (6) follows from the substitution
of the top half of equation (6) into equation (2). Equation () is graphed in Figure 2. Bánkövi (1962) provides an alternate derivation for a restricted version of equation (6). Widon (1966), Gonazlez et al. (1974), Hemmer (1989), and Krapivsky (1992) describe more complete derivations. Note that for any fixed finite value of ν, the top half of equation (6) is a simple exponential
decay in x. Equation () can also be expressed in forms that are less compact, but that facilitate numerical computations. This is also
true of all of the equations derived in this paper from equation (6). These forms can be recovered by applying basic techniques
of integration. The resulting equations are too bulky to be conveniently presented in this paper.
The top half of equation (6) follows from equations (1), (3), and (4). The bottom half of equation (6) follows from the substitution
of the top half of equation (6) into equation (2). Equation () is graphed in Figure 2. Bánkövi (1962) provides an alternate derivation for a restricted version of equation (6). Widon (1966), Gonazlez et al. (1974), Hemmer (1989), and Krapivsky (1992) describe more complete derivations. Note that for any fixed finite value of ν, the top half of equation (6) is a simple exponential
decay in x. Equation () can also be expressed in forms that are less compact, but that facilitate numerical computations. This is also
true of all of the equations derived in this paper from equation (6). These forms can be recovered by applying basic techniques
of integration. The resulting equations are too bulky to be conveniently presented in this paper.
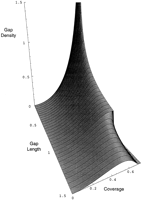
Gap length distribution. Gap density is the average number of left endpoints of gaps of a particular length that will be found in a unit interval of the infinite line at a particular time. The upper limit of coverage is the jamming limit, Rényi's number. The graph is arbitrarily truncated at a gap length of 1.5. For any fixed time, a cusp exists in the curve for gap density at a gap length equal to unity. At the jamming limit, all gaps are less than the length of a clone (L = 1; φ = 0).
From equation (6), we can calculate the target coverage as a function of time as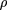 Equation () is graphed in Figure 3 (as the case of φ = 0). Hemmer (1989) provides an alternative derivation of equation (7). An immediate result is that at infinite time, which corresponds to characterization
of an infinitely deep clone library, we have
Equation () is graphed in Figure 3 (as the case of φ = 0). Hemmer (1989) provides an alternative derivation of equation (7). An immediate result is that at infinite time, which corresponds to characterization
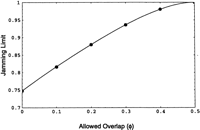
of an infinitely deep clone library, we have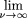 This jamming limit is known eponymously as Rényi's number (Rényi 1958). For an infinite target, the jamming limit is independent of L. Since the jamming limit is less than unity, it is clear that it is impossible to reach complete target coverage with a strict-parking
strategy. More particularly, it is impossible to achieve coverage > 75%. For finite targets, the jamming limit will vary about
a mean near Rényi's number. Solomon and Weiner (1986)reviewed results for the variance of the jamming limit. Dvoretzky and Robbins (1964) provided the first proof of the central limit theorem for the jamming limit.
This jamming limit is known eponymously as Rényi's number (Rényi 1958). For an infinite target, the jamming limit is independent of L. Since the jamming limit is less than unity, it is clear that it is impossible to reach complete target coverage with a strict-parking
strategy. More particularly, it is impossible to achieve coverage > 75%. For finite targets, the jamming limit will vary about
a mean near Rényi's number. Solomon and Weiner (1986)reviewed results for the variance of the jamming limit. Dvoretzky and Robbins (1964) provided the first proof of the central limit theorem for the jamming limit.
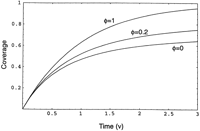
Coverage versus time. Coverage is asymptotic to the jamming limit, which varies with the allowed overlap φ.
The above equations provide the target coverage and distribution of gap sizes as a function of the number ν of clones analyzed rather than the number of clones sequenced, Gρ(ν). Often one is most interested in a project's status as a function of ρ(ν). In this case, one must numerically solve equation (7) for ν, given ρ(ν). The resulting function is the inverse of the function graphed in Figure3 (for the case φ = 0). For strict parking, target coverage equals the number of clones sequenced multiplied by their length, L.
Parking with Overlap
A modification to the parking strategy allows a sequenced clone to partially overlap previously sequenced clones. Let φ be
the allowed overlap as a fraction of clone length (φε[0,1]). We note that there is an exclusion zone of length L(1 − φ) centered at the midpoint of each sequenced clone. No portion of the exclusion zone of a sequenced clone may lie within
an exclusion zone of any previously sequenced clone (Fig. 4). This sets up an analysis exactly analogous to that of the previous section. For this, one rescales the parking length by
a factor of 1 − φ. Define (x,ν) as the distribution of the distances between the edges of adjacent exclusion zones. A modification of equation 6 gives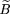 The coverage of the target by exclusion zones is, analogously to equation (7), thus
The coverage of the target by exclusion zones is, analogously to equation (7), thus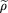 Since there is a one-to-one correspondence between exclusion zones and clones,
Since there is a one-to-one correspondence between exclusion zones and clones,
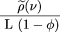 is the number of left endpoints of sequenced clones per unit length of the target.
is the number of left endpoints of sequenced clones per unit length of the target.
Cartoon of overlap parking. The central exclusion zone of a clone of length (1 − φ)L, shaded gray in the figure, may not overlap any other exclusion zone. Clones a and boverlap to the maximum possible extent, φL. The gap between clones b and c is the smallest gap that still allows for an additional clone to fit. However, the probability of a clone randomly being placed in this gap in any finite interval of time is zero. A single clone can fit with room to spare between clonesc and d.
If the distance between adjacent exclusion zones is x, then the length of the corresponding gap between clone ends, if it exists (i.e., if x > φL), is x − φL. Therefore, for φ ≥ ½ one has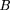 and for φ < ½ one has
and for φ < ½ one has
 Equation () is the special case of equation (11b) when φ = 0.
Equation () is the special case of equation (11b) when φ = 0.
One intuits that as φ → 1 the parking strategy will bcome asymptotically identical to a random subcloning strategy. This corresponds
to the case where every clone is sequenced after it is chosen from the clone library, regardless of the results of the screening
analysis of that clone. Indeed, for φ = 1, as it would be for random subcloning, one has Equation () is the gap distribution for a random subcloning project on an infinitely long target. Note that this distribution,
as well as many other properties of random subcloning on an infinite target, can be readily derived from the observation that
the left endpoints of random subclones will have a Poisson distribution (Port et al., 1995).
Equation () is the gap distribution for a random subcloning project on an infinitely long target. Note that this distribution,
as well as many other properties of random subcloning on an infinite target, can be readily derived from the observation that
the left endpoints of random subclones will have a Poisson distribution (Port et al., 1995).
The number of gaps in a project is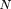 For strict parking, the number of gaps equals the number of sequenced clones. A tabulation of the number of gaps in a project
as a function of overlap is provided in Table 1. At infinite time (when a project has reached its jamming limit), the number of gaps decreases monotonically to zero as the
allowed overlap increases from zero to fifty percent. If projects are stopped at timepoints corresponding to fifty-percent
coverage, then cost reaches a minimum with an allowed overlap of eighteen percent.
For strict parking, the number of gaps equals the number of sequenced clones. A tabulation of the number of gaps in a project
as a function of overlap is provided in Table 1. At infinite time (when a project has reached its jamming limit), the number of gaps decreases monotonically to zero as the
allowed overlap increases from zero to fifty percent. If projects are stopped at timepoints corresponding to fifty-percent
coverage, then cost reaches a minimum with an allowed overlap of eighteen percent.
Optimization of Parking Strategies with Overlap (G = 3 Gb;L = 150 kb)
Target coverage may again be computed by subtracting the sum of all the gap lengths from the target length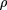 Equation () is graphed for several values of φ in Figure 3. In particular, we note that if φ = 1 one has
Equation () is graphed for several values of φ in Figure 3. In particular, we note that if φ = 1 one has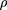 Equation is the Clarke-Carbon equation. Roach (1998) reviewed other derivations of the Clarke-Carbon equation.
Equation is the Clarke-Carbon equation. Roach (1998) reviewed other derivations of the Clarke-Carbon equation.
The limit as ν ➞ ∞ in equation (14) is the jamming limit. When φ = 0, this limit is Rényi's number. As the allowed overlap φ increases, the jamming limit increases to a maximum of 1 at φ = ½. At values of φ ≥ ½, there are no gaps too small to accommodate a new clone; so with an infinite number of screens, eventually a clone will be found to fill every gap. Jamming limit as a function of allowed overlap φ is graphed in Figure5.
Jamming limit versus allowed overlap, φ. The jamming limit is unity for all allowed overlaps greater than or equal to one-half. The gray points are the averages of ten simulations of parking 150 kb clones on a 3Gb target.
The parking with overlap strategy introduces an inefficiency not present in the strict-parking strategy. This results from
sequencing overlapping clones. This inefficiency is counterbalanced by improved gap filling, described by equation (11,) and
a resulting higher jamming limit, described by the limit as ν ➞ ∞ of equation (14). We define a measure of the inefficiency
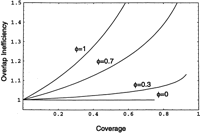
of excess coverage as the number of clones sequenced times their length divided by target coverage This gives a relative measure of the amount of overlap present in sequenced clones. This inefficiency measure is graphed for
several values of φ in Figure 6. Note that this measure ignores the cost of screening, which we will address in the next section.
This gives a relative measure of the amount of overlap present in sequenced clones. This inefficiency measure is graphed for
several values of φ in Figure 6. Note that this measure ignores the cost of screening, which we will address in the next section.
Overlap inefficiency of parking. Overlap inefficiency is the ratio of the sum of the lengths of the clones sequenced to the length of unique target sequence produced. There is no such inefficiency for strict parking with no allowed overlap (φ = 0). Overlap inefficiency and coverage are parametrically related as functions of time ν; the resulting curves do not extend beyond their respective jamming limits. The curve for φ = 1 corresponds to the Clarke-Carbon equation.
The average fractional overlap fo
(ν) of a newly sequenced clone is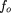 The average fractional overlap will increase as a project proceeds, until the jamming limit is reached.
The average fractional overlap will increase as a project proceeds, until the jamming limit is reached.
Cost of Parking
We computed the cost of parking as the cost of sequencing each selected clone, plus the cost of screening the clones. It is also possible to incorporate other factors into a cost analysis, such as the cost of library construction (see, for example, Roach et al. 1999). For computational simplicity, we ignored those factors here.
One might screen clones in a number of manners. These include partial sequencing, restriction mapping, sequence-tagged-site content mapping, array hybridization, mass spectrophotometry, or fluorescence sorting. Partial sequencing provides a robust screen if done to about 0.5-fold redundancy. It suffers from the drawback that it might screen out clones that are highly similar due to paralogous repeats. It has the advantage that if a clone is selected for complete sequencing, the sequencing from the screening effort can be utilized as part of the complete sequencing effort. In this case, if complete sequencing requires an effort equivalent to 7.5-fold shotgun sequencing, then the effective ratio of sequencing effort to screening effort will be 14 (r = 7.0/0.5 = 14). We used this ratio in our examples solely to provide conceptual concreteness, but we developed our equations generally for any ratio.
The actual cost of screening in the future, if a parking strategy is implemented, will be extremely small compared to the cost of sequencing a clone. Even now clones can be fingerprinted by restriction mapping at a much lower cost than fingerprinting by partial sequencing. Damping the gain of lower cost is a drop in the precision of overlap detection (Siegel et al. 1998a). However, Siegel et al. (1998b) analyzed approaches to maximize this precision. Beyond restriction mapping, numerous screening technologies are now under development that promise both low cost and high precision. Thus, it is likely that the cost of screening clones will eventually become nearly free compared to the cost of sequencing clones. As shown below, this drop in screening cost will nevertheless not have a large impact on overall project cost. This has permitted us to use a potentially outdated screening methodology (partial sequencing) as an example without invalidating the applicability of our results to future projects.
In the case of strict parking, cost per unit length can be expressed in terms of the number of clones screened per unit length,
ν, and the ratio, r, of the cost of completely sequencing a single clone to the cost of screening a single clone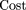 Here cost is expressed in terms of units of the cost of completely sequencing a clone (including screening). The clone coverage
function ρ(ν) is that of equation (7). Equation () assumes that a clone that has been screened is less expensive to sequence
than a clone that has not been screened. This may not be the case for some screening techniques, such as restriction mapping.
Equation () is easily modified for these cases by subtracting one from the denominator; qualitative conclusions are not affected.
Here cost is expressed in terms of units of the cost of completely sequencing a clone (including screening). The clone coverage
function ρ(ν) is that of equation (7). Equation () assumes that a clone that has been screened is less expensive to sequence
than a clone that has not been screened. This may not be the case for some screening techniques, such as restriction mapping.
Equation () is easily modified for these cases by subtracting one from the denominator; qualitative conclusions are not affected.
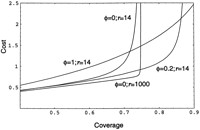
When clones are allowed to overlap during parking, equation (18) becomes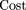 The exclusion-zone coverage function ρ̃(ν) is that of equation 10. Parking costs as a function of coverage are graphed in
Figure7. Cost and coverage are related parametrically through the variable ν. Costs parameterized for a prototypical human genome
project are tabulated in Table 1.
The exclusion-zone coverage function ρ̃(ν) is that of equation 10. Parking costs as a function of coverage are graphed in
Figure7. Cost and coverage are related parametrically through the variable ν. Costs parameterized for a prototypical human genome
project are tabulated in Table 1.
Parking costs as a function of coverage. For small to moderate values of coverage, parking costs are roughly proportional to coverage, demonstrating that the cost burdens of screening and of overlap inefficiency are initially quite small. Near the jamming limit, these costs rise sharply as the number of screening operations to identify an appropriate clone for sequencing rises sharply. Dropping the cost of screening by almost two orders of magnitude provides only a marginal benefit shortly before the jamming limit. Allowing modest overlaps permits progress toward higher jamming limits at little cost increase. The curve for φ = 0 and r = 14 intersects the curve for φ = 0.2 and r = 1000 at 0.4493 coverage. In practice, the curve for φ = 1 and r = 14 would run at a slightly lower cost, as no screening would actually be done (any screening results would be ignored). For screening by partial sequencing, this cost savings would be small, as it would apply only to clones not fully sequenced. If this factor is taken into account, the curve for φ = 0 and r = 1000 also must be slightly adjusted. We left the curves unadjusted to facilitate comparison of the parameterization of the underlying equations.
Approximations
Many of the exact equations developed here to model the parking strategy are complex. In some cases, it might be desirable to approximate these equations. For example, analytic solutions may be desired for parameter optimizations. The presence of a cusp atL (or L(1 − φ) when overlap is allowed) suggests that a piecewise approximation might be appropriate. We present the results of polynomial and exponential curve fits to the strict-parking curve, equation (6), for a variety of target coverages in Table 2. Curve fits may also be made to equation (11) with similar results.
Approximation of the Strict-Parking-Strategy Gap Distribution
A curve of the form ae bxprecisely fits the parking curve for gap lengths longer than L. The residual standard error for this curve in Table 2 is a limit of machine precision. This precise fit is expected as ae bx is the form of equation (6) for gap lengths longer than L. Polynomial curves provide better fit than exponential curves for gap lengths shorter than L. If a single curve is fit to the entire distribution, rather than two curves piecewise, polynomial curves do better than exponential curves. Therefore, if an approximation is desired, we recommend a curve defined piecewise with a polynomial form over [0,L] and an exponential form over [0,∞). Laguerre polynomials also work extremely well; we illustrate one example in Table 2. Nevertheless, as the low standard errors in Table 2 demonstrate, almost any reasonable approximation will serve adequately.
Rationale for using an approximation can be generated by noting the similarities of the parking strategy to other strategies, particularly random subcloning. However, these approximations are limited by the differences between strategies. Random subcloning strategies are distinct from parking strategies in that they do not iterate clone characterization, in which the use of the termcharacterization implies either screening or complete sequencing. In random subcloning, the decision to characterize a clone is made independently of the results of the characterization of other clones. Walking strategies are also distinct from parking strategies. In walking strategies, additional clones are characterized until a clone that overlaps an existing contiguous sequence is found. The fundamental differences between parking strategies and other strategies limit the direct application or comparison of theory developed for other strategies to the parking problem.
At low coverages, the effect of the parking strategy's iterative screening will be minimal due to the low probability that any two screened clones will overlap. Also the more overlap is allowed in a parking strategy, the more the strategy resembles random subcloning. Therefore, parking-strategy and random-subcloning theories under some circumstances may produce nearly identical results. Poisson analysis has been successful in predicting gap distributions for random subcloning on an infinite target. Poisson analysis for this purpose was introduced by Lander and Waterman (1988) and refined by Arratia et al. (1991, 1996). An excellent presentation of Poisson analysis on infinite targets is provided in the preamble of Port et al. (1995). Poisson analysis predicts gap distributions that are exponential in form. As seen in Table 2, these exponential forms are capable of providing adequate approximations to the parking-gap distribution. This approach is followed by Batzoglou et al. (1999).
Gap Closing
If a project begins with a parking-strategy phase, then at the end of this phase gaps will remain that must be closed if the project is to reach completion. A variety of closing strategies exist, but here we will focus on a strategy based on walking. For unidirectional walking, each step is of length l drawn from a distributionf(l). For walking by sequencing BACs, this lengthl represents the portion of each BAC that represents novel sequence extending to the right. If BAC length and overlap are constant, then so is l. In such a case, f(l) would be a Dirac-delta function. Depending on the method of BAC library construction and technique for overlap detection,f(l) is more typically approximated as a square, normal, or gamma distribution, all of which can be chosen with an arbitrary mean, μ, and standard deviation, ς, to fit to the empirically observed parameters of the BAC library. We chose the gamma distribution for our analysis here, preferring it to the normal distribution, as it is strictly positive. In any case, the choice of distribution has no substantial effect on our results or conclusions. For simultaneous bidirectional walking, f(l) would be the twofold convolution of the step-length distribution for unidirectional walking. We focused the following discussion on unidirectional walking, noting that, with this modification, the resulting model is directly applicable to bidirectional walking.
The BAC sequenced as the last step in a unidirectional left-to-right walk across a gap overlaps the right edge of the gap. The amount of this overlap represents redundant sequencing effort. Determining the mean and distribution of this overlap as a function of gap size is fundamental to predicting the cost of gap closing. We assume that all nonzero, rightmost overlaps are detectable. This assumption is easily modified if additional complexity is desired.
Walking across a gap is a renewal process and can be modeled with results from renewal theory. Cox (1962) provided an excellent monograph on renewal theory. In this context, the amount of rightward overlap of the last BAC across
a gap of length x is termed the forward recurrence time, Vx
. The probability density function of Vx
is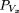 where h(p) is the renewal density, interpreted as the probability that a walking step begins at position p in the gap.
where h(p) is the renewal density, interpreted as the probability that a walking step begins at position p in the gap.
For very large gaps, as x → ∞, noting also thatl→∞lim
f(l) → 0 and thatp→∞lim
h(p) →
 , we have from equation (20)
, we have from equation (20)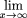 where F(·) is the cumulative distribution function off(·). This permits us to calculate the asymptotic limit of the average forward recurrence time:
where F(·) is the cumulative distribution function off(·). This permits us to calculate the asymptotic limit of the average forward recurrence time: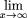
 If ς << μ, as is often the case for BAC libraries, thenx→∞lim
Vx
≈
If ς << μ, as is often the case for BAC libraries, thenx→∞lim
Vx
≈
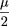 .
.
Equation () shows that the average overlap at the end of long gaps is roughly half of the length of an average BAC. However, this result is of limited value for analyzing the redundant overlaps of walks across short gaps (i.e., less than about ten times the average clone length). Most of the gaps in the final stages of a genome project will be short, so one is motivated to analyze the redundancies associated with walks across short gaps.
Now, the renewal density h(p) can be expressed as an infinite sum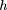 where kn
(p) is the probability density that the nth step begins at position p in the gap.
where kn
(p) is the probability density that the nth step begins at position p in the gap.
The mean forward recurrence time can be calculated as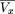
 Each of the three terms of equation (24) can be interpreted in terms of their separate contributions. First, the mean forward
recurrence time when x = 0 is μ, as all walking steps are synchronized. Second, as x increases, the mean recurrence time decreases linearly as one proceeds across steps that have previously initiated, but third,
increases by an average of μ every time a new step intiates.
Each of the three terms of equation (24) can be interpreted in terms of their separate contributions. First, the mean forward
recurrence time when x = 0 is μ, as all walking steps are synchronized. Second, as x increases, the mean recurrence time decreases linearly as one proceeds across steps that have previously initiated, but third,
increases by an average of μ every time a new step intiates.
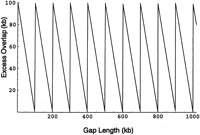
For a constant clone length, then f(l) is the Dirac-delta function δ(l − μ). Consequently,kn
(p) is the Dirac-delta function δ(np − μ). Equation () then simplifies to the periodic sawtooth function (where frc(·) designates the fractional part function):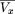 This sawtooth function illustrates the oscillatory nature of the expected excess overlap (Figure 8).
This sawtooth function illustrates the oscillatory nature of the expected excess overlap (Figure 8).
When f(l) is not a Dirac-delta function, then these oscillations are damped, decaying asymptotically to the limit of2μ
μ2+ς2established in equation (22). The damping comes about as the possible positions for the end of a walk become progressively
out of phase with each other. We illustrate this by choosing f(l) to be the gamma distribution with parameters α and β, such that μ =β
αand ς = β
√α̅
: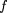 We compute kn
(p) as then-fold convolution of f(l):
We compute kn
(p) as then-fold convolution of f(l):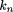 Substituting equation (27) into equation (24), we have
Substituting equation (27) into equation (24), we have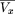 where Qu,w
is the cumulative distribution function of the gamma distribution Γu,w. Equation () is convenient for numerical calculations with software such as Mathematica 4.0 (Wolfram Research). Results are graphed in Figure 9. Note the decaying oscillations that tend towards the2μ
μ2+ς2 asymptote.
where Qu,w
is the cumulative distribution function of the gamma distribution Γu,w. Equation () is convenient for numerical calculations with software such as Mathematica 4.0 (Wolfram Research). Results are graphed in Figure 9. Note the decaying oscillations that tend towards the2μ
μ2+ς2 asymptote.
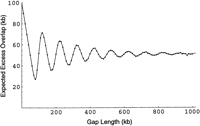
Expected excess overlap versus gap length (variable clone length). The model from the text is implemented such that the length for each walking step is drawn from a gamma distribution with mean 100 kb and standard deviation 14.4 kb. Each gray point represents the average of 10,000 simulations of this process; the simulations are consistent with the model. The damped oscillations decay towards an asymptote near 51 kb, just over half the average length of a clone.
Simulations
We performed simulations with results that were consistent with the predictions of our analytic model of the parking strategy. For example, the jamming limits reached in our simulations were within ± 0.12% of the predicted jamming limits (Fig. 5). For the purpose of simulating jamming limits, each iteration of our algorithm picked one new left clone endpoint uniformly from all possible positions that could result in clones that would not exceed the allowed overlap. However, this speedy algorithm does not fully reflect the time dependency of the coverage process. Therefore, we performed additional simulations with an algorithm that picked new left clone endpoints uniformly from all possible positions, rejecting clones that exceeded the allowed overlap. These simulations resulted in distributions of gaps that were consistent with the distribution predicted by equation (6), both with respect to the number of observed gaps of particular size ranges and with respect to time dependency (data not shown). We employed MATLAB (MathWorks, Inc.) as the simulation environment.
Our simulations were constrained to clone endpoints at integer positions and were performed for finite choices of target length,G. The consistency of our simulations with the predictions of our analytical model suggests minimal impact to our model from our enabling assumptions that target length could be considered infinite and that clone endpoints could occur at noninteger points along the target.
We performed additional simulations to support our model for the excess overlap of gap closing (Fig. 9). Our analytic model explains 99.9% of the variation in the simulation data (r 2 coefficient of determination). We performed additional simulations based on the assumption that clone lengths were distributed as a square wave with the same mean and standard deviation as the gamma distribution previously employed. A square-wave distribution is close to that usually obtained by cutting a band of fragments from a gel. Our analytical model implemented with the gamma distribution explained 98.5% of the variation in our square-wave simulation data (not shown). This suggests that knowledge of the mean and standard deviation of the lengths of clones in a library is sufficient for useful implementation of our model.
DISCUSSION
We have described a mathematical model for parking strategies for genome mapping and sequencing. We anticipate that this model will be useful for comparing the parking strategy to other strategies and for optimizing the parameters of the parking strategy. Our analysis ignores several biological and experimental issues, such as cloning bias. These issues are difficult to incorporate into a mathematical model and are best treated with simulations adapted to a particular cloning and sequencing methodology. Batzoglou et al. (1999) reviewed several other caveats associated with modeling genome-sequencing strategies. Our mathematical model forms a basis for comparing the parking strategy and its derivative hybrid strategies to other strategies. Roach et al. (1999) provided an example of a set of such comparisons, with attention to a hybrid strategy consisting of an initial strict-parking phase followed by walking to close the resulting gaps.
Our mathematical model is derived from models developed primarily for packing problems related to physical chemistry. For tractability, this model assumes an infinite target. In general, the assumption of an infinite target for modeling genome strategies can lead to difficulties in predicting certain parameters of finite targets (Roach 1998). For example, the expected amount of sequencing needed to close all the gaps in a finite target is not possible to determine under this assumption. This is related to the persistence of gaps in an infinite target even as time tends toward infinity, although at an increasingly vanishing density. In practice, genome parking strategies will never be continued to coverages that are close to a jamming limit. Therefore, in practice, it is unlikely that our assumption of an infinite target will significantly impact our predictions.
The parking strategy is marked by highly efficient generation of sequence during the early stages of a project with faster-than-exponential (i.e., asymptotic to a vertical line) increases in cost in the late stages. Thus, the parking strategy may be particularly useful for projects in which the complete sequence of the target is not sought. For projects in which complete sequence is sought, the parking strategy can only be used for a first stage and another strategy must be used to close the gaps left by the parking strategy.
One approach for combining strategies is to use the parking strategy to determine approximately 50% of the target sequence and then to switch to a gap-closing strategy. If this is done, one may wish to pursue a modified parking strategy that allows each sequentially chosen clone to be sequenced even if it overlaps a prior clone up to a maximum allowed overlap. Allowing such overlaps decreases the number of wasted screens, screens that result in a clone being rejected for sequencing. Allowing overlaps also reduces the number of gaps by allowing gaps smaller than the length of a clone to be filled. However, this comes at an increase in inefficiency due to redundant sequencing. A major utility of the model presented in this paper is for optimizing the choice of maximum allowed overlap during a parking strategy. For example, if the sole goal is to minimize the cost of reaching 50% coverage, then the maximum allowed overlap should be 18%. Even fewer gaps would be expected if the allowed overlap was set at > 18%, but this would result in a cost increase. However, this cost might be recovered with compensatory savings during gap closing. Therefore, this trade-off presents an additional opportunity for optimization, in conjunction with a model for the cost of gap closing.
Sequence walking is a common strategy for gap closing. The sequence-tagged-connector approach is a suitable walking strategy for large genomes (Venter et al. 1996). PCR is an alternative for short gaps. The major inefficiency of sequence walking results from redundant sequencing of the target due to imprecise overlap of the last walking clone sequenced. As a rough approximation, this inefficiency per gap is constant. As we show here, the more variability in the clone library for a given average length, the greater this constant (i.e., asymptotically2μ μ2+ς2). In practice, inefficiency will tend to be slightly greater than this asymptotic constant, as all random sequencing strategies create gaps that are distributed with a monotonically decreasing density. Therefore, the actual average inefficiency of gap closure will tend to be slightly greater than the asymptotic inefficiency, since there will be more than an even chance that the length of a gap modulo the average step length is less than half that average step length.
It is difficult to model the costs of gap closing, particularly as there are a large number of gap-closing techniques, making it difficult for one model to cover all situations. Additionally, any given gap-closing technique may vary highly and unpredictably in cost from gap to gap. Nevertheless, predictions of gap-closing costs are necessary for a complete cost analysis of an entire genome project. In this paper, we specifically modeled the costs for one particular gap-closing strategy. Although the cost inefficiency per gap for this strategy depends on the length of the gap, it does so in oscillatory manner. The period of the oscillations is generally shorter than either the resolution of a genomicist's ability to measure a gap or the standard deviation of gap sizes generated by a particular strategy. Therefore, models for hybrid strategies should primarily treat cost inefficiency as a constant per gap rather than as a function of the total sum of gap lengths. This will hold true for most gap-closing strategies but perhaps for slightly different reasons than the walking strategy modeled in this paper. For example, there are fixed costs in designing PCR primers and amplifying products. These costs are largely independent of product length.
Our model for gap closing assumes a rather simple-minded procedure for closing gaps, but we anticipate that our basic approach can be extended to more sophisticated closing procedures. For example, we assume that all gaps are closed by walking, even if they are short enough to be spanned by PCR. Also if the library used for walking contains clones of variable length that have been characterized at both ends, vast improvements in efficiency can be made. Batzoglou et al. (1999)demonstrated this point for several particular cases and provided a convincing argument that this is true generally.
Pairwise end sequencing is an inexpensive alternative for generating incomplete sequence from a target (Roach et al. 1995). This strategy has been employed for the first stage of generating the sequence of many bacterial genomes, as well as that of Drosophila melanogaster, and currently is being employed by Celera Genomics to sequence the human genome (Venter et al. 1998). Pairwise end sequencing and parking are similar in that they both generate a lot of sequence quickly and inexpensively but result in projects that have a large number of short gaps. Thus, for either of these strategies to be used for generating complete target sequence, efficient gap-closing strategies must be employed.
The two strategies differ in that pairwise end sequencing results in ordered and oriented contiguous sequences. This is a major advantage over parking. Furthermore, pairwise end sequencing is extremely powerful for resolving assembly ambiguities, such as those due to repeats. However, there are several advantages to parking. In particular, parking strategies produce higher-quality sequence in longer contiguous tracts. A potential disadvantage of the parking strategy is that it may underrepresent target sequences that are members of long genomic repeat families. This will occur to the extent that a screen rejects a clone for sequencing because it is very similar to a previously sequenced clone, even if it does not overlap that clone.
We anticipate that the parking strategy may form an important component of hybrid strategies for the future sequencing of large genomes. In particular, parking may be useful for sequence sampling large genomes for which there might be no plans to produce a finished sequence. Sampling by parking would give longer and higher-quality tracts of sequence than other sampling strategies, such as pairwise end sequencing. These long tracts might be particularly useful for gene and regulatory element identification, comparative genomics, and polymorphism studies.
Acknowledgments
The work of Vesteinn Thorsson was supported in part by a Sloan Foundation/DOE Fellowship in Computational Molecular Biology. Andrew F. Siegel holds the Grant I. Butterbaugh Professorship at the University of Washington. Lee Hood provided helpful comments on this paper.
The publication costs of this article were defrayed in part by payment of page charges. This article must therefore be hereby marked “advertisement” in accordance with 18 USC section 1734 solely to indicate this fact.
Footnotes
-
↵4 Corresponding author. Present address: The Institute for Systems Biology, 4225 Roosevelt Way NE, Suite 200, Seattle, Washington 98105 USA.
-
E-MAIL jroach{at}systemsbiology.org; FAX (206) 685-7301.
-
- Received February 2, 2000.
- Accepted May 10, 2000.
- Cold Spring Harbor Laboratory Press