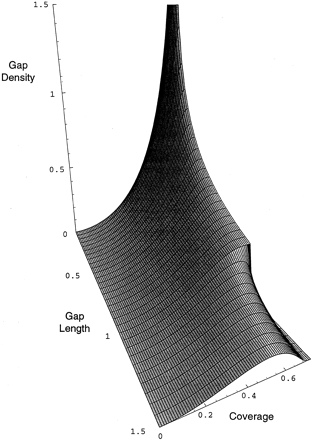
Gap length distribution. Gap density is the average number of left endpoints of gaps of a particular length that will be found in a unit interval of the infinite line at a particular time. The upper limit of coverage is the jamming limit, Rényi's number. The graph is arbitrarily truncated at a gap length of 1.5. For any fixed time, a cusp exists in the curve for gap density at a gap length equal to unity. At the jamming limit, all gaps are less than the length of a clone (L = 1; φ = 0).











