The Relative Power of Family-Based and Case-Control Designs for Linkage Disequilibrium Studies of Complex Human Diseases. II. Individual Genotyping
Abstract
In this paper we consider test statistics based on individual genotyping. For sibships without parents, but with unaffected as well as affected sibs, we introduce a new test statistic (referred to asTDS ), which contrasts the allele frequency in affected sibs versus that estimated for the parents from the entire sibship. For sibships without parents, this test is analogous to the TDT and is completely robust to nonrandom mating patterns. The efficiency of the TDS test is comparable to that of the THS test (which compares affected vs. unaffected sibs and was based on DNA pooling), for sibships with one affected child. However, as the number of affected sibs in the sibship grows, the relative efficiency of the TDS test versus theTHS test also increases. For example, for sibships with three affected, one-third fewer families are required; for families with four affected, nearly half as many are required. Thus, when sibships contain multiple affected individuals, theTDS test provides both an increase in power and robustness to nonrandom mating.
In the first paper in this series, Risch and Teng (1998), we considered statistics based on data derived from DNA pooling. Only overall allele frequency estimates for a pool are available from such experiments; hence, only statistics based on pooled allele frequencies are possible, such as the haplotype-based haplotype relative risk (HHRR) (Falk and Rubinstein 1987; Terwilliger and Ott 1992). Such statistics are not automatically robust to nonrandom mating, although they are conservative under population stratification. Furthermore, such statistics may not extract all the available information in some study designs if individual genotyping is performed. Therefore, in this paper we consider analyses of data obtained from individual genotyping of all study subjects. We compare the same family constellations as described in Risch and Teng (1998). As individual genotyping provides more information than DNA pooling, it enables us to improve the statistical treatment in two ways: by increasing robustness and power.
We consider statistics of the form (p̂ 1 − p̂ 2)/ς̂, in which the numerator contrasts the estimated allele frequencies in two groups (affected sibs vs. parents) and the denominator is the estimated standard deviation of the numerator. Typically, the variance of (p̂ 1 − p̂ 2) is a function of genotype frequencies in the parents. When DNA pooling has been performed, this variance has to be estimated based on the assumption of Hardy–Weinberg equilibrium. On the other hand, individual genotyping allows us to get an unbiased estimate of the variance under more general conditions and thus provides further robustness to non-random mating. More importantly, in the case where parents are unavailable, individual genotyping gives us a greater choice of the contrast we can make in the numerator, which potentially can improve the power of the test.
Study designs that include affected offspring with parents lend themselves to the calculation of a TDT statistic, provided individual genotyping is performed. Although the TDT offers additional robustness to nonrandom mating in this case, the power of this test statistic is generally comparable to that of the HHRR statistic, at least when mating is nearly at random. This is because the Hardy–Weinberg estimator of parental heterozygosity, used in the denominator of the HHRR statistic, is close to the directly counted parental heterozygosity estimate used in the TDT (Risch and Teng 1998, formula 4). Thus, sample size requirements using individual genotyping for designs involving affected offspring with parents, based on TDT, are essentially identical to those we have presented previously (Risch and Teng 1998) for the same designs based on DNA pooling and HHRR statistics (calculations performed but not presented). Therefore, we use the sample size requirements for affected sibships with parents derived in Risch and Teng (1998) for comparison with individually genotyped sibships without parents.
In the classic TDT, p 1 is the allele frequency in the affected child (or children) and p 2 the allele frequency in the parents. For sibships without parents, the test described in Risch and Teng (1998) proposes p 1 to be the allele frequency in the affected sibs, and p 2the allele frequency in the unaffected sibs. When the locus-related penetrance is low, the allele frequency p 2 in unaffected sibs can also be viewed as providing a nearly unbiased estimate of the allele frequency in the parents (in this sense, it is similar to the TDT, in which p 2 is the observed allele frequency in the parents). When more than one child has been individually genotyped, however, it is possible to obtain a more efficient estimate of the parent allele frequencyp 2, as well as an estimate of the variance ofp̂ 1 − p̂ 2 that is robust to nonrandom mating. We derive such a statistic below and describe its properties.
We use the same notation as given in Risch and Teng (1998); namely,mij
denotes the conditional probability of mating type (i,j) given an affected child (and similarlym
(r)
ij for r affected children), in which i and j are the number ofA alleles in the two parents (we use parentheses in subscripts to denote unordered genotypes); fk
is the ratio of penetrance in individuals with k D alleles compared withdd individuals; hats over letters (circumflexes) denote sample estimates. To simplify some formulas, we also introduce the following
notation: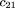
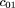
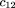 We assume, as in Risch and Teng (1998), that unaffected sibs have a random genotype distribution (low penetrance) given the parental mating type.
We assume, as in Risch and Teng (1998), that unaffected sibs have a random genotype distribution (low penetrance) given the parental mating type.
Affected–Unaffected Sib Pairs
We first examine the case of one affected and one unaffected sib, without parents. For this case, there are nine possible
marker genotype outcomes for the sib pair, as listed in Table 1, along with their probabilities of occurrence. To estimate the frequency of allele A in the parents (p
2), we notice that under the null hypothesis, f
2 = f1= 1 and the affected and unaffected sibs become symmetric; so Table1 can be simplified to six possible outcomes: (1) Both sibs areAA; (2) both sibs are aa; (3) both sibs areAa; (4) one is AA, the other is Aa; (5) one is Aa, the other is aa; and (6) one is AA,the other is aa. There are also the same six possible genotype combinations (mating types) for the parents with respective probabilitym
(ij). Because there is an equal number of parameters and independent observations, maximum likelihood estimates of the parental
mating type frequencies m(ij)
can be calculated by equating the sample frequency of each sib-pair outcome with its respective probability, namely
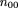
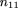
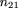
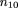
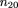 Solving these equations, we get the unbiased maximum likelihood estimators m̂ij
. These are given by
Solving these equations, we get the unbiased maximum likelihood estimators m̂ij
. These are given by
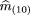
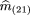
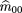
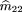
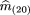 Then the frequency of A in the parents can be estimated by
Then the frequency of A in the parents can be estimated by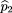

 which, in this case, is the same as the A allele frequency in the combined sibling sample. Because
which, in this case, is the same as the A allele frequency in the combined sibling sample. Because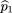 we have
we have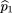 The variance of p̂
1 −p̂
2 is a function of h, the frequency of heterozygosity in the parents. Whereas DNA pooling required us to use the Hardy-Weinberg assumption in the
estimation of h(formula 5 of Risch and Teng 1998), individual genotyping allows us to obtain a more direct estimate, robust to nonrandom mating. Specifically,
The variance of p̂
1 −p̂
2 is a function of h, the frequency of heterozygosity in the parents. Whereas DNA pooling required us to use the Hardy-Weinberg assumption in the
estimation of h(formula 5 of Risch and Teng 1998), individual genotyping allows us to obtain a more direct estimate, robust to nonrandom mating. Specifically,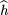
 In this case, under the null hypothesis, var(p̂
1 − p̂
2) =h/16n (e.g., this can be calculated from the variance of S in Table 1 using f
2 =f
1 = 1). Therefore, we can construct the statistic
In this case, under the null hypothesis, var(p̂
1 − p̂
2) =h/16n (e.g., this can be calculated from the variance of S in Table 1 using f
2 =f
1 = 1). Therefore, we can construct the statistic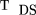 The subscripts on T denote that we do not assume Hardy-Weinberg equilibrium and that sibs are used to contruct the parent allele frequency.
The subscripts on T denote that we do not assume Hardy-Weinberg equilibrium and that sibs are used to contruct the parent allele frequency.
Genotype Outcomes, Scores, and Probabilities for Affected–Unaffected Sib Pair
To calculate the power of statistic 1, we reformat TDS to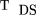 We assume the denominator converges to its expected value (by the Law of Large Numbers), and thus, we need only calculate
this expectation along with the mean and variance of the numerator under the alternative hypothesis. We denote the expectation
of the square of the denominator as E(ς2
0) and the mean and variance of the numerator as √
n
ν and ς2
a. From Table 1,
We assume the denominator converges to its expected value (by the Law of Large Numbers), and thus, we need only calculate
this expectation along with the mean and variance of the numerator under the alternative hypothesis. We denote the expectation
of the square of the denominator as E(ς2
0) and the mean and variance of the numerator as √
n
ν and ς2
a. From Table 1,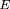

 and
and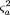 Then, the power is given by
Then, the power is given by
r Affected and s Unaffected Sibs
By using the same logic described above for one affected and one unaffected sib, we can construct a sibship-based disequilibrium test statistic for the general case of r affected and sunaffected sibs. We classify the various outcomes into six groups based on the possible matings that could have produced them: (I) All sibs areAA; (II) all sibs are aa; (III) all sibs areAa; (IV) all sibs are either AA or Aa; (V) all sibs are either Aa or aa; and (VI) the genotypesAA and aa (and possibly Aa) appear among the sibs. These categories are meant to be mutually exclusive, so that, for example, group IV excludes the case of all sibs being AA. In theory, it may be possible to obtain additional information by subdividing groups IV and V by the number of Aa individuals; however, by the above grouping scheme, we are able to obtain analytic formulas for power and sample size, as described below. We can characterize each possible outcome as a vector with the six elements (j 2, j 1, j 0,k 2, k 1, k 0) where ji is the number of affected sibs with i A alleles, and ki is the number of unaffected sibs with i A alleles. Note thatj 2 + j 1 + j 0 = r, andk 2 + k 1 + k 0 = s, and we define t = r + s. The possible outcomes, by group, are listed in Table 2, along with their probabilities under the alternative hypothesis. Under the null hypothesis, the corresponding probabilities can be obtained by using the population mating-type frequencies instead of the conditional (on having r affected children) mating-type frequencies and substituting in f 2 = f 1 = 1.
Probabilities of Different Outcomes for r Affected ands Unaffected Sibs and Scores for the TDSStatistic
To derive the TDS
statistic, we first sum up the probabilities across all possible outcomes within each group under the null hypothesis. We
obtain the following totals:


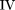
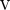
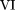 We denote by n
I the number of observations that fall into group I and similarly for the other groups. By equating the sample frequencies
of each group, that is,n
I/n, n
II/n, etc., with their respective probabilities, and solving the six equations, we can get unbiased maximum likelihood estimates
of them
(ij)’s under the null hypothesis, which are denoted by m̂
(ij). Recalling that p
2 = m
22 + ¾ m
(21) + ½m
(20) + ½ m
11 + ¼ m
(10), and using the maximum likelihood estimates of the mij
based on the simplified classification scheme given above, we can estimatep
2 by
We denote by n
I the number of observations that fall into group I and similarly for the other groups. By equating the sample frequencies
of each group, that is,n
I/n, n
II/n, etc., with their respective probabilities, and solving the six equations, we can get unbiased maximum likelihood estimates
of them
(ij)’s under the null hypothesis, which are denoted by m̂
(ij). Recalling that p
2 = m
22 + ¾ m
(21) + ½m
(20) + ½ m
11 + ¼ m
(10), and using the maximum likelihood estimates of the mij
based on the simplified classification scheme given above, we can estimatep
2 by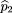 This formula can be easily derived by taking the linear combination in equation 5 applied to the formulas in equation 4. Then,
to obtainp̂
2, we can simply assign a scoreS(p
2) of 1, 3/4, 1/2, 1/4, or 0 depending on the group membership of the outcome; these scores are given in Table 2.
This formula can be easily derived by taking the linear combination in equation 5 applied to the formulas in equation 4. Then,
to obtainp̂
2, we can simply assign a scoreS(p
2) of 1, 3/4, 1/2, 1/4, or 0 depending on the group membership of the outcome; these scores are given in Table 2.
This derivation is similar to the approach we took for the simple case of one affected and one unaffected sib. However, in this general case, collapsing all possible sibship outcomes (ignoring affection status) into the six groups defined above, although unbiased, does not use all of the information available. Specifically, within group IV there is additional information about parental mating type based on the frequency of sibships defined by the number of AA andAa sibs. For example, in sibships of size 3, this would correspond to the relative frequency of sibships with two AAand one Aa sib versus those with one AA and twoAa sibs, which provides some information on the relative frequency of the parental mating type AA × Aaversus Aa × Aa. A similar comment applies to group V (for matings Aa × aa andAa × Aa). For the four other sibship groups, further subdivision is either not possible (groups I, II, and III) or provides no additional information about mating type (group VI, in which the parental mating type is automaticallyAa × Aa). By not further subgrouping groups IV and V, we are able to derive formulas for the estimate ofp 2 and Var(p̂ 1 − p̂ 2) that are simple and robust and can therefore also perform all power calculations and sample estimates analytically. Presumably, there is also some loss of efficiency in doing so, although much of the information about parental-mating type frequencies is contained in the relative frequency of groups I to VI. A maximum likelihood solution to estimate the parental mating type frequencies allowing for subgrouping of groups IV and V may be possible by numerical means; however, no simple formulas for parameter estimation, power calculations, or sample size estimates are possible in this case. Furthermore, we demonstrate below in numerical examples that our simple statistic is more efficient than one based on comparing the frequency of allele A in affected versus unaffected sibs, for sibships of size 3 or greater.
Scores can also be assigned for the estimate of p 1. To do so, we simply take (j 2 + 1/2j 1) / r, independent of which group contains the outcome. These scores [S(p 1)] are also given in Table 2. To estimate p 1 − p 2, we can then assign scores based on the difference in the scoresS(p 1) andS(p 2); these scores,S(p 1 − p 2), are also given in Table 2. As can be seen there, the score is (j 2 − j 1) / 4r in sibships with only AA and Aa sibs, (j 1 − j 0) / 4r in sibships with only Aa and aa sibs, and (j 2 − j 0) / 2r in sibships with AA and aa sibs.
In some sense, some of the scoring of sibships, as given in Table 2, may seem counterintuitive. Consider a sibship of two affected and one unaffected. For groups I to III, the uniform scoring of 0 is straightforward, as all sibs (affected and unaffected) have the same genotype. Now, suppose the two affected sibs have genotypes AAand Aa. This sibship will be scored the same (0) if the unaffected sib has genotype AA or Aa. This is because, in either case, the sibship belongs to group IV, and the unaffected child does not change the possible mating types of the parents. On the other hand, if the unaffected sib is genotypeaa, the sibship now belongs to group VI and gets a score of +1/2 because the parental mating type isAa × Aa. As another example, suppose the two affected sibs have genotypes AA and aa. Then the sibship will be scored 0 whatever the genotype of the unaffected sib (i.e., AA, Aa, or aa) because the sibship automatically belongs to group VI. A scoring routine based on the frequency of the A allele in the affected sibs versus the unaffected sib would score this family differently based on whether the unaffected sib was AA, Aa, or aa (e.g., −1/2 if the unaffected sib is AA, 0 if Aa, and +1/2 if aa). However, it is clear that in the creation of a TDT-type statistic (comparing offspring with parents’ allele frequency), in this case the unaffected child provides no additional information.
Under the null hypothesis,E(p̂
1 − p̂
2) = 0.To calculate Var(p̂
1 − p̂
2), we note thatp̂
1 − p̂
2 =[ΣS
i(p
1 = p
2)] / n is the average of n independent, identically distributed scores, so that Var(p̂
1 − p̂
2) =
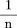 Var[S(p
1 − p
2)], where the subscript i has been suppressed. BecauseE[S(p
1 − p
2)] = 0, we simply calculate Var[S(p
1 − p
2)] = E{[S(p
1 − p
2)]2}. After some lengthy algebra, we obtain
Var[S(p
1 − p
2)], where the subscript i has been suppressed. BecauseE[S(p
1 − p
2)] = 0, we simply calculate Var[S(p
1 − p
2)] = E{[S(p
1 − p
2)]2}. After some lengthy algebra, we obtain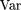
 By using logic similar to that used in the derivation ofp̂
2 and using the maximum likelihood estimates of the mij, we can estimate this variance by
By using logic similar to that used in the derivation ofp̂
2 and using the maximum likelihood estimates of the mij, we can estimate this variance by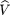
 (6)
(6)
Thus, the TDS statistic, for the general case of raffected and s unaffected sibs, is given by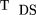 in which the scores are given in Table 2 and ς̂0 by the square root of formula 6. Under the null hypothesis, the TDS statistic is approximately normally distributed with mean 0 and variance 1.
in which the scores are given in Table 2 and ς̂0 by the square root of formula 6. Under the null hypothesis, the TDS statistic is approximately normally distributed with mean 0 and variance 1.
To calculate the power of this test, we need to determine ν =E[S(p
1 −p
2)],E(ς̂0
2), and Var[S(p
1 − p
2)] under the alternative hypothesis. Then, using the formulas in Table 2, and after some tedious algebra, we obtain the following results:



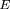




 and
and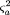





 The power can then be calculated using formula 3, substituting formulas 7, 8, and 9 for ν, E(ς̂2
0), and ς2
a, respectively.
The power can then be calculated using formula 3, substituting formulas 7, 8, and 9 for ν, E(ς̂2
0), and ς2
a, respectively.
Numerical Results—Individual Genotyping vs. Pooling
Using the power formulas described above, we can calculate required sample sizes to detect linkage disequilibrium. The logic is the same as described in Risch and Teng (1998) for sample pooling; again, we use a significance level of 5 × 10−8 and 80% power. The required sample sizes are given in Table 3. Using theTDS test for sibships without parents with individual genotyping can produce a significant advantage over the pooled statistic (THS ), depending on the family structure (compare with Table 4 in Risch and Teng 1998). For families with one affected sib, the sample sizes are roughly comparable, with low allele frequencies slightly favoring theTDS statistic but high allele frequencies slightly favoring the THS statistic. As the number of affected sibs increases, however, the advantage of theTDS statistic increases. For two affected sibs, on average (across genetic models), 25% fewer families are required; for three affected sibs, 35% fewer are needed, whereas for four affected sibs, nearly half as many families are necessary using individual genotyping and the TDS statistic. As in the case for one affected child, the ratios are highest at low allele frequencies. The only exception is the high frequency dominant situation, in which the THS test may retain a slight advantage. We note also that these conclusions are reasonably independent of the number of unaffected sibs used.
Number of Sibships Without Parents Required to Detect LD Using Individual Genotyping
From Table 2 and Table 3 of Risch and Teng (1998), we can also contrast the number of families required under individual genotyping when both parents are available versus using two unaffected sibs when they are not (giving an identical number of family members). Using two unaffected sibs requires ∼50% more families, roughly independent of the number of affected sibs and genetic model. This number can be substantially higher, however, for a very common dominant allele.
Combining Families of Different Structure
As described previously in Risch and Teng (1998), it is typical that an investigator will have families of different structure, including different numbers of affected sibs and possibly unaffected sibs. As in the case for pooled samples, we suggest taking a weighted sum of allele frequency differences (p̂ 1 − p̂ 2) for the various family structures, in which the weight is according to the number affected in the family and the number of families of that structure. Thus, for families with r affected sibs, we multiply (p̂ 1 − p̂ 2) byrnri before summing, in which nri is the number of families with r affected of structurei, and then divide the total byN = Σrnri . To obtain the denominator, we simply sumr 2 n 2 riVar(p̂ 1 − p̂ 2), in which the variance ofp̂ 1 − p̂ 2 for a given family structure under the null hypothesis is given in the formulas above, divide by N 2, and then take the square root.
DISCUSSION
We have considered test statistics that can be created when individual genotyping is performed in nuclear families containing affected and unaffected sibs without parents. We have shown previously that to calculate the TDT for families with parents, individual genotyping is only required for the parents, to obtain a direct estimate of h. The child allele frequencies can still be obtained by DNA pooling, which could lead to a significant reduction in genotyping effort, especially for larger sibships.
Because it is possible to estimate the variance in the allele frequency difference between the affected and unaffected sibs without the Hardy–Weinberg assumption in families without parents, estimators that are immune to population stratification artifacts can be constructed. The statistic we have described, the TDS test, is analogous to the TDT because it contrasts allele frequencies between parents and affected offspring, as in the TDT, and uses a variance estimate independent of the Hardy–Weinberg assumption. In this case, the parent allele frequencies are estimated from the total offspring sibship, including both the affected and unaffected offspring.
When the tested sibship contains only a single affected, the power of the TDS statistic is quite close to the pooledTHS statistic, so the primary advantage of theTDS statistic is its robustness. However, as the number of affected in the sibship increases, the power of theTDS test increases relative to theTHS test, providing an additional advantage. We also note that the TDS statistic is easily calculated using the scores given in Table 2 and its variance by formula 6 above.
When families with multiple affected sibs are used, neither the pooled statistic THS described in Risch and Teng (1998) nor the TDS test described here compare favorably in terms of power with tests based on using unrelated controls instead of unaffected sibs. Thus, strategies involving both family-based as well as unrelated controls may be preferable.
It may be tempting to use the same group of affecteds in a two-stage process—that is, first comparing them to unrelated controls to increase power to identify candidate loci and then comparing these same affected individuals to family-based controls (parents or unaffected sibs) for robustness. However, in this approach, the two tests will be positively correlated under the null hypothesis, and so the threshold for significance for the second test needs to be constructed taking this correlation into account.
Other tests of linkage disequilibrium based on sibships without parents and individual genotyping have been proposed. Penrose first suggested the use of unaffected sibs as controls in association studies to protect against artifactual results owing to population stratification (Clarke et al. 1956). The method of C.A.B. Smith (Smith 1961), as also described in Clarke et al. (1956), is essentially based on a comparison of genotypes in affected children with their unaffected sibs. The proposal of Curtis (1997) is similar in this regard. Since our paper was submitted, two additional papers (Boehnke and Langefeld 1998;Spielman and Ewens 1998) have appeared describing sibship-based statistics. These tests are also based on allele (or genotype) frequency difference between affected and unaffected sibs, similar to the original Smith test. For sibships with one affected and one unaffected sib, all of these tests (including ours) are equivalent. However, for larger sibships the tests diverge.
We have chosen to focus on a TDT-like statistic, estimating parental allele and heterozygosity frequency, as this approach yields a more efficient test for sibships with multiple affecteds. However, a critical assumption underlying this advantage is that unaffected sibs reflect a random distribution of parental alleles. This will certainly be nearly true whenever the “locus-specific” penetrance for the tested locus is low and the unaffected sibs are selected randomly. However, this statistic would not necessarily be more efficient than a statistic based on comparison of allele frequencies in affected versus unaffected sibs, when the locus-specific penetrance is high or when the unaffected sibs are chosen from the opposite extreme of a continuous distribution from which the affecteds are chosen (e.g., lean sibs of obese sib pairs) (Eaves and Meyer 1994; Risch and Zhang 1995). In this case, the allele frequency in unaffected sibs is also expected to deviate from the parental allele frequency. The relative efficiency of the two types of tests, in this case, will depend on the degree to which the allele frequency in affected sibs is expected to deviate from that in unaffected sibs relative to that in the parents, and on the number of unaffected sibs.
At first glance, it may seem mysterious as to why theTDS statistic has increased efficiency over other sibship-based statistics that compare affected and unaffected sibs. These latter statistics are based solely on comparisons of genotypeswithin sibships. However, there is additional information available in the sample that our statistic incorporates, namely, the relative frequency of the different sibship genotype constellations (ignoring affection status in the sibship). For example, for sibships of size 3, we also use the frequency of sibships with three AAsibs, two AA and one Aa sib, two AA and oneaa sib, and so on (for all possible genotype combinations). This distribution of sibship genotypes provides information regarding the frequency of the six possible parent mating types. Because the mating-type frequencies are estimated without assuming random mating, the estimation procedure is robust to any deviation from random mating including population stratification. For example, in the extreme stratification case in which half the sibships have three AAsibs and the other half three aa sibs, our procedure estimates half the parent mating types to be AA × AA and the other half to be aa × aa, a complete deviation from random mating and Hardy–Weinberg genotype frequencies.
The analogy of the TDS statistic to the TDT statistic may also seem mysterious if the latter is viewed as a statistic derivable only from intact nuclear families. As we showed in Risch and Teng (1998), however, the TDT is calculated from three components: (1) the frequency of allele A in the offspring (p 1); (2) the frequency of alleleA in the parents (p 2); and (3) the frequency of heterozygous parents (h). It is entirely unnecessary to have intact families to derive these statistics. For example, p 1 and p 2 can be obtained, in theory, by DNA pooling, whereby all children are pooled together and all parents are pooled together. Even if parent DNA samples are separated from their offspring’s, a TDT can still be calculated. All that is required is knowing that a sample is from a child or a parent. Thus, it is obviously unnecessary to know which child genotypes are associated with which parent genotypes to construct a TDT.
In the TDS statistic, we are effectively recreating a TDT-type statistic. In this case, however, parental allele frequencies and heterozygosity are not estimated directly from the parents, who are missing, but from the offspring. That this can be done without bias derives from the fact that there are at least as many different possible sibship genotype constellations as parent mating types.
Acknowledgments
This work was supported, in part, by grants from the National Human Genome Research Institute (HG00348) and the Nancy Pritzker Foundation. We are grateful to Dr. Michael Boehnke for many helpful comments and suggestions on this manuscript and to Drs. David Curtis and Cedric Clarke for pointing out the Clarke et al. reference.
The publication costs of this article were defrayed in part by payment of page charges. This article must therefore be hereby marked “advertisement” in accordance with 18 USC section 1734 solely to indicate this fact.
Footnotes
-
↵4 Corresponding author.
-
EMAIL risch{at}lahmed.stanford.edu; FAX (650) 725-1534.
-
Received January 7, 1998; accepted in revised form January 20, 1999.
-
- Received November 9, 1998.
- Accepted January 20, 1999.
- Cold Spring Harbor Laboratory Press











