The Distribution of Variation in Regulatory Gene Segments, as Present in MHC Class II Promoters
Abstract
Diversity in the antigen-binding receptors of the immune system has long been a primary interest of biologists. Recently it has been suggested that polymorphism in regulatory (noncoding) gene segments is of substantial importance as well. Here, we survey the level of variation in MHC class II gene promoters in man and mouse using extensive collections of published sequences together with unpublished sequences recently deposited by us in the EMBL gene bank using the Shannon entropy to quantify diversity. For comparison, we also apply our analysis to distantly related MHC class II promoters, as well as to class I promoters and to class II coding regions. We observe a high level of intraspecies variability, which in mouse but not in man is localized to a significant extent near the binding sites of transcription factors—sites that are conserved over longer evolutionary distances. This localization may both indicate and enhance heterozygote advantage, as the presence of two functionally different promoters would be expected to confer flexibility in the immune response.
A surge of interest in the variability of regulatory, noncoding gene segments is under way. Collections have been made of promoter sequences for MHC class I and class II genes in man (Louis et al. 1993; Yao et al. 1995) and class II in mouse (Janitz et al. 1997a), which add substantially to the information previously available for promoter sequences in the hemoglobin (Weatherall 1986;Labie and Elion 1996) and glucose-6-phosphate dehydrogenase (Vulliamy et al. 1992) genes. These are all genes that encode “extrovert” proteins that handle diverse foreign structures such as antigens and parasites, in contrast to the “introvert” proteins that handle conserved structures internal to the body (Mitchison 1997); hemoglobin and glucose-6-phosphate dehydrogenase have been included in this list as extrovert proteins, as the high level of polymorphism evident in their structural genes results largely from their interaction with malaria parasites. The genes that encode extrovert proteins often vary in their coding sequences, so as to provide a range of binding sites for these foreign structures, and vary also in their noncoding regions (for reference, see Mitchison 1997). Variation in noncoding gene segments is also evident to a lesser extent among genes encoding introvert proteins, particularly among cytokines (and their receptors and natural antagonists) (Daser et al. 1996). The functional consequences of this promoter sequence variation is not generally known, but its importance in determining expression level is becoming clearer for the class II MHC genes (Louis et al. 1994; Woolfrey and Nepom 1995), the ACE I gene (Villard et al. 1996), and cytokines genes (Messer et al. 1991; Pociot et al. 1992). For these MHC genes, valuable collections have been made of very distantly related sequences (Benoist and Mathis 1990), which enable comparisons to be made with the level of intraspecific variation. Thus, the basis for systematic study of this form of variation is now available, in a preliminary way at least.
One of the main functions of regulatory DNA sequences is to provide sequences recognized by transcription factors. These sites in the MHC class II promoter region are grouped in the S, X (X1 and X2), and Y boxes, although there are other regulatory sites farther upstream (Glimcher and Kara 1992; M. Janitz, L. Reiners-Schramm, and R. Lauster, in prep.) and within the 5′-untranslated region (Janitz et al. 1997b). This grouping leads one to ask two simple questions: To what extent are these box sequences conserved during evolution, and how is variation within a species distributed in relation to the boxes? Over long evolutionary distances the box sequences are known to be conserved (Benoist and Mathis 1990; Sültmann et al. 1993), but the expectation for intraspecific variation is less clear. To the extent that the expression of these genes is under balancing selective pressure, one would expect to find variation at the boxes. It is important to add that the available information does not allow exact comparison to be made between different genes in this form of variation. That is because the sequence collections do not themselves contain information about gene frequencies in the natural population nor are the phenotypic effects of these genes known. Indeed, the role of natural selection cannot be addressed in laboratory mice or other domesticated species.
Class II MHC genes have been chosen for this study not only because their promoters are relatively well understood and their alleles available in quantity, but also because the proteins that they encode have been studied in depth (for thorough discussions, see Germain 1993;Hansen et al. 1993). Each class II molecule is composed of one α chain comprising an outer (membrane–distal) α1 and an inner (membrane–proximal) α2 domain, and a β chain likewise divided into β1 and β2 domains. The membrane–distal domains contain the residues that make contact with peptide and the T-cell receptor; the only known natural function of these molecules is to present peptide to T cells. These distal domains are encoded in the 5′ half of the structural gene of these type-1 membrane proteins. Class I MHC molecules have a fundamentally similar structure, although the two domains that make up the peptide-binding site are the α 1and α 2 domains of a singleα chain; the analog of the class IIβ 2 domain is a single-domain molecule that is encoded outside the MHC. It is the contact residues that are most variable in amino acid and base sequence. The crystal structure of both class I and class II MHC molecules has been determined (Madden 1995), thus enabling the contact residues to be defined in detail. For present purposes the important point is that the 5′ half of the class II coding genes are most variable, as is the 5′ one-third of the class I coding gene. This variability is concentrated at the peptide binding residues.
We are not aware of previous attempts to measure noncoding variation in this context, except by simply counting the positions where bases vary (Guardiola et al. 1996). In immunology, the Wu and Kabat (1970)approach is used frequently to measure protein sequence variability. We suggest, however, that both are inadequate measures of diversity. For the present analysis, therefore, we use the Shannon entropy (Shannon and Weaver 1949), a convenient and natural general measure of diversity (Patil and Taillie 1982).
RESULTS
Mus musculus MHC class II Promoter Sequences
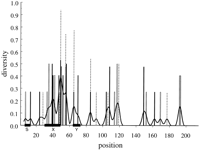
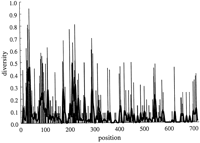
The diversity index Hi (see Methods) was computed for each position in the alignment of Mus musculus Aα, Aβ, andEβ MHC class II haplotypes. Most of the positions in all three data sets are invariant withHi = 0 or are invariant with the exception of a single differing nucleotide and haveHi = 0.27178. As can be seen in Figure 1, positions with a larger diversity index are clustered together in two groups, with one loosely clustered group in the 3′ half of the promoter and one dense group centered over the X box. The S box is diverse in comparison to the flanking regions but is relatively invariant when compared to the X and Y boxes. The region of greatest diversity begins 5′ of the X box in the pyrimidine tract where transcription factors are known to bind, peaks over the X box, and extends into the region just 3′ of X.
The diversity of the promoter regions measured by the Shannon entropy for the Mus Eβ (open bar),Aα (solid bar), Aβ(hatched bar) loci (shown stacked). Each locus is represented by eight haplotypes. The solid lines are moving averages computed using a Gaussian kernel 2 nucleotides wide. The width of this smoothing kernel is chosen to be the minimum length that produces smoothing sufficient for ease of visual inspection. Small variations in this width do not have an appreciable impact on the appearance of this plot. The locations of the promoter boxes are indicated by heavy lines on the abscissa. Base numbers start 6 nucleotides 5′ of the S box. Sequence lengths are as follows where the last 3 bases form the transcription start site ATG: Eβ, 215 bases; Aα, 174 bases; Aβ, 199 bases.
The average diversity of the boxes, H b (see Methods, below), was computed for each set of sequences by averaging Hi over all positions occurring in any one of the boxes. The average diversity outside the boxes, H n was computed by averaging over the rest of the positions. The combined difference H T b − H T n , where H T = H Aα + H Aβ + H Eβ ,is 0.0737. It was tested for statistical significance, as described in Methods, below with a resulting P = 0.0135. Using the Nei index of diversity, we find a combined difference value of 0.0798, with a corresponding P = 0.028. Thus, the variability in theMus promoter proximal region is concentrated to a significant extent in the regions of transcription factor binding, namely the S, X, and Y boxes. The difference H b − H ncomputed for each locus separately (Table 1), however, is not statistically significantly different from 0 at the traditional 0.05 level; under the null hypothesis, the probability of obtaining the differences seen for each locus independently were between P = 0.143 and P = 0.158. This is clearly dependent on the number of positions 5′ of the S box in the analysis. We included just five or six positions.
Results of the Promoter Sequence Analysis
Interspecies Comparison of MHC Class II Promoter Sequences
Six α-chain sequences from M. musculus (Aand E), Homo sapiens (DQ, DR, andDP), and zebrafish and seven β chains from M. musculus (A and E), H. sapiens (DQ, DR, and DP), Spalax ehrenbergi (DP), and chicken (B–L) were aligned. Hi, H b , and H n were computed as described in Methods, below. Our results, shown in Table 1, are consistent with the expectations and results of Benoist and Mathis (1990) andSültmann et al. (1993). The boxes, defined by their conservation over long evolutionary distances, vary much less than the non-box regions. The difference H b − H nis statistically highly significant (P < 10−3). In the α chains, all but 2 of 15 invariant positions are located in the boxes. In the β chains, all but 8 of 20 invariant positions are located in the boxes and 5 of these 8 positions are immediately 5′ of X in the pyrimidine tract where the binding factors RF-X and NF-X are known to contact the DNA (Benoist and Mathis 1990).
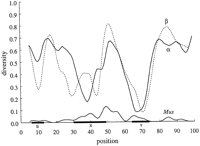
In Figure 2, one can see that for the α and β chains there are distinct points of low diversity centered over the S, X, and Y boxes. The diversity within the boxes is approximately half that outside the boxes (Table 1). Figure 2 reveals that the distribution of diversity differs little between the α and β chains, especially in the 3′ half of the promoter. When examining the 5′ half, one sees that the diversity in the S box is much lower in the β chains. There are no invariant positions in the S box of the α chains, but the overall level of diversity is clearly lower in this region when compared to non-box regions. In the β chains, there is an additional point of low diversity 5′ of the X box over the pyrimidine tract. The overall diversity in the X box for the α and β chains is greater than that in the Y box. It is interesting to note that the point of low diversity centered over the X box in the α chains occurs at the 5′ end of the box in the X1 portion of the box, whereas in the β chains, this point occurs at the 3′ end of the box in the region known as X2. This may be related to the fact that the X2binding factors are thought to be members of the Fos/Jun/CREB family, whose other members, TRE and CRE, are known to bind to half-sites (Benoist and Mathis 1990).
(Top two curves) Diversity of promoter sequences in distantly related class II genes over 6 sequences (104 bases in length) from 3 species (α chain) and 7 sequences (103 bases in length) from 4 species (β chain) (see Methods). The diversity is represented by a moving average computed with a Gaussian kernel 2 nucleotides wide. (Bottom curve) Moving average over Mus promoters (repeated from curve in Fig. 1).
When comparing the interspecies and Mus intraspecies distributions (Fig. 2), it is evident that the two distributions are mirror images of each other with the interesting exceptions that there is a corresponding peak just 3′ of the X box in all three sets of sequences. The distribution inside the X box of the Mussequences follows the distribution seen in the β chains, namely diversity in the X1 region and similarity in the X2region, whereas the distribution seen in the X box of the α chains mirrors the two.
Human MHC Promoter Sequences
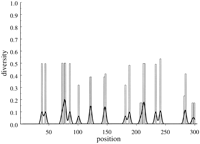
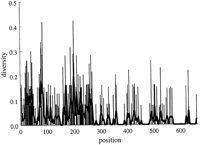
As can be seen in Figure 3, variability in the human MHC class II promoter region is distributed more evenly across the promoter and not concentrated near the X- and Y-box regions. The non-box region may have a higher average diversity value, although this difference, as seen here, is not significant (see Table 1 for exact values). As in the mouse, most of the variable positions are invariant, with the exception of just one or two sequences, and have correspondingly low Hi values, but there are many more variable positions.
The diversity of the promoter regions for the human DRβ locus (open bars), represented by 32 haplotypes. The solid line indicates the moving average. (Details as in Fig. 1.) Base numbers start 15 nucleotides 5′ of the X box; 277 bases were included in the analysis.
No conserved boxes have been located in the MHC class I promoter sequences. But when looking at overall diversity and its general distribution, one sees (Fig. 4) the opposite picture as that seen in the case of human MHC class II promoters. Here there are very few variable positions, but most of those that vary haveHi values near 0.5. This tends to result from the occurrence of two different nucleotides at one position with approximately equal frequencies. The overall diversity is almost half that seen in the human class II promoter sequences (Table 1).
Diversity over MHC HLA-B locus (open bars) (31 haplotypes). The solid line indicates the moving average. Sequences are 303 bases long. (Details as in Fig. 1.)
MHC Class II Coding Sequences
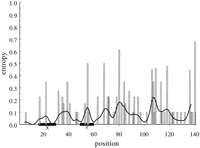
An examination of the human class II coding sequences reveals diversity throughout both of the extracellular domains, but at a higher level in the β1 domain (Fig. 5). As expected, the level of diversity is highest in the areas of peptide binding, especially in amino acid residues 9, 11, 13, 70, and 71. Residues 13, 70, and 71 all correspond to pocket 4, whereas residue 11 is the only β-chain residue in pocket 6 (Travers 1997). In the mouse, the diversity is also concentrated in exon 1, where the peptide binding residues are located (Fig. 6). The overall level of diversity is highest for the Aβ sequences. This is due not only to the presence of more variable positions, but also to the occurrence of more positions with a large index value. The overall level of diversity in the Eβ sequence set is much lower than either of the other two. Caution must be applied when comparing the human and mouse coding sequences. The entropy has been estimated using very different sample sizes, and it can be shown that the sample entropy is a downward-biased estimator for the population entropy, with bias decreasing for decreasing sample size.
Diversity over human DRβ coding regions. Sequences are 718 bases long. Average diversity over all positions at this locus is 0.06825. (Other details as in Fig. 1.)
Diversity over Mus Eβ, Aα, andAβ coding regions. Sequences are 667 bases long. Bars are averages over the three loci. (Other details as in Fig.1.) Note that the ordinate is scaled to show a maximum value of 0.5 rather than 1 as in Figs. 1 F2 F3 F4 F5. The average diversity over all positions for each locus is as follows: Eβ,0.02995; Aα, 0.04143;Aβ, 0.05141.
DISCUSSION
Measurement of Diversity
The concept of diversity as a property of a group of objects is of interest in many different disciplines including genetics, linguistics, business, economics, and ecology (Patil and Taillie 1982). This broad interest in quantifying diversity and comparing diversity has led to the development of several different diversity indices along with an analytic framework for examining the models behind the various indices and their properties (Patil and Taillie 1982). We have chosen to use the Shannon entropy as a measure of diversity in this analysis. The use of the Shannon entropy as a measure of diversity may be novel for many in our intended readership; therefore, in addition to the brief comments in the discussion to follow, please see the , which presents a slightly broader background for the mathematical issues involved. Those wishing a more extensive discussion of the quantitation of diversity can find such treatments in Hill (1973), Kempton (1979),Patil and Taillie (1982), and Pielou (1977).
The Shannon entropy was originally devised in the development of information theory (Shannon and Weaver 1949) and can be interpreted as the information gain expected in the performance of a single measurement from the population under discussion. This aspect of entropy has been exploited within molecular biology (Román-Roldán et al. 1996) and, in particular, with regard to DNA regulatory binding sites and the question of how much “information” is required to identify such regions (Schneider et al. 1986). These formal aspects of the entropy are of secondary importance for the present analysis. Entropy, and even diversity per se, are not the quantities of ultimate interest to us. The quantity that most unambiguously measures the effect we seek to document, however, will depend on many biological features: the specifics of DNA-protein binding, the mechanisms of evolutionary diversification and selection, the details of differential gene regulation, and the extent of the advantage gained through the increased flexibility of the immune response. In short, this ideal measurement is not yet available. The entropy is very likely to be highly correlated with this unknown index over the range of its observed variation and will therefore serve as an adequate indicator. More detailed models of the underlying mechanisms will eventually provide more powerful statistical tests.
To the best of our knowledge, investigators addressing the question of promoter sequence variability in the past have used the frequency of variable bases per region as a measure of region variability. This is clearly inadequate in that all information included in the knowledge of the number of different nucleotides appearing at a position is lost as well as all information contained in knowledge of their relative abundances. The Wu and Kabat (1970) approach to measuring sequence variation has been applied extensively in immunology, namely to amino acid sequences in antibodies (Kabat et al. 1991) and MHC molecules (Parham et al. 1989). It is thus worth mentioning that we also explicitly prefer the Shannon entropy over the Wu–Kabat index. The Wu–Kabat index played a valuable role in early qualitative discussions of diversity, but in contrast to the Shannon entropy, has no obvious natural interpretation and is not well suited to quantitation. [For a more detailed discussion of the mathematical deficiencies of the Wu–Kabat index, and a comparison of its properties with those of indices based on the Shannon entropy, see Shenkin et al. (1991).] The nucleotide diversity index of Nei (1987) is also widely used. We have repeated our primary analyses using the Nei index in place of the Shannon index for the sake of historical continuity; the findings are consistent between the two indices. A brief discussion of the Nei and Shannon indices is included in the .
Intra- and Interspecies Variation
The S, X, and Y boxes of the MHC class II promoters were initially identified by the level of their conservation across species. Our analyses are consistent with these observations: in interspecies comparisons, the noncoding DNA within the S, X, and Y boxes show significantly lower diversity than the noncoding DNA outside these boxes (Fig. 2). The contrast between intra- and interspecific variation is shown in Figure 2, where the Mus average diversity curve is plotted together with that for interspecific variation. [Mus castaneus does not figure as distant, as its promoter fits within the same group as the laboratory strains examined here (Janitz et al. 1997a; M. Janitz, L. Reiners-Schramm, and R. Lauster, in prep.), as was shown by tree analysis (result not shown).] Within Mus MHC class II promoters, we find greater diversity within the S, X, and Y boxes than outside them (Fig. 1 and accompanying statistical analysis). We take this as evidence for diversifying selection within the boxes.
The human class II promoters examined did not show the same pattern of localized variation but rather were consistently variable over the entire promoter region. It is difficult to arrive at any specific conclusions about this latter fact. Although the boxes are not overly diverse, they are also not overly conserved. The extent of variation within the boxes in this series has excited comment previously (Louis et al. 1993). We suggest two alternative perspectives. On the one hand, the level of variation in the promoter box regions may simply be tolerated rather than actively selected for. On the other hand, it may be that diversity in the boxes actually was selected for in the past but has reached its maximum tolerable level, whereas the non-box regions have continued to accumulate changes.
Selective Pressure
MHC promoter polymorphism is likely to be maintained by balancing selection in favor of heterozygotes. The presumed advantage of heterozygosity lies in the flexibility that it confers on the immune response: The protein under the control of the promoter in one allele is better able to mediate resistance to one type of pathogen, whereas the other allele is better suited to defense against another pathogen. The means by which this is brought about is likely to be in selective expression in particular cell types (Daser et al. 1996; Mitchison 1997). It is thus interesting that the one Mus MHC class II locus with an invariant promoter, Eα is the only locus with a variant upstream enhancer (M. Janitz, L. Reiners-Schramm, and R. Lauster, in prep.); this enhancer variation has also been shown to have functional consequences (M. Janitz, L. Reiners-Schramm, and R. Lauster, in prep.). Whether the lack of localized variation in the human promoter sequences implies a difference in the selective pressures on the two species cannot be inferred from this analysis. That is, however, an important question, and a similiar study including additional human MHC class II loci as well as intraspecific comparisons with a variety of other species is needed. There are other aspects of variation in human MHC class II promoters, including allele frequencies and the consequences of haplotype selection, that are important but necessitate extensive review, beyond the scope of the present work.
Further information about the functional significance of this promoter polymorphism is likely to be acquired through expression studies on naturally occurring variants (for review, see Guardiola et al. 1996;Müller and Mitchison 1997). More critical testing is likely to come from site-specific mutagenesis and promoter/exon reshuffling in cell lines and eventually in mice.
The relative conservation of MHC class I promoters in comparison with those of class II is not surprising. Class II MHC proteins, expressed primarily on specialized antigen-presenting cells, mediate a number of subtly different immunoregulatory cell–cell interactions that require precise control of expression level (Guardiola et al. 1996;Constant and Bottomly 1997) as well as tissue specificity of expression. In contrast, class I MHC proteins are expressed by nearly all cells; their expression is up-regulated drastically at sites of inflammation, thus enabling virus-infected cells to function simply as antigen-presenting machines (Germain 1993).
In their MHC class II promoters, Mus and Spalax show very little similarity outside the conserved S, X, and Y boxes, in contrast to the close similarity of laboratory mice and M. castaneus. Mus and Spalax have separate ancestry tracing back into the Oligocene, soon after the origin of the rodents, so it would be of interest to compare species related more closely to the mouse, such as Rattus, Mastacomys (both of which have laboratory strains), and Apodemus, all of which diverged post-Miocene (Thenius 1980). The EMBL database does not contain promoter sequences for these species.
Within the promoter boxes, the diversity is comparable to that in the coding sequences. Coding sequences within the MHC have been shown to be subject to diversifying selection (Hughes and Nei 1988). We suggest that the advantage conferred by this exon diversity is further enhanced by diversity in the associated promoters (Mitchison 1997). Once functional diversity of the protein has been established, the potential exists for differential expression of the proteins to effect immunoregulation. Variability in the promoters accomplishes this and provides additional flexibility to the immune response. Thus, we expect that the extent of diversity in the exons and promoters may be correlated.
METHODS
To address the question of how diversity is distributed within regulatory sequences, we have made several comparisons focusing on diversity of MHC class II promoter sequences. The first comparison examines the level of diversity seen within the conserved boxes versus that seen outside of these boxes. For the intraspecies comparisons, 8 haplotypes from laboratory strains of M. musculus were used for the Aα, Aβ, andEβ loci, as well as 32 haplotypes for the humanDRβ genes. The alignment and sequences for theMus b, d, k, and q haplotypes (all three loci) were taken from Janitz et al. (1997a). Haplotypes z, p, j1, andj2 (Eβ locus) and haplotypes z, p1, p2, and j (both A loci) can be found in GenBank under accession numbers Y13072–Y13083. They were aligned to the original alignment using the program GeneWorks 2.1 (Oxford Molecular Group). The 32 human sequences and their alignment were taken from Louis et al. (1993). The Mus Eα locus was not included in the analysis because it is known to be invariant. For the interspecies comparison, the alignment and sequences for six α chains and seven β chains were taken from Benoist and Mathis (1990). An additional sequence, a zebrafish α chain sequence, was taken from Sültmann et al. (1993) and was aligned to the Benoist and Mathis sequence using GeneWorks 2.1 (Oxford Molecular Group). For all species, the sixth base 5′ of S was used as the 5′ boundary; the 3′ boundary corresponds to that used in Benoist and Mathis (1990). These MHC class II promoter sequence comparisons are supplemented with a comparison between human MHC class I and class II promoter sequences, as well as an examination of the diversity seen in human and Mus MHC class II coding sequences. Thirty-one haplotypes of the HLA-B locus were used for the class I analysis. All sequences and their alignment are taken from Yao et al. (1995). For each set of sequences, the 5′ and 3′ boundaries, as well as the location of the boxes in promoters, is consistent with that in the cited references unless otherwise noted.
To examine the class II coding sequence diversity, 41 alleles of theDRβ genes in humans were used along with 9, 10, and 12 haplotypes for the Mus Aα, Aβ, and Eβ loci, respectively. For the human DRβ sequence set, the alignment and sequences for the following alleles were taken fromFigueroa et al. (1991): DRB1*1603, DRB1*0411, DRB1*0801, DRB1*08022, DRB1*08031, DRB1*09011, DRB3*0101, DRB3*0301, andDRB4*0103. The allele DRB1*1302 (accession no.U83584) was taken from GenBank; all of the DRB1, DRB3, DRB4,and DRB5 alleles available in the Graphical Interface to MHC Sequence Database (Histo) were also included (Travers 1997). Sequences taken from the Histo database are accessed by their allele designation. These sequences were aligned to the alignment of Figueroa et al. (1991)using the program GeneWorks 2.1 (Oxford Molecular Group). For theMus sequence sets, all sequences and their alignment were taken from the Histo database. The following haplotypes were used:I-A K-A′ CL, I-A B-A′ CL, I-A F-A′ CL, I-A U-A′ CL, I-A D-A′ CL, I-A S-A′ CL, I-A R-A′ CL, I-A Q-A′ CL, NON Aa′, I-A K-B′ CL, I-A K-B′ ′CL, I-A U-B′ CL, I-A b NOD′ CL, I-A F-B′ CL, I-A S-B′ ′CL, H-2 Ab/p′ CL, I-A D-B′ CL, I-A B-B′ CL, I-A Q-B′ CL, I-E (I-E) D-B EB24-1′ CL, I-E U-B′ CL, I-E B EBB24′ CL, I-E S-B′ CL, I-E K-B′ CL, MOUSE H-2 (H-2) Z′ CL, H-2 EbW17′ CL, NON Eb′ CL, B10.A(3R)-E-β′ CL, and NOD Eb′ CL (Travers 1997). Only the exons for theβ1 and β2 domains were considered.
In each case, the Shannon entropy (Patil and Taillie 1982) was computed for each position in the alignment. For purposes of this analysis, gaps are ignored, that is, at each position
where gaps occur, those sequences with gaps are omitted. The Shannon entropy is defined by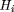
(Shannon and Weaver 1949). The position in the alignment is indexed byi, whereas j indexes the four nucleotides.pi,j
is the frequency of nucleotide j at position i. The average Hi,H, was computed over position within the regions of interest and then used to compare the diversity of the regions. Positions
occurring in any one of the boxes were grouped into one region with average diversity
H
b and the remaining positions were grouped into a second region with average diversity
H
n
. To detect statistically significant differences in the diversity of the two regions, a t statistic was computed for the difference
H
b −
H
n
.Let this value of t be denoted t
0.Hi
is not normally distributed, hence a comparison of t
0 to Student’s t is not appropriate. Therefore, the probability of obtaining t such that |t| > t
0 under the null hypothesis (that diversity between the two regions does not differ) was estimated by randomizing the positions
in the alignment 1000 times, calculatingt for each permutation and then counting the frequency of permutations yielding t such that |t| > t
0.
Additionally, we wanted to estimate the probability under the null hypothesis of observing a combined difference as large as or larger than that observed in our three Mus data sets. We summed H n over all three data sets, H n Aα + H n Aβ + H n Eβ ,and subtracted that from the sum of H b over all three data sets. Call this difference Θ0. We then randomized the positions in the alignments of each data set independently two thousand times and computed the difference Θ for each permutation. The probability of observing a difference greater than or equal to that present in our data sets was then estimated by the frequency of Θs such that |Θ| > Θ0.
This analysis was repeated using the Nei index of nucleotide diversity (Nei 1987) in place of the Shannon entropy. A brief discussion of the measurement of nucleotide diversity is included in the .
We developed Fortran 90 programs (available on request, fromlgcowell{at}unity.ncsu.edu) using the Microsoft Developer Studio with Fortran Powerstation 4.0 (Copyright 1994–1995 Microsoft Corporation) to compute sitewise diversity indices and perform permutations. Remaining computations were done using the commercially available software package Splus version 3.2 (Statsci, a division of Mathsoft).
Acknowledgments
This work was supported by a Fulbright grant (to L.G.C.), by National Science Foundation award MCB–9357637 (to T.B.K.), and by the Deutsche Forschungsgemeinschaft and the Senate Administration for Research and Education of the City of Berlin. We are grateful to T. Shiroishi and Sonoko Habu for genomic DNA from the MSM strain and P.-A. Cazenave for genomic DNA from M. castaneus.
The publication costs of this article were defrayed in part by payment of page charges. This article must therefore be hereby marked “advertisement” in accordance with 18 USC section 1734 solely to indicate this fact.
Footnotes
-
↵3 Corresponding author.
-
E-MAIL kepler{at}stat.ncsu.edu; FAX (919) 515-1909.
-
- Received July 28, 1997.
- Accepted January 5, 1998.
- Cold Spring Harbor Laboratory Press
