Dissecting multilayer cell–cell communications with signaling feedback loops from spatial transcriptomics data
- 1School of Mathematics, Sun Yat-sen University, Guangzhou 510275, China;
- 2Zhongshan School of Medicine, Sun Yat-sen University, Guangzhou 510080, China;
- 3Department of Mathematics and Department of Developmental and Cell Biology, NSF-Simons Center for Multiscale Cell Fate Research, University of California Irvine, Irvine, California 92697, USA
-
↵4 These authors contributed equally to this work.
Abstract
The emergence of spatial transcriptomics (ST) provides unprecedented opportunities to better decipher cell–cell communication (CCC). How to integrate spatial information and complex signaling mechanisms to infer functional CCC, however, remains a major challenge. Here, we present stMLnet, a method that takes into account spatial information and multilayer signaling regulation to identify signaling feedback loops within multilayer CCCs from ST data. To this end, stMLnet quantifies spatially dependent ligand–receptor signaling activity based on diffusion and mass action models, and maps it to intracellular targets. We benchmark stMLnet against seven representative methods and find that stMLnet performs better in both intercellular ligand–receptor inference and intracellular target gene prediction. We apply stMLnet to analyze data from diverse ST techniques like seqFISH+, Slide-seq v2, MERFISH, and Stereo-seq, verifying its robustness and scalability on ST data with varying spatial resolutions and gene coverages. Particularly, stMLnet reveals multilayer signaling feedback loops underlying the inflammatory response in ST data of COVID-19-infected lung tissue. Our study provides an effective tool for dissecting multilayer ligand/receptor-target regulation and multicellular signaling circuits from ST data, which can advance understanding of the mechanistic and functional roles of spatial CCC.
The coordinated activities of cells serve as fundamental building blocks for achieving the fate and function of multicellularity, with cellular activities dependent on cell–cell interactions among different cell types and tissues within an organism. Cells interact in different ways, such as physical cell-to-cell contact (e.g., cell adhesion) and biochemical cell–cell communication (CCC) mediated by diffusible molecules (Armingol et al. 2021). Among these interactions, CCC plays a pivotal role in multicellular physiological processes, primarily mediated through signaling events of ligand–receptor (L-R) binding, which induces downstream responses shaping development, differentiation, or homeostasis (Pires-daSilva and Sommer 2003; Quail et al. 2016; Armingol et al. 2021; Moss et al. 2021). Dysregulation of CCC often contributes to the development and progression of many diseases (Pires-daSilva and Sommer 2003).
Recently, single-cell RNA sequencing (scRNA-seq) technology enables sequencing of tissues with unprecedented resolution and gene coverage (Svensson et al. 2018). Consequently, many recent studies have developed CCC inference tools aimed at deciphering the mechanisms of CCC from scRNA-seq data (Browaeys et al. 2020; Cillo et al. 2020; Efremova et al. 2020; Zhang et al. 2020; Cheng et al. 2021; Jin et al. 2021; Noël et al. 2021; Hu et al. 2021b; Wilk et al. 2024). These CCC inference methods can be divided into two categories (Luo et al. 2023). One is to infer intercellular L-R signaling networks. For instance, CellChat (Jin et al. 2021), CellPhoneDB (Efremova et al. 2020), ICELLNET (Noël et al. 2021), and CellTalker (Cillo et al. 2020) infer CCC between cell populations by analyzing cell type–specific expression of ligands and receptors, whereas Scriabin (Wilk et al. 2024) infers intercellular communication at single-cell resolution. The other category is inferring both intercellular and intracellular signaling networks, such as scMLnet (Zhang et al. 2020; Cheng et al. 2021; Ni et al. 2022), NicheNet (Browaeys et al. 2020), and CytoTalk (Hu et al. 2021b), which predict links between ligand/receptor and downstream genes by considering intracellular signaling. These CCC inference tools have been widely applied across various systems (Bonnardel et al. 2019; Hu et al. 2021a; Kuppe et al. 2021). However, because of the lack of positional information in scRNA-seq data, the CCC inference methods based on scRNA-seq data cannot utilize the spatial information of cells and may produce potential false positives and false negatives.
Spatial transcriptomics (ST) can simultaneously measure gene expression and location information of cells or spots (Longo et al. 2021), and its emergence is beneficial to solving the above problems (Armingol et al. 2022; Walker et al. 2022). Although the scRNA-seq data-based tools have been often applied to infer CCCs in ST data (Dries et al. 2021; Hao et al. 2021; Palla et al. 2022; Pham et al. 2023; Wilk et al. 2024), a few specifically tailored methods designed for ST data (Shao et al. 2022; Tanevski et al. 2022; Cang et al. 2023; Fischer et al. 2023; Li et al. 2023; Jin et al. 2025) have been developed very recently. For example, MISTy utilizes explainable machine learning models to extract the spatially constrained intercellular links between ligands/receptors and target genes (TGs) (Tanevski et al. 2022). COMMOT builds a collective optimal transport model to infer L-R connections for cells/spots in the ST data, considering competition among multiple molecular species and spatial distances between cells (Cang et al. 2023). NCEM constructs node-centric expression models based on graph neural networks to predict cell's observed gene expression vector (Fischer et al. 2023). In addition, CytoSignal (Liu et al. 2024) and DeepTalk (Yang et al. 2024) decipher spatial CCC at single-cell resolution. Although these methods provide promising advancement in CCC inference, the elaborate mechanisms underlying CCC have not been fully exploited. In fact, the signaling mechanisms within CCC encompass not only intercellular L-R interactions but also intracellular signal transduction and transcriptional regulation, involving receptor–transcription factor (R-TF) pathways and transcription factor–target gene (TF-TG) interactions. Hence, these elements constitute a multilayer signaling network (Zhang et al. 2020; Cheng et al. 2021; Ni et al. 2022). However, current ST data–based CCC methods seldom consider multilayer signaling network structure involved in CCCs. Moreover, existing methods fall short on capturing signaling feedback loops among cells that are important for understanding multicellular organizations in a systematic manner (Su et al. 2014; Barone et al. 2017; Jing et al. 2021).
To address the above challenging gap, we present stMLnet, an ST-based multilayer network method for inferring multilayer signaling paths and multicellular signaling feedback circuits involved in CCCs. stMLnet integrates two scales (i.e., intercellular scale and intracellular scale) and four layers (i.e., L-R-TF-TG), facilitating the identification of feedback loops among multicellular signaling systems. To this end, we first construct a comprehensive signaling molecule interaction database stMLnetDB, which contains the multilayered signaling structure of “L-R-TF-TG.” Next, stMLnet mechanistically quantifies the spatially dependent L-R signaling activity based on a mathematical model of ligand diffusion and the L-R interaction. It then quantitatively maps the intercellular L-R signals to intracellular gene expressions using explainable machine learning. Together, our method provides a unified framework for multiscale inference of spatial CCC through a model and data codriven approach.
Results
Overview of stMLnet
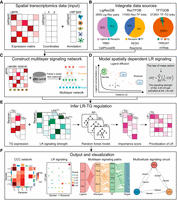
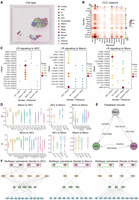
stMLnet requires a gene expression matrix, a cell location matrix, and cell type annotations from ST data as user input (Fig. 1A). It infers CCC by integrating this input data with prior knowledge of the interactions between signaling ligands, receptors, transcription factors (TFs), and TGs. Upon receiving input data, stMLnet models intercellular and intracellular communications through the following four modules.
Overview of stMLnet. (A,B) Required input of stMLnet. (A) The input data consist of a gene expression matrix, spatial locations of cells/spots, and the cell type annotation vector.
(B) stMLnet integrates molecular interactions from multiple data sources (including ligand–receptor [L-R] interactions, signaling
pathways, and transcriptional regulation) to generate a prior knowledge database called stMLnetDB. Specifically, LigRecDB
contains 3659 nonredundant LR interactions, comprising 920 ligands and 751 receptors. RecTFDB includes 17,450 nonredundant
receptor–transcription factor (TF) links, consisting of 751 receptors and 525 TFs. TFTGDB consists of 373,501 transcription
factor–target gene (TF-TG) interactions, with 525 TFs and 23,021 target genes. (C–E) Workflow of stMLnet. (C) Statistical inference of multilayer signaling network. Combining the stMLnetDB and gene expression data, stMLnet uses Fisher's
exact test (optional) to construct multilayer signaling network of ligand-receptor–transcriptional factors–target genes (L-R-TF-TG).
(D) Quantification of LR signaling activity. Based on the ligand diffusion model and the law of mass action, stMLnet employs
a distance-dependent function to calculate the LR signaling activity. (E) Linking LR activity to TG expression using random forest regression algorithm. stMLnet calculates the importance score of
the specific LR signaling contributing to the TG expression, which could be used to prioritize the ligands or receptors as
upstream regulators of a given target gene. LRSTGt represents the signaling scores of LR pairs (i.e., 
) that modulate TGt. (F) Output and visualization of inferred CCCs. stMLnet provides a variety of intuitive visualization outputs, including heatmap
plot, bubble plot, waterfall plot, and multilayer path and circuit visualization.
Construction of prior knowledge base
We curated multiple literature-supported databases that encompass various molecular interactions, such as L-R interactions, signaling pathways, and transcriptional regulation. These prior databases were integrated using random walk with a restart algorithm on directed weighted graphs, resulting in the construction of our in-house knowledge base, stMLnetDB (see details in Methods section and Supplemental Text S1, S2). stMLnetDB is organized into three subdatabases: LigRecDB, RecTFDB, and TFTGDB. This comprehensive database captures the multilayer signaling structure of “L-R-TF-TG,” providing a robust foundation for studying complex intercellular communication processes (Fig. 1B).
Inference of multilayer signaling network
To predict significant multilayer signaling networks, we first identify specific ligand genes, receptor genes, and feature genes from the input data. Next, stMLnet utilizes LigRecDB to search for the paired links between the identified ligands and receptors, constructing a Lig-Rec subnetwork. Feature genes are then intersected with the TG nodes in TFTGDB and linked to their corresponding TFs to form a TF-TG subnetwork. Subsequently, the TF nodes in the TF-TG subnetwork are matched with RecTFDB to construct the Rec-TF subnetwork. The Lig-Rec subnetwork is further updated by incorporating receptor nodes involved in the Rec-TF subnetwork. Additionally, a Fisher's exact test can be applied to further refine the network by filtering out inactive TFs, receptors, and their associated interactions. Finally, the individual subnetworks are integrated to construct a comprehensive multilayer signaling network (Fig. 1C).
Quantification of spatially dependent L-R signaling activity
Based on the assumption of ligand diffusion, stMLnet quantifies L-R signaling activity by considering that the ligand signal intensity sensed by the receiver cell is inversely proportional to the distance from the sender cell to the receiver cell and then calculates the spatially dependent L-R signaling strength according to the law of mass action (Fig. 1D).
Prioritization of L-R pairs contributing to TG expression
Because of the complex nonlinear regulation relationships between L-R pairs and TGs, stMLnet employs random forest regression to associate L-R activity with TG expression. For each TG, stMLnet trains a random forest model and calculates the importance score of each upstream L-R pair to the TG expression, thereby ranking L-R pairs that mediate spatially resolved CCC (Fig. 1E). In addition, we refined the permutation importance score to assess the individual contribution of L or R alone to the TG expression, which is referred to as the partial importance score.
The output of stMLnet includes the multilayer signaling network (L-R-TF-TG), L-R signaling activity, and importance ranking of L-R pairs or L-Rs with respect to their abilities to regulate TG expression. Therefore, stMLnet provides various visualization methods to display the results more intuitively (Fig. 1F). For instance, the heatmap plot of the CCC network shows the number of L-R pairs between any pair of two cell groups; the bubble plot depicts the signaling activity of different L-R pairs from the sender cell group to the receiver cell group; the waterfall plot displays the signaling paths with importance scores from upstream L-R pairs to TFs and then to the downstream TGs; and the multicellular signaling circuit indicates the inferred feedback loop between different cell types.
Performance comparison of stMLnet with other methods
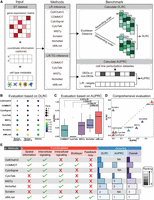
To benchmark stMLnet, we designed a benchmark framework to evaluate and compare its performance with other representative CCC inference methods in inferring intercellular and intracellular communications (Fig. 2A). Seven state-of-the-art CCC inference methods, including CellChatV2 (Jin et al. 2025), COMMOT (Cang et al. 2023), CytoSignal (Liu et al. 2024), CytoTalk (Hu et al. 2021b), MISTy (Tanevski et al. 2022), NicheNet (Browaeys et al. 2020), and Scriabin (Wilk et al. 2024), were used for comparison. The implementation process and parameter settings of these methods are described in Supplemental Text S3. We evaluated these eight methods on three ST data sets, including two breast cancer ST data sets and one glioma ST data set (Supplemental Text S4). We chose these data sets because they are associated with 15 sets of cell line perturbation expression data, providing ground truth of L-R-TG regulation for benchmarking.
Benchmarking the performance of stMLnet. (A) Overview of benchmark framework. It involves three components: input, methods, and benchmark metrics. We benchmark the performance of stMLnet and the other seven representative CCC inference methods on ST data sets. Specifically, CellCahtV2, COMMOT, CytoSignal, CytoTalk, MISTy, NicheNet, Scriabin, and stMLnet can all infer intercellular ligand–receptor (LR) interactions, whereas COMMOT, CytoTalk, MISTy, NicheNet, and stMLnet can further infer LR-TG regulation, namely, intracellular signaling. We used DLRC to evaluate intercellular LR inference and AURRC to evaluate the accuracy of intracellular target gene predictions. (B) Evaluation and comparison of the eight LR inference methods based on the DLRC metric. Rank indicates the performance ranking of a method on a data set according to the DLRC value (i.e., score). The higher the DLRC value, the lower the rank number. (C) Evaluation and comparison of the five LR-TG inference methods using the AUPRC metric. The statistical significance of difference in AUPRC values between stMLnet and each other method was assessed using the Wilcoxon rank-sum test. (D) Comprehensive evaluation of stMLnet with other methods from both intercellular and intracellular communication aspects. (E) Summary of properties/functionalities and benchmarking results for the eight CCC inference methods. (a) The names of CCC methods. (b) The properties/functionalities of different CCC methods. We list the properties of each method, including the spatial information utilization, and the prediction capacities on intercellular LR interactions, intracellular LR-TG regulation, multilayer network structures, and feedback loops. (c) Accuracy and overall ranking of different methods according to the two metrics. (NA) Not applicable. The lighter the color, the higher the ranking, indicating better method performance.
Based on the above three ST data sets with cellular perturbation data, we benchmark the performance of stMLnet and other seven CCC inference methods in inferring intercellular L-R interactions and intracellular L-R-TG regulation using the metrics including differential L-R correlation (DLRC) and area under the precision recall curve (AUPRC), respectively (see Methods). Briefly, we divide sender–receiver cell pairs into close and distant groups in different proportions based on Euclidean distance (Fig. 2A). We then calculate DLRC to assess the difference of L-R correlations in the close and distant cell groups for each method across the three ST data sets, under the hypothesis that closer cells are more likely to communicate with each other (Hu et al. 2021b; Jin et al. 2021). Based on the rankings of the DLRC values across three ST data sets, we found that stMLnet outperforms other CCC inference methods in predicting intercellular L-R interactions (Fig. 2B). In addition, we evaluate the performance of stMLnet on inferring intercellular communication between rare cell types on the breast cancer-2 data set. The number of endothelial cells accounts for only 1.92% of the total number of cells (Supplemental Fig. S1A). We then calculated the DRLC values of seven L-R inference methods on the communication between endothelial cells and other cell types. We found that stMLnet still show improvement compared with the other seven methods in this case (Supplemental Fig. S1B).
Furthermore, we benchmarked the L-R-TG prediction by comparing the regulatory scores of ligand/receptor–targets predicted by CCC methods that can infer intracellular signaling (including COMMOT, CytoTalk, MISTy, NicheNet, and stMLnet) with DEGs (serving as ground-truth labels) in cell line perturbation data. If the predicted TG is a DEG, the L-R-TG is marked as true; otherwise, it is marked as false, and then the values of AUPRC (Fig. 2C) and area under the ROC curve (AUROC) (Supplemental Fig. S2) are calculated. In this study, we focus on the AUPRC value because it is more appropriate than AUROC when evaluating classifiers using imbalanced data sets (Saito and Rehmsmeier 2015, 2017). The results demonstrate that stMLnet significantly outperforms other methods in L-R-TG predictions. Specifically, among the five methods evaluated, stMLnet has the best performance with a median AUPRC close to 0.6, followed by NicheNet and MISTy, both with a median AUPRC near 0.3 (Fig. 2C). In addition, we noticed that CytoTalk frequently failed to predict the ligands or receptors corresponding to the cell line perturbation–expression data sets in most situations (Supplemental Fig. S3). This occurred because most ligands/receptors of interest have a negative priority expression metric defined in CytoTalk, causing their node rewards being calculated as zero by the Steiner forest algorithm. Consequently, these ligand/receptor nodes were filtered during the construction of signaling networks in CytoTalk. Overall, stMLnet has superior performance over other methods in both intercellular L-R interaction inference and L-R-TG prediction (Fig. 2D).
We summarize the functionalities and the benchmark results of stMLnet compared with the other seven CCC inference methods (Fig. 2E). We list the properties of each method, including the spatial information utilization, the prediction capacities on intercellular L-R interactions, intracellular L-R-TG regulation, multilayer network structures, and feedback loops. In detail, only CellChatV2, COMMOT, and stMLnet consider the spatial information of ST data when inferring intercellular interactions. Among the eight methods we compared, all can predict L-R interactions between cells, among which COMMOT, CytoTalk, MISTy, NicheNet, and stMLnet can further infer intracellular L-R-TG regulation. Particularly, only stMLnet, COMMOT, and NicheNet can infer multilayer signaling network structures. Furthermore, stMLnet uniquely predicts signaling pathway feedback loops mediated by L-R, which will be demonstrated in the following sections. In addition, we calculate the average DLRC for each CCC method across the three data sets, as well as the average AUPRC across different cell line data sets, and rank the methods based on these values. Higher values indicated better performance and higher rankings. Furthermore, we derived the overall ranking of each CCC method by averaging their DLRC and AUPRC rankings (with NA values set to zero) (Fig. 2E(c)). According to the result, we found stMLnet, Scriabin, and NicheNet rank among the top three in terms of their ability to infer intercellular communication, whereas stMLnet performs best in inferring intracellular regulation, followed by NicheNet and MISTy. Overall, stMLnet offers more functionalities and exhibits the best performance in inferring CCC.
In addition, we compared the computational resources consumed by stMLnet with those of the seven other methods (Supplemental Fig. S4). The results show that stMLnet's running time across all three data sets is shorter than that of CytoTalk and comparable to that of COMMOT. Although stMLnet's memory usage is somewhat higher than most methods, it is still smaller than that of CytoTalk. The increased memory usage of these two methods is mainly owing to their modeling of complex intracellular signaling regulation. Nevertheless, the overall computational resources required by stMLnet fall within a reasonable and manageable scope.
Analysis of spatially dependent L-R signaling in stMLnet
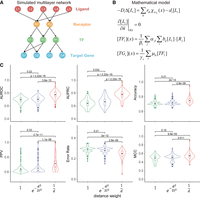
To scrutinize the distance-weighted L-R signaling activity, we performed a simulation study based on a mathematical model of ligand diffusion and L-R-TF-TG regulation (for details, see Supplemental Text S5). We generated three categories of simulated data sets with distinct spatial characteristics, each comprising 100 sets of synthetic data. (Fig. 3A,B; Supplemental Figs. S5–S10). In simulation data set 1, the three cell types are randomly distributed across the domain (Supplemental Fig. S5). In simulation data set 2, cells of Sender 1 and Receiver 3 are colocalized randomly distributed within a circular region, whereas cells of Sender 2 are randomly distributed across the entire domain (Supplemental Fig. S6). Finally, in simulation data set 3, each spatial position corresponds to one or more cells (Supplemental Fig. S7), mimicking spatial embedding in which the true cell position is rasterized by a synthetic microarray (e.g., 10x Visium or Slide-seq arrays).
Verifying distance-weighted LR signaling activity in the stMLnet model using synthetic data. The performance of stMLnet in LR-target prediction was compared to those of its variants with modified distance weighting functions in LR activity scoring. The distance weighting functions are the reciprocal function (i.e., 1 / d) as used in stMLnet and radial basis function (i.e., exp(−d2 / 2l2)) that is used in other tools (e.g., MISTy) or constant function (i.e., one) in the two variants, respectively. (A) Ground truth of the multilayer network structure used to generate synthetic data. (B) The mathematical model used for simulation. (C) Based on simulation data set 1, the performances of stMLnet with the reciprocal weighting function and the two variants in predicting L-R-TG regulation were evaluated and compared. The Wilcoxon rank-sum test P-value was used to assess the statistical significance. (AUROC) Area under the ROC curve, (AUPRC) area under the precision/recall curve, (PPV) positive predictive value, (MCC) Matthews correlation coefficient.
We substituted the weighting function of L-R signaling quantification in the stMLnet model (i.e., the reciprocal function
(
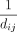); Equation 5) with the alternative constant (1) or radial basis function (
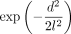). Note that the constant weight corresponds to spatially independent model, and the radial basis weight represents the one
used by previous methods such as MISTy (Tanevski et al. 2022), in which the parameter l = 100 is set for the radial basis function. We compared the performance of stMLnet with the two counterparts using the three
simulation data sets. The simulated spatial expression data were used as input for stMLnet and its variants (without using
the prior information of the predefined multilayer network) to infer the regulation of TGs’ expression by L-R pairs. The predicted
importance scores for L-R-TG regulation were benchmarked with the ground truth of the simulated network topology. Various
evaluation metrics, including AUROC, AUPRC, positive predictive value (PPV), accuracy, error rate, and Matthews correlation
coefficient (MCC), were used for assessment. The evaluation of the six metrics on three simulation data sets (Fig. 3C; Supplemental Fig. S11) showed that the reciprocal function used in stMLnet significantly outperformed the other two variants of weighting functions.
Furthermore, we evaluated the effect of the hyperparameter l on the performance of stMLnet when using the radial basis function as the weight function. In detail, when the radial basis function is used as the weight function, we compared the results with different values of l (i.e., l = 20, 40, 60, or 100) on three data sets and compared them with the results when the constant function or the reciprocal function was used as the weight function (Supplemental Fig. S12). Based on the evaluation of the six metrics across the three simulation data sets, we found that the performance of stMLnet using the reciprocal function as the weight function is still better than that of the constant function and the radial basis function under different values of l. Overall, these results affirm the rationale and effectiveness of stMLnet in modeling spatial distance-dependent cell communication and gene regulation.
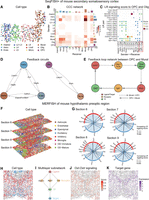
stMLnet traces signaling feedback loops within multilayer CCCs across diverse types of ST data
To showcase the wide applicability of stMLnet across various ST data types, we deployed it on multiple ST data sets generated by different techniques, such as sequential fluorescence in situ hybridization (seqFISH+), MERFISH, Slide-seq v2, and Stereo-seq. We first analyzed seqFISH+ data of mouse cerebral cortex with 10,000 genes measured in 523 single cells (Fig. 4A,E; Eng et al. 2019). We observed that stMLnet inferred abundant and active intercellular communication between different cell types. Among them, oligodendrocytes (Oligs) and endothelial cells (Endos) emerged as key intercellular communication “hubs,” exhibiting the highest number of interactions as sending cells to other cell types within the microenvironment (Fig. 4B). When setting oligodendrocyte precursor cells (OPCs) and Oligs as the receiver cells, we identified Sema5a-Plxnb3 transmitted from L6 as the most active upstream L-R signaling in OPCs. Moreover, the Sema5a-Plxnb3 L-R signal was found to mediate reciprocal communication between Oligs and OPCs. Specifically, Sema5a of Olig cells imposed strong influence on the expression of downstream TGs (e.g., Sox10) of OPCs. In turn, Sema5a of OPCs binds to Plxnb3 on Olig cell surfaces, regulating the expression of multiple TGs (Mag, Pcyt2, etc.) by activating the TFs including Nfkb1 (Supplemental Fig. S13). In addition, based on the inferred multilayer networks, we identified bidirectional feedback loops between Astro, Mural, and Endo, as well as between OPCs and Mural. Several ligand genes, such as Esam, Fn1, and Nid1 in Endos, Lamc1 in Mural, Vegfa in Astro, and Vcan in OPCs, also function as TGs within the multilayer networks of these cell types (Fig. 4D). Figure 4E illustrates the feedback loop networks between OPCs and Mural. Specifically, Mural secretes the ligand Lamc1, which interacts with the receptors Dag1 and Sv2a in OPCs, whereas the ligand Vcan from OPC interacts with the receptor Itgb1 on Mural. Furthermore, Lamc1 acts as a downstream target of Vcan via Stat3 (TF) in the signaling pathway from OPCs to Mural. Similarly, Vcan is a downstream target of Lamc1 through Rela and Nfkb1 (TFs) in the signaling pathway from Mural to OPCs (Fig. 4E). Additionally, the feedback loop networks between Astro, Mural, and Endo were shown in Supplemental Figure S14.
Multilayer signaling analysis of inferred CCC in seqFISH+ data and MERFISH data using stMLnet. (A–E) Multilayer signaling analysis of seqFISH+ of mouse secondary somatosensory cortex. (A) Spatial distribution of different cell types. (Adarb2) Adarb2-iNeruon, (Astro) astrocytes, (L2-L3) L2-L3-eNeuron, (Endo) endothelial, (L4) L4-eNeuron, (L5) L5-eNeuron, (L6) L6-eNeuron, (Lhx6) Lhx6-iNeuron, (Micro) microglia, (Olig) oligodendroglia, and (OPC) oligodendrocyte precursor cells. (B) Heatmap plot of inferred CCC network. “Number” in the plot represents the number of LR pairs between any two cell groups. The top color bar plot represents the sum of column of values displayed in the heatmap. The right color bar plot represents the sum of row of values. (C) Bubble plot of inferred LR signaling activity from other cell types to OPCs and Oligs. Score in the plot denotes the LR signaling activity. (D) The feedback circuits between Astro, Mural, and Endo (left) and the feedback circuits between OPC and Mural (left). Representative ligand/target genes are shown. (E) The feedback loop network between OPC and Mural. Lamc1 (ligand; red) interacts with Dag1/Sv2a (receptor; yellow), whereas Vcan (target gene; red) interacts with Itgb1 (receptor; yellow). Additionally, Lamc1 (target gene; red) is a downstream target from Vcan (ligand; red) via Stat3 (TF; green). Similarly, Vcan is a downstream target from Lamc1 through Rela/Nfkb1 (TF; green). Solid arrows represent signaling from OPC to Mural, and dashed arrows indicate signaling from Mural to OPC. (F–K) Multilayer signaling analysis of MERFISH of mouse hypothalamic preoptic region. (F) Spatial distribution of cell types in multiple tissue slices from MERFISH data. (G) Chord plot of LR signaling activity between excitatory and inhibitory. The links start from a sender cell type (excitatory; blue) and end in a receiver cell type (inhibitory; red) and each line link also connects a ligand–receptor pair. The thickness of the line represents LR signaling score: The thicker the line, the higher corresponding score. (H) Spatial distribution of excitatory and inhibitory in a section 6 slice. (I) Multilayer subnetwork of Oxt-Oxtr. The multilayer signaling subnetwork indicates the regulatory paths from a specific ligand/receptor to its downstream transcriptional factors and then to target genes. (J) The spatial distribution of specific Oxt-Oxtr signaling score. (K) The spatial distribution of target gene (Oxt).
We then analyzed the multiplexed error-robust fluorescence in situ hybridization (MERFISH) data, which measured the expression of 161 genes in the mouse hypothalamic preoptic region (Fig. 4F–K; Moffitt et al. 2018). The data set consists of 12 spatially adjacent slices along the anterior–posterior axis, among which we selected four slices (sections 6–9) for CCC analysis (Fig. 4F). Because of the limited number of genes included in the MERFISH gene panel, the application of a Fisher's exact test for secondary screening during the construction of a multilayer signaling network may result in the exclusion of key signaling molecules. Therefore, we chose to omit the Fisher's exact test when constructing the multilayer signaling network for the MERFISH data set. Setting excitatory cells as sender cells and inhibitory cells as receiver cells, we found that Pnoc-Oprl1 was the most active upstream L-R signal in all slices, dominating cell interactions. Moreover, Oxt-Oxtr L-R signaling was found in every slice (Fig. 4F). Specifically, excitatory neurons regulate Inhibitory neurons through Oxt signaling, which explains why Oxt-Oxtr L-R signaling can regulate social behavior, as reported in the literature (Warfvinge et al. 2020; Froemke and Young 2021). Particularly, we selected a section 6 slice to conduct further downstream analysis from the Oxt-Oxtr L-R signal (Fig. 4G–J). The multilayer signaling subnetwork depicts the regulatory paths from a specific ligand to downstream TFs and then to TGs. We found that Oxt secreted by excitatory cells binds to Avpr1a, Avpr2, and Oxtr on the inhibitory surface, regulating the expression of TG Oxt through activation of the TF Esr1 (Fig. 4H). Furthermore, we visualized the spatial distribution of the L-R signaling activity of Oxt-Oxtr (Oxtr in excitatory cells and Oxt from other cells) (Fig. 4I) and the spatial distribution of TG expression in excitatory cells (Fig. 4J), and we found that the distributions of the two were consistent. This finding is consistent with the hypothesis of stMLnet in modeling spatially dependent L-R signaling activity.
We also employed stMLnet to investigate a layer-scale ST data, the Slide-seq v2 data of mouse hippocampus, which measured the expression of 23,264 genes in 53,173 beads (Stickels et al. 2021). The results of L-R signal analysis and multilayer signaling networks are described in Supplemental Text S6 and are presented in Supplemental Figures S15 and S16.
Moreover, to evaluate how sensitive stMLnet is to changes in hyperparameters, we conducted a series of experiments on the above three ST data sets (for details, see Supplemental Text S7). We varied three key hyperparameters and assessed the consistency of the inferred networks using Jaccard coefficients. The results (Supplemental Figs. S17A–D, S18) indicate that stMLnet maintains a high level of robustness across different parameter settings, providing valuable guidance for parameter selection.
We further examined stMLnet's scalability using a large Stereo-seq data set from an E16.5 mouse embryo section (Chen et al. 2022). This data set includes 155,741 cells and 28,579 genes (Supplemental Fig. S17E). Through down-sampling analysis, we found that the running time and memory usage of stMLnet increase almost linearly with the number of cells (Supplemental Figs. S17F, S19), suggesting good scalability of stMLnet on large-scale ST data sets. Furthermore, the consistency among the subnetworks identified by stMLnet across various down-sampling rates verifies its robustness against variations in cell type abundance (Supplemental Fig. S20).
Lastly, we evaluated the robustness of stMLnet with respect to gene dropout using the MERFISH data set. The results demonstrate that, within the multilayer network constructed from the MERFISH data set, the Lig-Rec subnetwork exhibits higher robustness to gene dropout compared with the Rec-TF and TF-TG subnetworks (Supplemental Fig. S21).
stMLnet reveals positive cellular feedback circuits and multilayer signaling regulation in a COVID-19 microenvironment
To investigate CCCs underlying the inflammatory response to SARS-CoV-2 infection, we applied stMLnet to a set of Visium ST data of COVID-19-infected lung tissue (Fig. 5A; Supplemental Fig. S22; Gracia Villacampa et al. 2021). The CCC network (Fig. 5B) showed abundant and active intercellular interactions between various cell types, indicating dysregulated hyperinflammation in the COVID-19-infected lung tissue microenvironment.
stMLnet reveals positive cellular feedback circuits and multilayer signaling regulation in ST data of COVID-19. (A) Spatial distribution of cell types in COVID-19-infected lung tissue. (B) Heatmap plot of inferred CCC network. Number in the plot represents the number of LR pairs between any two cell groups. The top color bar plot represents the sum of column of values displayed in the heatmap. The right color bar plot represents the sum of row of values. (C) Bubble plots show the LR signaling from other cell types to AEC (left panel), Macro (middle panel), and Mono (right panel), respectively. Score denotes the LR signaling activity. Top 20 LR pairs were plotted for visualization purpose. (D) Correlations between ligand genes’ expressions (intracellular targets) and their upstream LR signaling activities. Most PCC values (R) were positive except for a small fraction of monocytes. (E) Positive feedback loops between AEC, Macro, and Mono. Representative ligands acting as paracrine cytokines are shown. (F) Multilayer signaling subnetworks from representative paracrine ligands to target genes in AEC (left panel), Macro (middle panel), and Mono (right panel). Top-ranked target genes according to importance scores were prioritized for visualization.
We focused on communications between alveolar epithelial cells (AECs), macrophages (Macro), and monocytes (Monos), as the latter two are pivotal innate immune cells against SARS-CoV-2 infection (Merad and Martin 2020), whereas AECs express a high level of the SARS-CoV-2 receptor ACE2 (Zhao et al. 2020), acting as a master communicator during viral infection (Miura 2019). The L-R signaling analysis (Fig. 5C) depicted paracrine signaling from other cell types to AECs (left panel), Macros (middle panel), and Monos (right panel). Relatively stronger activities of L-R signaling were observed for each pair of the above three cell types. For example, FN1-SDC4 signaling from Macros to AECs, C3-CD81 signaling from AECs to Macros, SFTPA1-TLR2 signaling from AECs to Monos, and B2M-HLA-F signaling from Macros to Monos exhibited clearly stronger activities than other L-R pairs; the spatial distributions of signaling scores for these L-R pairs are presented in Supplemental Figure S23. Moreover, we found that many ligand genes (e.g., FN1 and TGM2 in Macros, C3 and GPC3 in AECs, and NID1, VCAN in Monos) were also TGs in the multilayer networks of the three cell types (Supplemental Table S1; Supplemental Fig. S24) and that almost all these ligand genes as targets were positively correlated with their upstream L-R signaling (Fig. 5D). Collectively, these results suggest positive feedback loops between AECs, Macros, and Monos through paracrine signaling interactions (Fig. 5E), which may account for the sustained production and accumulation of inflammatory cytokines and dysregulated hyperinflammation in severe COVID-19 patients (Chen et al. 2021).
Furthermore, the multilayer subnetworks (Fig. 5F; Supplemental Fig. S25) demonstrate the signaling paths from representative ligands to targets in AECs, Macros, or Monos. Several TFs, such as NFKB1, RELA, and JUN, were inferred to be involved in the intracellular signaling pathways underlying the above intercellular feedback circuits. These TFs are reportedly critical in regulating the gene expressions of inflammatory cytokines during SARS-CoV-2 infection, and they are targets of FDA-approved drugs (Santoso et al. 2021), indicating their therapeutical values for COVID-19 by disrupting the above feedback circuits. In addition, we investigated the biological functions of the above intercellular feedback circuits by performing functional enrichment analysis for their intracellular TGs. The GO and KEGG pathway enrichment (Supplemental Fig. S26) demonstrated that biological processes or pathways related to COVID-19, immune response, cell adhesion, and the extracellular matrix (ECM) were significantly enriched for communications among AECs, Macros, and Monos. These results indicate the important roles of the abovementioned intercellular feedback loops in pulmonary injury and immune disorders in response to SARS-CoV-2 infection, and they are consistent with the results of previous studies (Romero et al. 2015; Peteranderl et al. 2016).
Discussion
In this paper, we introduce stMLnet, a tool designed for dissecting multiscale CCCs in ST data. The methodological innovations of stMLnet include the following aspects. First, stMLnet provides a unified framework for multiscale inference of spatial CCC. Our modeling framework (Supplemental Fig. S27) integrates two scales (i.e., intercellular scale and intracellular scale) and four layers (i.e., L-R-TF-target), facilitating the identification of feedback loops among multicellular signaling systems (Fig. 2E). Second, stMLnet represents a model and data codriven computational approach for CCC inference. At the intercellular scale, we develop mechanistic models (i.e., diffusion and mass-action models) to quantify the strength of intercellular L-R signaling. At the intracellular scale, we employ a random walk algorithm and a Fisher's exact test to infer the structure of multilayer networks. Moreover, we construct a nonlinear regression model (e.g., random forest) to quantify the regulatory scores of L-R-TGs by connecting intercellular L-R signaling to intracellular targets. Therefore, our method simultaneously infers intercellular signaling and intracellular gene regulation. Third, we develop an effective model-solving method, yielding a parameter-free formula for spatially dependent L-R signaling, significantly reducing the model complexity (Supplemental Fig. S28). stMLnet can serve as a hypothesis-generating tool in CCC studies, which can guide further experimental validations. For example, the L-R signaling-mediated feedback loops between different cell types predicted by stMLnet could be validated using cell coculture experiments and in vivo animal models (Su et al. 2014; Barone et al. 2017; Jing et al. 2021).
The advances of stMLnet include the following aspects. First, the L-R-TF-TG multilayer network framework constructed based on the cell type level is adequate and effective in depicting intercellular communication-mediated gene expression. This multilayer network method evaluates the upstream activities using the downstream responses, which may reduce false-positive predictions. To fulfill this objective, we integrate carefully curated prior network database information with context-specific and cell type–specific expression data to discover potential causal relationships between the upstream signaling and the downstream targets by employing the random walk algorithm and statistical inference method (e.g., Fisher's exact test). In our analysis, we found that applying multiple testing correction could lead to a more stringent filtering process, potentially excluding many TFs and receptors. This could result in a network with fewer nodes, increasing the risk of omitting key signaling pathways and critical interactions. Therefore, we chose not to apply multiple testing correction for the Fisher's exact test in this study. Second, for the L-R pairs in the multilayer network constructed above, we leverage the spatial information in the ST data to mechanistically quantify their signaling activities between sender and receiver cells, using a mathematical diffusion model of microenvironmental ligands. This analysis is conducted at the single-cell level. This leads to a parameter-free reciprocal relationship between effective ligand signals receipted by the receiver cells and physical distance between cells. Although simplified, it avoids unfeasible estimation or calibration of ligand-specific parameters (e.g., diffusion rate and degradation rate). Third, we employ an explainable random forest regression model to measure the contribution of each ligand, receptor, or L-R pair in regulating TG expression. This analysis is performed for each TG. We found that stMLnet with random forest regression (stMLnet-RF) has higher accuracy in L-R-TG prediction than stMLnet with neural network regression (stMLnet-NN) (Supplemental Fig. S29A), and stMLnet-RF runs faster than stMLnet-NN (Supplemental Fig. S29B). As such, we used random forest regression instead of neural network regression in stMLnet for modeling L-R-TG regulation. These advantages possibly contribute to the superiority of stMLnet compared with the other existing methods.
Admittedly, our study had some limitations. For example, our method makes several simplified assumptions. We employed a partial differentia equation (PDE) model to explicitly account for the weight of intercellular distance in paracrine L-R signaling, based on the assumption of ligand diffusion. This assumption may not be exactly realistic, especially in the context of complex cell microenvironment and various forms of ligand molecules. Actually, ligands can be secretory proteins or membrane proteins. The PDE model may not be very appropriate for the latter. But given that the cells carrying the membrane proteins are also undergoing migration or “diffusion” in the niche, the PDE model can also capture this equivalent distance-dependent effect in CCC. Nevertheless, our approach provides an explicit approach to weight the distance-dependent interaction potential. In future work, we will clearly distinguish between secreted ligands and membrane-bound ligands in the existing L-R interaction database and then infer diffusion-based interaction, contact-based interaction, and cell-self interaction based on the characteristics of the signaling molecules (i.e., paracrine, juxtacrine, and autocrine). Furthermore, for contact-based interactions, the L-R signaling scores can be calculated between directly adjacent cells, which can be identified using geometric algorithm such as Delaunay triangulation. For autocrine signaling, because the signal is directly fed back to itself, the influence of distance on signal degradation can be ignored. Therefore, for direct interactions and autocrine signaling, we propose to redefine dij in Equation 5 as one when the relative distance between cells is nearly zero, and zero otherwise. In addition, like many other tools (e.g., Scriabin, MISTy, NicheNet, CytoTalk, CellTalker, NATMI, Domino) (Cherry et al. 2021), each subunit of ligand/receptor is viewed as an independent ligand/receptor in stMLnet. StMLnet represents the total effect of different ligand/receptor subunits by summarizing them according to Equation 5. In the future studies, we will explicitly consider ligand/receptor complexes during the multilayer network construction.
Additionally, the TF-target information comes from prior databases, which are not cell type specific. These drawbacks can be addressed by integrating ST data with emerging single-cell multiomics data, such as single-cell proteomics data and single-cell ATAC sequencing data, thanks to the fast development of sequencing technology. Moreover, inferring CCC based on gene expression levels from spatial transcriptomic data has limitations, because the abundance of ligands, receptors, and TFs at the RNA level may not always be directly correlated with their protein levels. We observed that in the CID4465 data set, stMLnet failed to predict TGs downstream from several L-R interactions associated with certain cell line perturbations (Supplemental Fig. S3). The false-negative inaccuracy was likely owing to unrealistically low signaling scores for the corresponding L-R pairs, which were quantified based on their RNA levels in this data set. This prevented stMLnet from effectively inferring downstream TGs. In future work, we will consider combining ST with spatial proteomics (e.g., Spatial-CITE-Seq [Liu et al. 2023] or CODEX [Kennedy-Darling et al. 2021]) to improve the accuracy of inferred interactions. Additionally, our simulation study used a small-scale signaling network to generate synthetic data but did not incorporate large-scale biological network information. In future studies, we will develop novel multiscale models that integrate multiomics data across multiple layers to make better inferences of CCC and gene–gene regulation.
In summary, stMLnet, a method for modeling spatially dependent intercellular signaling and intracellular regulation, serves as a valuable tool for analyzing multiscale signaling and functioning of CCCs in ST data.
Methods
The proposed method stMLnet mainly encapsulates four components (Fig. 1), namely, constructing prior knowledge base of multilayer signaling interactions based on multiple data sources, inferring multilayer signaling networks, calculating distance-dependent L-R signaling activity, and quantifying regulatory relationships between upstream L-Rs and downstream TGs in the inferred multilayer network.
Collection and integration of prior network information
To infer inter- and intra-cellular signaling networks, we manually collected multiple data sources of molecular interactions as prior network information (Supplemental Text S1). We then processed and integrated them into prior knowledge databases of stMLnet, called stMLnetDB. stMLnetDB is a database of literature-supported human molecular interactions, which consists of three signal transduction scales: LigRecDB (L-R prior database), TFTGDB (TF-TG prior database), and RecTFDB (receptor-TF prior database) (Supplemental Fig. S30; Supplemental Table S2).
To infer links from receptors to TFs in RecTFDB, we used R package graphite (Sales et al. 2019) in R v 4.0.5 (R Core Team 2021) to extract information of intracellular signaling pathways or molecular interactions from eight existing databases (Supplemental Figs. S30, S31A). Based on such information, we constructed directed-weight graphs and employed the random walk with restart (RWR) algorithm (László 1996) to infer receptor-TF links (Supplemental Text S2). To enhance the reliability of receptor-TF link prediction, we employed threefold cross-validation and random subsampling validation (Lü and Zhou 2011) approaches to determine the restart-probability in the RWR algorithm and to test the accuracy of receptor-TF link prediction (Supplemental Fig. S30B). We further used 129 sets of cell line perturbation data (Supplemental Table S3) to determine significant receptor-TF links that mostly preserve the information of DEGs in the cell line data and simultaneously ensure the sparsity of the RecTF matrix (Supplemental Fig. S30C). Finally, 17,450 nonredundant receptor-TF links were obtained, comprising 751 receptors and 525 TFs, which compose the RecTFDB database.
The comparison of the prior databases of stMLnet with those of NicheNet (Browaeys et al. 2020) and Omnipath (Türei et al. 2016) is described in Supplemental Text S8 and Supplemental Figure S31. When applying stMLnet to mouse data sets, we mapped human genes in stMLnetDB to mouse orthologs.
Inference of multilayer intercellular and intracellular signaling networks
The multilayer signaling network consists of four layers of signaling molecules (ligands, receptors, TFs, and TGs), organized into three coherent subnetworks: L-R signaling, receptor-TF pathways, and TF-TG interactions. It is important to note that this multilayer signaling network is a simplified model designed to represent complex signal transduction pathways. Given the numerous signaling molecules involved in each receptor-TF pathway, it is challenging to explicitly incorporate all of them into the analysis and visualization of the multilayer network. As a result, we adopted the “L-R-TF-TG” multilayer network structure in our study, which aligns with our previous work on scMLnet (Zhang et al. 2020; Cheng et al. 2021; Ni et al. 2022), as well as other methods such as CellCall (Zhang et al. 2021) and exFINDER (He et al. 2023). The details of the multilayer network structure inference are described in Supplemental Text S9.
Modeling spatially dependent L-R signaling activity
We next quantified signaling activities of L-R pairs identified in the above multilayer signaling network NL−R−TF−TG. We employed a mechanistic modeling approach by considering ligand diffusion in the microenvironment. Assume that the spatial
coordinates of cell i and cell j are (xi, yi, zi) and (xj, yj, zj), respectively. The Euclidean distance between cell i and cell j is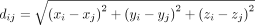 
. Denote LRk as the kth pair of ligand-receptor, and denote 
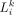and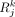 
as the corresponding ligand expression in the ith cell and receptor expression in the jth cell, respectively.
The ligand is a type of cytokine that can diffuse in the microenvironment following release by the sender cells. The spatial-temporal
distribution of the ligand concentration u(x, y, z) during diffusion can be described by a PDE as follows:
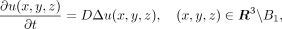(1)
where Δ is the Laplace operator, defined as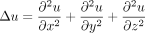 
. D is the diffusion coefficient. B1 represents a unit ball in a dimensionless scale, assuming that the cytokine signals are secreted from a single spherical
surface source (Francis and Palsson 1997). We assume that the diffusion of the ligand is relatively fast and that the above equation quickly reaches to the steady-state.
Therefore,
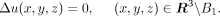(2)
We further assume that the diffusion of the ligand across the local microenvironment is homogenous, and thereby the solution
to the above equation is radially symmetric, that is, u(x, y, z) = u(r), where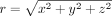 
. Consequently, the above steady-state diffusion model could be simplified to an ordinary differential equation (ODE):
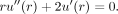(3)
Solving the above ODE, we get
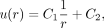(4)
where C1 and C2 are constants. Assume that the ligand concentration is u1 along the boundary of B1 and zero far away from the boundary of B1. So, we impose the boundary conditions u(1) = u1, u(∞) = 0. As such,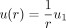 
. We used the ligand expression in the sender cell (
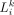) as a proximity of u1. Therefore, the signaling strength of 
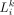received by the jth cell is 
.
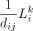Furthermore, based on the law of mass-action, the signaling strength of the kth L-R pair activated at the jth cell could be defined as
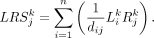(5)
dij represents the relative distance between sender cell i and receiver cell j.
These equations quantitatively describe the influence of relative distance between sender–receiver cells on L-R signaling intensity, so that the ligands from the sender cells with different distances react with the receptor of the receiver cell in different extent. As a result, the samples of L-R signals (i.e., receiver cells) are consistent with those of the corresponding TGs, allowing mapping L-R signal to the intracellular TG expression.
Random forest regression for L-R-TG regulation
We then model nonlinear relationship between the L-R signaling activities and the TG expression. Assume m TGs (i.e., TG1, TG2, …, TGm) in the inferred multilayer network and nt pairs of L-Rs linked to each TG, TGt. To decipher quantitative regulation relationship between the signaling activities of L-R pairs and the TGs, we divided this
task into m subproblems by decoding the following functions:
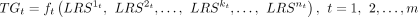(6)
Because of complex regulation relationship between L-Rs and the TG, the above ft is generally nonlinear. We thus employed explainable tree-based regression to learn ft. We constructed random forest regression model for each of the m TGs (Fig. 1E). We used the signaling activities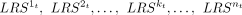 
(calculated from Equation 5) across the receiver cells as input to predict the expression of TGt.
Importance score of the ligand/receptor-target regulation
Based on the random forest model, we could calculate the importance score of the ktth feature (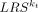
) contributing to the expression of TGt and thereby rank L-R pairs. Moreover, we also refined the permutation importance score to account for the disassembled importance
of L or R alone, which was referred to as partial importance score. The details are described in Supplemental Text S10.
Identifying signaling feedback loops within multilayer CCC networks
We integrate multilayer networks between different cell types and search for cycle in the hypergraph to identify the multilayer feedback loops of CCC. Specifically, cell type 1 acts as a sender and secretes ligand L1 to activate R1 in cell type 2 as a receiver. Then, R1 activates downstream TF1, and TF1 regulates TG1. We record each pathway in the multilayer network of cell type 1→cell type 2 as “L1 − R1 − TF1 − TG1.” Conversely, when cell type 2 acts as a sender, it releases ligand L2 and communicates with cell type 1 as a receiver through L1 − R2. Then R2 activates downstream TF2, and TF2 regulates TG2. We record each pathway in the multilayer network of cell type 2→cell type 1 as “L2 − R2 − TF2 − TG2.” When L1 and TG2 are the same gene and TG1 and L2 are also the same gene, it is considered that cell type 1 and cell type 2 have two-way communication, indicating a feedback loop of CCC signaling between these two cell types. Therefore, signal pathways [L1 − R1 − TF1 − L2] ↔ [L2 − R2 − TF2 − L1], in which L1 and L2 are reciprocal TGs, involved in bidirectional communications of cell type 1↔cell type 2 are identified as one of the multicellular signaling feedback loops.
ST data sets
To demonstrate the applicability of stMLnet, we applied it to five ST data sets, including seqFISH+ data of the mouse cortex (Eng et al. 2019), Slide-seq v2 data of the mouse hippocampus (Stickels et al. 2021), MERFISH data of the mouse hypothalamus preoptic region (Moffitt et al. 2018), Stereo-seq data of the developing mouse embryo (Chen et al. 2022), and Visium data of human COVID-19 (Gracia Villacampa et al. 2021). To benchmark the performance of stMLnet, we utilized three Visium data sets, including two from human breast cancer (Wu et al. 2021; https://www.10xgenomics.com/datasets/human-breast-cancer-block-a-section-1-1-standard-1-1-0) and one from human glioma (Ravi et al. 2022). Corresponding scRNA-seq data sets were collected to annotate these ST data sets. Detailed information on these data sets can be found in Supplemental Table S4, with their collection and processing described in Supplemental Text S4.
Benchmarking study
One of the challenges in CCC inference is the lack of appropriate benchmarking, which impedes the methodological development and practical applications of such tools (Dimitrov et al. 2022; Liu et al. 2022; Luo et al. 2023). In this study, we designed a benchmark framework to quantitatively evaluate the performance of different methods in both intercellular L-R interaction inference and intracellular L-R-TG predictions.
Benchmarking intercellular L-R interaction inference
To evaluate the performance of different methods for inferring intercellular L-R interactions, we analyzed the differences in L-R pair correlations between close and distant cell pairs in ST data. This analysis is based on the assumption that nearby cells are more likely to signal each other than distant ones, resulting in stronger communication signals (Jin et al. 2021; Hu et al. 2021b). This assumption aligns with prior studies, such as Dimitrov et al. (2022), who hypothesized that “colocalized cell populations are expected to have a higher chance of interacting than other nonadjacent cell types,” and Hu et al. (2021b), who used mutual information to evaluate and validate the differential spatial expression correlations of the inferred pathway genes between proximal and distal cell pairs.
First, for each sender–receiver cluster pair, we paired each cell in the sender cluster to cells in the receiver cluster to
create sender–receiver cell pairs. Specifically, we used si − rj to represent the sender–receiver cell pair, where si denotes the ith sender cell and rj denotes the jth receiver cell, respectively. Therefore, the sender–receiver cell pairs are represented as follows:
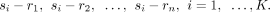Next, we divided the sender–receiver cell pairs into close and distant groups according to Euclidean distance. We sorted the
sender–receiver cell pairs in ascending order of their physical distances and subsequently selected the top 10%, 20%, 30%,
or 40% of cell pairs to construct close cell pair group. Similarly, the distant cell pair groups were constructed using bottom
10%, 20%, 30%, or 40% cell pairs, accordingly. Denote the close group with cell pair proportion of the top Hv (Hv = 10%, 20%, 30%, or 40%) as Cv (v = 1, 2, 3, 4) and the distant group with cell pair proportion of the down Hv as Dv (v = 1, 2, 3, 4).
Furthermore, we utilized mutual information (MI) to assess the correlation between the expression levels of ligand and receptor
in each L-R interaction within close or distant group, where L-R interactions were inferred by different CCC methods. Specifically,
for each L-R interaction Lx-Ry, the expression level of ligand Lx in sender cells among M sender–receiver cell pair is denoted as X = [x1, …, xi, …, xM], where xi represents the expression level of ligand Lx in sender cell si. Similarly, the expression level of receptor Ry in receiver cells among M sender–receiver cell pair is denoted as Y = [y1, …, yj, …, yM], where yj represents the expression level of receptor Ry in receiver cell rj. The MI value for the L-R interaction Lx-Ry was then computed using the following equation:
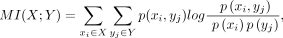(7)
where p(xi, yj) represents the joint probability distribution of X and Y. p(xi) and p(yj) are the marginal distributions of X and Y, respectively. The MI was calculated in R v 4.0.5 (R Core Team 2021) using the infotheo R package (Meyer 2008).
In particular, we calculated the MI values of each L-R interaction in the close group and distant group, respectively. The
MI value for each L-R interaction Lx-Ry in the close group Cv was calculated as follows:
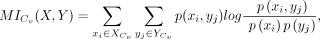(8)
where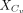 
represents the expression values of the ligand Lx in the close group Cv, and 
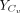represents the expression values of the receptor Ry in the close group Cv.
Similarly, for the distant group Dv, the MI value for each L-R interaction Lx-Ry in this group was calculated as follows:
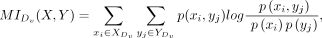(9)
where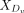 
and 
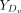represent the expression values of the ligand Lx and receptor Ry, respectively, in the distant group Dv.
We then calculated the difference of the MI values of L-R interactions in the close and distant groups and employed a Wilcoxon rank-sum test to assess the statistical significance of the difference of L-R correlations between the close and distant groups.
Finally, we integrated three factors, including the difference of MI between close and distant groups, the statistical significance,
and the proportions of cell pairs, to define the differential L-R correlation (DLRC) metric as follows:
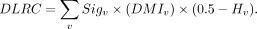(10)
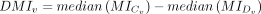represents the difference in the medians of MI values between the two groups, where 
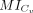and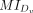 
are two vectors representing the MI values of L-R interactions inferred by a given method in the close group Cv and distant group Dv, respectively. Sigv (zero or one) denotes whether the difference in MI values between the close group Cv and distant group Dv is statistically significant (P < 0.05), as determined by the Wilcoxon rank-sum test.
Of note, for nonspatial CCC methods, we used gene expression matrix and cell type metadata as input of these tools for L-R pairs prediction but ignored the spatial coordinates in the ST data, whereas in the evaluation and benchmarking phase, we leveraged spatial information in the ST data by dividing cell pairs into close and distant groups for calculating DLRC of the predicted L-R pairs by those nonspatial CCC methods.
Benchmarking intracellular TG prediction
To benchmark the performance of different CCC methods in predicting intracellular TGs downstream from L-R interactions, namely, inferring the L-R-TG links, we gathered expression data sets perturbed for 15 cell lines, involving perturbations in ligands or receptors, spanning conditions such as breast cancer, ductal carcinoma in situ, and glioma. Supplemental Table S5 provides the information of these cell line perturbation–expression data sets. Cell line perturbation–expression data sets refer to data generated from experiments in which specific perturbations (such as knockdown, mutations, etc.) are applied to cell lines to investigate the resulting changes in gene expression. For example, data obtained from the NCBI Gene Expression Omnibus (GEO; https://www.ncbi.nlm.nih.gov/geo/) under accession number GSE120268 provides the gene expression profile of a cell line subjected to AXL receptor knockdown. The DEGs in these could serve as ground truth for evaluating the accuracy of CCC methods in predicting TGs’ responses to L-R perturbations.
In detail, the DEGs with P-values less than 0.05, calculated using the limma algorithm (Ritchie et al. 2015), were utilized as the ground truth for subsequent evaluations. If the predicted TG belongs to the DEG set of each perturbation–expression cell line, we labeled the L-R-TG as true; otherwise, it was marked as false. Then, we calculated AUPRC or AUROC by comparing the regulatory scores of L-R-TGs predicted by each CCC inference tool with the ground-truth labels. In this study, we focus on the AUPRC value because it is more appropriate than AUROC when evaluating classifiers using imbalanced data sets.
For the ST data of breast cancer and ductal carcinoma in situ, we set the tumor cells as the receiver cell type and other cell types as sender cell types to infer L-R-TG regulation. We then evaluated the prediction accuracy of each CCC method using 15 sets of cell line perturbation–expression data consisting of six ligands (i.e., CXCL12, TGFB1, DLL4, JAG1, IL6, and IGF1) and three receptors (i.e., AXL, NRP1, CXCR4) (Supplemental Table S5). For glioma ST data, we set Macros as receiver cell type and the rest of the cell types as sender cell types to infer L-R-TG regulation, because the CSF1R perturbation is performed for Macros in the corresponding cell line expression data set.
Simulation study
To test the impact of different distance-weighted L-R signaling activity on stMLnet performance, we generated 100 sets of synthetic data to compare the three different weighting functions in L-R signaling quantification. The details were described in Supplemental Text S5. The three simulation data sets are provided in Supplemental Tables S6–S11, as well as at GitHub (https://github.com/SunXQlab/stMLnet-simulation).
Software availability
The R package of stMLnet is available as Supplemental_Code_stMLnet and at GitHub (https://github.com/SunXQlab/stMLnet). The source code for the data analysis in this paper is also available as Supplemental_Code_stMLnet-AnalysisCode and at GitHub (https://github.com/SunXQlab/stMLnet-AnalysisCode). The source code for generating simulation data sets is available as Supplemental_Code_stMLnet-simulation and at GitHub (https://github.com/SunXQlab/stMLnet-simulation).
Competing interest statement
The authors declare no competing interests.
Acknowledgments
We acknowledge members in the Sun laboratory at SYSU for valuable discussion and technical assistance. X.S. was supported by grants from the National Natural Science Foundation of China (62273364, 11871070), the National Key R&D Program of China (2021YFF1200903), the Guangdong Basic and Applied Basic Research Foundation (2020B1515020047), the Guangzhou Science and Technology Programme (no. 2025A04J2562), and the Fundamental Research Funds for the Central Universities, Sun Yat-sen University (231lgbj025).
Authors contributions: L.Y. and J.C. performed research, analyzed data, and wrote the draft. Q.N. designed study and edited the paper. X.S. designed the study, performed research, analyzed data, and wrote the paper.
Footnotes
-
[Supplemental material is available for this article.]
-
Article published online before print. Article, supplemental material, and publication date are at https://www.genome.org/cgi/doi/10.1101/gr.279857.124.
- Received October 23, 2024.
- Accepted April 10, 2025.
This article is distributed exclusively by Cold Spring Harbor Laboratory Press for the first six months after the full-issue publication date (see https://genome.cshlp.org/site/misc/terms.xhtml). After six months, it is available under a Creative Commons License (Attribution-NonCommercial 4.0 International), as described at http://creativecommons.org/licenses/by-nc/4.0/.
