Geometric deep learning framework for de novo genome assembly

  1. Mile Šikić1,2
  1. 1Genome Institute of Singapore, A*STAR, Singapore 138672;
  2. 2Faculty of Electrical Engineering and Computing, University of Zagreb, 10000, Zagreb, Croatia;
  3. 3School of Computing, National University of Singapore, Singapore 117417;
  4. 4Department of Mathematics, Loyola Marymount University, Los Angeles, California 90045, USA
  • Corresponding authors: lovro_vrcek{at}gis.a-star.edu.sg, mile_sikic{at}gis.a-star.edu.sg
    •  
    Next Section

    Abstract

    The critical stage of every de novo genome assembler is identifying paths in assembly graphs that correspond to the reconstructed genomic sequences. The existing algorithmic methods struggle with this, primarily due to repetitive regions causing complex graph tangles, leading to fragmented assemblies. Here, we introduce GNNome, a framework for path identification based on geometric deep learning that enables training models on assembly graphs without relying on existing assembly strategies. By leveraging only the symmetries inherent to the problem, GNNome reconstructs assemblies from PacBio HiFi reads with contiguity and quality comparable to those of the state-of-the-art tools across several species. With every new genome assembled telomere-to-telomere, the amount of reliable training data at our disposal increases. Combining the straightforward generation of abundant simulated data for diverse genomic structures with the AI approach makes the proposed framework a plausible cornerstone for future work on reconstructing complex genomes with different degrees of ploidy and aneuploidy. To facilitate such developments, we make the framework and the best-performing model publicly available, provided as a tool that can directly be used to assemble new haploid genomes.

    De novo genome assembly provides essential insights into organism's biology and evolution by reconstructing its genome from short DNA fragments (or reads), without the access to the original genomic sequence. The assembly process is based on intricate methods on strings and graphs which were first introduced by Esko Ukkonen (Peltola et al. 1984) and later enhanced by Myers (1995), and many other scholars. This approach is known as the overlap–layout–consensus (OLC) paradigm, and the initial step is to build an assembly graph where each node represents an individual read, whereas pairs of overlapping reads are linked by an edge. The next step, layout, is tasked with placing the reads in the correct order—which is equivalent to finding a path through the graph—and is the core of the genome assembly. An alternative paradigm, based on finding paths in de Bruijn graphs, has been developed shortly after (Idury and Waterman 1995; Pevzner et al. 2001) and these two de novo assembly approaches are the most common ones today.

    The OLC method does have its challenges. Identifying a path in the graph where each node is visited only once is a nondeterministic polynomial time– (NP-)complete problem. Furthermore, due to imperfections in the overlap algorithms, certain edges are erroneously missing or falsely present. As a result, much of the research has shifted toward graph simplification, where spurious nodes and edges are eliminated (Myers 2005; Zerbino and Birney 2008; Brankovic et al. 2016; Li 2016; Vaser and Šikić 2021). In many regions, these refined methods yield unique solutions. However, they struggle to handle highly complex, repetitive regions in the graph, and resort to cutting them out. The approaches based on de Bruijn graphs are also often unable to find a unique solution in such regions. Thus, the problem of fragmentation in de novo genome assembly persists, unless different types of data and manual curation are used, leading to a slower, more expensive assembly. For more information about the computational methods for genome assembly, readers can refer to Garg (2021) and Garg et al. (2022).

    Recently, a tremendous achievement has been accomplished through a combination of both different types of data and manual curation—the complete reconstruction of the human genome (Nurk et al. 2022). This was primarily enabled by the latest advancements in the sequencing technologies, with PacBio HiFi reads and Oxford Nanopore Technologies (ONT) ultra-long reads at the forefront. While the HiFi reads are ∼15 kb in length and with an error rate of <0.5%, the ONT ultra-long reads have error rates ∼5%, but can reach the length of over 100 kb (Li and Durbin 2024). Even though using a combination of these complementary reads achieves state-of-the-art assemblies (Cheng et al. 2024), certain regions of the human genome had to be resolved manually in order to ensure correctness.

    This, and similar accomplishments enabled us to develop a novel paradigm for de novo assembly, one based on geometric deep learning (Bronstein et al. 2021). Here, we present GNNome, a framework which uses an accurate, manually curated reference genome to produce an arbitrary number of training samples, allowing us to train a model based on graph neural networks (GNNs) (Scarselli et al. 2009) and detect paths in the graph corresponding to genome reconstruction. The model presented here, which we make publicly available, yields assemblies with contiguity and quality comparable to the assemblies of the state-of-the-art tools, even though no a priori knowledge about the algorithmic simplification steps is implemented into the framework. The models trained only on HiFi graphs can produce meaningful assemblies from ONT data as well, although such direct transfer is suboptimal both for the AI methods and the algorithmic approaches. Nonetheless, the framework itself is agnostic to the underlying sequencing technology and can adapt to both HiFi and ONT assembly graphs.

    Previous SectionNext Section

    Results

    Overview of the GNNome framework

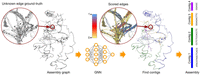
    General overview of assembling genomes with GNNome is shown in Figure 1. It starts with an assembly graph, constructed solely using either PacBio HiFi or ONT reads by an OLC-based genome assembler. Such a graph is passed to a trained model (Supplemental Fig. S1) which assigns a probability to each edge in the graph, reflecting the likelihood that the edge contributes to the optimal assembly. Subsequently, a certain number of edges is sampled as starting points for a search algorithm, which navigates through the probabilities with each walk resulting in a contig (Methods). We demonstrate that a well-trained model can confidently guide a search algorithm to avoid incorrect edges.

    Figure 1.
    View larger version:
    Figure 1.

    Overview of the assembly workflow with GNNome. An assembly graph is passed to a trained neural network which produces a probability for each edge. The probabilities are visualized in the zoomed-in region in the middle, with the color scheme that increases the visibility of the edges with probability ∼0.5. The graph shown here represents entangled Chromosomes 21 and 22 of CHM13 (Nurk et al. 2022) generated with hifiasm (Cheng et al. 2021), as well as the four longest contigs found by GNNome. The graph was visualized with Graphia (Freeman et al. 2022).

    In conventional assemblers, the assembly graphs are typically simplified with the removal of transitive edges (Myers 2005), trimming of dead ends (Li 2016), and popping of bubbles (Zerbino and Birney 2008). While these steps are generally reliable and effective, they greatly reduce the number of edges in the graph and thus diminish the amount of information conveyed in the GNN's message passing. Therefore, we use graphs before any simplifications.

    The model presented in this study was trained on a data set constructed from six chromosomes of the human HG002 reference genome (Wang et al. 2022b; Rautiainen et al. 2023) using the PBSIM3 simulator (v3.0.0) (Ono et al. 2022), while the validation data set, constructed in the same fashion, consisted of five different chromosomes (Methods). The assembly graphs were generated with hifiasm (v0.18.7-r514) (Cheng et al. 2021) as it produces state-of-the-art HiFi-only assemblies, although any OLC-based assembler could be used. Using the saved information about the reads, we implement an algorithm alike breadth-first search (BFS) that determines the label for each edge in the constructed training graphs, allowing for a supervised training of the model (Methods).

    Most of the existing algorithms for de novo assembly are hand-crafted and their parameters are tuned to several well-known genomes. Usually, it is uncertain whether the good performance transfers to other genomes as well, and fine-tuning the algorithm parameters from scratch for a new set of genomes can be tedious. Here, learning-based methods facilitate transferability, as the new genomes can easily be introduced into the training set and the model can be retrained with minimal modifications to the framework.

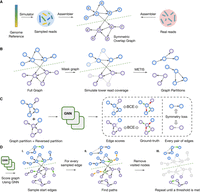
    In this work, we borrow the terminology and the definition of assembly graph from miniasm (Li 2016), where the assembly graph is symmetric since each read is represented with two nodes—one representing the original sequence, and its virtual pair representing the reverse complement of that sequence (Fig. 2A). Such a definition also ensures that the graph is directed instead of bidirected (Edmonds and Johnson 2003) as some representations are (Myers 2005), which would complicate training of the neural network. To use these symmetries during training, we devise a novel GNN layer named SymGatedGCN (Methods; Supplemental Fig. S2) and use a loss symmetric with respect to the strand (Fig. 2C). These symmetries were also addressed in several data augmentation steps during the training, such as masking and partitioning of the graph (Fig. 2B) as well as running a search algorithm over the edge probabilities (Fig. 2D). For more details, see Methods.

    Figure 2.
    View larger version:
    Figure 2.

    Schematic visualization of the training and decoding pipeline. (A) Generating and processing of the synthetic reads for training and real reads for inference. Different colors of the simulated reads indicate that their positions on the reference genome are known, unlike the positions of the real reads. The green dashed line shows the line of mirror symmetry. (B) Data augmentation during training. The grayed-out nodes and edges are the ones that are masked. (C) Training the model by computing the strand-wise symmetric loss over the edges. The shade of the edges indicates the values of the scores, while red and green colors indicate negative/positive edge labels. (D) Iterative decoding on a new graph during inference. Green nodes indicate the starting edges for walks, and orange edges represent the steps taken by a decoding algorithm. The grayed-out nodes and edges represent the ones that are previously traversed and are thus discarded in the next iteration of the decoding algorithm.

    Since our methodology is optimized for haploid genome assembly, we evaluate GNNome on the homozygous human genome CHM13 (Nurk et al. 2022) derived from a hydatidiform mole, along with the inbred genomes of Mus musculus (Hon et al. 2020) and Arabidopsis thaliana (Wang et al. 2022a), all of which are backed by high-quality reference genomes. Additionally, we evaluate on the maternal genome of Gallus gallus (Vertebrate Genome Project), for which the sequencing data were obtained with trio binning.

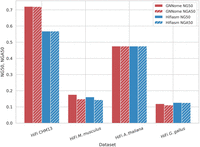
    Contiguity is one of the critical aspects of genome assembly and it is typically assessed using NG50 and NGA50 metrics. GNNome is run on the assembly graphs generated by hifiasm (Cheng et al. 2021) from HiFi reads and achieves similar or higher NG50 and NGA50 than the respective assembler while relying only on the predicted edge probabilities. The overview of these results can be seen in Figure 3. A more detailed analysis, including other measures and the comparison with the state-of-the-art tools as well as transferability to ONT data, is presented in Tables 1 and 2.

    Figure 3.
    View larger version:
    Figure 3.

    Contiguity on different haploid data sets. Comparison of contiguity of assemblies generated with GNNome and hifiasm (Cheng et al. 2021) for HiFi data. The NG50 of the assembly is defined as the sequence length of the shortest contig that, together with longer contigs covers the 50% of the total genome. The NGA50 is computed similarly like NG50, but instead of considering contigs, we consider blocks correctly aligned to the reference. Both NG50 and NGA50 are presented as proportions of the maximum achievable NG50 (NGA50) values for each respective genome.

    View this table:
    Table 1.

    Results on HiFi reads

    View this table:
    Table 2.

    Results on ONT data

    Assembling HiFi data sets

    We first evaluate GNNome (v0.4.0) along with hifiasm (v0.18.7-r514) (Cheng et al. 2021), which was used to construct the starting assembly graphs provided to GNNome, on four HiFi samples—CHM13 (Nurk et al. 2022), C57BL/6J strain of M. musculus (Hon et al. 2020), Col-0 strain of A. thaliana (Wang et al. 2022a), and G. gallus maternal genome (bGalGal1 isolate obtained from Vertebrate Genome Project). The coverages of these samples are roughly 32×, 25×, 35×, and 30×, respectively. Additionally, on the same data sets, we evaluate HiCanu (v2.2) (Nurk et al. 2020) and Verkko (v1.4.1) (Rautiainen et al. 2023), both popular de novo assemblers. Although hifiasm and Verkko can use different types of data in their pipelines, here we focus on HiFi-only assembly.

    From Table 1, we see that GNNome achieves higher NG50 and NGA50 on CHM13 and M. musculus than hifiasm by 25% and 3%, respectively. In the case of A. thaliana, the NGA50 is the same for both methods, and on G. gallus GNNome lags behind hifiasm by 11%. When evaluating on G. gallus, HiCanu encountered an error after running for 14 days. On the other three data sets, HiCanu achieved lower contiguity by 30% or more. Similarly, Verkko also achieves lower contiguity across the data sets, by more than 15%. It is also worth noting that in the case of A. thaliana, the length of the GNNome's assembly is the closest to the length of the reference. We hypothesize that the difference in the contiguity improvements GNNome achieves on CHM13 compared to other genomes stems from more similar graphs seen during the training phase. If this hypothesis proves correct, adding new, high quality, telomere-to-telomere genomes to the training set as they appear will lead to higher-quality reconstructions of nonhuman genomes. We discuss training data in Methods.

    In addition to the contiguity of the assemblies, we evaluated their gene completeness, QVs, and misassemblies. While the percentage of duplicated genes on CHM13 and A. thaliana is similar for GNNome, hifiasm, and Verkko, for HiCanu it is considerably higher. The percentage of complete genes is the lowest for Verkko, while for the other three approaches, it is similar. On M. musculus and G. gallus, however, it is GNNome that has more duplicated genes than the other three assemblers. The graph of M. musculus seems to be substantially more complex than that of CHM13, even though the M. musculus genome is slightly shorter and the coverage of the corresponding read sample is also lower. While the CHM13 graph has 2.4 million nodes and 18.5 million edges, the M. musculus graph has 3.7 million nodes and 44.6 million edges. We assume that this higher graph complexity led to lower contiguity and higher percentage of duplicated single-copy genes.

    In terms of quality, GNNome produces assemblies with slightly lower QV for CHM13 and G. gallus than hifiasm, but with a notably higher QV than assemblies of all the other tools on A. thaliana. Similarly, the number of GNNome's structural misassemblies is higher on CHM13 and G. gallus, and comparable or lower than that of other assemblers on M. musculus and A. thaliana. We analyze the misassemblies of GNNome and hifiasm on CHM13 and find that 21 out of 44 of GNNome's structural misassemblies come from Chromosomes 9 and 16 (Supplemental Fig. S3). Moreover, we observe that GNNome and hifiasm produce misassemblies on different chromosomes rather than always on the same ones. For example, on Chromosome 2 GNNome has 44 local misassemblies and hifiasm has only 1, while on Chromosome 18 hifiasm has 71 local misassemblies and GNNome has none (Supplemental Fig. S3). This analysis indicates that GNNome provides an alternative way to assemble genomes as compared to hifiasm, even though the underlying assembly graphs are the same.

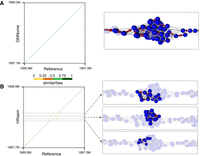
    Another notable difference between the CHM13 assemblies of GNNome and hifiasm is in the case of Chromosome 11 (Fig. 4A,B). Whereas hifiasm splits a tangle in the centromeric region into three different contigs (Fig. 4B), GNNome manages to correctly traverse the nodes in the tangle, leading to no breaks and no repetitiveness (Fig. 4A).

    Figure 4.
    View larger version:
    Figure 4.

    Assembly comparison of Chromosome 11 centromeric region. (A) GNNome's assembly of the region. (B) Hifiasm's assembly of the region. Mappings of the assembly to the reference are visualized with dotplots, which were created with D-Genies (Cabanettes and Klopp 2018)—a tool based on minimap2 (Li 2018) alignment. The nodes that comprise each contig are visualized on the right with the help of Graphia (Freeman et al. 2022). The region covered by the tangle is ∼264.5 kb long.

    Next, we analyze how different assemblers resolve regions with perfect repeats by setting up a simulation with a short, synthetic genome carrying a variable number of identical repeat units. The number of repeat units varies from 2 to 15, covering cases both where reads easily bridge the entire repetitive region and when they do not. We observe that not only do all the tested assemblers commonly produce misassemblies, but also that GNNome and hifiasm produce highly similar assemblies in nearly all scenarios (Supplemental Note S1; Supplemental Fig. S4). One exception, when their assemblies are different, is visualized in Supplemental Figure S5. This high similarity between GNNome's and hifiasm's assemblies implies that the degree to which a repeat can be resolved heavily depends on the overlap phase of the assemblers, which is shared between GNNome and hifiasm.

    It is noteworthy that the model underwent training on graphs of notably smaller sizes—graphs of individual chromosomes further partitioned with METIS (Karypis and Kumar 1998) contained roughly 50,000 nodes (Methods). Meanwhile, the full graph of the CHM13 genome graphs consists of 2.3 million nodes, showing that the model can generalize well to graphs even 50 times larger and substantially more complex.

    Assembling ONT data sets

    We investigate whether the model trained only on HiFi graphs can also generalize to ONT graphs constructed with Raven (v1.8.1) (Vaser and Šikić 2021), without ever seeing any ONT data. Although the idea seems far-fetched at first, both assemblers follow the same sequence alignment principles and construct the graphs in the same fashion, only from the different underlying data. For this purpose, we compare the GNNome's assemblies of CHM13 and Col-0 strain of A. thaliana with Raven's, starting from the same assembly graphs. The coverage of both samples is roughly 120×. Additionally, we also compare with two other popular assemblers for ONT reads, Flye (v2.9.2-b1786) (Kolmogorov et al. 2019) and Shasta (v0.11.1) (Shafin et al. 2020). The results are available in Table 2.

    On CHM13, GNNome again achieved far higher NG50 and NGA50 than any other assembler. However, we notice a gap between NG50 and NGA50, which is also accompanied by a higher number of misassemblies and lower QV. On A. thaliana NG50 and NGA50 are of similar values, and comparable to those achieved by Raven. The number of complete single-copy genes on A. thaliana is higher than for other tools, but so is the number of misassemblies. We observe that Raven also has a notably higher number of misassemblies than Flye and Shasta, and hypothesize that the large amount of GNNome's misassemblies can partially be attributed to relying on Raven's overlap phase. It is also worth noting that Flye and Shasta are not based on the OLC paradigm, but rather on de Bruijn graph approach. Both of these assemblers achieve an order of magnitude less misassemblies on both data sets, though also lower contiguity—except for Flye's assembly of CHM13, whose contiguity is comparable to Raven's.

    The results suggest that, while the general idea of the framework can be transferred to ONT reads and the assemblies produced by GNNome are still meaningful, directly transferring the model to a different type of data is not the optimal solution. This also indicates topological differences between HiFi and ONT graphs. Better results might be achieved by training the model on ONT data from scratch, but this approach is not practical from the computational standpoint. The ONT data sets typically have a sequencing depth above 100-fold, considerably higher than the HiFi ones, while also containing sequences of longer lengths. This makes the creation of the read samples, as well as generating the graphs, notably slower. Despite this, the resulting graphs are around two orders of magnitude smaller than the HiFi graphs, primarily due to many reads being discarded as contained. For example, the hifiasm-constructed graph of human Chromosome 1 from reads with 60-fold coverage has 311,000 nodes and 4.1 million edges, while the Raven-constructed graph from ONT reads with 120-fold coverage has only 5600 nodes and 22,000 edges. Thus, to have the same number of edges in the training set, for each HiFi graph we would require substantially more ONT graphs—making the data set preparation considerably more computationally expensive.

    Comparing different layout algorithms

    It might be assumed that layout algorithms are interchangeable among different genome assemblers, offering little benefit from new implementations. However, when we applied Raven's layout process to hifiasm-generated graphs, the results contradicted this assumption. According to Supplemental Table S3, the performance of Raven's algorithm significantly lagged behind hifiasm's when applied to the same assembly graphs. Specifically, the NG50 and NGA50 metrics for Raven were roughly 25%–50% lower than those achieved by hifiasm across all four evaluated genomes, demonstrating the distinct effectiveness of layout algorithms.

    This indicates that tailoring assembly algorithms to the particular type of assembly graphs may be present in the existing de novo assemblers. Worse performance of Raven's layout on hifiasm's graphs is similar to what we observed when we transferred the GNNome model trained only on hifiasm graphs to ONT data. This experiment further shows that the direct transfer of methods to a different type of data is not the optimal strategy, both for the algorithms and machine learning models.

    SymGatedGCN outperforms other GNN layers

    SymGatedGCN layer was inspired by GatedGCN (Bresson and Laurent 2017) due to its performance on several benchmarks (Dwivedi et al. 2023), but additionally includes an edge feature representation and uses a dense attention map for the edge gates (Bresson and Laurent 2019; Joshi et al. 2019). Furthermore, most off-the-shelf GNN layers are devised for undirected graphs. In our earlier efforts (Vrček et al. 2022), we noticed that this is a significant limitation when working with directed graphs. Thus, we devise a bidirectional message-passing procedure with an independent set of trainable parameters for each direction (Methods; Supplemental Fig. S2). Our findings on training on directed graphs were later more formally confirmed (Rossi et al. 2024).

    First, we test the effectiveness of SymGatedGCN against a baseline—a model that predicts the same score for every edge, resulting in random walks during the decoding. We demonstrate that random walks vastly underperform when compared to decoding with the model scores (Supplemental Note S2; Supplemental Fig. S6).

    Next, we compare the performance of SymGatedGCN to other popular GNN layers—GCN (Kipf and Welling 2016), GraphSAGE (Hamilton et al. 2017), GAT (Veličković et al. 2017), and GatedGCN (Bresson and Laurent 2017)—which were run on both directed and undirected graphs, and show consistently superior performance of SymGatedGCN (Supplemental Note S2; Supplemental Fig. S7). Additionally, we compare the influence of node and edge features and show that all the features contribute to the performance (Supplemental Note S3; Supplemental Fig. S8).

    Previous SectionNext Section

    Discussion

    This is the first attempt to solve de novo genome assembly using deep learning. Untangling the graph is the central part of the problem, and GNNs are perfect for this task—with large amounts of data and complex patterns difficult to recognize, machine learning offers an advantage over engineered algorithms.

    Lately, we have seen an increase in the genomes assembled telomere-to-telomere. Those have mostly been achieved with a combination of different types of data and often manual curation, increasing the time and the cost of the assembly. Improving single-technology assembly leads to not only lower time and cost, but also democratization of assembling new genomes, allowing the laboratories that do not have access to different data types to assemble high-quality draft references.

    It is worth noting that all assemblers yield superior results for the human genome compared to other genomes evaluated in this study, likely because of our more comprehensive understanding of human genomics and the greater abundance of such data. This highlights the critical need for intensified efforts toward high-quality genome assemblies of nonhuman eukaryotic organisms. Similarly, the GNNome model that was trained on a subset of HG002 data achieves the best results on CHM13—both human genomes. As the volume of reliable genome data continues to grow, we anticipate further enhancements in the performance of our deep learning approach, especially on nonhuman data, and foresee our method serving as a foundation for future approaches designed to leverage this expanding genome data set.

    Drawing inspiration from the pioneering telomere-to-telomere human genome assembly project, which started with a haploid genome (CHM13), our innovative approach also concentrates on haploid assembly. This strategy significantly streamlines the process relative to the assembly of higher ploidy genomes. Moreover, while there exist tools—based on classical algorithms—capable of assembling diploid and even polyploid genomes, they necessitate the use of various sequencing technologies and sequencing of parental genomes to phase the genome reliably. We believe the proposed method can greatly benefit sequence reconstruction when a homozygous or inbred sample is at hand, thereby reducing the need for a large amount of genomic material and cutting sequencing costs, which are often prohibitive. Moreover, the proposed deep learning paradigm, with its capacity to generate abundant simulated data sets and graphs combined with the usage of AI methodologies rather than relying on manual inspection and hand-crafted heuristics, is expected to significantly accelerate the development of assembly tools. This advancement will be particularly beneficial for the reconstruction of both diploid and polyploid genomes, as well as in addressing the complexities of aneuploid genomes, where chromosome numbers vary. Such variations are frequently observed in cancerous cells, making this approach highly relevant in cancer research. These more difficult tasks will be the focus of our future work.

    We demonstrate the applicability of the proposed framework to OLC graphs. However, the same approach can be applied to de Bruijn graphs as well. Moreover, many problems in computational genomics including mapping reads to pangenome graphs belong to combinational optimization problems on graphs which are usually computationally intractable, and the proposed framework can be easily adapted to them.

    Finally, even the best layout algorithms are limited by the graphs they are given. The missing edges that were not created during the graph construction cannot be introduced in the layout, at least not with the currently available approaches. The increasing popularity of geometric deep learning could open a new frontier here as well—a deep learning-based method for the overlap phase.

    Previous SectionNext Section

    Methods

    Data sets

    For training, the data were simulated from HG002 draft reference (v0.7) (downloaded from HG002 GitHub) and PBSIM3 (Ono et al. 2022). The training set consisted of Chromosomes 1, 3, 5, 9, 12, and 18, while the validation set consisted of Chromosomes 6, 11, 17, 19, and 20. The acrocentric chromosomes were not considered for either set due to their incompleteness in the draft reference. Moreover, we do not use all the chromosomes from the reference in order to better show the generalization capability of our model to the full human genome CHM13—even though not all the chromosomes were seen in either training or validation, our model consistently performs well. The chromosomes chosen for training were sampled 15 times each to produce samples of reads, which resulted in 15 hifiasm-constructed assembly graphs for each chromosome. Similarly, each chromosome in the validation set was sampled five times. We present the results of the best-performing model's predictions of edge class for each training and validation chromosome in Supplemental Table S4. Each time the sampling of the reference was different, which led to differences in the assembly graphs used for training and validation. This was a convenient way to synthetically increase the size of our data set. Note that the graph of each chromosome is considered as a separate data point—the network was not trained on a graph of a combination of reads coming from different chromosomes. We show that, while the specific choice of training and validation chromosomes does not play a major role in the performance, the number of copies of the chromosomes in the training and validation sets does, as less edges to train on leads to worse performance (Supplemental Note S4; Supplemental Fig. S9; Supplemental Table S5). Additionally, adding data from the recently assembled ape X and Y Chromosomes (Makova et al. 2024) improves the performance, even with less training examples (Supplemental Note S4; Supplemental Fig. S9; Supplemental Table S5). For parsing FASTA/Q files, we used Biopython (Cock et al. 2009).

    Labels

    The algorithm that determines the label for each edge in the training graphs consists of two steps. In the first step, it uses the positional information of each read—start, end, and strand with respect to the reference. It first identifies all edges which are not sampled from the same strand, and which do not have a valid suffix–prefix overlap. 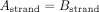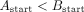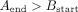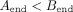More formally, for edge A → B connecting nodes A and B, the following relations must hold:Formula Formula Formula Formula

    All edges that do not satisfy these criteria are labeled as incorrect and removed from the graph. However, even in such a reduced graph where all the overlaps are valid, not every edge leads to the optimal assembly, the best example being dead ends. Thus, in the second step of the algorithm, a node with the lowest starting position is first identified and BFS is run from it. Of all the visited nodes, the one with the highest end position is picked. Then, we again run BFS, but this time backward—the opposite of the direction of the edges. The edges that are visited by both BFS runs lead to the optimal assembly of that part of the graph and are labeled as positive, while those visited by just one BFS are labeled as negative. In some cases, the assembly graphs can consist of more than one component, so this algorithm is repeated for each of them, until all the edges are labeled. In the implementation of this algorithm, we used NetworkX (Hagberg et al. 2008).

    The labels we get are highly imbalanced, with ∼99.75% of the edges being labeled as positive. This is expected as hifiasm connects nodes with an edge only if the overlap between the corresponding sequences is of high quality. Thus, most of the false overlaps stem from repetitive regions.

    SymGatedGCN

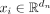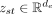    Let i and s → t be the node and the directed edge whose representations we want to update, respectively. We will use st to denote s → t for simplicity. The node features Formula and edge features Formula are first transformed into their embeddings in the latent space with linear layers. It was shown that, for low-dimensional features, it is beneficial to encode them into highly dimensional representations in a two-step process (Laurent et al. 2022). In our case, the node features are only in-degree and out-degree of each node, while the edge features are the length and the similarity of the overlap, thus dn = de = 2. 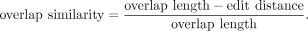Similarity is computed asFormula

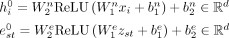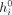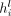    Edit distance computes an approximate string matching between a suffix and the prefix of the overlapping reads (Navarro 2001), and was obtained with Edlib (Šošić and Šikić 2017). The embedding of the features is then performed with:Formula where Formula is the initial representation of the node i, est is the initial representation of the edge st, and all the W and b are learnable parameters. The main part of the model consists of a stack of SymGatedGCN layers which update the representations of both the nodes and the edges iteratively. 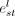Let the representations of node i and edge st at layer l be Formula and Formula. Also, let all the predecessors of node i be denoted with j and all its successors with k. 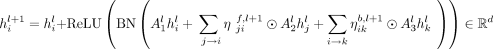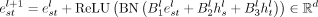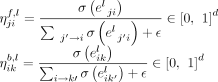Then, the node and edge representations at layer l + 1 will be computed asFormula Formula where all A, B ∈ ℝd×d are learnable parameters, ReLU stands for rectified linear unit, BN for batch normalization, and ⊙ for Hadamard product. The edge gates are defined asFormula where σ is the sigmoid function, and ϵ is a small value to avoid division by zero.

    Note that we distinguish between the messages 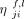Formula passed along the edges, and in the reverse direction of the edges 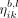Formula. The diagram of this layer, inspired by the diagram of GatedGCN (Dwivedi et al. 2023), can be seen in Supplemental Figure S2.

    Finally, we use a multilayer perceptron (MLP) on the node and edge representations produced by L SymGatedGCN layers to classify the edges. For each directed edge s → t, a probability pst is computed and trained such that it leads to the optimal assembly. The probability is given by passing the concatenated node representation of nodes s and t, as well as the edge representation of the directed edge s → t: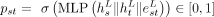Formula where σ is the sigmoid function, L denotes the last SymGatedGCN layer, and || is the concatenation operator. The diagram of the whole model can be seen in Supplemental Figure S1.

    Data augmentation during training

    All the samples of reads were initially generated with a 60-fold coverage, slightly higher than the typical sequencing depth of HiFi reads (30- to 50-fold). This allows us to use the reads more efficiently and virtually increase the size of the data set through masking (Fig. 2B). Every epoch, a subset of nodes of each 60-fold graph is masked to resemble the coverage of between 25× and 60×, with the exact number being randomly chosen. The nodes to be masked are also chosen randomly, so each graph can be reused many times as an entirely new data point. Additionally, masking of the nodes is done in a strand-wise manner to retain the symmetry of the assembly graph—either both the node and its virtual pair are masked, or neither of them is.

    Since the graphs are simulated from different chromosomes, and then even further reduced while simulating different coverages, their sizes vary greatly. Moreover, training even on the smallest graphs would exceed the graphics processing unit's (GPU's) memory. Thus, we partition them into smaller partitions of uniform sizes with METIS (Fig. 2B; Karypis and Kumar 1998). This ensures that the partitions are roughly uniform in size and that they can be loaded into a GPU memory, which would otherwise be impossible given that even the smallest graphs in the training set consist of ∼80,000 nodes and 800,000 edges. METIS partitions the graph by cutting the least number of edges needed to achieve a certain number of partitions. Since the edges connecting these partitions are cut out, the model would not make predictions on them during the training, which might hinder the predictions on the similar edges in the inference. Therefore, we add 1-hop neighborhood to each partition to tackle this issue (He et al. 2023).

    Learning objective

    The learning objective of the task is binary edge classification, where for each edge the model predicts whether it leads to the optimal assembly if traversed during the decoding. We use the symmetry of the graph and the fact that if an edge A → B leads to the optimal solution, then necessarily the edge 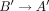Formula, connecting the virtual pairs of nodes A and B, also leads to the optimal solution on the reverse strand (Fig. 2C). 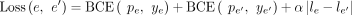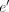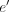More concretely, we devise a loss symmetric with respect to the strand:Formula where BCE stands for binary cross entropy, α ≥ 0 is a scalar, e and Formula are an edge and its virtual pair, whereas p, y, and l denote probability, label, and logit corresponding to the edge e or Formula.

    To compute such loss of a certain set of edges, each partition should also include their virtual pairs. This is not guaranteed by METIS. Thus, for each partition a virtual partition is also created, with all the edges reversed, to facilitate the computation of the strand-wise symmetric loss. Those two partitions are considered as a mini-batch, and the backpropagation was performed on the loss averaged over all the edges in the partition (Fig. 2C).

    Training setup

    The model used in this study had latent dimension d = 64, number of GNN layers L = 8, and three layers in the MLP classifier. Node and edge features were first linearly transformed to 16-dimensional tensors and then to the 64-dimensional latent space. This results in roughly 220,000 parameters—a small model compared to today's standards. Dropout of 0.2 was used on node representations after every GNN layer. METIS partitions consisted of roughly 50,000 nodes. The scaling factor α in the loss was 0.1. The network was trained with Adam (Kingma and Ba 2014) optimizer with an initial learning rate of 10−4 and decay of 0.95 after two consecutive epochs of no improvement in the loss on the validation set. Test set, consisting of real genomes presented in Table 1, was held out during the training. Minimal validation loss values of the trained models can be found in Supplemental Table S6. The results in Tables 1 and 2 correspond to the model with the lowest validation loss.

    The training was done on a single NVIDIA A100 GPU with 40 gigabytes (GB) of memory and took ∼9 h and 15 min. For training the model, we used Python (Van Rossum and Drake 2009), PyTorch (Paszke et al. 2019), DGL (Wang et al. 2019), and NumPy (Harris et al. 2020). DGL used 32 threads on AMD EPYC 7702 64-Core processor.

    Decoding and inference setup

    At inference, METIS is not used in order to avoid cutting any edges in the graph. Thus, we cannot load full graphs into a GPU memory, and instead run inference on a central processing unit (CPU). We perform this on AMD EPYC 7742 processor. A full graph is passed to a trained model, which produces a probability for each edge. The next step is to decode these probabilities and obtain paths representing the genome reconstruction. This is done by sampling the starting edges and running a greedy search from them. Once again, due to the nature of the graph, we opt for the symmetric approach—after sampling a certain number of starting edges, the greedy search in the forward direction is run from the target node of each chosen starting edge, whereas the backward search is run from the virtual pair of the starting edges’ source node (Fig. 2D). The nodes that are not traversed, yet they have a predecessor and a successor that are traversed consecutively, are labeled as visited and discarded—this is equivalent to traversing a transitive edge.

    We investigate how the number of starting edges in the decoding influences contiguity. As expected, the higher the number of starting edges, the better the contiguity of the genome, as there is a higher chance that a valid path will be found. However, after increasing the number of starting edges from 100 to 250, on most of the data sets the average results improve only slightly or not at all (Supplemental Note S5; Supplemental Fig. S10). Thus, 100 starting edges give a good tradeoff between the contiguity and the execution speed. The decoding is performed as long as the found contigs are longer than 70 kb. We noticed that if we keep decoding for shorter contigs, this significantly increases execution time and the number of duplications in our assemblies, stemming from the fact that we use nonreduced assembly graphs.

    Time and memory consumption

    We report the time and memory needed for executing the assembly pipeline, both for our method and for other assemblers. The comparison with the other assemblers is not entirely fair, due to the fact that we cannot independently evaluate different parts of their assembly pipelines, such as read overlap, graph construction, and layout. Thus, the time and memory consumption of the other assemblers is provided for their entire pipeline, whereas for our tool we measure each stage independently. Nevertheless, we believe that such analysis gives an insight into the complexity of our approach and the approach of the assemblers, showing that our method is not a bottleneck in the pipeline. These results can be found in Supplemental Table S7.

    Data sets analyzed

    All data used in this study are publicly available. For training, we used HG002 draft reference v0.7 which can be found at https://github.com/marbl/HG002. HiFi CHM13 data set, sequenced with the depth of ∼32×, is available from the NCBI Sequence Read Archive (SRA; https://www.ncbi.nlm.nih.gov/sra) under accession numbers SRR11292120, SRR11292121, SRR11292122, and SRR11292123. M. musculus data set, sequenced with ∼25× coverage, is available under SRA accession number SRR11606870. A. thaliana data set, sequenced with ∼157× coverage and downsampled to ∼35× with SeqKit (Shen et al. 2016) v2.5.1, is available at https://ngdc.cncb.ac.cn/gsa/browse/CRA004538/CRX257575. G. gallus HiFi data set, sequenced with ∼77× coverage was downsampled to ∼30× with SeqKit and is available https://www.genomeark.org/genomeark-all/Gallus_gallus.html. Parental Illumina short reads of G. gallus, used in trio binning, are available at the same link.

    ONT CHM13 data set is available at https://github.com/marbl/CHM13. A. thaliana ONT data set, sequenced with 388× and downsampled to ∼120× with SeqKit, is available at https://ngdc.cncb.ac.cn/gsa/browse/CRA004538/CRX257574. For computing QV, Illumina short reads were downloaded from https://www.ncbi.nlm.nih.gov/sra/?term=SRX1082031 for CHM13, https://ngdc.cncb.ac.cn/gsa/browse/CRA004538/CRX257577 for A. thaliana, and from https://www.ncbi.nlm.nih.gov/sra/SRX4381453[accn] for M. musculus (Sarsani et al. 2019).

    The CHM13 reference (v1.1) can be downloaded from https://s3-us-west-2.amazonaws.com/human-pangenomics/T2T/CHM13/assemblies/chm13.draft_v1.1.fasta.gz. The M. musculus reference GRCm39 (strain C57BL/6J) is available at https://www.ncbi.nlm.nih.gov/datasets/genome/GCF_000001635.27/.

    The A. thaliana reference Col-XJTU (strain Col-0) can be downloaded from https://download.cncb.ac.cn/gwh/Plants/Arabidopsis_thaliana_AT_GWHBDNP00000000.1/GWHBDNP000000 00.1.genome.fasta.gz. The maternal G. gallus reference (isolate bGalGal1) is available at https://www.ncbi.nlm.nih.gov/datasets/genome/GCF_016699485.2/. All the assemblies evaluated in this work are available at Zenodo (https://doi.org/10.5281/zenodo.13881591).

    Software availability

    Source code for GNNome framework (data set construction, model training, and inference), together with the model weights, is available at GitHub (https://github.com/lbcb-sci/GNNome) and as Supplemental Code. The commands we used to run the tools discussed in this paper are available in Supplemental Note S6.

    Previous SectionNext Section

    Competing interest statement

    M.Š. has been jointly funded by Oxford Nanopore Technologies and AI Singapore for the project AI-driven De Novo Diploid Assembler. The remaining authors declare no competing interests.

    Previous SectionNext Section

    Acknowledgments

    We thank Robert Vaser and Filip Tomas for help regarding Raven and Racon, especially for implementing functionality that helped our research. We also thank Haoyu Cheng who implemented the graph-printing functionality into hifiasm. Finally, we thank Raden Indah Kendarsari for comments on the manuscript. L.V. has been supported by “Young Researchers” Career Development Program DOK-2018-01-3373, ARAP scholarship awarded by A*STAR, and the core funding of Genome Institute of Singapore, A*STAR. X.B. has been supported by NUS-R-252-000-B97-133. M.S. has been supported by the SINGA scholarship awarded by A*STAR. M.Š. has been supported in part by the European Union through the European Regional Development Fund under the grant KK.01.1.1.01.0009 (DATACROSS), by the Croatian Science Foundation under the project Single genome and metagenome assembly (IP-2018-01-5886), and by the core funding of Genome Institute of Singapore, A*STAR.

    Author contributions: M.Š. and X.B. led the research. L.V., X.B., T.L., and M.Š. developed the neural network architecture, training pipeline, the decoding approach, and curated the data. L.V. implemented the framework, where X.B. contributed to the training and decoding implementation, and M.S. implemented the algorithm for determining the labels of edges in the training graphs. L.V., X.B., and M.Š. devised the experiments, while L.V. performed them and analyzed the results. M.S. composed the figures. M.Š. and K.K. devised the symmetric loss used during the training. M.Š. conceived the initial idea. L.V. and M.Š. wrote the paper, while all the other authors provided feedback.

    Previous SectionNext Section

    Footnotes

    • Received March 11, 2024.
    • Accepted October 18, 2024.

    This article is distributed exclusively by Cold Spring Harbor Laboratory Press for the first six months after the full-issue publication date (see https://genome.cshlp.org/site/misc/terms.xhtml). After six months, it is available under a Creative Commons License (Attribution-NonCommercial 4.0 International), as described at http://creativecommons.org/licenses/by-nc/4.0/.

    Previous Section
     

    References

    1. ↵
      Brankovic L, Iliopoulos CS, Kundu R, Mohamed M, Pissis SP, Vayani F. 2016. Linear-time superbubble identification algorithm for genome assembly. Theor Comput Sci 609: 374–383. doi:10.1016/j.tcs.2015.10.021
      CrossRefGoogle Scholar
    2. ↵
      Bresson X, Laurent T. 2017. Residual gated graph ConvNets. arXiv:1711.07553 [cs.LG]. http://arxiv.org/abs/1711.07553
      Google Scholar
    3. ↵
      Bresson X, Laurent T. 2019. A two-step graph convolutional decoder for molecule generation. arXiv:1906.03412 [cs.LG]. http://arxiv.org/abs/1906.03412
      Google Scholar
    4. ↵
      Bronstein MM, Bruna J, Cohen T, Veličković P. 2021. Geometric deep learning: grids, groups, graphs, geodesics, and gauges. arXiv:2104.13478 [cs.LG]. http://arxiv.org/abs/2104.13478
      Google Scholar
    5. ↵
      Cabanettes F, Klopp C. 2018. D-GENIES: dot plot large genomes in an interactive, efficient and simple way. PeerJ 6: e4958. doi:10.7717/peerj.4958
      CrossRefMedlineGoogle Scholar
    6. ↵
      Cheng H, Concepcion GT, Feng X, Zhang H, Li H. 2021. Haplotype-resolved de novo assembly using phased assembly graphs with hifiasm. Nat Methods 18: 170–175. doi:10.1038/s41592-020-01056-5
      CrossRefGoogle Scholar
    7. ↵
      Cheng H, Asri M, Lucas J, Koren S, Li H. 2024. Scalable telomere-to-telomere assembly for diploid and polyploid genomes with double graph. Nat Methods 21: 967–970. doi:10.1038/s41592-024-02269-8
      CrossRefGoogle Scholar
    8. ↵
      Cock PJA, Antao T, Chang JT, Chapman BA, Cox CJ, Dalke A, Friedberg I, Hamelryck T, Kauff F, Wilczynski B, et al. 2009. Biopython: freely available Python tools for computational molecular biology and bioinformatics. Bioinformatics 25: 1422–1423. doi:10.1093/bioinformatics/btp163
      arXivCrossRefMedlineGoogle Scholar
    9. ↵
      Dwivedi VP, Joshi CK, Luu AT, Laurent T, Bengio Y, Bresson X. 2023. Benchmarking graph neural networks. J Mach Learn Res 24: 1–48.
      Google Scholar
    10. ↵
      Edmonds J, Johnson EL. 2003. Matching: a well-solved class of integer linear programs. In Combinatorial optimization—Eureka, you Shrink!, Lecture notes in computer science (ed. Jünger M, Reinelt G), pp. 27–30. Springer, Berlin, Heidelberg.
      Google Scholar
    11. ↵
      Freeman TC, Horsewell S, Patir A, Harling-Lee J, Regan T, Shih BB, Prendergast J, Hume DA, Angus T. 2022. Graphia: a platform for the graph-based visualisation and analysis of high dimensional data. PLoS Comput Biol 18: e1010310. doi:10.1371/journal.pcbi.1010310
      CrossRefMedlineGoogle Scholar
    12. ↵
      Garg S. 2021. Computational methods for chromosome-scale haplotype reconstruction. Genome Biol 22: 101. doi:10.1186/s13059-021-02328-9
      CrossRefMedlineGoogle Scholar
    13. ↵
      Garg S, Balboa R, Kuja J. 2022. Chromosome-scale haplotype-resolved pangenomics. Trends Genet 38: 1103–1107. doi:10.1016/j.tig.2022.06.011
      CrossRefMedlineGoogle Scholar
    14. ↵
      Hagberg AA, Schult DA, Swart PJ. 2008. Exploring network structure, dynamics, and function using NetworkX. In Proceedings of the 7th Python in Science Conference (ed. Varoquaux G, Vaught T, Millman J), pp. 11–15, Pasadena, CA.
      Google Scholar
    15. ↵
      Hamilton WL, Ying R, Leskovec J. 2017. Inductive representation learning on large graphs. In 31st Conference on Neural Information Processing Systems (NIPS 2017), Long Beach, CA. Advances in neural information processing systems, Vol. 30.
      Google Scholar
    16. ↵
      Harris CR, Millman KJ, van der Walt SJ, Gommers R, Virtanen P, Cournapeau D, Wieser E, Taylor J, Berg S, Smith NJ, et al. 2020. Array programming with NumPy. Nature 585: 357–362. doi:10.1038/s41586-020-2649-2
      CrossRefMedlineGoogle Scholar
    17. ↵
      He X, Hooi B, Laurent T, Perold A, LeCun Y, Bresson X. 2023. A generalization of ViT/MLP-mixer to graphs. In Proceedings of the 40th International Conference on Machine Learning, Honolulu, HI. PMLR 202: 12724–12745. https://github.com/XiaoxinHe/Graph-ViT-MLPMixer
      Google Scholar
    18. ↵
      Hon T, Mars K, Young G, Tsai Y-C, Karalius JW, Landolin JM, Maurer N, Kudrna D, Hardigan MA, Steiner CC, et al. 2020. Highly accurate long-read HiFi sequencing data for five complex genomes. Sci Data 7: 399. doi:10.1038/s41597-020-00743-4
      CrossRefGoogle Scholar
    19. Huang N, Li H. 2023. compleasm: a faster and more accurate reimplementation of BUSCO. Bioinformatics 39: btad595. doi:10.1093/bioinformatics/btad595
      CrossRefMedlineGoogle Scholar
    20. ↵
      Idury RM, Waterman MS. 1995. A new algorithm for DNA sequence assembly. J Comput Biol 2: 291–306. doi:10.1089/cmb.1995.2.291
      CrossRefMedlineGoogle Scholar
    21. ↵
      Joshi CK, Laurent T, Bresson X. 2019. An efficient graph convolutional network technique for the Travelling Salesman Problem. arXiv:1906.01227 [cs.LG]. http://arxiv.org/abs/1906.01227
      Google Scholar
    22. ↵
      Karypis G, Kumar V. 1998. A fast and high quality multilevel scheme for partitioning irregular graphs. SIAM J Sci Comput 20: 359–392. doi:10.1137/S1064827595287997
      CrossRefGoogle Scholar
    23. ↵
      Kingma DP, Ba J. 2014. Adam: a method for stochastic optimization. arXiv:1412.6980 [cs.LG]. http://arxiv.org/abs/1412.6980
      Google Scholar
    24. ↵
      Kipf TN, Welling M. 2016. Semi-supervised classification with graph convolutional networks. arXiv:1609.02907 [cs.LG]. http://arxiv.org/abs/1609.02907
      Google Scholar
    25. ↵
      Kolmogorov M, Yuan J, Lin Y, Pevzner PA. 2019. Assembly of long, error-prone reads using repeat graphs. Nat Biotechnol 37: 540–546. doi:10.1038/s41587-019-0072-8
      CrossRefMedlineGoogle Scholar
    26. ↵
      Laurent T, von Brecht JH, Bresson X. 2022. Long-tailed learning requires feature learning. arXiv:2205.14553 [cs.LG]. http://arxiv.org/abs/2205.14553
      Google Scholar
    27. ↵
      Li H. 2016. Minimap and miniasm: fast mapping and de novo assembly for noisy long sequences. Bioinformatics 32: 2103–2110. doi:10.1093/bioinformatics/btw152
      CrossRefMedlineGoogle Scholar
    28. ↵
      Li H. 2018. Minimap2: pairwise alignment for nucleotide sequences. Bioinformatics 34: 3094–3100. doi:10.1093/bioinformatics/bty191
      CrossRefMedlineGoogle Scholar
    29. ↵
      Li H, Durbin R. 2024. Genome assembly in the telomere-to-telomere era. Nat Rev Genet 25: 658–670. doi:10.1038/s41576-024-00718-w
      CrossRefGoogle Scholar
    30. Li H, Feng X, Chu C. 2020. The design and construction of reference pangenome graphs with minigraph. Genome Biol 21: 265. doi:10.1186/s13059-020-02168-z
      CrossRefMedlineGoogle Scholar
    31. ↵
      Makova KD, Pickett BD, Harris RS, Hartley GA, Cechova M, Pal K, Nurk S, Yoo D, Li Q, Hebbar P, et al. 2024. The complete sequence and comparative analysis of ape sex chromosomes. Nature 630: 401–411. doi:10.1038/s41586-024-07473-2
      CrossRefGoogle Scholar
    32. Mikheenko A, Prjibelski A, Saveliev V, Antipov D, Gurevich A. 2018. Versatile genome assembly evaluation with QUAST-LG. Bioinformatics 34: i142–i150. doi:10.1093/bioinformatics/bty266
      CrossRefMedlineGoogle Scholar
    33. ↵
      Myers EW. 1995. Toward simplifying and accurately formulating fragment assembly. J Comput Biol 2: 275–290. doi:10.1089/cmb.1995.2.275
      CrossRefMedlineGoogle Scholar
    34. ↵
      Myers EW. 2005. The fragment assembly string graph. Bioinformatics 21 Suppl 2: ii79–ii85. doi:10.1093/bioinformatics/bti1114
      CrossRefGoogle Scholar
    35. ↵
      Navarro G. 2001. A guided tour to approximate string matching. ACM Comput Surv 33: 31–88. doi:10.1145/375360.375365
      CrossRefGoogle Scholar
    36. ↵
      Nurk S, Walenz BP, Rhie A, Vollger MR, Logsdon GA, Grothe R, Miga KH, Eichler EE, Phillippy AM, Koren S. 2020. HiCanu: accurate assembly of segmental duplications, satellites, and allelic variants from high-fidelity long reads. Genome Res 30: 1291–1305. doi:10.1101/gr.263566.120
      Abstract/FREE Full Text
    37. ↵
      Nurk S, Koren S, Rhie A, Rautiainen M, Bzikadze AV, Mikheenko A, Vollger MR, Altemose N, Uralsky L, Gershman A, et al. 2022. The complete sequence of a human genome. Science 376: 44–53. doi:10.1126/science.abj6987
      CrossRefMedlineGoogle Scholar
    38. ↵
      Ono Y, Hamada M, Asai K. 2022. PBSIM3: a simulator for all types of PacBio and ONT long reads. NAR Genom Bioinform 4: lqac092. doi:10.1093/nargab/lqac092
      CrossRefGoogle Scholar
    39. ↵
      Paszke A, Gross S, Massa F, Lerer A, Bradbury J, Chanan G, Killeen T, Lin Z, Gimelshein N, Antiga L, et al. 2019. PyTorch: an imperative style, high-performance deep learning library. In Advances in neural information processing systems (ed. Wallach H, et al.), Vol. 32, pp. 8024–8035. Curran Associates, Inc., Newry, Northern Ireland, UK. https://proceedings.neurips.cc/paper/2019/hash/bdbca288fee7f92f2bfa9f7012727740-Abstract.html
      Google Scholar
    40. ↵
      Peltola H, Söderlund H, Ukkonen E. 1984. SEQAID: a DNA sequence assembling program based on a mathematical model. Nucleic Acids Res 12: 307–321. doi:10.1093/nar/12.1Part1.307
      CrossRefMedlineGoogle Scholar
    41. ↵
      Pevzner PA, Tang H, Waterman MS. 2001. An Eulerian path approach to DNA fragment assembly. Proc Natl Acad Sci 98: 9748–9753. doi:10.1073/pnas.171285098
      Abstract/FREE Full Text
    42. ↵
      Rautiainen M, Nurk S, Walenz BP, Logsdon GA, Porubsky D, Rhie A, Eichler EE, Phillippy AM, Koren S. 2023. Telomere-to-telomere assembly of diploid chromosomes with Verkko. Nat Biotechnol 41: 1474–1482. doi:10.1038/s41587-023-01662-6
      CrossRefGoogle Scholar
    43. ↵
      Rossi E, Charpentier B, Di Giovanni F, Frasca F, Günnemann S, Bronstein M. 2024. Edge directionality improves learning on heterophilic graphs. In Proceedings of the Second Learning on Graphs Conference. PMLR 231: 25:1–25:27.
      Google Scholar
    44. ↵
      Sarsani VK, Raghupathy N, Fiddes IT, Armstrong J, Thibaud-Nissen F, Zinder O, Bolisetty M, Howe K, Hinerfeld D, Ruan X, et al. 2019. The genome of C57BL/6J “Eve”, the mother of the laboratory mouse genome reference strain. G3 (Bethesda) 9: 1795–1805. doi:10.1534/g3.119.400071
      Abstract/FREE Full Text
    45. ↵
      Scarselli F, Gori M, Tsoi AC, Hagenbuchner M, Monfardini G. 2009. The graph neural network model. IEEE Trans Neural Netw 20: 61–80. doi:10.1109/TNN.2008.2005605
      CrossRefMedlineGoogle Scholar
    46. ↵
      Shafin K, Pesout T, Lorig-Roach R, Haukness M, Olsen HE, Bosworth C, Armstrong J, Tigyi K, Maurer N, Koren S, et al. 2020. Nanopore sequencing and the Shasta toolkit enable efficient de novo assembly of eleven human genomes. Nat Biotechnol 38: 1044–1053. doi:10.1038/s41587-020-0503-6
      CrossRefMedlineGoogle Scholar
    47. ↵
      Shen W, Le S, Li Y, Hu F. 2016. SeqKit: a cross-platform and ultrafast toolkit for FASTA/Q file manipulation. PLoS One 11: e0163962. doi:10.1371/journal.pone.0163962
      CrossRefMedlineGoogle Scholar
    48. ↵
      Šošić M, Šikić M. 2017. Edlib: a C/C++ library for fast, exact sequence alignment using edit distance. Bioinformatics 33: 1394–1395. doi:10.1093/bioinformatics/btw753
      CrossRefMedlineGoogle Scholar
    49. ↵
      Van Rossum G, Drake FL Jr.. 2009. Python 3 reference manual. CreateSpace, Scotts Valley, CA. https://dl.acm.org/doi/book/10.5555/1593511
      Google Scholar
    50. ↵
      Vaser R, Šikić M. 2021. Time- and memory-efficient genome assembly with Raven. Nat Comput Sci 1: 332–336. doi:10.1038/s43588-021-00073-4
      CrossRefMedlineGoogle Scholar
    51. Vaser R, Sović I, Nagarajan N, Šikić M. 2017. Fast and accurate de novo genome assembly from long uncorrected reads. Genome Res 27: 737–746. doi:10.1101/gr.214270.116
      Abstract/FREE Full Text
    52. ↵
      Veličković P, Cucurull G, Casanova A, Romero A, Liò P, Bengio Y. 2017. Graph attention networks. arXiv:1710.10903 [stat.ML]. http://arxiv.org/abs/1710.10903
      Google Scholar
    53. ↵
      Vrček L, Bresson X, Laurent T, Schmitz M, Šikić M. 2022. Learning to untangle genome assembly with graph convolutional networks. arXiv:2206.00668 [q-bio.GN]. http://arxiv.org/abs/2206.00668
      Google Scholar
    54. ↵
      Wang M, Zheng D, Ye Z, Gan Q, Li M, Song X, Zhou J, Ma C, Yu L, Gai Y, et al. 2019. Deep Graph Library: a graph-centric, highly-performant package for graph neural networks. arXiv:1909.01315 [cs.LG]. http://arxiv.org/abs/1909.01315
      Google Scholar
    55. ↵
      Wang B, Yang X, Jia Y, Xu Y, Jia P, Dang N, Wang S, Xu T, Zhao X, Gao S, et al. 2022a. High-quality Arabidopsis thaliana genome assembly with nanopore and HiFi long reads. Genomics Proteomics Bioinformatics 20: 4–13. doi:10.1016/j.gpb.2021.08.003
      CrossRefGoogle Scholar
    56. ↵
      Wang T, Antonacci-Fulton L, Howe K, Lawson HA, Lucas JK, Phillippy AM, Popejoy AB, Asri M, Carson C, Chaisson MJP, et al. 2022b. The Human Pangenome Project: a global resource to map genomic diversity. Nature 604: 437–446. doi:10.1038/s41586-022-04601-8
      CrossRefMedlineGoogle Scholar
    57. ↵
      Zerbino DR, Birney E. 2008. Velvet: algorithms for de novo short read assembly using de Bruijn graphs. Genome Res 18: 821–829. doi:10.1101/gr.074492.107
      Abstract/FREE Full Text
    | Table of Contents

    This Article

    1. Published in Advance October 29, 2024, doi: 10.1101/gr.279307.124 Genome Res. 35: 839-849 © 2025 Vrček et al.; Published by Cold Spring Harbor Laboratory Press

    Article Category

    ORCID

    1. Profile for Vrček, L.http://orcid.org/0000-0001-6977-4002
    2. Profile for Šikić, M.http://orcid.org/0000-0002-8370-0891

    Share

    Preprint Server



    Navigate This Article

    Current Issue

    1. February 2026, 36 (2)
    1. Current Issue
    1. Alert me to new issues of Genome Research