Single-cell methylation sequencing data reveal succinct metastatic migration histories and tumor progression models
- Yuelin Liu1,2,3,9,
- Xuan Cindy Li1,4,9,
- Farid Rashidi Mehrabadi1,5,6,9,
- Alejandro A. Schäffer1,
- Drew Pratt7,
- David R. Crawford1,4,8,
- Salem Malikić1,
- Erin K. Molloy2,3,
- Vishaka Gopalan1,
- Stephen M. Mount8,
- Eytan Ruppin1,
- Kenneth D. Aldape7 and
- S. Cenk Sahinalp1
- 1Cancer Data Science Laboratory, Center for Cancer Research, National Cancer Institute, National Institutes of Health, Bethesda, Maryland 20892, USA;
- 2Department of Computer Science, University of Maryland, College Park, Maryland 20742, USA;
- 3Center for Bioinformatics and Computational Biology, University of Maryland, College Park, Maryland 20742, USA;
- 4Program in Computational Biology, Bioinformatics, and Genomics, University of Maryland, College Park, Maryland 20742, USA;
- 5Department of Computer Science, Indiana University, Bloomington, Indiana 47408, USA;
- 6Laboratory of Human Carcinogenesis, Center for Cancer Research, National Cancer Institute, National Institutes of Health, Bethesda, Maryland 20892, USA;
- 7Laboratory of Pathology, Center for Cancer Research, National Cancer Institute, National Institutes of Health, Bethesda, Maryland 20892, USA;
- 8Department of Cell Biology and Molecular Genetics, University of Maryland, College Park, Maryland 20742, USA
-
↵9 These authors contributed equally to this work.
Abstract
Recent studies exploring the impact of methylation in tumor evolution suggest that although the methylation status of many of the CpG sites are preserved across distinct lineages, others are altered as the cancer progresses. Because changes in methylation status of a CpG site may be retained in mitosis, they could be used to infer the progression history of a tumor via single-cell lineage tree reconstruction. In this work, we introduce the first principled distance-based computational method, Sgootr, for inferring a tumor's single-cell methylation lineage tree and for jointly identifying lineage-informative CpG sites that harbor changes in methylation status that are retained along the lineage. We apply Sgootr on single-cell bisulfite-treated whole-genome sequencing data of multiregionally sampled tumor cells from nine metastatic colorectal cancer patients, as well as multiregionally sampled single-cell reduced-representation bisulfite sequencing data from a glioblastoma patient. We show that the tumor lineages constructed reveal a simple model underlying tumor progression and metastatic seeding. A comparison of Sgootr against alternative approaches shows that Sgootr can construct lineage trees with fewer migration events and with more in concordance with the sequential-progression model of tumor evolution, with a running time a fraction of that used in prior studies. Lineage-informative CpG sites identified by Sgootr are in inter-CpG island (CGI) regions, as opposed to intra-CGIs, which have been the main regions of interest in genomic methylation-related analyses.
The problem of algorithmically inferring a phylogenetic tree that may be interpreted as a tumor progression history from multiple samples per patient has been widely studied in the past decade. Methods developed to address this problem include TuMult (Letouzé et al. 2010), PhyloSub (Jiao et al. 2014), PyClone (Roth et al. 2014), SciClone (Miller et al. 2014), MEDICC (Schwarz et al. 2014), PhyloWGS (Deshwar et al. 2015), AncesTree (El-Kebir et al. 2015), CITUP (Malikic et al. 2015), Canopy (Jiang et al. 2016), Treeomics (Reiter et al. 2017), MACHINA (El-Kebir et al. 2018), and others. Tumor phylogenies and the implied intratumor heterogeneity are occasionally used to make clinical decisions (Beerenwinkel et al. 2015). For understanding basic cancer biology, a key question is whether tumor progression is more branched (leading to a wider and shallower tree) or more linear (leading to a narrower and deeper tree) (Turajlic and Swanton 2016). For metastases, results on the question of branched versus linear evolution are mixed (e.g., Brastianos et al. 2015; Gundem et al. 2015; Zhao et al. 2016). Hong et al. (2015) showed that results are sensitive to the method used for phylogeny inference. Complicating matters further is that most of the methods listed above use bulk sequencing data as input, and El-Kebir et al. (2018) showed that under reasonable models, the optimal phylogeny from bulk sequencing data may not be unique. Therefore, recent efforts have looked beyond bulk sequencing data to elucidate the progression history of a tumor. In a major step toward this goal, Quinn et al. (2021) introduced technologies for cell lineage tracing and applied those technologies to study single-cell data in xenograft tumor models. To our knowledge, lineage tracing is not yet possible in human cancer samples, but analysis of single-cell data of other types is possible.
The recent rise of single-cell sequencing technology empowers more accurate tumor lineage inference by allowing the examination of intratumor heterogeneity at cellular resolution. However, because single-cell sequencing data are derived from a limited amount of genetic material, the signals obtained are scarcer than those from bulk sequencing (Lähnemann et al. 2020). Genomic events commonly used in bulk tumor lineage inference, such as single-nucleotide variations (SNVs) and copy number aberrations (CNAs), are observed with less frequency or are measured with less confidence in single-cell data sets. Single-cell tumor lineage inferences using SNVs often suffer from false negatives in the data sets, which calls for data imputation or aggregation; on the other hand, tumor lineage inference using CNAs called from single-cell sequencing data often involves ambiguities in the determination of chromosomal breakpoints that may mislead the conclusion. DNA methylation, the addition of a methyl group to cytosine, which results in the formation of 5-methylcytosine (5mC) especially in the context of CpG sites, is an epigenetic marker that has been extensively studied for its role in regulating gene expression and maintaining cellular memory (Kim and Costello 2017). As Gaiti et al. (2019) importantly noted, the methylation maintenance machinery has been shown to have an error rate four orders of magnitude higher than that for DNA replication (Ushijima et al. 2003; Biezuner et al. 2016) and therefore may provide a greater amount of observable evidence for tumor evolution than alternative data modalities, which is a critical asset especially in the single-cell context.
Recent studies have leveraged CpG methylation in single cells sampled from colorectal cancer (CRC) (Bian et al. 2018), chronic lymphocitic leukemia (CLL) (Gaiti et al. 2019), glioblastoma (GBM), and IDH-mutant glioma (Chaligne et al. 2021) tumors to construct lineages, showing CpG methylation to be a valuable signal for lineage inference. Gabbutt et al. (2022) recently developed a method to sample methylation data in single gastrointestinal crypts (containing multiple cells) and a mathematical method to estimate the number of stem cells in each crypt. They referred to the problem of estimating the stem cell replacement rate as “lineage tracing,” but that is different from the tumor phylogenetics problems we address here. More relevant to our work, Gabbutt et al. (2022) established that some CpG sites vary their methylation state at a predictable time rate, which exemplifies the potential of using fine-grained methylation data to make biological inferences.
There are two main challenges in constructing single-cell CpG methylation-based tumor lineage trees. First, detailed examination reveals that data obtained via single-cell bisulfite sequencing (scBS-seq) (Bian et al. 2018), single-cell reduced representation bisulfite sequencing (scRRBS) (Guo et al. 2013, 2015), or multiplexed scRRBS (MscRRBS) (Gaiti et al. 2019) protocols show high levels of sparsity. Cells with subpar bisulfite conversion rates have information at few CpG sites, and of the millions of unique CpG sites across all cells in a data set, less than one out of a hundred are sequenced in a sufficient number of cells to be useful in lineage reconstruction. Furthermore, even when a CpG site is sequenced in a cell, it is oftentimes covered by less than a few sequencing reads, which is not likely to capture heterozygosity in aneuploid cancers.
Besides sparsity, another key challenge is that not all CpG sites have their methylation statuses stably retained during tumor evolution. In particular, Meir et al. (2020) posited two models of methylation dynamics: mixture, in which the methylation status of a CpG site is resampled (from the parental status) in each cell replication, and persistency, in which that is an exact copy of the parent cell. It is the CpG sites whose status follows the persistency model that would be informative in tumor lineage reconstruction because the maintenance of information from the parental generation is the necessary condition for the infinite sites assumption (Kimura 1969; Ma et al. 2008) and Dollo parsimony (Dollo 1893), which form the basis for tumor lineage inference tools based on mutation profiles. However, as of now, there is no known set of CpG sites that follow either inheritance model, highlighting the necessity to perform intentional CpG site selection while reconstructing tumor lineages by CpG methylation.
To address these two challenges, in this work, we introduce Single-cell Genomic methylatiOn tumOr Tree Reconstruction (Sgootr), the first distance-based computational method to jointly select informative CpG sites and reconstruct tumor lineages from single-cell methylation data.
Methods
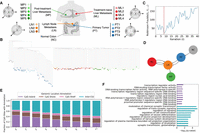
Sgootr (Fig. 1) consists of five components: (1) optional biclustering of cells and sites for reducing sparsity-induced noise, (2) likelihood-based sequencing error correction accounting for copy number estimates, (3) expected distance calculation between cell pairs for tree construction, (4) pruning of CpG sites according to a tree-based methylation status persistence measure, and (5) inference of migration history from the lesion-labeled tree leveraging prior knowledge on migration patterns. Components 3 and 4 are iteratively applied. The code for this work is available on GitHub as a Snakemake (Mölder et al. 2021) workflow. Results from this work are reproducible, and intermediate experiment outputs of Sgootr are available for further analysis.
Overview of Sgootr. Sgootr leverages single-cell methylation sequencing data from tumor samples, incorporating copy number information when available, to jointly infer a single-cell tumor lineage tree and identify CpG sites that may harbor lineage-informative methylation changes.
Biclustering of cells and sites for reducing sparsity-induced noise
Sgootr requires a fairly accurate estimate of the differences between the methylation status of distinct CpG sites across
all cell pairs. Before submitting the input data set to Sgootr, it is advisable that one filters out cells for which the number
of CpG sites with nonzero read coverage is low and CpG sites with nonzero coverage in only a few cells. For example, for the
Bian et al. (2018) metastatic CRC data set, which we will analyze further in depth in the Results section, we apply the following heuristic
filters to the cells and sites: (1) Among all input cells, remove low-quality ones with coverage in fewer than 4 million CpG
sites, and (2) remove CpG sites covered in less than 
of the remaining cells. For that particular data set, we additionally removed CpG sites on sex chromosomes, which may confound
the findings, and in Chromosome 21 peri-centromeric regions (hg19, Chr 21: 9,825,000–9,828,000), which we discovered to be
an overlooked alignment artifact. After filtering the input for reducing sparsity, we perform sequencing error correction
as described in the following section. Because this may further introduce sparsity, in an additional post error correction
step, we may remove sites covering 
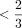of cells and then remove cells with coverage in 
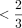of the remaining CpG sites. Overall, our filtering approach aims to make sure that the cells remaining are well covered and
that each cell pair has at least 
of the selected CpG sites as shared dimensions along which cell-to-cell distance can be measured.
Our main results on the Bian et al. (2018) data set show the heuristic filtering scheme described above is effective in practice; however, in principle, the filtering
of cells and CpG sites should ideally be coordinated in order to minimize information loss. For that purpose, we present an
integer linear program (ILP)–based biclustering formulation as follows. Let the site coverage data be represented in a cell-by-site
matrix Mv×u, where v is the number of cells and u is the number of CpG sites; mij = 1 if site j is covered (by at least one read) in cell i, and mij = 0 otherwise. Let α and β, respectively, be the specified fraction of cells and sites to be kept. Given M, α, and β, we wish to compute a biclustering, namely, a selection of rows of columns, of M,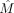 
, so that we maximize the number of CpG sites covered in the resulting 
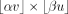submatrix in which rows and columns, respectively, correspond to the selected cells and sites.
To solve this biclustering problem, let C ∈ {0, 1}v, S ∈ {0, 1}u be (unknown) binary vectors, respectively, indicating whether a cell or site is kept. In addition, let A ∈ {0, 1}v×u denote (unknown) binary matrix such that aij = 1 if and only if ci = 1 and sj = 1 (i.e., if cell i and site j are both kept). The ILP formulation is
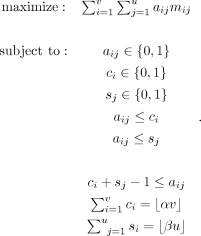The output submatrix 
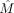is obtained by taking cells {i|ci = 1} and sites {j|sj = 1} from M.
We implement the above formulation as an optional step in our software using the Gurobi ILP solver, a licensed software that is free to use for academic purposes (https://www.gurobi.com). The performance of our implementation in terms of run time, memory, and accuracy (i.e., optimality gap), with respect to the input size and other parameters, and a strategy on setting α and β are explored in detail in Supplemental Section S1 (Supplemental Tables S1, S2; Supplemental Figs. S1–S3). For a typical computational environment, the current implementation of the biclustering formulation may not be practical for the scale of the single-cell CpG methylation data sets analyzed in this study (see Supplemental Sec. S1). However, because for given α and β values the ILP formulation produces a submatrix no sparser than that produced by the heuristic filters, it should be the preferred choice whenever it is feasible. In Supplemental Section S1, we show that memory consumption is likely to be the bottleneck and provide a way to estimate memory consumption of our biclustering implementation given the size of the input so that the users may determine whether performing biclustering may be appropriate for their own data sets of interest. It is intuitive that the single-cell tumor lineage tree constructed from input data resulting from biclustering is as reliable, if not more reliable, than the tree constructed from heuristically filtered data, because the former will be constructed from at least as much information from the unfiltered data as the latter. Improving the run time and memory efficiency of our ILP implementation and devising alternative strategies to perform biclustering are among our future objectives.
Likelihood-based sequencing error correction accounting for copy number estimates
Errors in sequencing may provide false evidence for an underlying allele methylation status different from the truth. A common strategy used in prior works to mitigate the effect of such sequencing errors in downstream tasks is to use the 90% rule, which assigns a CpG site in a cell the methylation status with support from 90% of the reads available for the site in the cell and discards the site if no status can be assigned (Bian et al. 2018; Gaiti et al. 2019; Chaligne et al. 2021). This approach has two drawbacks. First, the binarization of methylation status disallows heterozygosity. Second, although there are high levels of copy number gains in some cancer types, this approach does not distinguish between having reads sampled from two underlying alleles and having reads sampled from many. For a CpG site in a cell, we would like a copy number–aware way to determine, if we observe both reads with the site methylated and reads with it unmethylated, whether they are truly sampled from heterozygous alleles or they are sampled from homozygous alleles and the methylation statuses on the disagreeing reads need to be corrected.
To this end, we present a maximum log-likelihood-based approach to correct likely errors in methylation reads, incorporating
site copy number estimates in each cell (Algorithm 1). For a CpG site in a cell, given n ≥ 0 reads with a methylated status, m ≥ 0 reads with an unmethylated status, its copy number c, and sequencing error probability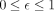 
(which we set to .01 in our experiments to proxy the per-base sequencing error rate in Illumina sequencing instruments),
we can enumerate the likelihood of having drawn the observed reads from all possible underlying allele statuses, letting 0
≤ γ ≤ c be the number of alleles with the CpG site methylated. Note that in Algorithm 1, 1c and 0c, respectively, denote the events that all c alleles are methylated and unmethylated; 
denotes the event in which γ alleles are methylated and c − γ are not.
Sequencing error correction accounting for copy number
n,m ← number of methylated and unmethylated reads for a CpG site in a cell, respectively
c ← copy number for the CpG site in the cell
ϵ ← sequencing error probability
function SequencingErrorCorrection(
)
if c = 0 then return None ▹ site is discarded in case of deletion event
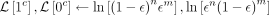
for 0 < γ < c do
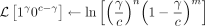
end for
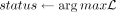
if [status = 1c OR status = 0c] AND [n ≠ 0 AND m ≠ 0] then
if n > m then n, m ← n + m, 0
else if n < m then m, n ← n + m, 0
else return None ▹ site is discarded if correction is impossible
end if
return n, m
end function
Sequencing error correction takes place when we have n > 0 and m > 0, but the allele status with the highest log-likelihood is homozygous. In that case, we correct the reads with the minority methylation status to the majority one. When c = 1, the site will implicitly be identified as homozygous, and the methylation status of any read that does not conform to the majority allele will be corrected. In the case in which sequencing error is needed yet n = m, which will likely happen for c = 1, the CpG site is discarded. In case copy number information is not available, one can assume an appropriate (uninformative) copy number for all sites in all cells (e.g., c = 2 for diploid). Sex chromosomes are always excluded from our analysis. We use the sequence error–corrected reads for pairwise distance estimation between cells, as described in the following section.
Expected distance calculation between cell pairs for tree construction
In this section, we present a formulation for computing the expected distance between two cells given their respective copy number and (sequencing error–corrected) reads. We consider such a formulation with the goal of correcting for the potential bias contributed by low-coverage CpG sites. Intuitively, this distance measure serves as an estimate for the expected proportion of methylation statuses altered across all CpG sites between a cell pair.
Given a cell, let the copy number at a CpG site be c, and we have 0 ≤ γ ≤ c alleles with the CpG site methylated and c − γ alleles with the CpG site unmethylated. To allow modeling preferential allele sampling based on site methylation status as
previously observed (Olova et al. 2018), we additionally introduce parameter p, probability of drawing a read from the allele with the CpG site methylated given a pair of alleles heterozygous for the
site. We set p to the uninformative 0.5 in our experiments (for when to choose alternative values, see Supplemental Sec. S8). Then, we can compute the probability of drawing from an allele with the CpG site methylated by normalizing over all alleles
(Equation 1):
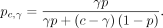(1)
It follows that the probability of drawing from an allele with the CpG site unmethylated is 1 − pc,γ.
Consider the case in which we observe n reads at a CpG site for a cell, and all n reads are methylated for the site. Let the copy number at the site for the cell be c. The probability of sampling all n methylated reads from c alleles with the CpG site methylated (i.e., γ = c) is P(reads|1c) = 1; here, 1c is the event that in all c copies, the CpG site is methylated, and reads is the event that all n sampled reads are methylated. The probability of drawing all n methylated reads from c alleles with the CpG site unmethylated (i.e., γ = 0) is P(reads|0c) = 0. To compute the probability of drawing n methylated reads from c alleles with mixed methylation status for the site, we need to sum the probabilities over all other possible values of γ, the number of alleles with the site methylated, assuming that all other possible values of γ are equally likely and that when there is a copy number loss (i.e., c = 1), the formulation assigns only nonzero probability to a homozygous combined allele status:
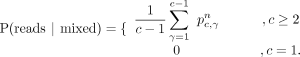Given user-defined prior probabilities P(1c), P(0c), and P(mixed), which we all set to the uninformative 0.33 in our experiments (for when to choose alternative values, see
Supplemental Sec. S8), let a = P(reads | 1c)P(1c) + P(reads | mixed)P(mixed) + P(reads | 0c)P(0c). Then, we apply Bayes’ theorem to get the likelihood of any allele status given the observed reads (Equations 2):
(2)
In the case in which the n reads all have the CpG site unmethylated, the three values can be computed similarly with P(reads|1c) = 0 and P(reads|0c) = 1. In the case that we observe among the n reads both ones with the CpG site methylated and ones with the site unmethylated, we have P(mixed | reads) = 1 and P(1c|reads) = P(0c|reads) = 0. Then, for a given CpG site s in cell A and cell B, the respective copy numbers cA,s, cB,s, and respective reads, we can compute the expected distance over the possible combinations of allele status between the two
cells at s (Equation 3):
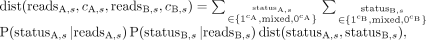(3)
where dist(11,11) = dist(10,10) = dist(00,00) = 0, dist(11,10) = dist(10,11) = dist(00,10) = dist(10,00) = 0.5, and dist(11,00)
= dist(00,11) = 1.
The total expected distance between cells A and B can now be computed with some distance function over the vector of expected
distances over all shared sites. The L1 norm normalized by the number of shared sites is computed via Equation 4. The use of shared CpG sites between pairs of single cells to estimate their distances was established by Hui et al. (2018):
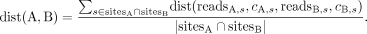(4)
A comparison of our distance formulation against a baseline distance measure commonly used in prior studies (Gaiti et al. 2019; Chaligne et al. 2021) on simulated data can be found in Supplemental Section S2.1 (Supplemental Figs. S4–S6). After computing the distance between each pair of cells, one can incorporate any distance-based tree reconstruction method
into Sgootr to obtain the lineage tree and arbitrarily choose a single cell from the normal tissue as the root. We use the
scikit-bio implementation of the neighbor-joining (NJ) algorithm (Saitou and Nei 1987) for our main analysis. It is possible to replace NJ with an alternative distance-based tree construction method in Sgootr.
We compare Sgootr’s performance while using FastME 2.0 (Lefort et al. 2015), a popular alternative, against using NJ in Supplemental Section S5 and show that they lead to similar results (Supplemental Figs. S15–S17).
Pruning of CpG sites according to a tree-based methylation status persistence measure
The main body of Sgootr consists of an iterative procedure: At each iteration, it (1) computes the pairwise distances among single cells to form the tumor lineage tree using a distance-based algorithm, then (2) measures the methylation persistence score of each CpG site along the tumor lineage tree and prunes away a fraction of CpG sites that has the lowest scores before continuing onto the next iteration, and (3) outputs the tumor lineage tree of the particular iteration where distance from the tumor lineage trees obtained in consecutive iterations is the minimum possible.
We have described how to compute pairwise distance among single cells in the previous section, and we leverage the widely used Robinson–Foulds (RF) distance (Robinson and Foulds 1981; Sul and Williams 2008) to measure the differences among the tumor lineage trees constructed on the same set of cells in consecutive iterations. Note that it is possible to incorporate alternative tree distance or similarity measures in using Sgootr, and we provide a brief comparison of RF distance against four other tree distance and similarity measures in Supplemental Figure S8. In this section, we focus on how we measure the methylation persistence of CpG sites at each iteration given the tumor lineage tree obtained for these CpG sites. In particular, we define the methylation persistence score for a CpG site given a tumor lineage tree (Equation 6): The higher the methylation persistence score for a CpG site, the more stably maintained is its methylation status change along a tumor lineage tree.
To facilitate the analysis, we assign to each CpG site covered in each cell its most likely methylation status: Given sequencing error–corrected reads from component 2 of Sgootr, we call a site homozygously methylated if all of its reads have the site methylated, homozygously unmethylated if all unmethylated, and heterozygous if the read status for the site is mixed. The status remains unknown if there are no reads covering the CpG site. After this step, we measure the persistence of each CpG site independently: first at each branch of the tree and then for the overall tree.
Methylation persistence score for a CpG site at a particular branch in the lineage tree
Each branch in the methylation tumor lineage tree induces a bipartition of the tree and subsequently of the leaf nodes, which
represent single cells. In other words, let TN denote the full set of leaf nodes in a methylation tumor lineage tree t; cutting a branch b in the tree creates disjoint subsets of leaf nodes TNb and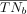 
. Let Qs,tn denote the probability distribution across three possible methylation statuses–—homozygously methylated, heterozygously methylated,
and homozygously unmethylated—at CpG site s across a subset of cells tn, and let Is represent the set of cells with status information at site s. Then, we define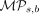 
, the methylation persistence score of CpG site s at branch b (Equation 5):
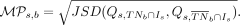(5)
Here JSD(X, Y) denotes the Jensen–Shannon divergence (Wong and You 1985; Lin 1991) for a pair of distributions X, Y and is defined as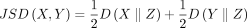 
, with 
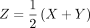and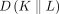 
denoting the Kullback–Leibler divergence measure for any arbitrary distributions K and L (Kullback and Leibler 1951). It is worth noting that the square root of the Jensen–Shannon divergence measure, which computes 
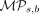(Equation 5), is metric (Endres and Schindelin 2003; Österreicher and Vajda 2003) and is commonly referred to as the Jensen–Shannon distance in popular implementations.
The intuition is that if the change in methylation status of CpG site s has an observed persistent effect in tumor progression, namely, s is lineage-informative, there exists a branch b* in the methylation tumor lineage tree such that the leaf nodes in the two subtrees induced by b* show very different distributions of methylation statuses. In other words,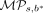 
will be large for such b*. In contrast, suppose the bipartitions contain the same distributions for methylation statuses for s—either that most cells share the same status or that both bipartitions are similarly heterogeneous—the score will be low.
Overall methylation persistence score for a CpG site in the lineage tree
We define the overall methylation persistence score of CpG site s in methylation tumor lineage tree t as the maximum methylation persistence score the site s has across all valid bipartitions (Equation 6). We recognize that (1) an extreme difference in the number of cells between the bipartitions or (2) a severe lack of cells
with status information could both lead to meaningless divergence measurements. Therefore, we only consider bipartitions induced
by branch b such that (1) both partitions contain no fewer than a user-defined fraction δ of total number of leaves, and (2) there is read information in no fewer than a user-defined fraction ω of cells in both partitions. In our experiments, we set δ = .05 and ω = .5.
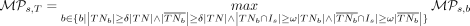(6)
Iterative joint tumor lineage tree reconstruction and lineage-informative site identification
In a given iteration i, Sgootr first computes the tumor lineage tree ti with the distances between pairs of cells based on the persistent sites identified in iteration i − 1 (for iteration i = 0, the entire set of sites remaining after component 1 and 2 of Sgootr are used). Then, for each CpG site s used in computing ti, Sgootr calculates its overall methylation persistence score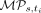 
. Among the CpG sites with overall methylation persistence scores, Sgootr prunes away a user-defined fraction κ of the CpG
sites with the lowest scores, along with those with tying scores at the threshold. It outputs the remaining CpG sites to be
used in iteration i + 1. The process continues for a user-defined maximum number of iterations, and Sgootr outputs t* = ti, where i is the last iteration, with RF(ti, ti−1) equal to the global minimum across iterations.
Intuitively, we would like to detect an approximate point in the iterative procedure at which most non-lineage-informative CpG sites have been pruned out (leading to the initial roughly decreasing trend of RF distance) but most lineage-informative CpG sites still remain (whose further elimination will lead to increasingly inaccurate distance measurements between cell pairs and therefore increasingly unstable tree topologies, which is reflected in a once-again increasing trend of RF distance). We show empirical observations corroborate with such intuition (Fig. 2C, Supplemental Figs. S11, S17) and provide practical recommendations for choosing κ and the maximum number of iterations in Supplemental Section S9.
Application of Sgootr to patient CRC01 scTrio-seq data by Bian et al. (2018). (A) The multiregional patient data consist of single cells sampled from four distinct lesions (in addition to normal tissue) and multiple sampling locations within each lesion. (B) Tumor lineage tree constructed by Sgootr with κ=0.1. Each single cell is represented as a leaf, colored by its sampling location. (C) RF distances between the trees of consecutive iterations of the pruning procedure, with the global minimum occurring at t* = t8. (D) Tumor migration history inferred by Sgootr for patient CRC01. (E) Fraction of CpG sites located in CpG island (CGI; regions with overrepresentation of CpG sites) (Cross and Bird 1995), CpG shore (2-kb-long regions flanking both sides of CGIs) (Irizarry et al. 2009), CpG shelf (2-kb-long regions adjacent to CpG shores on the side away from CGIs) (Irizarry et al. 2009), and inter-CGI regions in the CRC01 trees at each iteration of the pruning procedure of Sgootr, from t0 to t*. (F) Top 10 GO terms with significant (<0.05) q-values in enrichment analysis of nonpseudo, protein-coding genes spanning lineage-informative sites in intra-CGI and inter-CGI regions, respectively, in CRC01. For a full list of enriched terms, see Supplemental Figure S12A.
Inference of migration history from lesion-labeled tumor lineage tree leveraging prior knowledge on migration patterns
Given a rooted tumor lineage tree t* produced by Sgootr through the procedures described above, provided that the single cells in the tree are labeled by their lesion of origin, we can infer the underlying tumor migration history, which we represent as a directed multigraph (without self-loops) in which each vertex represents a distinct lesion and each edge represents a distinct migration event from the source lesion to the target lesion. This intuitive representation of metastatic migration events was introduced as a “migration graph” by El-Kebir et al. (2018). We accomplish this by first adapting the well-known Fitch–Hartigan algorithm (Fitch 1971; Hartigan 1973) with slight modification to obtain a unique, maximally parsimonious labeling of the internal nodes of t* and then by identifying the migration events.
The Fitch–Hartigan algorithm was originally intended to solve the small parsimony problem, namely, labeling the internal nodes of a character-based evolutionary tree in which every leaf is labeled with a single character and the objective is to minimize the total number of changes (i.e., mutations from parent node to child node) (Fitch 1971; Hartigan 1973). In our reuse, the bottom-up phase of the Fitch–Hatigan algorithm computes in a tree the number of migration events—in other words, the change of lesion of origin labels from a parent node to a child—in the most parsimonious labeling of its internal nodes. This phase also produces a set of possible labels for each internal node in the tree. The top-down phase, then, assigns each internal node a label from its set, as described in Algorithm 2, starting with the root node of t*.
Partial order-guided modification to the Fitch-Hartigan top-down node label assignment
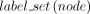← maps a node to the set of labels it is given by the bottom-up phase of Fitch–Hartigan algorithm (Fitch 1971; Hartigan 1973)
parent(node), children(node) ← returns the parent and the two children of node, respectively
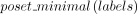← returns the minimal element in subset labels of a poset L, breaking ties arbitrarily
assignment[node] ← records the final label assignments of all nodes
node ← a node in the tree
function LabelAssignment(node)
if node is not root AND assignment[parent(node)] is in 
then
assignment[node] ← assignment[parent(node)]
else
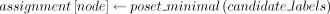
end if
if node is not a leaf then
child1, child2 ← children(node)
LabelAssignment(child1)
LabelAssignment(child2)
end if
end function
A general formulation of Fitch-Hartigan algorithm may produce multiple optimal labeling of the internal nodes, and there are
existing tools to capture the space of all optimal labeling: For example, MACHINA by El-Kebir et al. (2018) enumerates optimal solutions allowing restrictions on the types of transition events, and FitchCount by Quinn et al. (2021) generates a stochastic matrix summarizing all transition events in the optimal solution space. However, some of these optimal
labelings may adhere to our prior understanding of the sequential-progression (a.k.a. metastatic-cascade) model of tumor evolution
(Lambert et al. 2017) better than others. One can encode such prior understanding as a partial order over the lesion of origin labels of single
cells. For example, in this work, we leverage the following partial order:
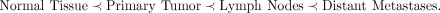In our modification to the Fitch–Hartigan algorithm, during the top-down phase, when a node cannot inherit the label of
its parent, we assign it the minimal element in its candidate label set according to the partial order, breaking ties arbitrarily
when the elements in the label set cannot be compared (Algorithm 2). This returns a maximally parsimonious labeling of the internal nodes in the tree that also acknowledges the sequential-progression
model.
With a fully labeled tree, we produce a directed multigraph that corresponds to the tumor migration history as follows. First, we generate a vertex for each distinct lesion represented in the tree. Then, as we traverse down the tree from the root, for each label change from a parent to a child in the tree, we add one directed edge to the multigraph, from the lesion vertex corresponding to the parent label to that corresponding to the child label. Parallel edges between a pair of vertices correspond to a polyclonal seeding event, and any back edge indicates a reseeding event.
Note that our proposed method resolves equally optimal labeling of the internal nodes with prior knowledge on the likely migration patterns among sampled sites. We have that prior knowledge for the primary data set we analyze in this work, and the method provides a basis on which we compare single-cell lineage trees with lesion-labeled leaves constructed with Sgootr or alternative methods. In the case in which no prior knowledge is available and the goal is to survey the whole space of parsimonious migration histories possibly suggested by a lesion-labeled lineage tree, users may instead use tools like MACHINA (El-Kebir et al. 2018) or FitchCount (Quinn et al. 2021). It may also be intuitive to more directly encode such prior knowledge by assigning different weights to migration events between distinct lesions and to solve the weighted version of the small parsimony problem with Sankoff's algorithm (Sankoff 1975); however, the output of Sankoff's algorithm is highly sensitive to the input weights, and it is not immediately clear which set of weights would be most appropriate for our purpose.
Results
The performances of Sgootr’s distinct components on simulated data are described in the Supplemental Sections S1 (biclustering), S2.1 (distance calculation), and S2.2 (iterative pruning) (Supplemental Fig. S7). Each of these components improves upon the respective baseline approach on a wide range of settings, and the results of the iterative pruning component show that Sgootr can capture the migration history of a tumor accurately. Furthermore, we applied Sgootr to scRRBS data of single cells from an U87MG GBM cell line ex vivo clone tree experimentally generated by Wei and Zhang (2020). We show in Supplemental Section S3 that, even though the original study fails to construct an accurate lineage tree from microsatellite allelotype data (see Supplemental Fig. S10 in Wei and Zhang 2020), Sgootr is able to reconstruct a CpG methylation-based lineage tree that accurately captures the ground truth clonal relationships (Supplemental Fig. S9).
In the remainder of the paper, we focus on the application of Sgootr to the scBS-seq data set generated by Bian et al. (2018) on nine metastatic CRC patients (out of 12 total patients in the Bian et al. (2018) cohort, we excluded those without scBS-seq data [CRC03 and CRC06] and those without metastasis information [CRC09]), among whom two (CRC01 and CRC04) have matching scRNA-seq data (via the scTrio-seq2 protocol) from both normal and tumor cells with which copy number calling can be performed. We highlight results from patient CRC01 because in addition to having copy number calls available, they have the largest number of distinct tissue types, sampling locations, and treatment conditions. Full details and results for the other eight patients can be found in Supplemental Section S4 (Supplemental Table S3; Supplemental Fig. S10). We additionally present in Supplemental Section S7 Sgootr’s results on a GBM patient by Chaligne et al. (2021), which show the applicability of our approach to MscRRBS data (Supplemental Fig. S19). To the best of our knowledge, this is the only other scBS-seq data set with multiregional tumor sampling that is publicly available.
Sgootr obtains a simple tumor migration history with scBS-seq and scRNA-seq data from patient CRC01
The single cells of CRC01 are sampled from four distinct lesions—primary tumor (PT), lymph node metastasis (LN), liver metastasis (ML), and post-treatment liver metastasis (MP)—and normal colon tissue (NC) adjacent to the primary lesion; furthermore, there are multiple sampling locations within each lesion (Fig. 2A). We only include cells with both scBS-seq and scRNA-seq data, and use inferCNV (from the Trinity CTAT Project, https://github.com/broadinstitute/inferCNV) to call the copy number from scRNA-seq data. We apply Sgootr with κ=0.1, terminating the iterative procedure after 40 rounds. A unique global minimum among the RF distances is identified at iteration 8 (Fig. 2C); hence, t* = t8 (Fig. 2B) is output as the lineage tree. The tumor migration history inferred by Sgootr (Fig. 2D) is simpler than the CNA-based results previously reported (Supplemental Fig. S7 in Bian et al. 2018): NC grows into PT, followed by a polyclonal migration to LN, which appears to proceed to seed both ML and MP. Although the migration history also suggests a polyclonal reseeding from ML to LN, both edges in the graph have low support: They are both owing to a subtree of a particular cellular origin harboring a (potentially mislabeled) singular cell of a different origin.
For comparison, we also present in Supplemental Section S6 the tumor lineage tree we constructed on mutations called from the matching scRNA-seq data from patient CRC01 using the Trisicell toolkit (Rashidi Mehrabadi et al. 2021). Because of the high level of sparsity in the mutation calls, we clustered single cells before constructing the mutation tree. We observed a high level of heterogeneity in terms of lesion of origin and sampling locations in the cell clusters (Supplemental Fig. S18), which makes inferring simple tumor migration history from trees constructed on them unlikely. Together with the CNA-based results (Supplemental Fig. S7 in Bian et al. 2018), this mutation-based result further highlights the usefulness of CpG methylation in reconstructing single-cell lineage trees when sparse SNV and CNA data fail to provide sufficient signal for lineage reconstruction.
Sgootr infers migration histories simpler than alternative methods for the Bian et al. (2018) CRC cohort
We benchmark Sgootr against (1) a naive baseline distance-based tree construction method (column “baseline” in Fig. 3A); (2) IQ-TREE (Nguyen et al. 2015) with the two-state general time reversible model (GTR2), an instance of the popular maximum-likelihood-based tool used for inferring lineage trees from scBS-seq data in prior studies (Fig. 3A, column “IQ-TREE”; Gaiti et al. 2019; Chaligne et al. 2021); and (3) IQ-TREE (with GTR2 model) preceded by four-gamete analysis (FG), a lineage-informative site-selection method previously described by Gaiti et al. (2019), which returns a subset of input CpG sites with a lower than expected epimutation rate (Fig. 3A, column “FG + IQ-TREE”). Note that it is IQ-TREE preceded by FG that was used exactly in previous studies (Gaiti et al. 2019; Chaligne et al. 2021). However, as discussed in more detail below, the FG step is not only very slow, it also leads to highly complex migration histories. These observations lead us to additionally benchmark against IQ-TREE without the FG step, even though it had not been directly applied to scBS-seq data in prior studies. For further experiment details, see Supplemental Section S10.
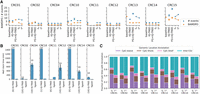
Overview of results from the Bian et al. (2018) metastatic CRC cohort. (A) Number of migration events and BAMDPO values of migration histories obtained via (1) naive baseline method, (2) IQ-TREE, (3) IQ-TREE on FG-selected CpG sites, (4) Sgootr intermediate tree before iterative procedure (t0), and (5) final tree output by Sgootr (t*). The IQ-TREE result is represented by the mean across 10 runs with different random seeds, with the error bars denoting the 95% confidence interval of the mean. The lack of data points in the “IQ-TREE” columns means IQ-TREE failed to finish the model optimization to start tree search after 24 h, and that in “FG + IQ-TREE” columns means FG analysis fail to terminate after 100 h. (B) Run time comparison between Sgootr and IQ-TREE. Each experiment is performed on four cores. The number in brackets next to “IQ-TREE” on the x-axis represents the number of IQ-TREE runs (out of 10) that have converged within 24 h. The number above each IQ-TREE bar represents the total number of runs (out of 10) with any tree search output (converged or intermediate after 24 h) and, hence, contributes to the run time and migration history comparison. (C) Fraction of CpG sites located in CpG island, CpG shore, CpG shelf, and inter-CGI regions before (t0) and after (t*) the iterative pruning component of Sgootr.
For each benchmarking experiment, we take as input the cell-by-site read count matrices resulting from the first-pass heuristic
filtering step of Sgootr, namely, removing low-quality cells, CpG sites with coverage in less than 
of remaining cells, sites on sex chromosomes, and sites within Chromosome 21 peri-centromeric regions. Then, for each CpG
site covered in each cell, call whether it is methylated or not by the 90% rule (Bian et al. 2018; Gaiti et al. 2019; Chaligne et al. 2021). This binarization step is necessary in generating input for the GTR2 model. For the FG + IQ-TREE experiments, we further
perform FG (Supplemental Sec. S10; Supplemental Figs. S20, S21) to select CpG sites to input to IQ-TREE. Additionally, we further filter the input to the benchmarking experiments so that
all experiments (Fig. 3A) on a particular patient act on the same set of input cells. This calibration is to ensure fair comparisons among results
from different methods using the two performance measures we will introduce below. To facilitate fair runtime comparison between
IQ-TREE and Sgootr, we also filter to ensure the input to IQ-TREE for each patient is the same set as those to Sgootr, so
that the runtime measurements in Figure 3B are taken on the same set of cells and CpG sites for each patient.
For each patient in the Bian et al. (2018) cohort, we generate a baseline lineage tree by first computing the Hamming distance between every pair of cells over their binarized CpG site methylation status vectors, averaging across the sites covered in both cells and then applying NJ to the distance matrix. As IQ-TREE is a stochastic method, we perform 10 separate runs of each IQ-TREE experiment with different random seeds and for each instance report the intermediate tree at convergence or after 24 h if convergence has yet to be achieved by then. If none of the 10 runs of IQ-TREE for a particular experiment have finished model optimization, started tree search, and produced some intermediate result, we do not report the IQ-TREE result for that experiment. Similarly, if FG does not terminate in 100 h, we do not report the FG + IQ-TREE result for that experiment. We root the baseline and IQ-TREE trees with the same normal cells we used to root the trees by Sgootr, and we infer the tumor migration histories from them via Sgootr’s modified Fitch–Hartigan algorithm.
We compare the migration histories inferred via Sgootr and the three alternative approaches by two measures: (1) the total number of migration events, namely, the number of edges in our multigraph representation, and (2) one we name binary adjacency matrix distance from partial order (BAMDPO), which is the Hamming distance between the binary adjacency matrix of the simple directed acyclic graph induced by the lesion partial order and that obtained by collapsing all parallel edges in the migration history multigraph. Intuitively, the first measure (output from Fitch–Hartigan algorithm) captures the conventional definition of parsimony, and the latter measures the degree the inferred history deviates from the sequential-progression model of tumor evolution. Together, they offer complementary perspectives on the complexity of the inferred histories. For both measures, a lower value would correspond to a simpler history.
Figure 3A compares the tree t* obtained by Sgootr against the alternatives with respect to the two measures. The figure also includes results of t0 for each patient, the tree obtained by Sgootr before its iterative site pruning procedure. Comparisons of the measures for t0 against those for t* show Sgootr’s iterative procedure almost always reduces the complexity of the inferred migration history, provided such a reduction is at all possible. In the case of patient CRC15, even though the total number of migration events increases from t0 to t*, BAMDPO decreases; this suggests that what first appeared to be deviations from the simple sequential-progression model could potentially be resolved as polyclonal seeding events more in concordance with the model, once the tree structure becomes more refined through the iterative procedure. Compared with naive baseline and the two IQ-TREE-based methods, Sgootr typically infers as simple, if not simpler, migration histories; the only exception is patient CRC10, for which IQ-TREE (without FG site-selection) infers a migration history with the lowest BAMDPO.
Note that all patients except CRC01 and CRC15 have single cells sampled from only two lesions in addition to the normal tissue (Supplemental Table S3); among them, patients CRC02, CRC04, CRC12, and CRC14 have a low number of input cells. For that reason, one may expect a lower number of migration events detected from the constructed lineage trees. Furthermore, Sgootr has achieved the minimal possible values in terms of BAMDPO before the iterative procedure in CRC02, CRC04, CRC11, CRC12; for CRC02, CRC04, and CRC12, Sgootr has also achieved the minimal possible value for the number of events before the iterative procedure. In those cases, there are no changes in terms of those two measures between the initialized tree (t0) and the optimal tree (t*).
Sgootr-identified lineage-informative CpG sites construct lineages suggesting simpler migration histories than those identified via FG
Specifically, comparisons between the measures from running IQ-TREE on FG-selected sites and those from Sgootr show that Sgootr consistently outperforms the former in terms of the number of events and BAMDPO when further improvements were possible. This suggests the sites selected by Sgootr may be more meaningful for the purpose of lineage reconstruction than those by FG. FG is also time-consuming: For patients CRC11 and CRC12, FG failed to complete after 100 h, and no experimental result was reported (Fig. 3A).
Sgootr is orders-of-magnitude faster than IQ-TREE
Although Sgootr produces an as simple, if not simpler, migration history than IQ-TREE (without FG site-selection) in terms of the two measures in all but one case, Sgootr obtains the results in a fraction of time IQ-TREE took given the same input dimensions. Each IQ-TREE run was allotted 24 h. If the program converged within 24 h, we report the wall clock time elapsed; if the program did not converge within 24 h but produced some intermediate output from tree search, we report the program run time as 24 h; and if IQ-TREE failed to produce any intermediate result from tree search within 24 h, we do not include the elapsed time from that run. Within the allotted time, IQ-TREE produces converged results in six out of nine patients and some (intermediate) results for eight out of nine patients. IQ-TREE is not able to finish model optimization and start tree search within 24 h for any of the 10 runs for CRC11 (Fig. 3B). Sgootr is deterministic and obtains lineage trees suggesting simpler histories in a mere fraction of the time when given the same number of cores and memory as IQ-TREE, positioning itself as the better option in more time-frugal settings.
Sgootr-identified lineage-informative CpG sites are enriched in inter-CGI regions
In all nine CRC patients in the Bian et al. (2018) cohort, as well as the multiregional GBM patient MGH105 in the Chaligne et al. (2021) cohort, the set of lineage-informative sites identified by Sgootr shows enrichment in inter-CGI regions (Figs. 2E, 3C; Supplemental Fig. S19F). The median distances between CpG sites and their closest CGIs also increase as the iterations approach t* across all patients (Supplemental Fig. S14).
Genes associated with Sgootr-identified lineage-informative CpG sites are enriched for pan-cancer and CRC-related terms
To examine whether the lineage-informative sites discovered by Sgootr in the Bian et al. (2018) cohort have potential functional implications, we stratified lineage-informative sites by their genomic annotations with respect to CGIs, for each group finding a set of nonpseudo, protein-coding genes whose gene bodies and 1000 bp upstream promoter regions contain the sites, and performed Gene Ontology (GO) (Ashburner et al. 2000; The Gene Ontology Consortium 2021) enrichment analyses, respectively, using GOrilla (Eden et al. 2007, 2009). All annotated nonpseudo, protein-coding genes in the genome were used as the background set. A hypergeometric test was used to measure the overrepresentation of the genes in associated GO terms, and the Benjamini–Hochberg false-discovery rate–adjusted P-values (q-values) are presented. In five out of nine CRC patients, genes mapped to lineage-informative sites within CGI are strongly associated with transcription regulation and DNA binding (Fig. 2F; Supplemental Fig. S12), processes known to be linked to cancer onset (Corces et al. 2018). Among informative sites mapped to inter-CGI regions, prominent enrichment in neural activities including ion transport and gated channel activities were observed across all nine CRC patients (Fig. 2F; Supplemental Fig. S12), concurring with recent studies that support the cross talk between the neural system and CRC development (Rademakers et al. 2021; Zhu et al. 2022). Enrichment results using an alternative tool, DAVID (Huang et al. 2009; Sherman et al. 2022), are also included for comparison (Supplemental Fig. S13). Although the GO terms discovered are not identical between the tools, the results highly concur as indicated by the overlap coefficients of the terms (Supplemental Table S4).
Discussion
In this work, we present Sgootr, the first distance-based tool to jointly infer tumor lineage using single-cell CpG methylation data and select for lineage-informative CpG sites. Sgootr concomitantly tackles two key challenges in lineage reconstruction from single-cell methylation data: sparsity and diverse inheritance dynamics of CpG methylation. We show Sgootr is able to construct lineage trees that suggest simpler tumor migration histories, perform CpG site selection, and obtain results orders-of-magnitude faster than alternative methods in applications to real multiregionally sampled single-cell methylation data in CRC and GBM.
In addition to tumor lineage inference, Sgootr captures meaningful biological insights of identified lineage-informative CpG sites. In both CRC and GBM, the two cancer types included in our study, we discovered the enrichment of lineage-informative sites in inter-CGI regions across patients. We also observed that the variability of the methylation status of a CpG site among sequenced cells seems to increase with its distance from the closest CGI (Supplemental Table S5). Although the underlying mechanisms of these phenomena are yet to be elucidated and are beyond the scope of this study, a plausible explanation is that CpG sites in islands are protected by the reduced chromatin accessibility in the region marked by histone modifications (Cedar and Bergman 2009), whereas inter-CGI sites harbor more stochastic changes owing to malfunctioning of DNA methyltransferases and TET enzymes (Du et al. 2015). Although CGIs have attracted much attention in the studies of tumor epigenetic changes and are more frequently covered in methylation arrays, our findings suggest that inter-CGI regions should not be overlooked, especially in the context of tumor lineage tracing. We are looking to further study the relations between the methylation status of lineage-informative inter-CGI CpG sites and gene expression and explore their prognostic potentials in our subsequent studies.
Leveraging single-cell methylation data while accounting for CNA data when available, Sgootr is also among many recent efforts in integrating information from multiple data modalities in inferring tumor evolution trees from cancer data sets. Indeed, combining different types of omics data is a major algorithmic challenge in tumor phylogenetics (Schwartz and Schäffer 2017). Because this work concerns single-cell methylation data, we focus this list of examples on methods that analyzed a combination of at least one type of (relatively rare, potentially more informative) single-cell data with at least one type of (more abundant) bulk data. Malikic et al. (2019a,b) pioneered methods called B-SCITE and PhISCS to integrate bulk and single-cell sequencing data to infer tumor phylogenetics trees using a Monte Carlo Markov chain algorithm and combinatorial optimization, respectively. Zeira and Raphael (2020) introduced a different method for inferring copy-number tumor evolution trees that can combine bulk and single-cell DNA sequencing data. Lei et al. (2021) presented a method to combine bulk copy number sequence data, single-cell sequence data, and fluorescence in situ hybridization data. Satas et al. (2020) developed the method SCARLET to infer tumor phylogenies from single-cell DNA data while accounting for CNAs, which might be inferred from either single-cell or bulk data. How to best integrate single-cell methylation data with both single-cell and bulk gene expression data and perhaps also copy number data is a natural question for future research.
Software availability
Sgootr is implemented as a Snakemake workflow available at GitHub (https://github.com/algo-cancer/Sgootr) and as Supplemental Code.
Competing interest statement
E.R. is a cofounder of Metabomed, Medaware, and Pangea Biomed (divested and serving as a nonpaid scientific consultant).
Acknowledgments
This work was in part supported by the Intramural Research Program of the National Institutes of Health (NIH), National Cancer Institute (NCI), Center for Cancer Research. This work used the computational resources of the NIH HPC Biowulf cluster (http://hpc.nih.gov). Y.L. and X.C.L. are funded by the NCI-UMD Partnership Program. E.K.M. is funded by the state of Maryland. We thank the reviewers for their valuable comments and suggestions, which improved the quality of the manuscript.
Author contributions: Y.L., X.C.L., F.R.M., A.A.S., and K.D.A. curated the data used in this study. X.C.L. and F.R.M. performed preliminary analysis of the Bian et al. (2018) data set and called copy number using the matching scRNA-seq data from CRC01 and CRC04. Y.L., A.A.S., S.M., and S.C.S. developed the methods. Y.L. designed, implemented, and tested the software and applied the software on available data sets. Y.L., A.A.S., S.M., E.K.M., and S.C.S. performed simulations and benchmarking of the methods. X.C.L. and E.K.M. experimented with incorporating alternative tree distance measures. F.R.M. constructed the mutation tree for patient CRC01 using Trisicell. X.C.L., A.A.S., D.P., D.R.C., S.M., and V.G. performed gene enrichment analysis and biological interpretations. Y.L., X.C.L., F.R.M., A.A.S., and S.C.S. wrote and edited the manuscript. A.A.S., E.K.M., S.M.M., E.R., K.D.A., and S.C.S. supervised the study.
Footnotes
-
[Supplemental material is available for this article.]
-
Article published online before print. Article, supplemental material, and publication date are at https://www.genome.org/cgi/doi/10.1101/gr.277608.122.
- Received January 12, 2023.
- Accepted June 6, 2023.
This article is distributed exclusively by Cold Spring Harbor Laboratory Press for the first six months after the full-issue publication date (see https://genome.cshlp.org/site/misc/terms.xhtml). After six months, it is available under a Creative Commons License (Attribution-NonCommercial 4.0 International), as described at http://creativecommons.org/licenses/by-nc/4.0/.
