Leveraging family data to design Mendelian randomization that is provably robust to population stratification

  1. Sriram Sankararaman1,3,4
  1. 1Department of Computer Science, University of California Los Angeles, Los Angeles, California 90095, USA;
  2. 2Department of Statistics, University of California Los Angeles, Los Angeles, California 90095, USA;
  3. 3Department of Computational Medicine, University of California Los Angeles, Los Angeles, California 90095, USA;
  4. 4Department of Human Genetics, University of California Los Angeles, Los Angeles, California 90095, USA

  1. ↵5 These authors contributed equally to this work.

  • Corresponding authors: nathanl2012{at}gmail.com, sriram{at}cs.ucla.edu
    •  
    Next Section

    Abstract

    Mendelian randomization (MR) has emerged as a powerful approach to leverage genetic instruments to infer causality between pairs of traits in observational studies. However, the results of such studies are susceptible to biases owing to weak instruments, as well as the confounding effects of population stratification and horizontal pleiotropy. Here, we show that family data can be leveraged to design MR tests that are provably robust to confounding from population stratification, assortative mating, and dynastic effects. We show in simulations that our approach, MR-Twin, is robust to confounding from population stratification and is not affected by weak instrument bias, whereas standard MR methods yield inflated false positive rates. We then conduct an exploratory analysis of MR-Twin and other MR methods applied to 121 trait pairs in the UK Biobank data set. Our results suggest that confounding from population stratification can lead to false positives for existing MR methods, whereas MR-Twin is immune to this type of confounding, and that MR-Twin can help assess whether traditional approaches may be inflated owing to confounding from population stratification.

    Mendelian randomization (MR) is a widely used analytical tool that uses genetic variants (“genetic instruments”) to determine whether one trait (the “exposure”) has a causal effect on another (the “outcome”). With the availability of massive biobank data sets such as the UK Biobank (Bycroft et al. 2018), MR analyses have become increasingly powerful and have been used to identify causal relationships between numerous pairs of traits (Haase et al. 2012; Haycock et al. 2017; Lyall et al. 2017; Hemani et al. 2018; Wade et al. 2018). The validity of MR rests on three key assumptions (Lawlor et al. 2008): (1) that the genetic instrument is significantly associated with the exposure, (2) that the genetic instrument is independent of confounders of the exposure–outcome relationship, and (3) that the genetic instrument affects the outcome only through its effect on the exposure.

    Unfortunately, the latter two assumptions are often violated in practice, owing to several factors, including horizontal pleiotropy, population stratification (and related phenomena such as assortative mating and dynastic effects), and batch effects. Even when these assumptions are met, the weak effects of typical genetic instruments on the exposure coupled with spurious correlation between genetic instruments and confounders (Burgess et al. 2011) can bias the results of MR analyses (“weak instrument bias”). The problem of population stratification has been extensively studied in the Genome-Wide Association Study (GWAS) literature, and approaches for mitigating its effects have been developed, including the usage of principal component analysis (PCA) and linear mixed models (LMMs) (Price et al. 2010). These approaches have generally been found to be effective at reducing the confounding introduced by population stratification (Price et al. 2010).

    However, recent studies have shown that, with sample sizes as large as those found in modern biobanks, even a small amount of residual population stratification can cause a considerable amount of bias (Berg et al. 2019; Haworth et al. 2019; Brumpton et al. 2020; Cook et al. 2020) and may even cause false positives in MR analysis (Haworth et al. 2019; Cinelli et al. 2022). In addition, although the confounding effects of population stratification are well known, less attention has been directed toward confounding from other phenomena such as (cross-trait) assortative mating and dynastic effects, which can also cause MR false positives (Hartwig et al. 2018; Brumpton et al. 2020). Recent work has shown that cross-trait assortative mating is widespread and substantially inflates genetic correlation estimates between many trait pairs (Border et al. 2022).

    It has recently been proposed that family-based genetic data sets could be used in MR studies to avoid confounding from population stratification (Pingault et al. 2018; Brumpton et al. 2020). A recent suite of methods has been developed for this purpose and was shown to reduce the bias from this type of confounding (Brumpton et al. 2020). However, like other MR methods, these methods are susceptible to weak instrument bias, which can be substantial for small family-based data sets (Brumpton et al. 2020). In this paper, we introduce MR-Twin, a test for causal effects between pairs of traits that is able to leverage family-based genetic data to provably control for population stratification and to use publicly available summary statistics estimated in large biobank data sets to achieve power competitive with the top existing methods for the same sample size. We develop versions of MR-Twin for trio, parent–child duo, and sibling data; evaluate MR-Twin's ability to control false positives owing to population stratification and weak instrument bias; and compare it with existing methods.

    Previous SectionNext Section

    Results

    Methods overview

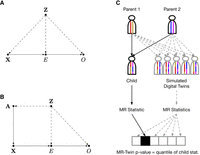
    In an MR analysis, we wish to determine whether one phenotype (the “exposure”) has a causal effect on another phenotype (the “outcome”) using genetic instrumental variables, which can be either single-nucleotide polymorphisms (SNPs), a polygenic score, or other genetic features. Under the assumption that the genetic instruments are associated with the exposure and are independent of the outcome given the exposure, the MR effect estimate of the exposure on the outcome will be valid even if there are unobserved confounders of the exposure–outcome relationship. The independence assumption, however, is often violated by population stratification (Fig. 1A) or horizontal pleiotropy, as these phenomena cause the genetic instruments to be correlated with the outcome through pathways other than those through the exposure.

    Figure 1.
    View larger version:
    Figure 1.

    Illustrations of Mendelian randomization (MR) assumptions and the MR-Twin framework. (A) Directed acyclic graph (DAG) depicting variables and their relationships in a typical MR study, where X is the genotypic instrument, E is the exposure trait, and O is the outcome trait. An external confounder Z, such as population stratification, can cause violations of the MR assumptions. (B) If we have the parental haplotypes A, then X is independent of Z given A. (C) Illustration of the MR-Twin workflow. Digital twin genotypes are sampled from the parental genotypes. MR-Twin is a conditional randomization test, conditioned on A and therefore immune to confounding from Z, in which the P-value is computed based on the quantile of the true offspring's MR-Twin statistic compared with the digital twins’ statistics.

    MR-Twin is a method that uses family-based genetic data to construct a test for whether the exposure has an effect on the outcome that is immune to confounding from population structure. It is based on the key idea that the genotypes of observed individuals are independent of population structure given the genotypes of the individuals’ parents, because the mechanisms by which genetic information is passed from parents to offspring are known (Fig. 1B). In other words, conditioned on the parental genotypes, population structure provides no additional information about the distribution of the offspring's genotypes. Thus, by conditioning on the parental genotypes, confounding from population stratification can be avoided (Fig. 1C), along with confounding from other phenomena such as cross-trait assortative mating and dynastic effects that operate through the parental genotypes (see Fig. 1 of Brumpton et al. 2020).

    We now outline the algorithm in the context of a trio design in which we have genetic data on the parents and the offspring. Let X and O denote the genotypes and outcome phenotype values, respectively, for some individual, and let 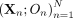Formula denote these across N trios. Also let P1 and P2 denote the genotypes of the parents of the individual with genotypes X, and let A: = (P1, P2) refer to the set of parental genotypes. Let Z denote the set of external confounders measured on the same individual, which we define as the set of confounders that satisfy X⫫Z|A. Thus, population stratification is an external confounder (as are assortative mating and dynastic effects), whereas horizontal pleiotropy is not. The key idea is that we can formulate a hypothesis test of a causal effect conditional on the parental haplotypes A. Bates et al. (2020) show that such a test is also a test of the stronger null hypothesis of a causal effect conditional on (A, Z).

    The way that this is accomplished is through a conditional randomization test, similar to the digital twin test (DTT) proposed by Bates et al. (2020) in the context of GWAS (Candès et al. 2018). The idea is to sample so-called “digital twins” 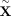Formula from each set of parents A such that 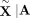Formula has the same distribution as 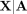Formula, which can easily be accomplished using the laws of Mendelian inheritance (Methods). 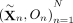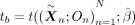We construct B such random samples across all trios, Formula, and for each set b of twins, we compute a test statistic Formula, representing the strength of association between the genetically predicted exposure and the outcome. 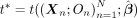We also compute a test statistic for the true offspring of the trios, Formula.

    We can then obtain a P-value for a nonzero causal effect of the exposure on the outcome, 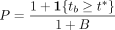Formula. The set of B statistics derived from the digital twins represents a null distribution conditioned on the parental genotypes. If there is a true nonzero effect of the exposure on the outcome, we expect the statistic derived from the true offspring to be stronger than statistics derived from digital twins whose genotypes are randomly sampled from the parental genotypes. The test statistic and algorithm are explained in more detail in the Methods section.

    MR-Twin controls for arbitrarily strong population stratification confounding in simulations

    Algorithm 1.

    Simulate genotypes under population structure

    1: procedure SimGeno(FST, groups, N,M) ▷ FST is the fixation index, groups is the number of populations, N is number of samples, M is number of SNPs.

    2:  Initialize the average Formula for each SNP j.

    3:  for k ≤ groups do

    4: 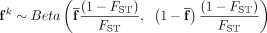  Formula

    5:   Generate genotype matrix X(k) of population k such that 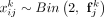Formula for each individual i and SNP j.

    6:  end for

    7:  X = [X(1); . . . ;X(groups)] . ▷ Stack the rows of each genotype matrix

    8:  return Genotype matrix X

    9:  end procedure

    Algorithm 2.

    Simulate population-stratified phenotypes

    1: procedure getPheno(X, U, h2, αE, γue, γuo) ▷ X is the normalized genotype matrix, U is a vector with the fixed population label for each sample, h2 is heritability of exposure E, αE is effect of E on outcome O, γue and γuo are fixed confounding effects of U on E and O.

    2:  Generate genetic coefficient 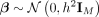Formula

    3:  Compute 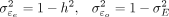Formula

    4:  Simulate E = Xβ + γueU + ɛe where 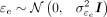Formula

    5:  Simulate O = αEE + γuoU + ɛo where 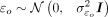Formula

    6:  return (E,O)

    7:  end procedure

    We compared the performance of MR-Twin to other MR methods via simulations consisting of two populations with allele frequency differences modeled according to the standard Balding–Nichols model (Balding and Nichols 1995), following the method of previous works (Pritchard et al. 2000; Price et al. 2006; Hubisz et al. 2009; Chen et al. 2015; Conomos et al. 2016; Ochoa and Storey 2021). The procedure for simulating the genotypes is outlined in Algorithm 1. We use this algorithm to simulate “external” samples (nontrio data, e.g., from a biobank), as well as the parents for the trios. The offspring genotypes for the trios can then be easily sampled given the parental genotypes (Methods). For each sample, we retain the population label, a binary variable indicating to which population each sample belongs. Unless otherwise specified, each simulation had 50,000 (false-positive rate [FPR] simulations) or 100,000 (power simulations) external samples and 1000 trio samples evenly split between two populations with a fixation index FST = 0.01 and 100 SNPs, 50 of which were causal for the exposure trait. Unless otherwise specified, the heritability of the exposure trait was set to h2 = 0.2.

    Next, we simulate both the exposure and outcome phenotypes following a linear model, as outlined in Algorithm 2. This model allows the population labels from the first step to have an effect on the exposure and outcome phenotypes, which models population stratification that violates the MR assumptions. We use this setting to assess the FPR of methods under population stratification, allowing the effects of the population labels on the exposure and outcome phenotypes to range from zero (no confounding) to 0.8 (substantial confounding). In a separate set of simulations to assess power, we set the confounding effect to zero and varied the causal effect.

    We performed 1000 simulation replicates under these settings, each time simulating a set of external and trio genotypes and phenotypes according to the chosen parameters, performing linear regression between each SNP and the exposure and outcome phenotypes, and using the resulting association statistics as input to each of the MR methods. We excluded SNPs with association P-values of above 0.05/M (M=100) with the exposure phenotypes in the external data in order to limit weak instrument bias (Burgess et al. 2011). The methods we assessed include the trio mode of MR-Twin, standard inverse-variance weighted (IVW) MR (Burgess et al. 2013), MR-Egger (Bowden et al. 2015), the weighted median estimator (Median) (Bowden et al. 2016), the mode-based estimator (Mode) (Hartwig et al. 2017), and a method introduced by Brumpton et al. (2020) to use family data to control for confounding owing to population stratification and other population-related effects. Brumpton et al. (2020) provide a suite of methods for different family data sets, following previous work such as that by Fulker et al. (1999); here we focus on the trio-based method they describe, and simply refer to that method as “Brumpton” below.

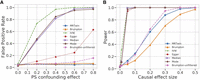
    The trio mode of MR-Twin maintained a calibrated FPR irrespective of the strength of confounding (Fig. 2A). Non-family-based methods such as IVW, Egger, Median, and Mode all displayed substantially inflated FPR in the face of confounding, consistent with their sensitivity to potential residual population stratification. The Brumpton method also displayed slightly inflated FPR, which increased with the strength of the confounding effect, likely owing to weak instrument bias (Brumpton et al. 2020). To mitigate the impact of weak instrument bias, we applied a common approach used in MR studies (Burgess et al. 2011) that involves filtering out variants for which the F-statistic of the association signal is low (F < 10 following previous recommendations). This rendered the FPR inflation negligible but also rendered Brumpton substantially less powerful than MR-Twin, whereas the “unfiltered” mode had similar power to MR-Twin (Fig. 2B). Results with confidence intervals are shown in Supplemental Figure S10. We further investigated the weak instrument bias by running simulations with no SNP filtering based on external data and with increasing numbers of SNPs—settings expected to generate large numbers of weak instruments—and confirmed that Brumpton had greater FPR inflation in these settings, whereas MR-Twin remained calibrated (Supplemental Fig. S11) and did not lose power (Supplemental Fig. S12).

    Figure 2.
    View larger version:
    Figure 2.

    False-positive rate (FPR) and power comparison between various methods run on simulated data. (A) FPR (y-axis) under varying levels of confounding owing to population stratification (PS), with the x-axis describing the magnitude of the confounding effect of population labels on the exposure and outcome trait. (B) Power (y-axis) as a function of the magnitude of the causal effect of the exposure on the outcome trait (x-axis) in a setting with no confounding. Results are averaged over 1000 simulation replicates.

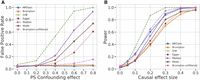
    The standard MR methods (IVW, Egger, Median, and Mode), when run on the external data, had substantially higher power than the family-based methods, MR-Twin and Brumpton (Fig. 2B). We performed additional simulations to understand if the lower power of MR-Twin was owing to the smaller number of trios as opposed to methodological limitations. When applied to the offspring in each trio (Fig. 3), the standard MR methods still had substantially inflated FPR (Fig. 3A) but similar power to MR-Twin and Brumpton (Fig. 3B). We also evaluated the FPR and power of these methods under varying number of trios (Supplemental Fig. S1). We observed that increasing the number of trios increased power for all methods, as expected, suggesting that the family-based methods can be expected to obtain increased power as more genetic family data are ascertained in the future. The relative power of the methods remained roughly consistent across these experiments.

    Figure 3.
    View larger version:
    Figure 3.

    FPR and power comparison between various methods run on simulated trio data. This is similar to Figure 2 except that IVW, Egger, Median, and Mode are run on the offspring of the trio data set instead of the large “external” group of unrelated individuals, such that all methods have the same sample size. (A) FPR (y-axis) under varying levels of confounding owing to population stratification (PS), with the x-axis describing the magnitude of the effect of the population labels on the exposure and outcome trait. (B) Power (y-axis) as a function of the causal effect size (x-axis). Results are averaged over 1000 simulation replicates.

    We also evaluated the area under the receiver operating characteristic curve (AUC-ROC) (Supplemental Figs. S5, S6). Comparing the two main family-based approaches, MR-Twin generally had higher AUC than Brumpton (filtered). Predictably, the AUC of standard MR methods drops sharply when there is confounding, and MR-Twin outperforms these methods in most such cases, although Egger was a notable exception in our findings and remained competitive with family-based approaches even under confounded settings. Similar to our findings in Figures 2 and 3, family-based methods are more competitive with standard MR methods when run on similar sample sizes. As an additional sensitivity analysis, we also assessed the FPR (Supplemental Fig. S7) and power (Supplemental Fig. S8) of methods in settings in which there are very few instruments or very low heritability. The trends were broadly similar to those seen in Figures 2 and 3. MR-Twin maintained a calibrated FPR in all settings, although it did suffer a loss of power when heritability was very low (Supplemental Fig. S8B,D).

    We performed simulations increasing the magnitude of population structure as measured by the FST (without necessarily increasing the confounding strength), and observed that increasing the population structure leads to further FPR inflation for standard MR methods (Supplemental Fig. S2). We observed inflated FPR for standard MR methods even when there is no confounding (stratification) for large values of FST (Supplemental Fig. S2) likely owing to correlation or linkage disequilibrium (LD) among the genetic variants induced by population structure. The standard implementation of IVW and Egger (Yavorska and Burgess 2017; Broadbent et al. 2020) allows the user to pass in a variant correlation matrix, which removed the FPR inflation with no stratification (Supplemental Fig. S2); other methods such as Median and Mode do not currently have this option.

    Next, we assessed the runtime of methods run on the trio data (Supplemental Fig. S3). Brumpton, along with non-trio-based methods (e.g., IVW), had similar run times (<1–5 sec per simulation replicate); for succinctness, only Brumpton is shown. MR-Twin (with 100 simulated digital twins) took ∼1 min per simulation replicate under the simulation settings described above, with time increasing to up to 4 min if the number of families or SNPs was increased. The number of digital twins to simulate for MR-Twin involves a trade-off between speed and stability of results. We assessed the stability of MR-Twin with different numbers of digital twins, with the results shown in Supplemental Figure S9. We interpreted these findings as indicating that 100 digital twins are likely stable enough for simulations for which many replicates are run and speed is a priority, but 1000 or more digital twins are recommended for one-off real data analysis. Therefore, we simulated 100 digital twins in our simulations and 1000 in our real data analysis. We note, however, that although the MR-Twin runtime increases linearly with the number of digital twins simulated, the generation and statistic computation for the digital twins can be performed in parallel, so many twins can be simulated efficiently given multiple compute cores or nodes. For clarity of results, we did not take advantage of this in our runtime assessment.

    Finally, MR-Twin also enables users to use parent–child duo or sibling data sets (Methods). We assessed the performance of these modes versus the trio mode of MR-Twin (Supplemental Fig. S4). We found that the duo and sibling modes, although having lower FPR than most standard MR methods, did not maintain a calibrated FPR at high levels of confounding, which is expected because the precise sampling of offspring genotypes from parents is not possible when either or both of the parental genotypes are not available.

    Application to trio data in the UK Biobank

    To assess the results given by MR-Twin relative to other approaches in a real data context, we next applied MR-Twin and four other MR methods (IVW, Egger, Median, and the Brumpton et al. method) (Brumpton et al. 2020) to 144 real trait pairs in the UK Biobank (Bycroft et al. 2018). These consisted of all pairwise combinations of 12 metabolic, anthropometric, and socioeconomic traits that were widely measured among the UK Biobank participants (listed in Supplemental Table S1). We isolated 955 White British genetic trios from the full UK Biobank data set (Supplemental Materials) and used PLINK (Purcell et al. 2007) to run linear regression on the remaining unrelated White British individuals for these 12 traits, including the top 20 principal components (PCs), age, and sex as covariates. The genetic instruments selected for each analysis were the SNPs with genome-wide significant P-values ( < 5.0 × 10−8) for the exposure trait, after LD pruning was performed so that none of these instruments were in substantial LD with one another (Supplemental Materials). Ignoring the degenerate cases in which the exposure and outcome were the same trait or in which there were no significant SNPs for the exposure trait (as was the case for the Townsend deprivation index [TDI]), there were 121 usable trait pairs.

    Table 1 shows the results for six selected trait pairs (excluding Median for brevity because it gave similar results to IVW), and Supplemental Table S2 shows the full set of analyses. Brumpton was run with several different variant filtering settings to assess the impact of potential weak instrument bias (Supplemental Materials); results for all runs are given in Supplemental Table S2. For Table 1, we selected six analyses: two positive controls representing causal effects that are true by definition (LDL cholesterol → total cholesterol and weight → body mass index [BMI]), two negative controls that represent seemingly implausible effects (glucose → TDI and height → body fat), and two trait pairs with unclear or conflicting evidence (BMI → diastolic blood pressure [DBP] and BMI → TDI). In particular, previous studies have identified a significant effect for BMI → DBP (Lyall et al. 2017) and for BMI → TDI in women (Tyrrell et al. 2016) with IVW analysis, although Egger analysis did not replicate the significant findings in either case (Tyrrell et al. 2016; Lyall et al. 2017).

    View this table:
    Table 1.

    Traditional MR results and MR-Twin results on selected trait pairs from the UK Biobank

    All methods performed as expected on the controls, with highly significant P-values for positive controls and insignificant P-values for negative controls. For BMI → DBP, IVW and Brumpton yielded significant results, whereas Egger and MR-Twin did not. For BMI → TDI, IVW and Egger yielded significant results, whereas Brumpton and MR-Twin did not. In general, IVW tended to yield much stronger P-values than other methods, and the family-based methods (Brumpton and MR-Twin) tended to be conservative (Supplemental Table S2), in line with our simulation results. In particular, of the 121 usable trait pairs, IVW identified 78 as significant, Egger identified 56 as significant, Brumpton identified 20 as significant, and MR-Twin identified 19 as significant.

    Previous SectionNext Section

    Discussion

    We introduced MR-Twin, a method for testing causal effects between pairs of traits within an MR framework, which is provably robust to confounding of any strength resulting from population stratification. Our primary contributions are the following: (1) developing a DTT, originally proposed by Bates et al. (2020) in the context of genetic association studies, for MR, coupled with a novel statistic for this test; (2) showing that, by leveraging trio data, our proposed framework is robust to confounding owing to population stratification and to biases from the inclusion of genetic instruments with weak effects; (3) extending our framework to the setting of sibling data, a setting not considered by Bates et al; and (4) conducting the first (to our knowledge) large-scale evaluation of the DTT framework in comparison with existing methods for MR. We showed that existing MR methods, including those designed to correct for confounding resulting from horizontal pleiotropy, are prone to false positives when there is confounding from population stratification.

    Although population stratification was the focus of this paper, the MR-Twin framework also provides immunity to several other types of confounding effects. Theory dictates that MR-Twin is immune to confounding from familial effects such as assortative mating and dynastic effects because these effects operate through the parental genotypes (see Fig. 1 of Brumpton et al. 2020), although we do not explicitly test this in this paper. As recently shown, cross-trait assortative mating is pervasive and impacts many common genetic analyses (Border et al. 2022), including MR (Hartwig et al. 2018), so this represents another valuable aspect of MR-Twin even if population stratification is believed to be well controlled in a particular study. In general, MR-Twin is immune to any confounder that is independent of the genotypes of offspring given the genotypes of their parents. We note that when we refer to “immunity” we mean this in a theoretical sense, for instance, under the assumption that the model for Mendelian inheritance is correct. In our particular implementation, we assume that the genetic instruments have been selected to be roughly independent, and thus, we can sample digital twin genotypes from the parental genotypes using a binomial model. In practice, of course, genetic variants on the same chromosome are never perfectly independent, although with appropriate caution, the dependence is weak enough that the effect on calibration should be negligible. More complex models of meiosis will also rely on other factors such as haplotype phasing accuracy.

    In addition to population and familial effects, we highlight two underappreciated sources of bias in MR studies, both of which MR-Twin avoids without requiring the user to modify any parameters or arguments. The first is weak instrument bias (Burgess et al. 2011), which can bias the effect estimate of standard MR methods, including the Brumpton approach (Brumpton et al. 2020). This accounts for the Brumpton method yielding inflated FPRs when the confounding effects were strong (Fig. 2A). One of the most common ways to control for weak instrument bias is by filtering out variants with a weak association signal, often with a threshold of F < 10 for the association between a variant and the exposure trait. However, this procedure has been criticized (Burgess et al. 2011) and may not fully correct for weak instrument bias. Other MR methods may also be affected by this bias. In two-sample study designs, the direction of the bias is toward the null rather than the confounded exposure–outcome association estimate (Lawlor 2016), but the bias remains.

    Additionally, we found that standard MR methods (IVW, Egger, Median, Mode, etc.) may have inflated FPR when there is population structure that induces correlation between variants, even in the absence of stratification (Supplemental Fig. S2). The reason for the induced correlation is that, even though the variants were simulated independently, they were correlated with one another through the population labels. For example, suppose we have two variants, X1 and X2, and a population label U. The causal diagram for these three variables is X1 ← U → X2, so X1 and X2 are correlated. Our findings corroborate earlier findings that correlation between SNPs can cause calibration issues in MR methods (Burgess et al. 2013). This phenomenon should be taken into account when performing MR simulations or when applying MR to real data sets where variants may be correlated. In the latter case, users should obtain SNP correlations from an appropriately population-matched (Peterson et al. 2019) and sufficiently large (Benner et al. 2017) reference panel.

    MR-Twin avoids both of these issues, without requiring the user to specify an SNP correlation matrix or apply various approaches to mitigate weak instrument bias. First, both MR-Twin and Brumpton avoid the correlated-variant issue because they condition on parental genotypes, severing the link between the offspring genotypes and the population structure. Second, MR-Twin would not lose FPR calibration owing to weak instrument bias, because this phenomenon has nothing to do with the aspects of the MR-Twin test that guarantee immunity from confounding owing to population and familial effects (sampling digital twin genotypes conditioned on parental genotypes). Theoretically, it is possible that the bias in the MR effect estimate used in the MR-Twin statistic (Methods) could lower power, but because the MR effect estimate equally affects both the digital twin statistics and the true offspring statistics, a reduction in power seems unlikely and was not observed empirically (Supplemental Fig. S12).

    There is extensive literature on family-based methods for avoiding confounding owing to population structure in genome-wide association studies or linkage analysis (Spielman et al. 1993; Thomson 1995; Fulker et al. 1999; Abecasis et al. 2000; Laird and Lange 2006; Weiner et al. 2017). One prominent example is the transmission disequilibrium test (TDT) (Spielman et al. 1993) and the more recent polygenic TDT (pTDT) (Weiner et al. 2017). Bates et al. (2020) compare the DTT to the TDT and show that the DTT is a generalization of the TDT and highlight some of its benefits. Because it is not immediately obvious how to adapt the TDT and pTDT to MR, we do not evaluate their potential use in this context.

    There are several considerations that come into play when applying the MR-Twin method, which we note here. First, the number of digital twins simulated involves a trade-off between speed and precision (Supplemental Fig. S9). Although MR-Twin was slower than competing MR methods (Supplemental Fig. S3), it still ran in a few minutes or less per run on both simulated and real data analyses, justifying the use of a fairly large number of digital twins if possible. Consequently, we recommend 1000 or more digital twins for real data analysis, which should be computationally feasible and precise (and, again, parallelization can make this quite efficient). One hundred digital twins are likely sufficient in simulations in which there are many replicates and speed is the paramount concern. Second, the populations of the external and family data sets should be similar. This is natural for biobanks like the UK Biobank but can be more challenging when attempting to combine separate data sets. Third, care should be taken to ensure that the normalization method used and covariates controlled for are similar in the external and trio data sets in order to avoid potential loss of power.

    Although the genetic trio offspring used in our UK Biobank analysis were all adults (as all participants in this data set were aged 40–69 at collection time) (Bycroft et al. 2018), other trio data sets may contain young children. This is a potential issue because some commonly analyzed traits such as height and weight may not have the same relationship in youths or adolescents as they do in adults, and variants that affect these traits may not yet have realized their full effect in the children yet. Dealing with such time-varying exposures in the context of MR is an area of ongoing research (Labrecque and Swanson 2019), and it is not clear how this would impact MR-Twin results. Even when the offspring of the trios are all adults, it may be difficult to adequately sample certain traits. For example, we were not able to perform MR analysis for complex traits such as heart disease, because none of the offspring in our sample had developed heart disease, largely because all offspring in our sample were aged 40–49.

    We note a few trends seen across many trait pairs in the real data results, reflecting some practical considerations. First, all standard MR methods identified substantially more trait pairs than did either family-based approach. Given our simulation results showing a large power difference in the methods when run with different sample sizes (Fig. 2) but similar power when run with the same sample size (Fig. 3), along with the fact that the UK Biobank has many more unrelated individuals than trios, we believe that this difference is largely because of the difference in the available sample sizes between unrelated and trio data. The number of trios available as part of public data sets is currently relatively small, limiting the power of family- or trio-based methods, but future increases in the number of available trios will lead to increases in the power of MR-Twin and other family-based methods. Second, some trait pairs had quite different results when the exposure and outcome traits were switched. For example, none of the standard MR methods had significant P-values for DBP → weight, but all were significant for weight → DBP (Supplemental Table S2). This may be owing to one causal direction being correct while the other is incorrect but may also be affected by factors such as differences in the heritability and/or polygenicity between the two traits.

    Several extensions to the methods presented here are also possible. Although we explored continuous traits in this paper, further work needs to be performed to apply MR-Twin to binary phenotypes such as disease labels. First, a different statistic such as binary cross entropy (rather than our negative squared loss statistic) may be more appropriate. Second, the use of the external effect size estimates in the statistic may have to be modified, depending on the regression method used and the interpretation of the estimates. For example, it would be inappropriate to replace the effect size estimates in our statistic with odds ratios produced by logistic regression. Even for linear data, it is possible that a different statistic than the one we proposed would be more powerful in some situations. Finding the most powerful statistics for a given significance threshold is a direction for future work. Future work could also improve upon the sibling mode of MR-Twin by using population-based priors to infer parental genotypes with a greater level of accuracy, thereby obtaining superior control of false positives. This approach could, in principle, be developed for and applied to more extended pedigrees.

    In the DTT paper, Bates et al. (2020) propose using a hidden Markov model (HMM) to simulate digital twins from the parental haplotypes, the latter being generated by phasing the parental genotypes. For the simplicity of avoiding this phasing step and because genetic instruments in MR studies are usually selected to be roughly independent (Burgess et al. 2013), we used a simpler method for simulating digital twins using binomial draws from the parental genotypes (Methods). However, the variants used may not be independent even if they appear to be (Burgess et al. 2013), or one may wish to include correlated variants to increase power. Extending MR-Twin to perform the HMM-based digital twin simulation could therefore increase power.

    Finally, a preprint from Tudball et al. (2022) proposes a randomization-based approach to MR that, although being conceptually similar, differs from MR-Twin in a few practical aspects. First, Tudball et al. (2022) do not discuss the use of external summary statistics to increase power, whereas this is a core part of the MR-Twin approach (as well as in the DTT of Bates et al. 2020). Second, Tudball et al. develop family-based propensity scores for individual SNPs and suggest aggregating them with Fisher's method or another P-value aggregation method, which is substantially different from our proposed sum-of-squares statistic over all SNPs (Methods). Finally, Tudball et al. used the HMM-based digital twin simulation model, whereas (as discussed above) we use the simpler binomial model. Nevertheless, the broad conceptual similarities between the two methods highlight the promise of randomization-based approaches to make MR findings more robust and the value of continued development to extend these approaches to more complex pedigrees.

    Previous SectionNext Section

    Methods

    The MR-Twin framework

    We first introduce the standard MR model, without any confounding. Suppose that for a collection of N individuals we obtain their genotypes at M SNPs, as well as a phenotypic measure for an exposure trait and an outcome trait. For a given individual n, we denote the genotype vector as Xn, the genotype at some SNP j as Xnj, the exposure trait as En, and the outcome trait as On. Let 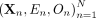Formula denote the collection of these genotypes and traits over all N individuals, where (Xn) is an (N × M) matrix, and (En) and (On) are (N × 1) vectors. Finally, let X, E, and O refer to the genotype vector, exposure trait, and outcome trait for a generic individual.

    MR uses the genetic “instrument” X to estimate the effect of an “exposure” trait E on an “outcome” trait O. This estimate is valid regardless of any confounder U of the association between E and O, assuming that the following conditions hold (Lawlor et al. 2008):

    1. The genetic instrument X is significantly associated with the exposure trait E;

    2. The genetic instrument X is independent of any variables (such as those in U) that confound the relationship between E and the outcome trait O; and

    3. The genetic instrument X is not associated with O except owing to its association with E.

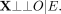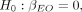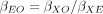    The latter two criteria can be captured by the independence statementFormula (1) Assuming these conditions hold and assuming a linear model for the relationships between the genotypes and phenotypes (a typical assumption in MR analyses), we can test the null hypothesis that there is no direct causal effect of E on O:Formula (2) where βEO is not obtained by direct regression but rather via instrumental variables estimators such as the ratio estimator Formula (when a single instrument is used) or by two-stage least squares or inverse-variance weighting (when multiple instruments are used) (Burgess et al. 2013).

    However, in the case in which we have residual population stratification, denoted Z (Fig. 1A), this independence assumption is violated. This is because, using terminology from Pearl's graphical formalism (Pearl 1995), X ← Z → O is a backdoor path between X and O, so the two are not marginally independent. Conditioning on E fails to block this backdoor path (i.e., see Fig. 1A). Residual population stratification generally cannot be controlled for directly, although approaches such as PCAs and LMMs have been used to reduce its effect (Price et al. 2010).

    MR-Twin (Fig. 1C) is a method that uses family-based genetic data to avoid this confounding. Suppose that we also observe, corresponding to each individual's genotypes X, the genotypes P1 and P2 of their parents (we later relax the trio assumption to allow for parent–child duo or sibling data). Let A: = (P1, P2). According to the graphical criteria for d-separation developed by Pearl (1995), A d-separates X from Z (Fig. 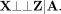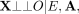1B):Formula (3) This means that, assuming X does not affect some unmeasured variable which in turn affects O (i.e., no horizontal pleiotropy), Formula (4) thereby satisfying the MR conditions regardless of any residual population stratification.

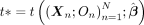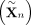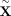    As shown by Bates et al. (2020), the DTT framework outlined in Algorithm 3 can be used to perform a hypothesis test conditioned on A. The resulting test involves computing the test statistic Formula (we give the statistic used in this paper in the subsection “MR-Twin test statistic incorporating external weights”). To perform a test, we construct B random samples Formula where each Formula is a random sample given A with the same distribution as X given A (such a sample can be easily constructed using Mendelian inheritance; see subsection “Generating digital twins”). 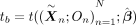We refer to these samples as “digital twins.” For each such sample b, we then compute Formula, representing a null distribution of genotypes conditioned on the parental genotypes. This, in turn, gives us a P-value for 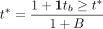Formula, where B is the total number of permutations we perform. The MR-Twin test is therefore a kind of conditional randomization test (Candès et al. 2018; Bates et al. 2020).

    Importantly, the proposed algorithm can leverage effect size estimates 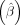Formula from any external GWAS data sets (even GWAS data sets in which such estimates might be biased owing to population stratification) while providing valid tests. The proposed algorithm is robust to any external confounder satisfying Equation 3, such as population stratification, assortative mating, and dynastic effects.

    Algorithm 3.

    Outline of MR-Twin

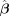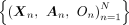
     1. Input: Effect sizes for SNPs: Formula, trio data Formula

     2. Compute the MR-Twin test statistic 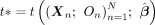Formula

     3. For b = 1 to B:

       (a) Sample digital twins 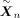Formula given their ancestors An.

       (b) Compute the MR-Twin test statistic 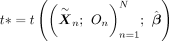Formula

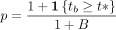
     4. Formula

    Output: P-value: P

     Next, we detail the MR-Twin test statistic, digital twin generation algorithms, and formal proofs of the exchangeability of digital twins with each other and their real counterparts.

    Conditional randomization test for MR

    The MR-Twin test is related to the DTT (Bates et al. 2020) and, likewise, is a kind of conditional randomization test (Candès et al. 2018). Like the DTT, MR-Twin leverages the fact that offspring genotypes are conditionally independent of “external” confounders such as population structure given the parental genotypes, and uses a conditional randomization test to test the weaker, but equivalent, null hypothesis of no effect conditioned upon the parental genotypes.

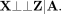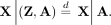    Let X be a vector of offspring genotypes, and let A be the genotype vectors of the two parents of the offspring. A may be directly observed, as in trio data, or inferred using parent–child duo or sibling data (see subsection “Generating digital twins”). Let Z be one or more “external” confounders, defined (Bates et al. 2020) asFormula (5) Thus, population structure is an external confounder, whereas horizontal pleiotropic traits are not. 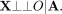We therefore haveFormula (6) Assuming that all confounders are external and that X is significantly associated with E, O is independent of X given A under the MR null hypothesis that E has no effect on O. This is because X would not have any effects on O mediated by E (because E does not affect O under the MR null hypothesis), and all paths not through E are blocked by conditioning on A as shown in Equation 6. We therefore want to testFormula (7) If this holds, then we cannot rule out that either X has no effect on E or E has no effect on O. We test this null hypothesis via a conditional randomization test (Candès et al. 2018).

    In testing this null hypothesis, it is helpful to be able to leverage SNP effect sizes estimated from large, external data sets (such as publicly released summary statistics for resources like the UK Biobank) (Bycroft et al. 2018), as this will often yield more statistically significant variants and better effect size estimates than those generated using small genetic family data sets. 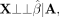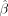We therefore note that the following property also holds:Formula (8) where we use the shorthand Formula to refer to the estimated effect sizes of each SNP on the exposure and outcome traits.

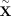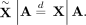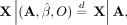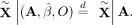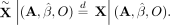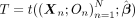    We construct “digital twins” Formula sampled from the parental genotypes via Mendelian inheritance (see subsection “Generating digital twins”) such thatFormula (9) Given Equations 7, 8, and 9, we have the following under the null hypothesis:Formula (10) Formula (11) It follows from Equations 9, 10, and 11 that the digital twins are exchangeable under the null hypothesis:Formula (12) Therefore, given some statistic Formula, where N is the number of families,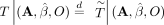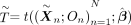Formula (13) under the null, where Formula. We can then use the procedure outline in Algorithm 3 to obtain a P-value for this test statistic (Candès et al. 2018).

    MR-Twin test statistic incorporating external weights

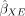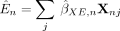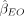    We construct a test statistic based on a negative sum of squares loss when using X to predict O via an MR estimate for the effect of E on O. First, we leverage the effect sizes from the external data set of the genotype on the exposure trait Formula to obtain the genetically predicted exposure trait values:Formula (14) for each individual n and SNP j. We then compute the MR estimate for the effect of the exposure trait on the outcome trait, Formula. This estimate may be a conventional IVW estimate (Burgess et al. 2013) or various statistics designed to be robust to pleiotropy such as the Egger-based statistic (Bowden et al. 2015), the weighted median statistic (Bowden et al. 2016), or others. We then predict the outcome trait for each individual n as 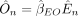Formula. Finally, we compute the negative squared error of these predictions 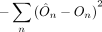Formula, summed across all individuals. The full statistic is then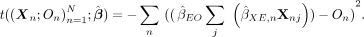Formula (15)

    Generating digital twins

    We have assumed that trio data are available thus far for simplicity. However, the MR-Twin framework can also be used when parent–child duo data or sibling data are available. Here we discuss the algorithms used to generate digital twins given trio, parent–child duo, or sibling data.

    Trio and duo modes

    We assume that the SNPs used in the MR instrument are independent, a common assumption when multi-SNP instruments are used in MR (Burgess et al. 2013). Therefore, we separately sample the genotype of each SNP of the digital twin given the parent and/or offspring genotypes at that SNP. Let (Dn) be the (N × M) matrix of digital twin genotypes we will sample, corresponding to the true “offspring” genotypes in (Xn). Further, let n index some family and j index some SNP, such that P1nj (e.g.) is the genotype for one parent in family n at SNP j. If we have both parents available, sampling Dnj is straightforward. Because the SNPs are considered independent, we do not need to know the parental haplotypes. If a parental genotype P1nj is zero or two, respectively, then a zero or one, respectively, is inherited by Dnj. If the parent genotype is one, then either zero or one is inherited with 50% probability each. Dnj inherits alleles from the two parents independently. This can be summarized as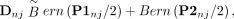Formula (16) where Bern stands for the Bernoulli distribution, for each family n and SNP j.

    If we only have one parent genotype available, then following the method of Bates et al. (2020), we fix the offspring's haplotype from the unobserved parent and only simulate a random draw from the observed parent's haplotype. If the observed parent is homozygous, then the allele inherited from that parent is fixed as well, so Dnj = Xnj. Otherwise, the allele inherited from this parent will be Bern(0.5). In principle, 0.5 could be replaced with some value based on population allele frequencies. Similar to that above, the model for the allele from the other parent can be written as Bern(Xnj/2). Thus, if the parent is a heterozygote, we have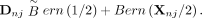Formula (17)

    Sibling mode

    In the case in which we observe sibling genotypes but not the genotypes of their parents, we assessed two potential approaches. In either case, the observed sibling information is used to infer the probabilities of digital twin genotypes based on the fact that the sibling genotypes give information about the probabilities of various parental genotypes. For instance, a child with a two genotype at an SNP guarantees that neither parent has a zero genotype at that SNP and makes it more likely that the parents have two genotypes than one genotypes. Most simply, if one sibling has a two genotype at an SNP and the other sibling has a zero, then the parents must both be heterozygotes. In all other cases, approximation is needed.

    The first approach is straightforward and involves randomly drawing two haplotypes from the observed sibling haplotypes to generate a digital twin. This shuffling approach gives a rough approximation of the likelihood of digital twin genotypes given the information the observed siblings provide. The second approach, described in the Supplemental Materials, involves using the sibling data to infer a distribution over the possible parents and then performing a weighted random draw of digital siblings based on those parents. In practice, we found that the shuffling approach was faster and yielded lower FPR than the probabilistic approach while achieving similar power, so we used the shuffling approach for the results in this paper.

    Software availability

    The code implementing the MR-Twin package can be found at GitHub (https://github.com/nlapier2/MR-Twin) and as Supplemental Code. Scripts and instructions for repeating the experiments in this paper can be found at GitHub (https://github.com/nlapier2/MRTwin-replication) and as Supplemental Code. Please note that UK Biobank genotypes are not publicly released, so those wishing to replicate the experiments will first have to get access to that data via the UK Biobank (https://www.ukbiobank.ac.uk/enable-your-research/apply-for-access).

    Previous SectionNext Section

    Competing interest statement

    The authors declare no competing interests.

    Previous SectionNext Section

    Acknowledgments

    This research has been conducted using the UK Biobank Resource under application number 33127. B.F. and S.S. were supported in part by National Institutes of Health (NIH) R35GM125055 and National Science Foundation (NSF) CAREER-1943497, III-2106908. E.E. and N.L. are funded by NSF award 2106908 and NIH awards U01HG011715 and R56HG010812. We thank Matthew J. Tudball for productive discussions on potential future work and our respective efforts to develop family-based MR methods.

    Author contributions: S.S. and E.E. conceived of and supervised the project. N.L., B.F., and S.S. developed the methods and wrote the manuscript. N.L., B.F., and S.T. wrote the software code and performed the analyses. All authors read and approved the final manuscript.

    Previous SectionNext Section

    Footnotes

    • Received January 5, 2023.
    • Accepted April 16, 2023.

    This article is distributed exclusively by Cold Spring Harbor Laboratory Press for the first six months after the full-issue publication date (see https://genome.cshlp.org/site/misc/terms.xhtml). After six months, it is available under a Creative Commons License (Attribution-NonCommercial 4.0 International), as described at http://creativecommons.org/licenses/by-nc/4.0/.

    Previous Section
     

    References

    1. ↵
      Abecasis GR, Cardon LR, Cookson W. 2000. A general test of association for quantitative traits in nuclear families. Am J Hum Genet 66: 279–292. doi:10.1086/302698
      CrossRefMedlineGoogle Scholar
    2. ↵
      Balding DJ, Nichols RA. 1995. A method for quantifying differentiation between populations at multi-allelic loci and its implications for investigating identity and paternity. Genetica 96: 3–12. doi:10.1007/BF01441146
      CrossRefMedlineGoogle Scholar
    3. ↵
      Bates S, Sesia M, Sabatti C, Candès E. 2020. Causal inference in genetic trio studies. Proc Natl Acad Sci 117: 24117–24126. doi:10.1073/pnas.2007743117
      Abstract/FREE Full Text
    4. ↵
      Benner C, Havulinna AS, Järvelin MR, Salomaa V, Ripatti S, Pirinen M. 2017. Prospects of fine-mapping trait-associated genomic regions by using summary statistics from genome-wide association studies. Am J Hum Genet 101: 539–551. doi:10.1016/j.ajhg.2017.08.012
      CrossRefGoogle Scholar
    5. ↵
      Berg JJ, Harpak A, Sinnott-Armstrong N, Joergensen AM, Mostafavi H, Field Y, Boyle EA, Zhang X, Racimo F, Pritchard JK, et al. 2019. Reduced signal for polygenic adaptation of height in UK Biobank. eLife 8: e39725. doi:10.7554/eLife.39725
      CrossRefMedlineGoogle Scholar
    6. ↵
      Border R, Athanasiadis G, Buil A, Schork AJ, Cai N, Young AI, Werge T, Flint J, Kendler KS, Sankararaman S, et al. 2022. Cross-trait assortative mating is widespread and inflates genetic correlation estimates. Science 378: 754–761. doi:10.1126/science.abo2059
      CrossRefGoogle Scholar
    7. ↵
      Bowden J, Davey Smith G, Burgess S. 2015. Mendelian randomization with invalid instruments: effect estimation and bias detection through Egger regression. Int J Epidemiol 44: 512–525. doi:10.1093/ije/dyv080
      CrossRefMedlineGoogle Scholar
    8. ↵
      Bowden J, Davey Smith G, Haycock PC, Burgess S. 2016. Consistent estimation in Mendelian randomization with some invalid instruments using a weighted median estimator. Genet Epidemiol 40: 304–314. doi:10.1002/gepi.21965
      CrossRefMedlineGoogle Scholar
    9. ↵
      Broadbent JR, Foley CN, Grant AJ, Mason AM, Staley JR, Burgess S. 2020. MendelianRandomization v0.5.0: updates to an R package for performing Mendelian randomization analyses using summarized data. Wellcome Open Res 5: 252. doi:10.12688/wellcomeopenres.16374.2
      CrossRefGoogle Scholar
    10. ↵
      Brumpton B, Sanderson E, Heilbron K, Hartwig FP, Harrison S, Vie GÅ, Cho Y, Howe LD, Hughes A, Boomsma DI, et al. 2020. Avoiding dynastic, assortative mating, and population stratification biases in Mendelian randomization through within-family analyses. Nat Commun 11: 3519. doi:10.1038/s41467-020-17117-4
      CrossRefMedlineGoogle Scholar
    11. ↵
      Burgess S, Thompson SG, CRP CHD Genetics Collaboration. 2011. Avoiding bias from weak instruments in Mendelian randomization studies. Int J Epidemiol 40: 755–764. doi:10.1093/ije/dyr036
      CrossRefMedlineGoogle Scholar
    12. ↵
      Burgess S, Butterworth A, Thompson SG. 2013. Mendelian randomization analysis with multiple genetic variants using summarized data. Genet Epidemiol 37: 658–665. doi:10.1002/gepi.21758
      CrossRefMedlineGoogle Scholar
    13. ↵
      Bycroft C, Freeman C, Petkova D, Band G, Elliott LT, Sharp K, Motyer A, Vukcevic D, Delaneau O, O'Connell J, et al. 2018. The UK Biobank resource with deep phenotyping and genomic data. Nature 562: 203–209. doi:10.1038/s41586-018-0579-z
      CrossRefMedlineGoogle Scholar
    14. ↵
      Candès E, Fan Y, Janson L, Lv J. 2018. Panning for gold: ‘model-X’ knockoffs for high dimensional controlled variable selection. J R. Statist Soc B 80: 551–577. doi:10.1111/rssb.12265
      CrossRefGoogle Scholar
    15. ↵
      Chen G, Yuan A, Shriner D, Tekola-Ayele F, Zhou J, Bentley AR, Zhou Y, Wang C, Newport MJ, Adeyemo A, et al. 2015. An improved Fst estimator. PLoS One 10: e0135368. doi:10.1371/journal.pone.0135368
      CrossRefGoogle Scholar
    16. ↵
      Cinelli C, LaPierre N, Hill BL, Sankararaman S, Eskin E. 2022. Robust Mendelian randomization in the presence of residual population stratification, batch effects and horizontal pleiotropy. Nat Commun 13: 1093. doi:10.1038/s41467-022-28553-9
      CrossRefGoogle Scholar
    17. ↵
      Conomos MP, Reiner AP, Weir BS, Thornton TA. 2016. Model-free estimation of recent genetic relatedness. Am J Hum Genet 98: 127–148. doi:10.1016/j.ajhg.2015.11.022
      CrossRefMedlineGoogle Scholar
    18. ↵
      Cook JP, Mahajan A, Morris AP. 2020. Fine-scale population structure in the UK Biobank: implications for genome-wide association studies. Hum Mol Genet 29: 2803–2811. doi:10.1093/hmg/ddaa157
      CrossRefGoogle Scholar
    19. ↵
      Fulker D, Cherny S, Sham P, Hewitt J. 1999. Combined linkage and association sib-pair analysis for quantitative traits. Am J Hum Genet 64: 259–267. doi:10.1086/302193
      CrossRefMedlineGoogle Scholar
    20. ↵
      Haase CL, Tybjærg-Hansen A, Ali Qayyum A, Schou J, Nordestgaard BG, Frikke-Schmidt R. 2012. LCAT, HDL cholesterol and ischemic cardiovascular disease: a Mendelian randomization study of HDL cholesterol in 54,500 individuals. J Clin Endocrinol Metab 97: E248–E256. doi:10.1210/jc.2011-1846
      CrossRefMedlineGoogle Scholar
    21. ↵
      Hartwig FP, Davey Smith G, Bowden J. 2017. Robust inference in summary data Mendelian randomization via the zero modal pleiotropy assumption. Int J Epidemiol 46: 1985–1998. doi:10.1093/ije/dyx102
      CrossRefMedlineGoogle Scholar
    22. ↵
      Hartwig FP, Davies NM, Davey Smith G. 2018. Bias in Mendelian randomization due to assortative mating. Genet Epidemiol 42: 608–620. doi:10.1002/gepi.22138
      CrossRefMedlineGoogle Scholar
    23. ↵
      Haworth S, Mitchell R, Corbin L, Wade KH, Dudding T, Budu-Aggrey A, Carslake D, Hemani G, Paternoster L, Smith GD, et al. 2019. Apparent latent structure within the UK Biobank sample has implications for epidemiological analysis. Nat Commun 10: 333. doi:10.1038/s41467-018-08219-1
      CrossRefMedlineGoogle Scholar
    24. ↵
      Haycock PC, Burgess S, Nounu A, Zheng J, Okoli GN, Bowden J, Wade KH, Timpson NJ, Evans DM, Willeit P, et al. 2017. Association between telomere length and risk of cancer and non-neoplastic diseases: a Mendelian randomization study. JAMA Oncol 3: 636–651. doi:10.1001/jamaoncol.2016.5945
      CrossRefGoogle Scholar
    25. ↵
      Hemani G, Zheng J, Elsworth B, Wade KH, Haberland V, Baird D, Laurin C, Burgess S, Bowden J, Langdon R, et al. 2018. The MR-Base platform supports systematic causal inference across the human phenome. eLife 7: e34408. doi:10.7554/eLife.34408
      CrossRefMedlineGoogle Scholar
    26. ↵
      Hubisz MJ, Falush D, Stephens M, Pritchard JK. 2009. Inferring weak population structure with the assistance of sample group information. Mol Ecol Resour 9: 1322–1332. doi:10.1111/j.1755-0998.2009.02591.x
      CrossRefMedlineGoogle Scholar
    27. ↵
      Labrecque JA, Swanson SA. 2019. Interpretation and potential biases of Mendelian randomization estimates with time-varying exposures. Am J Epidemiol 188: 231–238. doi:10.1093/aje/kwy204
      CrossRefMedlineGoogle Scholar
    28. ↵
      Laird NM, Lange C. 2006. Family-based designs in the age of large-scale gene-association studies. Nat Rev Genet 7: 385–394. doi:10.1038/nrg1839
      CrossRefMedlineGoogle Scholar
    29. ↵
      Lawlor DA. 2016. Commentary: two-sample Mendelian randomization: opportunities and challenges. Int J Epidemiol 45: 908–915. doi:10.1093/ije/dyw127
      CrossRefMedlineGoogle Scholar
    30. ↵
      Lawlor DA, Harbord RM, Sterne JA, Timpson N, Davey Smith G. 2008. Mendelian randomization: using genes as instruments for making causal inferences in epidemiology. Stat Med 27: 1133–1163. doi:10.1002/sim.3034
      CrossRefMedlineGoogle Scholar
    31. ↵
      Lyall DM, Celis-Morales C, Ward J, Iliodromiti S, Anderson JJ, Gill JM, Smith DJ, Ntuk UE, Mackay DF, Holmes MV, et al. 2017. Association of body mass index with cardiometabolic disease in the UK Biobank: a mendelian randomization study. JAMA Cardiology 2: 882–889. doi:10.1001/jamacardio.2016.5804
      CrossRefMedlineGoogle Scholar
    32. ↵
      Ochoa A, Storey JD. 2021. Estimating FST and kinship for arbitrary population structures. PLoS Genet 17: e1009241. doi:10.1371/journal.pgen.1009241
      CrossRefGoogle Scholar
    33. ↵
      Pearl J. 1995. Causal diagrams for empirical research. Biometrika 82: 669–688. doi:10.1093/biomet/82.4.669
      CrossRefGoogle Scholar
    34. ↵
      Peterson RE, Kuchenbaecker K, Walters RK, Chen CY, Popejoy AB, Periyasamy S, Lam M, Iyegbe C, Strawbridge RJ, Brick L, et al. 2019. Genome-wide association studies in ancestrally diverse populations: opportunities, methods, pitfalls, and recommendations. Cell 179: 589–603. doi:10.1016/j.cell.2019.08.051
      CrossRefMedlineGoogle Scholar
    35. ↵
      Pingault JB, O'Reilly PF, Schoeler T, Ploubidis GB, Rijsdijk F, Dudbridge F. 2018. Using genetic data to strengthen causal inference in observational research. Nat Rev Genet 19: 566–580. doi:10.1038/s41576-018-0020-3
      CrossRefGoogle Scholar
    36. ↵
      Price AL, Patterson NJ, Plenge RM, Weinblatt ME, Shadick NA, Reich D. 2006. Principal components analysis corrects for stratification in genome-wide association studies. Nat Genet 38: 904–909. doi:10.1038/ng1847
      CrossRefMedlineGoogle Scholar
    37. ↵
      Price AL, Zaitlen NA, Reich D, Patterson N. 2010. New approaches to population stratification in genome-wide association studies. Nat Rev Genet 11: 459–463. doi:10.1038/nrg2813
      CrossRefMedlineGoogle Scholar
    38. ↵
      Pritchard JK, Stephens M, Donnelly P. 2000. Inference of population structure using multilocus genotype data. Genetics 155: 945–959. doi:10.1093/genetics/155.2.945
      Abstract/FREE Full Text
    39. ↵
      Purcell S, Neale B, Todd-Brown K, Thomas L, Ferreira MA, Bender D, Maller J, Sklar P, De Bakker PI, Daly MJ, et al. 2007. PLINK: a tool set for whole-genome association and population-based linkage analyses. Am J Hum Genet 81: 559–575. doi:10.1086/519795
      CrossRefMedlineGoogle Scholar
    40. ↵
      Spielman RS, McGinnis RE, Ewens WJ. 1993. Transmission test for linkage disequilibrium: the insulin gene region and insulin-dependent diabetes mellitus (IDDM). Am J Hum Genet 52: 506–516.
      MedlineGoogle Scholar
    41. ↵
      Thomson G. 1995. Mapping disease genes: family-based association studies. Am J Hum Genet 57: 487.
      MedlineGoogle Scholar
    42. ↵
      Tudball MJ, Smith GD, Zhao Q. 2022. Almost exact Mendelian randomization. arXiv:2208.14035 [stat.ME].
      Google Scholar
    43. ↵
      Tyrrell J, Jones SE, Beaumont R, Astley CM, Lovell R, Yaghootkar H, Tuke M, Ruth KS, Freathy RM, Hirschhorn JN, et al. 2016. Height, body mass index, and socioeconomic status: Mendelian randomisation study in UK Biobank. BMJ 352: i582. doi:10.1136/bmj.i582
      Abstract/FREE Full Text
    44. ↵
      Wade KH, Carslake D, Sattar N, Davey Smith G, Timpson NJ. 2018. BMI and mortality in UK Biobank: revised estimates using Mendelian randomization. Obesity 26: 1796–1806. doi:10.1002/oby.22313
      CrossRefMedlineGoogle Scholar
    45. ↵
      Weiner DJ, Wigdor EM, Ripke S, Walters RK, Kosmicki JA, Grove J, Samocha KE, Goldstein JI, Okbay A, Bybjerg-Grauholm J, et al. 2017. Polygenic transmission disequilibrium confirms that common and rare variation act additively to create risk for autism spectrum disorders. Nat Genet 49: 978–985. doi:10.1038/ng.3863
      CrossRefMedlineGoogle Scholar
    46. ↵
      Yavorska OO, Burgess S. 2017. MendelianRandomization: an R package for performing Mendelian randomization analyses using summarized data. Int J Epidemiol 46: 1734–1739. doi:10.1093/ije/dyx034
      CrossRefMedlineGoogle Scholar
    | Table of Contents

    This Article

    1. Published in Advance May 17, 2023, doi: 10.1101/gr.277664.123 Genome Res. 33: 1032-1041 © 2023 LaPierre et al.; Published by Cold Spring Harbor Laboratory Press

    Article Category

    ORCID

    1. Profile for LaPierre, N.http://orcid.org/0000-0003-2394-8868
    2. Profile for Fu, B.http://orcid.org/0000-0002-0082-8735
    3. Profile for Eskin, E.http://orcid.org/0000-0003-1149-4758
    4. Profile for Sankararaman, S.http://orcid.org/0000-0003-1586-9641

    Share

    Preprint Server



    Navigate This Article

    Current Issue

    1. February 2026, 36 (2)
    1. Current Issue
    1. Alert me to new issues of Genome Research