Assembler artifacts include misassembly because of unsafe unitigs and underassembly because of bidirected graphs
- 1Department of Computer Science and Engineering, The Pennsylvania State University, University Park, Pennsylvania 16802, USA;
- 2Department of Biochemistry and Molecular Biology, The Pennsylvania State University, University Park, Pennsylvania 16802, USA;
- 3Huck Institutes of the Life Sciences, The Pennsylvania State University, University Park, Pennsylvania 16802, USA
Abstract
Recent assemblies by the T2T and VGP consortia have achieved significant accuracy but required a tremendous amount of effort and resources. More typical assembly efforts, on the other hand, still suffer both from misassemblies (joining sequences that should not be adjacent) and from underassemblies (not joining sequences that should be adjacent). To better understand the common algorithm-driven causes of these limitations, we investigated the unitig algorithm, which is a core algorithm at the heart of most assemblers. We prove that, contrary to popular belief, even when there are no sequencing errors, unitigs are not always safe (i.e., they are not guaranteed to be substrings of the sequenced genome). We also prove that the unitigs of a bidirected de Bruijn graph are different from those of a doubled de Bruijn graph and, contrary to our expectations, result in underassembly. Using experimental simulations, we then confirm that these two artifacts exist not only in theory but also in the output of widely used assemblers. In particular, when coverage is low, then even error-free data result in unsafe unitigs; also, unitigs may unnecessarily split palindromes in half if special care is not taken. To the best of our knowledge, this paper is the first to theoretically predict the existence of these assembler artifacts and confirm and measure the extent of their occurrence in practice.
Reconstructing the full sequence of a genome from its sequencing data remains one of the most challenging problems in bioinformatics. Assemblers have suffered both from misassemblies (putting together sequences that should not be adjacent) and underassemblies (not putting together sequences whose adjacency should be apparent from the data) (Alkan et al. 2011; Simpson and Pop 2015). Recent efforts by the Telomere-to-Telomere (T2T) consortium (Miga et al. 2020; Nurk et al. 2022) and the Vertebrate Genome Project (VGP) (Rhie et al. 2021) showed how long-read technologies, long-range contact mapping, and manual curation can alleviate these errors. However, the time and cost of those efforts remain prohibitive for most biology laboratories. In such cases, mis- and underassemblies continue to be a major limitation (e.g., Yang et al. 2021).
Understanding the common algorithm-driven causes of these limitations is made complicated by the diversity and complexity of assembly algorithms. We can start by focusing on assemblers that use de Bruijn graphs (dBGs) (Idury and Waterman 1995), which continue to be popular even for long-read data (Bankevich et al. 2022). But even dBG-based assemblers differ on how they handle complexities arising from sequencing errors, heterogeneity, or DNA double-strandedness. Nevertheless, most assemblers are built on top of the unitig algorithm, which returns all the maximal unitigs in an assembly graph (Simpson and Pop 2015); a unitig is a path whose vertices have exactly one incoming and one outgoing edge, with the exception that the first and last vertex can have any number of incoming and outgoing edges, respectively. Being a common denominator of most assemblers, the unitig algorithm is a good target for investigating shared sources of mis- and underassemblies.
It is already known that the unitig algorithm contributes to underassembly (e.g., see the safe and complete framework of Tomescu and Medvedev 2016; Cairo et al. 2020) and can trivially create misassemblies when there are sequencing errors. The effect of sequencing errors on assembly errors has even been theoretically studied more broadly by Shomorony et al. (2015, 2016a,b). However, it is widely assumed that if it were not for sequencing errors, unitigs would always be safe (i.e., substrings of the sequenced genome). In an earlier work (Medvedev 2019), we attempted to formally prove this but could only do so by assuming perfect coverage. This assumption was also necessary in another earlier work (Tomescu and Medvedev 2016), where it was suggested that without it, unitigs may not be safe. Unitigs were also implied to be unsafe in certain models of the assembly problem (Cairo et al. 2020). We therefore hypothesize that, contrary to popular belief, there are noncontrived conditions that lead to unsafe unitigs on error-free data.
The unitig algorithm also needs to account for the fact that the strand from which a read is sequenced is unknown. Most assemblers do so via two common approaches to constructing the dBG. In one, every k-mer is “doubled” before constructing the dBG; that is, for every k-mer in the input, both it and its reverse complement are added to the dBG (e.g., SPAdes) (Bankevich et al. 2012). In the other approach, edges are given two instead of one orientation, thereby capturing the way that double-stranded strings can overlap. This results in a bidirected dBG (Medvedev et al. 2007), used in assemblers such as ABySS (Simpson et al. 2009; Jackman et al. 2017). Because this is a more elegant construction for capturing the double-stranded nature of the data, one would hypothesize that it should not hurt assembly accuracy. In this paper, we will perform a theoretical and empirical study to validate our two hypotheses about common algorithm-driven sources of mis- and underassemblies.
Results
Summary of findings
First, despite widespread belief, we show that even on error-free data, unitigs do not always appear in the sequenced genome (i.e., they are unsafe). Our experimental results confirm that at least two different assemblers show this behavior in practice. Second, we establish that there is a bijection between maximal unitigs in the doubled and bidirected dBGs, except that palindromic unitigs in the doubled dBG are split in half in the bidirected dBG. This shows that, contrary to intuition, naively using the bidirected graph actually contributes to underassembly compared with the doubled graph. Our experimental results confirm that this artifact appears in some assemblers but not in others. Nevertheless, we also find that the extent of these two artifacts is limited. To the best of our knowledge, this paper is the first to theoretically predict the existence of these assembler artifacts and confirm and measure the extent of their occurrence in practice.
Theoretical results
The main theoretical results in this paper are two theorems, whose precise statement is given in the Methods. Theorem 1 gives a characterization of unitigs that are unsafe; that is, they are not present in the sequenced parts of the genome. Theorem 2 breaks down the categories of maximal unitigs in the doubled dBG and the bidirected dBG and gives a relationship between the two. For the doubled graph, the set of maximal unitigs is partitioned into nonpalindromic strings (Dnon-pal) and palindromic strings (Dpal). For the bidirected graph, the maximal unitigs is partitioned into three sets: Bno-loop, Bfirst-loop, and Blast-loop. Theorem 2 states that there is a one-to-one correspondence between Dnon-pal and Bno-loop. However, each Dnon-pal unitig is split in half in the bidirected graph, with one half appearing in Bfirst-loop and the other half appearing in Blast-loop.
Occurrence of unsafe unitigs in real genomes
Theorem 1 predicts the possibility of unsafe unitigs. To verify the extent to which this happens with real genomes, we use T2T human reference Chromosome 1 (Nurk et al. 2022). We simulated error-free reads of length 100 with varying target coverages and varying k. Note that for this experiment, we want to test if misassemblies occur even when the data are perfect, so making the reads error-free is necessary. The sequenced read intervals correspond to the source location of each simulated read, and the sequenced segments are defined as in previous section. From these reads, we constructed the basic dBG and output its maximal unitigs, using a version of BCALM (Chikhi et al. 2014; Chikhi 2016) modified to ignore reverse complementary. We confirmed that the unitigs that were unsafe (i.e., not a substring of the sequenced segments) were exactly the unitigs that satisfied the conditions of Theorem 1.
Table 1 shows the number of unsafe unitigs, as a function of the coverage and of k. There are as many as 17,635 unsafe unitigs (at coverage 2 × and k = 71). The best indicator for the number of unsafe unitigs is the percentage of k-mers sampled (or the number of sequenced segments); that is, the number of unsafe unitigs goes down as the percentage of sampled k-mers goes up. This trend is in line with the prediction of Corollary 1, which states that once the coverage is perfect, we expect to see at most one unsafe unitig. Our results indicate that the artifacts identified by Theorem 1 do occur in real genomes, although they become less common as more of the genomic k-mers are sampled.
The presence of unsafe and misassembled unitigs in human Chromosome 1, using simulated error-free reads
An unsafe unitig is not necessarily a misassembly, as it may be a substring of the unsequenced genome by luck. We define an unitig to be misassembled if its spelling is not a substring of the reference. Table 1 shows that the number of misassembled unitigs is substantially lower than the unsafe unitigs, for example, with 708 misassembled unitigs at 2 × coverage and k = 71. Thus, the potential for misassembly does not usually translate into a real misassembly, although many misassemblies remain.
We further check how many of these misassembled unitigs fit the example in Figure 3. A formal definition to capture this example is included in Corollary 2 for reference. Table 1 shows that the vast majority of misassembled cases are in fact caused by this situation, in which a repeat has an occurrence in which its start is unsequenced and another occurrence in which its end is unsequenced.
The simulations in Table 1 suggest that the misassembly artifact can be removed by simply increasing coverage. In a metagenome experiment, however, this is not always possible. Even when one increases the number of reads, there will continue to be genomes in the sample whose abundance is low enough that their coverage is low. To verify this intuition, we used a standard benchmark data set generated by the CAMI competition (Sczyrba et al. 2017), containing 70 million synthetic reads from 30 genomes. Table 2 shows there are 33–37 misassembled unitigs, indicating that this artifact remains under realistic coverage of a metagenomic data set. The section “CAMI dataset” in Supplemental Material, section C contains more details about the experiment, including Supplemental Table S1 which shows the details of the data set (Nurk et al. 2017; Fritz et al. 2019).
The presence of unsafe and misassembled unitigs in the CAMI data set, using simulated error-free reads
Presence of unsafe unitigs in the contig output of real assemblers
We investigated the extent to which the artifact predicted by Theorem 1 appears in output of real assemblers. Assemblers do not simply output the unitigs of a graph but perform many other steps; hence, it was not clear if this artifact would appear in the output contigs. It is not clear how to verify this artifact with real data, as sequencing errors make it difficult to know which of the misassembled contigs are caused by the conditions of Theorem 1. We therefore again used a simulated error-free data set from the T2T Chromosome 1, using the ART simulator (Huang et al. 2012), with read length of 250 and varying coverages. This time, we simulated reads from either strand, because assemblers are not typically run in single-stranded mode. We also used the CAMI data set, but simulating reads in double-stranded mode. We then constructed the doubled dBG using k = 74 and outputting its maximal unitigs (note that Theorem 1 holds for even k). We also ran SPAdes (Bankevich et al. 2012) and MEGAHIT (Li et al. 2015) to assemble the reads (for parameter details, see Corollary 2). We then identified unitigs and the assembler contigs that were misassembled, but allowed for reverse complements. We will say that a string x matches a string y with a threshold of t if a fraction t of the k-mers of x occur in y.
Tables 3 and 4 show that nearly all of the misassembled unitigs matched at least one misassembled SPAdes contig with a threshold of one. For MEGAHIT, the threshold of one turned out to be stringent; this is not surprising, because assemblers have many steps that may add or remove k-mers from the graph. In addition, MEGAHIT varies the value of k internally and may therefore join k-mers that do not have an overlap of length k − 1. Using a threshold of 0.5, however, we found that, similar to SPAdes, most misassembled unitigs matched a misassembled contig of MEGAHIT. These results indicate that the artifact predicted by Theorem 1 appears not only in unitigs of the raw graph but also in the output of widely used assemblers like SPAdes and MEGAHIT.
The extent to which misassembled unitigs contribute to misassembled contigs of real assemblers
The extent to which misassembled unitigs contribute to misassembled contigs of real assemblers for the CAMI metagenomic data set
Presence of palindrome splitting in a real genome
To measure the extent of the “palindrome splitting” artifact predicted by Theorem 2, we let K be the set of all constituent k-mers in human Chromosome 21 (GRCh38.p13), after excising the Ns. We confirmed the correctness of Theorem 2 by verifying that the spellings of Dnon-pal are equal to the spellings of Bno-loop and that the spellings of Blast-loop are equal to the spellings of Dpal and are the reverse complements of the spellings of Bfirst-loop. Table 5 shows that the splitting artifact is present but rare; for example, for k = 15, there were 186 palindromic maximal unitigs in Gdbl(K) that were split in Gbid(K). The artifact becomes rarer with increasing k (e.g., for k = 43, there were only three split palindromes), which is expected because palindrome frequency in real genomes decreases with length.
Extent of the palindrome splitting artifact predicted by Theorem 2 in Chr 21
Presence of palindrome splitting in real assemblers
Most assembler papers do not contain enough detail to ascertain what kind of dBG they use to handle reverse complements nor what modifications, if any, they make to the unitig algorithm used for the final output. Looking at MEGAHIT (Li et al. 2015), SPAdes (Bankevich et al. 2012), ABySS (Simpson et al. 2009; Jackman et al. 2017), and minia (Chikhi and Rizk 2013), only the SPAdes paper is unambiguously clear in saying how it handled reverse complements (it used the doubled dBG). Furthermore, because these assemblers implement many heuristics, the splitting artifact may be absent (respectively, present) even if they did (respectively, did not) use bidirected graphs. We therefore tested the behavior of these assemblers by looking for evidence of palindrome splitting in their output rather than in their technical descriptions.
Because large exact palindromes are uncommon in typical genomes, we created a synthetic genome by modifying an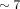 
million-bp-long contig from human Chromosome 4 (GRCh38.p13) as follows. We randomly sampled a 1000-bp-long region and replaced
the last 500 bp by the reverse complement of first 500 bp; we then repeated the sampling process 700,000 times. We then simulated
error-free Illumina reads with ART. We used a read length of 100 bp so that assemblers will not be able to supplement the
dBG with read information in a way that hides the palindrome splitting artifact. We used 10× coverage so that most k-mers would be sampled.
First, we find the reference location of each unitig w in Dpal. Then, we find all exact alignments of the assembler contigs to the reference. We say that w is fully covered if there exists a contig whose alignment spans w’s. Otherwise, we say w is split if one-half of w’s region does not overlap with any contig alignments whereas the other half has a contig aligned that ends precisely in the middle of w at one end and extends past w at the other end. A unitig is ambiguous if it does fall into either category. Corollary 2 contains a more precise definition of these cases.
Table 6 shows that ABySS clearly shows the palindrome splitting artifact, with all nonambiguous unitigs being split and none fully covered. In fact, this is because of a heuristic that breaks unitigs at any palindromic edges or vertices (see relevant code at https://github.com/bcgsc/abyss/blob/master/Common/Kmer.cpp). The opposite was true for SPAdes and MEGAHIT, with all nonambiguous unitigs being fully covered and none split. minia, on the other hand, showed mixed behavior. Of the 417 nonambiguous cases, 34 were split and 383 were fully covered. These results indicate that the palindrome splitting artifact of Theorem 2 does persist all the way to the contig output stage in some assemblers. However, this artifact requires the presence of long exact palindromes in the reference, which is uncommon in most genomes.
Presence of the palindrome splitting artifact in real assemblers on a synthetic genome
Discussion
Our theoretical study uncovered two artifacts of the unitig algorithm for genome assembly. The first is that even without sequencing errors, it can create misassemblies in places of imperfect coverage. The second is that when the bidirected graph is used to model double-strandedness, the unitig algorithm underassembles by failing to merge the two halves of palindromes. Our experiments confirmed the presence of these theoretically predicted artifacts in real genomes and popular assemblers. Fortunately, the impact of these artifacts is not large and can be addressed. Misassembly issues owing to the first artifact can be resolved by increasing coverage or, potentially, breaking unitigs at places where the coverage along them is uneven. Underassembly issues owing to the palindrome artifact are rare in real genomes and, moreover, can sometimes be fixed by forcing the unitigs to “push their way through” lonely inverted loops (however, it is not always possible) (e.g., Bushmanova et al. 2019; Meleshko et al. 2021).
One of the tangential outcomes of this paper is that we have given proper definitions for things like walks and unitigs in the context of bidirected graphs. Previous papers used these concepts somewhat informally; when definitions were given, they worked in the context of that paper but failed to have more general desired properties. For example, our previous work had an inconsistency in the way that a walk was defined on a single vertex versus on many vertices (Rahman et al. 2021). One key takeaway is that as a rule of thumb, when working with bidirected graphs one should avoid thinking in terms of vertices but think instead of vertex-sides. The definitions we have provided in this paper generalize further than previous ones and are able to form the basis for the type of analysis we have performed in this paper. For example, we are the first to prove the bijection between walks in the doubled and bidirected dBGs. We hope that these definitions will facilitate future attempts to formally study questions in bidirected graphs.
Bidirected graphs give an elegant way to capture the double-stranded nature of DNA in a dBG, but our results here indicate that, for the unitig algorithm, they do not give any theoretical advantage. One of the claimed advantages of using the bidirected graph framework in assembly is that it allows one to take advantage of results from graph theory that may otherwise be hidden. The primary example of this is a result (involving one of the investigators) in work by Medvedev et al. (2007), in which a variant of the assembly problem was theoretically solved in polynomial time by relying on a reduction to the flow problem in bidirected graphs (Gabow 1983). When viewed in retrospect, however, it is not clear that this connection was necessary. The algorithm being reduced to that of Gabow (1983) was too cumbersome to implement, and when the assembly problem later necessitated a software solution, an approximation algorithm was used instead (Medvedev and Brudno 2008; Medvedev et al. 2010). But the approximation algorithm worked on the doubled graph, erasing the advantage of having initially formulated the problem on bidirected graphs. Therefore, it remains to be seen if there are situations in which the connection to graph theoretical results on bidirected graphs can prove useful for genome assembly. Alternatively, using a different setting may better help identify the advantages of bidirected graphs, for example, pangenomics (Paten et al. 2017), rearrangement analysis (Bergeron et al. 2006), or compression (Rahman and Medevedev 2021). Quantifying these advantages would be an exciting future direction.
Methods
Preliminaries
In this section, we give the formal definitions for our paper. The reader may wish to delay reading the last three paragraphs (relating to bidirected graphs) until they are used later in the text.
Strings
In this paper, we assume all strings are over the four-letter DNA alphabet. A string of length k is called a k-mer. We define sufk(x) (respectively, prek(x)) to be the last (respectively, first) k characters of x. When the subscript is omitted from pre and suf, we assume it is k − 1. For x and y with suf(x) = pre(y), we define gluing x and y, denoted by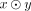 
, as x concatenated with the last |y| − k + 1 characters of y. Given two strings x and y, we define occy(x) as the number of times that x occurs in y. The reverse complement of x is denoted as 
. For a set of strings S,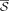 
denotes the set of the reverse complements of all strings of S. A string x is a palindrome iff 
. A string x is canonical if it is the lexicographically smaller of x and 
. For s ∈ {0, 1}, we define orient(x, s) to be x if s = 0 and to be 
if s = 1. To canonize x is to replace it by its canonical version,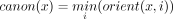 
. We say that x0 and x1 have a (s0, s1)-oriented overlap if suf(orient(x0, 1 − s0)) = pre(orient(x1, s1)). Informally, such an overlap exists between two strings if we can orient them in such a way that they are glueable. For
example, GTT and TTG have a (1, 0)-oriented overlap, and AAC and TTG have a (0, 0)-oriented overlap. We define the noncanonical k-spectrum spk(x) as the set of all k-mer substrings of x.
Directed dBGs
Given a set of k-mers K, the basic node-centric-directed dBG, Gbasic(K), is directed graph where nodes are the k-mers of K, and an edge exists from k-mer x to k-mer y iff suf(x) = pre(y). A double-directed dBG on K, Gdbl(K) is a basic dBG on the set of k-mers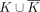 
; that is, 
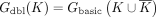. Observe that for any k-mer x such that 
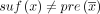, the existence of the edge from x to y in Gdbl(K) implies the existence of a different edge from 
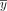to 
. We refer to such a pair of edges as mirrors. For a k-mer x such that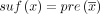 
, the Gdbl(K) will contain an edge from x to 
; we call this edge a self-mirror.
Walks and unitigs in directed graphs
For a vertex x in a directed graph, the in-degree d−(x) (respectively, out-degree d+ (x)) is the number of edges incoming to (respectively, outgoing from) it. The sequence of vertices w = (x0, …, xn), for n ≥ 0, is a walk iff for all 1 ≤ i ≤ n, there exists an edge from xi−1 to xi. Vertices x0 and xn are called endpoints, and a walk sometimes has one endpoint. The spelling of a walk is defined as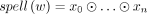 
. A walk is said to be circular iff n ≥ 1 and x0 = xn, and as a simple cycle if for all i and j such that 0 ≤ i < j ≤ n, xi = xj implies i = 0 and j = n. A simple periodic cycle is a walk that starts with a simple cycle and then keeps on looping around it without ever exiting;
formally, a walk is a simple periodic cycle if there exists 0 ≤ i ≤ n − 1 such that (x0, …, xi) is a simple cycle and xi+1, …, xn is a repetition of x0, …, xi, except the last repetition may be partial. A walk is a unitig if it is not a periodic cycle and for all 1 ≤ i ≤ n, d−(xi) = 1 and for all 0 ≤ i ≤ n − 1, d+ (xi) = 1. A unitig is maximal if it is not a proper subwalk of another unitig.
Bidirected dBG
A bidirected graph G is a pair (V, E) in which the set V is called vertices and E is a set of edges. Informally, every vertex has two sides; formally, a vertex-side is a pair (u, s), in which u ∈ V and s ∈ {0, 1}. An edge e is a set of two vertex-sides {(u0, s0), (u1, s1)}, where ui ∈ V and si ∈ {0, 1}, for i ∈ {0, 1}. Informally, an edge is an undirected connection between two (not-necessarily-distinct) vertex-sides. We say that an edge e is incident to each of the two vertex-sides. Note that there can be multiple edges between two vertices, but only one edge once the sides are fixed. A labeled bidirected graph is a bidirected graph G in which every vertex u has a string label lab(u) and for every edge e = {(u0, s0), (u1, s1)}, there is a (s0, s1)-oriented overlap between lab(u0) and lab(u1). G is said to be overlap-closed if there is an edge for every such overlap. Let K be a set of canonical k-mers. The node-centric bidirected dBG, denoted by Gbid(K), is the overlap-closed-labeled bidirected graph in which the vertices and their labels correspond to K. Supplemental Figure S1A shows an example of a bidirected graph.
Walks and unitigs in bidirected graphs
An edge in a bidirected graph is an inverted loop if its two vertex-sides are equal. An inverted loop {(u, s), (u, s)} is lonely if it is the only edge incident to (u, s). We define the degree of a vertex-side d(u, s) to be the number of edges incident to it, but with an inverted loop contributing two to the degree. A sequence t = (u0, s0, u1, s1, …, un, sn) with n ≥ 0 is a walk if for all 1 ≤ i ≤ n, there exists an edge ei = {(ui−1, 1 − si−1), (ui, si)}. The vertex-sides (u0, s0) and (un, 1 − sn) are called the first and last endpoint sides, respectively. Note that even when n = 0, there are two endpoint sides. The spelling of a walk is defined as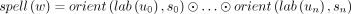 
. The reverse of t is rev(t) = (un, 1 − sn, …, u0, 1 − s0). Note that, as expected, 
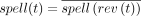. Note that if t′ is a subwalk of t, then rev(t′) is a subwalk of rev(t) and spell(t′) is a substring of spell(t) (the converse is not necessarily true when k is even). Supplemental Figure S1B,C gives an example illustrating a walk in a bidirected graph, and Supplemental Figure S1D shows a corresponding walk in a double-directed dBG.
A walk w = (u0, s0, …, un, sn) is said to be circular iff n ≥ 1 and (u0, s0) = (un, sn) and to be a simple cycle if for all i and j such that 0 ≤ i < j ≤ n, (ui, si) = (uj, sj) implies i = 0 and j = n. A simple periodic cycle is a walk that starts with a simple cycle and then keeps on looping around it without ever exiting; formally, w is a simple periodic cycle if there exists 0 ≤ i ≤ n − 1 such that (u0, s0, …, ui, si) is a simple cycle and (ui+1, si+1, …, un, sn) is a repetition of (u0, s0, …, ui, si), except the last repetition may be partial. A walk is a unitig if it is not a periodic cycle and for all 1 ≤ i ≤ n, d−(xi) = 1 and for all 0 ≤ i ≤ n − 1, d+ (xi) = 1. A walk (u0, s0, …, un, sn) is a unitig if it is not a periodic cycle and for all 0 ≤ i < n, d(ui, 1 − si) = 1 and for all 0 < i ≤ n, d(ui, si) = 1. A unitig is said to be maximal if it is not a proper subwalk of another unitig. Note that all the subwalks of a unitig must themselves be unitigs.
Safety of unitigs
In this subsection, we will give necessary and sufficient conditions for a unitig to be unsafe in the basic dBG constructed from error-free reads. To properly formulate this question, we define a sequenced read interval as a genomic interval that generated a read, that is, from which a read was sequenced. A sequencing experiment then corresponds to a set of sequenced read intervals. A sequenced interval is then defined as a maximal interval that is covered by sequenced read intervals, with the additional constraint that any two consecutive sequenced intervals overlap by at least k − 1. We define a sequenced segment as the string corresponding to a sequenced interval.
Observe that the sequenced intervals do not overlap by more than k − 2 bases (otherwise they would not be maximal), but the sequenced segment may have longer overlaps owing to repeats. A set
of reads then induces a set 
of sequenced segments. Figure 1 illustrates this formulation. In this subsection, we do not explicitly account for reverse complements, because they will
be considered in the next subsection.
Illustration of sequenced segments. The black text on top shows the reference genome of length 26. The seven sequences in red are reads aligned to the reference. The green boxes highlight the resulting sequenced segments when k = 3. Note that the reads TACCG and GCCTA form two separate segments as the k-mer CGC is not present in K.
Given a set of sequenced segments S, we say that a unitig w in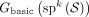 
is unsafe iff spell(w) is not a substring of a string in S. Equivalently, w is unsafe iff it is not a subwalk of a walk that corresponds to a string in S. Our definition of unsafe captures the notion
of a potential misassembly, as the unitig is not present in the sequenced part of the genome. (The safety of unitigs has been
previously studied for other notions of “safety” by Cairo et al. [2020]. Although the investigators did not make the explicit conclusion and did not verify it in practice, their Theorem 6.1(d)
implies that unitigs are not guaranteed to be safe in the model of assembly they consider. Concretely, although a suffix or
prefix of the unitig may be present at the starts and ends of parts of the genome, the whole unitig might never be contained
as a contiguous sequence.)
Observe that in formulating the problem, we start with the set of sequenced segments themselves; the read set that induced them is irrelevant. We can now state the main result of this subsection, which gives the necessary and sufficient conditions for a unitig to be unsafe. The proof of this theorem, along with the necessary lemmas, is left for Corollary 2 owing to space constraints.
Theorem 1. Let S be a set of sequenced segments, and let w = (x0, …, xm) be a unitig in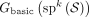 
. Then w is unsafe if and only if for all 
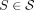, one of the following holds:
-
S does not contain any k − mer of w,
-
occS(prek(S)) = 1 and prek(S) = xi for some 1 ≤ i ≤ m,
-
occS(sufk(S)) = 1 and sufk(S) = xj for some 0 ≤ j ≤ m − 1, or
-
occS(prek(S)) = occS(sufk(S)) = 2 and there exists 1 ≤ i ≤ j ≤ m − 1 such that prek(S) = xi and sufk(S) = xj.
The cases of Theorem 1 are illustrated in Figure 2 and can be understood informally as follows. Because every k-mer of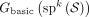 
is in S, every k-mer of w must be touched by some 
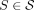. Then, consider a walk g corresponding to such a string S. If g starts in the middle of w and does not visit its own starting vertex again, then g does not fully contain w (case 2). Similarly, if g ends in the middle of w and did not visit its own ending vertex previously, then g does not fully contain w (case 3). If g starts and ends in the middle of w, with the ending vertex to the right of the starting vertex, and contains each of those vertices exactly twice, then g does not fully contain w (case 4). This is the “if” direction of Theorem 1, with the “only if” direction further stating that under all other conditions,
g fully contains w.
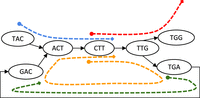
Illustration of the cases in Theorem 1. The graph in the figure represents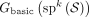 
, where k = 3 and 
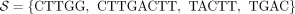. The segments are marked by dashed lines with their starts marked with a dot and their ends marked with a diamond. The unitig
w = {ACT, CTT, TTG} is unsafe because for each of the segment, one of the cases in Theorem 1 is true. For segment colored in green, case 1 holds;
for red, case 2; for blue, case 3; and for orange, case 4.
When the genome is a single chromosome and the coverage is high enough so that every k-mer is sequenced, the whole genome becomes one sequenced segment. In this case, Theorem 1 simplifies because the genome has only one starting and ending vertex and, for a unitig w to be unsafe, the genome must somehow contain every vertex of w without containing w as a subwalk.
Corollary 1. Let X be a string and let w = (x0, …, xm) be a unitig in Gbasic(spk(X)). Then spell(w) is not a substring of X iff one of the following holds:
-
occX(prek(X)) = occX(sufk(X)) = 1, prek(X) = xi, sufk(X) = xi−1 for some 1 ≤ i ≤ m.
-
occX(prek(X)) = occX(sufk(X)) = 2, prek(X) = xi, sufk(X) = xj for some 0 < i ≤ j < m. Moreover, this can hold for at most one unitig in Gbasic(spk(X)).
This corollary tells us that with perfect coverage, all unitigs, except possibly one, are safe. Note that this is a stronger version of the perfect coverage case than the one given by Medvedev (2019), which made an assumption that the starting vertex of X is a source and the ending vertex of X is a sink.
A natural question is how a scenario that gives an unsafe unitig looks like in terms of the original genome. Figure 3, A and B, visualized the following natural possibility. Suppose that the sequenced genome X has a repeat that appears as a maximal unitig ψ in Gbasic(spk(X)). Then, suppose that the region encompassing the start of one copy and the region encompassing the end of the other copy
is not sequenced. Then ψ loses its maximality in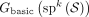 
and becomes a subwalk of a bigger unitig w. Although w is a unitig in the graph from the sequencing data, it would not be a unitig if all the k-mers of X were included in the graph. In the Results section, we show that this situation accounts for the majority of our experimental
observations.
Illustration of an unsafe unitig. Panel A shows two parts of a sequenced genome X. Regions surrounded by green dashed boxes are the sequenced segments S. The solid blue boxes represent two copies of a repeat.
Panel B shows the resulting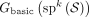 
, with dashed vertices and edges representing vertices that are in Gbasic(spk(X)) but not sequenced.
The relationship between the doubled dBG (Gdbl(K)) and the bidirected dBG (Gbid(K))
In this subsection, we will characterize the relationship between the maximal unitigs of Gdbl(K) and the maximal unitigs of Gbid(K) (Theorem 2). Because of space constraints, the lemmas and proofs needed to prove Theorem 2 are in Corollary 2. Here, we will instead give an informal walk-through to elucidate the relationship between the two graphs. We will incrementally show the relationship between objects in the doubled graph and the bidirected graph: first between vertices and vertex-sides, then between edges, then between walks, and finally between maximal unitigs.
Let K be a set of canonical k-mers, with k as odd. We only consider the case of odd k; when k is even, there may be palindrome k-mers, which create special cases to handle both in the practical assembler implementation and in the theoretical analysis. Because most assemblers anyway restrict k to be odd, we limit ourselves to this case as well.
There is a natural mapping between vertices of Gdbl(K) and vertex-sides of Gbid(K). For a vertex x in Gdbl(K), define FV(x) = (u, s), where u is a vertex in Gbid(K) and s ∈ {0, 1} such that lab(u) = orient(x, s). By the definition of Gbid(K), there exists a unique u and unique s that satisfy this condition. The uniqueness of s is guaranteed by the fact that x cannot be a palindrome. Formally, FV is a bijection between vertices of Gdbl(K) and vertex-sides of Gbid(K) (Lemma B.10).
There is also a natural mapping between edges in Gdbl(K) and Gbid(K). Let x1 and x2 be two k-mers in Gdbl(K) and let (u1, s1) = FV(x1) and (u2, s2) = FV(x2). We define the mapping FE(x1, x2) = {(u1, 1 − s1), (u2, s2)} such that (x1, x2) is an edge in Gdbl(K) if and only if FE(x1, x2) is an edge in Gbid(K) (Lemma B.11). Note, however, that FE is not a bijection, because a pair of mirror edges (x, y) and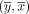 
map to the same bidirected edge; that is, 
.
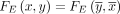The FV and FE mappings allow us to naturally define a mapping from walks in Gdbl(K) to walks in Gbid(K). Let w = (x0, …, xn) be a walk in Gdbl(K). For each 0 ≤ i ≤ n, let (ui, si) = FV(xi) and define FW(w)≜(u0, s0, …, un, sn). FW is a spell-preserving bijection between the set of walks in Gdbl(K) and the set of walks in Gbid(K) (Lemma B.12).
One might hypothesize that FW is also a bijection between the maximal unitigs of Gdbl(K) and the maximal unitigs of Gbid(K). It turns out to not be the case, although the following more careful analysis reveals a close relationship. For Gdbl(K), let us partition the set of maximal unitigs into nonpalindromic strings Dnon−pal and palindromic strings Dpal. For Gbid(K), let Bno−loop be the set of maximal unitigs in which neither endpoint side has an incident lonely inverted loop, let Bfirst−loop be the set of maximal unitigs in which the only endpoint side with a lonely inverted loop is the first one, and let Blast-loop be the set of maximal unitigs in which the only endpoint side with a lonely inverted loop is the last one. To avoid corner cases, let us further assume that there are no circular unitigs in Gdbl(K), which eliminates the possibility of a maximal unitig having lonely inverted loops at both endpoint sides and implies that Bno-loop, Bfirst-loop, and Blast-loop are a partition of the maximal unitigs of Gbid(K) (Lemma B.16). Figure 4, A and B, shows an example.
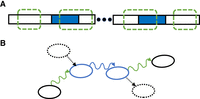
Example of a bidirected dBG (Gbid(K)) (panel A) and a doubled dBG (Gdbl(K)) (panel B) on the same underlying set of k-mers K = {CAC, AAC, ACT, CTA, ATA}. Each vertex-side in Gbid(K) and each in- and outside of a vertex in Gdbl(K) is numbered with the corresponding degree. All maximal unitigs are shown using a long, filled rectangle with an arrow. The maximal unitigs of Gbid(K) are color-coded so that red is Bno-loop, dark green is Blast-loop, and light green is Bfirst-loop. The maximal unitigs of Gdbl(K) are color-coded so that dark red is Dnon-pal and blue is Dpal. Self-mirror edges in Gdbl(K) are shown in blue.
We also need to define a function head that, informally, takes a maximal palindromic unitig in Gdbl(K), extracts the first half of it, and maps it to Gbid(K). Formally, head(w) maps a walk w = (x0, …, xn) in Dpal to the walk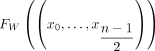 
in Gbid(K). Note that 
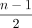is necessarily an integer because w is a palindrome, and hence, n must be odd (Lemma B.1). We can now state the main theorem of this subsection.
Theorem 2. Let K be a set of canonical k-mers where k is odd and Gdbl(K) does not contain a circular unitig.
-
1. The function Fw is a bijection from Dnon-pal to Bno-loop.
-
2. The function rev is a bijection between Blast-loop and Bfirst-loop.
-
3. head is a bijection from Dpal and Blast-loop
Figure 5 schematically illustrates the relationship captured by Theorem 2. The theorem says that for maximal unitigs that are nonpalindromic in Gdbl(K) and do not have inverted self-loops incident at the endpoint sides in Gbid(K), FW is in fact a bijection. However, every maximal unitig w that is palindromic in Gdbl(K) is split into two maximal unitigs in Gbid(K): one that spells the first half of w and has a self-loop incident at the last endpoint side, and one that spells the second half of w and has a self-loop at the first endpoint side. These are necessarily reverses of each other.
Overview of relationship between maximal unitigs in double and bidirected graph for odd k. We use the example from Figure 4, in which K = {AAC, ACT, CTA, CAC, ATA}. The set of maximal unitigs from Gdbl(K), D, is partitioned into Dpal and Dnon-pal. The set of maximal unitigs from Gbid(K), B, is partitioned into Blast-loop, Bfirst-loop, and Bno-loop. The arrows between different subsets of D and B denote bijections.
Inverted loops are caused by k-mers x where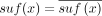 
(e.g., GTA). When these type of k-mers are not present in K, there are no inverted loops in Gbid(K) or palindromic unitigs in Gdbl(K). Hence, 
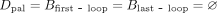, and Theorem 2 immediately simplifies.
Corollary 2. Let K be a set of k-mers, with odd k, which does not contain any x such that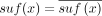 
. Then FW is a bijection from the maximal unitigs in Gdbl(K) to the maximal unitigs in Gbid(K).
Software availability
Scripts for the experimental evaluations are available at GitHub (https://github.com/medvedevgroup/assembly-artifacts-paper-experiments) and as Supplemental Code.
Competing interest statement
The authors declare no competing interests.
Acknowledgments
P.M. thanks Rayan Chikhi, Alexandru Tomescu, and Mihai Pop for useful discussions. This material is based upon work supported by the National Science Foundation under grant nos. 1453527 and 1931531. A.R. was supported by the National Institutes of Health Computation, Bioinformatics, and Statistics (CBIOS) training program.
Author contributions: Both P.M. and A.R. took part in all aspects of the project, except that A.R. was the one who performed all the experiments.
Footnotes
-
[Supplemental material is available for this article.]
-
Article published online before print. Article, supplemental material, and publication date are at https://www.genome.org/cgi/doi/10.1101/gr.276601.122.
- Received January 17, 2022.
- Accepted July 26, 2022.
This article is distributed exclusively by Cold Spring Harbor Laboratory Press for the first six months after the full-issue publication date (see https://genome.cshlp.org/site/misc/terms.xhtml). After six months, it is available under a Creative Commons License (Attribution-NonCommercial 4.0 International), as described at http://creativecommons.org/licenses/by-nc/4.0/.
