Network-based hierarchical population structure analysis for large genomic data sets

  1. Noah A. Rosenberg1
  1. 1Department of Biology, Stanford University, Stanford, California 94305, USA;
  2. 2Department of Computer Science, Ben-Gurion University of the Negev, Be'er-Sheva, 8410501, Israel;
  3. 3Department of Biology, Washington University, St. Louis, Missouri 63130, USA;
  4. 4Department of Evolutionary and Environmental Ecology, University of Haifa, Haifa, 31905, Israel
  • Corresponding author: gili.greenbaum{at}gmail.com
    •  
    Next Section

    Abstract

    Analysis of population structure in natural populations using genetic data is a common practice in ecological and evolutionary studies. With large genomic data sets of populations now appearing more frequently across the taxonomic spectrum, it is becoming increasingly possible to reveal many hierarchical levels of structure, including fine-scale genetic clusters. To analyze these data sets, methods need to be appropriately suited to the challenges of extracting multilevel structure from whole-genome data. Here, we present a network-based approach for constructing population structure representations from genetic data. The use of community-detection algorithms from network theory generates a natural hierarchical perspective on the representation that the method produces. The method is computationally efficient, and it requires relatively few assumptions regarding the biological processes that underlie the data. We show the approach by analyzing population structure in the model plant species Arabidopsis thaliana and in human populations. These examples illustrate how network-based approaches for population structure analysis are well-suited to extracting valuable ecological and evolutionary information in the era of large genomic data sets.

    Population structure is ubiquitous in natural populations, and the ability to detect it from information on genetic variation has been instrumental to our understanding of evolution and ecology. By studying population structure, researchers can investigate processes of gene flow and migration, quantify the evolutionary impacts of fragmentation and movement barriers, inform decisions concerning the conservation and management of populations, and interpret selection signals found in genomic studies. Currently, population structure analysis is an essential element in the toolkit of evolutionary biologists, conservation biologists, and ecologists, both for exploratory data analysis and for hypothesis testing (Guillot et al. 2009; Allendorf et al. 2010; Novembre and Peter 2016).

    As genome sequencing technology advances, large-scale whole-genome sequencing is becoming possible not only for describing genetic variation among species, but also for reporting similarities and differences among individuals within populations. Data sets describing genome-wide sequence variation for multiple conspecific individuals are emerging (e.g., Li et al. 2008; The 1000 Genomes Project Consortium 2015; The 1001 Genomes Consortium 2016; Martin et al. 2018; Armstrong et al. 2019), and a surge of whole-genome population data sets is expected in the coming years. Whole-genome population structure analysis presents the promise of high-resolution population structure inference, such as multiple hierarchical levels and detection of fine-scale structure. However, the era of large genomic data sets also introduces challenges for extracting and interpreting population structure at a genomic scale, as well as significant computational difficulties.

    Methods such as F-statistics (Excoffier et al. 1992; Holsinger and Weir 2009), principal components analysis (PCA) and other representations of data sets using techniques of multivariate analysis (Menozzi et al. 1978; Jombart et al. 2009), tree-based inference (Bowcock et al. 1994; Pickrell and Pritchard 2012), and STRUCTURE-like methods (Pritchard et al. 2000; Alexander et al. 2009), have been exceedingly successful in enabling inference of population structure from genetic data. Each type of method has distinctive features and disadvantages. F-statistics (e.g., FST) are easily communicated summary statistics for measuring genetic differentiation in hierarchically defined population structures, but they require putative groupings of individuals before data analysis. Multivariate analysis methods such as PCA do not require a prior grouping of individuals into populations, but they do require visual interpretation or post-analysis clustering to place individuals into clusters, and they do not naturally represent hierarchical structure. Tree-based hierarchical analyses depict evolutionary relationships between individuals or putatively defined groups (e.g., neighbor-joining, TreeMix) (Bowcock et al. 1994; Pickrell and Pritchard 2012); a limitation is that rigid tree-based representations might poorly depict the data when evolution has been particularly non-tree-like. STRUCTURE-like methods cluster individuals into groups based on a predefined model inherent to the analysis. Like multivariate analyses, they have the feature that they do not require prior assignment of individuals into groups, and they have the limitation that a hierarchical representation is not intrinsic to the approach. Multiple hierarchical levels can be explored in STRUCTURE-like methods by repeatedly clustering individuals using models with different numbers of assumed clusters or subsets of the data. Although hierarchical structure is often observed, identification of multiple hierarchical levels depends on the nature of the structure in the data and is not integral to the method. We are unaware of any population structure inference method that clusters individuals into groups without placing individuals into populations before the analysis, and that as a feature intrinsic to the method detects and represents multiple hierarchical levels in a flexible form.

    In recent years, network approaches have been introduced to model and analyze population structure (Dyer and Nason 2004; Rozenfeld et al. 2008; Greenbaum et al. 2016; Greenbaum and Fefferman 2017; Han et al. 2017; Kuismin et al. 2017). In network-based population structure inference, the genetic relationships between individuals within the populations are formulated as a network, incorporating the many complexities that result from evolutionary processes in natural populations, with few prior assumptions regarding the biological processes involved in generating these relationships. The resulting mathematical construct, the network, is then subjected to analyses developed in network science (Newman 2010) to identify topological characteristics that can be interpreted as population structure. Network approaches have shown promise in the detail with which population structure can be described and in computational efficiency (Greenbaum et al. 2016).

    Here, we describe a network-based population structure inference approach that allows for efficient clustering of individuals based on genetic information and that produces hierarchical population structure diagrams. Cluster representations containing many clusters at different levels in a hierarchy can then assist in evaluation and interpretation of the significance of the population structure detected. We provide examples of analyses of population structure in two large well-studied genomic data sets, Arabidopsis thaliana (Durvasula et al. 2017) and humans (Li et al. 2008), emphasizing the applicability of our approach for studying ecology and evolution.

    Previous SectionNext Section

    Results

    Detecting hierarchical population structure using networks

    The problem of detecting population structure from genetic data has a particular emphasis on the hierarchical nature of many natural population structures. To use networks to detect population structure, we first formulate genotype data as a genetic-similarity network, with individuals as nodes and inter-individual genetic similarities as edges. To construct a genetic-similarity network, we use a frequency-weighted allele-sharing similarity measure (Greenbaum et al. 2016), with the weighting scheme designed to increase the contribution assigned to shared rare alleles. Constructing pairwise genetic-similarity networks for large numbers of loci is a computationally intensive process; however, it is also highly parallelizable and can therefore be completed in reasonable time with the readily available computation clusters available today, even for whole-genome data sets (see “Computational efficiency” in Methods).

    In our approach, the problem of detecting population structure—groups of individuals sharing common evolutionary histories—is equated with the problem of detecting dense subnetworks within the genetic-similarity network. In other words, we identify groups of individuals that are highly interconnected. In network science, such dense groups are termed “communities,” and many community-detection methods have been developed in recent years (Newman 2002, 2006; Fortunato 2010).

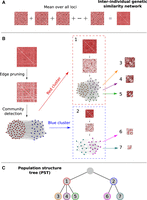
    The genetic-similarity network summarizes genetic variation from across the entire genome. However, the network is expected to be extremely dense, with most pairs connected, because any two individuals, even if belonging to distinct subpopulations, are expected to share some alleles inherited from distant common ancestors. This property adds much noise to any signal of structure, potentially decreasing the ability to detect fine-scale structure. In particular, fine-scale population structure is characterized by smaller groups of individuals that share a more recent genetic history within the group than do larger groups representing coarser-scale structure. Therefore, genetic similarity within fine-scale clusters, which are expected to contain only strong genetic similarities, is expected to be higher than that in coarser clusters, which are expected to contain weaker but nontrivial network connections. Consequently, we explore population structure across many hierarchical scales by iteratively pruning weak edges from the network and applying community-detection procedures (Fig. 1). By removing weak edges from a coarse cluster, the population structure signals characteristic of fine-scale clusters within the coarser cluster become distinguishable, and another hierarchical level can be revealed. The resulting set of clusters can be described as a tree-like hierarchy of nested clusters, which we term a “population structure tree” (PST). In a PST, the root cluster contains all individuals, the leaf clusters describe the finest-scale structure, and the clusters represented by internal nodes describe intermediate levels of clustering (Fig. 1). The internal clusters overlap with clusters emerging from them as “descendants,” whereas all the leaf clusters are nonoverlapping. Note that in PSTs, no assumptions are made regarding the evolutionary processes that give rise to the hierarchical structure, and the branches need not represent groups that have evolved in isolation.

    Figure 1.
    View larger version:
    Figure 1.

    Schematic representation of a network-based construction of a population structure tree (PST) from genomic data. (A) For each SNP, an inter-individual genetic-similarity network (adjacency matrix) is constructed using a frequency-weighted allele-sharing genetic-similarity measure (Equation 1). To produce a genome-wide genetic-similarity matrix, the mean over all loci is taken. (B) Weak edges are pruned from the matrix, by setting low matrix entries to 0 until a community structure emerges, as detected using network community-detection algorithms. Each community (numbered submatrices) is then analyzed independently in a similar manner. Notice that finer-scale clusters are characterized by darker matrices, indicating structures characterized by higher genetic similarities. (C) The analysis is summarized as a PST diagram, summarizing the hierarchical levels of population structure and their relationships.

    PST visualization

    An important aspect of interpreting population structure analyses is visualization of the outputs. We visualize population structure on geographic maps using a coloring scheme designed to reflect the topology of the inferred PST. We start with a color interval (e.g., “rainbow colors”), and assign it to one of the clusters, which becomes the root cluster for that coloring. Our coloring scheme seeks to describe the topology of the branch connecting the selected root cluster and the leaves. For the selected root cluster, each daughter cluster—a cluster emerging from a parent cluster through the edge-pruning and community-detection process—inherits an equal fraction of the color interval, in no particular order. This process of transmission of color intervals to daughter clusters is then repeated until the leaves of the hierarchy are reached on all branches. Each cluster is then assigned a color that corresponds to the midpoint of its assigned color interval. The scheme results in a coloring of a branch of the PST, such that closer clusters in the hierarchy, within and between hierarchical levels, are assigned closer colors on the initial color interval (for examples, see Figs. 2⇓⇓–5).

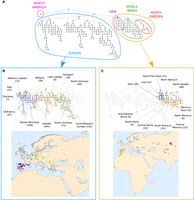
    Figure 2.
    View larger version:
    Figure 2.

    Broad-scale population structure of A. thaliana. (A) The inferred population structure tree (PST). Each element in the hierarchy represents a cluster of individuals, and each cluster contains those clusters below it in the hierarchy. The root element represents the entire sample of 1214 individuals. In colored dashed lines, the main regions corresponding to sampling locations are indicated (with the labels defined post hoc). (B) Visualization of the branch corresponding to most European sampling locations. Each cluster is assigned a color such that “closer” colors represent closer clusters in the PST. On the map, each individual is placed at its sampling location and colored according to the finest-scale cluster to which it was assigned. (C) Visualization of the branch corresponding to Africa, Asia, North Sweden, and some samples in the Iberian Peninsula.

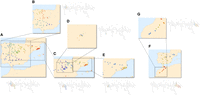
    Figure 3.
    View larger version:
    Figure 3.

    Fine-scale population structure of A. thaliana in the Iberian Peninsula and Morocco. On each map, a branch of the inferred PST from Figure 2 is visualized. Adjacent to each map is the PST colored in the same manner as in the map. A–E show subbranches of the primarily European branch (blue branch in Fig. 2A), and F and G show subbranches of the primarily non-European branch (orange branch in Fig. 2A). (A) Branch corresponding to most of the Iberian population (Iberian Peninsula branch in Fig. 2B). (B) Branch corresponding to the western part of the Iberian Peninsula, with differentiation along a north–south gradient. (C) Branch corresponding to the northeastern part of the peninsula, with differentiation along an east–west gradient. (D) Branch corresponding to a small area in the center of the peninsula. (E) Branch corresponding to north Spain, with a differentiated subbranch along the northeast coast. (F) Branch not belonging to the primary European branch in Figure 2A, corresponding to the Iberian Peninsula and Morocco. Population structure extends on a north–south axis from Africa to Europe over the Strait of Gibraltar. (G) Branch corresponding to Morocco, showing fine-scale population structure in Morocco.

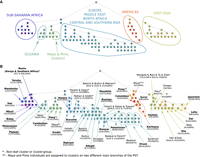
    Figure 4.
    View larger version:
    Figure 4.

    Population structure tree in humans. Closer colors represent closer clusters on the PST. (A) Main branches corresponding to continental groups have been labeled based on assignment of individuals in the branches to population groups (labels defined post hoc). Maya and Pima individuals are found in two subgroups, one within the Americas branch and one outside it. (B) Fine-scale structure revealed by the PST. Clusters or cluster groups in which a majority (>50%) of individuals have a particular label or labels are circled and marked with the corresponding group labels. Under each label, detailed assignments are given in the format x/y(z%): (x) number of individuals with the marked label assigned to the cluster group; (y) number of individuals in the data set with that label; (z) proportion of individuals with the marked labels among all individuals assigned to the cluster group. In the case of cluster groups with more than one hierarchical level, the detailed assignments refer to the cluster at the highest hierarchical level in the cluster group. For non-leaf cluster groups (marked with *), the proportion z is taken among all individuals in the cluster group, omitting all individuals in all descendant clusters assigned a label different from the label of the cluster group. Labels in bold indicate clusters or cluster groups (not considering omitted individuals, if relevant) that contain only individuals that have the marked labels (i.e., z = 100%).

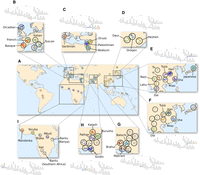
    Figure 5.
    View larger version:
    Figure 5.

    Fine-scale human population structure. Shown is a visualization of the PST on a world map. Each open circle corresponds to one of the 52 groups of the HGDP data set; group coordinates from Rosenberg (2011) were used, but adjusted such that circles do not overlap (for group labels, see Supplemental Fig. S3). Individuals were positioned randomly within their corresponding circles and colored according to the finest-scale cluster to which they were assigned. To illustrate fine-scale structure at a local level, a variety of regions are shown in detail. (A) World map, with colors corresponding the coloring of the entire PST, as in Figure 4. (B) Branch corresponding to Europe. (C) Branch corresponding to the Mediterranean region. (D) Branch corresponding to northern China. (E) Branch corresponding to Japan and central and southern China. (F) Branch corresponding to central and southern China. (G) Branch corresponding to Balochi, Brahui, and Makrani groups. (H) Branch corresponding to Burusho, Kalash, Pathan, and Sindhi groups. (I) Branch corresponding to sub-Saharan Africa. In each inset, the branch has been re-colored according to an automatic coloring scheme, which assigns closer colors to clusters positioned closer in the PST, except in B and G, where each cluster was assigned a color manually, irrespective of positioning in the PST.

    Once the clusters are assigned colors, each individual is assigned a color corresponding to the finest-scale cluster to which it is assigned. On a geographic map of the region of interest, each individual is placed in its geographic sampling position and colored with its assigned color. This step results in a map reflecting the topology of a particular branch of the PST. By selecting different root clusters and repeating the process, different geographic regions and different levels of structure can be emphasized (e.g., Figs. 3, 5).

    Population structure tree in Arabidopsis thaliana

    Understanding the population structure of the model plant species A. thaliana has been of great interest both for explaining patterns of natural variation and for correctly interpreting signatures of selection and association inferred from genome-wide association studies (Sharbel et al. 2000; Jørgensen and Mauricio 2004; Nordborg et al. 2005; Bakker et al. 2006; François et al. 2008; Platt et al. 2010; Provart et al. 2016; The 1001 Genomes Consortium 2016; Durvasula et al. 2017; Lee et al. 2017). Within Eurasia, population structure has been characterized in one study by nine clusters—the group of highly differentiated individuals found primarily in the Iberian Peninsula, and eight other clusters, broadly corresponding to north Sweden, south Sweden, the Iberian Peninsula, Asia, Germany, Italy/Balkans/Caucasus, west Europe, and central Europe (The 1001 Genomes Consortium 2016). Recently, evidence provided by samples from Africa has suggested that African populations are distinct from Eurasian populations (Durvasula et al. 2017). In North America, the population has been found to be relatively unstructured (Jørgensen and Mauricio 2004; Hagmann et al. 2015; The 1001 Genomes Consortium 2016).

    Here, we analyzed worldwide population structure of A. thaliana using our network-based method, to better understand hierarchical levels and fine-scale structure in this model species. We studied 1135 individuals (accessions) from Eurasia and North America (The 1001 Genomes Consortium 2016), and 79 individuals from Africa (Durvasula et al. 2017), with the combined data set containing 1214 individuals and 2,367,560 SNPs.

    We detected a highly hierarchical population structure, with 247 (overlapping) clusters overall and 96 fine-scale (nonoverlapping) leaf clusters at the tips of the hierarchy (Fig. 2A). The topology of the inferred PST is highly unbalanced, with one main branch consisting of a single cluster (left main branch in Fig. 2A), and the other main branch containing 246 clusters (right main branch in Fig. 2A). All individuals in the single-cluster left main branch are from North America, representing 71% of the North American sampled population (89 of 125). The right main branch consists of two subbranches, one representing European individuals (Fig. 2B) and the other representing African, Asian, and northern Swedish individuals, and some Iberian individuals designated as “relicts” by previous studies (Fig. 2C; The 1001 Genomes Consortium 2016; Durvasula et al. 2017; Lee et al. 2017). Population structure in the primary European branch shows relatively continuous genetic differentiation over space, as evidenced by the fact that geographically close samples are closely positioned in the PST topology (Fig. 2B). In the primarily non-European branch, population structure is more discontinuous geographically, with a large “gap” between the Asian, Iberian, and northern Swedish branches (Fig. 2C). However, looking at fine-scale population structure in Africa and Iberia (Fig. 3F,G) and in Asia (Supplemental Fig. S1), population structure appears to be more geographically continuous within these smaller branches. Note that in north Sweden, the sampled area was too small to examine geographic patterns of differentiation within the region.

    The separation, at a high hierarchical level, between the European branch and the African, Asian, and northern Swedish branches could reflect an ancestral split between these groups (Durvasula et al. 2017), but how these spatially distant populations are related, and why a geographic gap exists in the primarily non-European branch, remain to be investigated. Alternatively, the split partitioning these three groups from the European group may reflect strong genetic similarity within the European branch, rather than genetic similarity between these three groups. Therefore, further study of the population in north Sweden, and increased geographic sampling in Africa and Asia, could help explain these patterns (e.g., Hsu et al. 2019). The continuous differentiation, across hierarchical scales, in the European branch accords with past studies of this geographic region (Sharbel et al. 2000; Nordborg et al. 2005; François et al. 2008; The 1001 Genomes Consortium 2016).

    Structure can also be ascertained at a very fine scale by examining branches close to the tips of the hierarchy. In the Iberian Peninsula, for example, genetic differentiation can be observed at several scales (Fig. 3). At the broader scale (Fig. 3A), in the western part of the peninsula, genetic differentiation is aligned along a north–south gradient (Fig. 3B), whereas in the northeastern region, genetic differentiation more closely follows an east–west gradient (Fig. 3C). Distinct groups, correlated with geography, can be seen at fine spatial scales, such as along the northeastern coast (Fig. 3E), in the north (Fig. 3B), and in the central region (Fig. 3D). In Morocco and the Iberian Peninsula, for those individuals belonging to the primary non-European branch in Figure 2A, population structure follows a north–south gradient, with clusters corresponding to small and specific regions in Morocco (Fig. 3G) and to larger regions in the Iberian Peninsula (Fig. 3F). In Asia, population structure corresponds to broad regions (e.g., Altai Mountains, central Asia, Ural Mountains), but finer-scale patterns are also observed within these regions (Supplemental Fig. S1).

    The formation of such small-scale structure might be attributable to small-scale landscape barriers and resistance to gene flow, but also to adaptation of A. thaliana to specific local conditions (Li et al. 2010; Fournier-Level et al. 2011; Horton et al. 2012). For example, the branch corresponding to the coastal population in northeastern Spain has been suggested to be locally adapted to high salinity (Busoms et al. 2015). Selective sweeps suggesting significant local adaptation have also been reported for the population in north Sweden (Long et al. 2013; Huber et al. 2014). Such events could have led to decreased fitness of hybrids and decreases in effective migration, intensifying the differentiation of this population. This phenomenon could perhaps contribute to explaining the nonintuitive placement of north Sweden in the PST, separate from most European samples (Fig. 2C).

    The single cluster associated with North America represents most of the samples from that region. This lack of structure, which accords with previous studies (Jørgensen and Mauricio 2004; Platt et al. 2010; Hagmann et al. 2015), could result from a founder effect followed by rapid expansion, producing a fairly homogeneous but widespread population (Platt et al. 2010). However, 29% of the North American samples are clustered within the European branch: 20 in a UK/France cluster, 14 in a Central European cluster, and two in a south Sweden/north-Europe cluster (Supplemental Fig. S2). These samples include five of the six individuals sampled along the western coast of North America. The clustering of North America individuals in European clusters suggests a history more complex than a single colonization event. Most individuals perhaps descend from a founder population in the eastern United States (Sharbel et al. 2000; Jørgensen and Mauricio 2004), but other migration events, possibly from western European sources, might also have contributed to the population.

    Population structure tree in humans

    The Human Genome Diversity Project (HGDP), in collaboration with Centre Etude Polymorphism Humain (CEPH), has collected genomic samples from 52 human populations from across the world, which is referred to as the “HGDP-CEPH Human Genome Diversity Cell Line Panel” (Cann et al. 2002; Cavalli-Sforza 2005). This set of populations is particularly well-suited as an example, because it has served as a test set for a variety of population structure methods (Corander et al. 2004, 2008; Corander and Marttinen 2006; François et al. 2006; Patterson et al. 2006; Nievergelt et al. 2007; Hubisz et al. 2009; Shringarpure and Xing 2009; Jombart et al. 2010; Lawson and Falush 2012; Lawson et al. 2012; Pickrell and Pritchard 2012; San Lucas et al. 2012; Loh et al. 2013; Frichot et al. 2014; Raj et al. 2014; Gopalan et al. 2016; Granot et al. 2016; Hao et al. 2016; Hunley et al. 2016; Zheng and Weir 2016). We generated a PST from 938 HGDP individuals, typed at 647,976 SNPs.

    The PST consists of 108 clusters overall, and 57 leaf clusters (Fig. 4). The main branches of the PST correspond to continental-level patterns of human groups, such as sub-Saharan Africa, east Asia, and the Americas (Fig. 4A), recapitulating structure observed with other methods in these samples (Rosenberg et al. 2002; Jakobsson et al. 2008; Li et al. 2008). Several populations, including Cambodians, Melanesians, Papuans, and Yakut, are not placed within any main continental branch (Fig. 4B). These positionings highlight persistent variability in the placement of these populations; the Oceanians and the Yakut population generally emerge as clusters in detailed analyses, but they have variable placement in relation to the largest clusters in analyses with lower clustering resolution.

    Two Native American groups, Maya and Pima, are split into two positions in the PST—one within the branch corresponding to the Americas (four Maya and eight Pima individuals) (Fig. 4B), and one outside any main continental group (14 Maya and six Pima individuals) (Fig. 4B). This pattern may reflect previous observations of apparent admixture in the Maya sample, with possible genetic contributions from east Asian and European populations (e.g., Rosenberg et al. 2002; Pickrell and Pritchard 2012). The Pima sample has not previously been detected as an intercontinentally admixed group; because our analysis is based on genetic similarity between individuals, and because the Maya and Pima groups are genetically similar, the clustering of six Pima individuals outside the main branch of the Americas might reflect their similarity to admixed Maya individuals, rather than admixture in the Pima themselves.

    The PST reveals fine-scale structure, which generally agrees with previous analyses, but in some cases provides finer details (Fig. 5A). Most groups can be associated with a single cluster or a small cluster group in the PST (Fig. 4B). Detailed previous analyses of the HGDP sample have been able to clearly separate groups particularly in the Americas and the Middle East, and to some extent in sub-Saharan Africa (Jakobsson et al. 2008; Li et al. 2008). These groups are also clearly separated in the PST (Figs. 4B, 5C,I). Fine-scale structure has been more difficult to resolve in central/south Asia, east Asia, Europe, and in some sub-Saharan African populations. Our network-based approach is able to identify finer-scale structure for many groups in these regions. In central and western Africa, Biaka, Mandenka, Mbuti, and Yoruba are each clustered to a different leaf cluster, with each cluster consisting of individuals from a single group (Figs. 4B, 5I). In Europe, we identified two Orcadian leaf clusters, containing all individuals from that group, and a leaf cluster consisting of a subset of Basque individuals (Fig. 4B). At higher hierarchical levels, we identified a Basque and French cluster (Figs. 4B, 5B). In central/south Asia, we identified leaf clusters corresponding to many of the groups in the HGDP: Balochi, Brahui, Burusho, Hazara, Kalash, and Makrani (Fig. 4B).

    Non-leaf clusters also inform population structure, with clusters corresponding to a Hazara and Uygur group; a Pathan and Sindhi group; a Balochi, Brahui, and Makrani group; and a Burusho, Kalash, Pathan, and Sindhi group (Figs. 4B, 5G,H). In east Asia, three northern Chinese groups are separated in the PST, and the Hezhen and Oroqen groups are each assigned a leaf cluster (Figs. 4B, 5D). The Japanese, Lahu, and Yi groups are also clearly separated, and each is assigned a leaf cluster (Figs. 4B, 5E). A cluster of groups from China is separated into six clusters: Dai, Miao, She and three clusters containing Han and Tujia individuals (Figs. 4B, 5F).

    Because our coloring scheme differentiates between individuals assigned to leaf clusters and those that are not, it aids in observing groups that are not grouped exclusively in a leaf cluster. For example, in the branch corresponding to northern China, eight of the nine Daur individuals are assigned to a non-leaf cluster, but not to the leaf clusters below it, whereas the Hezhen and Oroqen individuals are assigned to leaf clusters. Therefore, although the Daur group is not characterized by any exclusive leaf cluster, it can be visually differentiated from the other two populations in Figure 5D. Similarly, by subtracting individuals from leaf clusters, an Italian and Tuscan grouping can be observed in Figure 5B, and a Bantu (Kenya and southern Africa) grouping can be observed in Figure 5I, although individuals from those groups are not a majority in any specific cluster.

    Comparing population structure trees

    Large genomic data sets provide opportunities to conduct subsampling analyses on the same data set, for example, to investigate population structure inferred from different genomic regions, or to study the effect of different genome sequencing schemes. To interpret such subsampling analyses, a coherent method for comparing population structure outputs is needed. We therefore developed an approach to compare different PSTs derived from the same data set.

    The approach is based on normalized mutual information (NMI), an information-theoretic measure that evaluates, for a pair of variables, the amount of information gained about a variable by observing a second variable. This measure can be adjusted to apply to a set of hierarchical sets of clusters (Lancichinetti et al. 2009), such as PSTs. Given two PSTs derived from the same set of individuals but not necessarily from the same similarity matrix, the measure produces a score that ranges from 0 to 1, in which higher scores indicate greater similarity between the PSTs (for details, see Methods). Notably, two PSTs might differ both in the topological ordering of the clusters in the tree and in the assignment of individuals to clusters, but they are still comparable using the NMI measure.

    Our implementation of the NMI measure is flexible in the sense that it is possible to conduct comparisons not only between two PSTs, but also between subsets of the PSTs. This type of comparison enables a focus on comparing certain features of the PSTs. For example, the approach can compare specific branches of interest, or only fine-scale leaf clusters, by considering in the NMI comparisons only specified subsets of clusters (see Methods; Supplemental Information).

    Information gain by increased SNP coverage

    We estimated the effect of increasing the number of loci used in the inference of PSTs by comparing the PST inferred from an entire data set with PSTs inferred from subsamples of the data set, using the information-theoretic NMI measure. This step was accomplished by evaluating NMI between PSTs, one inferred from the full data set (Figs. 2, 4), and one inferred from a subsample of the data. We also computed NMI for fine-scale structure by examining only the leaves of the hierarchies. For this purpose, without considering SNP positions, we randomly subsampled all SNPs to produce subsets of 0%–98% of the original data set, in increments of 2%. For each frequency value, 100 random subsamples were taken, and from each of these subsamples, a PST was inferred and compared to the full-data PST.

    The results (Fig. 6) indicate that information gain is rapid for the first 50,000 SNPs, in both the A. thaliana and human data sets. In A. thaliana, further SNP coverage results in only modest information gain, suggesting that most population structure is revealed in this data set using about 100,000 SNPs (Fig. 6A). For the human data set, more information was gained as SNP coverage continued to increase (Fig. 6B). These results, particularly for the A. thaliana data set, are consistent with previous studies on lower-density genetic data that have shown that the resolution of population structure detected tends to saturate when enough loci are included in the analysis (e.g., Manel et al. 2002; Turakulov and Easteal 2003; Rosenberg et al. 2005; Morin et al. 2009; Haasl and Payseur 2011; Bryc et al. 2013); however, for the human data set, information gain is not saturated even with several hundred thousand SNPs. In both data sets, with increased SNP coverage, more information is gained regarding fine-scale structure than about coarse-scale structure. For example, increasing the number of SNPs from 10% of the data set (236,756 SNPs for A. thaliana and 64,797 SNPs for humans) to 90% SNP coverage (2,130,804 SNPs for A. thaliana and 583,173 SNPs for humans), increases NMI by 3.7% for A. thaliana and 23.7% for humans when considering the entire PST, whereas the increase is larger when considering the finest-scale clustering at the PST leaves, with NMI increases of 11.1% for A. thaliana and 77.1% for humans (Fig. 6).

    Figure 6.
    View larger version:
    Figure 6.

    Normalized mutual information (NMI) between the PST inferred using the entire genome and PSTs inferred from subsampled fractions of the genome. The NMI values evaluate the amount of information gained on hierarchical population structure by sampling a fraction of the data set. The mean NMI across 100 random subsamples for each SNP coverage value considering the entire PST topology is shown in purple; mean NMI considering only the finest-scale leaf clusters is shown in orange. Shaded regions show standard deviations across 100 sampling replicates. (A) A. thaliana data set. Inset shows NMI for subsamples below 200,000 SNPs. (B) Human data set. NMI values saturate at values below 1 because cluster assignments often switch at fine scales (e.g., between PST leaves) when PSTs are inferred from subsampled data.

    Previous SectionNext Section

    Discussion

    Population structure inference using networks

    The evolutionary processes shaping genetic variation are often complex, occurring at multiple spatial levels and over multiple time periods. Network-based methods are well-suited for population structure inference because they enable a natural hierarchical perspective. Our approach is data-driven and does not require assumptions or prespecified models regarding the biological processes responsible for shaping the genetic patterns. The visualization technique presented here, with PST diagrams and corresponding map colorings, is useful for summarizing information on population structure while preserving information at both broad and fine scales.

    We showed the applicability of the NMI measure for comparing PSTs to understand the information gained by an increased number of genetic markers. This measure can also be useful for other types of analyses, such as for comparing PSTs inferred from different genomic regions or different types of genetic markers.

    Comparison to other approaches

    In Table 1, we summarize the features of our network approach in relation to those of popular classes of population structure inference approaches.

    View this table:
    Table 1.

    Comparison of features of selected population structure inference approaches representing the major families of methods

    The network-based approach, unlike F-statistics or some commonly used tree-based methods, does not require an assumption of putative populations, and it clusters individuals into groups in a data-driven manner. Unlike in multivariate analysis methods such as PCA, in the network method, clustering is naturally conducted using community-detection procedures. Unlike in STRUCTURE-like methods, the PST generated by the network method depicts hierarchical levels of structure without the need to predefine the number of clusters or to run the analysis at different values for this quantity. Detection of multiple hierarchical levels of structure is integral to the network approach, without assumptions on the number of clusters, the hierarchical topology of population structure, or putative groupings of individuals; all these characteristics are generated from the data. Such features of the method are beneficial particularly when little information is available for specifying models or for defining putative groups, and when the hierarchical level of interest is unclear.

    We showed the features of our approach in two data sets. In our application to A. thaliana and humans, the PSTs distinguish between groups on a fine scale. The method uncovers clusters that have not been straightforward to distinguish in PCA or STRUCTURE-like analyses in previous studies (Li et al. 2008; Durvasula et al. 2017).

    Ideally, inference of population structure should be conducted using more than one approach, to show robustness and to capitalize on the different features of the different approaches (Table 1). For example, in some cases, we observe in a PST a split between a large group and several smaller groups. These splits are sometimes difficult to interpret, because it is unclear whether they represent genetic similarity between the smaller groups, or strong genetic similarity between individuals in the larger group. For example, the A. thaliana split between a branch with African/Asian/north Sweden groups and a large European branch (Fig. 2), and the human split between the Oceanian/Cambodian/Yakut/North American groups and a large mainly Eurasian branch (Fig. 4A), might be driven by genetic similarities between the groups in the same finer-scale branch, or by strong between-individual genetic similarities in the coarser branch. The distinction of these two scenarios can be examined by leveraging advantages of different classes of methods. For example, once clusters and groups of interest have been ascertained by an approach that does not require definition of putative populations, genetic similarities between the identified groups can be computed using methods that rely on putative group assignments (Table 1); network methods can also aid in investigating the cohesiveness of different clusters, for example, using strength-of-association distribution (SAD) analysis (Greenbaum et al. 2016).

    We have presented a network-based approach for revealing population structure at multiple hierarchical levels. This structure is summarized in a novel form, the PST, and can be visualized on geographic maps. The method is applicable to whole-genome data. The approach is data-driven and computationally efficient, allowing analysis of large genomic data sets. Our method for comparing PSTs using the NMI measure is potentially useful for conducting studies that investigate population structure inferred from subsamples of the data.

    Previous SectionNext Section

    Methods

    Constructing genetic-similarity networks

    The first step of network-based population structure detection is to use genomic data to generate a genetic-similarity network, with individuals treated as nodes and inter-individual genetic similarities as edges (Fig. 1). Here, we use a frequency-weighted allele-sharing similarity measure. Allele-sharing measures count the number of shared alleles between each pair of individuals over all loci. Because individuals that share rare alleles are more likely to belong to the same subpopulation than are those that share common alleles, we assign more weight to shared rare alleles than to shared common alleles. There are different ways to design weighting schemes to generate genetic-similarity networks (Greenbaum et al. 2016); here, we adopt a linear weighting scheme for its simplicity, but this weighting scheme can in principle be replaced by other weighting schemes if there is reason to tailor weights such that different weights are assigned to different allele frequency classes.

    Considering a locus ℓ, for individual i with alleles a and b and individual j with alleles c and d, the frequency-weighted allele-sharing similarity is defined as follows (Greenbaum et al. 2016): Formula (1) where Ixy = 1 if x and y are identical and Ixy = 0 otherwise, and fa and fb are the frequencies of alleles a and b in the entire sample. The genetic-similarity edge connecting individuals i and j is weighted by the mean genetic similarity over all L loci available for this pair of individuals, Formula. When some data are missing, Aij is computed based on all those loci for which both individuals i and j are scored. This measure is symmetric (Aij = Aji) and defines an inter-individual genetic-similarity network, where Aij is the adjacency matrix of the network.

    Community detection

    By a subpopulation in a structured population, we mean a group of individuals that share a common genetic history, and that are therefore more related to one another on average than they are to individuals outside the group. Individuals are then expected to share more genetic-similarity edges within subpopulations than between subpopulations. In network science, groups of nodes that are strongly connected within the group, forming dense subnetworks, are termed “communities” (Newman 2002). By detecting the community structure of genetic-similarity networks, the genetic population structure can be revealed (Greenbaum et al. 2016).

    Many algorithms for community detection have been developed, including for weighted networks for which weights are assigned to the edges (Fortunato 2010; Yang et al. 2016). Many of these methods are based on a quality function that evaluates community partitions and that is termed “modularity” (Newman 2006). This function, given a network and a partition of the network, returns a value between −1 and 1. Modularity is computed by analytically comparing the intra-community densities of a partition of the network with the expectation of intra-community densities over an implicit distribution of “random networks” that preserve the node-weighted degrees (Newman 2006; Greenbaum et al. 2016, Eq. 1). Therefore, high modularity scores reflect a community partition in which within-community connections are more frequent and more highly weighted than would be expected in a random network with the same degree distribution. Many community-detection algorithms aim to efficiently identify a community partition that maximizes the modularity score. Here, we use a particularly time-efficient weighted community-detection method, the Louvain method (Blondel et al. 2008), which attempts to maximize modularity through a greedy search using a deterministic iterative process.

    Edge pruning

    In structured populations, genetic variants are more likely to be shared within subpopulations than between subpopulations. Different genetic processes might have occurred over different spatial scales, either at different points in time or simultaneously, and therefore, the genetic signature is a complex aggregate of structure at several scales. Fine-scale population structure is characterized by groups of individuals that are strongly related and that therefore are expected to be represented in subnetworks that contain only the strongest genetic-similarity edges. Coarse-scale population structure, in contrast, is characterized by both strong and weak genetic similarities.

    To detect population structure at multiple hierarchical levels, we perform an iterative edge-pruning process, in which we sequentially remove edges below a genetic-similarity threshold. Here, we start at threshold 0 (i.e., all edges are included), and calculate the community structure. If only a single community is detected (no community structure), then we increment the threshold, remove the edges below the threshold, and again apply community detection. Once community structure is detected, the network is split, and the process is repeated for each community independently. This process of subdividing communities forms a PST, where clusters closer to the root represent coarse-scale structure and clusters at the leaves represent fine-scale structure.

    We selected a threshold increment of 10−4 for the analysis of the A. thaliana data set and 10−3 for the human data set, such that the final output, the PST, does not substantially change with each increment. For other data sets, we recommend inspecting the typical differences between the sorted weights of the edges, selecting a threshold larger than the typical gaps between consecutive edge weights, and testing several threshold increments, at different orders of magnitudes, to identify stable outputs. Higher threshold increments are expected to result in fewer hierarchical levels in the PST, because removal of many edges between applications of the community-detection procedure may result in hierarchical levels being skipped over.

    The PST generated in this way is entirely data driven, with the number of fine-scale and coarse-scale clusters determined only from the genetic data. Note that the population structure could include small clusters containing relatively few individuals. In some cases, even clusters containing only a few individuals might be informative, because they might represent sparsely sampled population fragments or familial groups. In other cases, such small groups may not be of interest. We therefore impose a condition on the process by specifying the minimum number of individuals in a cluster, so that communities below that size are not considered clusters and do not induce a split in the PST. Because large genomic data sets can potentially generate a fine-scale level of structure, we kept these minimum sizes small and ignored clusters smaller than five individuals for both data sets. In other data sets, keeping small clusters may reveal fine-scale structure, but this high-resolution structure could be less reliable because of potentially nonrepresentative individuals; we recommend testing several minimum cluster sizes and keeping in mind the minimal group sizes for which meaningful interpretation can be given (e.g., the smallest predefined group in the human data set includes five individuals).

    Generating geographical PST maps

    We use a coloring scheme to visualize population structure. This scheme represents fine-scale structure while accounting for the hierarchical topology of population structure, and it allows identification of relevant differentiation patterns (Figs. 2⇑⇑–5). For each coloring, we select a root cluster from the PST. This cluster defines the scale and focus of the coloring; the coloring is intended to visualize the branch leading from this root cluster to the leaves.

    We start with an interval [0, 1] representing a color gradient. Here, we use the “Rainbow” color gradient, with each number in the interval representing a color on the gradient; see Supplemental Figure S4 for an explicit representation of this color scheme function. We assign the starting interval to the root cluster. We then evenly split the interval among all immediate daughter clusters of the selected root cluster. We repeat this process, so that in each step, a subinterval of the parental interval is inherited by daughter clusters. In other words, if a cluster C is assigned the interval [a, b], and it has n daughter clusters C1, …,Cn, then the daughter cluster Ci is assigned the interval 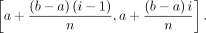Formula This method assigns smaller intervals to clusters as we advance toward the leaves.

    The process is terminated when leaves have been reached on all subbranches. We then assign a single color to each cluster, by taking the color associated with the midpoint of the interval assigned to that cluster. In other words, if cluster C is assigned the interval [d, e], then C is assigned the color corresponding to (d + e)/2. In this way, fine-scale clusters that are far from the root cluster and that share a common parent cluster one level above will tend to be assigned “closer” colors than will clusters that share a parent cluster nearer to the root cluster.

    Each individual can be assigned to multiple clusters in different hierarchical levels, and we assign a color to an individual based on the finest-scale cluster to which it is assigned (i.e., the cluster closest to a leaf). This color assignment of individuals is then used for plotting geographic maps, so that for each individual, a point is plotted at its sampling location, colored in its assigned color.

    In this way, the many fine-scale clusters that are detected in large genomic data sets can be represented simultaneously, while allowing the broader genetic patterns to be clear on each map and at each scale by the coloring scheme. For example, although Figures 2 and 3 use many colors, some of which are visually indistinguishable, the broad patterns of genetic differentiation can be easily comprehended. When structure at a fine scale is of interest, the coloring scheme can be repeated while selecting different root clusters, thus focusing on different subbranches of the PST. This method makes it possible to rescale the coloring scheme to the appropriate geographic scale, and finer-resolution genetic differentiation patterns become apparent (e.g., Fig. 3). A caveat of our coloring scheme is that when the number of daughter nodes is odd, one of the daughter nodes and the parent node are assigned the same color; this may limit visual interpretation, particularly when a parent cluster and its daughter clusters are visualized near the leaves of the tree. In such cases, we suggest assigning colors manually (e.g., Fig. 5B,G). It is important to note that the PST holds information on all hierarchical levels; the coloring strategy we suggest only aids with visualizing the relationship of genetic differentiation patterns to geography.

    All maps were plotted using Mathematica GeoGraphics (www.wolfram.com/mathematica), which imports maps from Wolfram|Alpha (www.wolframalpha.com).

    Preprocessing of the data sets

    For A. thaliana, we used data from the 1001 Genomes project, extracted from www.mpipz.mpg.de/hancock/downloads, which stores a unified data set of the 1001 Genomes database (also found at 1001genomes.org) and the data from Durvasula et al. (2017). The data set includes whole-genome SNP data of 1135 A. thaliana diploid individuals (accessions) from Eurasia and North America (The 1001 Genomes Consortium 2016), and data from Durvasula et al. (2017) on 79 individuals from Africa. For the combined data set of 1214 individuals, we considered only biallelic SNPs, and filtering included removal of all SNPs with more than 10% missing data and all SNPs with minor allele frequencies <0.01. After filtering, the combined data set included 1214 individuals and 2,367,560 SNPs. Geographic locations of the A. thaliana samples were extracted from the 1001 Genomes database at 1001genomes.org and from Durvasula et al. (2017).

    For humans, we used 938 individuals from the HGDP data set, downloaded from the HGDP website hagsc.org/hgdp. This subset of individuals contain those that remain after removing low-quality samples, replicated samples, and closely related individuals (Rosenberg 2006; Li et al. 2008). We used the same data filtering as for the A. thaliana data set for the purpose of tractability, that is, only biallelic SNPs were considered, and SNPs with >10% missing data were removed, as were loci with minor allele frequencies <0.01. After filtering, the data set included 938 individuals and 647,976 SNPs (of the 660,918 SNPs in the initial HGDP data set).

    Comparing PSTs using NMI

    To compare two PSTs derived from the same set of individuals I, we compute the normalized mutual information (NMI) between representations of the two PSTs as sets of partitions of I (Lancichinetti et al. 2009; McDaid et al. 2013). NMI quantifies the amount of information shared by two random variables, or the amount of uncertainty on one variable that is reduced by observing the other variable, as measured in bits.

    To apply this measure, we represent a PST, X, with k clusters, as a partition X1, … ,Xk of the set of individuals I (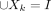Formula … Formula). The sets X1, … ,Xk need not be mutually disjoint, and indeed in PSTs, clusters can be nested within other clusters (e.g., a daughter cluster is nested in the parent cluster). The NMI measure computes, for two PSTs X and Y represented as partitions, a score between 0 and 1, in which higher scores represent higher similarities between the PSTs. We summarize the computation in Supplemental Information and Supplemental Figure S5, and refer the readers to Lancichinetti et al. (2009) and McDaid et al. (2013) for the full details of this computation.

    In some cases, it is of interest to compute NMI not for the entire PST, but rather for a subset of the clusters. For example, we computed NMI for leaf clusters of PSTs to compare the fine-scale structure described by the PSTs. Given two PSTs, X and Y, represented as partitions X1, … ,Xk and Y1, … ,Ym, this computation is performed by considering only a subset of the sets in the partition, and computing NMI using only these subsets. However, because NMI requires both PSTs to be defined on the same set of individuals, a problem arises when the unions of the subsets of clusters are different. In other words, if we consider a subset of k′ ≤ k clusters from PST X and a subset of m′ ≤ m clusters from PST Y, we might have 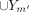Formula … Formula … Formula. This problem can be addressed by removing or adding individuals to clusters in a standardized way, so that the unions of the subsets of clusters become equal; our analysis of information gain by increased genomic density provides an example of how such a case can be addressed.

    Information gain by increased sequencing

    The NMI measure quantifies the information shared between two PSTs. If one of the PSTs considered was ascertained using strictly lower-density genetic data, then NMI can be used to evaluate the information gained by increasing the genomic density of the data, as we have done here for the A. thaliana and human data sets.

    We calculated NMI for PSTs constructed from a subsample of the genome to simulate different fractions of the genome sequenced (0% to 98% in intervals of 2% of the number of SNPs in the data set). First, the data were randomly partitioned into 10,000 approximately evenly sized groups of SNPs, subsampled randomly from all SNPs without replacement, regardless of position in the genome. For each fraction of the genome, f, 100 random subsamples of the genome, each summing up to a fraction f of the genome, were taken without replacement (constructed using the SNP groups, for computational efficiency). For each such subsample, the PST was derived, and the NMI between that PST and the PST derived from the entire genome (Figs. 2A, 4A) was computed. The mean NMI and standard deviations for each f were then calculated.

    In addition, we also considered the information gained when considering only fine-scale structure. This step used a similar process, only that the NMI was calculated by considering only the leaf clusters of the PSTs. Because some individuals are possibly not being assigned to any leaf, the union of the leaf clusters does not necessarily cover the entire population. To address this, each individual not assigned to any leaf was added to all the leaves in the branch below the finest-scale cluster to which that individual was assigned. 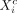In other words, for PSTs X and Y, with leaf clusters X1, … ,Xr and Y1, … ,Ys, respectively, we added each individual d in Formula (where Formula is the complement of Xi) to all leaf clusters that belong to the branch emerging from the cluster 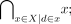Formula we do the same for all individuals in Formula (see Supplemental Information for an illustrative example). We compute NMI for the sets X1, … ,Xr and Y1, … ,Ys with the added individuals, which now cover the full set of individuals. This procedure generates a comparison between the finest-scale structures described by the PSTs.

    Computational efficiency

    A major issue with analyses of large genomic data sets is computational efficiency. The method we present requires two stages: (1) construction of the genetic-similarity network, and (2) construction of the PST. The first stage amounts to construction of a pairwise matrix of size n2, where n is the number of individuals. Each element requires ℓ calculations, where ℓ is the number of loci. To apply Equation 1, calculation of allele frequencies for all loci is required. The computation time for the first stage is therefore O(ℓn2 + ℓn) = O(ℓn2) time. This computation time can be reduced substantially by computing the elements of the matrix for each of the loci in parallel: Given c computation threads, the computation time can be reduced to O(ℓn2/c) time.

    The computation time of the second stage depends on the topology of the PST. With the community-detection Louvain algorithm, each community-detection computation takes O(i log i) time, where i is the number of individuals in the network examined (Blondel et al. 2008). Therefore, for each level of the hierarchy, assuming we have k clusters in that level, in which cluster j has size ij, the computation time is 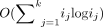Formula for that hierarchical level. Because 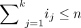Formula and ij ≤ n (and therefore log ij ≤ log n) for any j, the run time of each level is bounded above by O(n log n). For a PST with d levels, the overall computational time of this step is, therefore, smaller than O(dn log n). The factor d is not known a priori, and could differ for different data sets; d is bounded by d ≤ n, although in practice it would typically be much smaller.

    In practice, for whole-genome data, the first step (constructing the matrix) takes substantially more time to compute than the second stage (iterative edge-pruning and community detection); the second step does not depend on the number of loci in the data. Using a single computation thread, the first step would require ∼82 d for the A. thaliana data set and ∼14 d for the human data set. We used 1000 computation threads, and the computation took 2 h for the A. thaliana data set and 20 min for the human data set. The second step, using a single computation thread, required 49 min for the A. thaliana data set and 1.5 min for the human data set.

    Software availability

    The code for running the analyses (called NetStruct_Hierarchy) can be found as Supplemental Code and at https://github.com/amirubin87/NetStruct_Hierarchy along with a user manual and a tool for plotting maps and coloring the clusters.

    Previous SectionNext Section

    Acknowledgments

    We thank Arun Durvasula, Andrea Fulgione, and Angela Hancock for help with the A. thaliana data, and Jonathan Kang for help with the HGDP data set. We also thank Ellie E. Armstrong, Danny Hendler, and Stefan Prost for helpful discussions. This study was supported by National Institutes of Health grant R01HG005855 awarded to N.A.R.

    Author contributions: G.G. conceived the study and drafted the manuscript. G.G. and A.R. developed and implemented the approach and analyzed the A. thaliana and human data sets. A.R.T. and N.A.R. contributed ideas to the framing and implementation of the project. All authors read and commented on the manuscript.

    Previous SectionNext Section

    Footnotes

    • Received March 6, 2019.
    • Accepted November 1, 2019.

    This article is distributed exclusively by Cold Spring Harbor Laboratory Press for the first six months after the full-issue publication date (see http://genome.cshlp.org/site/misc/terms.xhtml). After six months, it is available under a Creative Commons License (Attribution-NonCommercial 4.0 International), as described at http://creativecommons.org/licenses/by-nc/4.0/.

    Previous Section
     

    References

    1. ↵
      The 1000 Genomes Project Consortium. 2015. A global reference for human genetic variation. Nature 526: 68–74. doi:10.1038/nature15393
      CrossRefMedlineGoogle Scholar
    2. ↵
      The 1001 Genomes Consortium. 2016. 1,135 Genomes reveal the global pattern of polymorphism in Arabidopsis thaliana. Cell 166: 481–491. doi:10.1016/j.cell.2016.05.063
      CrossRefMedlineGoogle Scholar
    3. ↵
      Alexander DH, Novembre J, Lange K. 2009. Fast model-based estimation of ancestry in unrelated individuals. Genome Res 19: 1655–1664. doi:10.1101/gr.094052.109
      Abstract/FREE Full Text
    4. ↵
      Allendorf FW, Hohenlohe PA, Luikart G. 2010. Genomics and the future of conservation genetics. Nat Rev Genet 11: 697–709. doi:10.1038/nrg2844
      CrossRefMedlineGoogle Scholar
    5. ↵
      Armstrong E, Khan A, Taylor R, Gouy A, Greenbaum G, Thiéry A, Kang J, Redondo S, Prost S, Barsh G, et al. 2019. Recent evolutionary history of tigers highlights contrasting roles of genetic drift and selection. bioRxiv doi:10.1101/696146
      Abstract/FREE Full Text
    6. ↵
      Bakker EG, Stahl EA, Toomajian C, Nordborg M, Kreitman M, Bergelson J. 2006. Distribution of genetic variation within and among local populations of Arabidopsis thaliana over its species range. Mol Ecol 15: 1405–1418. doi:10.1111/j.1365-294X.2006.02884.x
      CrossRefMedlineGoogle Scholar
    7. ↵
      Blondel VD, Guillaume JL, Lambiotte R, Lefebvre E. 2008. Fast unfolding of communities in large networks. J Stat Mech Theory Exp 10: P10008. doi:10.1088/1742-5468/2008/10/P10008
      CrossRefGoogle Scholar
    8. ↵
      Bowcock AM, Ruiz-Linares A, Tomfohrde J, Minch E, Kidd JR, Cavalli-Sforza LL. 1994. High resolution of human evolutionary trees with polymorphic microsatellites. Nature 368: 455–457. doi:10.1038/368455a0
      CrossRefMedlineGoogle Scholar
    9. ↵
      Bryc K, Bryc W, Silverstein JW. 2013. Separation of the largest eigenvalues in eigenanalysis of genotype data from discrete subpopulations. Theor Popul Biol 89: 34–43. doi:10.1016/j.tpb.2013.08.004
      CrossRefMedlineGoogle Scholar
    10. ↵
      Busoms S, Teres J, Huang XY, Bomblies K, Danku J, Douglas A, Weigel D, Poschenrieder C, Salt DE. 2015. Salinity is an agent of divergent selection driving local adaptation of Arabidopsis to coastal habitats. Plant Physiol 168: 915–929. doi:10.1104/pp.15.00427
      Abstract/FREE Full Text
    11. ↵
      Cann HM, de Toma C, Cazes L, Legrand MF, Morel V, Piouffre L, Bodmer J, Bodmer WF, Bonne-Tamir B, Cambon-Thomsen A, et al. 2002. A human genome diversity cell line panel. Science 296: 261–262. doi:10.1126/science.296.5566.261b
      CrossRefMedlineGoogle Scholar
    12. ↵
      Cavalli-Sforza LL. 2005. The human genome diversity project: past, present and future. Nat Rev Genet 6: 333–340. doi:10.1038/nrg1596
      CrossRefMedlineGoogle Scholar
    13. ↵
      Corander J, Marttinen P. 2006. Bayesian identification of admixture events using multilocus molecular markers. Mol Ecol 15: 2833–2843. doi:10.1111/j.1365-294X.2006.02994.x
      CrossRefMedlineGoogle Scholar
    14. ↵
      Corander J, Waldmann P, Marttinen P, Sillanpää MJ. 2004. BAPS 2: enhanced possibilities for the analysis of genetic population structure. Bioinformatics 20: 2363–2369. doi:10.1093/bioinformatics/bth250
      CrossRefMedlineGoogle Scholar
    15. ↵
      Corander J, Marttinen P, Sirén J, Tang J. 2008. Enhanced Bayesian modelling in BAPS software for learning genetic structures of populations. BMC Bioinformatics 9: 539. doi:10.1186/1471-2105-9-539
      CrossRefMedlineGoogle Scholar
    16. ↵
      Durvasula A, Fulgione A, Gutaker RM, Alacakaptan SI, Flood PJ, Neto C, Tsuchimatsu T, Burbano HA, Picó FX, Alonso-Blanco C, et al. 2017. African genomes illuminate the early history and transition to selfing in Arabidopsis thaliana. Proc Natl Acad Sci 114: 5213–5218. doi:10.1073/pnas.1616736114
      Abstract/FREE Full Text
    17. ↵
      Dyer RJ, Nason JD. 2004. Population graphs: the graph theoretic shape of genetic structure. Mol Ecol 13: 1713–1727. doi:10.1111/j.1365-294X.2004.02177.x
      CrossRefMedlineGoogle Scholar
    18. ↵
      Excoffier L, Smouse PE, Quattro JM. 1992. Analysis of molecular variance inferred from metric distances among DNA haplotypes: application to human mitochondrial DNA restriction data. Genetics 131: 479–491.
      Abstract/FREE Full Text
    19. ↵
      Fortunato S. 2010. Community detection in graphs. Phys Rep 486: 75–174. doi:10.1016/j.physrep.2009.11.002
      CrossRefGoogle Scholar
    20. ↵
      Fournier-Level A, Korte A, Cooper MD, Nordborg M, Schmitt J, Wilczek AM. 2011. A map of local adaptation in Arabidopsis thaliana. Science 334: 86–89. doi:10.1126/science.1209271
      Abstract/FREE Full Text
    21. ↵
      François O, Ancelet S, Guillot G. 2006. Bayesian clustering using hidden Markov random fields in spatial population genetics. Genetics 174: 805–816. doi:10.1534/genetics.106.059923
      Abstract/FREE Full Text
    22. ↵
      François O, Blum MGB, Jakobsson M, Rosenberg NA. 2008. Demographic history of European populations of Arabidopsis thaliana. PLoS Genet 4: e1000075. doi:10.1371/journal.pgen.1000075
      CrossRefMedlineGoogle Scholar
    23. ↵
      Frichot E, Mathieu F, Trouillon T, Bouchard G, François O. 2014. Fast and efficient estimation of individual ancestry coefficients. Genetics 196: 973–983. doi:10.1534/genetics.113.160572
      Abstract/FREE Full Text
    24. ↵
      Gopalan P, Hao W, Blei DM, Storey JD. 2016. Scaling probabilistic models of genetic variation to millions of humans. Nat Genet 48: 1587–1590. doi:10.1038/ng.3710
      CrossRefGoogle Scholar
    25. ↵
      Granot Y, Tal O, Rosset S, Skorecki K. 2016. On the apportionment of population structure. PLoS One 11: e0160413. doi:10.1371/journal.pone.0160413
      CrossRefGoogle Scholar
    26. ↵
      Greenbaum G, Fefferman NH. 2017. Application of network methods for understanding evolutionary dynamics in discrete habitats. Mol Ecol 26: 2850–2863. doi:10.1111/mec.14059
      CrossRefGoogle Scholar
    27. ↵
      Greenbaum G, Templeton AR, Bar-David S. 2016. Inference and analysis of population structure using genetic data and network theory. Genetics 202: 1299–1312. doi:10.1534/genetics.115.182626
      Abstract/FREE Full Text
    28. ↵
      Guillot G, Leblois R, Coulon A, Frantz AC. 2009. Statistical methods in spatial genetics. Mol Ecol 18: 4734–4756. doi:10.1111/j.1365-294X.2009.04410.x
      CrossRefMedlineGoogle Scholar
    29. ↵
      Haasl RJ, Payseur BA. 2011. Multi-locus inference of population structure: a comparison between single nucleotide polymorphisms and microsatellites. Heredity (Edinb) 106: 158–171. doi:10.1038/hdy.2010.21
      CrossRefMedlineGoogle Scholar
    30. ↵
      Hagmann J, Becker C, Müller J, Stegle O, Meyer RC, Wang G, Schneeberger K, Fitz J, Altmann T, Bergelson J, et al. 2015. Century-scale methylome stability in a recently diverged Arabidopsis thaliana lineage. PLoS Genet 11: e1004920. doi:10.1371/journal.pgen.1004920
      CrossRefGoogle Scholar
    31. ↵
      Han E, Carbonetto P, Curtis RE, Wang Y, Granka JM, Byrnes J, Noto K, Kermany AR, Myres NM, Barber MJ, et al. 2017. Clustering of 770,000 genomes reveals post-colonial population structure of North America. Nat Commun 8: 14238. doi:10.1038/ncomms14238
      CrossRefMedlineGoogle Scholar
    32. ↵
      Hao W, Song M, Storey JD. 2016. Probabilistic models of genetic variation in structured populations applied to global human studies. Bioinformatics 32: 713–721. doi:10.1093/bioinformatics/btv641
      CrossRefMedlineGoogle Scholar
    33. ↵
      Holsinger KE, Weir BS. 2009. Genetics in geographically structured populations: defining, estimating and interpreting FST. Nat Rev Genet 10: 639–650. doi:10.1038/nrg2611
      CrossRefMedlineGoogle Scholar
    34. ↵
      Horton MW, Hancock AM, Huang YS, Toomajian C, Atwell S, Auton A, Muliyati NW, Platt A, Sperone FG, Vilhjálmsson BJ, et al. 2012. Genome-wide patterns of genetic variation in worldwide Arabidopsis thaliana accessions from the RegMap panel. Nat Genet 44: 212–216. doi:10.1038/ng.1042
      CrossRefMedlineGoogle Scholar
    35. ↵
      Hsu CW, Lo CY, Lee CR. 2019. On the postglacial spread of human commensal Arabidopsis thaliana: journey to the East. New Phytol 222: 1447–1457. doi:10.1111/nph.15682
      CrossRefGoogle Scholar
    36. ↵
      Huber CD, Nordborg M, Hermisson J, Hellmann I. 2014. Keeping it local: evidence for positive selection in Swedish Arabidopsis thaliana. Mol Biol Evol 31: 3026–3039. doi:10.1093/molbev/msu247
      CrossRefMedlineGoogle Scholar
    37. ↵
      Hubisz MJ, Falush D, Stephens M, Pritchard JK. 2009. Inferring weak population structure with the assistance of sample group information. Mol Ecol Resour 9: 1322–1332. doi:10.1111/j.1755-0998.2009.02591.x
      CrossRefMedlineGoogle Scholar
    38. ↵
      Hunley KL, Cabana GS, Long JC. 2016. The apportionment of human diversity revisited. Am J Phys Anthropol 160: 561–569. doi:10.1002/ajpa.22899
      CrossRefGoogle Scholar
    39. ↵
      Jakobsson M, Scholz SW, Scheet P, Gibbs JR, VanLiere JM, Fung HC, Szpiech ZA, Degnan JH, Wang K, Guerreiro R, et al. 2008. Genotype, haplotype and copy-number variation in worldwide human populations. Nature 451: 998–1003. doi:10.1038/nature06742
      CrossRefMedlineGoogle Scholar
    40. ↵
      Jombart T, Pontier D, Dufour AB. 2009. Genetic markers in the playground of multivariate analysis. Heredity (Edinb) 102: 330–341. doi:10.1038/hdy.2008.130
      CrossRefMedlineGoogle Scholar
    41. ↵
      Jombart T, Devillard S, Balloux F. 2010. Discriminant analysis of principal components: a new method for the analysis of genetically structured populations. BMC Genet 11: 94. doi:10.1186/1471-2156-11-94
      CrossRefMedlineGoogle Scholar
    42. ↵
      Jørgensen S, Mauricio R. 2004. Neutral genetic variation among wild North American populations of the weedy plant Arabidopsis thaliana is not geographically structured. Mol Ecol 13: 3403–3413. doi:10.1111/j.1365-294X.2004.02329.x
      CrossRefMedlineGoogle Scholar
    43. ↵
      Kuismin MO, Ahlinder J, Sillanpää MJ. 2017. CONE: community oriented network estimation is a versatile framework for inferring population structure in large-scale sequencing data. G3 (Bethesda) 7: 3359–3377. doi:10.1534/g3.117.300131
      Abstract/FREE Full Text
    44. ↵
      Lancichinetti A, Fortunato S, Kertész J. 2009. Detecting the overlapping and hierarchical community structure in complex networks. New J Phys 11: 033015. doi:10.1088/1367-2630/11/3/033015
      CrossRefGoogle Scholar
    45. ↵
      Lawson DJ, Falush D. 2012. Population identification using genetic data. Annu Rev Genomics Hum Genet 13: 337–361. doi:10.1146/annurev-genom-082410-101510
      CrossRefMedlineGoogle Scholar
    46. ↵
      Lawson DJ, Hellenthal G, Myers S, Falush D. 2012. Inference of population structure using dense haplotype data. PLoS Genet 8: e1002453. doi:10.1371/journal.pgen.1002453
      CrossRefMedlineGoogle Scholar
    47. ↵
      Lee CR, Svardal H, Farlow A, Exposito-Alonso M, Ding W, Novikova P, Alonso-Blanco C, Weigel D, Nordborg M. 2017. On the post-glacial spread of human commensal Arabidopsis thaliana. Nat Commun 8: 14458. doi:10.1038/ncomms14458
      CrossRefGoogle Scholar
    48. ↵
      Li JZ, Absher DM, Tang H, Southwick AM, Casto AM, Ramachandran S, Cann HM, Barsh GS, Feldman M, Cavalli-Sforza LL, et al. 2008. Worldwide human relationships inferred from genome-wide patterns of variation. Science 319: 1100–1104. doi:10.1126/science.1153717
      Abstract/FREE Full Text
    49. ↵
      Li Y, Huang Y, Bergelson J, Nordborg M, Borevitz JO. 2010. Association mapping of local climate-sensitive quantitative trait loci in Arabidopsis thaliana. Proc Natl Acad Sci 107: 21199–21204. doi:10.1073/pnas.1007431107
      Abstract/FREE Full Text
    50. ↵
      Loh PR, Lipson M, Patterson N, Moorjani P, Pickrell JK, Reich D, Berger B. 2013. Inferring admixture histories of human populations using linkage disequilibrium. Genetics 193: 1233–1254. doi:10.1534/genetics.112.147330
      Abstract/FREE Full Text
    51. ↵
      Long Q, Rabanal FA, Meng D, Huber CD, Farlow A, Platzer A, Zhang Q, Vilhjálmsson BJ, Korte A, Nizhynska V, et al. 2013. Massive genomic variation and strong selection in Arabidopsis thaliana lines from Sweden. Nat Genet 45: 884–890. doi:10.1038/ng.2678
      CrossRefMedlineGoogle Scholar
    52. ↵
      Manel S, Berthier P, Luikart G. 2002. Detecting wildlife poaching: identifying the origin of individuals with Bayesian assignment tests and multilocus genotypes. Conserv Biol 16: 650–659. doi:10.1046/j.1523-1739.2002.00576.x
      CrossRefGoogle Scholar
    53. ↵
      Martin HC, Batty EM, Hussin J, Westall P, Daish T, Kolomyjec S, Piazza P, Bowden R, Hawkins M, Grant T, et al. 2018. Insights into platypus population structure and history from whole-genome sequencing. Mol Biol Evol 35: 1238–1252. doi:10.1093/molbev/msy041
      CrossRefGoogle Scholar
    54. ↵
      McDaid AF, Greene D, Hurley N. 2013. Normalized mutual information to evaluate overlapping community finding algorithms. arXiv: 1110.2515v2 [physics.soc-ph].
      Google Scholar
    55. ↵
      Menozzi P, Piazza A, Cavalli-Sforza L. 1978. Synthetic maps of human gene frequencies in Europeans. Science 201: 786–792. doi:10.1126/science.356262
      Abstract/FREE Full Text
    56. ↵
      Morin PA, Martien KK, Taylor BL. 2009. Assessing statistical power of SNPs for population structure and conservation studies. Mol Ecol Resour 9: 66–73. doi:10.1111/j.1755-0998.2008.02392.x
      CrossRefMedlineGoogle Scholar
    57. ↵
      Newman MEJ. 2002. Random graphs as models of networks. In Handbook of graphs and networks: from the genome to the internet (ed. Bornholdt S, Schuster HG), pp. 34–68. Wiley-VCH, Darmstadt, Germany.
      Google Scholar
    58. ↵
      Newman M. 2006. Modularity and community structure in networks. Proc Natl Acad Sci 103: 8577–8582. doi:10.1073/pnas.0601602103
      Abstract/FREE Full Text
    59. ↵
      Newman MEJ. 2010. Networks: an introduction. Oxford University Press, Oxford.
      Google Scholar
    60. ↵
      Nievergelt CM, Libiger O, Schork NJ. 2007. Generalized analysis of molecular variance. PLoS Genet 3: e51. doi:10.1371/journal.pgen.0030051
      CrossRefMedlineGoogle Scholar
    61. ↵
      Nordborg M, Hu TT, Ishino Y, Jhaveri J, Toomajian C, Zheng H, Bakker E, Calabrese P, Gladstone J, Goyal R, et al. 2005. The pattern of polymorphism in Arabidopsis thaliana. PLoS Biol 3: e196. doi:10.1371/journal.pbio.0030196
      CrossRefMedlineGoogle Scholar
    62. ↵
      Novembre J, Peter BM. 2016. Recent advances in the study of fine-scale population structure in humans. Curr Opin Genet Dev 41: 98–105. doi:10.1016/j.gde.2016.08.007
      CrossRefGoogle Scholar
    63. ↵
      Patterson N, Price AL, Reich D. 2006. Population structure and eigenanalysis. PLoS Genet 2: e190. doi:10.1371/journal.pgen.0020190
      CrossRefMedlineGoogle Scholar
    64. ↵
      Pickrell JK, Pritchard JK. 2012. Inference of population splits and mixtures from genome-wide allele frequency data. PLoS Genet 8: e1002967. doi:10.1371/journal.pgen.1002967
      CrossRefMedlineGoogle Scholar
    65. ↵
      Platt A, Horton M, Huang YS, Li Y, Anastasio AE, Mulyati NW, Ågren J, Bossdorf O, Byers D, Donohue K, et al. 2010. The scale of population structure in Arabidopsis thaliana. PLoS Genet 6: e1000843. doi:10.1371/journal.pgen.1000843
      CrossRefMedlineGoogle Scholar
    66. ↵
      Pritchard JK, Stephens M, Donnelly P. 2000. Inference of population structure using multilocus genotype data. Genetics 155: 945–959.
      Abstract/FREE Full Text
    67. ↵
      Provart NJ, Alonso J, Assmann SM, Bergmann D, Brady SM, Brkljacic J, Browse J, Chapple C, Colot V, Cutler S, et al. 2016. 50 years of Arabidopsis research: highlights and future directions. New Phytol 209: 921–944. doi:10.1111/nph.13687
      CrossRefGoogle Scholar
    68. ↵
      Raj A, Stephens M, Pritchard JK. 2014. fastSTRUCTURE: variational inference of population structure in large SNP data sets. Genetics 197: 573–589. doi:10.1534/genetics.114.164350
      Abstract/FREE Full Text
    69. ↵
      Rosenberg NA. 2006. Standardized subsets of the HGDP-CEPH human genome diversity cell line panel, accounting for atypical and duplicated samples and pairs of close relatives. Ann Hum Genet 70: 841–847. doi:10.1111/j.1469-1809.2006.00285.x
      CrossRefMedlineGoogle Scholar
    70. ↵
      Rosenberg NA. 2011. A population-genetic perspective on the similarities and differences among worldwide human populations. Hum Biol 83: 659–684. doi:10.3378/027.083.0601
      CrossRefMedlineGoogle Scholar
    71. ↵
      Rosenberg NA, Pritchard JK, Weber JL, Cann HM, Kidd KK, Zhivotovsky LA, Feldman MW. 2002. Genetic structure of human populations. Science 298: 2381–2385. doi:10.1126/science.1078311
      Abstract/FREE Full Text
    72. ↵
      Rosenberg NA, Mahajan S, Ramachandran S, Zhao C, Pritchard JK, Feldman MW. 2005. Clines, clusters, and the effect of study design on the inference of human population structure. PLoS Genet 1: e70. doi:10.1371/journal.pgen.0010070
      CrossRefMedlineGoogle Scholar
    73. ↵
      Rozenfeld AF, Arnaud-Haond S, Hernández-García E, Eguíluz VM, Serrão EA, Duarte CM. 2008. Network analysis identifies weak and strong links in a metapopulation system. Proc Natl Acad Sci 105: 18824–18829. doi:10.1073/pnas.0805571105
      Abstract/FREE Full Text
    74. ↵
      San Lucas FA, Rosenberg NA, Scheet P. 2012. Haploscope: a tool for the graphical display of haplotype: structure in populations. Genet Epidemiol 36: 17–21. doi:10.1002/gepi.20640
      CrossRefMedlineGoogle Scholar
    75. ↵
      Sharbel TF, Haubold B, Mitchell-Olds T. 2000. Genetic isolation by distance in Arabidopsis thaliana: biogeography and postglacial colonization of Europe. Mol Ecol 9: 2109–2118. doi:10.1046/j.1365-294X.2000.01122.x
      CrossRefMedlineGoogle Scholar
    76. ↵
      Shringarpure S, Xing EP. 2009. mStruct: inference of population structure in light of both genetic admixing and allele mutations. Genetics 182: 575–593. doi:10.1534/genetics.108.100222
      Abstract/FREE Full Text
    77. ↵
      Turakulov R, Easteal S. 2003. Number of SNPS loci needed to detect population structure. Hum Hered 55: 37–45. doi:10.1159/000071808
      CrossRefMedlineGoogle Scholar
    78. ↵
      Yang Z, Algesheimer R, Tessone CJ. 2016. A comparative analysis of community detection algorithms on artificial networks. Sci Rep 6: 30750. doi:10.1038/srep30750
      CrossRefGoogle Scholar
    79. ↵
      Zheng X, Weir BS. 2016. Eigenanalysis of SNP data with an identity by descent interpretation. Theor Popul Biol 107: 65–76. doi:10.1016/j.tpb.2015.09.004
      CrossRefMedlineGoogle Scholar
    | Table of Contents

    This Article

    1. Published in Advance November 6, 2019, doi: 10.1101/gr.250092.119 Genome Res. 29: 2020-2033 © 2019 Greenbaum et al.; Published by Cold Spring Harbor Laboratory Press

    Article Category

    ORCID

    1. Profile for Greenbaum, G.http://orcid.org/0000-0002-1631-8203

    Share

    Preprint Server



    Navigate This Article

    Current Issue

    1. February 2026, 36 (2)
    1. Current Issue
    1. Alert me to new issues of Genome Research