Parente2: a fast and accurate method for detecting identity by descent
- 1Biomedical Informatics Program,
- 2Department of Computer Science, Stanford University, Stanford, California 94305, USA
- Corresponding author: serafim{at}cs.stanford.edu
-
↵3 These authors contributed equally to this work.
Abstract
Identity-by-descent (IBD) inference is the problem of establishing a genetic connection between two individuals through a genomic segment that is inherited by both individuals from a recent common ancestor. IBD inference is an important preceding step in a variety of population genomic studies, ranging from demographic studies to linking genomic variation with phenotype and disease. The problem of accurate IBD detection has become increasingly challenging with the availability of large collections of human genotypes and genomes: Given a cohort’s size, a quadratic number of pairwise genome comparisons must be performed. Therefore, computation time and the false discovery rate can also scale quadratically. To enable accurate and efficient large-scale IBD detection, we present Parente2, a novel method for detecting IBD segments. Parente2 is based on an embedded log-likelihood ratio and uses a model that accounts for linkage disequilibrium by explicitly modeling haplotype frequencies. Parente2 operates directly on genotype data without the need to phase data prior to IBD inference. We evaluate Parente2’s performance through extensive simulations using real data, and we show that it provides substantially higher accuracy compared to previous state-of-the-art methods while maintaining high computational efficiency.
When two individuals co-inherit a genomic segment from a common ancestor, the shared haplotypes are identical to each other except for occasional lineage-specific de novo mutations. Such shared segments are called identical-by-descent (IBD).
Computational detection of IBD segments from genotyping or sequencing data serves as the foundation for many downstream applications (Browning and Browning 2012). IBD detection is the prevalent method for finding familial relatives in direct-to-consumer genomics companies such as 23andMe (23andme.com) and AncestryDNA (ancestry.com) and is a key step in analyzing relatedness within a population and across populations; for example, IBD analysis was applied to study the demographic history across Ashkenazi Jewish and Masai populations (Palamara et al. 2012), to demonstrate increased sharing across Welsh individuals as compared to individuals from other regions in the United Kingdom (Browning and Browning 2011), and to compare relatedness across hunting-gathering, agricultural, and pastoralist African populations (Soi et al. 2011). IBD detection was also shown to be useful in estimating narrow-sense (additive) heritability (Yang et al. 2010; Price et al. 2011) and imputation (Kong et al. 2008; Setty et al. 2011). In genome-wide association studies, IBD detection has been applied to remove the confounding effect of hidden relatedness in cohorts of individuals that are assumed to be unrelated to each other (Gusev et al. 2009; Pemberton et al. 2010; Kyriazopoulou-Panagiotopoulou et al. 2011) and to correct for hidden relatedness when inferring associations between genotype and phenotype (Slager and Schaid 2001; Bourgain et al. 2003; Browning et al. 2005; Choi et al. 2009; Thornton and McPeek 2010).
IBD segment detection can be applied directly as a way to identify regions of the genome associated with a phenotype with a technique called IBD mapping (Alkuraya 2010; Bercovici et al. 2010; Moltke et al. 2011; Browning and Thompson 2012; Thompson 2013), narrowing the search to regions in which most cases are identical by descent (Roach et al. 2010; Rodelsperger et al. 2011; Smith et al. 2011). Examples of successfully applying IBD mapping include the study of genes related to an individual’s plasma plant serol (PPS) level, a surrogate measure of cholesterol absorption from the intestine (Kenny et al. 2009), where an analysis of 44 individuals from the Micronesian island of Kosrae identified a 526-kbp shared haplotype that led to the discovery of a putative missense causal variant. Simulation studies have shown that IBD mapping has higher statistical power to detect disease susceptibility genes when multiple rare causal variants cluster within them (Browning and Thompson 2012).
Extensive previous work has focused on developing methods for IBD segment detection. One of the earlier methods, PLINK (Purcell et al. 2007), uses a three-state hidden Markov model (HMM) with states corresponding to zero, one or two co-inherited copies of the genome, and assumes that all markers are in linkage equilibrium. BEAGLE IBD (Browning and Browning 2010) uses a model of haplotype frequencies that simultaneously phases and infers the particular shared haplotype by a pair of individuals. BEAGLE IBD is based on a factorial HMM that incorporates a model of IBD and a descriptive model of linkage disequilibrium. IBDMap (Bercovici et al. 2010) uses a factorial HMM that explicitly models the inheritance vector capturing the relationship between two individuals. IBDMap models linkage disequilibrium (LD) with a first-order Markov model of the founders. In an effort to reduce the computational cost of IBD detection among all pairs of individuals in a group, GERMLINE (Gusev et al. 2009) is a hash-map-based method that relies on string matching; it uses a sliding window based on hashing of haplotype strings, hence scaling linearly with the number of individuals analyzed. Similarly, toward the goal of reducing running time, fastIBD (Browning and Browning 2011) incorporates a sliding window approach like GERMLINE and uses the phasing and haplotype frequency model of BEAGLE (Browning 2006; Browning and Browning 2007). fastIBD identifies pairs of individuals sharing the same state in its factorial HMM and extends shared haplotype segments when the probability of IBD is high. Henn et al. (2012) developed a method for detecting longer IBD segments that identifies long stretches of markers where the individuals share at least one allele in common. Moltke et al. (2011) developed a Markov chain Monte Carlo (MCMC) method designed to identify IBD shared among many individuals within a cohort rather than focusing on each pair independently. Recently we developed Parente (Rodriguez et al. 2013), a method that estimates the likelihood of windows of markers under both related and unrelated states producing a likelihood ratio score, followed by estimating the empirical likelihood of that score under the two states; we refer to this technique as the embedded likelihood ratio. Parente assumes that markers are in linkage equilibrium and does not require phasing for inference. As a result, the method is computationally efficient.
While there have been numerous advances in this field, improvement in accuracy as well as speed compared to the state-of-the-art is necessary in order to handle increasingly large cohorts of individuals. As the number of individuals increases, the number of pairs of individuals that need to be analyzed and the number of falsely discovered segments grow quadratically.
In this work we present Parente2, a novel method for IBD detection that incorporates a model accounting for linkage disequilibrium by explicitly modeling haplotype frequencies, as well as a novel technique of aggregating informative overlapping windows of nonconsecutive, randomly selected markers. We demonstrate that these novel steps result in significant improvements in accuracy over previous state-of-the-art methods such as Parente and fastIBD. Furthermore, Parente2 requires significantly less total computational time than fastIBD and GERMLINE.
Results
Overview of algorithms
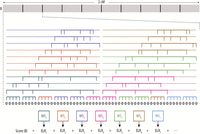
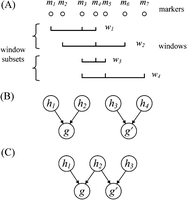
Parente2 uses a sliding-window approach for detecting IBD across the genomes of two individuals. Inspired by bootstrap aggregating (bagging), multiple weak haplotypic models are aggregated to estimate the likelihood of genotypes under both related and unrelated models. These weak haplotypic models are independently constructed by the random selection of features, which correspond in our case to the observed markers. The construction of these weak models is as follows. Given a target IBD segment length (in our experiments, 1–4 cM), a block B of that length is examined, starting at every marker of the genomes. Each sliding block B covers multiple overlapping window subsets, which in turn are composed of multiple overlapping windows (Fig. 1). A window is defined as a set of markers, which may be nonconsecutive. A window subset is defined as a set of such windows. In the results described, all windows have the same number of markers, controlled by the parameter winsize (typically, five to 10); all window subsets have the same number of windows, controlled by the parameter subsetsize (by default, five). As illustrated in Figure 1, the default set of windows consists of: (1) all nonoverlapping windows of consecutive markers tiling B (referred to as the basic windows), and (2) an additional c (by default, 10) sets of overlapping windows tiling B, where each such window samples winsize random markers out of a region of length r markers (by default, 40) (referred to as the augmented windows).
Overview of Parente2. A sliding block B of equal size to the minimum target size for IBD segment detection is examined, starting at every marker of the genome. In this figure, a block B of length 2 cM is displayed. The block contains windows, which are sets of winsize possibly nonconsecutive markers (by default, winsize = 8; in our benchmarks against other methods prior to optimizing this parameter, winsize = 5). A set of consecutive-marker windows tiles B; these are called the basic windows. In addition, c sets of nonconsecutive-marker windows tile B (by default, c = 10). Each such nonconsecutive window is generated by choosing winsize markers out of r markers (by default, r = 40; in this figure, r = 30). These are called the augmented windows. Windows are ordered lexicographically by their leftmost markers and grouped into window subsets by forming a subset out of each successive subsetsize window (by default, subsetsize = 5). Each window subset WSi is scored according to the outer log-likelihood ratio (Equation 6 in Methods) to yield ELRi; the score of B is the sum of these window subset scores according to Equation 7 in Methods.
The above windows are sorted by the genomic coordinate of their first marker; a window subset is formed for every successive subsetsize window. Each window subset is scored by the outer log-likelihood ratio (Equation 5 in Methods), which is a score computed from the empirical distribution of the inner log-likelihood ratio (Equation 1 in Methods) in the training data. This latter quantity, the inner log-likelihood ratio, is defined here as the log-likelihood ratio of two scenarios: (1) The observed genotypes within the windows of the subset originated from related individuals that share a common ancestor, and (2) the observed genotypes correspond to nonrelated individuals. Our model assumes that the windows are independent. The markers within each window, however, are derived by a haplotype distribution that accounts for LD, as well as for genotyping or sequencing errors (see Methods). Once all window subsets’ likelihoods are estimated, the corresponding scores are summed up for the block B. Block B will be reported as IBD in all cases where the resulting score exceeds a predefined threshold T.
Benchmark data sets
We benchmark the performance of Parente2 in two data sets: the HapMap Phase III panel (HapMap) (The International HapMap 3 Consortium 2010) and The Wellcome Trust Case Control Consortium (WTCCC) (The Wellcome Trust Case Control Consortium 2007). In HapMap we used haplotypes from three Asian populations: Han Chinese in Beijing, China (CHB); Japanese in Tokyo, Japan (JPT); and Chinese in metropolitan Denver, Colorado (CHB), resulting in a total of 520 haplotypes. Because haplotypes are required to perform simulations, the genotype data in WTCCC was first phased using HAPI-UR (Williams et al. 2012), which resulted in 2960 haplotypes. To expedite running time, we restricted benchmarks to the long arm of Chromosome 1, spanning 46,580 markers for HapMap and 14,777 markers for WTCCC. For each data set, we randomly partitioned individuals into training and testing sets; one-third was used for training and two-thirds were used for testing. To train its underlying model of IBD, Parente2 generated from the training data 1000 pairs of individuals sharing one haplotype along the entire length of the chromosome and 1000 pairs of individuals without any IBD segments. In order to break up latent IBD segments in the testing data set, we generated composite individuals from the original haplotype pairs for each individual in a manner similar to previous work (Browning and Browning 2011), except that our protocol retained 50% of the data rather than the 10% that was suggested in previous work. Each composite individual was generated by tiling 0.2-cM segments from different haplotypes in the testing data. When generating a composite individual, at each marker position, each source was guaranteed to appear in at most one composite individual (see Methods for details).
For each benchmark experiment, we generated simulated pairs of related individuals that shared one IBD segment of a fixed size. We performed benchmarks for segments of size 2 cM and 4 cM on HapMap and WTCCC. We name these data sets HapMap-2cM, HapMap-4cM, WTCCC-2cM, and WTCCC-4cM. In our experiments HapMap-2cM is the default data set unless otherwise specified. Each simulation was composed of 30 bootstrapped trials that sampled from the training and testing sets described above. For each trial, we generated a number of pairs of individuals sharing an IBD segment (termed related pairs of individuals) by choosing two random haplotypes per individual without replacement; 28 pairs were generated for each HapMap simulation and 40 pairs were generated for each WTCCC simulation. Within each trial, no haplotype from the testing data set was used in more than one pair; however, each haplotype was used in multiple trial data sets. To simulate an IBD segment in each pair, we chose a random location to start the IBD segment and copied the alleles of one haplotype from one individual in the pair over one of the haplotypes of the other individual. Next, we simulated genotyping errors for each generated individual using a genotyping error rate of 0.005, such that when an error was introduced, the genotype was changed to one of the other two genotypes with equal probability. Thus, each HapMap trial contained 56 individuals, so that 1540 pairs of individuals were evaluated. Each WTCCC trial data set contained 80 individuals, so that 3160 pairs were evaluated.
Comparison against other methods
We benchmarked the performance of Parente2 against Parente, fastIBD, and GERMLINE on the HapMap-2cM and HapMap-4cM data sets. We ran each method with parameters as described in Methods. We evaluated the overall accuracy of these methods with respect to detecting pairs of individuals that share at least one IBD segment, as well as the positional accuracy, which is defined as the ability to detect the exact IBD status per position across the examined segments (see Methods for details). We set the scoring threshold of each method so as to fix to a given false-positive rate (FPR) of detecting pairs of related individuals. We compared each method’s sensitivity (SN) at both low FPR and at higher FPR (Table 1) and found that Parente2 outperforms the earlier methods in both scenarios. We also measured the positional accuracy of each method and found that Parente2 infers the location of IBD segments more accurately than other state-of-the-art methods.
Pairwise accuracy of Parente2 and other methods
For effective IBD detection in large cohorts, both computational efficiency and low FPR are key for practical use; both running
time as well as number of false-positive IBD segments grow quadratically with cohort size. Parente2 can be tuned to run with
a variety of parameters that affect both running time and accuracy, allowing one to trade between those two core aspects based
on the application and problem at hand. To further lower the running time, and independently from the parameter choices, Parente2
can be applied in conjunction with SpeeDB (Huang et al. 2014), a coarse-grained filter designed to reduce running time of IBD detection within a large cohort. When considering a pair
of individuals, SpeeDB rapidly filters out regions of the genome that are unlikely to be IBD between the two individuals,
while it rarely filters out true IBD segments. Filtered-out regions can then be ignored by a downstream IBD detection method
such as Parente2. SpeeDB is based on a statistical model that identifies regions where a pair of individuals has too many
opposite homozygous loci for the region to be within an IBD segment (Huang et al. 2014). We compared the running time and accuracy of Parente2 to Parente and other methods on the HapMap-2cM data set (Table 2). Running Parente2 using the augmented window set was five times faster than running fastIBD and also resulted in significantly higher accuracy.
When using the SpeeDB filter, Parente2 ran 50 times faster than fastIBD and also had slightly higher accuracy than without
the filter (SpeeDB’s threshold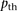 
was set to 0.1). If even lower running time is required, Parente2 can be run using the basic window set instead of the augmented
window set, which in our experiments resulted in a further threefold reduction in running time; this change, however, came
at the cost of reduced accuracy.
Accuracy and running time of evaluated IBD inference methods
Application of Parente2 to the discovery of cryptic relationships
We evaluated the performance of Parente2 on the discovery of IBD segments among the 368 haplotypes from Maasai in Kinyawa, Kenya (MKK) in the HapMap Phase III panel, in which a large number of cryptic relationships across individuals were previously reported (Pemberton et al. 2010), and assessed the ability of Parente2 to discover such relationships as compared to previous work. First, we performed simulations on the long arm of chromosome 1 to establish baseline IBD detection accuracy on 2-cM and 4-cM segments using the same procedures as we used for generating HapMap-2cM and HapMap-4cM. As in all our simulations, latent IBD was broken up through shuffling (see Methods, “Generation of benchmark test individuals”). Parente2 achieved 100% sensitivity and no false positives (i.e., zero FPR) on the African-4cM data set, and 98.9% sensitivity at 1% FPR on the African-2cM data set.
We then applied Parente2 to every pair of the 184 MKK samples. We set the target IBD length minimum to 4 cM and a strict scoring threshold and performed whole-genome IBD detection. The region near the telomere of Chromosome 15 (0–4.35 cM), where an abnormally high number of IBD segments were detected, were removed from our analysis. We compared the related individuals inferred by Parente2 to the discovered relationships previously reported (Pemberton et al. 2010), which included 68 parent-offspring pairs, 16 full-sibling pairs, and 80 second-degree relative pairs. Using Parente2 we confirmed all previously identified pairs (Supplemental Fig. 1; Supplemental Table 1). The minimum percentage of genome in IBD detected was 99.05% for parent-offsprings (mean, 99.29%), 66.24% for siblings (mean, 74.89%), and 28.81% for other relatives (mean, 49.01%). In addition, of the remaining 16,672 pairs of individuals, we identified 677 pairs to have blocks of IBD covering at least 6.75% of their genomes, of which 318 pairs have IBD covering at least 12.5% of their genomes, and 83 pairs have IBD covering at least 25% of their genomes (Supplemental Table 2). In addition, we identified four new putative relationships between individual NA21737 and individuals NA21344, NA21366, NA21301, and NA21302 with IBD levels 99.33%, 99.09%, 78.39%, and 55.2%, respectively. Also, individual NA21318 exhibited IBD with individuals NA21455, NA21678, and NA21597 at levels 34.88%, 34.26%, and 34.08%. A full demographic and family analysis of this data set is beyond the scope of this work.
Performance on homozygous IBD detection
The IBD model used by Parente2 assumes that the two examined individuals share either zero or one IBD segment at any location of the genome. When examining populations for cryptic relationships, it may be important to detect IBD in regions where pairs of individuals share two haplotypes; such cases may arise when a small population has significant inbreeding, or when applying the analysis on siblings. We performed simulations similar to HapMap-2cM and HapMap-4cM, except that the simulated individuals shared IBD segments in both haplotypes and evaluated the ability of Parente2 to discover pairs of individuals who share IBD under that scenario. Parente2 performed better under the homozygous IBD scenario, exhibiting 99.8% sensitivity with 0.03% FPR in the 4-cM case and 82.9% sensitivity with 1% FPR in the 2-cM case.
Amount of training data required for Parente2
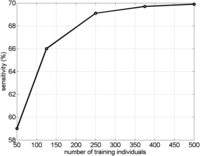
In order to perform inference, Parente2 requires haplotype frequencies that are empirically estimated from phased training data. To estimate the amount of training data required for high performance, we measured the sensitivity of Parente2 while varying the number of training individuals from 50 to 500 (Fig. 2). We used the WTCCC-2cM data set for this experiment due to the larger number of available training individuals than HapMap, allowing for better trend resolution. We observed diminishing returns as the number of training individuals increased: 250 training individuals were sufficient to achieve near-peak performance. In all of our experiments on the HapMap data set, we used only 85 training individuals, so the WTCCC results suggest that Parente2’s performance on HapMap may increase with additional training data. The number of training individuals needed to reach saturation is likely to depend on the window size used as well as the haplotype diversity within the cohort.
Parente2’s sensitivity as a function of the number of training individuals. Parente2 was run on the WTCCC-2cM data set. The vertical axis shows sensitivity at a 1% false-positive rate.
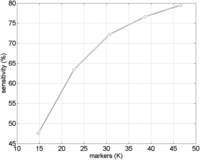
We evaluated the accuracy of Parente2 as a function of density of assayed positions. Figure 3 shows the sensitivity of Parente2 at a 1% FPR when run on the HapMap data set after downsampling the markers to various densities. We observe that increasing marker density results in an increase in sensitivity, and the curve has yet to reach a saturation point. We expect that Parente2 will perform better on high-density sequencing-based genotyping studies. Parente2’s runtime is linear in the number of markers used, so the running time will increase with an increase in marker density. However, as previously demonstrated, SpeeDB is more effective at filtering out non-IBD segments with higher marker density (Huang et al. 2014). Therefore, when using Parente2 in conjunction with SpeeDB, we expect a lower-than-linear increase in running time as marker density increases.
Performance of Parente2 as a function of marker density. Parente2 performance is shown as a function of marker density; tests are performed on the HapMap-2cM benchmark with FPR fixed at 1%.
Recommended settings for Parente2
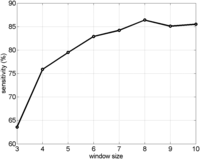
Subsequent to obtaining the above results with parameters set as described in Methods, we sought to derive a final default parameter set that is informed by our extensive experimentation. We tested Parente2 on the HapMap-2cM benchmark with and without the basic and augmented window sets, with and without using the window filter (set to filtering winfilter = 20% of the windows, see Methods), and with and without using the outer-LLR (Supplemental Fig. 2). We confirmed that the best settings for Parente2 are using the augmented window set, the window filter, and the outer-LLR. In all settings of window sets and filter, the outer-LLR scoring significantly outperforms the inner-LLR. Furthermore, all of our experiments indicated that SpeeDB resulted in a significant decrease in running time, and in a small and often positive effect on accuracy. To measure the effect of window size on performance, we ran Parente2 using the augmented window set by setting winsize between 3 and 10, and reported sensitivity at 1% FPR (Fig. 4). These results indicate that window size 8 provided the highest accuracy, with slightly decreased accuracy as window size is further increased to 9 or 10. Finally, we ran Parente2 using different levels of window filtering, setting winfilter = 0%–90%, and found that performance was best for values between 30% and 70% (results not shown). Based on our above experiments, we modified two parameters to the final default values winsize = 8 and winfilter = 50%. Using the new parameters, we tested Parente2 on the HapMap and WTCCC-2cM and -4cM benchmarks and also on an additional HapMap-1cM benchmark, and we confirmed that performance is significantly improved under these parameters (Table 3).
Effect of window size on Parente2’s performance. Increasing the window size of Parente2 results in better performance (test performed on the HapMap-2cM benchmark).
Accuracy of Parente2 with the recommended default settings
We note that the performance of Parente2 is still low in the 1-cM IBD inference. We evaluated the performance of fastIBD in the 1-cM IBD inference on the HapMap data set. To accomplish the highest accuracy for fastIBD, we set its minimum IBD segment size to 0.8 cM. We found that fastIBD achieved per-pair sensitivity of 1.6%, 27%, 41.2%, and 47.5% with per-pair FPR of 0.1%, 1%, 5%, and 10%, respectively, and positional sensitivity of 24%, 33%, and 36% with positional FPR of 0.01%, 0.05%, and 0.1%, respectively, and thus performed slightly worse than Parente2 on most measures (see Table 3). We conclude that given the size of the data set used, detection of IBD with 1 cM resolution is a challenging task for all existing methods.
Discussion
In future applications of Parente2 on new cohorts, training data from the cohort’s population may not be available. When only a single genotyped cohort is available, one may attempt to estimate haplotype frequencies from the cohort directly after first phasing the data; building our haplotypic model on the “test” data could in principle lead to overfitting. To quantify the impact on performance under this scenario, we measured Parente2’s accuracy on WTCCC-2cM when haplotype frequencies are estimated from the testing data itself and compared the results to Parente2’s performance when haplotype frequencies are estimated using a separate training data sampled from the same population. In both cases we used 370 individuals to control for training set size. The previous default parameters were used for this test. The sensitivity of Parente2 on the testing data was 68.7% when trained on training data and 72.0% when trained on the testing data, with FPR set to 1%. With a difference in sensitivity of only 3.3% in this experiment, we expect that Parente2 will perform reasonably well in a real-world scenario when one does not have access to separate training data.
As DNA sequencing is increasingly replacing genotyping, there will be a dramatic increase in the number of variants observed, including additional types of variants beyond SNVs, such as insertions and deletions. While some recent work has explored methods specifically for sequencing (Browning and Browning 2013), Parente2 is a general method that operates on observed polymorphic sites. In a naïve approach, Parente2 can be applied to sequencing data by simply restricting analysis to SNVs in known sites of variation such as sites from HapMap III. Equation 4, however, can be adjusted to more accurately account for both of the genotyping errors, as well as the missing, or poorly covered, variants. Namely, the standard phred-scaled likelihoods provided with the sequencing-based genotypes can be directly incorporated to compute the probability of the sequencing reads given the two assumed haplotypes and the derived expected genotype. In cases where only very low coverage data is available for sampled individuals, many of the variation sites will remain unobserved; the likelihood function in Equation 4 can be extended to account for missing data by using a uniform probability for all possible genotypes given the assumed haplotypes. We leave such extensions for future work.
Parente2 provides substantial improvements in accuracy as well as speed over previous state-of-the-art methods, and as such, is more suitable for performing IBD analysis of large cohorts. In addition, the novel use of sparse window sets for capturing the statistics of LD across a population may prove useful in other population genetic applications such as ancestry inference and imputation. Parente2 is open source and publicly and freely available at http://parente.stanford.edu.
Methods
Description of algorithm
Let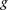 
denote an individual’s genotype, represented as a vector of M bi-allelic markers 
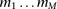. Let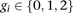 
represent the observed genotype at marker 
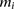as the number of minor alleles the individual has at 
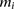. The alleles at 
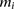on the individual’s chromosomes are denoted by 
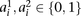, where 0 represents the minor allele and 1 represents the major allele. A window 
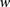is defined as a set of winsize possibly nonconsecutive markers, and 
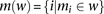is defined as the set indices corresponding to the markers associated with a window 
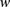(Fig. 5A). A window haplotype 
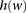is defined to refer to the alleles at markers 
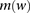, i.e., 
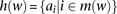. The frequency of a haplotype 
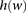within the examined population is denoted by 
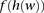. The underlying idea is that intermarker LD may be captured by different sets 
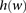of markers within the block B. Given a set of windows defined over a set of markers on a chromosome, a window subset s is defined simply as a subset of windows (Fig. 5A).
(A) Example of windows and window subsets. Here, windows contain three markers and window subsets contain two windows. (B,C) Graphical models used for the inner log-likelihood ratio described in Equation 2. (B) Model for two unrelated individuals that do not share an IBD segment in the window. (C) Model for two related individuals sharing a single IBD segment in the window. The variables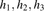 
and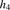 
represent hidden haplotypes for a given window of markers. The variables g and g′ represent the observed genotype vectors from the first and second individual in a pair of individuals being evaluated for
IBD in the window.
For a target IBD block length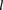 
(in cM), the Parente2 method is defined as follows. Given the genotype calls of two individuals, g and g′, the genome is scanned by sliding a block B for each marker across each chromosome. B spans a set of windows w, into window subsets grouped into window subsets 
as defined precisely in the corresponding subsections of Methods (see also Fig. 1). Within B, and specifically within each associated window subset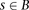 
, the inner log-likelihood ratio (inner-LLR) is computed by estimating the likelihood of the individuals’ genotypes within
each block under two models: a model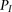 
corresponding to the hypothesis that the two examined individuals are IBD; and a model 
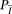corresponding to the hypothesis that the two individuals are not IBD (Fig. 5B,C).
We model the genotypes within a window subset s using a naïve Bayes approach, whereby windows are independent given the IBD status of the two examined individuals within
s. The probabilities of the genotypes within each window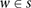 
are considered separately, and the product of these probabilities defines the probability of the observed genotypes within
s (or as a sum, under our log formulation). Namely, given s, and given the genotype of two examined individuals g and g′, the inner-LLR score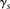 
is defined as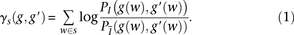
To calculate these joint probabilities of observed genotypes, we sum over all possible underlying haplotypes h. We denote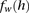 
as the frequency of a haplotype h with respect to the markers within window 
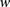. Once established or approximated, 
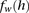is used to compute the probability of the observed genotypes under both models, namely, 
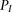and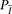 
, as follows: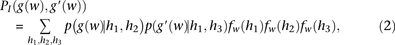
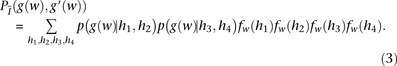
The probability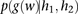 
that the genotype 
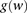was sampled, conditioned on haplotypes 
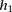and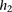 
, needs to account for genotyping errors. Hence, we define 
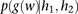as follows: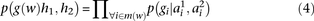
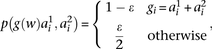where the parameter 
is tuned to capture the amount of expected genotyping error, using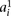 
and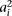 
to correspond to the allele associated with marker i in haplotype 
and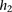 
, respectively. To reduce FPR, during inference we replace 
in the above equation with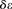 
, where 
is a scaling factor that increases the contrast between IBD and non-IBD segments. In all benchmarks, we use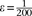d 
and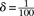 
. Finally, to accommodate for missing data, whenever a genotype value for a particular window 
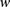is missing the probabilities under both models 
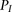and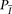 
are set to 1, which will not affect the 
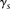score.
In the above model, the individuals share zero or one haplotype in a given genomic region. Homozygous IBD resulting from inbreeding
is not explicitly modeled; however, homozygous IBD regions across two individuals should be significantly more likely under
the IBD scenario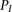 
rather than under 
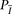, and thus easily detectable. This is indeed the case in our experiments, as reported in Results.
As the size of window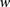 
grows, enumerating over all possible haplotypes 
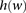becomes impractical: Given k markers in a window, there are 
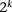possible distinct haplotypes; when k = 10, iterating more than 1 million haplotype pairs would be necessary to evaluate the likelihood of an individual’s genotype
at each window. While there are 1024 distinct 10-marker possible haplotypes, the number of observed haplotypes in an examined population is significantly smaller. To reduce computation time at the possible cost of accuracy
of the likelihood function estimation, we only iterate over the top H most common window haplotypes observed in training data. In practice, we found that for a window size of 10 markers, 99%
of windows on the long arm of Chromosome 1 had no more than 50 distinct haplotypes in our data sets. Therefore, in all of
our experiments we set H = 50. We note that setting H = 50 only impacted experiments where windows could have more than 50 distinct haplotypes per window (i.e., when window size
was at least 6).
Outer log-likelihood ratio
The model described thus far can be utilized directly for IBD detection by simply summing Equation 1 over all window subsets
scores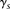 
within a block B (i.e., 
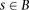) and reporting as IBD blocks with scores higher than a threshold. Nonetheless, computing a single naïve Bayes LLR score may
be sensitive to a small subset of windows that exhibit scores with high variance. To correct for potentially high-variance
windows, we empirically examine the performance of each window subset s on the training set. Specifically, we treat the inner-LLR described in Equation 1 as a random variable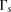 
. We then define two empirical models 
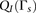and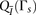 
for the distribution of 
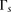given related individuals, and given unrelated individuals, respectively. We estimate these distributions by using phased
training haplotypes that we use to simulate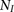 
pairs of individuals sharing IBD along the entire chromosome, and 
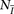individuals without any IBD segments. Then, we compute the LLR for each window subset for the IBD and non-IBD pairs and estimate
the probability density functions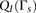 
and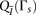 
via binning. We define numbins as equally sized, nonoverlapping bins that span the domain of each distribution and we use a pseudocount 
for each bin. Our modified score, which we call the outer log-likelihood ratio (outer-LLR), is defined as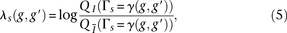
and the scores of all window subsets associated with a block 
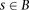are combined via a naïve Bayes model, to produce the block score: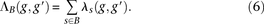
The above block score is used to infer IBD segments. We call a pair of individuals IBD in block B whenever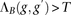 
, where T is a predefined threshold. Since each marker may be contained in several blocks, Parente2 reports, for each marker, the maximum
block score of any block containing the marker. We call a pair of individuals related if any block in the genome is called
to be IBD. The block score 
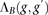can be computed efficiently: As we slide B across the genomes of two individuals, scores corresponding to windows that are
no longer part of the block are subtracted from the current block score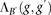 
, and scores corresponding to newly joining windows are added.
The phased haplotypes used for training could be either generated from data sets containing trios, or via computationally
phased individuals. Current phasing methods offer a sufficiently low switch-error rate for their performance to have a negligible
effect when considering haplotypes within a window of moderate size. For our experiments in the Results and Discussion sections,
we set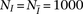 
, 
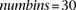, and 
.
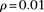Windows and window subsets
In the above description of our model, both windows and window subsets were defined in general terms. There are several ways to instantiate the definitions of windows. We have tested two different ways, which we term the basic and augmented windows:
-
The basic windows set is the set of all nonoverlapping windows of winsize markers. Formally, the ith window is composed of markers in the interval
.
-
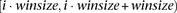The augmented windows set is the set of windows that includes the basic windows as well as a set of overlapping windows defined as follows. We let r > winsize be the number of markers in a region, and define the ith region to span the markers in the interval
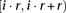. We construct 
windows for each such region by picking for each such window winsize markers at random. For most of our experiments we used winsize = 5; r = 40; c = 10, which for a genome of length L markers resulted in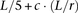 
windows (ignoring boundary effects), each of them sampling five markers.
We then defined window subsets as follows. We first sorted all of the above windows by their leftmost marker and then separately by their rightmost marker. Then, window subsets were defined by successively picking the next subsetsize windows of the sorted list. Because we perform this procedure twice, for leftmost marker-sorted and rightmost marker-sorted windows, each of the windows appears in exactly two window subsets. For our experiments, we used as default subsetsize = 5.
Finally, we use a window filter to remove the least informative windows for predicting IBD in each local region. Informally, an informative window is one that reliably outputs low scores for non-IBD pairs and high scores for IBD pairs. We performed experiments that revealed that informative windows tend to have low variance in the outer-LLR scores of the simulated training IBD pairs (results not shown). Therefore, we used the negative variance of the IBD training scores as a proxy of informativeness. The window filter examines all nonoverlapping 0.05-cM segments that tile the chromosome, and removes the winfilter percent of the windows of lowest informativeness within each segment.
Generation of benchmark test individuals
For each benchmark data set (HapMap Phase III and WTCCC), we randomly partitioned individuals into one-third training and
two-thirds testing sets. To break up latent IBD segments in a testing data set of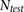 
individuals (
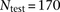for HapMap and 
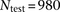for WTCCC), we generated 
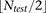composite individuals as follows. For the ith composite individual, we first choose a random offset, O, in cM such that 
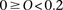. The first segment of each composite individual was established as O cM (the 0th segment), and each subsequent segment was 0.2 cM in size (segments 1 to S). For example, assuming N = 6 and a chromosome of 1.8 cM in size, this procedure produces three composite individuals each with nine segments with
source individuals of each segment as seen in Table 4. In this way, we significantly reduced latent IBD in the testing data sets prior to simulating IBD individuals, as in previous
practice (Browning and Browning 2011).
Example of tiling method used to break up latent IBD
Parameters for each IBD detection method
We set initial parameters of Parente2 at values that we obtained during development of the method with limited training on HapMap populations in small subsets of Chromosome 1 (experiments not shown). These initial parameters were used for all experiments described in Results and Discussion, with the exception of Table 3, which was obtained after setting the final default parameters. The following initial parameters were used: The augmented window set was set to r = 40, c = 10, winsize = 5, and subsetsize = 5, which resulted in each marker being included in 11 windows on average.
We sought to run other methods in the best possible settings. fastIBD was run using a minimum IBD segment size of 1 cM since this resulted in better performance than the default or than using an IBD segment size close to the target IBD segment size, and the nsamples parameter was set to 20 to achieve better performance given relatively small simulation sizes. For each run, fastIBD was provided with both the training and testing data sets, which resulted in better accuracy than if given only the testing data sets (results not shown); accuracy was measured only using inferred pairs where both individuals were in the testing data set. Therefore, for each benchmark, fastIBD’s model was built on strictly more data than Parente2’s model. Following the authors’ recommendations to achieve higher accuracy, fastIBD was run 10 times with 10 different seeds and the results were merged by setting the score of each position to be the maximum score observed in any of the 10 runs. All other parameters of fastIBD were left at their default values. To evaluate GERMLINE, the data was first phased using BEAGLE according to the pipeline provided with the GERMLINE software. GERMLINE was applied on the phased data with default parameters, except that the -bits parameter was set to 128 to achieve higher specificity and set to 64 for the results to achieve higher sensitivity.
Measuring accuracy
In our benchmarks, we measured the positional accuracy and pairwise accuracy of each method. Accuracy was taken as the average over all the trials in each simulation. For positional accuracy, the basic units evaluated were tuples containing a marker, a pair of individuals, and a label indicating whether or not the marker was a part of an IBD segment shared by the two individuals in the pair. A tuple was considered to be labeled true by an IBD inference method if the marker in the tuple appeared in a predicted IBD segment output by the method. Likewise, the actual label for a tuple was considered true if the marker was within a simulated IBD segment of the two individuals. For pairwise accuracy, the position information was disregarded so that the tuples evaluated contained only a pair of individuals and a label. In this case, a tuple was considered to be labeled true by an IBD inference method if it predicted at least one IBD segment between the pair of individuals and its actual label was true if the pair of individuals were simulated to share an IBD segment.
To estimate sensitivity (SN) and false-positive rate (FPR), we generated many points along a receiver operator curve (ROC curve) for each method by adjusting a score threshold on the output scores of the method. The exception to this was GERMLINE—since it did not output a score its performance points were collected based on changing nonthreshold parameters. For Parente2, Parente, and fastIBD, we estimated SN and FPR values between points on the curve via linear interpolation.
Competing interest statement
S. Batzoglou is a founder of DNAnexus and a member of the scientific advisory boards of 23andMe and Eve Biomedical. S. Bercovici is Chief Technology Officer of SVBio.
Acknowledgments
This material is based upon work supported in part by the National Science Foundation Graduate Research Fellowship under grant no. DGE-1147470. Any opinions, findings, and conclusions or recommendations expressed in this material are those of the authors and do not necessarily reflect the views of the National Science Foundation. This work is also supported by a grant from the Stanford-KAUST alliance for academic excellence. L.H. was supported in part by a Stanford Graduate Fellowship. We thank Dorna Kashef-Haghighi for producing Figure 1.
Footnotes
-
[Supplemental material is available for this article.]
-
Article published online before print. Article, supplemental material, and publication date are at http://www.genome.org/cgi/doi/10.1101/gr.173641.114.
Freely available online through the Genome Research Open Access option.
- Received February 5, 2014.
- Accepted September 30, 2014.
This article, published in Genome Research, is available under a Creative Commons License (Attribution-NonCommercial 4.0 International), as described at http://creativecommons.org/licenses/by-nc/4.0/.
