Extensive Genome-wide Linkage Disequilibrium in Cattle

RESULTS

Evidence for Long-range Linkage Disequilibrium in Cattle

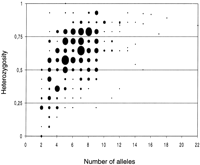
The first data set used to measure LD in the dutch black-and-white population was a previously described granddaughter design (GDD), with 22 paternal half-sib families comprising a total of 949 bulls (Coppieters et al. 1998). This sample was genotyped for a battery of 284 autosomal microsatellites for a total of 276,048 genotypes. Figure1 reports for each marker the heterozygosity measured in the 22 founder sires as well as the number of alleles observed in the overall population. The average heterozygosity as measured in the founder sires was 59%, whereas the average number of alleles was 6.6. Linkage maps were constructed for all autosomes as described (Georges et al. 1995), yielding a total map length of 2702 cM (Kosambi map) with an average between-marker interval of 13.4 cM. Order and distance between markers as well as estimates of total map length were in good agreement with Kappes et al. (1997).

The most likely linkage phase of the 22 founder-sires and their respective sons was estimated for the 29 autosomes as described in Materials and Methods. The maternally inherited chromosomes of the sons were considered to be a representative sample of the dutch black-and-white breeding population. For dams having multiple sons in the GDD, only one of the sons was considered in the analysis. In total, we selected 581 such maternal “gametes” for further analysis. The corresponding genotypes were used to estimate LD between all 40,186 pairs of markers, using Lewontin's (1964) normalized D′ measure (see Materials and Methods).

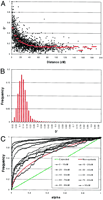
The extent of LD was first evaluated for syntenic marker pairs. Figure2A shows the distribution of D′ values as a function of genetic distance in centimorgans. D′ averaged 50% for marker pairs <5 cM apart, decayed rapidly to values of the order of 16% for distances of 50 cM, and then reached a plateau slightly below 14% for more distant markers. The statistical significance of the corresponding LD, α, was estimated by Monte-Carlo approximation of Fisher's exact test as described by Weir (1996). More specifically (see Materials and Methods), we examined the cumulative frequency distribution of α values for syntenic marker pairs grouped by distance in recombination units (Fig. 2C). All observed frequency distributions differed dramatically from that expected under the null hypothesis of linkage equilibrium (P < 0.001), clearly indicating that substantial levels of intrachromosomal LD can be captured with the utilized marker density, not only for closely linked, but even for the most distant, syntenic markers. Grouping marker pairs <5 cM apart in 1-cM bins, indicates that average D′ values continue to increase with decreasing distance between markers, providing no evidence for a saturation of the LD signal <5 cM (data not shown).

Intrigued by the long-range LD observed between syntenic markers, we then looked for possible gametic phase disequilibrium between nonsyntenic loci. Figure 2B reports the frequency distribution ofD′ values measured between nonsyntenic marker pairs. The average D′ value was 12%, therefore quite similar to theD′ value found for distant (>50 cM) though syntenic loci. Examination of the corresponding cumulative frequency distribution of α-values (Fig. 2C) indicates that the observed gametic phase disequilibrium between nonsyntenic loci was highly significant as well (P < 0.001).

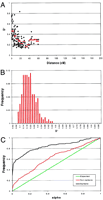
The results described previously were obtained using gametes from so-called bull-dams, that is, elite cows selected to produce top bulls. One could argue that this so-called “active breeding population” is not representative of the breed in general. We therefore examined a second data set assumed to be more representative of the general population. We collected DNA from 627 cows, daughters of four sires, as well as from their respective dams in a large number of dutch herds. The four sires, all daughters, and their corresponding dams were genotyped for eight microsatellite markers located on different autosomes. 175 daughters and their dams were genotyped for an additional 19 markers, 16 of these located on chromosome 14 and three on chromosome six. We determined the genotype of the gamete transmitted to the daughter as well as its “complement” (see Materials and Methods), yielding a total of 1254 gametes. Figure 3shows the distribution of D′ values obtained for the 123 tests performed between syntenic markers (Fig. 3A) as well as for the 228 nonsyntenic tests (Fig. 3B). D′ averaged 46% for marker pairs <5 cM apart, decaying to 24% on average for marker pairs at a distance of 30 cM or more. The average D′ value measured between nonsyntenic markers was 20%, therefore even higher than the value observed with the bull-dam gametes. The departure from expectation proved to be highly significant (P < 0.001) for both syntenic and nonsyntenic marker pairs (Fig. 3C). Overall, these results provide strong evidence that long-range LD and gametic association between nonsyntenic loci is a genuine feature characterizing the dutch black-and-white dairy cattle population in general and not only the elite bull-dam population.

Random Drift Accounts for Most of the Observed Disequilibrium

The observation of this unexpectedly high degree of linkage disequilibrium poses the question of its origin. It is well established from classical population genetics theory that drift (Hill and Roberston 1968; Ohta and Kimura 1969), migration (admixture) (e.g.,Stephens et al. 1994), mutation, and selection (Bulmer 1971) generate linkage disequilibrium. Worldwide, the black-and-white dairy population counts >25 million animals. In the Netherlands only, the population of black-and-white cattle comprises 1.2 million lactating cows. Estimates of effective population size, however, yield numbers as low as 50 (Boichard 1996). This is primarily attributable to the widespread use of artificial insemination (A.I.) and the intense selection for increased milk production. As an example, in the Netherlands 95% of cows are bred by A.I. and the 10 top sires account for 40% of the inseminations.

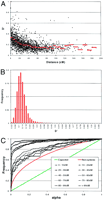
To evaluate whether the population structure of the dutch black-and-white population alone could account for the observed linkage disequilibrium, we collected the known genealogies of the studied bull-dams (data set 1). The average number of recorded ancestors per bull-dam was 40.4, whereas up to 11 generations separated the bull-dams from their most distant ancestor. Based on the available pedigree data and assuming that the “founders” were unrelated, we estimated the average inbreeding coefficient, F, of the bull-dams at 1.3% (range: 0%–14%), and their average kinship coefficients, f, at 4% (range: 0%–57%). We simulated the segregation in this pedigree material of 29 autosomes covered with markers mimicking the actual microsatellite map (see Material and Methods). A gamete was drawn at random from each bull-dam and the resulting collection of genotypes used to measure LD between syntenic markers as well as gametic phase disequilibrium between nonsyntenic markers (Fig.4). D′ values averaged 33% for syntenic marker pairs <5 cM apart, that is, slightly lower than the values observed with the real data. As expected, D′ values decreased with increasing distance between markers to plateau at a value of 14.7% for marker pairs >50 cM apart, therefore very similar if not slightly superior to the corresponding value of 13.8% obtained with the real genotypes (Fig. 4A). For nonsyntenic marker pairs, the average D′ value was 12%, therefore virtually identical to the value found with the real data set (Fig. 4B). The cumulative frequency distributions of α values were shown to depart very significantly from the distribution expected in case of linkage equilibrium (P < 0.001), both for syntenic marker pairs sorted by distance as well as nonsyntenic markers (Fig. 4C). These results therefore clearly indicated that the population structure alone suffices to generate substantial levels of both syntenic and nonsyntenic LD, very similar in magnitude to that observed with the real data. The most striking difference between the real and the simulated results are that for closely linked markers (<5 cM apart) the average D′ values are considerably higher for the real data (50%) when compared with the simulated data (33%). The intrinsic differences between the real and simulated data sets therefore seem to affect the level of disequilibrium between closely linked versus distant markers more profoundly. Note that despite the extensive pedigree recording that is customary in dairy cattle breeding, the available genealogies of the bull-dams are far from complete (see above). In the simulations, all “founder” chromosomes were assumed to be in linkage equilibrium (see Materials and Methods), which would be expected to reduce the overall level of LD when compared with the real data.

In addition to random drift, migration (admixture) is likely to have contributed to the observed levels of LD as well. The globalization of semen trade has caused considerable gene flow between demes, particularly from the United States to the rest of the world (e.g.,Goddard 1992). Differences in allelic frequencies between demes could only have increased the level of LD.

Lack of Evidence in Favor of the Bulmer Effect

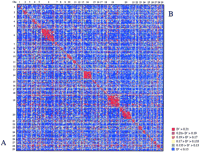
Selection is also predicted to cause gametic phase disequilibrium (Bulmer 1971). Contrary to the other factors that cause LD, however, selection will preferentially generate disequilibrium between loci influencing the selected phenotype. Directional and stabilizing selection for instance tend to generate negative gametic-phase disequilibrium (alleles increasing the character value at one locus preferentially associated with alleles decreasing the character value at other loci and vice versa), whereas disruptive selection and directional selection on characters displaying certain patterns of epistasis will generate positive gametic-phase disequilibrium (Walsh and Lynch 1999). Therefore, if selection were to contribute significantly to the observed genome-wide LD, one would predict thatD′ values would not be distributed uniformly across the genome-wide nonsyntenic LD map but would have a tendency to be higher for chromosome pairs harboring Quantitative Trait Loci (QTL) undergoing selection. Figure 5 illustrates the genome-wide LD map obtained with both the real (data set 1) and simulated data. We analyzed the nonsyntenic D′ values using a linear model including the effect of the two corresponding chromosomes, as well as a term testing for the interaction between these chromosomes (see Materials and Methods). A significant interaction term would have been interpreted as being in favor of the Bulmer effect. As expected, the interaction term was not significant for the simulated data set (P = 0.97), as the simulation was performed in the absence of selection. This term was also not significant, however, with the real data (P = 0.98), therefore providing no evidence in favor of a strong contribution of selection to the gametic association observed between nonsyntenic marker loci. Examination of the genomic distribution of nonsyntenic marker pairs exhibiting D′ values >0.3 did not point toward the preferential involvement of specific chromosomes, including those that are known to harbor QTL, influencing milk yield and composition (e.g., Georges et al. 1995;Coppieters et al. 1998).

Interestingly, the chromosome effects proved to be highly significant for both the real and simulated data sets (P < 0.0001). Despite the fact that D′ is assumed to be a frequency-independent measure of LD (Hedrick 1987), we attribute this significant chromosome effect to differences in information content between markers.

DISCUSSION

Our results suggest that mapping strategies exploiting LD may be particularly effective in dairy cattle (e.g., Charlier et al. 1996;Riquet et al. 1999). Whereas the present study concentrated on the dutch black-and-white population, we predict that similar situations will be encountered in most other dairy cattle populations were A.I. is widespread. Contrary to the situation in the human where genome-wide LD mapping may require a marker density two orders of magnitude higher than that required for conventional linkage mapping (Kruglyak 1999), the available battery of ≅1,500 microsatellites (Kappes et al. 1997) could be sufficient for first-pass LD screening in dairy cattle. The corollary of this observation, however, is that the mapping resolution to be gained from LD is likely to be limited in these populations as well. In this work, we still observed a considerable drop in D′ values between 1 and 5 cM, suggesting that it should nevertheless be possible to achieve resolution down to the centimorgan level. Further analyses will be required to evaluate the benefit of LD mapping at the sub-centimorgan level in these populations.

Because of their higher mutation rate, the usefulness of microsatellite markers for LD mapping when compared with single nucleotide polymorphisms (SNPs) has been questioned by some. The extensive LD observed suggests, however, that in cattle populations Identity By Descent (IBD) chromosome segments will on average coalesce within considerably fewer generations when compared with most human populations. The relatively high mutation rate of microsatellite markers, susceptible to erase part of the LD signal in humans, is therefore less likely to cause a problem for LD mapping in cattle.

The common occurrence of gametic-phase disequilibrium between nonsyntenic loci raises serious concerns about the generation of false-positive results when using association studies as the only means to locate genes underlying complex traits in these populations. Preference should therefore be given to mapping methods that combine linkage and LD information. This could be achieved using a two-tiered approach in which the rough map position of the genes of interest is first determined by linkage analysis followed by their fine-mapping using LD. Alternatively, one could use approaches akin to the Transmission Disequilibrium Test (e.g., Spielman et al. 1993), which are simultaneously testing for linkage and LD.

The fact that we were not able to provide evidence in favor of the Bulmer effect, does not mean that it doesn't operate in the studied population. More refined methods are probably required to reveal the specific contribution of selection to the gametic-phase disequilibrium observed between chromosome regions harboring QTL. As several QTL influencing milk yield and composition have now been uncovered and marker haplotypes associated with specific QTL alleles are being detected (e.g., Riquet et al. 1999), such experiments should become feasible in the near future.

MATERIALS AND METHODS

Genotype Determination

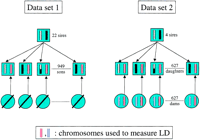
Microsatellite genotypes, marker maps, and the most likely linkage phase of the founder sires were obtained as described (Georges et al. 1995). Assuming known linkage phase of the sires, we determined the most likely linkage phase of each offspring accounting for the marker genotype of the dam when available (data set 2) or marker allele frequencies in the general population when not (data set 1) (F. Farnir, unpubl.). For data set 1, the maternal gametes transmitted to the sons were used to estimate LD. This yielded a sample of 581 gametes. For data set 2, the maternal gametes transmitted to the daughters as well as the “complementary” gamete (the genotype of which could be inferred by substracting the genotype of the transmitted gamete from the known genotype of the dam) were used to estimate LD. This yielded a sample of 1,254 gametes. Figure 6 summarizes the pedigree structure for data sets 1 and 2.

Measuring Linkage Disequilibrium

Following Hedrick (1987), LD between two polyallelic lociA and B was measured as: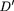 where u and v are the respective number of alleles at the two marker loci, p_i andq_j are the population frequencies of marker allelei at locus A and marker allele j at locusB, and ‖D′_ij‖ is the absolute value of Lewontin's (1964) normalized LD measure computed as:  =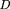 

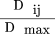
with: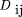 where x_ij is the observed frequency of gametes A_iB_j , and p_i and q_j are the frequencies of allelesA_i and B_j respectively, and: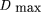 The statistical significance (α) of the observed allelic association under the null hypothesis of random allelic assortment, was estimated by Monte-Carlo approximation of Fisher's exact test as described by Weir (1996). Briefly, assume a sample of ngametes genotyped for marker loci A and B having respectively u and v alleles. The sample is fully characterized by allele counts n_i. . (locusA) and n_.j (locus B) and haplotype counts n_ij , as illustrated in the following table for a simple example where locus A and B are characterized by three and two alleles, respectively. The probability of a given sample, P, can be computed as:

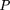The value of α for a given marker pair corresponds to the proportion of all possible tables with same allele counts (n_i. and n_.j ) that have equal or lower P. α can be estimated by simulating such tables under the hypothesis of random assortment and counting the proportion of tables that have equal or lower P than the real sample. In this study, the estimates of α were based on the simulations of 16,590 such tables.

The α values generated as described do not account for the large number (40,186) of tests performed. Rather than applying a Bonferroni correction on individual α values (and essentially lose all power to detect non random assortment), we compared the observed cumulative frequency distribution of α values with that expected under the null hypothesis of random allelic assortment. The statistical significance of the departure from expectation of the observed cumulative frequency distribution was estimated from the area bounded by the expected and observed lines. The corresponding surface was computed by numerical integration. The distribution of this area under the null hypothesis of random assortment was obtained by Monte-Carlo simulation (1,000 simulations) as well.

Determination of Kinship and Inbreeding Coefficients

Pedigree information was directly obtained from the NRS (Arnhem, The Netherlands). Kinship and inbreeding coefficients were computed using PROC INBREED from the SAS package version 6.12.

Simulating Chromosome Segregation in the Bull–Dam Genealogy

We simulated the segregation of 29 autosomes covered with a map of 284 markers. Number of markers per chromosome, their order, distance and allelic frequencies mimicked the real microsatellite data. Chromosomes were first generated for all founder individuals in the pedigree (i.e., individuals missing one generation of one chromosome) or both parents (generation of two chromosomes). Founder chromosomes were generated stochastically by drawing an allele at random for each marker and assuming linkage equilibrium between markers. Founder chromosomes were then allowed to segregate within the pedigree, including recombination with their homologs at a rate determined by the genetic distance between adjacent markers.

Testing for the Bulmer Effect

D′ values for nonsyntenic marker pairs were analyzed with the following linear models: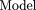  = μ + C_i + C_j + ɛ_n,m 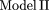 = μ + C_i + C_j + C_i * C_j + ɛ_n,m

where:

D′_n(i),m(j) is the D′ value computed for marker n, located on chromosome i, and marker m, located on chromosome j; μ is the average D′ value over all marker pairs;C_i and C_j are the effects of chromosomes i and j respectively;C_i * C_j is the interaction effect between chromosomes i and j, and ε_n,mis the error term.

Chromosome and interaction effects were estimated using standard least square methodology (Searle 1971).

The significance of the chromosome effects was estimated from: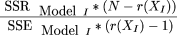 where SSR is the sum of squares caused by the chromosome effects, SSE is the residual sum of squares, N is the number of nonsyntenic marker pairs, andr(X_I ) is the rank of the incidence matrix for Model I, that is, 29.

The significance of the interaction term was estimated from: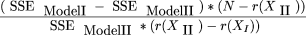 where r(X_II ) is the rank of the incidence matrix for Model II, that is, 406.