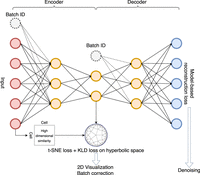
Complex hierarchical structures in single-cell genomics data unveiled by deep hyperbolic manifold learning

  1. Hakon Hakonarson1,3
  1. 1Center for Applied Genomics, Children's Hospital of Philadelphia, Philadelphia, Pennsylvania 19104, USA;
  2. 2Department of Computer Science, Ying Wu College of Computing, New Jersey Institute of Technology, Newark, New Jersey 07102, USA;
  3. 3Division of Human Genetics, Department of Pediatrics, The Perelman School of Medicine, University of Pennsylvania, Philadelphia, Pennsylvania 19104, USA

  1. ↵4 These authors contributed equally to this work.

  • Corresponding author: zhiwei{at}njit.edu
    •  
    Next Section

    Abstract

    With the advances in single-cell sequencing techniques, numerous analytical methods have been developed for delineating cell development. However, most are based on Euclidean space, which would distort the complex hierarchical structure of cell differentiation. Recently, methods acting on hyperbolic space have been proposed to visualize hierarchical structures in single-cell RNA-seq (scRNA-seq) data and have been proven to be superior to methods acting on Euclidean space. However, these methods have fundamental limitations and are not optimized for the highly sparse single-cell count data. To address these limitations, we propose scDHMap, a model-based deep learning approach to visualize the complex hierarchical structures of scRNA-seq data in low-dimensional hyperbolic space. The evaluations on extensive simulation and real experiments show that scDHMap outperforms existing dimensionality-reduction methods in various common analytical tasks as needed for scRNA-seq data, including revealing trajectory branches, batch correction, and denoising the count matrix with high dropout rates. In addition, we extend scDHMap to visualize single-cell ATAC-seq data.

    Single-cell RNA-seq (scRNA-seq) has provided plenty of new opportunities for exploring cell development and differentiation (Tanay and Regev 2017). Computation methods to accurately reveal and display the cell development process from large single-cell data have grown tremendously in recent years (Saelens et al. 2019). The progression of cells in continuous trajectories is like a hierarchical tree, with multiple branches typically, such as in Waddington's classic epigenetic landscape (Goldberg et al. 2007). Methods for analyzing these complex structures in the single-cell data have been published, including visualization (Haghverdi et al. 2015; Ding et al. 2018; Lopez et al. 2018; Amodio et al. 2019; Moon et al. 2019; Wolf et al. 2019), clustering (Levine et al. 2015; Wang et al. 2017; Tian et al. 2019), and pseudotime inference (Haghverdi et al. 2016; Qiu et al. 2017). Visualizing large-scale single-cell data in low dimensions will effectively reveal high-level structural information, which often provides interesting insights for downstream analyses. Despite the compelling potential of scRNA-seq, we note that scRNA-seq data are highly noisy, full of zeros (the dropout phenomenon), and highly dimensional, which makes dimensionality reduction a daunting task. An ideal dimensionality-reduction method is desired to address all these challenges to effectively reveal biological structural patterns in the data.

    Numerous embedding methods have been proposed to reduce the high-dimensional scRNA-seq data for downstream analysis. Most of these methods act on Euclidean space, including t-SNE (van der Maaten and Hinton 2008), UMAP (McInnes et al. 2018), PaCMap (Wang et al. 2021), diffusion map (Haghverdi et al. 2015), PAGA (Wolf et al. 2019), PHATE (Moon et al. 2019), Monocle (Qiu et al. 2017), scVI (Lopez et al. 2018), SAUCIE (Amodio et al. 2019), and scvis (Ding et al. 2018), among others. Although these methods of Euclidean space have different features (Supplemental Table 1; Supplemental Note 1), they share a common limitation; namely, they would distort the high-dimensional pairwise distance and would result in suboptimal downstream analysis, such as clustering and trajectory inference.

    Compared with Euclidean space, hyperbolic space can help to reduce distorting the high-dimensional pairwise distance. Hyperbolic space is a non-Euclidean space with a constant negative curvature. It can be considered as a continuous version of hierarchical trees and has the advantage of low distortion in low-dimensional embedding, even in two-dimensional space (Gromov 2007). Hyperbolic embedding has been successfully applied to various data types for representing complex hierarchical structures, including word embedding (Nickel and Kiela 2017), image embedding (Mathieu et al. 2019; Ovinnikov 2019), and graph embedding (Chami et al. 2019). Recently, two main methods, PoincaréMap (Klimovskaia et al. 2020) and scPhere (Ding and Regev 2021), acting on hyperbolic space, have been proposed for visualizing single-cell trajectory. In the cell-differentiation process, the number of cells can grow exponentially. The volume of balls also grows exponentially in the hyperbolic space with respect to the radius, which is a helpful property for the visualization of single-cell lineage. However, in the Euclidean space, the volume of balls only increases polynomially, which results in insufficient space for the exponentially growing number of cells and would distort the high-dimensional distances in the embedding. PoincaréMap is a hyperbolic version of t-SNE, which reduces scRNA-seq data to a 2D Poincaré ball. The scPhere is a deep variational autoencoder (Kingma and Welling 2014) that represents scRNA-seq data in a low-dimensional hyperbolic embedding. To characterize scRNA-seq count data, scPhere uses negative binomial (NB) reconstruction loss and integrates data from different sources via a conditional autoencoder (Sohn et al. 2015). Both of these two hyperbolic embedding methods have been proven to outperform Euclidean embedding methods empirically.

    Despite the superiority of these existing hyperbolic embedding methods, they are not optimized for computational challenges of single-cell data. Dropout events cause high proportions of zeros in scRNA-seq data, making the structural pattern vague; integrating data of different sources to a unified embedding with the batch effect eliminated is a common task in the single-cell analysis, but PoincaréMap fails to tackle these problems. Furthermore, PoincaréMap relies on a graph Laplacian of the pairwise distance matrix and a symmetric Kullback–Leibler (KL) divergence for local and global structure proximities. Calculating the Laplacian matrix is very time- and memory-consuming (Jianbo and Malik 2000), and the symmetric KL divergence requires the memory to store the whole similarity matrix, which makes PoincaréMap infeasible for large data sets. As a workaround, down-sampling has to be used to run PoincaréMap analysis on large data sets (Klimovskaia et al. 2020). For scPhere, which is an autoencoder-based model, it does not guarantee similarity preservation during the dimensionality reduction, making it not applicable for trajectory inference at single-cell resolution.

    To address these issues, we propose a model-based deep hyperbolic manifold learning approach: single-cell deep hierarchical map (scDHMap) (Fig. 1). To characterize the overdispersed and zero-inflated count matrix of the scRNA-seq data, we apply a zero-inflated negative binomial (ZINB) model-based loss function. The ZINB model has been successfully applied to various single-cell analyses, including imputation, dimensionality reduction, and clustering (Lopez et al. 2018; Risso et al. 2018; Eraslan et al. 2019; Tian et al. 2019). The scDHMap model can be used for versatile types of single-cell analysis. To represent the continuous hierarchical structures, we use the ZINB model–based variational autoencoder to map the high-dimensional-count data into a 2D hyperbolic space. Like in scvis, the structure of high-dimensional data is preserved by t-SNE regularization in our model but using the hyperbolic distance metric. The architecture of scDHMap can be considered as a model-based parametric t-SNE (van der Maaten 2009) in the hyperbolic space, which combines the strength of local structure preservation from t-SNE and global structure preservation from autoencoder (Ding et al. 2018; Graving and Couzin 2020), thus making it a strong candidate for representing complex hierarchical structures. We regularize the latent embedding by following a standard wrapped normal distribution via the variational inference (Kingma and Welling 2014), which makes the embedding normally distributed for better visualization. The deep generative model has recently emerged as a powerful method for representation learning of single-cell genomics data (Ding et al. 2018; Lopez et al. 2018; Ding and Regev 2021; Liu et al. 2021). To integrate data sets from different batches to a joint embedding, we combine the strength of Harmony (Korsunsky et al. 2019) with a conditional autoencoder (Sohn et al. 2015) responding to batch IDs. Following the previous studies (Lopez et al. 2018; Eraslan et al. 2019), estimated mean parameters in the ZINB model can be used as the denoised counts. Our model can be optimized per mini-batch on the graphic processing unit (GPU), which can be easily scaled to large data sets. Using both simulated and real data sets, we illustrate that scDHMap outperforms competing methods in various embedding tasks in terms of embedding quality metrics and visualizing developmental trajectories. Finally, we extend scDHMap to visualize the differential trajectories of single-cell ATAC-seq (scATAC-seq) data.

    Figure 1.
    View larger version:
    Figure 1.

    Network architecture of scDHMap. The encoder and decoder are fully connected neural networks. The latent embedding is in a 2D hyperbolic space for visualization and with the t-SNE regularization for structural preservations. KL divergence loss minimizes the divergence between the posterior and prior distributions of the latent embedding. Batch IDs can be incorporated to align different batches. Zero-inflated negative binomial (ZINB) reconstruction loss characterizes single-cell count data.

    Previous SectionNext Section

    Results

    Simulation evaluation of dimensionality reduction

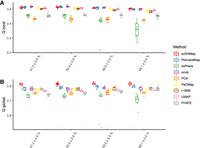
    Dropout events are pervasive in the scRNA-seq data and cause the main computational challenge in the single-cell analysis. To evaluate the dimensionality-reduction performance, we generated simulated data sets with various dropout rates. Each setting is repeated 10 times with different random seeds. Two embedding quality metrics are used to quantify the embedding performance: Q local and Q global, which reflect the local and global structural preservations, respectively (Supplemental Note 2). Larger Q scores mean better preservations of local and global high-dimensional distances. In the simulated data sets, we know the true counts, which are counts without the interference of dropout events. We built the ground-truth high-dimensional similarities by the 50 principal components (PCs) of analytic Pearson residuals (Lause et al. 2021) normalized true counts. All embedding methods received the 50 PCs of normalized raw counts as the input (except scDHMap and scPhere; scDHMap used both normalized raw counts and 50 PCs, and scPhere used raw counts), which are counts after adding dropout events. We simulated data sets having a hierarchical tree structure with various branches. We compared the embedding performance of scDHMap with various methods, including PoincaréMap (Klimovskaia et al. 2020), scPhere (Ding and Regev 2021), scvis (Ding et al. 2018), principal component analysis (PCA), PaCMap (Wang et al. 2021), t-SNE (van der Maaten and Hinton 2008), UMAP (McInnes et al. 2018), and PHATE (Moon et al. 2019). All methods reduce the high-dimensional count data to 2D representations. Simulation results are summarized in Figure 2, A and B. As we observed, scDHMap outperformed all competing methods, especially in terms of Q global. Although PoincaréMap and scvis had comparable Q local scores with scDHMap, they performed worse than scDHMap in terms of Q global. Hyperbolic embedding methods, including scDHMap and PoincaréMap, outperformed Euclidean embedding methods such as PaCMap, t-SNE, UMAP, and PHATE in all settings. ScPhere is a hyperbolic variational autoencoder but is not designed for similarity preservation, and it performed poorly on all simulated data sets. We also visualized embeddings of all the methods in Supplemental Figures S1 and S2. We noted that hyperbolic methods, including scDHMap and PoincaréMap, can accurately reveal the continuous trajectory paths. Methods of Euclidean space, including scvis, PaCMap, and UMAP, had some breaking points in trajectory paths, making a continuous path into multiple parts. With the increase of dropout rates, we observed that embeddings of competing methods become noisier, such as scPhere, scvis, and PHATE, whereas scDHMap's performance was unaffected. These results illustrated that scDHMap could reveal complex hierarchical structures better than the competing methods, even with high dropout rates. To make a further comparison, we conducted an experiment reducing the simulated data into 3D representations. We found that scDHMap showed similar superiority in the 3D embeddings, with the best Q scores (Supplemental Fig. S3A,B).

    Figure 2.
    View larger version:
    Figure 2.

    Embedding quality metrics of different methods on simulated data sets with various dropout rates. Q values measure the local (A) and global (B) structure preservations. Larger values mean better preservations. Each setting generated 10 data sets.

    Next, we conducted an ablation study with two variant models: one with NB reconstruction loss and another one discarding the ZINB model–based decoder of scDHMap. The evaluation of the embedding qualities is summarized in Supplemental Figure S4, A and B. We observed that scDHMap performed better than the model with NB loss and the model without decoder in terms of Q local (paired one-sided t-test P-value < 0.01 for the dropout rates is 50.4%, 68.1%, 75.6%, 81.7%, and 86.6%) (Supplemental Fig. S4C). The improvements became more significant with the increase of dropout rates, which reflected the contribution of the ZINB model–based decoder. We also tested the performance of scDHMap with different network architectures. We found that scDHMap is quite robust against different numbers of hidden layers in the encoder and decoder (Supplemental Fig. S5A,B). The contribution of pretraining scDHMap (the ZINB model–based autoencoder without the t-SNE loss) was shown in Supplemental Figure S6, A and B, and we found that pretraining can slightly improve the embedding quality, especially in terms of Q local (paired one-sided t-test P-value < 0.05 for dropout rates is 50.4%, 59.6%, and 68.1%). Perplexity is an important parameter in the t-SNE algorithm, which controls the number of neighbors that the model focuses on during dimensionality reduction. We reported the performance of scDHMap with different perplexity values in Supplemental Figure S7, A and B. Notably, scDHMap was robust against a large range of perplexity values from 10–50, and perplexity value 30 was the best choice based on the performance of both local and global structural preservations. So, we suggest perplexity = 30 as the default setting for scDHMap. Because scDHMap calculates the t-SNE regularization per mini-batch, if the perplexity is 30, then the effective perplexity of the whole data will be 30/512 · n ≈ 5.8% · n, where n is the number of total cells and 512 is the mini-batch size. This setting is similar to the suggestion of the previous study using t-SNE to scRNA-seq data (Kobak and Berens 2019).

    With the accumulation of scRNA-seq data, it is a common request to include new samples into the existing latent representations. Traditional nonparametric methods such as PoincaréMap, t-SNE, and UMAP are not possible for this out-of-sample support, but scDHMap can use the learned neural network to include new samples. To evaluate the out-of-sample performance, we randomly split the simulated data sets into training and testing sets with the proportions of 90% and 10%. We trained scDHMap on training sets and then mapped testing sets to the embeddings. Q scores were calculated for both training and testing sets, respectively. As shown in Supplemental Figure S8, A and B, scDHMap could preserve global structures in testing sets well but was not so good at preserving local structures. We further plotted the embeddings of training and testing sets in Supplemental Figure S9 and confirmed that testing sets were mapped to the expected positions. These results show that scDHMap can be used for embedding new samples after model training.

    We summarized the running time of scDHMap on simulated data sets of various cell numbers in Supplemental Figure S10. Each data set had been repeated three times. Although there are different numbers of iterations before the early stop, we noted that the running time scaled roughly linearly with the number of cells. This result is consistent with the computational complexity analysis in the scvis paper (Ding et al. 2018). For a mini-batch with a given size, the computational complexity of scDHMap is constant, which is quadratic to the mini-batch size. Large data sets need more iterations to converge, and the number of iterations scales linearly with the cell number when the mini-batch size is given (with some variances owing to different numbers of iterations before the early stop). As a result, the total running time of scDHMap scales linearly with the number of cells in the data set. This property makes it useful for analyzing large scRNA-seq data sets.

    scDHMap for batch correction

    Integrating data sets from different batches is a common task in single-cell analysis. Integrating means eliminating the technical batch effects in separate experiments and revealing real biological signals. Methods for correcting batch effects have been proposed, such as Harmony (Korsunsky et al. 2019), Seurat (Butler et al. 2018), and MNN (Haghverdi et al. 2018). Most embedding methods do not consider batch effects, but these methods can be used as upstream tools before the dimensionality reduction. In the scDHMap, we propose an integrated pipeline to correct batch effects. Conditional autoencoder is applied to improve embedding quality for the autoencoder part, and for the t-SNE regularization, Harmony (a method that iteratively removes batch effects in PCs) is used for correcting batches. To evaluate the performance, we simulated data sets with six different batches, and batches had varied sizes from 5% to 25% of the total number of cells. This simulation represents a setting of complex batch effects. We tested methods including scDHMap, PCA + PoincaréMap (50 PCs for PoincaréMap), Harmony + PoincaréMap (Harmony-corrected 50 PCs for PoincaréMap), scPhere, and a batch-aware version of t-SNE–BC-t-SNE (Aliverti et al. 2020) on these simulated data sets.

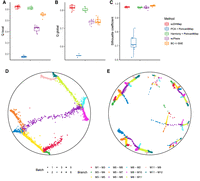
    The Harmony-corrected 50 PCs of analytic Pearson residual normalized true counts were used for ground-truth high-dimensional similarities. We display the embedding results in Figure 3. We found that scDHMap had the best Q scores among the different methods (Fig. 3A,B), which meant that scDHMap performed best in local and global structural preservations. Next, we quantified the alignment between different batches by the silhouette coefficient (SIL) (Fig. 3C). Although BC-t-SNE had the best SIL, it failed to display the continuous hierarchical trajectories (Supplemental Fig. S11). We observed that scDHMap had a better SIL than Harmony + PoincaréMap's (paired one-sided t-test P-value = 0.01), indicating that the cooperation of Harmony and the conditional autoencoder could improve the batch alignment and the embedding quality simultaneously. It is not surprising that scPhere had a fair result in batch correction but a poor performance in the Q values, because there is no guarantee of distance preservation. Plotting the 2D embedding confirmed that scDHMap could effectively eliminate batch effects (Fig. 3D), and if using PCA + PoincaréMap, the batch effect made the embedding meaningless (Fig. 3E). We conducted an ablation study of the two components (Harmony and conditional autoencoder) in scDHMap to integrate batches. We observed that although the batch effect was corrected primarily by Harmony, the conditional autoencoder could improve the quality of embedding further (Q locals of scDHMap vs. scDHMap without conditional autoencoder, paired one-sided t-test P-value = 0.01) (Supplemental Fig. S12A–G).

    Figure 3.
    View larger version:
    Figure 3.

    Evaluation of embeddings for batch alignment. (A,B) Embedding quality metrics of methods on simulated data sets with six batches. Ten data sets had been generated. (C) Silhouette coefficient (SIL) for quantifying the batch alignments. Larger values mean better alignments. (D) Embedding of scDHMap. (E) Embedding of PCA + PoincaréMap. Colors represent branches, and dot shapes represent batches (D,E).

    scDHMap for trajectory interpretation and denoising counts

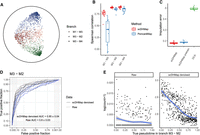
    The cell ordering among the trajectory path or trajectory pseudotime inference is the essential analysis in trajectory inference. For this experiment, we generate simulated data sets having three branches with high dropout rates (∼75%). We performed embedding of scDHMap and PoincaréMap on these simulated data sets and quantified the quality by Q scores (Supplemental Fig. S13A,B). We observed that scDHMap outperformed PoincaréMap in both Q local scores and Q global scores. The embedding of scDHMap had placed points following the true trajectory order correctly, but the embedding of PoincaréMap was chaotic (Fig. 4A; Supplemental Fig. S13C). The Poincaré norm is the geodesic distance between a point and the origin and can be used as the trajectory pseudotime to order cells in the trajectory path (Klimovskaia et al. 2020). In the simulated data sets, for each branch, we transformed the origin to the starting points (in the simulation, one branch could have multiple points with starting state; we used the hyperbolic centroid of these points as the starting point) and summarized the trajectory pseudotime of points in the three branches. As plotted in Figure 4B, the Spearman's correlations between the pseudotime inferred by scDHMap and ground-truth pseudotime were significantly better than PoincaréMap's correlations. These results concluded that scDHMap could order cells better, matching the true trajectory order, than PoincaréMap even in a challenging situation with high dropout rates.

    Figure 4.
    View larger version:
    Figure 4.

    scDHMap can be used for trajectory interpretation and denoising counts. (A) Embedding of scDHMap on the simulated data set with three branches (M1–M3, M3–M2, and M3–M4). Dot shapes represent branches; red, blue, and green colors from shallow to deep represent ground-truth pseudotime. Ten data sets had been generated, and one example is displayed. (B) Spearman's correlation coefficient between the Poincaré pseudotime inferred by scDHMap, PoincaréMap, and the ground-truth pseudotime in the three branches. (C) Imputation errors of scDHMap pretraining, scDHMap final training, and deep count autoencoder (DCA) on the simulated data sets. (D) Area under the curve (AUC) plots of trajectory differential expression (DE) of raw counts and scDHMap-denoised counts (final training). (E) One DE gene in the branch M3–M2; plots display raw counts and scDHMap-denoised counts against the ground-truth pseudotime. Trend lines are smoothed by the LOESS regression.

    The ZINB model–based decoder of scDHMap can be used for denoising the count matrix of scRNA-seq data. We calculated the imputation errors of scDHMap pretrained, scDHMap trained with the t-SNE part, and a ZINB autoencoder model, DCA (Eraslan et al. 2019), that measures the relative difference between denoised and true counts at the zero measures of the count matrix. We found that scDHMap-denoised counts were significantly better than DCA's, and adding t-SNE regularization could improve the imputation accuracy of scDHMap significantly (scDHMap vs. scDHMap pretrain, paired t-test P-value = 3.3 × 10−5) (Fig. 4C). This observation is expected because autoencoder imputes dropout counts by borrowing information from neighbors, and the t-SNE regularization could pull neighbors together, thus improving the imputation accuracy effectively. Next, we conducted a trajectory differential expression (DE) test by tradeSeq, which identifies the DE gene among the trajectory path by the NB spline regression (Supplemental Note 3; Van den Berge et al. 2020). Ground-truth pseudotime was used for tradeSeq analysis. As displayed in Figure 4D and Supplemental Figure S14, A–C, after denoising, the areas under the curve (AUCs) of DE analysis were significantly improved in the branches M3–M2 and M3–M4 (paired t-test P-values < 0.05). We picked one gene as an example and showed that dropout made the trend among the trajectory path very obscure, but after scDHMap denoising, the trend became much clearer (Fig. 4E).

    Application to real scRNA-seq data

    We applied scDHMap to three scRNA-seq data to illustrate the performance of different embedding tasks. Real data sets do not have so-called “true counts,” so we used 50 PCs of analytic Pearson residual normalized counts for evaluating structural preservations. We first evaluated the embedding qualities of Q scores, as shown in Figure 5A, scDHMap was the best in the three data sets compared with the hyperbolic embedding methods and Euclidean embedding methods. In most cases, the hyperbolic embedding methods, including scDHMap and PoincaréMap, outperformed the Euclidean methods, including PaCMap, t-SNE, UMAP, and PHATE, which indicated the low distortion of representing hierarchical structures in the hyperbolic space.

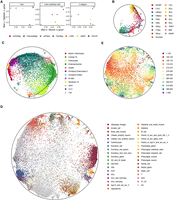
    Figure 5.
    View larger version:
    Figure 5.

    Embeddings of scDHMap on three real scRNA-seq data sets. (A) Embedding quality metrics of methods on real scRNA-seq data sets. (B) scDHMap embedding of the Paul cells. Colors represent cell types. (C) scDHMap embedding of the colon epithelial cells. Colors represent cell types. Arrowed lines indicate the suggested trajectory paths (B,C). (D,E) scDHMap embedding of the C. elegans embryonic cells. Colors represent cell types (D), and colors represent embryonic time bins (E).

    In the Paul data (Paul et al. 2015), there are about 2000 cells profiled from murine bone marrow. The investigators identified 19 clusters in the data. We projected the Paul data to 2D Poincaré space by scDHMap in Figure 5B. As we can see, the data contained two main branches, and the cell types were posed in the expected orders. This result is consistent with the previous trajectory analysis (Haghverdi et al. 2016). Visualizations of other methods had similar two main branches (Supplemental Figs. S15, S16A,B). The data have a predefined root cell. In the embedding of scDHMap, we transformed the origin of the Poincaré ball to the root and ordered cells by their geodesic distance to the new origin as the Poincaré pseudotime (Supplemental Fig. S17A–C). Using a similar branching method to that of Haghverdi et al. (2016), we divided the data set into three branches: two long branches and one short trunk based on the Poincaré pseudotime (Supplemental Fig. S17D; Supplemental Note 4). In branch 2, most cells were basophils, monocytes, and neutrophils. We selected marker genes in these cell types and plotted the raw and scDHMap-denoised counts along the Poincaré pseudotime in branch 2 (Supplemental Fig. S17E). In branch 3, most cells were erythroids, and we also plotted the marker genes (Supplemental Fig. S17F). As the plots show, dropouts were pervasive in the raw counts; however, after scDHMap denoising, the changing trend through the pseudotime became much clearer, including the marker genes Cebpe, Csf1r, Gfi1, Irf8, Epor, and Gypa.

    The colon epithelial cells (Smillie et al. 2019) were collected from various people and profiled by different sequencing platforms. We selected healthy individuals for the analysis. The batch effects were first corrected by Harmony and then used as input for embedding methods. We found two clear trajectories in the embedding of scDHMap (Fig. 5C), which were stems → cycling TA → secretory TA → immature goblet → goblet and stems → TA2 → immature enterocytes → enterocytes. PoincaréMap and scPhere can also reveal the two trajectories but with some noise (Supplemental Fig. S18A). For example, goblets should be adjacent to immature goblets, but goblet cells were close to enterocytes in the embedding of Harmony + PoincaréMap. The methods of Euclidean space had some distortions of the cell developmental order (Supplemental Fig. S19A,C), especially in the embeddings of UMAP and PHATE. In the embedding of PaCMap, it pushed Best4+ enterocytes far away from other enterocytes. Next, we plotted the embeddings of different methods against patient IDs in Supplemental Figures S18B and S19D. The embedding of PCA + PoincaréMap confirmed that different individuals had undesired technical variances, and batches were not aligned. After Harmony corrected the 50 PCs, embeddings from different subjects were merged in most methods. However, some batches were still unaligned, such as points from patient 4 in the embeddings of PoincaréMap (Supplemental Fig. S18B), PaCMap, t-SNE, UMAP, and PHATE (Supplemental Fig. S19D). Meanwhile, scDHMap could merge points from different individuals well (Supplemental Fig. S18B), indicating the combining of conditional autoencoder and Harmony in scDHMap could improve batch integration and embedding quality together. We have observed similar results in the simulation experiment already. The quantitative SIL coefficient of batch alignment further confirmed that scDHMap had the best SIL score (Supplemental Figs. S18C, S19B).

    Finally, we applied scDHMap to Caenorhabditis elegans embryonic cells (Packer et al. 2019), collected along with a series from <100 min to >650 min of embryonic time. Cells were profiled in different batches, and we first corrected 50 PCs by Harmony. In the embedding of scDHMap, we observed clear developmental paths showing that various main cell types originated from the same root and then differentiated to different places (Fig. 5D) and that cells were ordered by embryonic time (Fig. 5E). We displayed the embedding per embryonic time bin and confirmed that within the same cell type, cells were also ordered by embryonic time (Supplemental Fig. S20). For example, body wall muscle (BWM) cells first appeared in the time bin 130–170 and then moved to the boundary of the Poincaré ball along the embryonic time. Other hyperbolic embedding methods, including PoincaréMap and scPhere, had similar properties (Supplemental Fig. S21A,B). The embedding of PoincaréMap had some isolated small clusters, which made the trajectory paths not as smooth as scDHMap's. The embedding of scPhere had ordered cell types according to embryonic time well, but high-dimensional distance preservation was not as good as scDHMap's (Fig. 5A). Our scDHMap could combine the advantages of the two hyperbolic methods. Same as with the previous studies (Packer et al. 2019; Klimovskaia et al. 2020; Ding and Regev 2021), all the Euclidean embedding methods failed to display trajectory paths correctly (Supplemental Fig. S22A–C). Only PaCMap's embedding had placed main cell types among continuous hierarchical paths, but with some incorrect groups. The embeddings of t-SNE and UMAP clustered cells into many isolated small groups, which were unfavorable for trajectory interpretation. These results illustrate that only hyperbolic methods can learn a smooth and interpretable embedding of C. elegans embryonic cells and that scDHMap captures the preferred features of both PoincaréMap and scPhere. To explore the trajectory branches in the data set further, we provide an optional parameter, γ, to control the intensity of the repulsive force between nonneighboring points. As we can see in Supplemental Figure S23, A and B, a larger value of γ brings greater repulsive force and could separate different branches more clearly. This feature is useful when users want to visualize the branches more closely.

    Application to scATAC-seq data

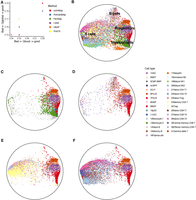
    We analyzed Satpathy's scATAC-seq data (Satpathy et al. 2019) by scDHMap. scATAC-seq profiles genome-wide chromatin accessibility. The data matrix of scATAC-seq is close to binary and extremely sparse, and the features in scATAC-seq are not genes but peaks. To make it fit the scDHMap model, we first aggregated peaks into genes and obtained the gene activity scores by Signac (Stuart et al. 2021), which quantifies the activity of each gene by assessing the chromatin accessibility associated with each gene. The gene activity matrix is cell by gene, and we used it as the input for embedding methods. Figure 6A displays the embedding qualities of different methods. Again, we found scDHMap had the best Q values. Figure 6B plotted the scDHMap embedding and different cell types. Satpathy's scATAC-seq data contain about 58,000 human bone marrow and blood cells and can be divided into several major groups, from progenitor cells (including hematopoietic stem cell [HSC], lymphoid-primed multipotent progenitor [LMPP], common lymphoid progenitor [CLP], megakaryocyte–erythroid progenitor [MEP], basophil–mast cell progenitor [BMP], Pro-B, and Pre-B) to end-stage cell types, such as myeloid cells, B cells, CD4+ T cells, CD8+ T cells, basophils, and NK cells. We selected progenitors and some groups in the scDHMap embedding for plotting (Fig. 6C–F). In Figure 6C, we observed the trajectory path from HSC to myeloid cells (HSC, CMP → GMP → MDP → pDC, cDC, monocytes); in Figure 6D, we observed the trajectory path from HSC to B cells (HSC, LMPP → CLP → Pro-B → Pre-B → naïve and memory B cells); in Figure 6, E and F, we observed the trajectory path from HSC to T cells (HSC, LMPP → CLP → naïve CD4+ and CD8+ T cells → memory CD4+ T cells and CD8+ T cells). These differentiation trajectories were consistent with known bone marrow differentiation orders (Satpathy et al. 2019). Next, we compared the embedding of scDHMap with embeddings of other methods (Supplemental Fig. S24A,B) and further focused on the subsets of the specified cell types (Supplemental Fig. S25A–D). Competing methods did not recover differentiation orders correctly in some cell types. For example, in the embeddings of PaCMap, t-SNE, and UMAP, B cells were separated far from Pro B cells (Supplemental Fig. S25B), and in the embeddings of PoincaréMap and PHATE, naive B cells were adjacent to HSC but not to Pro-B and Pre-B. We observed many compact small clusters in the t-SNE and UMAP embeddings, similar to the observations of the C. elegans cells, which indicated these methods mainly focusing on local but not global structures. The embedding of scDHMap was not affected by this problem.

    Figure 6.
    View larger version:
    Figure 6.

    Embedding of scDHMap on Satpathy's scATAC-seq data. (A) Embedding quality metrics of different methods. (B) scDHMap embedding of Satpathy's scATAC-seq data. (C–F) scDHMap embedding of different cell types. (C) Progenitor cells (cluster 1–9) and myeloid cells (cluster 10–13). (D) Progenitor cells and B cells (cluster 14–16). (E) Progenitor cells and CD4+ T cells (cluster 21–25). (F) Progenitor cells and CD8+ T cells (cluster 26–31). (HSC) Hematopoietic stem cell; (LMPP) lymphoid-primed multipotent progenitor; (CLP) common lymphoid progenitor; (MEP) megakaryocyte–erythroid progenitor; (BMP) basophil–mast cell progenitor.

    Previous SectionNext Section

    Discussion

    In summary, we have developed a deep hyperbolic manifold learning approach scDHMap for visualizing complex trajectories in single-cell genomics data. The model is a hyperbolic t-SNE parametrized by a model-based deep variational autoencoder. We compared scDHMap with several state-of-the-art dimensionality-reduction methods, including the recently published hyperbolic methods, on various embedding tasks of simulated and real data sets and illustrated scDHMap as having the best performance. By aggregating peaks into genes, we showed that scDHMap could be applied to visualize scATAC-seq data. The model can be optimized per mini-batch, making it efficient for visualizing large data sets. Because of the parametric model, it can easily include out-of-sample points after training. All these advantages make scDHMap a strong candidate for the visualization and discovery of complex hierarchical structures in single-cell genomics data.

    ScDHMap is an end-to-end deep learning approach that accepts the raw count matrix with several building blocks accounting for different tasks. The encoder part accounts for learning a low-dimensional embedding, and the decoder part accounts for denoising dropout events in the count matrix. The wrapped normal prior distribution in the variational inference makes the embedding of scDHMap more favorable for visualization. To eliminate batch effects, we combine two blocks: the conditional autoencoder explicitly accounts for batch IDs, and Harmony corrects batches in the input of the t-SNE regularization. The combination results in better batch alignment and embedding quality. The most critical hyperparameter in the t-SNE regularization is perplexity, which controls how many neighbors will be considered. We showed that scDHMap is robust in a range of different perplexities.

    So far, all results have been obtained on the data sets with continuous hierarchical structures. To illustrate the universality of visualization of single-cell genomics data, we further applied scDHMap to the data sets with different cell types. For this purpose, we used four real scRNA-seq data sets from various species and tissues: 10X PBMC (Zheng et al. 2017), mouse embryonic stem cells (Klein et al. 2015), mouse bladder cells (Han et al. 2018), and worm neuron cells (Cao et al. 2017). We found that scDHMap retained good performance in embedding qualities, whereas it was able to separate cell types decently (Supplemental Fig. S26A–C). This result suggests that, although not designed for this type of data, scDHMap can still be used for visualizing the data sets with different cell types.

    Our method provides a flexible hyperbolic embedding framework that can be extended in several ways. For example, we can extend it to visualize multi-omic data by joint high-dimensional distances (Do and Canzar 2021) or to preserve local densities by adding a regularization term (Narayan et al. 2021). Another extension is to include prior information into the embedding learning process. The prior information can be cell types, time points, etc., that could guide the model to group or separate different cells (Tian et al. 2021; Zhai et al. 2022). Given the efficiency, flexibility, and extensibility, we expect scDHMap to be a valuable tool for the analysis of single-cell genomics data.

    We have illustrated the advantage of the hyperbolic embedding in visualizing of complex hierarchical structures in single-cell data, but the downstream analysis tools are currently underdeveloped. For example, in the pseudotime inference analysis, after obtaining the low-dimensional embedding, practitioners often expect to do clustering, to build a minimum spanning tree (MST), and to run principal curve regression (Qiu et al. 2017; Street et al. 2018). The hyperbolic version of these popular analytic methods is desired to exploit the advantageous hyperbolic embedding. We hope our study can motivate the development of more supportive tools acting on hyperbolic space, which is a promising future study direction.

    Previous SectionNext Section

    Methods

    Feature selection and preprocessing of scRNA-seq data

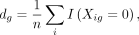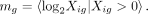
    Following the method of Kobak and Berens (2019), we apply the mean-variance relationship for feature selection. We first filter out genes that have a non-zero expression in fewer than 10 cells. Given by their mean, genes with large variance are selected. For each gene g, we compute the fraction of zero counts Formula where n is the number of cells, and the mean of log non-zero expression is Formula

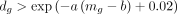    To select a predefined number M of genes (we set M = 1000), we use a heuristic approach of finding a value b such that Formula is true for exactly M genes. Here b is found by binary search, and a is set to be 1. The feature selection procedure is conducted on raw counts directly, and the selected n × M raw count matrix is used for the ZINB reconstruction part of the decoder. Following our previous work (Tian et al. 2019, 2021), the input for the autoencoder is library size normalized, log-transformed, and scaled counted. Briefly, we calculate a library size factor of each cell, so cells share the same library size. Next, we log-transform and scale counts, so genes have unit variance and zero mean. 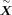The preprocessed count is denoted as Formula. These steps are conducted by the Python package SCANPY (Wolf et al. 2018).

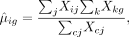
    We use PCs of the data matrix as the input for the t-SNE regularization part. After selecting top M genes, we apply analytic Pearson residual normalization (Lause et al. 2021) to correct sequencing depth and stabilize the variance across genes in the count data. Specifically, for gene g in cell i, Pearson residuals are calculated by 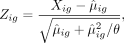Formula Formula where Xig is the raw count of gene g in cell i, and θ is the dispersion parameter of the NB distribution and is set to be 100. Pearson residual normalized count data are reduced from n × M to n × 50 by PCA. As Kobak and Berens (2019) suggested, the usual number of PCs in single-cell data is around 50, so the top 50 PCs are used as the input for the t-SNE part of our model to keep the structural topology of the data during dimensionality reduction.

    Hyperbolic geometry and Poincaré ball

    Hyperbolic geometry is a non-Euclidean geometry having a constant sectional curvature of −1. Because of the geometric analog, hyperbolic space can be considered as a continuous version of discrete trees. Poincaré ball is a projection that represents the hyperbolic space in a unit ball in the Euclidean space: 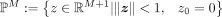Formula, where ℙM is a M dimensional Poincaré ball, ℝM+1 is a M + 1 dimensional Euclidean space, and z = (z0, z1, …, zM)T. 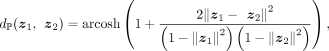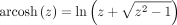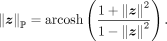In the Poincaré ball, the distance between two points z1, z2 is defined as Formula where Formula is the inverse hyperbolic cosine function, and Formula is the Euclidean norm. The distance between z and the origin is the Poincaré norm Formula

    As we can see, the Poincaré ball represents Euclidean space near the origin of the unit hyperball, and the Poincaré norm grows exponentially when z approach to the border 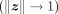Formula. These properties are very useful for representing the hierarchical tree structure.

    The Lorentzian model is a type of hyperbolic space that all points satisfy ℍM: = {z ∈ ℝM+1|z0 > 0, 〈z, z〉ℍ = −1}, where ℍM is a M-dimensional Lorentzian model, ℝM+1 is a M + 1-dimensional Euclidean space, and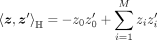Formula is the Lorentzian inner product. Lorentzian norm is defined as 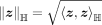Formula. The origin of the Lorentzian model is o0 = (1, 0, …, 0)T. 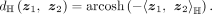The distance between two points z1, z2 in the Lorentzian model is defined as Formula

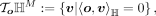    The tangent space at point o is defined as all vectors that passing point o and are orthogonal to vector o Formula and the resulting tangent space is a Euclidean subspace in ℝM+1. The mapping between hyperbolic space and tangent space can be performed by the exponential map and inverse exponential map (also called logarithm map) (Nickel and Kiela 2018; Grattarola et al. 2019; Nagano et al. 2019). 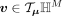For point Formula and o ∈ ℍM, the exponential map is 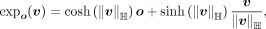Formula where sinh and cosh are hyperbolic sine and cosine, respectively. For point o, z ∈ ℍM and o ≠ z, we can obtain the inverse exponential map as 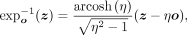Formula where η = −〈o, z〉ℍ.

    We build our model with a latent representation of the 2D Lorentzian model. For visualization, we can easily project the 2D Lorentzian model to Poincaré ball 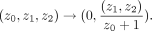Formula We discard the first dimension because it is a constant zero for plotting.

    Hyperbolic variational autoencoder with the ZINB reconstruction loss

    ScDHMap receives preprocessed count and reduces it to a two-dimensional hyperbolic space by a ZINB model–based variational autoencoder (VAE). ZINB model–based autoencoder has been applied to scRNA-seq count data in previous studies successfully (Lopez et al. 2018; Eraslan et al. 2019; Tian et al. 2019, 2021). VAE is a deep generative model that characterizes data by a neural-network parametrized distribution with a low-dimensional latent variable (Kingma and Welling 2014), which is appropriate for visualization. 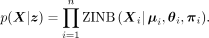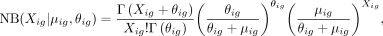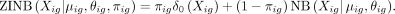The variational inference models the count matrix X by the likelihood of ZINB distribution: Formula Here the ZINB likelihood of Xig is calculated by two components: the NB likelihood and the point mass of probability at zero (the probability of dropout events): Formula Formula ZINB parameters mean μ, dispersion θ, and dropout probability π are parametrized by decoder networks with the latent variable z. 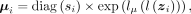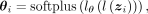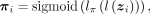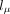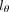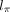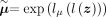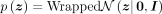Specifically, Formula Formula Formula where Formula, Formula, and Formula are three neural networks that parametrize mean, dispersion, and dropout probability, respectively; si is the library size factor of cell i that is calculated in the preprocessing step; and l is the latent decoder. Different activation functions (exponential, softplus, and sigmoid) are appended to the three networks, because mean and dispersion are always positive, and dropout probability is in the range from zero to one. In keeping with the method of Eraslan et al. (2019), the estimated mean Formula can be used as denoised counts, which eliminates the effect of library size. In the typical VAE model, the latent variable z is generated from a standard multivariate normal prior, but in scDHMap model, to represent the continuous hierarchical structure, we use a wrapped normal prior Formula in the hyperbolic space (Mathieu et al. 2019; Nagano et al. 2019; Ovinnikov 2019; Ding and Regev 2021).

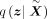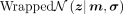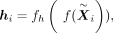
    The posterior distribution Formula is parametrized by the encoder and a wrapped normal posterior Formula. Here latent mean m and latent variance σ are estimated by neural networks 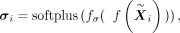Formula Formula where f is the latent encoder. Then hi is projected to hyperbolic space by the exponential map (from the tangent space around the origin o0 = (1, 0, …, 0)T to the hyperbolic space): 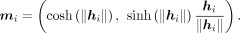Formula We use m as the low-dimensional embedding for the visualization.

    Combining encoder and decoder parts, we can write the learning objective as maximizing the evidence lower bound (ELBO) (Kingma and Welling 2014): 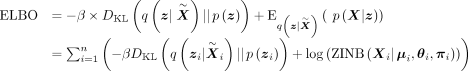Formula (1) where the KL divergence measures the difference between the wrapped normal prior and the wrapped normal posterior of the latent variable, and β controls the weight of KL divergence (Higgins et al. 2017). The second term is the ZINB likelihood of the raw count matrix.

    The wrapped normal prior distribution 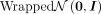Formula is built by two steps. First, a standard normal distribution in the tangent space Formula at the origin o0 = (1, 0, …, 0)T is defined. Next, samples of the standard normal distribution are parallel-transported to the desired locations and projected to the hyperbolic space by the exponential map.

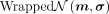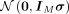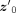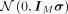    For sampling the wrapped normal posterior distribution Formula, where m ∈ ℍM and σ ∈ ℝM, we use a set of invertible functions to transform samples from a normal distribution Formula in ℝM to the hyperbolic space, where IM is the identity matrix in ℝM(Nagano et al. 2019). 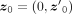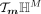First, we sample Formula from Formula and then let Formula, which can be considered as a sample vector in the tangent space Formula. 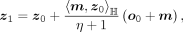Next, z0 is parallel-transported to z1 in the tangent space Formulaat m: Formula where η = −〈o0, m〉ℍ. The parallel-transport keeps the direction and the vector norm. 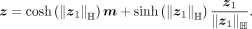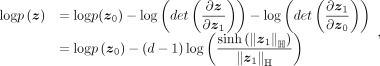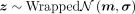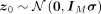Finally, z1 is projected back to the hyperbolic space by the exponential map Formula The likelihood of z can be calculated by Formula where d is the dimension of vectors, Formula and Formula.

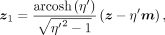
    For a given sample z from the wrapped normal, we need the corresponding z1 and z0 to evaluate the wrapped normal density p(z). These can be obtained by the inverse exponential map and the inverse parallel transport 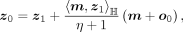Formula Formula where η′ = −〈m, z〉ℍ and η = −〈o0, m〉ℍ.

    Finally, we have all components to calculate the KL divergence in the ELBO Equation (1) 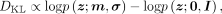Formula where p(z;m, σ) is the wrapped normal density with mean m and variance σ, and p(z;0, I) is the wrapped normal density with mean 0 and variance I.

    The t-SNE regularization function

    The t-SNE function preserves the similarity of high-dimensional space during dimension reduction (van der Maaten and Hinton 2008). Specifically, t-SNE measures a directional similarity of point j to point i in high-dimensional space (here we use 50 PCs of analytic Pearson residual normalized counts), 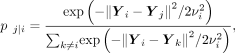Formula where the variance of the Gaussian kernel 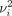Formula is chosen such that the perplexity 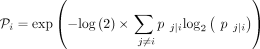Formula has a predefined value. 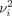Formula can be found by the binary search, and perplexity controls the variance of the kernel. 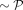Importantly, for a given P, all but Formula nearest neighbors of point i have a near-to-zero pj|i, so P can guide the t-SNE algorithm to focus on how many neighbors of each point. 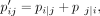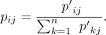For mathematical and computational convenience, we use the symmetric SNE Formula Formula

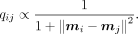
    The similarity between points in the low-dimensional embedding is measured by a heavy-tailed Student's t-distribution Formula

    Additionally, to separate trajectory branches more clearly, we provide an optional parameter γ (Cauchy distribution) to strengthen the repulsive force between nonneighboring points 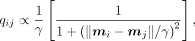Formula where γ controls the heavy-tail property of the Cauchy distribution. If setting γ = 1, the Cauchy distribution reduces to the Student's t-distribution. With the larger γ, the repulsive force will also increase.

    The t-SNE algorithm optimizes the low-dimensional embedding such that the similarity between qij and pij as close as possible in terms of the KL divergence.

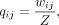
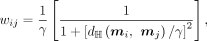
    In the scDHMap model, we use the ZINB model–based hyperbolic variational autoencoder to learn the low-dimensional embeddings m, and the low-dimensional similarity is calculated by the hyperbolic distance 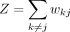Formula Formula Formula and the t-SNE KL divergence is obtained by (Ding et al. 2018): Formula (2) In the t-SNE KL divergence, the first term is an attractive force between point i and j whenever pji ≠ 0, and the second term is a repulsive force between point i and j.

    Total loss function

    The total learning objective of scDHMap combines the ELBO of ZINB model–based hyperbolic variational autoencoder (1) and the t-SNE regularization (2): 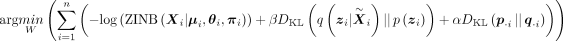Formula (3) where α controls the weight of the t-SNE part, β controls the weight of the wrapped normal prior, and W is trainable parameters in the variational autoencoder. The loss function is optimized per min-batch. For the t-SNE regularization, the variance of the Gaussian kernel is also searched per mini-batch.

    Batch correction and evaluation

    We combine Harmony (Korsunsky et al. 2019) with a conditional variational autoencoder (Sohn et al. 2015) to correct batch effect in the data. The conditional variational autoencoder has been applied in scVI and scPhere for integrating scRNA-seq data of different batches (Lopez et al. 2018; Ding and Regev 2021). We encode the batch ID by a one-hot encoding B, and then the conditional encoder becomes 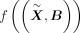Formula and the conditional decoder becomes l((z, B)). As a result, the learned latent embedding should be batch independent. For the input of the t-SNE part, the 50 PCs are corrected by Harmony respecting the batch information. scDHMap combines the strength of conditional variational autoencoder and Harmony for batch correction.

    The result of batch correction is quantified by the silhouette coefficient (SIL) (Cole et al. 2019): 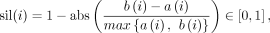Formula where a(i) denotes the average distance (for methods of hyperbolic space, e.g., scDHMap, PoincaréMap, and scPhere, we use Poincaré distance; for other methods, we use Euclidean distance) between the embedding of the ith cell and other cells in the same batch, and b(i) denotes the minimum average distance between the embedding of the ith cell and cells in other batches. The SIL of the whole data set is the average of SILs of all cells. The larger SIL means the learned embedding has better alignment between batches.

    Model implementation

    The scDHMap model is implemented in Python3 using PyTorch (Paszke et al. 2017). All layers are fully connected neural networks. Layer sizes of latent encoder and decoder are (128, 64, 32, 16) and (16, 32, 64, 128), and each layer uses the ELU activation function (Clevert et al. 2016) with the batch normalization technic (Ioffe and Szegedy 2015). The bottleneck layer size is set to be two for visualization. The model learns the latent representation in the Lorentzian model and then projects the embedding to the 2D Poincaré ball for plotting. The Adam (Kingma and Ba 2015) with AMSGrad (Reddi et al. 2018) optimizer is used to train the model, with the parameters of learning rate lr = 0.001, β1 = 0.9, and β2 = 0.999 and a weight decay of 0.001. The model is first pretrained without the t-SNE loss for a predefined number of iterations (400 epochs for most data sets and 200 epochs for large data sets with more than 10,000 cells) and then trained to optimize the total loss. The early stop criterion is set to be the t-SNE KL divergence loss not improving for 150 epochs. The size of mini-batch is 512. The most time-consuming step in the model is to find the best variance of the Gaussian kernel with the given perplexity in each mini-batch. We accelerate this step by parallelly calculating the variance for each sample, which is implemented by the Python package numba (Lam et al. 2015). Values of the hyperparameters are α = 1000 for balancing the number of input features and the dimensions of latent embeddings and β = 10. The perplexity is set to be 30, and the default parameter of the Cauchy distribution is γ = 1. We use float64 for all tensor operations in PyTorch to achieve better calculation precision.

    Embedding quality metric

    Following the method of Lee and Verleysen (2010), we use the embedding quality metric to quantify the performance of different dimension reduction methods. Basically, the metric is to measure how good preservation of local and global distance on the manifold. In this work, the high-dimensional distance is calculated by the pairwise Euclidean distance of 50 PCs of analytic Pearson residual normalized counts. A good dimensionality-reduction method should have a good preservation of local and global distance on the embedding, which means close neighbors should be placed closed to each other and distant points should be placed separately. Q local and Q global are focused on local and global distance preservation, respectively. The quantities of Q local and Q global range from zero to one; larger values mean better preservations.

    Translation in Poincaré space and Poincaré pseudotime

    In the embedding of Poincaré ball, we can perform an isometric transformation of the whole embedding that places a known root to the origin and preserve all pairwise distances. Particularly, if we want to translate the origin of the Poincaré ball to ν, point x is translated to 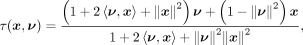Formula where 〈ν, x〉 is the inner product (〈ν, x〉 = ν1x1 + ν2x2 + …), and Formula is the Euclidean norm. In the Poincaré ball, the spatial resolution is amplified around the origin, so this translation can be also used as a method to zoom into the interested part of embedding.

    Pseudotime is referred to as a measure of how much process a cell has been differentiated through a trajectory path. Here, we use the Poincaré distance between an individual cell and the root as the Poincaré pseudotime.

    Methods comparison

    PoincaréMap (Klimovskaia et al. 2020), scPhere (Ding and Regev 2021), scvis (Ding et al. 2018), PaCMap (Wang et al. 2021), t-SNE (van der Maaten and Hinton 2008), UMAP (McInnes et al. 2018), PHATE (Moon et al. 2019), and BC-t-SNE (Aliverti et al. 2020) are used for comparisons. All methods reduce inputs to 2D representations. We first select the top 1000 genes by using the mean-variance relationship. Except for scPhare (which accepts raw counts as inputs), all competing methods use 50 PCs of analytic Pearson residual normalized raw counts as inputs. For data sets with batch effects, 50 PCs are corrected by Harmony (Korsunsky et al. 2019), respecting the batch IDs (except for scPhere and BC-t-SNE; these two methods can handle batch effects directly).

    PoincaréMap (https://github.com/facebookresearch/Poincare Maps) is set to the default setting: k_neighbours = 15, sigma = 1, gamma = 2, epochs = 1000, lr = 0.1, and earlystop = 0.0001 (except for the C. elegans data set: sigma = 2, gamma = 3, which is suggest by the investigators).

    scPhere (https://github.com/klarman-cell-observatory/scPhere) is a VAE-based dimensionality-reduction method, which maps the scRNA-seq data to the hyperbolic space. We project the VAE embedding from the hyperbolic space to the Poincare space as the model output. The parameters for scPhere are latent_dist = “wn,” max_epoch = 250, and the rest of the parameters are set to the default settings: z_dim = 2, observation_dist = “nb,” mb_size = 128, learning_rate = 0.001.

    Scvis (https://github.com/shahcompbio/scvis) is a deep generative dimensionality-reduction model for scRNA-seq data. The parameters are set to use the default settings: optimization = “Adam,” learning_rate = 0.01, batch_size = 512, max_epoch = 100, regularizer_l2 = 0.001, perplexity = 10.

    PaCMap (https://github.com/YingfanWang/PaCMAP), t-SNE (https://github.com/pavlin-policar/openTSNE), and UMAP (https://github.com/lmcinnes/umap) are nonlinear dimensionality-reduction methods. The parameters of PaCMap are n_dims = 2, n_neighbors = None, MN_ratio = 0.5, and FP_ratio = 2. The settings of t-SNE are perplexity = 30, initialization = “pca.” UMAP uses default settings, for example, n_neighbors = 15, min_dist = 0.1, n_components = 2.

    PHATE (https://github.com/KrishnaswamyLab/PHATE) uses default settings such as n_components = 2, knn = 5, t = “auto,” and gamma = 1.

    BC-t-SNE (https://github.com/emanuelealiverti/BC_tSNE) is a batch-aware t-SNE. The parameters are set to use default settings, k = 50, outDim = 2, perplexity = 30, maxIter = 1000.

    Data simulation

    Simulated data sets are generated by the R package Splatter (Zappia et al. 2017), and the tree structures are synthesized by dyntoy (Saelens et al. 2019).

    For the simulation experiments of various dropout rates, we first synthesized the hierarchical tree structure by the dyntoy function generate_milestone_network (“tree”) and then generated the true and raw count matrix of 4000 cells and 3000 genes by Splatter. The parameters for Splatter were set as n_batches = 1, pct_main_ features = 0.5, dropout_shape = −1, de_prob = 0.2, de_facScale = 0.3, n_steps_per_length = 100, and dropout_mid = (1.5, 2, 2.5, 3) for different dropout rates. True count matrix is the count matrix before dropout, and raw count matrix is the count matrix after dropout. For each setting, we generated 10 data sets with different random seeds. For the simulation experiments of batch effect, we set the parameter of Splatter as n_batches = 6, dropout_mid = 2.5, batchCells = (0.05, 0.1, 0.15, 0.2, 0.25, 0.25)*n_cells, and batch_facScale = 0.15, and others remained the same as previously described.

    For the simulation experiments of three branches, we first synthesized the tree structure by the dyntoy function generate_ milestone_network (“bifurcating”). The parameters for Splatter were n_batches = 1, pct_main_features = 0.5, dropout_mid = 4, dropout_shape = −1, de_prob = 0.1, n_steps_per_length = 100, and de_facScale = 0.4. Ten data sets were generated by different random seeds. In the generated data sets, the step value of each cell in the branch was used as a ground-truth pseudotime.

    Single-cell data sets

    Paul cell data (Paul et al. 2015) were downloaded from GitHub (https://github.com/theislab/scAnalysisTutorial). In the data set, investigators profiled 2730 murine myeloid progenitor cells by the MARS-seq (Jaitin et al. 2014). We used “data.debatched” matrix as the count matrix, which was regularized for the inter-batch differences. The cell types and the root were annotated by the investigators and provided in the tutorial of SCANPY package https://scanpy-tutorials.readthedocs.io/en/latest/paga-paul15.html.

    The colon mucosa cells (Smillie et al. 2019) were collected from various individuals and profiled by the 10x Chromium platform (v1 or v2). We downloaded it from https://singlecell.broadinstitute.org/single_cell/study/SCP551/scphere. We selected colon epithelial cells from the 12 healthy individuals, thus giving a matrix of 22,439 cells by 1361 genes.

    The C. elegans embryonic cell data set (Packer et al. 2019) consists of about 80,000 cells profiled by 10x Chromium (v2). The data set was download from the NCBI Gene Expression Omnibus (GEO; https://www.ncbi.nlm.nih.gov/geo/) under accession number GSE126954. We filtered out cells with fewer than 40 genes; as a result, 67,970 cells by 2766 genes were selected for the analysis.

    Satpathy's scATAC-seq data (Satpathy et al. 2019), including the cell barcodes, count matrix, peaks, and fragment files, of all the hematopoiesis cells were downloaded from the NCBI Gene Expression Omnibus (GEO) database under accession number GSE129785. This data set contains 63,882 cells. We extracted the bone marrow and peripheral blood immune cells, having 61,806 cells across 31 cell types. Before preprocessing, unsorted fragment files were sorted by BEDTools, and all the fragment files were indexed by Tabix. We preprocessed the data according to the Signac pipeline (https://stuartlab.org/signac/articles/monocle.html). Signac (Stuart et al. 2021) and Seurat (Butler et al. 2018) were used for all the preprocessing. Specifically, each fragment file was transformed into a Signac's fragment object by the “CreateFragmentObject” function. Then all the fragment objects were combined as a list and input into the “CreateChromatinAssay” function to create a chromatin assay. This assay was then transformed into a Seurat object for all the downstream processes. Quality control was performed to remove the outlier cells. Specifically, the scATAC-seq data were filtered by three criteria: (1) total counts per cell < 50,000, (2) transcriptional start site (TSS) enrichment score > 2, and (3) nucleosome signal (the ratio of mononucleosomal to nucleosome-free fragments) > 5. In addition, cells with a high proportion of reads in the black areas of the genome (the regions always with high artifactual signals) were also removed. Following the processing steps in the original paper, the reads were mapped to the gene regions of human genome 19 (hg19) by the “GeneActivity” function. The final count matrix was 58,711 cells by 20,010 genes used for the embedding analysis. Cell type annotations were provided by the original paper.

    The processed real single-cell data sets used in this study can be found at Figshare (https://figshare.com/s/64694120e3d2b87e21c3).

    The description of the four real scRNA-seq data sets with different cell types is in Supplemental Note 5. These data sets can be found at GitHub (https://github.com/ttgump/scDeepCluster/tree/master/scRNA-seq%20data).

    Software availability

    An open-source software implementation of scDHMap is available as Supplemental Code and on GitHub (https://github.com/ttgump/scDHMap).

    Previous SectionNext Section

    Competing interest statement

    The authors declare no competing interests.

    Previous SectionNext Section

    Acknowledgments

    We thank Dr. Yao Ma from the New Jersey Institute of Technology for valuable suggestions. We thank Dr. Ruihua Cheng from the Tianjin University of Finance and Economics for proofreading, which improved the clarity of the manuscript. This work used the Extreme Science and Engineering Discovery Environment (XSEDE) through the allocation CIE170034, supported by National Science Foundation grant number ACI-1548562. This work was supported by grant R15HG012087 (Z.W.) from the National Institutes of Health (NIH) and was partially supported by the National Center for Advancing Translational Sciences (NCATS), a component of NIH under award number UL1TR003017 (Z.W.).

    Author contributions: Z.W. and H.H. conceived and supervised the project. T.T. conceived and designed the method. T.T. and C.Z. conducted experiments. X.L. contributed to data processing. T.T., C.Z., Z.W., and H.H. wrote the manuscript. All authors approved the manuscript.

    Previous SectionNext Section

    Footnotes

    • Received June 28, 2022.
    • Accepted January 24, 2023.

    This article is distributed exclusively by Cold Spring Harbor Laboratory Press for the first six months after the full-issue publication date (see https://genome.cshlp.org/site/misc/terms.xhtml). After six months, it is available under a Creative Commons License (Attribution-NonCommercial 4.0 International), as described at http://creativecommons.org/licenses/by-nc/4.0/.

    Previous Section
     

    References

    1. ↵
      Aliverti E, Tilson JL, Filer DL, Babcock B, Colaneri A, Ocasio J, Gershon TR, Wilhelmsen KC, Dunson DB. 2020. Projected t-SNE for batch correction. Bioinformatics 36: 3522–3527. doi:10.1093/bioinformatics/btaa189
      CrossRefGoogle Scholar
    2. ↵
      Amodio M, van Dijk D, Srinivasan K, Chen WS, Mohsen H, Moon KR, Campbell A, Zhao Y, Wang X, Venkataswamy M, et al. 2019. Exploring single-cell data with deep multitasking neural networks. Nat Methods 16: 1139–1145. doi:10.1038/s41592-019-0576-7
      CrossRefGoogle Scholar
    3. ↵
      Butler A, Hoffman P, Smibert P, Papalexi E, Satija R. 2018. Integrating single-cell transcriptomic data across different conditions, technologies, and species. Nat Biotechnol 36: 411–420. doi:10.1038/nbt.4096
      CrossRefMedlineGoogle Scholar
    4. ↵
      Cao J, Packer JS, Ramani V, Cusanovich DA, Huynh C, Daza R, Qiu X, Lee C, Furlan SN, Steemers FJ, et al. 2017. Comprehensive single-cell transcriptional profiling of a multicellular organism. Science 357: 661–667. doi:10.1126/science.aam8940
      Abstract/FREE Full Text
    5. ↵
      Chami I, Ying Z, Ré C, Leskovec J. 2019. Hyperbolic graph convolutional neural networks. In Advances in neural information processing systems (ed. Wallach H, et al.). NIPS, Vancouver, Canada.
      Google Scholar
    6. ↵
      Clevert D-A, Unterthiner T, Hochreiter S. 2016. Fast and accurate deep network learning by exponential linear units (ELUs). In International Conference on Learning Representations (ICLR), San Juan, Puerto Rico.
      Google Scholar
    7. ↵
      Cole MB, Risso D, Wagner A, DeTomaso D, Ngai J, Purdom E, Dudoit S, Yosef N. 2019. Performance assessment and selection of normalization procedures for single-cell RNA-seq. Cell Syst 8: 315–328.e8. doi:10.1016/j.cels.2019.03.010
      CrossRefMedlineGoogle Scholar
    8. ↵
      Ding J, Regev A. 2021. Deep generative model embedding of single-cell RNA-Seq profiles on hyperspheres and hyperbolic spaces. Nat Commun 12: 2554. doi:10.1038/s41467-021-22851-4
      CrossRefGoogle Scholar
    9. ↵
      Ding J, Condon A, Shah SP. 2018. Interpretable dimensionality reduction of single cell transcriptome data with deep generative models. Nat Commun 9: 2002. doi:10.1038/s41467-018-04368-5
      CrossRefGoogle Scholar
    10. ↵
      Do VH, Canzar S. 2021. A generalization of t-SNE and UMAP to single-cell multimodal omics. Genome Biol 22: 130. doi:10.1186/s13059-021-02356-5
      CrossRefGoogle Scholar
    11. ↵
      Eraslan G, Simon LM, Mircea M, Mueller NS, Theis FJ. 2019. Single-cell RNA-seq denoising using a deep count autoencoder. Nat Commun 10: 390. doi:10.1038/s41467-018-07931-2
      CrossRefMedlineGoogle Scholar
    12. ↵
      Goldberg AD, Allis CD, Bernstein E. 2007. Epigenetics: a landscape takes shape. Cell 128: 635–638. doi:10.1016/j.cell.2007.02.006
      CrossRefMedlineGoogle Scholar
    13. ↵
      Grattarola D, Livi L, Alippi C. 2019. Adversarial autoencoders with constant-curvature latent manifolds. Appl Soft Comput 81: 105511. doi:10.1016/j.asoc.2019.105511
      CrossRefGoogle Scholar
    14. ↵
      Graving JM, Couzin ID. 2020. VAE-SNE: a deep generative model for simultaneous dimensionality reduction and clustering. bioRxiv doi:10.1101/2020.07.17.207993
      Abstract/FREE Full Text
    15. ↵
      Gromov M. 2007. Metric structures for Riemannian and non-Riemannian spaces. Springer Science & Business Media, Birkhäuser, Boston.
      Google Scholar
    16. ↵
      Haghverdi L, Buettner F, Theis FJ. 2015. Diffusion maps for high-dimensional single-cell analysis of differentiation data. Bioinformatics 31: 2989–2998. doi:10.1093/bioinformatics/btv325
      CrossRefMedlineGoogle Scholar
    17. ↵
      Haghverdi L, Büttner M, Wolf FA, Buettner F, Theis FJ. 2016. Diffusion pseudotime robustly reconstructs lineage branching. Nat Methods 13: 845–848. doi:10.1038/nmeth.3971
      CrossRefMedlineGoogle Scholar
    18. ↵
      Haghverdi L, Lun ATL, Morgan MD, Marioni JC. 2018. Batch effects in single-cell RNA-sequencing data are corrected by matching mutual nearest neighbors. Nat Biotechnol 36: 421–427. doi:10.1038/nbt.4091
      CrossRefMedlineGoogle Scholar
    19. ↵
      Han X, Wang R, Zhou Y, Fei L, Sun H, Lai S, Saadatpour A, Zhou Z, Chen H, Ye F, et al. 2018. Mapping the mouse cell atlas by Microwell-seq. Cell 172: 1091–1107.e17. doi:10.1016/j.cell.2018.02.001
      CrossRefMedlineGoogle Scholar
    20. ↵
      Higgins I, Matthey L, Pal A, Burgess C, Glorot X, Botvinick M, Mohamed S, Lerchner A. 2017. β-VAE: learning basic visual concepts with a constrained variational framework. In International Conference on Learning Representations (ICLR), Toulon, France.
      Google Scholar
    21. ↵
      Ioffe S, Szegedy C. 2015. Batch normalization: accelerating deep network training by reducing internal covariate shift. In Proceedings of the 32nd International Conference on Machine Learning (ed. Bach F, Blei D), Vol. 37, pp. 448–456. JMLR, Lille, France.
      Google Scholar
    22. ↵
      Jaitin DA, Kenigsberg E, Keren-Shaul H, Elefant N, Paul F, Zaretsky I, Mildner A, Cohen N, Jung S, Tanay A, et al. 2014. Massively parallel single-cell RNA-seq for marker-free decomposition of tissues into cell types. Science 343: 776–779. doi:10.1126/science.1247651
      Abstract/FREE Full Text
    23. ↵
      Jianbo S, Malik J. 2000. Normalized cuts and image segmentation. IEEE Transa Pattern Anal Mach Intell 22: 888–905. doi:10.1109/34.868688
      CrossRefGoogle Scholar
    24. ↵
      Kingma DP, Ba J. 2015. Adam: A method for stochastic optimization. In International Conference on Learning Representations (ICLR), San Diego.
      Google Scholar
    25. ↵
      Kingma DP, Welling M. 2014. Auto-encoding variational bayes. In International Conference on Learning Representations (ICLR), Banff, Canada.
      Google Scholar
    26. ↵
      Klein AM, Mazutis L, Akartuna I, Tallapragada N, Veres A, Li V, Peshkin L, Weitz DA, Kirschner MW. 2015. Droplet barcoding for single-cell transcriptomics applied to embryonic stem cells. Cell 161: 1187–1201. doi:10.1016/j.cell.2015.04.044
      CrossRefMedlineGoogle Scholar
    27. ↵
      Klimovskaia A, Lopez-Paz D, Bottou L, Nickel M. 2020. Poincaré maps for analyzing complex hierarchies in single-cell data. Nat Commun 11: 2966. doi:10.1038/s41467-020-16822-4
      CrossRefGoogle Scholar
    28. ↵
      Kobak D, Berens P. 2019. The art of using t-SNE for single-cell transcriptomics. Nat Commun 10: 5416. doi:10.1038/s41467-019-13056-x
      CrossRefMedlineGoogle Scholar
    29. ↵
      Korsunsky I, Millard N, Fan J, Slowikowski K, Zhang F, Wei K, Baglaenko Y, Brenner M, Loh PR, Raychaudhuri S. 2019. Fast, sensitive and accurate integration of single-cell data with harmony. Nat Methods 16: 1289–1296. doi:10.1038/s41592-019-0619-0
      CrossRefMedlineGoogle Scholar
    30. ↵
      Lam SK, Pitrou A, Seibert S. 2015. Numba: A LLVM-based Python JIT compiler. In Proceedings of the second workshop on the LLVM compiler infrastructure in HPC (ed. Finkel H), pp. 1–6. LLVM '15, Austin, TX.
      Google Scholar
    31. ↵
      Lause J, Berens P, Kobak D. 2021. Analytic Pearson residuals for normalization of single-cell RNA-seq UMI data. Genome Biol 22: 258. doi:10.1186/s13059-021-02451-7
      CrossRefGoogle Scholar
    32. ↵
      Lee JA, Verleysen M. 2010. Scale-independent quality criteria for dimensionality reduction. Pattern Recognit Lett 31: 2248–2257. doi:10.1016/j.patrec.2010.04.013
      CrossRefGoogle Scholar
    33. ↵
      Levine JH, Simonds EF, Bendall SC, Davis KL, Amir el AD, Tadmor MD, Litvin O, Fienberg HG, Jager A, Zunder ER, et al. 2015. Data-driven phenotypic dissection of AML reveals progenitor-like cells that correlate with prognosis. Cell 162: 184–197. doi:10.1016/j.cell.2015.05.047
      CrossRefMedlineGoogle Scholar
    34. ↵
      Liu Q, Chen S, Jiang R, Wong WH. 2021. Simultaneous deep generative modelling and clustering of single cell genomic data. Nat Mach Intell 3: 536–544. doi:10.1038/s42256-021-00333-y
      CrossRefGoogle Scholar
    35. ↵
      Lopez R, Regier J, Cole MB, Jordan MI, Yosef N. 2018. Deep generative modeling for single-cell transcriptomics. Nat Methods 15: 1053–1058. doi:10.1038/s41592-018-0229-2
      CrossRefMedlineGoogle Scholar
    36. ↵
      Mathieu E, Lan CL, Maddison CJ, Tomioka R, Teh YW. 2019. Hierarchical representations with poincaré variational auto-encoders. In Advances in neural information processing systems (ed. Wallach H, et al.), Vol. 32. NIPS, Vancouver, Canada.
      Google Scholar
    37. ↵
      McInnes L, Healy J, Melville J. 2018. UMAP: Uniform Manifold Approximation and Projection for dimension reduction. arXiv: 1802.03426.
      Google Scholar
    38. ↵
      Moon KR, van Dijk D, Wang Z, Gigante S, Burkhardt DB, Chen WS, Yim K, Elzen AVD, Hirn MJ, Coifman RR, et al. 2019. Visualizing structure and transitions in high-dimensional biological data. Nat Biotechnol 37: 1482–1492. doi:10.1038/s41587-019-0336-3
      CrossRefMedlineGoogle Scholar
    39. ↵
      Nagano Y, Yamaguchi S, Fujita Y, Koyama M. 2019. A wrapped normal distribution on hyperbolic space for gradient-based learning. In Proceedings of the 36th International Conference on Machine Learning (ed. Kamalika C, Ruslan S), Vol. 97, pp. 4693–4702. Proceedings of Machine Learning Research, Long Beach, CA.
      Google Scholar
    40. ↵
      Narayan A, Berger B, Cho H. 2021. Assessing single-cell transcriptomic variability through density-preserving data visualization. Nat Biotechnol 39: 765–774. doi:10.1038/s41587-020-00801-7
      CrossRefGoogle Scholar
    41. ↵
      Nickel M, Kiela D. 2017. Poincaré embeddings for learning hierarchical representations. In Proceedings of the 31st International Conference on Neural Information Processing Systems (ed. Guyon I, et al.), pp. 6341–6350. Curran Associates, Long Beach, CA.
      Google Scholar
    42. ↵
      Nickel M, Kiela D. 2018. Learning continuous hierarchies in the Lorentz model of hyperbolic geometry. In Proceedings of the 35th International Conference on Machine Learning, Stockholm (ed. Dy JG, Krause A), Vol. 80, pp. 3779–3788. Proceedings of Machine Learning Research, Stockholm.
      Google Scholar
    43. ↵
      Ovinnikov I. 2019. Poincaré Wasserstein autoencoder. In International Conference on Learning Representations (ICLR), Addis Ababa, Ethiopia.
      Google Scholar
    44. ↵
      Packer JS, Zhu Q, Huynh C, Sivaramakrishnan P, Preston E, Dueck H, Stefanik D, Tan K, Trapnell C, Kim J, et al. 2019. A lineage-resolved molecular atlas of C. elegans embryogenesis at single-cell resolution. Science 365: eaax1971. doi:10.1126/science.aax1971
      Abstract/FREE Full Text
    45. ↵
      Paszke A, Gross S, Chintala S, Chanan G, Yang E, DeVito Z, Lin Z, Desmaison A, Antiga L, Lerer A. 2017. Automatic differentiation in PyTorch. In Neural information processing systems (ed. Wallach HM, et al.). NIPS, Long Beach, CA.
      Google Scholar
    46. ↵
      Paul F, Arkin Y, Giladi A, Jaitin DA, Kenigsberg E, Keren-Shaul H, Winter D, Lara-Astiaso D, Gury M, Weiner A, et al. 2015. Transcriptional heterogeneity and lineage commitment in myeloid progenitors. Cell 163: 1663–1677. doi:10.1016/j.cell.2015.11.013
      CrossRefMedlineGoogle Scholar
    47. ↵
      Qiu X, Mao Q, Tang Y, Wang L, Chawla R, Pliner HA, Trapnell C. 2017. Reversed graph embedding resolves complex single-cell trajectories. Nat Methods 14: 979–982. doi:10.1038/nmeth.4402
      CrossRefMedlineGoogle Scholar
    48. ↵
      Reddi SJ, Kale S, Kumar S. 2018. On the convergence of Adam and beyond. In International Conference on Learning Representations. ICLR, Vancouver, BC, Canada.
      Google Scholar
    49. ↵
      Risso D, Perraudeau F, Gribkova S, Dudoit S, Vert JP. 2018. A general and flexible method for signal extraction from single-cell RNA-seq data. Nat Commun 9: 284. doi:10.1038/s41467-017-02554-5
      CrossRefMedlineGoogle Scholar
    50. ↵
      Saelens W, Cannoodt R, Todorov H, Saeys Y. 2019. A comparison of single-cell trajectory inference methods. Nat Biotechnol 37: 547–554. doi:10.1038/s41587-019-0071-9
      CrossRefMedlineGoogle Scholar
    51. ↵
      Satpathy AT, Granja JM, Yost KE, Qi Y, Meschi F, McDermott GP, Olsen BN, Mumbach MR, Pierce SE, Corces MR, et al. 2019. Massively parallel single-cell chromatin landscapes of human immune cell development and intratumoral T cell exhaustion. Nat Biotechnol 37: 925–936. doi:10.1038/s41587-019-0206-z
      CrossRefMedlineGoogle Scholar
    52. ↵
      Smillie CS, Biton M, Ordovas-Montanes J, Sullivan KM, Burgin G, Graham DB, Herbst RH, Rogel N, Slyper M, Waldman J, et al. 2019. Intra- and inter-cellular rewiring of the human colon during ulcerative colitis. Cell 178: 714–730.e22. doi:10.1016/j.cell.2019.06.029
      CrossRefMedlineGoogle Scholar
    53. ↵
      Sohn K, Lee H, Yan X. 2015. Learning structured output representation using deep conditional generative models. In Advances in neural information processing systems (ed. Cortes C, et al.), Vol. 28. NIPS, Montréal, Canada.
      Google Scholar
    54. ↵
      Street K, Risso D, Fletcher RB, Das D, Ngai J, Yosef N, Purdom E, Dudoit S. 2018. Slingshot: cell lineage and pseudotime inference for single-cell transcriptomics. BMC Genomics 19: 477. doi:10.1186/s12864-018-4772-0
      CrossRefMedlineGoogle Scholar
    55. ↵
      Stuart T, Srivastava A, Madad S, Lareau CA, Satija R. 2021. Single-cell chromatin state analysis with Signac. Nat Methods 18: 1333–1341. doi:10.1038/s41592-021-01282-5
      CrossRefMedlineGoogle Scholar
    56. ↵
      Tanay A, Regev A. 2017. Scaling single-cell genomics from phenomenology to mechanism. Nature 541: 331–338. doi:10.1038/nature21350
      CrossRefMedlineGoogle Scholar
    57. ↵
      Tian T, Wan J, Song Q, Wei Z. 2019. Clustering single-cell RNA-seq data with a model-based deep learning approach. Nature Machine Intelligence 1: 191–198. doi:10.1038/s42256-019-0037-0
      CrossRefGoogle Scholar
    58. ↵
      Tian T, Zhang J, Lin X, Wei Z, Hakonarson H. 2021. Model-based deep embedding for constrained clustering analysis of single cell RNA-seq data. Nat Commun 12: 1873. doi:10.1038/s41467-021-22008-3
      CrossRefGoogle Scholar
    59. ↵
      Van den Berge K, Roux de Bézieux H, Street K, Saelens W, Cannoodt R, Saeys Y, Dudoit S, Clement L. 2020. Trajectory-based differential expression analysis for single-cell sequencing data. Nat Commun 11: 1201. doi:10.1038/s41467-020-14766-3
      CrossRefGoogle Scholar
    60. ↵
      van der Maaten L. 2009. Learning a parametric embedding by preserving local structure. In Proceedings of the 12th International Conference on Artificial Intelligence and Statistics (ed. van Dyk DA, Max W), Vol. 5, pp. 384–391. Proceedings of Machine Learning Research, Clearwater Beach, FL.
      Google Scholar
    61. ↵
      van der Maaten L, Hinton G. 2008. Visualizing data using t-SNE. J Mach Learn Res 9: 2579–2605.
      CrossRefMedlineGoogle Scholar
    62. ↵
      Wang B, Zhu J, Pierson E, Ramazzotti D, Batzoglou S. 2017. Visualization and analysis of single-cell RNA-seq data by kernel-based similarity learning. Nat Methods 14: 414–416. doi:10.1038/nmeth.4207
      CrossRefMedlineGoogle Scholar
    63. ↵
      Wang Y, Huang H, Rudin C, Shaposhnik Y. 2021. Understanding how dimension reduction tools work: an empirical approach to deciphering t-SNE, UMAP, TriMAP, and PaCMAP for data visualization. J Mach Learn Res 22: 1–73.
      Google Scholar
    64. ↵
      Wolf FA, Angerer P, Theis FJ. 2018. SCANPY: large-scale single-cell gene expression data analysis. Genome Biol 19: 15. doi:10.1186/s13059-017-1382-0
      CrossRefMedlineGoogle Scholar
    65. ↵
      Wolf FA, Hamey FK, Plass M, Solana J, Dahlin JS, Göttgens B, Rajewsky N, Simon L, Theis FJ. 2019. PAGA: graph abstraction reconciles clustering with trajectory inference through a topology preserving map of single cells. Genome Biol 20: 59. doi:10.1186/s13059-019-1663-x
      CrossRefMedlineGoogle Scholar
    66. ↵
      Zappia L, Phipson B, Oshlack A. 2017. Splatter: simulation of single-cell RNA sequencing data. Genome Biol 18: 174. doi:10.1186/s13059-017-1305-0
      CrossRefGoogle Scholar
    67. ↵
      Zhai Z, Lei YL, Wang R, Xie Y. 2022. Supervised capacity preserving mapping: a clustering guided visualization method for scRNA-seq data. Bioinformatics 38: 2496–2503. doi:10.1093/bioinformatics/btac131
      CrossRefGoogle Scholar
    68. ↵
      Zheng GX, Terry JM, Belgrader P, Ryvkin P, Bent ZW, Wilson R, Ziraldo SB, Wheeler TD, McDermott GP, Zhu J, et al. 2017. Massively parallel digital transcriptional profiling of single cells. Nat Commun 8: 14049. doi:10.1038/ncomms14049
      CrossRefMedlineGoogle Scholar
    | Table of Contents

    This Article

    1. Published in Advance February 27, 2023, doi: 10.1101/gr.277068.122 Genome Res. 33: 232-246 © 2023 Tian et al.; Published by Cold Spring Harbor Laboratory Press

    Article Category

    Share

    Preprint Server



    Navigate This Article

    Current Issue

    1. February 2026, 36 (2)
    1. Current Issue
    1. Alert me to new issues of Genome Research