Estimating population genetic parameters and comparing model goodness-of-fit using DNA sequences with error
- Human Genetics Center, School of Public Health, The University of Texas Health Science Center at Houston, Houston, Texas 77030, USA
Abstract
It is known that sequencing error can bias estimation of evolutionary or population genetic parameters. This problem is more prominent in deep resequencing studies because of their large sample size n, and a higher probability of error at each nucleotide site. We propose a new method based on the composite likelihood of the observed SNP configurations to infer population mutation rate θ = 4Neμ, population exponential growth rate R, and error rate ɛ, simultaneously. Using simulation, we show the combined effects of the parameters, θ, n, ɛ, and R on the accuracy of parameter estimation. We compared our maximum composite likelihood estimator (MCLE) of θ with other θ estimators that take into account the error. The results show the MCLE performs well when the sample size is large or the error rate is high. Using parametric bootstrap, composite likelihood can also be used as a statistic for testing the model goodness-of-fit of the observed DNA sequences. The MCLE method is applied to sequence data on the ANGPTL4 gene in 1832 African American and 1045 European American individuals.
Population parameter inference is one of the most important tasks in theoretical and applied population genetics. Among all parameters, the scaled population mutation rate θ is probably the most important for modeling the evolution of a DNA locus in a population. The quantity θ equals 4Neμ for diploids or 2Neμ for haploids, where Ne is the effective population size and μ is the mutation rate per generation of the locus. The mutation rate describes the basic variability of DNA sequences in a population, and many summary statistics of DNA sequences are related to θ. Therefore, estimating θ plays a central role in understanding the evolution of a population. Other important population parameters include, but not limited to, the population exponential growth rate R, the scaled recombination rate ρ, and the migration rate.
One challenge of estimating these population parameters is how to incorporate sequencing error when it is not negligible, e.g., when the error rate is high and/or sample size is large. It is easy to understand that errors can bias the estimation of evolutionary or population genetic parameters with sequence samples (Clark and Whittam 1992; Johnson and Slatkin 2008). The sample size has a large impact because sequencing error increases linearly with sample size, while the expected number of true mutations increases more slowly, as implied by coalescent theory. As a rule of thumb, population genetic estimates that are uncorrected will be biased significantly if nɛ ≥ θ/L, where n is sample size (i.e., number of sequences sampled), ɛ is the average error rate per site, and L is the sequence length of the given locus (Johnson and Slatkin 2008).
The newer parallel DNA sequencing technologies have higher error rates compared to traditional Sanger sequencing, and at the same time their low cost per base pair (bp) encourages researchers to conduct larger-scale sequencing projects with larger sample sizes (Shendure and Ji 2008). While a typically finished sequence produced by Sanger sequencing has an error rate of 10−5 (Zwick 2005), the error rates of the newer parallel sequencers are typically 10-fold higher (Shendure and Ji 2008). Although technological advance may further decrease their error rate, the trend of balancing sequencing quality and quantity for the newer parallel sequencers is likely shifting toward larger quantities with higher error rates, e.g., on the scale of 10−4 on consensus reads. For some sequencing projects, such as metagenomic shotgun sequencing, each sequence can be considered as a random sample from a sequence pool of a whole population (or populations) (Whitaker and Banfield 2006), so that it is almost impossible to reduce error rate by multiple reads from the same sequence. In such cases, the error rate in the sequences can be higher than 10−3 (Shendure and Ji 2008).
In response to these challenges, new unbiased estimators for θ and other population parameters for sequence samples with error are proposed. Targeting metagenomic sequencing data, Johnson and Slatkin (2006) were probably the first to directly address the error problem. Incorporating sequencing errors via Phred quality scores,
they proposed a maximum composite likelihood estimator (MCLE) for θ and R using the SNP frequency spectrum. In a later study they corrected the sequencing error bias of two widely used θ estimators, Tajima's 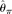 (Tajima 1983) and Watterson's
(Tajima 1983) and Watterson's 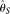 (Watterson 1975), assuming known ɛ (Johnson and Slatkin 2008). Another corrected
(Watterson 1975), assuming known ɛ (Johnson and Slatkin 2008). Another corrected 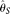 assuming known ɛ was proposed by Hellmann et al. (2008), which is similar to Johnson and Slatkin (2008), but accounts for the uncertainty of chromosome sampling in a shotgun resequencing of pooled diploid individuals. All the
above estimators of θ assume that ɛ is known. For sequence data with unknown error rate, several estimators have recently been developed. Achaz (2008) proposed two computationally efficient, moment-based estimators. Assuming a low but unknown ɛ, the estimators simply use the SNP number and frequency spectrum, while ignoring singletons, on which sequencing error is
most skewed. Knudsen and Miyamoto (2007) developed a full-likelihood coalescent model that incorporates missing data, sequencing error, and multiple reads of the
same sequence. Both θ and ɛ can be estimated jointly with their method. However, the computational intensity of calculating the likelihood is so high
that only small sample sizes (i.e., less than 20 sequences) can realistically be considered. By ignoring singletons, Knudsen and Miyamoto (2009) modified their original algorithm to improve its accuracy and computational speed. Targeting high-coverage shotgun resequencing
of a single diploid individual, Lynch (2008) proposed several methods to correct
assuming known ɛ was proposed by Hellmann et al. (2008), which is similar to Johnson and Slatkin (2008), but accounts for the uncertainty of chromosome sampling in a shotgun resequencing of pooled diploid individuals. All the
above estimators of θ assume that ɛ is known. For sequence data with unknown error rate, several estimators have recently been developed. Achaz (2008) proposed two computationally efficient, moment-based estimators. Assuming a low but unknown ɛ, the estimators simply use the SNP number and frequency spectrum, while ignoring singletons, on which sequencing error is
most skewed. Knudsen and Miyamoto (2007) developed a full-likelihood coalescent model that incorporates missing data, sequencing error, and multiple reads of the
same sequence. Both θ and ɛ can be estimated jointly with their method. However, the computational intensity of calculating the likelihood is so high
that only small sample sizes (i.e., less than 20 sequences) can realistically be considered. By ignoring singletons, Knudsen and Miyamoto (2009) modified their original algorithm to improve its accuracy and computational speed. Targeting high-coverage shotgun resequencing
of a single diploid individual, Lynch (2008) proposed several methods to correct 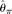 , assuming a known or unknown ɛ. Lynch (2009) further extended the method to estimate allele frequencies of each nucleotide site with multiple individuals. The combination
of Lynch (2008) and Lynch (2009) provides a method to estimate
, assuming a known or unknown ɛ. Lynch (2009) further extended the method to estimate allele frequencies of each nucleotide site with multiple individuals. The combination
of Lynch (2008) and Lynch (2009) provides a method to estimate 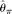 with high-coverage resequencing data of multiple individuals. Jiang et al. (2009) developed a method to estimate θ and ρ for shotgun resequencing data. Although they did not incorporate error rate into their method, they suggested some refinements
to make their method more robust to errors.
with high-coverage resequencing data of multiple individuals. Jiang et al. (2009) developed a method to estimate θ and ρ for shotgun resequencing data. Although they did not incorporate error rate into their method, they suggested some refinements
to make their method more robust to errors.
Recently, Liu et al. (2009) modified Fu's (Fu 1994) best linear unbiased estimator (BLUE) and proposed two types of θ estimators, based on generalized least squares (GLS) with either known or unknown ɛ. One type uses the full spectrum of SNP frequency and incorporates ɛ into the calculation, while the other type simply ignores singletons and treats ɛ = 0 for other SNP frequency classes. The two estimators either strictly or relaxedly assume that there is, at most, one error on any given nucleotide site of the whole sample, therefore their efficiency decreases with an increase of ɛ and they are more suitable for data with ɛ < 10−4 and moderate sample sizes (102 sequences). Another disadvantage is that they cannot handle missing data directly. For large resequencing projects and metagenomic sequencing projects, the missing data rate of the resulting sequences can be high. Especially with metagenomic shotgun resequencing, the nature of uneven coverage on different nucleotide sites will produce very different sample sizes for different sites, which can be considered as a type of missing data.
In this study we propose a MCLE of θ, R, and ɛ that is suitable for data with high error rates, large sample sizes and/or a high missing data rate. While the full likelihood method calculates the likelihood of sequences as a whole, the composite likelihood method first calculates the likelihood of each observed nucleotide site (or pair of sites) and then calculates the total likelihood of the sequences by multiplying these individual likelihoods as if they are independent (e.g., Nielsen 2000; Hudson 2001). The composite likelihood is an approximation of the full likelihood and MCLE should have larger variance than a full likelihood estimator. However, the computational burden is substantially reduced, so that in many cases a MCLE can be a good compromise between estimation efficiency and computational speed. A MCLE of θ and R was proposed by Johnson and Slatkin (2006) for metagenomic sequencing data. Compared to their method, ours is more suitable for resequencing data with a large sample size because of two major differences. First, we do not assume each nucleotide read has an associated quality score, but instead use an error rate ɛ for each nucleotide site for all samples. One reason for this is that some SNP calling software do not provide a quality score. Second, our method systematically handles cases when there are more than two allele types at a SNP site (due to sequencing error), which becomes more common when the sample size is large.
Besides parameter estimation, whether the observed sequence pattern of a gene or a DNA region fits a particular population genetic model, and which model fits the data better, are also important questions in population genetics. The composite likelihood of a DNA region can also be used as a summary statistic of the model's goodness-of-fit to the data. Therefore, the model goodness-of-fit test and model comparison can be conducted by parameter estimation followed by parametric bootstrap (see Methods for details).
Below we show the performance of our MCLEs of θ and R using computer simulation, and compare our MCLE of θ with other θ estimators. Then, we demonstrate its application for both parameter estimation and the model goodness-of-fit comparison using data from a resequencing project of the ANGPTL4 gene in 1832 African Americans and 1045 European Americans (Romeo et al. 2007).
Results
Simulation validation
Coalescent simulation (see Methods) was used to investigate the properties of our MCLE and its performance with changing population parameters, including ɛ, n, θ, and R. One obvious problem of MCLE is the treatment of each nucleotide site independently. Although recombination may validate the assumption for genetically unlinked sites, for any closely linked sequence the assumption is obviously invalid. To investigate the robustness of MCLE, we simulated sequences with no recombination. With different combinations of parameters, at least 10,000 samples were simulated assuming an exponential growth population model (R > 0) and at most three sequencing errors on any site (K = 3; see Methods; Supplemental Appendix). To investigate the performance of the MCLE with changing parameters, we used Brent's search algorithm (see Methods) to estimate θ or R with all other parameters fixed.
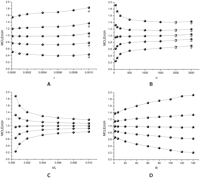
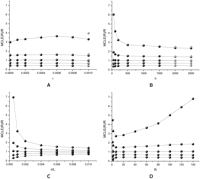
Black dots in Figure 1 show the ratios of 5%, 25%, 50%, 75%, and 95% percentiles of MCLE of θ [MCLE(θ)] versus the true value, with increasing ɛ, n, θ, and R. Figure 2 is similar to Figure 1, but shows the ratio of MCLE(R) versus R. The medians of MCLE(θ) and MCLE(R) fit well with the true values, with exception when ɛ is large or when n is large (details given below). The distribution of MCLE(θ) is more or less symmetric, while the distribution of MCLE(R) has a heavy right tail, which biases the mean of MCLE(R) upward. Increasing R increases the variance of MCLE(θ)/θ. The variance of MCLE(R)/R also increases with increasing R, except when R is near 0. In contrast, an increase of n or θ/L decreases the variance of MCLE(θ)/θ and MCLE(R)/R. With an increase of ɛ, we observe the variance of MCLE(R)/R increases with increasing ɛ and then decreases a little bit when ɛ is high (Fig. 2A). We also observe that the MCLE(θ) is biased upward when ɛ is large (ɛ = 10−3, Fig. 1A) or when n is large (n = 2000, 2500, Fig. 1B). Both the observations are due to the fact that when ɛ or n is near or out of the maximum applicable range of the MCLEs, MCLE(R) tends to underestimate R while MCLE(θ) tends to overestimate θ. The gray dots in Figures 1A,B and 2A,B are MCLEs calculated with assumption of, at most, four errors on any nucleotide site (K = 4). As we can see, by increasing the maximum allowable errors, we can obtain unbiased MCLEs.
Effects of ɛ (A), n (B), θ/L (C), and R (D) on the MCLE of θ. The five point-and-lines (top to bottom) represent 95%, 75%, 50%, 25%, and 5% percentiles of the MCLE, respectively. Unless shown on the x-axis, ɛ = 10−4, n = 200, θ/L = 10−3, R = 40, and L = 104. Black dots were percentiles of MCLEs calculated with K = 3 and gray dots were percentiles of MCLEs calculated with K = 4.
Effects of ɛ (A), n (B), θ/L (C), and R (D) on the MCLE of R. The five point-and-lines (top to bottom) represent 95%, 75%, 50%, 25%, and 5% percentiles of the MCLE, respectively. Unless shown on the x-axis, ɛ = 10−4, n = 200, θ/L = 10−3, R = 40, and L = 104. Black dots were percentiles of MCLEs calculated with K = 3 and gray dots were percentiles of MCLEs calculated with K = 4.
Compared to other θ estimators
Assuming constant population size and unknown ancestral states of the nucleotide alleles, we used coalescent simulation to
compare MCLE(θ) with some other θ estimators that take into account error or are robust to error, i.e., two modified 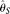 estimators (
estimators (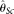 [Johnson and Slatkin 2008] and
[Johnson and Slatkin 2008] and 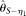 [Achaz 2008]), two modified
[Achaz 2008]), two modified 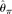 estimators (
estimators (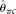 [Johnson and Slatkin 2008] and
[Johnson and Slatkin 2008] and 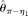 [Achaz 2008]), and two modified BLUE estimators (
[Achaz 2008]), and two modified BLUE estimators (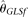 and
and 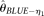 [Liu et al. 2009]). To provide performance standards,
[Liu et al. 2009]). To provide performance standards, 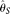 and
and 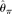 were also calculated using the TRUE SNP spectrum (i.e., no errors), which were designated as
were also calculated using the TRUE SNP spectrum (i.e., no errors), which were designated as 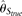 and
and 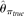 , respectively (see Methods). Among those estimators,
, respectively (see Methods). Among those estimators, 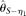 and
and 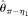 assume an unknown error rate ɛ, while
assume an unknown error rate ɛ, while 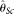 and
and 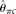 assume known ɛ. Our MCLE(θ) can be calculated with either known or unknown ɛ. In the former case, Brent's algorithm was used to find MCLE(θ). In the latter case, we used Powell's algorithm (see Methods) to find the MCLE of θ and ɛ simultaneously, but reported MCLE(θ) only (treating ɛ as a nuisance parameter). For each set of parameters, 10,000 samples were simulated and the mean, variance, and the root
mean squared error (RMSE) of each estimator were calculated.
assume known ɛ. Our MCLE(θ) can be calculated with either known or unknown ɛ. In the former case, Brent's algorithm was used to find MCLE(θ). In the latter case, we used Powell's algorithm (see Methods) to find the MCLE of θ and ɛ simultaneously, but reported MCLE(θ) only (treating ɛ as a nuisance parameter). For each set of parameters, 10,000 samples were simulated and the mean, variance, and the root
mean squared error (RMSE) of each estimator were calculated.
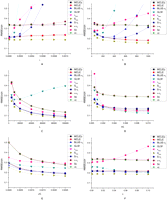
The results are shown in Figure 3. MCLE(θ) with either known or unknown ɛ is the overall best estimator with all ranges of parameters tested. It is always among the group of the most accurate estimators
in the comparison group as measured by the smallest RMSE. It shows clear advantage over other estimators with either high
error rate or large sample size. MCLE(θ) typically shows the same trend as 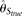 with the change of the parameters, but never outperforms
with the change of the parameters, but never outperforms 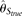 . On the other hand,
. On the other hand, 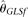 and
and 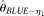 perform poorly with high error rates or large sample sizes, which is expected. The two modified
perform poorly with high error rates or large sample sizes, which is expected. The two modified 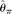 estimators have very similar performance as
estimators have very similar performance as 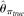 , but they never outperform MCLE(θ) throughout the range of parameters tested, due to their large variances. The RMSEs of
, but they never outperform MCLE(θ) throughout the range of parameters tested, due to their large variances. The RMSEs of 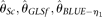 , and
, and 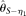 increase with increasing ɛ. For
increase with increasing ɛ. For 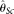 , this is largely due to the increase of variance, while for the remaining three this is largely because they are biased upward
with increasing ɛ. With increasing n, MCLE(θ) becomes more accurate while
, this is largely due to the increase of variance, while for the remaining three this is largely because they are biased upward
with increasing ɛ. With increasing n, MCLE(θ) becomes more accurate while 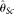 becomes less accurate, which is due to increased variance. The RMSEs of
becomes less accurate, which is due to increased variance. The RMSEs of 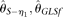 , and
, and 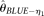 , first decrease and then increase with increasing n. The reason for
, first decrease and then increase with increasing n. The reason for 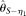 is that although its variance decreases with increasing n, it is biased upward at the same time. At a given range of relative small n,
is that although its variance decreases with increasing n, it is biased upward at the same time. At a given range of relative small n, 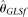 and
and 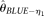 are unbiased estimators and their variances decrease with increasing n. While n is larger than the range, they are biased upward and their variances increase with increasing n. Both
are unbiased estimators and their variances decrease with increasing n. While n is larger than the range, they are biased upward and their variances increase with increasing n. Both 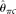 and
and 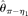 seem to be insensitive to n. With increasing L, all estimators become more accurate, with the only exception of
seem to be insensitive to n. With increasing L, all estimators become more accurate, with the only exception of 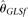 , which is biased upward with large L. On the other hand, while all estimators become more accurate with increasing θ/L,
, which is biased upward with large L. On the other hand, while all estimators become more accurate with increasing θ/L, 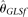 outperforms all other estimators (even
outperforms all other estimators (even 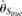 ) with large θ/L, due to its small variance. With increasing recombination rate ρ, all estimators increase their accuracy. At one extreme, when all nucleotide sites are independent, the RMSEs of MCLE(θ) can go down to 0.144 × θ, while that of
) with large θ/L, due to its small variance. With increasing recombination rate ρ, all estimators increase their accuracy. At one extreme, when all nucleotide sites are independent, the RMSEs of MCLE(θ) can go down to 0.144 × θ, while that of 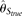 is 0.131 × θ (data not shown). Finally, we investigated the effect of the missing data rate δ, which is defined as the number of nucleotide alleles excluded from analysis (due to low-quality read, PCR failure, among
others) divided by the total number of alleles actually sequenced. As expected, MCLE(θ) is relatively insensitive to δ. However, it was unexpected to observe that with increasing δ, only
is 0.131 × θ (data not shown). Finally, we investigated the effect of the missing data rate δ, which is defined as the number of nucleotide alleles excluded from analysis (due to low-quality read, PCR failure, among
others) divided by the total number of alleles actually sequenced. As expected, MCLE(θ) is relatively insensitive to δ. However, it was unexpected to observe that with increasing δ, only 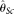 becomes less efficient, while
becomes less efficient, while 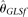 actually becomes slightly more efficient. After a closer look, we believe that this is due to the fact that the missing data
have two possibly positive effects on the estimators. First, it biases the θ estimators downward, which to some extent compensates for the upward bias caused by errors. Second, the higher the missing
data rate, the higher the chance an error is called missing, which is similar to the effect of removing putative errors by
increasing the standard of tolerable quality scores in sequence reading. Therefore, most of the estimators compared here should
be able to be applied to data sets with some extent of missing data. Further investigation is needed to clarify their tolerable
missing data rate.
actually becomes slightly more efficient. After a closer look, we believe that this is due to the fact that the missing data
have two possibly positive effects on the estimators. First, it biases the θ estimators downward, which to some extent compensates for the upward bias caused by errors. Second, the higher the missing
data rate, the higher the chance an error is called missing, which is similar to the effect of removing putative errors by
increasing the standard of tolerable quality scores in sequence reading. Therefore, most of the estimators compared here should
be able to be applied to data sets with some extent of missing data. Further investigation is needed to clarify their tolerable
missing data rate.
Effects of ɛ (A), n (B), L (C), θ/L (D), ρ/L (E), and δ (F) on the root mean squared error of different θ estimators. MCLE|ɛ: MCLE(θ) assuming known ɛ; MCLE: MCLE(θ) assuming unknown ɛ; BLUE-η1: 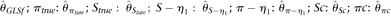 . Unless shown on the x-axis, ɛ = 10−4, n = 200, θ/L = 10−3, L = 104, ρ/L = 10−3, and δ = 0.
. Unless shown on the x-axis, ɛ = 10−4, n = 200, θ/L = 10−3, L = 104, ρ/L = 10−3, and δ = 0.
Applied to ANGPTL4 sequence data
Romeo et al. (2007) showed a significant excess of rare alleles in the exon regions of the ANGPTL4 gene from 1832 African Americans and 1045 European Americans (for details, see Methods; Supplemental Fig. S1). There can be different explanations for this observation, including purifying selection, population expansion, and sequencing error. However, the three neutrality tests the authors used, Tajima (1989)'s D and Fu and Li (1993)'s D and D*, cannot distinguish artificial significance (i.e., sequencing error) from biological significance (e.g., purifying selection and population expansion), because all assume no sequencing error in the data.
To show that the excess of rare alleles has biological significance, we need to test it with an error model. First, with an assumption of no error, we estimated MCLE(θ)s as 0.0020 for European Americans and 0.0026 for African Americans, respectively. Then we compared the model without error (null hypothesis) to the model with error (alternative hypothesis) using parametric bootstrap with the MCLE(θ)s (see Methods). The results showed that the alternative hypothesis is significantly better than the null hypothesis (P-value smaller than 0.01, one tail) based on 10,000 coalescent simulations, for both African Americans and European Americans. This suggests that sequencing error explains the excess of rare alleles better than the null hypothesis of no error.
Then we used a simple grid search method to estimate MCLEs of θ and ɛ simultaneously (assuming constant population size), with step widths 10−4 and 10−6 for θ and ɛ, respectively. We assume there are at most three errors at any nucleotide site, which will guarantee an applicable MCLE(θ) with an ɛ up to 7.5 × 10−5 (see Methods for explanation). For the African Americans, the estimated MCLE(θ) is 0.0017. Using parametric bootstrap, we estimated its approximate 95% confidence interval (CI) (0.0010, 0.0027) based on 10,000 coalescent simulations. The estimated MCLE(ɛ) for African Americans is 3 × 10−6. The same analysis was performed with European Americans. The results are MCLE(θ) = 0.0011, with 95% CI (0.0006, 0.0018); MCLE(ɛ) = 4 × 10−6.
To test neutrality under the error model, we conducted coalescent simulation (10,000 replications) with the MCLEs of θ and ɛ, to obtain the null distributions of the test statistics. Based on the empirical null distributions, empirical P-values of one-tail tests for an excess of rare alleles (test statistics significantly smaller than expected) were obtained. Besides the above three test statistics we added Achaz (2008)'s Y and Y* tests, which are modified Tajima (1989)'s D and supposed to be more robust to errors. We also conducted a model goodness-of-fit test using the composite likelihood (see Methods) to test the overall model goodness-of-fit. The results of the tests are as follows. For African Americans, only Achaz's Y (P = 0.045) and Y* (P = 0.045) rejected the null hypothesis of neutrality. For the European Americans, Tajima's D (P = 0.044) and Achaz's Y (P = 0.020) and Y* (P = 0.020) rejected the null hypothesis. Fu and Li (1993)'s D and D* and our model goodness-of-fit test failed to reject the null hypothesis in both cases. With the fact that the rare nonsynonymous changes have been verified experimentally (Romeo et al. 2007), singletons should have a lower error rate than other SNPs. Because this information is not incorporated in the current model, our MCLE(ɛ) should be an upper limit of ɛ. Even with an error model that has overestimated ɛ, Y and Y* rejected the null hypothesis of no excess of rare alleles, which suggests that sequencing error cannot explain the excess of rare alleles. This leaves alternative explanations including purifying selection (Romeo et al. 2007), population expansion, or mixed effects of multiple acting factors as mentioned above to explain the excess. The results also suggested that Tajima's D and Fu and Li's D and D* tests have higher type I error rates when there are sequencing errors and lose power under the error model. Model goodness-of-fit tests using composite likelihood may be too conservative because of no specified alternative hypothesis. The neutrality tests that take error into account, such as Achaz's Y and Y*, should be preferred if there are likely many errors in the sequences.
Finally, assuming an exponential growth model, we used a hybrid algorithm to estimate MCLEs of θ, ɛ, and R simultaneously (searching θ and ɛ using Powell's algorithm on a grid of R; see Methods for details). For African Americans, we estimated MCLE(θ) = 0.0027, MCLE(ɛ) = 2.3 × 10−6 and MCLE(R) = 5 (grid width = 1). With 10,000 parametric bootstrap samples, we estimated their approximate 95% CIs, which are (0.0018, 0.0040), (3 × 10−7, 6.8 × 10−6), and (1.4, 19.3), respectively. For European Americans, the corresponding estimates are: MCLE(θ) = 0.0121 with 95% CI (0.0080, 0.0166), MCLE(ɛ) = 1.7 × 10−6 with 95% CI (0, 4.0 × 10−6), and MCLE(R) = 738 with 95% CI (404.2, 1517.4).
Discussion
In this paper we propose a method based on the composite likelihood of SNP configurations for estimating population genetic parameters, such as the population mutation rate θ and scaled exponential growth rate R. There are several advantages of this method compared to available parameter estimation methods that incorporate error. First, it is relatively unbiased and can be efficiently computed with relatively large error rate ɛ or sample size n. Second, it is very flexible and can be used to estimate different sets of parameters assuming different models. The only requirement is the expected probabilities of SNP configurations under the model, which can be obtained either analytically or via computer simulation. Third, it fully models SNP configurations with more than two alleles. Fourth, the method can naturally handle missing data.
One limitation of our method is that it uses a single error rate ɛ for all sites and all sequences, which is an acceptable treatment when quality score or probability call of genotypes are unavailable or only an average error rate is known. When the quality score of each genotype is available, we can improve our method by using a site-specific error rate ɛi for site i instead of an average ɛ. That is, we replace ɛ with ɛi in Equation 3, see below, and ɛi can be calculated using quality scores. This treatment gains computational efficiency, but loses power because it does not make full use of the quality score of each genotype. However, calculating all combinations of possible SNP configurations using a quality score (as proposed in Johnson and Slatkin 2006) may cause a large computational burden when the sample size is large. Further development is needed to compute composite likelihood efficiently with quality scores.
Another limitation of our method is associated with the nature of the composite likelihood. Since the composite likelihood is not the true likelihood, it does not have some of the important properties of the true likelihood. For example, a likelihood ratio test using the composite likelihood may be biased. This is the reason we proposed to use a computational intensive parametric bootstrap method to compare models. Some kind of normalization is needed before comparing composite likelihoods directly. More thorough studies are needed to investigate the statistical properties of the composite likelihood.
As shown in the Results, the MCLE with known ɛ only slightly outperforms the MCLE with unknown ɛ. However, in regard to the computational speed, the former should be at least several-fold faster than the latter. As a simple case, if a grid-search algorithm is used and ɛ is searched on g grids, then the former should be approximately g times faster than the latter. If efficient search algorithms, such as Brent's algorithm for one-dimensional space or Powell's algorithm for multidimensional space (see Methods) is used, the search speed is largely affected by the initial value of the parameter(s). For example, in one comparison with 1000 simulated data sets with the default parameters used in Figure 3 (true θ = 10−3/bp and ɛ = 10−4/bp), the MCLE with known ɛ (via Brent's algorithm with initial θ = 2 × 10−3/bp) took 276 sec to obtain the estimations; while the MCLE with unknown ɛ (via Powell's algorithm with initial θ = 2 × 10−3/bp and ɛ = 10−5/bp) took 1294 sec on a PC using an Intel Pentium 4 CPU at 3.4 GHz. Applied to the same data set, Brent's algorithm with initial θ = 4 × 10−3/bp, took 286 sec to obtain the estimations; while Powell's algorithm with initial θ = 4 × 10−3/bp and ɛ = 10−5/bp took 2217 sec.
As mentioned in the Introduction, several θ estimators, including ours, have been proposed to incorporate sequencing error or to be robust to errors. So far, extensive comparison of these estimators is limited. However, these estimators are designed for analyzing different types of data and all have their own advantages and disadvantages. Here we try to provide our recommendations for choosing the appropriate estimators based on our understanding and experience. First, when the sample size is small (tens of sequences), especially when the missing data rate is high, e.g., metagenomic sequencing data, Johnson and Slatkin (2006)'s MCLE or Knudsen and Miyamoto (2007, 2009)'s full likelihood method is probably the best choice. The former is especially designed for metagenomic sequences when the quality score of each nucleotide read is available. The latter uses a model assuming no recombination. Therefore, if recombination is significant in the DNA sequences studied, Knudsen and Miyamoto (2007, 2009)'s method may not be appropriate. Second, when the sample size is large (thousands or even tens of thousands of sequences), the MCLE method proposed here is a suitable estimator to use. Third, when the sample size is moderate (hundreds of sequences), there are more choices. Johnson and Slatkin (2006)'s and our MCLEs may still be quite usable when the sample size is at the lower end or higher end of the hundreds, respectively. When the missing data rate and the error rate are relatively low, Liu et al. (2009)'s GLS estimator is a good choice. If the missing data rate is high or the error rate is high, Achaz (2008)'s corrected Watterson's estimator performs well with very little computational intensity.
One obvious dilemma in a resequencing study is how to balance sample size, the number of genes for sequencing and sequencing
error. With a fixed budget, increasing sequencing coverage for each sample decreases the error rate, but at the same time
decreases the total number samples or genes to be sequenced. A larger sample size provides higher power to discover rare alleles,
but decreases the number of genes to be sequenced. At the same time, error accumulates linearly with sample size and makes
it harder to identify true “signals” from “noises.” Although answering this question is beyond the scope of this paper, our
study does provide some clues. First, any methods using simple SNP counting regardless of errors, such as Watterson (1975)'s 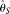 , may dramatically lose power when errors cannot be ignored (Liu et al. 2009). Second, using appropriate methods, such as our MCLE method, it is possible to achieve a similar power with higher error
rates, which means that a smaller budget is needed for sequencing. Third, the power gain of methods using the SNP spectrum
may diminish with increasing sample size, but the diminishing rate may be different for different estimators or different
tests. For example, the variance of MCLE(θ) decreases slower than MCLE(R) with increasing sample size. This means for different estimators or tests, the choice between more samples and fewer genes
or more genes and smaller sample may be different.
, may dramatically lose power when errors cannot be ignored (Liu et al. 2009). Second, using appropriate methods, such as our MCLE method, it is possible to achieve a similar power with higher error
rates, which means that a smaller budget is needed for sequencing. Third, the power gain of methods using the SNP spectrum
may diminish with increasing sample size, but the diminishing rate may be different for different estimators or different
tests. For example, the variance of MCLE(θ) decreases slower than MCLE(R) with increasing sample size. This means for different estimators or tests, the choice between more samples and fewer genes
or more genes and smaller sample may be different.
In this study, we build a probability model for the SNP spectrum with θ, R, and ɛ. With this model, we can estimate the three parameters by maximizing the composite likelihood of the spectrum. So far, we
have been focused on estimating θ and R, but also demonstrate the estimation of ɛ using the ANGPTL4 gene. Actually, with our limited comparison, MCLE of ɛ shows a higher efficiency compared to the simple ɛ estimations using 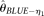 and
and 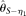 (Liu et al. 2009; Supplemental Fig. S2). However, our model is not proper for other kinds of errors contained in the DNA sequences, including
clone errors, PCR errors, and DNA degradation, all of which need specific probability models (e.g., Rambaut et al. 2009).
(Liu et al. 2009; Supplemental Fig. S2). However, our model is not proper for other kinds of errors contained in the DNA sequences, including
clone errors, PCR errors, and DNA degradation, all of which need specific probability models (e.g., Rambaut et al. 2009).
Several java programs for calculating MCLE of θ, R, and ɛ, and core programs for calculating MCLE(θ) are available at http://sites.google.com/site/jpopgen/.
Methods
Composite likelihood calculation
Let us first define the configuration of a SNP as a (possibly partially ordered) serial of allele counting at that site, in which the first number is the counting of the ancestral alleles, while the second (and third, fourth, when they exist) is the counting of derived alleles. For example, at a site we observed 10 “A” alleles, five “C” alleles, and one “T” allele, and we know the “A” alleles are the ancestral alleles. Then the configuration of that site is presented as [10, 5, 1] or [10, 1, 5]. That is, the numbers in [ ] are partially ordered, so that [10, 5, 1] ≠ [5, 10, 1], but [10, 5, 1] = [10, 1, 5]. On the other hand, if the ancestral state is unknown, we present the configuration as a set of unordered counting of alleles. In the previous example, if we do not know which allele is ancestral, then we represent its configuration as {10, 5, 1}, or {5, 10, 1}, or {1, 5, 10}, etc.
We designate 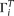 as the true allele configuration of site i, with the ancestral state either known or unknown. Assuming the infinite sites model, there are at most two alleles at a
given site. Let us separate
as the true allele configuration of site i, with the ancestral state either known or unknown. Assuming the infinite sites model, there are at most two alleles at a
given site. Let us separate 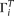 for two different conditions, ancestral state known or unknown. Suppose at site i there are j ancestral alleles and ni − j mutant alleles, where ni is the number of observed alleles on that site. If we assume a constant population size, the expected probability of observing
a true configuration [j, ni − j] is
for two different conditions, ancestral state known or unknown. Suppose at site i there are j ancestral alleles and ni − j mutant alleles, where ni is the number of observed alleles on that site. If we assume a constant population size, the expected probability of observing
a true configuration [j, ni − j] is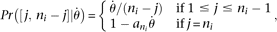 where Pr() means probability,
where Pr() means probability, 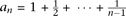 , and
, and 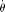 is θ per base pair
is θ per base pair 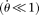 (Fu 1995). In an exponential growth model for the population, Ne(t) = Ne(0)exp(−rt), where Ne(t) is the effective population size t generations before the current time (generation 0). In population genetics, a scaled population growth rate, R = 2Ner for diploids or R = Ner for haploids, is often used as a demographic parameter. The expected probability of observing a true configuration [j, ni − j],
(Fu 1995). In an exponential growth model for the population, Ne(t) = Ne(0)exp(−rt), where Ne(t) is the effective population size t generations before the current time (generation 0). In population genetics, a scaled population growth rate, R = 2Ner for diploids or R = Ner for haploids, is often used as a demographic parameter. The expected probability of observing a true configuration [j, ni − j], 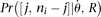 can be calculated using formulas described in Polanski et al. (2003) and Polanski and Kimmel (2003). More generally, assuming any demographic models and/or mutation models,
can be calculated using formulas described in Polanski et al. (2003) and Polanski and Kimmel (2003). More generally, assuming any demographic models and/or mutation models, 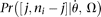 can be calculated either analytically, numerically or using a Monte Carlo simulation, given a set of model parameters Ω,
other than
can be calculated either analytically, numerically or using a Monte Carlo simulation, given a set of model parameters Ω,
other than 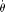 . If
. If 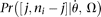 has to be evaluated via simulation and ni is different from site to site because of missing data, then it will be more efficient to evaluate only
has to be evaluated via simulation and ni is different from site to site because of missing data, then it will be more efficient to evaluate only 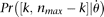 using simulation, where nmax is the maximum of all ni, and calculate
using simulation, where nmax is the maximum of all ni, and calculate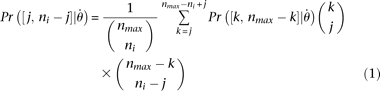 for ni ≠ nmax.
for ni ≠ nmax.
If the ancestral state of the site is unknown, then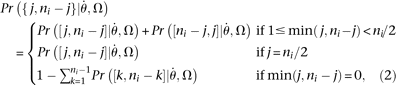 where min() means minimum.
where min() means minimum.
We designate 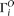 as the observed allele configuration of site i, with ancestral state either known or unknown.
as the observed allele configuration of site i, with ancestral state either known or unknown. 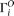 can be different from
can be different from 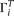 because of sequencing error. Given the error rate ɛ and
because of sequencing error. Given the error rate ɛ and 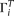 , we can calculate the expected probability
, we can calculate the expected probability 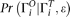 (details given below). Then
(details given below). Then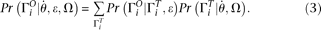 Then a composite likelihood (CL) of a range of sequence is calculated as the product of the expected probability of the observed
allele configuration of each site. That is,
Then a composite likelihood (CL) of a range of sequence is calculated as the product of the expected probability of the observed
allele configuration of each site. That is,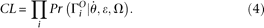
Probability of observed SNP configuration
Here we explain how to calculate 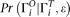 . Let us assume that on a given site the true SNP configuration is either [i, j] or {i, j}. Actually we do not need to distinguish [i, j] or {i, j} in this step because they are treated as the same. So in the following we simply use counting of the different allele types
to represent the observed configuration of SNP, in which there may be more than two types of alleles because of error. For
example, (i + 1, j − 2, 1) represents an observed SNP configuration with one type of allele with i + 1 counts, another type of allele with j − 2 counts, and a third allele with one count.
. Let us assume that on a given site the true SNP configuration is either [i, j] or {i, j}. Actually we do not need to distinguish [i, j] or {i, j} in this step because they are treated as the same. So in the following we simply use counting of the different allele types
to represent the observed configuration of SNP, in which there may be more than two types of alleles because of error. For
example, (i + 1, j − 2, 1) represents an observed SNP configuration with one type of allele with i + 1 counts, another type of allele with j − 2 counts, and a third allele with one count.
First, we assume there are, at most, K errors on any site. The choosing of K depends on L, n, and ɛ. A K that is too small may violate the assumption that there are at most K errors at any site, therefore the estimation will be biased. However, a larger K may significantly increase the computational burden. As a rule of thumb, we can choose the K as the minimum integer satisfying L × [1 − binomCDF (n, K, ɛ)] < 0.5, where binomCDF is the binomial cumulative distribution function that returns the probability of sequencing error, which occurs with a probability ɛ, occurring K or less times in n trials. However, ɛ is unknown in practice, therefore we choose a K to guarantee an applicable estimation with an upper limit of ɛ. For example, the largest n in the ANGPTL4 data equals 1832 × 2 = 3664 and L = 2604. Therefore, K = 2 will guarantee an applicable estimation with an ɛ up to 2.9 × 10−5, while K = 3 corresponds to an ɛ up to 7.5 × 10−5.
Now we show how to calculate the probabilities of different observed SNP configurations given i, j, and ɛ, assuming ΓiT is either [i, j] or {i, j}. Without loss of generality let us assume the allele with i copies is “A” and the other allele with j copies is “C.” Let us further assume that there are at most m (m ≥ 2) possible types of alleles at a site (if only point mutations are considered then m = 4), and when a sequencing error occurs at an allele, the allele has an equal probability u = 1/(m − 1) of changing to another type of allele. For the following, we show the derivation of the probabilities assuming there are at most two errors on each site (K = 2).
-
We consider three different cases, that is, there are 0, 1, or 2 sequencing errors on the site:
-
(1) There is 0 sequencing error:
Following a binomial distribution, this event has probability
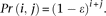
-
(2) There is 1 sequencing error:
If the error occurs at an “A” allele, the event can be further divided into two different cases. In the first case the error changes the “A” allele to a “C” allele, which produces a configuration (i − 1, j + 1) with probability
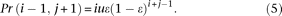
In the second case the error changes the “A” allele to a “G” or “T” allele, which produces a configuration (i − 1, j, 1) with probability
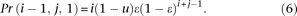
Similarly, if the error occurs on a “C” allele, the event produces the configuration (i + 1, j − 1) or (i, j − 1, 1). We can easily calculate Pr(i + 1, j − 1) and Pr(i, j − 1, 1) by switching i and j in Equations 5 and 6.
-
(3) There are 2 sequencing errors:
There are a total of 13 different possible configurations that can be produced by two errors. Their probabilities can be calculated as
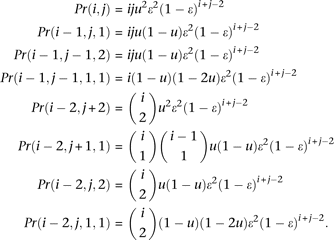
By switching i and j, we can obtain Pr(i, j − 1, 1), Pr(i + 2, j − 2), Pr(i + 1, j − 2, 1), Pr(i, j − 2, 2), and Pr(i, j − 2, 1, 1).
-
-
We combine the probabilities that produce the same configuration. Specifically,
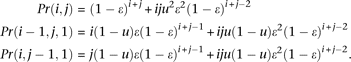
There are 32 possible configurations when there are three errors at a site. Their probabilities and combined probabilities for K = 3 and a method to compute the probabilities with K ≥ 4 can be found in the Supplemental Appendix.
Parameter estimation
Given the composite likelihood function (Equation 4), we can estimate the parameters based on the criterion of maximum composite likelihood. The simplest method is a grid search. Other algorithms are available for efficiently searching the parameter space for the optimal estimate without derivatives, such as Brent's algorithm for a one-dimensional space and Powell's algorithm or the downhill simplex algorithm for a multidimensional space (Press et al. 2007). Our limited experience shows that Brent's algorithm works reasonably well in most cases (estimating either θ or R). When estimating θ and ɛ simultaneously, both Powell's algorithm and the downhill simplex algorithm work reasonably well, while Powell's algorithm slightly outperforms the downhill simplex algorithm. On the contrary, when estimating θ and R simultaneously, the downhill simplex algorithm slightly outperforms Powell's algorithm, but it often fails to find the global maximum composite likelihood estimate. If all three parameters (θ, R, and ɛ) need to be estimated, both Powell's algorithm and the downhill simplex algorithm perform badly. In that case, grid search is a slow but reliable choice. A faster alternative is some kind of hybrid search algorithm, e.g., using Powell's algorithm to search the MCLEs of θ and ɛ on a grid of R.
Parametric bootstrap can be used to estimate an approximate confidence interval of a MCLE of a parameter. After the MCLEs
of the parameters of a given model are estimated using the original data (designated as 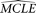 ), coalescent simulation is conducted with the
), coalescent simulation is conducted with the 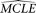 . With each replication, a sample of sequences with the same sample size and the same length as the original data are simulated.
Then the same missing data pattern on each site of the original data is superimposed onto the simulated sequence sample. Finally,
using the simulated sample, the MCLE of the given parameter (designated as
. With each replication, a sample of sequences with the same sample size and the same length as the original data are simulated.
Then the same missing data pattern on each site of the original data is superimposed onto the simulated sequence sample. Finally,
using the simulated sample, the MCLE of the given parameter (designated as 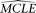 ) is estimated with all other parameters fixed to their
) is estimated with all other parameters fixed to their 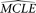 . After a large number of replications, the
. After a large number of replications, the 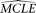 s of the given parameter form an empirical distribution from which the confidence interval of the
s of the given parameter form an empirical distribution from which the confidence interval of the 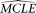 of the parameter can be approximated.
of the parameter can be approximated.
Model goodness-of-fit test and model comparison
To test the model goodness-of-fit, we first calculate the MCLE of all parameters of the model, 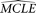 . Then a parametric bootstrap is conducted as described above. For each simulated sample, the set of MCLE(s) of the parameters
for the model,
. Then a parametric bootstrap is conducted as described above. For each simulated sample, the set of MCLE(s) of the parameters
for the model, 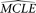 , is estimated, with a corresponding composite likelihood,
, is estimated, with a corresponding composite likelihood, 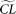 . The resulting composite likelihoods of all simulated samples (designated as
. The resulting composite likelihoods of all simulated samples (designated as 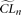 ) is considered as an empirical null distribution of the composite likelihood assuming
) is considered as an empirical null distribution of the composite likelihood assuming 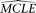 is the true model parameter. Finally, the composite likelihood of the observed sample (designated as CLo) is compared to the empirical null distribution. Given a small fraction α, if CLo is smaller than α/2 or larger than 1 − α/2 of all
is the true model parameter. Finally, the composite likelihood of the observed sample (designated as CLo) is compared to the empirical null distribution. Given a small fraction α, if CLo is smaller than α/2 or larger than 1 − α/2 of all 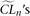 , we reject the null hypothesis of the model at the α level (two-tail test). Since recombination reduces the variance of the composite likelihood, a simulation of sequences without
recombination will make the test more conservative.
, we reject the null hypothesis of the model at the α level (two-tail test). Since recombination reduces the variance of the composite likelihood, a simulation of sequences without
recombination will make the test more conservative.
Since composite likelihood is not full likelihood, a simple likelihood ratio test cannot be directly applied. Fortunately,
parametric bootstrap can also be used for simple model comparisons. For example, suppose we want to compare two different
neutral population models with constant population size. The null model assumes ɛ = 0 and has one parameter θ. The alternative model makes no such assumption and has two parameters, θ and ɛ. To perform the comparison, we first estimate the MCLE(s) of the two models, designated as 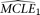 and
and 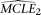 for the null and the alternative models, respectively. The corresponding CL's are designated as CL1 and CL2, respectively. Parametric bootstrap is conducted with the
for the null and the alternative models, respectively. The corresponding CL's are designated as CL1 and CL2, respectively. Parametric bootstrap is conducted with the 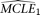 . For each simulated sample, the set of MCLE(s) of the parameters for the null model (in this case only θ),
. For each simulated sample, the set of MCLE(s) of the parameters for the null model (in this case only θ), 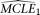 , is estimated, with a corresponding composite likelihood,
, is estimated, with a corresponding composite likelihood, 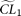 . With the same simulated sample, the set of MCLEs of the parameters for the alternative model (in this case, θ and ɛ),
. With the same simulated sample, the set of MCLEs of the parameters for the alternative model (in this case, θ and ɛ), 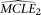 , is estimated with a corresponding composite likelihood
, is estimated with a corresponding composite likelihood 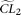 . Then the difference of the two composite likelihoods
. Then the difference of the two composite likelihoods 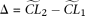 is calculated. With all replications, Δ forms an empirical null distribution with an assumption of the null model. Given
a small fraction α, if CL2 − CL1 is larger than 1 − α of the null distribution, we conclude that the alternative model is significantly better than the first model at the α level (one tail).
is calculated. With all replications, Δ forms an empirical null distribution with an assumption of the null model. Given
a small fraction α, if CL2 − CL1 is larger than 1 − α of the null distribution, we conclude that the alternative model is significantly better than the first model at the α level (one tail).
Computer simulation
Coalescent simulations (e.g., Hudson 2002) were used to validate our MCLE and compare the performance of different θ estimators. We assumed a Wright-Fisher model, neutrality, and the infinite sites model for mutation and unknown ancestral allele state. When validating the MCLE, we simulated sequences in an exponential growth population with parameter R and without recombination. When comparing the MCLE with other θ estimators, we simulated sequences with a given recombination rate ρ in a neutral population with constant size. When conducting model goodness-of-fit tests and model comparison for the ANGPTL4 gene, we simulated sequences assuming a neutral population with constant size and without recombination. Sequencing error on each site was simulated to follow a binomial distribution with parameter nɛ. Only point mutations (m = 4) were simulated. Missing data were simulated by random removal of simulated alleles according to the missing data rate.
Other θ estimators compared
As mentioned in the Introduction, there are several new θ estimators that incorporate error or are supposed to be robust to error. We selected six estimators that can be efficiently
calculated with a relatively large sample size to be compared with our MCLE of θ. We calculated the estimators assuming that the ancestral states of the alleles are unknown. All estimators assume constant
population size and neutrality. As standards of performance, two widely used θ estimators, Tajima (1983)'s estimator based on the average difference between two sequences (π) and Watterson (1975)'s estimator based on the total number of polymorphic sites (S), were also calculated with the simulated TRUE allele frequencies (i.e., no errors). Those two estimators were designated
as 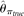 and
and 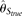 , respectively.
, respectively.
Two of the estimators we selected for comparison are modified Tajima (1983)'s estimators. They are Johnson and Slatkin (2008)'s 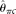 , assuming known ɛ, and Achaz (2008)'s
, assuming known ɛ, and Achaz (2008)'s 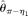 , assuming unknown ɛ. Another two estimators selected are modified Watterson (1975)'s estimators: Johnson and Slatkin (2008)'s
, assuming unknown ɛ. Another two estimators selected are modified Watterson (1975)'s estimators: Johnson and Slatkin (2008)'s 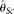 , assuming known ɛ, and Achaz (2008)'s
, assuming known ɛ, and Achaz (2008)'s 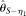 , assuming unknown ɛ. The remaining two estimators for comparison were recently proposed by Liu et al. (2009). They are the modified Fu (1994)'s BLUE estimators, assuming either known ɛ (designated as
, assuming unknown ɛ. The remaining two estimators for comparison were recently proposed by Liu et al. (2009). They are the modified Fu (1994)'s BLUE estimators, assuming either known ɛ (designated as 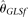 ) or unknown ɛ (
) or unknown ɛ (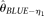 ). Because those two estimators cannot handle missing data directly, when there are alleles missing on a nucleotide site we
imputed them according to the observed allele frequency of that site. Detailed description of the calculation of the above
six estimators can be found in Liu et al. (2009).
). Because those two estimators cannot handle missing data directly, when there are alleles missing on a nucleotide site we
imputed them according to the observed allele frequency of that site. Detailed description of the calculation of the above
six estimators can be found in Liu et al. (2009).
Johnson and Slatkin (2006)'s estimator was not compared because of the requirement of a quality score for each nucleotide allele. Lynch (2008, 2009)'s method based on π was not compared because of the requirement of sequence coverage information for each individual. However, with high coverage
available, Lynch (2008, 2009)'s estimation is supposed to be close to 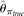 .
.
ANGPTL4 sequence data
The sequence data set of the ANGPTL4 gene was from the Dallas Heart Study (see Romeo et al. 2007, 2009 for a detailed description of the data and their supplemental tables for the SNP spectrum we analyzed in this study). The sequencing region consists of seven exons and the intron–exon boundaries of the gene, with a total length of 2604 bp. The randomly sampled individuals include 1832 African Americans, 1045 European Americans, 601 Hispanic, and 75 other ethnicities. In this study we only analyzed African American and European American data. There are a total of 79 polymorphic sites (excluding insertion/deletions) combining African Americans and European Americans (60 in African Americans alone and 44 European Americans alone). Because the missing data information is unavailable for the monomorphic sites, we used an average missing data rate of 6.24%, which is estimated from the polymorphic sites.
Acknowledgments
This research was supported by the MiCorTex study and National Institutes of Health grant 5P50GM065509. We thank Jonathan C. Cohen for kindly providing the ANGPTL4 data. We thank the three anonymous reviewers for their comments and suggestions. We thank Sara Barton for her help with polishing the language.
Footnotes
-
↵1 Corresponding author.
E-mail Xiaoming.Liu{at}uth.tmc.edu; fax (713) 500-0900.
-
[Supplemental material is available online at http://www.genome.org. Java programs for calculating MCLE of θ, R, and ɛ are freely available at http://sites.google.com/site/jpopgen/.]
-
Article published online before print. Article and publication date are at http://www.genome.org/cgi/doi/10.1101/gr.097543.109.
-
- Received June 18, 2009.
- Accepted October 8, 2009.
-
Freely available online through the Genome Research Open Access option.
- Copyright © 2010 by Cold Spring Harbor Laboratory Press