Compositional Gene Landscapes in Vertebrates
Abstract
The existence of a well conserved linear relationship between GC levels of genes' second and third codon positions (GC2, GC3) prompted us to focus on the landscape, or joint distribution, spanned by these two variables. In human, well curated coding sequences now cover at least 15%–30% of the estimated total gene set. Our analysis of the landscape defined by this gene set revealed not only the well documented linear crest, but also the presence of several peaks and valleys along that crest, a property that was also indicated in two other warm-blooded vertebrates represented by large gene databases, that is, mouse and chicken. GC2 is the sum of eight amino acid frequencies, whereas GC3 is linearly related to the GC level of the chromosomal region containing the gene. The landscapes therefore portray relations between proteins and the DNA environments of the genes that encode them.
Two-dimensional frequency distributions of the GC levels of second and third codon positions of protein-coding genes reveal compositional constraints and selection pressures: those acting on proteins on one hand, and those acting on DNA, RNA, and possibly translational accuracy on the other hand. Indeed, GC levels in third positions (GC3) are almost free of constraints at the amino acid level, whereas those in second positions (GC2) are almost completely determined by the gene product. Their joint distribution, or landscape, therefore displays relations between the DNA and the proteins that its embedded genes encode.
Among taxa that are well represented in sequence databases, genic GC2 and GC3 levels exhibit a tendency to cluster along a widely conserved, straight line in the landscape: the landscape's major axis or orthogonal regression line. The correlation to which this linearity corresponds is found in species as distant as human and Escherichia coli, and the major axis is consistently close to the line GC3 = 6 GC2 - 200%. In other words, a 1% change in GC2 corresponds roughly to a 6% change in GC3, and the two codon positions have similar GC levels around 40%. The intragenomic correlation, and the correlation between first/second and third codon positions (GC1 + 2 vs. GC3), are well conserved among vertebrates. Similar intergenomic correlations are also found, for eukaryotes or prokaryotes, when each genome is represented by its two genome-wide gene averages, that is, by the center of mass of its own intragenomic landscape (see Wada and Suyama 1985; Bernardi and Bernardi 1986; Sueoka 1988; D'Onofrio et al. 1991,1999; D'Onofrio and Bernardi 1992). The conservation of the major axis can be used to detect incorrectly predicted genes, even in previously uncharacterized species (Cruveiller et al. 2003, 2004; Jabbari et al. 2004).
The major axis runs parallel to, and very close to, a modal crest or ridge of the landscape of GC2 and GC3 levels, as can be seen in species for which a large number (>1000) of genes have been sequenced (see, e.g., Clay et al. 1996). The crest is almost linear and resembles a mountain ridge or range.
Very large numbers of nonredundant, reliable gene sequences, which are now available for several vertebrate species, allow higher levels of resolution than were previously possible.
This prompted us to analyze the detailed landscapes (two-dimensional distributions) for these species. We focused mainly on human, where a nonredundant set of 10,218 genes was available from a well curated human sequence database, and also studied the landscapes for three other vertebrates that are represented by large databases of experimentally verified protein-coding sequences, namely mouse, chicken, and Xenopus. Especially in the warm-blooded vertebrates, we observed a structure of peaks and valleys that extended along the landscapes' crests. This structure was indicated by raw 2D histograms for different bin sizes, and by standard algorithms for contour plots and 3D representations. We here present some views of these landscapes.
METHODS
Data Retrieval and Redundancy Elimination
The human sequence set used consisted of coding sequences extracted from the RefSeq database (Pruitt and Maglott 2001). All curated genes that had been confirmed, and genes that had been checked once (`provisional') were included (n = 10,218). For two other warm-blooded vertebrates (Mus musculus, Gallus gallus) and one cold-blooded vertebrate (Xenopus laevis), sequences were extracted from GenBank (release 130, April 2002) using the ACNUC retrieval system (Gouy et al. 1985). Redundant entries were removed using the Cleanup software developed by Grillo et al. (1996), yielding n = 16,383, 1389, and 1303 sequences for mouse, chicken, and Xenopus, respectively. As a robustness check, we also constructed a second human data set (n = 21,284) containing a larger proportion of predicted genes, by using the same protocol as for mouse, chicken, and Xenopus. We found a good general agreement between the results obtained from the two human data sets. Some predicted coding sequences that may be contained in our data sets should therefore not influence the general conclusions drawn here. For human, we present the results for the more reliable, smaller set of 10,218 curated coding sequences.
Descriptions and families of the genes in each peak region (families obtained by HOVERGEN, pbil.univ-lyon1.fr; Duret et al. 1994) confirmed that they were not the result of an accumulation in individual peaks of overrepresented gene families or superfamilies such as immunoglobulins, T-cell receptors, major histocompatibility complex, histones, or kinases. Furthermore, compositional dispersion (rather than accumulation) of paralogs from the same gene family appears to be the rule (∼80%) rather than the exception. For example, the GC3 levels of genes are correlated with the GC of their environments on the chromosome, yet the GC3 levels of the paralog pairs are not correlated (Jabbari et al. 2003b). Olfactory receptors (Glusman et al. 2001) present a good example of such compositional diversification of GC3 and GC.
Bivariate Analyses of Compositional Landscapes: Binning and Contouring
Compositional correlations are traditionally illustrated by 2D scatterplots (x,y plots). A regression line, an index of dispersion of the points (such as the correlation coefficient, or the standard deviation orthogonal to the regression line), and significance levels or confidence intervals can help to confirm visual impressions, but such basic information hardly shows how the points are distributed within the scatterplot. We therefore also plotted raw and smoothed 3D landscapes and contours (as implemented in the Statistica package; see, e.g., Douglas 1994 for details on the Coulthard contouring algorithm). Equal-sized bins were used along each axis, and contours were calculated with a mesh size of 150. Their number ranged between 17 and 35 bins, counting from minimal to maximal value of GC2 or GC3 (human: 21 × 21 bins, min/max = 24.6%/97.4% GC3; mouse: 35 × 35 bins, min/max = 15.6%/96.5% GC3; chicken: 21 × 17 bins, min/max = 14.1%/99.2% GC3; Xenopus: 22 × 22 bins, min/max = 20.6%/86.1% GC3).
If one uses wide bins to partition GC2 and GC3, automatic contour smoothing programs will not reveal fine-scale features: one loses resolution. If one uses narrow bins, the sample size per bin becomes low, and sampling or binning fluctuations obscure the fine-scale features. A landscape characterized by narrow as well as broad peaks may not be well captured by a single bin size. In our landscape, some peaks are apparently as narrow as 3% GC3, or even narrower along the GC2 axis. Thus, no fixed bin size may adequately capture all of the peaks. As a result, the number and precise positions of the peaks depend to some extent on the choice of bins. The sample settings used for the results shown in this report provide, in our opinion, a good tradeoff between resolution and reliability. Robustness checks (see below) suggest that the settings are close to optimal in human.
The peaks observed in human, for example, are rendered directly visible by a total of roughly 5% of the genes rising above the base level of the crest. The fraction of the genes that underlies each of the peaks is close to 20%.
Peak Locations, Comparison With Experimental Results Using Genomic DNA
Homo sapiens (Curated Data Set, n = 10,218)
The five observed peaks were located at approximately 43.4%, 52%, 60.7%, 73%, and 79.9% GC3. Via the relation GC3 = 2.92 GC - 74.3% (Zoubak et al. 1996), the GC3 values would correspond to estimated bulk DNA components (Macaya et al. 1976; Cuny et al. 1981; Bernardi et al. 1985) at 38.7%, 48.3%, 58.1%, 72.7%, and 84% GC3.
Mus musculus (GenBank-Derived Data Set, n = 16,383)
Approximate locations of the four observed peaks: 53.7%, 59.1%, 64.1%, and 67% GC3. The fewer peaks and narrower range they span, compared to human, are roughly what one would expect, in view of the erosion of the GC-poorest and GC-richest DNA in murids (see Bernardi 2000).
Gallus gallus (GenBank-Derived Data Set, n = 1389)
Approximate locations of the six observed peaks: 41.3%, 51.5%, 65%, 74.1%, 78.1%, and 86.4% GC3. Approximate locations corresponding to components of bulk DNA (Olofsson and Bernardi 1983; Bernardi et al. 1985), as calculated from the relation GC3 = 2.64 GC - 64 (Musto et al. 1999): 40%, 51.4%, 59.3%, 67.2%, 75.9%, and 87.8% GC3.
Xenopus laevis (GenBank-Derived Data Set, n = 1303)
Approximate locations of the two observed peaks: 39.9%, 45.8% GC3.
For all conversions between buoyant density ρ in CsCl and GC of genomic DNA, the relation by Schildkraut et al. (1962) was used, GC = 100% × (ρ - 1.66 g cm-3)/0.098.
Robustness Check: No Pigeonhole Artifact
For a collection of fixed-length sequences, narrow peaks can arise via a `pigeonhole' artifact if the bins unequally partition the finite number of possible values (e.g., of GC3). Some fluctuations of this kind are always present (except if all sequences happen to have exactly the same length), but they did not influence our landscapes at the settings we chose. Indeed, when we subjected a corresponding uniform distribution to the same binning procedures, we obtained a pattern that bore no relation to the gene landscapes' peaks or valleys. Kernel-based smoothing, a binless method (see below), confirmed that the peaks' presence is independent of binning or bin choices.
Robustness Check: The Peaks Persist Over a Wide Range of Bin Sizes
We gradually increased the number of bins (partitioning the same region) from 13 × 13 to 45 × 45 and counted the number of peaks in each of the contour plots for the human data. In the 33 counts obtained in this way, a plateau of relative stability extended from 20 × 20 to 33 × 33. In this range (i.e., in 14 consecutive bin sizes out of 33) the peak number was always five or six, except for one value of seven, for 25 × 25 bins; outside of this range the peak number changed more erratically between three and 12.
Kernel Smoothing and Silverman's Test for Multimodality
For the human data we also considered a cruder, but statistically simple, alternative to binning and contouring. In this variant, the height at any location is defined as the count of its neighboring points, weighted according to distance from the location following a single, radially symmetric Gaussian weighting scheme (kernel). Thus, at any location in the landscape, all points contribute to the height, but those farther away contribute less. This smoothing procedure is much simpler than binning and contouring in that it requires only one adjustable parameter, the Gaussian width. Although it is not flexible enough to yield accurate estimates of the peaks (e.g., for a Gaussian width of 1.7% it placed the peaks at 43.8%, 53.0%, 61.6%, 71.4%, and 76.9% GC3), its simplicity gives a reliable first idea of the multimodality's significance.
Image processing software that uses kernel smoothing or filtering, such as ImageJ (Wayne Rasband, NIH, http://rsb.info.nih.gov/ij), yields landscapes similar to that in Figure 1C, for example when a 1024 × 1024 pixel screen covers the raw scatterplot of Figure 1A and the dot image is then smoothed by convolving it with a square, discrete Gaussian kernel of 61 × 61 pixels (G. Joss, pers. comm.). Our operations are similar, but require fewer adjustable parameters and no `pixelization': we consider effectively a square scatterplot (0%–100% GC2/GC3) in order to achieve radial symmetry (isotropy), and all exact distances between the original data points are taken into account. Although such kernel smoothing is not fully equivalent to binning and contouring operations, quantitative results are available in this context, notably significance tests for multimodality and an algorithm for constructing a plausible null landscape (Silverman 1981, 1986; Minnotte and Scott 1993).
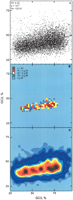
2D representations of the landscape of GC levels in second and third positions (GC2, GC3) of 10,218 curated human genes: (A) scatterplot, (B) bivariate histogram, and (C) smoothed contour plot. Bins were chosen to partition the range of GC2 and GC3 values found (minimum to maximum values) into 37 × 37 (B) or 21 × 21 (C) equal bins. Height (i.e., frequency) ranges are indicated by colors.
Gaussian kernel smoothing can be used to generate a mode tree for a data set: the width of the Gaussian kernel is plotted against the mode positions, which bifurcate to form a tree (Minnotte and Scott 1993). The idea is similar to our bin plateau analysis (see above), except that transient modes are absent. Indeed, as one gradually decreases the Gaussian width, the number of modes will increase monotonically (Silverman 1981). If a set of modes remains stable over a large range of Gaussian widths, the modes are likely to be real, robust features of the data, rather than just what one might expect from chance differences among randomly chosen samples. For our human landscape, radially symmetric Gaussian kernels with a `width parameter' (standard deviation along either axis, GC2 or GC3) between 5.6% and 2.9% all led to two modes (a stability that corresponds to the presence of the landscape's two broad hills), whereas widths from 2.8% down to 2.0% all led to four modes. This relatively abrupt jump from two modes (the basic background feature) to four modes (i.e., all but the GC-richest peak) is striking, as one would expect any reasonable null model to pass through a longer three-mode phase. Indeed, Silverman's (1981, 1986) smoothed bootstrap test for multimodality, when applied to test the jump from 2- to ≥4-modality, gave an estimate of p ≤ 0.01 supporting the presence of four or more modes. More precisely, in 50 smoothed bootstrap samples constructed from the critically smoothed landscape (width parameter 2.9%), only one sample appeared to lead to a (≥)4-mode landscape, but it turned out that two of its four modes essentially coincided (they were separated by only 0.4% GC3 and 0.1% GC2). Thus, 50 attempts to create four modes as chance artifacts, starting from the two broad hills, all failed. This smoothed bootstrap analysis supports the robust presence of ≥ four modes.
Comments on the Significance of Multimodality
Judging from the overall concordance between the peaks of different, well studied genomes and from bootstrapping, the peaks and valleys we observe seem unlikely to be just a result of some bias in the available gene samples.
If the peaks persist as the available sample of genes approaches all of the genes in a genome, the possibility of a sampling artifact will actually vanish, because we will then face, if anything, a descriptive problem, not a sampling problem: there will be no obvious larger set or population from which the genes were drawn. If, instead, we are interested in the human genome merely as a sample from a larger population of extant or possible vertebrate genomes, then this larger population would need to be precisely defined (not an easy task), and the danger of unwittingly considering an ill-posed (insufficiently specified) or biologically irrelevant problem should be kept in mind. Furthermore, we have not found quantitative results that would allow us to estimate `expected' changes of peak number in a generic or rugged landscape as it widens or narrows during evolution (see however Reidys and Stadler 2002 for research that may lead in this direction).
In our view, in-depth tracking of the landscapes created by selected gene families or gene subsets in human, mouse, chicken, and Xenopus should provide a more efficient way to understand the peaks and their biological significance than pursuing heuristic statistical calculations using toy null models. Furthermore, many biological questions (e.g., addressing the transcriptome or proteome) will effectively address weighted gene sets. Differently weighted sets would yield different landscapes (e.g., in the figures shown here, a coding region is represented only once, whereas rates of transcription and translation can vary considerably among genes).
RESULTS
Large-Scale Features of the Gene Landscapes
Figure 1 shows three `aerial' views of the (GC2, GC3) landscape of 10,218 well curated human coding sequences from RefSeq: a scatterplot (Fig. 1A), a 2D histogram (Fig. 1B; 37 × 37 bins), and a smooth contour plot of the same region, as obtained by interpolation (Fig. 1C; 21 × 21 bins). Where points are dense in the scatterplot, or where there are many genes per bin, the altitude of the GC2/GC3 landscape is high. It is difficult to see the structure by eye from the raw scatterplot, but the histogram and especially the contour representation reveal the high, narrow, nearly linear crest of the landscape, with peaks and valleys situated along it or very close to it. We have called such contour plots or 3D representations `Sorrento plots', after the 2002 symposium in which they were first presented and served as the logo.
The rise to the crest region is steep: few bins contain intermediate gene numbers between the high frequencies in the narrow crest region and the low frequencies in the surrounding plain. In the contour plot, five modes can be seen along the crest.
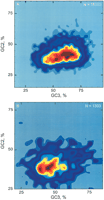
Similar landscapes, with analogous peaks but at different locations, were found for mouse (Fig. 2A), chicken (see Methods) and cow (not discussed here because its sequence set is small). The less extended crest of the mouse genome corresponds to its narrower nucleotide and dinucleotide distributions, compared to other warm-blooded vertebrates (reviewed in Bernardi 2000). The cold-blooded vertebrate Xenopus (Fig. 2B) differs from the warm-blooded vertebrates in having only a short crest with two peaks.
Frequency distributions of GC2 and GC3 values of mouse (A; 16,383 sequences) and Xenopus genes (B; 1303 sequences), represented as smoothed contour plots defining 3D compositional landscapes.
Details of the Crest
The multiple peaks in human are superimposed on a broad background feature of the crest, which is also present in cow and chicken: two smooth, broad hills of approximately the same size, separated by a wide pass or saddle (around 56% GC3 in human). The fine-scale features of the crest involve the number, positions, sizes, and shapes of the peaks along the crest, which rise above the two broad hills.
The smoothed plots presented in Figures 1 (panel C) and 2 constitute one characterization of each landscape. Because it is not the only possible one, we checked its relative robustness in the case of human, for example by gradually increasing the number of bins used to obtain the landscape. In 14 consecutive bin sizes out of 33, the peak number was five or six, with one transient exception (seven). According to current understanding, such a clear plateau indicates that the peaks are real, robust features of the data. This and other robustness checks, via kernel-based smoothing (a binless method) and bootstrapping are described in the Methods section.
The Gene Landscapes Appear to Correspond to Protein Landscapes
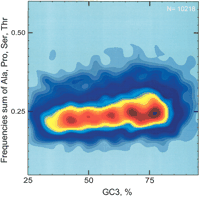
We tried to partially reconstruct or `reverse engineer' the human landscape, that is, the altitudes along the landscape's crest, using combinations from the eight amino acids having G or C in their second position. Figure 3 shows an example of a contour plot in which GC2 has been replaced by the frequency of the four residues having C in second position: Ala, Pro, Ser, and Thr. The general peak structure of this 4-amino acid landscape resembles that of the corresponding landscape for GC3 and GC2 (Fig. 1C), although there are still differences. Further studies along such lines may help to understand the factors contributing to the peaks, and which base compositions of DNA (represented by GC3) and/or amino acid compositions (represented by GC2) are preferentially encountered in vertebrate genomes.
Smoothed contour plot showing a variant of the landscape of 10,218 human genes: the vertical axis is the summed frequencies of alanine, proline, serine, and threonine instead of GC2; the horizontal axis is GC3. The four amino acids used to recreate this landscape are frequent, and all have cytosine in second position in four of their codons.
DISCUSSION
The Compositional Landscape of Available Genes Should Be Representative of the Genome
The 10,218 well curated human sequences shown in Figure 1 cover at least 15%–30% of all human genes as they are commonly defined (Fields et al. 1994; Venter et al. 2001). Unless there turn out to be major, unsuspected biases in identifying human genes, it seems reasonable to expect a similar landscape for all of the genes, including those that have not yet been reliably identified. Furthermore, the available set of bona fide genic sequences, that is, those that are experimentally verified or risk-free, is unlikely to grow much in the next few years. The human landscape presented here could therefore be as reliable as any that will be obtained from larger gene sets in the near future.
The Gene Landscapes Apparently Correspond to Experimentally Determined DNA Landscapes
The discovery of isochores was accompanied by the identification, and physical isolation, of a small number of DNA components of increasing GC level in several vertebrate species (Macaya et al. 1976; Cuny et al. 1981; Olofsson and Bernardi 1983; Bernardi et al. 1985). The isochores from which the DNA derived were correspondingly allocated, in each species, to a small number of isochore families: five in human, four in mouse, six in chicken, and two in Xenopus. Isochore families and their DNA components have served as useful concepts for almost three decades, and corresponding classifications are now routinely used for practical purposes, for example, in compositional mapping of sequenced chromosomes (Pavlícek et al. 2002; Ross 2003) and in gene-finding programs (Salamov and Solovyev 2000).
The number of peaks found in the human (five, or possibly six), mouse (four), chicken (six), and Xenopus landscapes (two) correspond to those that one might expect from the major components of bulk DNA. The latter were determined experimentally (Macaya et al. 1976; Cortadas et al. 1977; Cuny et al. 1981) by silver- and BAMD-assisted density gradient ultracentrifugation of DNA fragments ranging up to 50–100 kb. BAMD is an acronym for 3,6-bis (acetomercurimethyl) 1–4 dioxane, a mercury-based, sequence-specific DNA ligand that binds preferentially to AT-rich DNA, and that may also exhibit a preference for certain AT-rich oligonucleotides. The expected positions of the peaks were calculated from the positions of the experimental DNA components (see Methods). Such calculations use a well established linear relation between buoyant density and GC (Schildkraut et al. 1962). They also use the linear relation between GC3 levels of genes and the GC level of the chromosomal regions (∼50–100 kb) in which the genes are found (R ∼0.6–0.8). An analogous relation holds between genic GC1+2 levels and the chromosomal regions' GC (R ∼ 0.5; Jabbari et al. 2003a). The positions and extents of the two wide hills that define the main crest of the landscape correspond very well to the `L' (low GC) and `H' (high GC) DNA components in these species (cf. Bernardi 2001), and the individual peaks in the GC2, GC3 landscape show, in general, a good overall concordance with the experimental peaks deduced from bulk DNA. In particular, the expected and observed values for human almost coincide in the third (∼60% GC3) and fourth (∼73% GC3) peaks, and although the other maxima are slightly closer to each other than expected from the calculation (the GC-poorest peak is around 43%–44% GC3 instead of ∼39%), the corresponding difference at the bulk DNA level (40% GC vs. 39%) remains within experimental error margins.
An intriguing question is why the components of DNA (which were revealed by ligand-assisted fractionation experiments on DNA fragments) appear to be so much more clearly visible in gene sequences than in bulk genomic sequences, which do not explicitly show such pronounced multiple peaks of single-copy DNA in their GC histograms. Analyses of combinations of oligonucleotides (see above) may help in answering this question, although the computational complexity of exhaustively screening a draft sequence for such combinations is likely to be high, and analyses of this kind would lead outside the scope of the present study.
Evolutionary and Functional Implications of the Gene Landscapes
The two main hills of the landscapes, apparently conserved in a wide range of warm-blooded vertebrates and visible down to small subregions of protein-coding genes, can be regarded as representing essentially two classes of genes, with modest overlap. Two gene classes, observed on the basis of GC3 or GC distributions of exons and introns, were studied earlier in the contexts of plants and human (Carels and Bernardi 2000; Bernardi 2001 and references therein). The taxonomic range within which genomes exhibit two gene classes may, therefore, span a large part of the higher eukaryotes. The hills or classes correspond, in warm-blooded vertebrates, to preferential locations of the genes in isochores of low (L) or high (H) GC—or, rephrased: genes tend to avoid the intermediate GC saddle between the hills on the landscape. The important and well documented properties and functional correlates that exist for GC-poor and GC-rich isochores in mammals and birds, and for the GC-poor and GC-rich coding DNA located in them, have been reviewed in detail elsewhere (Bernardi 2000; Saccone et al. 2002), and include, for GC-rich isochores, their much higher gene densities, the shorter introns of their genes, and the different localization pattern of their DNA in the interphase nucleus, which extends away from the matrix in long loops.
We offer here a graphical representation of gene sets that involves, directly and visibly, an additional dimension, which can be interpreted as the amino acid composition of the encoded proteins. Although it may not come as a surprise that the protein products tend to group into two classes (because the amino acid compositions are linked to the GC of the encoding DNA), albeit with some overlap, this grouping can be seen with exceptional clarity in the landscapes. Phrased more pragmatically, a protein's most probable class can sometimes be guessed already to some extent from its amino acid composition (via GC2), but it can often be predicted more easily and with higher resolution if GC3 information, that is, its gene sequence, is available. This being said, it must however be kept in mind that some proteins may have `copies' in both classes, for example, when the GC3 level has diverged substantially between two paralogs, yet the amino acid sequence is largely conserved.
The landscapes show that when both DNA (GC3) and protein (GC2) dimensions are available one can, apparently, obtain enough resolving power to observe not only the two broad hills in warm-blooded vertebrates, but also multiple peaks rising up from each of them, that is, subclasses of the two classes of genes. The overall concordance among the peaks of different vertebrates, the correspondence with results of fractionation experiments on DNA using silver- or mercury-based ligands, and the fact that important functional correlates are already well documented for the broad hills, all suggest an evolutionary and/or functional significance also for the narrower peaks. To elucidate the functional properties of the peaks' genes and proteins, one general route that appears promising is to now select several gene families that have been extensively characterized in their functional roles and regulation, and then focus on the compositional properties and chromosomal environments of their paralogs and orthologs in different taxa.
Conclusion
Our analysis consistently yielded several marked peaks in the bivariate GC level histograms of vertebrate genes' codon positions. These peaks correspond to the experimentally observed components of bulk DNA. Thus, the human gene landscape appears to be the superposition of five underlying, narrower distributions of GC3 and GC2, presumably corresponding to particular types of genes, genic/protein regions, and/or chromosomal environments. To pursue their description further, a good strategy may be an exhaustive, in-depth tracking of gene families in different species, that is, of the genes in the peaks, their paralogs, and their orthologs in the corresponding peaks of other vertebrate species.
Acknowledgments
We thank David H. Douglas (Gävle, Sweden) for details on currently used contour programs, and two anonymous referees for valuable comments that allowed us to improve the manuscript. We especially thank Greg Joss (Macquarie University, Australia) for his image analysis of the human scatterplot, for suggesting kernel-based approaches, and for helpful discussions. We also thank Romy Sole for her assistance in preparing the figures.
The publication costs of this article were defrayed in part by payment of page charges. This article must therefore be hereby marked “advertisement” in accordance with 18 USC section 1734 solely to indicate this fact.
Footnotes
-
Article and publication are at http://www.genome.org/cgi/doi/10.1101/gr.2246704.
-
↵3 Present address: Atelier de Génomique Comparative, Genoscope, Centre National de Séquençage, CP 5706, 91057 Evry Cedex, France.
-
↵4 ENS/CNRS FRE 2433, Organismes Photosynthétiques et Environment, Département de Biologie, Ecole Normale Supérieure, 75230 Paris Cedex 05, France.
-
↵5 Corresponding author. E-MAIL bernardi{at}szn.it; FAX 39 081-764-1355.
-
- Accepted February 26, 2004.
- Received December 11, 2003.
- Cold Spring Harbor Laboratory Press