Interactive Exploration of Microarray Gene Expression Patterns in a Reduced Dimensional Space
Abstract
The very high dimensional space of gene expression measurements obtained by DNA microarrays impedes the detection of underlying patterns in gene expression data and the identification of discriminatory genes. In this paper we show the use of projection methods such as principal components analysis (PCA) to obtain a direct link between patterns in the genes and patterns in samples. This feature is useful in the initial interactive pattern exploration of gene expression data and data-driven learning of the nature and types of samples. Using oligonucleotide microarray measurements of 40 samples from different normal human tissues, we show that distinct patterns are obtained when the genes are projected on a two-dimensional plane spanned by the loadings of the two major principal components. These patterns define the particular genes associated with a sample class (i.e., tissue). When used separately from the other genes, these class-specific (i.e., tissue-specific) genes in turn define distinct tissue patterns in the projection space spanned by the scores of the two major principal components. In this study, PCA projection facilitated discriminatory gene selection for different tissues and identified tissue-specific gene expression signatures for liver, skeletal muscle, and brain samples. Furthermore, it allowed the classification of nine new samples belonging to these three types using the linear combination of the expression levels of the tissue-specific genes determined from the first set of samples. The application of the technique to other published data sets is also discussed.
[Online supplementary material available atwww.genome.org.]
DNA microarrays are presently used extensively for genome-wide gene expression measurements. Large-scale transcriptional studies have catalyzed new discoveries and are generating important new insights into the behavior and functioning of cells (Spellman et al. 1998; Perou et al. 1999; Alizadeh et al. 2000; Hughes et al. 2000). Class discovery tools have played a key role in this process. Class discovery methods are exploratory analysis tools used to organize, learn from, and discover patterns in the data. Of the various multivariable techniques available, clustering of genes and samples has been the most common tool used for the analysis of microarray data (Eisen et al. 1998; Spellman et al. 1998; Perou et al. 1999; Tamayo et al. 1999; Alizadeh et al. 2000; Hughes et al. 2000). Before proceeding to cluster, it is often advantageous to visualize the data to develop an understanding of underlying structure. This initial exploration is useful in revealing patterns and providing clues for further analysis.
Principal component analysis (PCA) is a linear projection method that defines a new dimensional space that captures the maximum information present in the initial data set by minimizing the error between the original data set and the reduced dimensional data set. Each principal direction of the projection space, or principal component (PC), is defined such as to be orthonormal to all others and to maximize the information in the data that has not already been captured by the previous (lower) dimensions. In this way, as the number of PCs progressively increases, a larger fraction of the total information content is accounted for. PCA is a linear projection in the sense that the variables of the projection space (PCs) are linear combinations of the original variables (i.e., the gene expressions). The coefficients of this linear combination are called loadings and the actual values of the projection of the samples are called scores. PCA is obtained from a singular value decomposition of the data, and the loadings are the entries in the singular vector and are associated with genes. The scores are contained in the matrix obtained from a multiplication of the original data matrix with the singular vectors and are associated with samples. Standard formulas are available for the determination of the projection variables, loadings, and captured variability (Dillon and Goldstein 1984), and many applications of PCA have been reported in a variety of different contexts (Kamimura 1997; Rannar et al. 1998;Alter et al. 2000; Holter et al. 2000).
In this paper we use PCA to analyze a set of microarray measurements on normal human tissues. Initial projection onto a lower dimensional space allows for better visualization of the entire data set. The loadings are subsequently used to select relevant genes while considering the impact of the removal of irrelevant genes on the patterns observed in the projection of the samples. This is an alternate approach to the problem of selection of relevant genes in the analysis of microarray data (Golub et al. 1999) and may be used to obtain a subset of genes that best describe the data. The observation of clear gene-expression patterns after the removal of irrelevant genes points to a high degree of structure in the measurements. Exploration of these gene expression patterns further revealed tissue-specific gene expression signatures. These signatures were further supported by the analysis of additional tissue samples that had not been used in the initial pattern-discovery step.
RESULTS
The data set used in this study comprised expression measurements of 7070 genes made in 40 normal human tissue samples using Affymetrix GeneChips. The data were generated at the Brigham and Women's Hospital (BWH) in Boston (Hsiao et al. 2001). Samples from several human tissues were analyzed, here we use the samples from brain, kidney, liver, lung, esophagus, skeletal muscle, breast, stomach, colon, blood, spleen, prostate, testes, vulva, proliferative endometrium, myometrium, placenta, cervix, and ovary.
PCA Loadings Can Be Used to Filter Irrelevant Genes
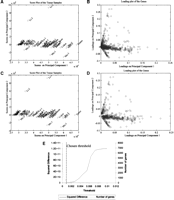
The data from the 40 human tissues were first projected using PCA, which may be used with or without scaling (mean-centering, or autoscaling, among others). Here, we did not scale the data, and comparisons with mean-centered results are provided in Discussion. The first and second PCs account for ∼70% of the information present in the entire data set. The score plot of the 40 samples using the entire gene expression set is shown in Figure 1A. Plotted in Figure 1B are the loadings for each of the 7070 genes for the first and second PCs. The loading plot reveals a large number of genes clustered around the origin, implying that they only marginally impact the projection onto the first and second PC. Because the relative magnitude of the loading is a measure of the importance of the corresponding gene in defining the PC, a small magnitude implies that the corresponding gene expression does not materially impact that particular PC. On this basis, a filter that eliminates genes with loadings below a threshold in all of the first five PCs was implemented. The decisions that went into the choice of the threshold are shown in Figure 1E. The threshold was varied over a large range, and at each threshold value a record was maintained of the number of genes retained for analysis and the distortions in the score plot due to the elimination of genes. As the threshold value was gradually increased, the samples were re-projected using the subset of genes passing the filter. The distortion from the original score plot was measured in terms of the squared difference, defined as the sum of the squares of the difference between the 40 original score values and the 40 score values produced with the filtered gene set (this is defined mathematically in Methods). In essence, this squared difference measures the error between the original projections and the new sample projections (or the distortion of the original pattern) as more and more genes are removed. When the threshold value exceeded 0.001, a large fraction of the genes were filtered out, precipitating large distortions in the patterns on the score plot. This criterion eliminated all but 425 genes with loadings in at least one of the first five PCs that exceeded the threshold value. A projection of the samples using only these 425 genes reveals an almost identical pattern on the score plot with the one obtained when all 7070 genes were used (Fig.1C). This suggests that the dramatic reduction from the initial 7070 genes to the 425 finally retained resulted in a minimal information loss relevant to the description of the samples in the reduced space. Thus, a PCA framework may be used to evaluate the effect of gene removal on expression patterns observed in the reduced dimensional space.
Gene selection based on the loadings on the principal components. Graphs A and B show the score plot of the samples and the loading plot of the genes, respectively, before any filtering is implemented. Graphs C and D show the score and loading plots after the filtering. Graph E displays quantitatively the decisions that went into the choice of the filtering threshold. It displays the distortion in the observed patterns, as measured through the squared difference, and the number of genes retained for analysis as the threshold is varied. The chosen filter threshold was 0.001. Filtering reduces the number of genes from 7070 to 425. At the same time, the score plot of the samples remains largely unchanged and displays the same initial patterns, signifying a minimal loss of information. The loading plot displays strong linear structures of genes. (For more details about the samples used, see Supplementary Material online at http://www.genome.org.)
Identification of Tissue-Specific Gene Expression Patterns: Correspondence between Score and Loading Plots
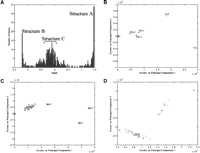
Three linear structures can be identified in the loading plot of the 425 genes selected by the above analysis, each structure comprising a set of genes arranged along a particular angle in Figure 1D. These linear structures suggest a certain degree of organization in gene expression reflected in the linear relationships between the loadings of the first and second PCs of the genes clustered in these structures. An obvious question is whether there is any correlation among the genes that define these structures. Figure 2shows the results of a systematic exploration of the patterns depicted in Figure 1D. Plotted in Figure 2A are the angles defined by theX-axis and the points representing the loadings of the first two PCs for the 425 consequential genes identified above. This histogram defines three clusters each corresponding to the three structures identified in Figure 1D. The first, termed structure A, comprises genes with angles between 1.452–1.469 radians. The second, structure B, is centered around the second peak, with angles between −1.222 and −1.205 radians, and the third is a set of genes between −0.328 and 0.054 radians, called structure C. The list of genes so selected was further refined to prevent the inclusion of genes that may have the same angle but are far removed from the structures in Figure1D by clustering the genes on the basis of their distance from the origin (the clustering results are discussed and provided in the Supplementary Materials available online at www.genome.org). The final list of selected genes is provided in Table1.
Identification of tissue-specific genes and validation using new samples. (A) Histogram of the angles between theX-axis and the points defined by the two principal loadings of each gene shown in Fig. 1D. Three main features, corresponding to the linear structures shown in Fig. 1D can be discerned and are labeled as A, B, and C. (B) PCA projection of all samples using the genes in structure A. The samples in the initial data set are represented by red circles and the new samples by blue asterisks. The two liver samples in the initial data set (Li-1 and Li-2) and the new liver samples (NLi-1, NLi-2, and NLi-3) are separated from the other samples, all of which cluster at the origin. (C) Projection of all samples using the genes in structure B. The muscle samples in the initial data set (Mu-1, Mu-2, and Mu-3) are separated from the other samples along PC1. All the other tissue samples cluster at the origin. The new muscle samples are also separated when projected using these genes (NMu-1, NMu-2, and NMu-3). (D) Projection of all samples using the genes in structure C. The six brain samples in the initial data set and the three new brain samples are separated from the other samples.
List of Genes Identified by Angle Selection
Although the identity of some genes in the above groups are suggestive of the type of tissue they represent (e.g., the genes in structure A contain an excess of genes related to the liver, such as albumins and apolipoproteins), the nature of each gene group is revealed when score plots are constructed using only the genes that are specific to the structures of Figure 1D or 2A. Thus, using only the 24 genes of structure A to project all the samples yields a score plot (Fig. 2B) that dramatically separates the two liver samples in the data set from all the remaining tissue samples. Similarly, projecting the expression data of the 19 genes in structure B separates the three skeletal muscle tissue samples from the remaining tissues along the first PC (Fig. 2C) and, finally, projection of the samples using the 86 genes of structure C separates all six brain samples from the remaining tissues (Fig. 2D).
Inspection of the genes in structure C revealed two broad classes of genes. One class of genes with low expression levels was largely related to ribosomal proteins and function; the other class of genes, with larger and more variable expression, are primarily brain-tissue-related genes. The loadings of these genes on the second PC support this observation, so that genes with high expression levels in the brain samples also had a high loading magnitude on the second PC, as shown in Table 1. This is also true of the genes in the other structures. This fact may be used for class discovery and data-driven learning and is a result of the observed correspondence between the score plot and the loading plot. Given the observed separation of the six brain samples on the second PC in Figure 2D, a learning approach for samples with unidentified characteristics would have consisted of the following steps: Select a set of genes with high loadings on the dominant PC, examine their function, and generate hypotheses as to the nature of the samples. This is a class-discovery approach, in contrast to a classification methodology, which relies on a priori labeling of the samples (Golub et al. 1999; Brown et al. 2000). Here, the methodology allows one to probe the nature of the sample, and simultaneously identify the genes that contribute to the differentiation of the sample(s) from the others.
The genes that were not part of these structures were also analyzed by projecting the samples using these genes; however, no clustering of samples or any noteworthy separation was observed.
Validation of Gene Expression Patterns Using New Samples
Additional samples (three each) from liver, muscle, and brain were collected in a subsequent experiment, profiled transcriptionally, and analyzed by applying the above projection methods. Figure 2B shows the projections of the gene expression data of the new liver samples using the loadings obtained from the projection of the genes in structure A (this discriminated the two liver samples from the remaining tissues in the initial data set). All three liver samples are clearly separated along the first PC from the nonliver tissues in the initial data set, underscoring the tissue-specific nature of these genes and hinting at the construction of a liver axis along the first PC. The genes distinguishing liver from nonliver tissues, include albumin and those associated with the coagulation pathway (e.g., factor IX, antithrombin III, and heparin cofactor), complement pathway (e.g., C8), lipid process (e.g., apolipoproteins), bile metabolism (e.g., fatty acid binding protein 1), xenobiotic metabolism (e.g., cytochrome P450), and iron homeostasis (e.g., hemopexin), a result which is to be expected based on the known biology of the liver. An examination of the 24 genes in this structure revealed that 33% of all gene pairs had correlation coefficients >0.88 for these five liver samples. This value of the coefficient is significant at the 95% confidence level. Thus, a subset of these genes are expressed proportionately to each other in the liver tissue. For instance, it is known that apolipoprot H binds to negatively charged heparin and the heparin cofactor and antithrombin III are serine proteases that inhibit the coagulation pathway (McNally et al. 1994; Vander et al. 1994).
The loadings of the 19 genes in structure B were similarly used to project the three new skeletal muscle samples; the results are shown in Figure 2C. Similar to the liver samples, the first PC clearly separates the new skeletal muscle samples and acts like a muscle axis. The genes include those associated with the cytoskeleton (e.g., actin, α1, actinin α3, and nebulin), contraction (e.g., tropomyosin, troponin, myosin), glucose metabolism (e.g., enolase 3β), CO2 metabolism (e.g., carbonic anhydrase III), and energy transduction (e.g., creatine kinase). Particularly, actinin α3 is known to have expression limited to skeletal muscle (North et al. 1999), and carbonic anhydrase III is strictly present at high levels in skeletal muscle and much lower levels in cardiac and smooth muscle (Lloyd et al.. 1986). About 74% of all gene pairs, after discounting ones with the same genes, had a correlation coefficient >0.811, the 95% confidence level with the given number of samples. This rather striking degree of linear correlation implies that these genes are expressed proportionately in skeletal muscle samples and may be coordinately regulated. For example, whereas both actin and myosin provide force for muscle contraction, troponin, a regulatory protein, prevents actin and myosin interaction in resting muscle tissue. And, tropomyosin, an actin filament-binding protein is required for the interaction of actin and troponin. It is also known that titin maintains resting tension in skeletal muscle (Vander et al. 1994).
Finally, the 86 genes in structure C were used to project the new brain samples, and as Figure 2D shows, the new brain samples are clearly separated from the other nonbrain samples and fall in the same region as the brain samples of the initial set. The genes include those associated with myelin structure (e.g., myelin basic protein), astrocytic differentiation (e.g., glial fibrillary acidic protein), synaptic reorganization (e.g., calmodulin, neurogranin, and GAP-43), and neurotransmission (e.g., glutamate receptor). Of note, many genes with no known functions are also reported here to be specific for the brain samples.
The use of projection methods to analyze the effect of these genes on the samples also led to the automatic construction of a reduced-dimension classifier space for the liver, muscle, and brain tissues. As shown here, new samples may be projected onto this space and the score value used to classify the tissue sample.
Application to Other Data Sets
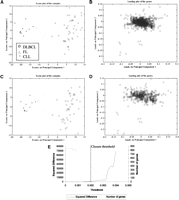
Figure 3 shows the result of the application of the current methodology to the gene expression data on lymphoid malignancies (Alizadeh et al. 2000). Expression phenotype of 62 samples of diffuse large B-cell lymphoma (DLBCL), follicular lymphoma (FL), and chronic lymphotic leukemia (CLL) were measured on 17,856 cDNA clones. A simple projection reveals the presence of two clusters and one intervening group of samples. Querying the nature of these samples reveals an almost perfect segmentation of the samples in a PC space that comprises a mere 35% of the information in the data. Implementing the thresholding procedure allows for the identification of 401 consequential genes, which maintain the patterns in the data with minimal distortion. No outstanding structures suggest themselves in the loading plot. The observation of linear structures is a unique characteristic of each data set and will not necessarily occur in all cases. In this particular case, just the thresholding procedure is sufficient to allow for segmentation of the samples and identification of consequential genes.
Projection of the lymphoma samples using the principal component analysis. The projection already reveals a fairly clear separation of the three classes in the data. The thresholding procedure allows for the identification of 401 genes from ∼850 cDNA clones, which are sufficient to describe the patterns observed. (A, B) The score and the loading plot prior to thresholding. (C,D) The score and loading plot post-thresholding. (E) The effect of thresholding on the number of genes retained and the squared difference. The chosen threshold, 0.002, is the point beyond which the squared difference explodes.
DISCUSSION
We have shown the utility of PCA as an initial step in the analysis of microarray data to extract and examine gene expression patterns. Previous work has applied a similar approach (singular value decomposition) to construct linear combinations of gene expressions (called characteristic modes, or eigengenes) from microarray measurements of time-series samples (Alter et al. 2000; Holter et al. 2000). Here, we extend the application of PCA to the analysis of nontime series data and the data-driven learning and sample classification problem. The reason for the broad applicability of the PCA lies in its strong, yet flexible, mathematical structure and the correspondence between the score plot and the loading plot. This latter feature is exploited in the interactive methodology presented for the elimination of redundant variables or genes. This method is general and may be applied to any data set.
Our methodology facilitated the identification of strong underlying structures in the data. The identification of such structures is uniquely dependent on the data and is not generally guaranteed. For example, the expression data on leukemia samples (Golub et al. 1999) was similarly analyzed; however, no evident patterns presented themselves, although diffuse structures containing some discriminatory information could be observed at higher, less informative PCs (data not shown). This may be due to the fact that the PCA attempts to maximize the variation that it captures in the data. In cases where the discriminatory information is not the most important type of variation (perhaps due to the presence of a large number of nondiscriminatory genes), the above analysis will not yield discriminatory patterns between two classes of tissues/sample. When discriminatory genes are preselected by applying a t-test on preclassified samples and used for projection, clear separations are obtained between acute myeloid leukemia (AML) and acute lymphoid leukemia (ALL) classes.
Several genes in the tissue-specific signatures identified here are justifiable with respect to known biology regarding the particular tissue. In the case of the liver and muscle samples, coordinate expression of some of these genes may also be biologically explained. Elucidation of the function and role of the other genes observed in these tissue-specific signatures must await further experiments.
In the current study, the data was not mean-centered. Mean-centering is geometrically equivalent to shifting the origin of the PCA coordinate system to the centroid of the data, a procedure which may or may not yield different results. For the purposes of comparison, the data was mean-centered and then analyzed as described above. The structures for the liver and muscle samples were identified in the first and second PC, whereas the identification of the brain structure required the inclusion of the third PC. The list of genes identified overlapped strongly with the one presented here. This raises our confidence in the significance of the genes identified but also underscores the fact that different processing methods will give rise to a slightly different list of genes; it may be best to adopt several processing methods and choose a common subset of genes.
Projection methods shift the focus of analysis from individual genes to the combined quantitative effect of several consequential genes. Here, due to the strong structures observed in the data, such a combination led to the construction of reduced dimension classifiers for the liver, muscle, and brain tissues. If the sole objective of the analysis is to yield a classifier, then other projection methods, such as Fisher discriminant analysis (Stephanopoulos et al. 2002), are more appropriate and rigorous. If the objective is data exploration, the PCA is better applied, because few a priori assumptions, such as sample class type, are made. Overall, due to their data reduction properties and their flexibility in dealing with large data sets, projection methods are an important class of tools for the analysis of microarray data.
METHODS
Data Treatment
Each array from the BWH data was scaled to a target intensity of 100. All negative expression values were reduced to zero for the purpose of analysis. For treatment of the lymphoma data, see Alizadeh et al. (2000). In the lymphoma data set, genes that had missing values for the 62 experiments were removed from the analysis. This gave an initial starting number of 854 cDNA clones.
Principal Components Analysis
Singular value decomposition is used to calculate the principal components of a data matrix (Dillon and Goldstein 1984). Any data matrix X with S samples (tissues) on the rows andV variables (genes) on the columns may be decomposed as follows: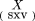 where T is a diagonal matrix with values that have the singular values of matrix X. The singular values of Xare the square roots of the nonzero eigenvalues of square matrixX′X, as well as XX′ (X′ being the transpose of X). The columns of U andL contain the eigenvectors of XX′ andX′X, respectively. R, the maximum number of independent dimensions, is determined by the rank of the matrixX.
where T is a diagonal matrix with values that have the singular values of matrix X. The singular values of Xare the square roots of the nonzero eigenvalues of square matrixX′X, as well as XX′ (X′ being the transpose of X). The columns of U andL contain the eigenvectors of XX′ andX′X, respectively. R, the maximum number of independent dimensions, is determined by the rank of the matrixX.
The loadings of the genes, or their coefficients in the linear combination that forms the principal component, is given by
the column vectors of matrix L. The magnitude of a gene loading is a measure of its importance in defining the principal component. The scores of the samples,
or the projections of the samples on the principal components, are given by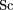 The amount of information in the data that the first rprincipal components capture may be quantified as
The amount of information in the data that the first rprincipal components capture may be quantified as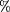 where SVi
is the ith singular value.
where SVi
is the ith singular value.
The filter on the loadings was implemented by dividing each loading by the sum of the magnitudes of all the other loadings
for that PC and then by rejecting all genes with a loading less than the threshold value. The distortion of patterns in the
score plot due to the removal of genes in this thresholding procedure was measured by the sum of the squares of the difference
between the 40 original score values and the 40 score values produced with the filtered gene set. Mathematically,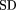 where SD is the squared difference,y
s,i,o is the score value of the s
th sample on the i
thPC in the projection using all the 7070 genes, whereasy
s,i,f is the score value of the s
th sample on the i
th PC obtained when a filtered gene set is used.
where SD is the squared difference,y
s,i,o is the score value of the s
th sample on the i
thPC in the projection using all the 7070 genes, whereasy
s,i,f is the score value of the s
th sample on the i
th PC obtained when a filtered gene set is used.
Acknowledgments
We thank the anonymous reviewers for their constructive suggestions for this paper. This work was supported by a grant from the Engineering Research Program of the Office of Basic Energy Science at the Department of Energy (DE-FG02-94ER-14487 and DE-FG02-99ER-15015) and an NIH grant (1-RO1-DK58533-01).
The publication costs of this article were defrayed in part by payment of page charges. This article must therefore be hereby marked “advertisement” in accordance with 18 USC section 1734 solely to indicate this fact.
Footnotes
-
↵3 Corresponding author.
-
E-MAIL gregstep{at}mit.edu; FAX (617) 253-3122.
-
Article and publication are at http://www.genome.org/cgi/doi/10.1101/gr.225302.
-
- Received November 26, 2001.
- Accepted April 16, 2002.
- Cold Spring Harbor Laboratory Press