A model-based constrained deep learning clustering approach for spatially resolved single-cell data

  1. Zhi Wei1
  1. 1Department of Computer Science, New Jersey Institute of Technology, Newark, New Jersey 07102, USA;
  2. 2Department of Computer Science, Wake Forest University, Winston-Salem, North Carolina 27109, USA;
  3. 3Department of Chemistry and Chemical Biology and Biological Sciences, College of Arts and Sciences, Cornell University, Ithaca, New York 14853, USA
  • Corresponding author: zhiwei{at}njit.edu
    •  
    Next Section

    Abstract

    Spatially resolved scRNA-seq (sp-scRNA-seq) technologies provide the potential to comprehensively profile gene expression patterns in tissue context. However, the development of computational methods lags behind the advances in these technologies, which limits the fulfillment of their potential. In this study, we develop a deep learning approach for clustering sp-scRNA-seq data, named Deep Spatially constrained Single-cell Clustering (DSSC). In this model, we integrate the spatial information of cells into the clustering process in two steps: (1) the spatial information is encoded by using a graphical neural network model, and (2) cell-to-cell constraints are built based on the spatial expression pattern of the marker genes and added in the model to guide the clustering process. Then, a deep embedding clustering is performed on the bottleneck layer of autoencoder by Kullback–Leibler (KL) divergence along with the learning of feature representation. DSSC is the first model that can use information from both spatial coordinates and marker genes to guide cell/spot clustering. Extensive experiments on both simulated and real data sets show that DSSC boosts clustering performance significantly compared with the state-of-the-art methods. It has robust performance across different data sets with various cell type/tissue organization and/or cell type/tissue spatial dependency. We conclude that DSSC is a promising tool for clustering sp-scRNA-seq data.

    Single-cell RNA sequencing (scRNA-seq) is a powerful, systematic biological tool that allows for transcriptomic analysis of cell heterogeneity and profiles thousands of cells at high resolution to ultimately reveal unidentified cellular subpopulations (Moncada et al. 2020). Despite this, conventional scRNA-seq alone leaves the tissue landscape undefined as cells are dissociated from their respective tissues and suspended in solution (Longo et al. 2021), neglecting the spatial complexity of cells and their relationships to function (Liao et al. 2021). Furthermore, cellular organization and intercellular communication networks for novel cell types identified by scRNA-seq remain uncharacterized unless ligand–receptor relationships are established (Skelly et al. 2018; Wang et al. 2019; Efremova et al. 2020). As cellular spatial distributions are deeply intertwined with gene expression and cell functions (Zhuang 2021), retaining this information is pivotal to further understanding the collective dynamics of biological activities. Spatially resolved single-cell transcriptomics (sp-scRNA-seq) provides an exciting opportunity to map RNA molecules in their tissue locations, allowing for comprehensive profiling of cell heterogeneity (Liao et al. 2021).

    The technologies used to profile spatially resolved single-cell transcriptomics (or targeted genes) can be divided into two types. The first type includes the hybridization-based (or image-based) approaches, such as MERFISH, smFISH, and osmFISH. These technologies profile the physical locations of cells by single-molecule fluorescence in situ hybridization (FISH) (Codeluppi et al. 2018; Miller et al. 2021). Pioneering studies in spatial genomics sought to explore FISH and digital imaging microscopy to allow for the detection of single RNA molecules in single cells (Femino et al. 1998). Thereafter, various FISH probes were developed for single-cell transcript profiling, allowing for higher accuracy and sensitivity when quantifying RNA molecules at the single-molecule level, such as single-molecule in situ hybridization (smFISH) (Femino et al. 1998; Lubeck and Cai 2012; Kwon 2013; Shah et al. 2016). As some smFISH methods are multiplexed by barcoding (Femino et al. 1998; Lubeck and Cai 2012), limitations such as optical crowding and transcript length hinder marker gene targeting and cell-type mapping (Femino et al. 1998; Shah et al. 2016). Codeluppi et al. (2018) developed a nonbarcoded and unamplified cyclic-ouroboros smFISH (osmFISH) method, optimized for brain tissue, to overcome the limitations of other smFISH methods. This method has the ability to process and map large tissue areas and allows for the construction of data-driven reference atlases of human tissue. The second type includes the sequencing-based approaches, such as 10x Visium and Slide-seq. A joint robust dissection of scRNA-seq data with spatially resolved single-cell transcriptomics captures a detailed illustration of the concerted cell–cell interactions within the tissue architecture. These technologies provide spatially resolved, untargeted transcriptomic profiling at the pixel level, with a pixel size of 10–100 μm (Larsson et al. 2021). Using Visium as an example, it uses spatially barcoded mRNA-binding oligonucleotides grouped in spots (larger than one cell) on the tissue slides. The mRNA from the specialized tissue will bind to the oligos. Then, based on the collected mRNA, a cDNA library with spatial barcodes will be built, preserving the spatial information of spots. In this way, both the gene expression level and the cells/spots spatial organization in the tissue can be measured. The two types of technologies have their own advantages and disadvantages. Briefly, imaging-based technologies can reach single-cell resolution, but they can only profile a limited number of targeted genes/proteins; on the other hand, some sequencing-based technologies can profile whole transcriptomes, but they cannot reach single-cell resolution.

    Clustering analysis is an essential step in most single-cell studies and has been utilized extensively. Based on the clustering results, researchers can explore the biological activities in cell-type or subtype level, which could not be reached by studying bulk data (Shapiro et al. 2013; Kolodziejczyk et al. 2015; Kiselev et al. 2019). It has been shown that some cell types, such as neurons, have high spatial dependencies and heterogeneities (Codeluppi et al. 2018). Specifically, tissues are an ensemble of cell types that interactively give rise to a specific function. It has been shown that endothelial cells in the brain are localized in certain spatial patterns (Xia et al. 2019; Stoltzfus et al. 2020). Furthermore, within cells of the same type, high spatial self-affinity was measured in ependymal cells, and spatial self-evasion was observed in inhibitory neurons such as microglia and astrocytes (Codeluppi et al. 2018). Cell neighbors identified by the spatiotemporal organization within tissues in complex organs (e.g., the brain) provide an important context to make inferences regarding cell interactions and behaviors. As such, highly accurate and sensitive mapping of tissue sections is important to reveal spatially dependent cells and can be used to understand the complexity of cell heterogeneity. The set of neighboring cells from spatial transcriptomics studies may provide valuable information for cell-type annotation. In other cases, such knowledge can lead to the identification of new cell types based on their neighborhood profiles. However, this requires that computational resources to analyze transcriptomic data are appropriately equipped with mechanisms to integrate the spatial features. However, traditional methods, such as Seurat (Butler et al. 2018) and SC3 (Kiselev et al. 2017), cannot use valuable spatial information in the clustering analysis.

    Some tools have been developed for spatial transcriptomic data. Giotto is a computational method specifically designed for spatial transcriptomic data analysis that performs cell-type enrichment analysis, spatially coherent gene detection, cell neighborhood and interaction analyses, and spatial pattern recognition (Dries et al. 2021). Unlike other computational methods that are geared toward scRNA-seq analysis but use spatial information to identify cell types (Stuart et al. 2019), marker genes (Svensson et al. 2018), or domain patterns (Zhu et al. 2018), Giotto is purely centered toward spatial data analysis but is capable of integrating scRNA-seq data to enhance spatial cell-type enrichment analysis. In the clustering analysis, Giotto uses graph clustering algorithms, such as Louvain (Blondel et al. 2008), to find cell communities. BayesSpace is a Bayesian statistical method that enhances spatial transcriptomic resolution and performs clustering analysis by modeling dimensionally reduced representations of the single-cell count matrix and grouping neighboring spots to the same cluster via spatial prior (Zhao et al. 2021). BayesSpace draws a distinction in the use of a t-distributed error model to identify spatial clusters and uses a Markov chain Monte Carlo to estimate model parameters. However, BayesSpace has a limited scope of application as it is primarily designed for decomposing the data with low resolution from sequencing-based technologies, such as 10x Visium. Some other methods, such as SpaGCN (Hu et al. 2021) and stLearn (Pham et al. 2020), use deep neural networks, such as CNN and GCN, to analyze the sp-scRNA-seq data. These tools can also integrate the information from H&E images to enhance cell clustering.

    It is widely shown that in many tissues, especially in the brain, many marker genes display strong spatial expression dependencies (Guillozet-Bongaarts et al. 2014; Zeisel et al. 2015; Maynard et al. 2021). Therefore, the information from the markers can be used as prior knowledge to guide the sp-scRNA-seq analyses, especially for the clustering analysis. However, none of the methods mentioned above can incorporate the marker gene information in the clustering process.

    In this article, we propose a novel clustering approach for sp-scRNA-seq data, Deep Spatially constrained Single-cell Clustering (DSSC). DSSC integrates prior information from both the physical organization of cells and the expression of the spatially dependent marker genes into the clustering process by a denoising graphical autoencoder with cell-to-cell constraints. Our extensive experiments indicate that DSSC outperforms the state-of-the-art methods in both simulated and real data sets, suggesting that it is a promising tool for clustering spatially resolved single-cell data.

    Previous SectionNext Section

    Results

    Simulation experiments

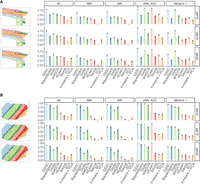
    DSSC is developed for clustering spatially resolved single-cell data by integrating prior knowledge from cell/spot location and marker genes. The overall architecture of the DSSC model is shown in Figure 1. In the simulation experiments, we test the performance of DSSC on data in different cell-type spatial organizations and dependencies. We simulated scRNA-seq data by Splatter and placed them in the spatial locations from two real data sets from (1) osmFISH data (Fig. 2A) and (2) sample 151507 from spatialLIBD data (Fig. 2B). We adjusted the cell-type spatial dependencies by perturbing the spatial coordinates of 10%, 15%, and 20% of the total cells (for details, see Methods). Constraints are built based on the true labels with 5% perturbations. We compared DSSC with seven existing clustering methods, including SpaGCN, stLearn, Seurat, Giotto, BayesSpace, k-means + PCA, and SC3. We compared both the clustering performance (measured by AC, NMI, and ARI) and the predicted label's spatial heterogeneity (denoted as PLSH, measured by k-nearest neighbors (kNN) accuracy (ACC) and Moran's I) of these methods. The results of the simulation experiments are shown in Figure 2. Generally, we found that the spatial-based clustering methods (DSSC, SpaGCN, stLearn, BayesSpace, and Giotto) have higher clustering performance and PLSH than the traditional scRNA-seq clustering methods (Seurat, SC3, and k-means). Cell-type spatial dependency is positively correlated with the performance of the spatial-based clustering methods, but it has no influence on the performance of the traditional clustering methods. BayesSpace cannot encode the spatial coordinates of the osmFISH data, so the clustering performance and PLSH are much higher in spatial organization 2 (Fig. 2B) than in spatial organization 1 (Fig. 2A). Although DSSC outperforms existing methods in both spatial organizations, its advantage is much higher in spatial organization 1 than in spatial organization 2. In summary, these results reveal that DSSC's performance is not affected by the sequencing technologies and cell-type spatial organizations, whereas other methods may prefer the sequencing-based technologies (such as the 10x Visium). DSSC demonstrates superior performance over the other methods under low, medium, and high cell-type dependencies. Therefore, these experiments show the robustness of DSSC's performance. The statistical tests of the clustering performance between DSSC and the other methods are shown in Supplemental Tables S1–S3.

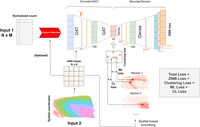
    Figure 1.
    View larger version:
    Figure 1.

    DSSC model architecture. The inputs of DSSC are the gene expression matrix and the cell coordinates. The outputs of DSSC are the low-dimension latent space (32D) and the predicted labels. Briefly, DSSC learns a low-dimensional representation of the gene expression matrix while simultaneously leveraging the prior knowledge from the spatial coordinates of cells/spots and the marker genes. Clustering is performed on latent space. Constraint loss, reconstruction loss, and clustering loss are optimized simultaneously. ML loss and CL loss are optimized alternately. (BN) Batch normalization, (ELU) ELU activation, (ML) must-links constraints, (CL) cannot-link constraints, (ZINB) zero-inflated negative binominal.

    Figure 2.
    View larger version:
    Figure 2.

    Simulation results from the spatial organization 1 (A; from osmFISH data) and 2 (B; from spatialLIBD sample 151507). True labels with 10%, 15%, and 20% perturbed coordinates are shown on the physical spaces (left). The corresponding clustering results are shown in the bar plots (right).

    Real data sets

    We then tested the performance of DSSC in three studies, including 25 real data sets with one data set from osmFISH (mouse cortex), 12 data sets from spatialLIBD (human cortex), and 12 data sets from 10x Genomics (mouse brain, denoted as 10xMBAD). In all data sets, we compared DSSC with seven competing methods as described above. For the data from spatialLIBD and 10xMBAD, we used the markers from the original spatialLIBD paper (Maynard et al. 2021) (see details in Methods and Supplemental Notes). Because osmFISH data only has 33 genes, we only used the genes with the top Moran's I as the marker genes to build constraints.

    OsmFISH data set

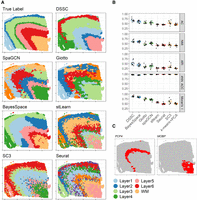
    The results of the osmFISH data set are shown in Figure 3. Because the latent dimension of SpaGCN is larger than the feature dimension of this data, we excluded SpaGCN from this experiment. BayesSpace cannot recognize the neighbors from the hybridization technologies, so the spatial information is not used by it for this data set. The marker genes used here for DSSC are Rorb and Syt6 (Fig. 3C). As expected, the expression of these genes has a high spatial dependency. We found that DSSC can profile the layer structures in the cortex (Fig. 3A). These layers are not clearly profiled by the other methods (Fig. 3B). DSSC outperforms the other methods in both clustering performance and PLSH (Fig. 3B). Some spatial-based methods, such as Giotto and stLearn, have very high kNN accuracy, but their clustering performance is much lower than DSSC. A potential reason for this result is that the spatial information overwhelms the clustering signal from gene expression during the clustering process, resulting in high spatial dependence but low clustering performance.

    Figure 3.
    View larger version:
    Figure 3.

    Results of osmFISH data set. (A) Predicted labels; (B) clustering performance; and (C) marker genes used for DSSC.

    SpatialLIBD data set

    We then tested all the methods on the spatialLIBD data sets (Fig. 4). We illustrated two marker genes, PCP4 and MOBP (Fig. 4C) for layer 5 and WM, respectively, from Maynard et al. (2021). It is noted that we checked the spatial dependencies of the marker genes before using them to build constraints. Figure 4A shows that DSSC is the only method that can identify five layers in sample 151673. Some other spatial-based methods, such as SpaGCN and BayesSpace, cluster some cells in clumps, not in layers. Figure 4B shows that DSSC outperforms all the other methods in the 12 spatialLIBD samples in both clustering performance and PLSH. Spatial-based methods have overall better performance than the traditional scRNA-seq clustering methods, revealing the benefits of using the spatial information. BayesSpace has the second-best performance in this data set because it can recognize the spatial neighbors for each spot in this data set. The statistical tests of the clustering performance between DSSC and the other methods are shown in Supplemental Table S4.

    Figure 4.
    View larger version:
    Figure 4.

    Results of spatialLIBD data sets. (A) Visualization of the predicted label for sample 151673; (B) clustering performance of the 12 samples; and (C) two marker genes used in this experiment.

    10xMBAD data set

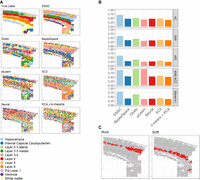
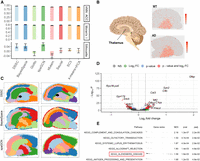
    We then applied DSSC on the 10xMBAD data set (Fig. 5). Because this data set has no true labels, we used a silhouette score (SS) to evaluate the clustering performance. We found that all the methods have similar predicted labels’ spatial heterogeneity on this data set (Fig. 5A). DSSC, BayesSpace, and SpaGCN have higher SSs than other methods. To further prove the accuracy of clustering of DSSC, we identified the cluster of thalami in a wild-type (WT) sample and an Alzheimer's disease (AD) sample by a marker gene Tcf7l2 (Fig. 5B; Lipiec et al. 2020) and then performed a differential expression (DE) analysis between the two groups of cells. We selected the thalamus because it has been widely shown to be associated with memory and cognition loss during AD (Pardilla-Delgado et al. 2021; van de Mortel et al. 2021). BayesSpace and SpaGCN fail to identify the region of the thalamus in the corresponding WT and AD samples (Fig. 5C). The DE results are shown in Figure 5D. Many genes that are overexpressed in the AD group are supported by previous studies. For example, Olfm1 has been shown to be a potential neuroprotective agent in AD (Takahama et al. 2014); Cst3 has been shown to increase the neuronal vulnerability and impaired neuronal ability to prevent neurodegeneration (Kaur and Levy 2012); and Syn2 is related to the onset and progression of AD (Kumar and Reddy 2020). As a result, in the pathway analysis of the KEGG gene set from the DE results (Fig. 5E), the AD pathway is significantly enriched in the thalamus of the AD sample. Another significant pathway, olfactory transduction, is also shown to be associated with AD in previous studies (Zou et al. 2016). The spliceosome is also shown to be altered in the Alzheimer transcriptomes (Koch 2018), which is down-regulated in the AD sample (marginally significant). These downstream analyses further consolidate the clustering results of DSSC. The statistical tests of the clustering performance (SS) between DSSC and the other methods are shown in Supplemental Table S5.

    Figure 5.
    View larger version:
    Figure 5.

    Results of 10xMBAD data sets. (A) Clustering performance (without true labels). (B) Cartoon of the brain showing the position of the thalamus and the expression of a marker gene, Tcf7l2, for the thalamus in a WT and an AD sample. (C) Predicted labels for a WT sample and an Alzheimer's disease (AD) sample from DSSC, BayesSpace, and SpaGCN; the black arrows indicate the thalamus regions. (D) Volcano plot from the differential expression analysis (DE) between the cells in the thalamus from the WT and the AD samples. (E) KEGG pathway analysis from the DE results in D. The pathway of AD is highlighted by the red box.

    Model test

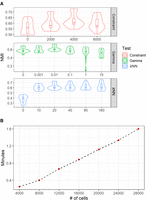
    We tested three parameters in DSSC: (1) the number of constraints (ML and CL, respectively), (2) the parameter that controls the clustering loss (gamma), and (3) the number of neighbors in the kNN graph for GAT layers on the 12 spatialLIBD data sets (Fig. 6A). We found that when the constraint number is zero (no constraints) or 6000 (too many constraints), the performance of DSSC becomes unstable. A suitable number of constraints (here we suggest setting the constraint number around the cell number) will not only improve the clustering performance but also make the model more stable. Compared with the model without clustering loss (gamma = 0), DSSC's performance is improved when the gamma is 0.01. However, a too-high gamma (greater than one) will seriously impact the model's performance. When the number of neighbors is higher than 10, DSSC's performance is not sensitive to them. However, a model without considering neighbors (K = 0) has much lower performance, revealing the contributions from using spatial information in clustering analysis. The results of the statistical tests of the parameter tuning experiments are in Supplemental Tables S6–S8. We then tested DSSC on the simulated data sets with increasing numbers of cells (Fig. 6B). We found that DSSC has a linearly ascending running time with the increased cell numbers. Thus, it can be easily used for analyzing large data sets. All experiments here are performed on the NVIDIA Tesla P100 with 16-GB memory.

    Figure 6.
    View larger version:
    Figure 6.

    Parameter tuning on the 12 spatialLIBD data sets (A) and running time test on the simulated data with increasing cell numbers (B).

    Previous SectionNext Section

    Discussion

    In this paper, we have developed a deep learning approach, DSSC, for clustering sp-scRNA-seq data. DSSC uses a denoising graphical autoencoder to learn a nonlinear representation of data. Spatial information is integrated into the clustering approach in two ways: (1) constraints from marker genes and (2) GAT encoders. To our knowledge, DSSC is the first model that can encode the information from both spatial coordinates and marker genes to guide the clustering. More broadly, DSSC is a flexible model in which its reconstruction loss function can be switched depending on the data structure. The available reconstruction loss includes zero-inflated negative binomial (ZINB) loss, NB loss, and MSE loss to deal with various scenarios. In this study, DSSC has been tested on both simulated and real data sets. The aim of our experiments is to test the robustness of DSSC's clustering performance over the data with different cell-type spatial organization and cell-type spatial dependency. The evaluation has been conducted regarding two aspects: clustering performance and space heterogeneity. Our results show that DSSC outperforms the state-of-the-art methods across different data sets.

    Recently, a new general-purpose density estimator has been introduced by using symmetrical and paired generative adversarial network (GAN) architecture (Liu et al. 2021b). Adopting this GAN architecture, a new method scDEC enables simultaneous learning of latent features and cell clustering and shows its superiority over competing methods in scATAC-seq analysis (Liu et al. 2021a). If spatial information could be accommodated in this GAN architecture, we may expect similar promising improvement in the analysis of sp-scRNA-seq data. We leave such exploration to future work.

    One limitation of the current model is its compatibility with the data sets with low spatial dependency. DSSC uses the spatial information of cells to boost the clustering performance, whereas not all tissue types have a high spatial dependency. For approaches like 10x Visium, our model is dependent on the assumption that all the cells in one spot are in the same cell type. In the future, this issue can be solved by performing the decomposition of spots. The latent representation of DSSC can be used for many downstream analyses, such as cell-to-cell communication and trajectory analysis.

    Previous SectionNext Section

    Methods

    Denoising autoencoder

    The autoencoder is a neural network for learning a nonlinear representation of data (Hinton and Salakhutdinov 2006). It receives corrupted data with artificial noise and reconstructs the original data (Vincent et al. 2008). It is able to learn a robust latent representation for noisy data. We use the denoising autoencoder for highly noisy count data of cells/spots. Let us denote the preprocessed count data as X and the corrupted data as Xc, formally: 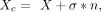Formula where n is the artificial noise in standard Gaussian distribution (with mean = 0 and variance = 1), and σ controls the weights of n. We set σ as 0.1.

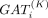    Next, we use an autoencoder to reduce the dimension of the count data. Encoders (E) are graphical attention network (GAT) layers, and decoders (D) are fully connected neural networks. Denoting the latent space as Z and the learnable weights of encoder as w, the encoder can be shown as Z = Ew(Xc). The GAT layers in E can be formalized as Formula where Xi is the output of the ith layer, Formula is the ith GAT layer with K heads, L is the total layers of encoder, and A is the adjacent matrix of a kNN graph G built based on the spatial coordinates of cells. Specifically, the distance between two cells i and j is measured by Euclidean distance: 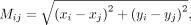Formula where x and y indicate the coordinates of cells i and j in a two-dimensional physical space.

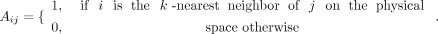
    Then Aij (i, j ε 1, 2, 3, …, N) is built by Formula

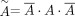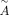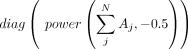    A is then normalized by Formula, where Formula is the normalized graph, Formula is Formula and ( · ) means dot product. Then 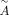Formula is used as the input for the GAT encoder. In this study, we set the number of heads as three. The decoder is 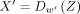Formula, where w′ is the learnable weight for the decoder, and X′ is the reconstructed counts from the decoder. The ELu activation function (Nair and Hinton 2010) and batch normalization are used for all the hidden layers in the encoder and decoder except the bottleneck layer. In the default setting, we use two layers of encoder and decoder. The default bottleneck layer is set as 32.

    We use a zero-inflated negative binomial (ZINB) model in the reconstruction loss function to characterize the zero-inflated and over-dispersed count data (Tian et al. 2019). Note, the raw count data, not the normalized data, are used in the ZINB model (Lopez et al. 2018; Eraslan et al. 2019; Tian et al. 2019). Let Xij be the count for cell i and gene j in the raw count matrix. The NB distributions are parameterized by μij and θij as means and dispersions, respectively. 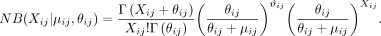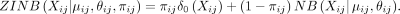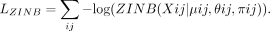Formally, Formula Then, the ZINB distribution is parameterized by the negative binomial and an additional coefficient πij for the probability of dropout events (zero mass): Formula The loss function of the ZINB-based autoencoder for the count data is defined as Formula We use independent fully connected layers to estimate these parameters in ZINB loss functions. We add three independent fully connected layers M, Θ, and Π after the last hidden layer of the decoder, which outputs the reconstructed matrix X′. 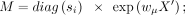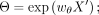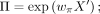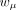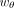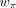The parameter layers are defined as Formula Formula Formula where M, Θ, and Π are the matrix of estimated mean, dispersion, and drop-out probability for the ZINB loss of count data.Formula, Formula, and Formula are the learnable weights for them, respectively. The size factor si for the cell i was calculated in the preprocessing step.

    The sizes of layers are set to (128, 32) for the GAT encoder and (32, 128) for the fully connected decoder.

    Deep embedded clustering

    Our model has two learning stages, a pretraining stage and a clustering stage. In the pretraining stage, we only train the autoencoder without considering the clustering loss and the constraint loss (see details below). Then, in the clustering stage, we simultaneously optimize the autoencoder and the clustering results. We perform unsupervised clustering on the latent space of the autoencoder (Xie et al. 2016). Our autoencoder transfers the input matrix to a low dimensional space Z. 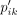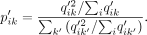The clustering loss is defined as the Kullback–Leibler (KL) divergence between the soft label distribution Q′ and the derived target distribution P′: Formula where the soft label Formula measures the similarity between zi and cluster center μk by Student's t-kernel (Maaten and Hinton 2008). The cluster center μk is initialized by applying a k-means on the bottleneck layer from the pretraining stage and then updated per batch in the clustering stage. Formally, Formula is defined as Formula The target distribution P′, which emphasizes the more certain assignments, is derived from Q′. Formally Formula is defined as Formula During the training process, Q′ and clustering loss are calculated per batch, and P′ is updated per epoch. This clustering loss will improve the initial estimate (from k-means) in each iteration by learning from the high-confident cell assignments, which in turn helps to improve the low-confident ones (Xie et al. 2016).

    Autoencoder with pairwise constraints

    Based on the autoencoder architecture, we add pairwise constraints of cells (Tian et al. 2021) on the latent space according to the expression of the marker genes. Similar to scDCC (Tian et al. 2021), we use the must-link constraints, which pull two cells to have similar soft labels if they have similar expression patterns of one or more marker genes, and cannot-link constraints, which encourage two cells to have different soft labels if they have different expression patterns of one or more marker genes.

    Constraints are built by six steps, considering both the spatial coordinates and the gene expression of the cells: (1) select the marker genes from literatures; (2) for each marker, say gene A, smooth the expression of A by averaging the normalized count data of k (k is defined according to the technology, we set it as six in this study) spatial neighbors of each cell/spot; (3) define the cells with the top 5% (cutoff1) expression of A as high, otherwise as low; (4) collect the cells as the confident cells if more than half (cutoff2) of its neighbors (and itself) have the high smoothed expression of A; (5) repeat steps 2–4 for all the marker genes; (6) because each marker gene represents a cell type (or a layer in cortex), we connect two confident cells by a must-link if they are selected by the markers for the same cell type (or layer); otherwise, we connect two confident cells by a cannot-link if they are selected by the markers for different cell types (or layers). It is noted that there is a tradeoff between the coverage and the reliability of constraints. A higher cutoff will decrease the coverage of constraints but also reduce the false-positive links. We denote all the constraints sampled here as the pool of constraints.

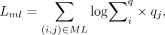
    The must-link and cannot-link constraints loss are defined as 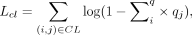Formula Formula where q is the soft labels described in the clustering section above. Must-links and cannot-links are used for training the model alternately and are updated (resampled from the pool) during the training. The number of constraints can be set according to the cell numbers. For example, for a data set with 4000 cells, we sample 4000 must-links and cannot-links, respectively.

    Combining the pairwise constraint loss, reconstruction loss, and clustering loss, the total loss of the DSSC is 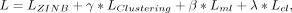Formula where γ, β, and λ are the coefficients for the clustering loss, must-link loss, and cannot-link loss, respectively. In the experiments of this study, γ is set to 0.01, and β and λ are set to 0.1 and one, respectively (for parameter tuning, see Results).

    Model implementation

    This model is implemented in Python3 using PyTorch (Paszke et al. 2019). Adam with AMSGrad variant (Kingma and Ba 2014; Reddi et al. 2018) with an initial learning rate = 0.001 is used for the pretraining stage and the clustering stage. The kNN graph is calculated by the “kneighbors_graph” function from the scikit-learn package. The top 2000 highly variable genes (HVGs) are selected to train the model. We pretrain the autoencoders for 200 epochs before entering the clustering stage. In the beginning of the clustering stage, we initialize K centroids by the k-means algorithm. During the clustering stage, reconstruction loss and clustering loss are optimized first. Then, constraint losses are optimized with reconstruction loss. ML and CL losses are optimized alternately. The centroids of clusters are also continuously updated by the learning process. Before each epoch, constraints are randomly sampled from the constraint pools. The soft label distribution Q′ is calculated in each batch, and the derived target distribution P′ is updated after each epoch. The convergence threshold for the clustering stage is that <0.1% of labels are changed per epoch. The marker genes used in this study are from the original spatialLIBD paper (Maynard et al. 2021), including PCP4, MOBP, FABP7, AQP4, CARTPT, KRT17, and so forth. More markers can be added if necessary. It is noted that we test the Moran's I and check the expression pattern of each marker before using it (for details, see Supplemental Notes). If a marker has very low spatial dependency in a data set, we exclude it from building constraints. For the osmFISH data set with only 33 genes, we just use the genes with the highest spatial dependency (Moran's I) as the markers. All experiments of DSSC in this study are conducted on a NVIDIA Tesla P100 with 16-GB memory.

    Marker and gene selection

    Before running the autoencoder model, we use Moran's I statistic (Moran 1950; Miller et al. 2021) to measure the spatial heterogeneity of marker genes. 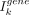Formula stands for the Moran's I of gene k, which is defined as 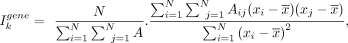Formula where Formula is the mean value of the normalized counts of the gene k over all cells/spots. A is the kNN graph from spatial information of cells. Marker genes with low Moran's I will not be used to build constraints. It is noted that gene filtering has a tiny influence on the performance of the osmFish data set because it only has 33 genes. These genes are all selected by the researchers so all of them are important for all or a part of cells in the tissue. In our experiments, because of the low feature number, we only select 30 HVGs out of 33 genes. On the other hand, sequencing-based methods profile the whole transcriptome (more than 20,000 genes). Many genes are not informative for clustering and even mislead the clustering so feature selection is essential for these data sets. In our experiments, we select the top 2000 HVGs for training DSSC. An optional feature selection approach is to use the genes with the top Moran's I.

    Evaluation metrics for clustering performance

    Adjusted Rand index (ARI) (Hubert and Arabie 1985), normalized mutual information (NMI) (Strehl and Ghosh 2003), and clustering accuracy (AC) are used as metrics to evaluate the performance of different methods.

    ARI measures the agreements between two sets, U and G. Assume a is the number of pairs of two cells in the same group in both U and G, b is the number of pairs of two cells in different groups in both U and G, c is the number of pairs of two cells in the same group in U but in different groups in G, and d is the number of pairs of two cells in different groups in U but in the same group in G. 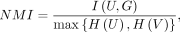The ARI is defined as Formula Let U = {U1, U2, …, Ctu} and G = {G1, G2, …, Gtg} be the predicted and ground truth labels on a data set with n cells. 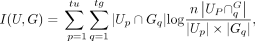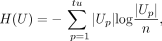NMI is defined as Formula where I(U,G) represents the mutual information between U and G and is defined as Formula and H(U) and H(G) are the entropies: 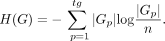Formula Formula AC is defined as the best matching between predicted and true clusters, which is given as 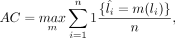Formula where Formula are the true labels, and li are the predicted labels from clustering algorithms. n is the number of cells, and m is the number of all possible one-to-one mapping between Formula and li. The best mapping is found by the Hungarian algorithm (Kuhn 1955).

    The SS is used to measure the clustering performance without labels. It compares how similar a cell is to its own cluster compared to other clusters. The SS ranges from −1 to +1, where a high value indicates better clustering. Let us denote the SS of cell i as Si, so we have Formula where ai stands for how well a cell i is assigned to its cluster based on the distance between this cell and all other cells in its cluster; bi stands for the smallest mean distance of the cell i to the cells in any other clusters. Then we use the mean value of Si over all the cells as the SS for a data set.

    Evaluation metrics for spatial heterogeneity and concentration

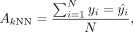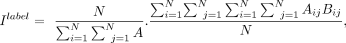    kNN accuracy measures the consistency of the labels between each cell and its spatial neighbors. It is defined as Formula where yi is the predicted label of cell i by clustering algorithms, and Formula is the major label of its neighbors (K = 20) on the physical space. We also use a variant of Moran's I (Moran 1950) to measure the cell-type spatial concentration. Let Ilabel be the Moran's I for the predicted labels (y1, y2, y3, …, yN) defined as Formula where Bij of cell i and j is defined as 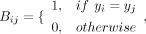Formula and A is the kNN graph (with k = 20) from spatial information of cells. The Ilabel measures the degree that the physically neighboring cells have the same label. Both metrics range from zero to one.

    Data simulation

    To test the model's performance to integrate spatial information for clustering, we simulate the single-cell RNA-seq data by Splatter package in R (Zappia et al. 2017; R Core Team 2021). The parameters for scRNA-seq data simulation are estimated from a real scRNA-seq data set (https://support.10xgenomics.com/spatial-gene-expression/datasets), and the parameter of clustering signal (de.scale) is fixed as 0.4. Besides simulating the count data, we place each cell on a 2D space with a coordinate (x,y). The physical space and coordinates are extracted from real data sets. The regions (domains) on the physical space in the real data sets are provided by the investigators. Specifically, let us denote the spot number in a layer k (from true label) as nk and the total layer number as K. During the simulation, for a layer k, we use Splatter to simulate nk cells and randomly assign these cells to the spatial coordinates of the spots in this layer. We do this for all K layers so the cell number in the simulated data sets should be the same as the spot number in the real data set. Then, we perturb the spatial coordinate of 10%, 15%, and 20% of cells to control the cell-type spatial dependency. We also use the spatial coordinates from two data sets (osmFISH [Codeluppi et al. 2018] and spatialLIBD 151507 [Maynard et al. 2021]) to simulate different spatial organizations. Therefore, our simulation experiments can test the robustness of DSSC's performance in the data with different cell-type spatial dependencies and cell-type spatial organizations. To simulate the constraints from markers, we randomly connect 3000 cells in the same cell type (from the true label) as the must-links. We then perturb the cells in 5% must-links to simulate the real accuracy (∼95%). Similarly, we randomly connect 3000 cells in the different cell types as the cannot-links.

    Real data sets

    We use data from three studies, including 25 sp-scRNA-seq data sets in this study. The first data set was measured by the osmFISH technology (Codeluppi et al. 2018), and the other two data sets were sequenced by the 10x Visium technology and provided by spatialLIBD (Pardo et al. 2022) and the 10x Genomics website, respectively. Specifically, the osmFISH data set of the somatosensory cortex was downloaded from Linnarsson laboratory website (http://linnarssonlab.org/osmFISH/). This data set contains 33 genes and 4839 cells. We did not implement the feature selection for this data set as the low dimension of features. All 10x Visium data sets are read by the “Load10x_Spatial” function and preprocessed by the “SCTransform” function by Seurat in R. The 10x mouse brain AD data set is downloaded from the website https://www.10xgenomics.com/resources/datasets. This data set contains 12 sp-scRNA-seq data with six WT samples and six CRND8 APP-overexpressing transgenic (AD) samples. The mice brains were sampled at 2.5, 5.7, and 13.2 mo of age. There were two replicates per phenotype per time point, resulting in 12 samples in total. The spatialLIBD data set is downloaded from the R package “spatialLIBD” (Pardo et al. 2022). This data set contains 12 spatially resolved RNA-seq data sets, which can be grouped into three spatial organizations. Specifically, samples 151507–151510 have similar spatial organizations; samples 151669–151672 have similar spatial organizations; and samples 151673–151676 have similar spatial organizations.

    Count data preprocessing

    The raw count data are preprocessed and normalized by the Python package SCANPY (Wolf et al. 2018). Specifically, the genes with no count are filtered out. The counts of a cell are normalized by a size factor si, which is calculated by dividing the library size of that cell by the median of the library size of all cells. In this way, all cells will have the same library size and become comparable. Then, the counts are logarithm transformed and scaled to have unit variances and zero means. The treated count data are used in our denoising autoencoder model. However, we use the raw count matrix to calculate the ZINB loss (Lopez et al. 2018; Eraslan et al. 2019).

    Comparisons to other methods

    For consistency, we use DSSC's data preprocessing and feature selection approaches for all the other methods, which include k-means (with PCA) (https://scikit-learn.org/stable/modules/generated/sklearn.cluster.KMeans.html), Seurat (Butler et al. 2018; https://github.com/satijalab/seurat), SC3 (Kiselev et al. 2017; https://github.com/hemberg-lab/SC3), BayesSpace (Zhao et al. 2021; https://github.com/edward130603/BayesSpace), Giotto (Dries et al. 2021; https://rubd.github.io/Giotto_site/), SpaGCN (https://github.com/jianhuupenn/SpaGCN), and stLearn (https://github.com/BiomedicalMachineLearning/stLearn). For Seurat and Giotto, we adjusted the resolution in the Louvain algorithm for a better K estimation (same or close to the real K). All other parameters in all the other methods are kept in the default setting or following the settings in the official pipelines. It is noted that the latent dimension of SpaGCN is higher than the feature dimension of osmFISH data so SpaGCN cannot be used to analyze osmFISH data. For consistency, H&E images are not used for all the methods.

    Statistical test

    The differences between the clustering performance of DSSC and the competing methods are tested by the one-sided paired t-test.

    Software availability

    Source code of DSSC is available at GitHub (https://github.com/xianglin226/DSSC) and as Supplemental Code.

    Previous SectionNext Section

    Competing interest statement

    The authors declare no competing interests.

    Previous SectionNext Section

    Acknowledgments

    This work was supported by grant R15HG012087 (Z.W.) from the National Institutes of Health and grant 1659472 (Z.W.) from the National Science Foundation.

    Author contributions: Z.W. conceived and supervised the project. X.L. designed the method and conducted the experiments. X.L., L.G., A.A., and N.W. wrote the manuscript. Z.W. revised the manuscript. X.L., L.G., N.W., and A.A. conducted experiments on the competing methods. All authors contributed to and approved the manuscript.

    Previous SectionNext Section

    Footnotes

    • Received December 8, 2021.
    • Accepted September 28, 2022.

    This article is distributed exclusively by Cold Spring Harbor Laboratory Press for the first six months after the full-issue publication date (see https://genome.cshlp.org/site/misc/terms.xhtml). After six months, it is available under a Creative Commons License (Attribution-NonCommercial 4.0 International), as described at http://creativecommons.org/licenses/by-nc/4.0/.

    Previous Section
     

    References

    1. ↵
      Blondel VD, Guillaume J-L, Lambiotte R, Lefebvre E. 2008. Fast unfolding of communities in large networks. J Stat Mech Theory Exp 2008: P10008. doi:10.1088/1742-5468/2008/10/P10008
      CrossRefGoogle Scholar
    2. ↵
      Butler A, Hoffman P, Smibert P, Papalexi E, Satija R. 2018. Integrating single-cell transcriptomic data across different conditions, technologies, and species. Nat Biotechnol 36: 411–420. doi:10.1038/nbt.4096
      CrossRefMedlineGoogle Scholar
    3. ↵
      Codeluppi S, Borm LE, Zeisel A, La Manno G, van Lunteren JA, Svensson CI, Linnarsson S. 2018. Spatial organization of the somatosensory cortex revealed by osmFISH. Nat Methods 15: 932–935. doi:10.1038/s41592-018-0175-z
      CrossRefMedlineGoogle Scholar
    4. ↵
      Dries R, Zhu Q, Dong R, Eng C-HL, Li H, Liu K, Fu Y, Zhao T, Sarkar A, Bao F. 2021. Giotto: a toolbox for integrative analysis and visualization of spatial expression data. Genome Biol 22: 78. doi:10.1186/s13059-021-02286-2
      CrossRefGoogle Scholar
    5. ↵
      Efremova M, Vento-Tormo M, Teichmann SA, Vento-Tormo R. 2020. CellPhoneDB: inferring cell–cell communication from combined expression of multi-subunit ligand–receptor complexes. Nat Protoc 15: 1484–1506. doi:10.1038/s41596-020-0292-x
      CrossRefMedlineGoogle Scholar
    6. ↵
      Eraslan G, Simon LM, Mircea M, Mueller NS, Theis FJ. 2019. Single-cell RNA-seq denoising using a deep count autoencoder. Nat Commun 10: 390. doi:10.1038/s41467-018-07931-2
      CrossRefMedlineGoogle Scholar
    7. ↵
      Femino AM, Fay FS, Fogarty K, Singer RH. 1998. Visualization of single RNA transcripts in situ. Science 280: 585–590. doi:10.1126/science.280.5363.585
      Abstract/FREE Full Text
    8. ↵
      Guillozet-Bongaarts A, Hyde T, Dalley R, Hawrylycz M, Henry A, Hof P, Hohmann J, Jones A, Kuan C, Royall J, et al. 2014. Altered gene expression in the dorsolateral prefrontal cortex of individuals with schizophrenia. Mol Psychiatry 19: 478–485. doi:10.1038/mp.2013.30
      CrossRefMedlineGoogle Scholar
    9. ↵
      Hinton GE, Salakhutdinov RR. 2006. Reducing the dimensionality of data with neural networks. Science 313: 504–507. doi:10.1126/science.1127647
      Abstract/FREE Full Text
    10. ↵
      Hu J, Li X, Coleman K, Schroeder A, Ma N, Irwin DJ, Lee EB, Shinohara RT, Li M. 2021. SpaGCN: integrating gene expression, spatial location and histology to identify spatial domains and spatially variable genes by graph convolutional network. Nat Methods 18: 1342–1351. doi:10.1038/s41592-021-01255-8
      CrossRefGoogle Scholar
    11. ↵
      Hubert L, Arabie P. 1985. Comparing partitions. J Classif 2: 193–218. doi:10.1007/BF01908075
      CrossRefGoogle Scholar
    12. ↵
      Kaur G, Levy E. 2012. Cystatin C in Alzheimer's disease. Front Mol Neurosci 5: 79. doi:10.3389/fnmol.2012.00079
      CrossRefMedlineGoogle Scholar
    13. ↵
      Kingma DP, Ba J. 2014. Adam: a method for stochastic optimization. arXiv:1412.6980 [cs.LG]. doi:10.48550/arXiv.1412.6980
      CrossRefGoogle Scholar
    14. ↵
      Kiselev VY, Kirschner K, Schaub MT, Andrews T, Yiu A, Chandra T, Natarajan KN, Reik W, Barahona M, Green AR, et al. 2017. SC3: consensus clustering of single-cell RNA-seq data. Nat Methods 14: 483–486. doi:10.1038/nmeth.4236
      CrossRefMedlineGoogle Scholar
    15. ↵
      Kiselev VY, Andrews TS, Hemberg M. 2019. Challenges in unsupervised clustering of single-cell RNA-seq data. Nat Rev Genet 20: 273–282. doi:10.1038/s41576-018-0088-9
      CrossRefMedlineGoogle Scholar
    16. ↵
      Koch L. 2018. Altered splicing in Alzheimer transcriptomes. Nat Rev Genet 19: 738–739. doi:10.1038/s41576-018-0064-4
      CrossRefGoogle Scholar
    17. ↵
      Kolodziejczyk AA, Kim JK, Svensson V, Marioni JC, Teichmann SA. 2015. The technology and biology of single-cell RNA sequencing. Mol Cell 58: 610–620. doi:10.1016/j.molcel.2015.04.005
      CrossRefMedlineGoogle Scholar
    18. ↵
      Kuhn HW. 1955. The Hungarian method for the assignment problem. Nav Res Logist Q 2: 83–97. doi:10.1002/nav.3800020109
      CrossRefGoogle Scholar
    19. ↵
      Kumar S, Reddy PH. 2020. The role of synaptic microRNAs in Alzheimer's disease. Biochim Biophys Acta Mol Basis Dis 1866: 165937. doi:10.1016/j.bbadis.2020.165937
      CrossRefGoogle Scholar
    20. ↵
      Kwon S. 2013. Single-molecule fluorescence in situ hybridization: quantitative imaging of single RNA molecules. BMB Rep 46: 65–72. doi:10.5483/BMBRep.2013.46.2.016
      CrossRefGoogle Scholar
    21. ↵
      Larsson L, Frisén J, Lundeberg J. 2021. Spatially resolved transcriptomics adds a new dimension to genomics. Nat Methods 18: 15–18. doi:10.1038/s41592-020-01038-7
      CrossRefGoogle Scholar
    22. ↵
      Liao J, Lu X, Shao X, Zhu L, Fan X. 2021. Uncovering an organ's molecular architecture at single-cell resolution by spatially resolved transcriptomics. Trends Biotechnol 39: 43–58. doi:10.1016/j.tibtech.2020.05.006
      CrossRefMedlineGoogle Scholar
    23. ↵
      Lipiec MA, Bem J, Koziński K, Chakraborty C, Urban-Ciećko J, Zajkowski T, Dąbrowski M, Szewczyk LM, Toval A, Ferran JL, et al. 2020. TCF7L2 regulates postmitotic differentiation programmes and excitability patterns in the thalamus. Development 147: dev190181. doi:10.1242/dev.190181
      Abstract/FREE Full Text
    24. ↵
      Liu Q, Chen S, Jiang R, Wong WH. 2021a. Simultaneous deep generative modelling and clustering of single-cell genomic data. Nat Mach Intell 3: 536–544. doi:10.1038/s42256-021-00333-y
      CrossRefGoogle Scholar
    25. ↵
      Liu Q, Xu J, Jiang R, Wong WH. 2021b. Density estimation using deep generative neural networks. Proc Natl Acad Sci 118: e2101344118. doi:10.1073/pnas.2101344118
      Abstract/FREE Full Text
    26. ↵
      Longo SK, Guo MG, Ji AL, Khavari PA. 2021. Integrating single-cell and spatial transcriptomics to elucidate intercellular tissue dynamics. Nat Rev Genet 22: 627–644. doi:10.1038/s41576-021-00370-8
      CrossRefMedlineGoogle Scholar
    27. ↵
      Lopez R, Regier J, Cole MB, Jordan MI, Yosef N. 2018. Deep generative modeling for single-cell transcriptomics. Nat Methods 15: 1053–1058. doi:10.1038/s41592-018-0229-2
      CrossRefMedlineGoogle Scholar
    28. ↵
      Lubeck E, Cai L. 2012. Single-cell systems biology by super-resolution imaging and combinatorial labeling. Nat Methods 9: 743–748. doi:10.1038/nmeth.2069
      CrossRefMedlineGoogle Scholar
    29. ↵
      Maynard KR, Collado-Torres L, Weber LM, Uytingco C, Barry BK, Williams SR, Catallini JL, Tran MN, Besich Z, Tippani M, et al. 2021. Transcriptome-scale spatial gene expression in the human dorsolateral prefrontal cortex. Nat Neurosci 24: 425–436. doi:10.1038/s41593-020-00787-0
      CrossRefGoogle Scholar
    30. ↵
      Miller BF, Bambah-Mukku D, Dulac C, Zhuang X, Fan J. 2021. Characterizing spatial gene expression heterogeneity in spatially resolved single-cell transcriptomics data with nonuniform cellular densities. Genome Res 31: 1843–1855. doi:10.1101/gr.271288.120
      Abstract/FREE Full Text
    31. ↵
      Moncada R, Barkley D, Wagner F, Chiodin M, Devlin JC, Baron M, Hajdu CH, Simeone DM, Yanai I. 2020. Integrating microarray-based spatial transcriptomics and single-cell RNA-seq reveals tissue architecture in pancreatic ductal adenocarcinomas. Nat Biotechnol 38: 333–342. doi:10.1038/s41587-019-0392-8
      CrossRefGoogle Scholar
    32. ↵
      Moran PA. 1950. A test for the serial independence of residuals. Biometrika 37: 178–181. doi:10.1093/biomet/37.1-2.178
      CrossRefMedlineGoogle Scholar
    33. ↵
      Nair V, Hinton GE. 2010. Rectified linear units improve restricted Boltzmann machines. In ICML’10. Proceedings of the 27th International Conference on Machine Learning, Haifa, Israel, pp. 807–814.
      Google Scholar
    34. ↵
      Pardilla-Delgado E, Torrico-Teave H, Sanchez JS, Ramirez-Gomez LA, Baena A, Bocanegra Y, Vila-Castelar C, Fox-Fuller JT, Guzmán-Vélez E, Martínez J, et al. 2021. Associations between subregional thalamic volume and brain pathology in autosomal dominant Alzheimer's disease. Brain Commun 3: fcab101. doi:10.1093/braincomms/fcab101
      CrossRefGoogle Scholar
    35. ↵
      Pardo B, Spangler A, Weber LM, Page SC, Hicks SC, Jaffe AE, Martinowich K, Maynard KR, Collado-Torres L. 2022. spatialLIBD: an R/Bioconductor package to visualize spatially-resolved transcriptomics data. BMC Genomics 23: 434. doi:10.1186/s12864-022-08601-w
      CrossRefGoogle Scholar
    36. ↵
      Paszke A, Gross S, Massa F, Lerer A, Bradbury J, Chanan G, Killeen T, Lin Z, Gimelshein N, Antiga L. 2019. PyTorch: an imperative style, high-performance deep learning library. In Advances in neural information processing systems 32. 33rd Conference on Neural Information Processing Systems (NeurIPS 2019), Vancouver, Canada.
      Google Scholar
    37. ↵
      Pham D, Tan X, Xu J, Grice LF, Lam PY, Raghubar A, Vukovic J, Ruitenberg MJ, Nguyen Q. 2020. stLearn: integrating spatial location, tissue morphology and gene expression to find cell types, cell-cell interactions and spatial trajectories within undissociated tissues. bioRxiv doi:10.1101/2020.05.31.125658
      Abstract/FREE Full Text
    38. ↵
      R Core Team. 2021. R: a language and environment for statistical computing. R Foundation for Statistical Computing, Vienna. https://www.R-project.org/.
      Google Scholar
    39. ↵
      Reddi SJ, Kale S, Kumar S. 2018. On the convergence of Adam and beyond. In International Conference on Learning Representations, Vol. 366.
      Google Scholar
    40. ↵
      Shah S, Lubeck E, Zhou W, Cai L. 2016. In situ transcription profiling of single cells reveals spatial organization of cells in the mouse hippocampus. Neuron 92: 342–357. doi:10.1016/j.neuron.2016.10.001
      CrossRefMedlineGoogle Scholar
    41. ↵
      Shapiro E, Biezuner T, Linnarsson S. 2013. Single-cell sequencing-based technologies will revolutionize whole-organism science. Nat Rev Genet 14: 618–630. doi:10.1038/nrg3542
      CrossRefMedlineGoogle Scholar
    42. ↵
      Skelly DA, Squiers GT, McLellan MA, Bolisetty MT, Robson P, Rosenthal NA, Pinto AR. 2018. Single-cell transcriptional profiling reveals cellular diversity and intercommunication in the mouse heart. Cell Rep 22: 600–610. doi:10.1016/j.celrep.2017.12.072
      CrossRefMedlineGoogle Scholar
    43. ↵
      Stoltzfus CR, Filipek J, Gern BH, Olin BE, Leal JM, Wu Y, Lyons-Cohen MR, Huang JY, Paz-Stoltzfus CL, Plumlee CR, et al. 2020. CytoMAP: a spatial analysis toolbox reveals features of myeloid cell organization in lymphoid tissues. Cell Rep 31: 107523. doi:10.1016/j.celrep.2020.107523
      CrossRefGoogle Scholar
    44. ↵
      Strehl A, Ghosh J. 2003. Cluster ensembles: a knowledge reuse framework for combining multiple partitions. J Mach Learn Res 3: 583–617. doi:10.1162/153244303321897735
      CrossRefGoogle Scholar
    45. ↵
      Stuart T, Butler A, Hoffman P, Hafemeister C, Papalexi E, Mauck WM III., Hao Y, Stoeckius M, Smibert P, Satija R. 2019. Comprehensive integration of single-cell data. Cell 177: 1888–1902.e21. doi:10.1016/j.cell.2019.05.031
      CrossRefMedlineGoogle Scholar
    46. ↵
      Svensson V, Teichmann SA, Stegle O. 2018. SpatialDE: identification of spatially variable genes. Nat Methods 15: 343–346. doi:10.1038/nmeth.4636
      CrossRefGoogle Scholar
    47. ↵
      Takahama S, Nakaya N, Tomarev SI. 2014. Olfactomedin 1 may suppress APP cleavage through its interaction with BACE1. Invest Ophthalmol Vis Sci 55: 2959.
      Google Scholar
    48. ↵
      Tian T, Wan J, Song Q, Wei Z. 2019. Clustering single-cell RNA-seq data with a model-based deep learning approach. Nat Mach Intell 1: 191–198. doi:10.1038/s42256-019-0037-0
      CrossRefGoogle Scholar
    49. ↵
      Tian T, Zhang J, Lin X, Wei Z, Hakonarson H. 2021. Model-based deep embedding for constrained clustering analysis of single cell RNA-seq data. Nat Commun 12: 1873. doi:10.1038/s41467-021-22008-3
      CrossRefGoogle Scholar
    50. ↵
      van de Mortel LA, Thomas RM, van Wingen GA, Initiative AsDN. 2021. Grey matter loss at different stages of cognitive decline: a role for the thalamus in developing Alzheimer's disease. J Alzheimers Dis 83: 705–720. doi:10.3233/JAD-210173
      CrossRefGoogle Scholar
    51. ↵
      van der Maaten L, Hinton G. 2008. Visualizing data using t-SNE. J Mach Learn Res 9: 2579–2605.
      CrossRefMedlineGoogle Scholar
    52. ↵
      Vincent P, Larochelle H, Bengio Y, Manzagol P-A. 2008. Extracting and composing robust features with denoising autoencoders. In Proceedings of the 25th International Conference on Machine Learning, Helsinki, Finland, pp. 1096–1103.
      Google Scholar
    53. ↵
      Wang S, Karikomi M, MacLean AL, Nie Q. 2019. Cell lineage and communication network inference via optimization for single-cell transcriptomics. Nucleic Acids Res 47: e66. doi:10.1093/nar/gkz204
      CrossRefGoogle Scholar
    54. ↵
      Wolf FA, Angerer P, Theis FJ. 2018. SCANPY: large-scale single-cell gene expression data analysis. Genome Biol 19: 15. doi:10.1186/s13059-017-1382-0
      CrossRefMedlineGoogle Scholar
    55. ↵
      Xia C, Fan J, Emanuel G, Hao J, Zhuang X. 2019. Spatial transcriptome profiling by MERFISH reveals subcellular RNA compartmentalization and cell cycle-dependent gene expression. Proc Natl Acad Sci 116: 19490–19499. doi:10.1073/pnas.1912459116
      Abstract/FREE Full Text
    56. ↵
      Xie J, Girshick R, Farhadi A. 2016. Unsupervised deep embedding for clustering analysis. In Proceedings of the 33rd International Conference on Machine Learning, New York, pp. 478–487.
      Google Scholar
    57. ↵
      Zappia L, Phipson B, Oshlack A. 2017. Splatter: simulation of single-cell RNA sequencing data. Genome Biol 18: 174. doi:10.1186/s13059-017-1305-0
      CrossRefGoogle Scholar
    58. ↵
      Zeisel A, Muñoz-Manchado AB, Codeluppi S, Lönnerberg P, La Manno G, Juréus A, Marques S, Munguba H, He L, Betsholtz C, et al. 2015. Cell types in the mouse cortex and hippocampus revealed by single-cell RNA-seq. Science 347: 1138–1142. doi:10.1126/science.aaa1934
      Abstract/FREE Full Text
    59. ↵
      Zhao E, Stone MR, Ren X, Guenthoer J, Smythe KS, Pulliam T, Williams SR, Uytingco CR, Taylor SE, Nghiem P, et al. 2021. Spatial transcriptomics at subspot resolution with BayesSpace. Nat Biotechnol 39: 1375–1384. doi:10.1038/s41587-021-00935-2
      CrossRefGoogle Scholar
    60. ↵
      Zhu Q, Shah S, Dries R, Cai L, Yuan G-C. 2018. Identification of spatially associated subpopulations by combining scRNAseq and sequential fluorescence in situ hybridization data. Nat Biotechnol 36: 1183–1190. doi:10.1038/nbt.4260
      CrossRefGoogle Scholar
    61. ↵
      Zhuang X. 2021. Spatially resolved single-cell genomics and transcriptomics by imaging. Nat Methods 18: 18–22. doi:10.1038/s41592-020-01037-8
      CrossRefGoogle Scholar
    62. ↵
      Zou Y-M, Lu D, Liu L-P, Zhang H-H, Zhou Y-Y. 2016. Olfactory dysfunction in Alzheimer's disease. Neuropsychiatr Dis Treat 12: 869. doi:10.2147/NDT.S104886
      CrossRefGoogle Scholar

    Articles citing this article

    • Conserved principles of spatial biology define tumor heterogeneity and response to immunotherapy bioRxiv December 16, 2025 0: 2024.10.18.619136v2-2024.10.18.619136
    • CONCERT predicts niche-aware perturbation responses in spatial transcriptomics bioRxiv November 24, 2025 0: 2025.11.08.686890v2-2025.11.08.686890
    | Table of Contents

    This Article

    1. Published in Advance October 5, 2022, doi: 10.1101/gr.276477.121 Genome Res. 32: 1906-1917 © 2022 Lin et al.; Published by Cold Spring Harbor Laboratory Press

    Article Category

    Share

    Preprint Server



    Navigate This Article

    Current Issue

    1. January 2026, 36 (1)
    1. Current Issue
    1. Alert me to new issues of Genome Research