Identification of polymorphic motifs using probabilistic search algorithms

Single nucleotide polymorphisms (SNPs) are abundant in the human genome and occur at roughly 1 per 2 kb spacing on the average (Balasubramanian et al. 2002). Alleles at SNP loci are often nonrandomly associated. Various evolutionary mechanisms, including drift and natural selection, maintain the association of specific nucleotides at two or more sites, which may not be contiguous. The search for nucleotides that exhibit association at a set of polymorphic sites is of interest in studies of common diseases (Sabeti et al. 2002) and in evolutionary genetics (Tateno et al. 1997; Daly et al. 2001). We define a set of nucleotides that occurs with a high frequency at multiple polymorphic DNA sites, not necessarily contiguous, in a group of individuals as a “polymorphic motif.” We note that our definition of a motif differs from the conventional definition, for example, that is used for finding regulatory sequences in promoter regions of genes (Keiler and Shapiro 2001), in two ways; (1) the sites included in our definition are polymorphic, and (2) the sites need not be contiguous. In conventional motif-identification problems, search is made for evolutionarily conserved nucleotide sequences at a contiguous set of nucleotide positions (Gupta and Liu 2003). In case-control studies of common diseases, it is of interest to find polymorphic motifs and to test whether there are differences in motif frequencies between cases and controls (Khani-Hanjani et al. 2002). Motifs that are found in significantly higher frequencies among cases are associated with the disease under study. If variants in multiple genes are indeed involved in the disease, the sites in such a motif may not be contiguous. Similarly, the discovery of polymorphic motifs is important in evolutionary genetics. Indeed, such motifs have been used to define subhaplogroups of specific clades (haplogroups) of the human mitochondrial (mt) DNA (Bamshad et al. 2001).

In the context of evolutionary or human genetic studies, there are two related issues. First, to identify motifs or haplotypes that occur at high frequencies in subsets of a large data set, such as those sampled from specific geographical regions or groups, or from individuals afflicted with a specific disease. Having identified such motifs, the second problem is to decipher the biological or population genetic processes (e.g., linkage, drift, selection, epistasis) that have resulted in the existence of these high-frequency motifs. In this study, we shall only address the first issue, viz., how to identify high-frequency motifs. To address the second issue, collection of further data (e.g., family data), statistical modeling, investigations of metabolic pathways, wet-laboratory experimentation, etc., may be required.

It is theoretically possible to discover polymorphic motifs in a set of N-aligned DNA sequences, each of length L nucleotides, by examining frequencies in all possible k × k tables, k = 2,3,...,L. However, this is computationally infeasible. The purpose of this study is to propose a set of computationally fast probabilistic search algorithms that may be used for motif finding, and to evaluate their efficiencies using both synthetic and real data sets. Keeping SNP loci in mind, which are usually biallelic, we formulate, describe, and assess these algorithms using sequences of binary characters. However, there is no inherent restriction in these algorithms that the search has to be confined to binary sequences. These algorithms can also be used on multilocus genotype data of diploid individuals. When genotype data are used, the distinct genotypes only need to be numerically recoded, as discussed later. Thus, the proposed algorithms are fairly general in nature, and can be put to diverse uses.

We first propose an algorithm for identifying a motif of a given length. We then extend this algorithm when the length is unknown. Finally, we propose a modification for identifying “variant” motifs. The problem of identifying a variant motif arises when, given a collection of DNA sequences derived from a set of individuals, it is of interest to identify whether an appropriately defined subset of individuals in this collection possesses a motif that is different from that possessed by the remaining subset of individuals. For example, in a case-control study, it is pertinent to identify whether the cases possess a motif at a certain number of sites that comprise nucleotides, each of which is different from the nucleotide possessed by the controls at the corresponding sites. Identification of such a variant motif can help in identifying SNPs associated with the disease in question. The problem of identifying variant motifs in subsets of a collection of sequences at the hypervariable segment-1 (HVS1) of human mtDNA has received a lot of attention (Quintana-Murci et al. 1999). In particular, efforts have been made to to identify contrasting motifs in HVS1 in subsets of individuals belonging to different haplogroups (HGs) that are defined by the presence of specific nucleotides at sites outside of the HVS1.

In each of these problems, a variant motif is defined in relation to another. For example, for case-control data, the variant motif among cases is defined in contrast to the one found among the controls. In the evolutionary analysis of mtDNA HVS1 sequences, search for a motif is made in contrast to the Cambridge Reference Sequence (CRS) (Anderson et al. 1981). In such cases, for motif searching, not only do we have to find a high-frequency motif, but this motif should contain nucleotides that are completely or largely different from those present in the reference sequence at the corresponding nucleotide positions.

Methods

Consider a data matrix ((a_ij))_N×L, where a_ij denotes a nucleotide (A,T,G, or C) at the j^th polymorphic site (j = 1,2,...,L) for the i^th individual (i = 1,2,..., N). The data matrix is generated from aligned DNA sequences of a specific genomic segment of N individuals, from which all monomorphic sites have been removed. We note that if these N individuals belong to a case-control study, then the data matrix needs to be initially created by pooling all cases and controls, and subsequently separated into two matrices, one for cases and another for controls. A similar strategy is also required in evolutionary studies, while simultaneously dealing with two populations. We also note that if disjoint segments of DNA are to be simultaneously examined for motif finding, then appropriate segments may be separately aligned, and the aligned segments concatenated in the data matrix.

Let V = {1,2,...,L} denote the set of all L polymorphic sites in the data. Let Π_p denote the set of all possible combinations of p sites in V. To fix ideas, consider the data matrix given in Table 1. In this matrix, N = 4, and L = 7. Thus, V = {1,2,...,7}. For p = 2, Π₂ = {{1,2}, {1,3},..., {1,7}, {2,3}, {2,4},..., {6,7}} = 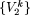, k = 1,2,...(). In general, Π_p = 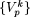, k = 1,2,...() and 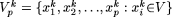. For a fixed k, we define the modal sequence on 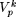as that particular combination of nucleotides at the sites 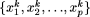included in 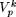, k = 1,2,...() which has the highest frequency. In the data matrix of Table 1, the modal sequence, for example, on 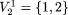is AG with frequency 2, on 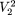= {1,3} is AT with frequency 3, etc. We define a motif of length p as the maximally frequent modal sequence on Π_p; that is, the sequence that occurs with the highest frequency (globally modal) among modal sequences on 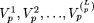. In our example, the motif of length 2 is AT on 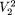= {1,3} with frequency 3.

In general, the problem of finding a motif of length p from an N×L data matrix reduces to identifying the set 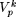, k = 1,2,..., (), from Π_p, such that the modal sequence on 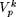is globally modal. With an N×L data-matrix, the search space Π_p has () elements. Obviously, each element of Π_p is a string, S, comprising the identities of those specific p sites chosen out of L. There are () such strings in Π_p. An exhaustive search of this space Π_p is computationally very expensive, and perhaps infeasible. We propose a stochastic search method, similar in spirit to the Metropolis-Hastings version (Metropolis et al. 1953) of simulated annealing, which is computationally fast and efficient. In this method, we maximize an objective function, G(S), that is naturally defined as the “frequency of the modal sequence on the string S ∈ Π_p.” By our definition, maximizing the frequency of the modal sequence on Π_p leads to identification of the motif of length p. Thus, the search comprises choosing both sites and characters at these sites, so that the chosen set of characters at the chosen set of sites has the maximum frequency in the data set.

Algorithm for finding a motif of a given length and assessing its statistical significance

Although in real problems, the motif length is usually unknown, for ease of exposition, we first describe an algorithm for a known motif length p, and then generalize it to the case of an unknown motif length. Instead of maximizing G(S), we shall consider the equivalent problem of minimizing a monotonically decreasing function, H(S), of G(S). The algorithm is iterative. We start with an arbitrary string S of length p; that is, a set of p distinct nucleotide sites drawn randomly from the L polymorphic sites. In each iterative step, an element (a specific site) of the string S is updated. The updating procedure requires the computation of G(S), which is done from the frequency distribution of all unique sequences at the sites included in the string S. For this purpose, given a specific string of sites, S, of length p, we enumerate from data the frequencies (f_l) of all unique nucleotide sequences ξ_l (l = 1,2,...), at the sites included in S. At each iterative step, we update a single site, and after p such iterative steps, we get a completely updated string. The procedure of updating a string completely is called a sweep. Thus, a sweep comprises p iterative steps. Let S_t denote the updated string after t sweeps.

We shall use the following notations:

1. Let 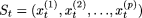, where 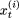denotes the i^th element (a site) of the string at the (t + 1)^th sweep.

2. Let 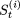denote a string in the (t + 1)^th sweep, whose first i (0 ≤ i ≤ p - 1) elements have already been modified.

3. Let 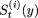denote a string in the (t + 1)^th sweep, whose first i (0 ≤ i ≤ p - 1) elements have already been modified and the (i + 1)^th element is replaced by element y.

4. Let 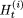denote the minimum value of H(S) after completion of the i^th iterative step in the (t + 1)^th sweep step.

5. Let 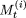denote the string of elements (array of sites) corresponding to .

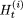We initially set 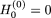, and 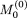as a “null” string, that is, a 1×p vector whose elements are all set to zero. The updating procedure for the i^th element in the (t + 1)^th sweep uses the idea underlying the Metropolis-Hastings algorithm (Metropolis et al. 1953), which can be described as follows:

We first calculate β_t = c.1n(t + 1); where c is a constant and c > 0. One element (x) is selected at random from the set 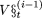; that is, from the set V = {1,2,..., L}, from which the elements included in the set 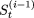have been removed. We then probabilistically update 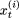to 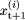according the following rule: 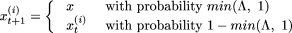where,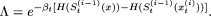

Obviously, the transition probability from one string to another depends only on the outcome of the current string (Markov property). As is easily understood from the above updating rule, at any step of the iteration, a new string that yields a smaller value of H(S) is always accepted, but to avoid being trapped at a local minimum, the new string with higher value of H(S) may also be retained with a small probability (that crucially depends on the preassigned control parameter c and the corresponding sweep step t). It may be noted, however, that as the number of sweeps, t, increases, the process stabilizes. In other words, the probability of accepting a worse string decreases as t increases. The algorithm converges to the global minimum if β_t increases to infinity logarithmically (Winkler and Lutz 2003), and the speed of convergence is determined by the local oscillations of the function H at various coordinates of its argument. (Detailed results on convergence of nonstationary Markov chains can be found in Winkler and Lutz [2003]). It is clear that our choice of β_t satisfies this general property. In practice, it is important to start with a small value of c (say, five), but also to try with larger values of c to examine convergence to the same optimal value of the function and the rate of convergence. Large values of c can substantially speed up convergence, but can also result in the algorithm being trapped in a local minimum, and a large number of sweeps may be required to get out of the trap.

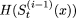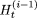After each iteration, we compare with . If, 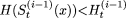, then 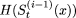is the new value for 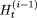and 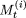is the updated string 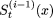. Otherwise, we do not change 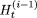and 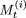. In each iteration, therefore, we compare the value of the objective function with the smallest value it has attained thus far. (If that smallest value remains the same over a large number of consecutive sweeps, then the entire procedure may have to be restarted with a new randomly chosen string. This is standard in most numerical optimization procedures.) This introduces the concept of elitism in our algorithm, which is popular in evolutionary computation (Goldberg 1989), and is done to retain the best value that was achieved during the entire run. Using available convergence results (Liu 2001; Winkler and Lutz 2003), it can be shown that as the number of sweeps goes to infinity, the value of the objective function converges to the global minimum. In practice, however, the procedure needs to be terminated after a finite number of sweeps. We have terminated when an upper bound (usually taken to be a large number; we have used the value of 5000 in our analyses) on the total number of sweeps was reached.

We note that, as with all numerical optimization procedures, it is desirable to repeat the procedure a certain number of times from different starting strings, and examine whether convergence to the same optimal value is obtained. The number of repetitions of the procedure that is practically feasible obviously depends on the availability of computing resources.

Having discovered a motif of a given length p in a data set, it is important to assess the statistical significance of the discovery. For this, we need to estimate the probability of existence of a motif of length p in a “random” data set of “similar” structure as the real data set in terms of nucleotide composition (as explained in detail in the Results section), that has a frequency higher than the motif discovered in the real data set. If this probability is smaller than a preassigned value (say, 0.05), then the motif that has been discovered can be declared to be statistically significant. To estimate this probability, we created a large number of random data sets, by randomly permuting the elements of each column of the real data set. For each random data set thus created, we used our algorithm to discover the motif of length p with the highest frequency, that is, the “best” motif. The proportion of random data sets in which the best motif had a frequency higher than that of the motif discovered in the real data set provided an empirical estimate of statistical significance. We note that for this purpose, ideally, the best motif in each random data set should be identified by a complete enumeration search, and not by using the algorithm proposed by us. However, this is infeasible unless the real data set is small. (We have actually carried out the complete enumeration search in many small data sets; the results are presented later.)

Extension of the algorithm when the motif length is unknown and assessment of statistical significance

In practical applications, the motif length (p) will usually be unknown. When p is unknown, one can start with a small value of p and increase this value sequentially, examining for each value of p the extent of decrease in the value of G(S). One can stop with that value of p when an increase to (p + 1) results in a “substantial” drop in the value of G(S). In practice, two values, p_min and p_max may be specified, and search for p may be made in the interval [p_min, p_max]. We now need a measure to evaluate whether the drop in the value of G(S) for two consecutive values of p is substantial to stop the iterative algorithm.

For any given value of the motif length p ∈ [p_min, p_max], we can use the algorithm described for identifying a motif of a given motif length, and obtain the (maximum) value of G(S) given p, which we shall denote as G(S|p). We, therefore, calculate G(S|p_min), G(S|p_min + 1),...,G(S|p_max). Let d(p_i) denote the value of G(S|p_i) - G(S|p_i + 1), where p_i ∈ [p_min, p_max-1].

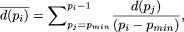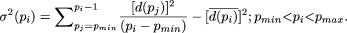To assess the statistical significance of a decrease in G(S|p) as the motif length (p) is increased, we propose the following criterion. Let and If 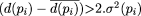, then we declare the decrease from G(S|p_i) to G(S|p_i + 1) as significant, and stop with the motif length p. The idea underlying this criterion is that we declare a drop in the value of the objective function to be statistically significant if this drop differs from the mean of all previous drops by more than two times the variance of all previous drops. In the rare event that σ²(p_i) = 0, we use the stopping criterion G(S|p_i - 1) > 2.G(S|p_i), and declare the length of the motif as p_i.

Although the above method of assessment of statistical significance is intuitively appealing, the choice of the value of the constant (=2) in the stopping criterion is somewhat arbitrary. Further, in the above search procedure, it is possible that the sets of sites included in motifs of length p and (p + 1) are disjoint. In many practical applications, this may not be desirable. Therefore, after the initial stage, new sites should be added to the set of sites included in the motif discovered thus far. Such an addition is made by searching for a site from among those sites not included in the identified motif. This strategy is not only more meaningful in many practical applications, but is also computationally less expensive. However, there is a trade-off. After convergence of this procedure, it is possible that the identified motif of length q (say) is suboptimal among all motifs of length q. When this procedure is adopted, we suggest the use of the criterion described below to assess statistical significance of increase of motif length from p to (p + 1). Let π_p and π_p+1 denote the probabilities of occurrence of the motifs of lengths p and (p + 1), respectively. Let θ_p+1 denote the probability of the nucleotide at the new site included in the motif as its length is increased from p to p + 1. We now wish to test the null hypothesis H₀: π_p+1 = π_p × θ_p+1, versus the alternative hypothesis H₁: π_p+1 > π_p × θ_p+1. In other words, we wish to test whether the additional site and the nucleotide at this site that were included to expand the motif of length p to p + 1 is associated, to a greater degree, with those sites and nucleotides already included in the motif (of length p) than is expected by chance. The level of significance of the test is given by: 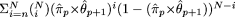, where `hats' denote the relative frequency estimates of the parameters and .

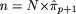Starting with a small motif length, one can continue to increase its length until the level of significance falls below a preassigned value (say, 0.05).

If the structure of a data set is such that sequential addition of sites leads to the same motif at every stage, compared with the direct procedure of identifying a motif of a certain length, then, as we shall show later, the use of these two procedures of testing statistical significance yield concordant inferences.

Identification and statistical significance of variant motifs

In a standard case-control study, a set of N individuals (cases) possessing a characteristic (e.g., a specific disease) and another set of N individuals (controls), usually matched for age and gender with the cases, not possessing that characteristic, are chosen. DNA sequence data are generated on these 2N individuals, and polymorphic sites identified. If the data are diploid, appropriate analyses are carried out (Stephens et al. 2001) to estimate the frequencies of distinct haploid sequences (haplotypes). The objective is to identify a haplotype—polymorphic motif—that occurs at a high frequency among cases, but in low frequency among controls, resulting in a high degree of association of the haplotype with disease. If, indeed, the association is due to causality, then it is expected that there will simultaneously exist a haplotype at a high frequency among controls that comprises alternative nucleotides at the same sites as those found in the high-frequency haplotype among cases. In other words, there will exist a variant motif occurring at a high-frequency among controls compared with that among cases. To identify such motifs among cases and controls, we need to maximize an objective function with respect to three parameters, which may be written in a general form as: G(S_p) = g(f₁,f₂,m), where f₁ and f₂ are, respectively, the frequencies of sequences of nucleotides at the sites in S_p among cases and controls, and m is the number of mismatches between the nucleotide sequences considered for cases and controls. The objective function is so chosen that it is monotonically increasing in f₁, f₂ and m and is to be maximized with respect to these three parameters. The idea is that, since we are searching for a variant motif among controls, we need to find a high-frequency motif among them that simultaneously exhibits a large number of mismatches with a high-frequency motif occurring among cases. Except for this natural modification in the objective function, no change in the search algorithm described earlier was made. An example and details of its implementation are given in Supplemental text 1.

Upon termination of the algorithm, we test whether the odds-ratio estimated from the 2 × 2 table comprising the frequencies of the two motifs identified among cases and controls (or in the two data matrices under consideration) was significantly different from unity (Breslow and Day 1993).

Following the same spirit as for a single data set discussed and described earlier, one may also assess the statistical significance of the discovered motif in case-control data by using a permutation algorithm to generate a large number of “random” data sets of a structure similar to that of the controls. We have done this. For each case-control data set, synthetic or real, after having identified a motif in the case data by using the variant-motif algorithm, we generated a large number of control data sets by permuting the elements of each column of the control data matrix. We then used the algorithm, and empirically estimated the probability that the odds-ratio obtained for the real data sets of cases and controls is lower than the odds-ratio obtained from the real case data and a randomly generated control data set. We have used this probability as a measure of statistical significance (p-value) of the motif discovered from the real data sets.

In data sets pertaining to evolution, the method of finding a variant motif is simpler because a specific reference sequence is generally given. In this setup, given a string, S_p, of length p, we enumerate from the data all possible sequences ξ_l,p (l = 1,2,...) of nucleotides, at the sites included in S_p. For each such sequence ξ_l,p, we calculate its frequency f_l,p. We then calculate the number of mismatches, m_l,p, of each of these sequences ξ_l,p (l = 1,2,...) with the reference sequence. The objective function is obviously to be modified as 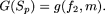It is evident from the objective function that the value of m_l,p, for which G(S_p) is maximized is ≤p. This indicates that, if the value of m_l,p realized at the maximum value of the above objective function is less than p, then there may exist sequences of length p with more than m_l,p mismatches with the reference sequence. But the frequency of such a sequence will be much smaller than f_l,p, resulting in a drop in the value of G(S_p). One effective strategy that we have used in implementing the above objective function is to start the algorithm with a large value of p. This enables us to find a sequence with a considerably high frequency, where m_l,p out of the p sites differ from the reference sequence. By keeping track of the sites at which the sequence differs from the reference sequence, we can find the sequence at the sites constituting the variant motif. Another advantage of using the algorithm is that, even without any prior on the actual length of the motif (discussed in detail in the previous section), the objective function obtains its maximum at some value of m_l,p, which enables us to get the motif length, the best estimate of which is m_l,p, from a single run.

To assess the statistical significance of the discovered motif, we generated a large number (10,000) of “random” data sets of a structure similar to the original. If the length of the motif discovered in the original data set was p, we restricted the search algorithm to maximize only over those sequences for which m_1,p was equal to p. That is, in the randomly generated data, given a string S_p, the frequency of a sequence was set to 0 if it had less than p mismatches with the reference sequence.

Results

Performance of the algorithms: Assessment using synthetic data sets

Data Set 1

We designed various synthetic data sets, so that the motif in each data set was known, to assess the performance of our algorithm. In our synthetic Data Set 1, a data matrix (N × L) was created, and a known motif of a fixed length (p) was planted in a proportion u of individuals. Data sets were created with different values of relevant parameters; details are given in Supplemental Text 2. The algorithm was applied on each synthetic data matrix, with different values of the control parameter c. As stated earlier, instead of maximizing G(S), we consider an equivalent problem of minimizing a monotonically decreasing function H(S) of G(S). We have taken 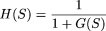in this and in all of the remaining analyses. This choice was subjective and was guided by its simplicity. 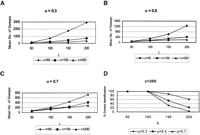However, any other monotonically decreasing function, H(S), of G(S) will also obviously work. The results are presented in Figure 1A–C, for N = 200, p = 10, L = 50, 100, 150, and 200, u = 0.3, 0.5, and 0.7, and c = 50, 100, and 200. (More detailed results for various other values of the parameters are presented in Supplemental Table 2.) For every combination of values of N, L, and p, with an appropriate choice of the control parameter c, our proposed algorithm correctly identified the planted motif in 100% of simulation runs. (Although, for brevity, we have presented results only for N = 200 and p = 10, results are similar for other values of N and p.) The role of the control parameter c is that it speeds up convergence with larger values, but the convergence may not be to the correct optimum. In our simulation experiments, while for values of c = 50, 100, and 150, the planted motif was correctly identified in 100% of simulation runs for any set of values of L and p, the proportion of correct identification was substantially smaller for c = 200 (Fig. 1D). For c = 200, the mean number of sweeps to convergence was the lowest compared with the other values of c (Fig. 1A–C). Thus, there is a trade-off between speed of convergence and convergence to the correct value. In any application of our algorithm, we recommend that multiple values of c be used, starting with a small value. In other words, we recommend that some experimentation on the convergence behavior of our algorithm with respect to c be done before accepting the results obtained by using a specific value of c.

For every synthetic data set (for different values of N and L) on which the algorithm was used to discover a motif of length p (= the length of the planted motif), we generated 10,000 random data sets of similar structure to test the statistical significance of the discovered motif, as explained earlier. In every case, the estimated probability that a random data set has a motif of frequency higher than that of the discovered motif was <10^-7. Thus, in every case, the discovered motif was statistically significant at a level <10^-7.

We have also assessed the levels of significance as the motif length was increased. The significance levels were all <0.005 as the motif length was increased from 2 to 10, but were >0.5 when the motif length was increased from 10 to 11. (Statistical significance was assessed using both the criteria described in an earlier section—assessing the significance of a “drop” in frequency with increase in motif length and also of the addition of a site. Both criteria yielded concordant inferences in every simulation run.) This indicates that our algorithm was not only able to discover the planted motif of length 10, but the discovery was statistically significant. Further, increase of length to 11 was not statistically significant. Detailed results are presented in Supplemental Table 2.

Some general results on the validity and good performance of the proposed method of assessing statistical significance of a motif discovered by our algorithm are presented in Supplemental text 3.

To examine the limits to which our algorithm can perform well, we constructed new data sets. The descriptions of the data sets and results are given in Supplemental texts 4 and 5.

Data Set 2

We created a synthetic data set analogous to that generated by a case-control study. Two separate data matrices, each of size N × L, corresponding to the cases and controls, were created. We planted, in the case data matrix, a motif of length p in a proportion u₁ of individuals. Under the common-disease, common-variant model (Collins et al. 1998), each of the p sites (SNPs) carries a small relative risk (RR) to the disease, that collectively results in a large haplotype (motif) relative risk. Hence, in the data matrix corresponding to the controls, we changed the proportion of the motif relative to the cases in such a way that the relative risk conferred by the high-risk variant at the i^th site of the motif was >0. Details of the methodology for creation of Data Set 2 are given in Supplemental text 6.

In creating synthetic data sets, we have used various values of u₁ and RR. The algorithm for finding variant motifs was used. Statistical significance was assessed by testing the null hypothesis of the odds-ratio being equal to unity, as described earlier.

The values of the parameters used in generating the synthetic data sets were as follows: N = 100; L = 100, 200, 300; p = 4 and 6; u₁ = 0.2, 0.4, and RR = 1.2, 1.5, and 2.0. For each combination of L and u₁, 1000 synthetic data sets were generated with each of the various combinations of the other parameters. The algorithm was run on each data set for values of the control parameter c = 50, 75, and 100. The results are given in Table 2, for c = 100. (For c = 50 and 75, the results, not shown, were virtually identical.) In general, our algorithm correctly identified the planted motif in a large proportion of simulation runs only when the RR attributable to a single site was high. The probability of correct identification decreased with decrease in RR. Further, for fixed values of the parameters u₁ and RR, this probability decreased with increase in the motif length, p, but was found to be not strongly dependent on the value of L. Although, for several combinations of simulation parameter values, the probability of correct identification was small or zero, we note that the number of sites and nucleotides that matched between the planted and identified motifs was large, except for RR = 1.2. This indicates that just by chance there may exist motifs with haplotype (motif) relative risks higher than that of the planted motif. However, it is clear that unless the relative risk is small, the true motif will share many sites and nucleotides with the identified motif.

Whether or not the identified motif matched with the planted motif in a synthetic data set, we carried out a test of statistical significance of the identified motif by generating 10,000 random data sets of a similar structure as the control data and estimating the odds-ratios, as explained earlier. The p-values corresponding to the identified motif in the real data, are given in Table 3. None of the identified motifs for the various combinations of the parameter values (motif-length, p; u₁; and the number of polymorphic sites) was statistically significant when RR was small (=1.2). However, when the RR was 1.5 or 2, the identified motifs were all statistically significant at the 5% level.

Data Set 3

This data set was constructed to mimic an evolutionary scenario. When two populations that have diverged from an ancestral population evolve separately, the daughter populations accumulate separate sets of mutations that increase in frequencies because of natural selection or other evolutionary forces. Thus, one may find motifs in the daughter populations, with some motif sites being shared between the two populations, while some being unshared (Schwaiger and Epplen 1995). The shared sites are presumably those sites that belonged to a motif that was present in the ancestral population, while the unshared sites are those that have arisen and increased in frequency since the divergence of the two populations from the ancestral population. We constructed a synthetic data set to mimic this evolutionary scenario (details are provided in Supplemental text 7) and applied our algorithm to assess whether it is possible to discover the relevant motifs. In this data set, the parental population (D₁) carried a motif of length 10, while each of the two daughter populations (D₂ and D₃) carried motifs of length 15, with the 10 parental sites and five additional sites in each motif.

We carried out 1000 independent simulation runs using the procedure described above, with c = 200. Detailed results for five runs are provided in Table 3, which show that our probabilistic search algorithm always converged and identified the correct motifs of correct lengths in the parental and in the daughter populations in a small number of sweeps. The final motifs were statistically significant at levels <0.005, as assessed by the procedure in which 10,000 random data sets were generated. As a matter of fact, correct convergence was achieved in every one of the 1000 runs (detailed results not provided) and the convergence using the proposed algorithm was fairly fast (Supplemental Table 6).

Identification of variant motifs: Applications to real data

Gilbert's syndrome: Case-control study

In an ongoing study on Gilbert's syndrome (OMIM #143500), we have generated DNA sequence data of the promoter of UGT1A1 gene among affected individuals and normal controls. The syndrome, characterized by elevated levels of unconjugated serum bilirubin, is caused primarily due to the homozygous insertion of a pair of nucleotides T and A at specific sites in this promoter (Bosma et al. 1995). However, a small fraction of normal individuals also carry these insertions in heterozygous form. In addition to these insertions, in our study, we have found a subset of affected individuals to carry an additional trinucleotide (CAT) insertion at a specific site in the promoter. This insertion has not been found in any of the unaffected control individuals. Haplotypes and their frequencies were estimated from the sequence data, separately for the cases and controls. The size (80 × 456) of the data matrix was the same for both cases and controls. We have used the algorithm for finding variant motifs (with c = 100) and were able to identify the 5-site motif (corresponding to the TA dinucleotide and the CAT trinucleotide insertions) correctly. The 5-site motif was estimated to be present in 11.25% of the cases and 0% of controls, which agreed with the actual count. Since none of the controls possessed this motif, the relative risk cannot be computed, but the finding is obviously significant (11.25% among cases, vs. 0% among controls). The exact p-value computed from the binomial distribution (using the estimate of the probability of the motif from the pooled data of cases and controls) is 9.74 × 10^-3.

LDL receptor haplotypes among individuals of European and African descent: The PARC study

In an ongoing project entitled “Pharmacogenomics and Risk of Cardiovascular Disease” (PARC) at the University of Washington, Seattle, data on haplotypes of individuals belonging to African descent (n = 48) and European descent (n = 46), pertaining to the LDL receptor gene (located on human chromosome 19p13.3), have been made available in the public domain (http://droog.gs.washington.edu/parc/data/ldlr/welcome.htm). The number of polymorphic sites (L) in this data set is 117. We have used our algorithm to find whether there are any high-frequency contrasting (variant) motifs present among individuals of European and African descent. We have used our algorithm for finding variant motifs (with c = 100) and discovered that the motif TTTGGTAGC of length 9 occurs at the nucleotide sites 26, 34, 41, 43, 50, 54, 57, 58, and 61 with a frequency of 19 (39.5%) among individuals of African descent, and a completely contrasting motif CCGACCCAT occurs at these sites with a frequency of 34 (73.9%) among individuals of European descent. The degree of association in the corresponding 2 × 2 table is statistically significant at a level <0.001. Both of these motifs were statistically significant with estimated p-values < 10^-7. (To test the significance of the discovered motif among Europeans, we generated 10,000 random data sets of a structure similar to that of African-descent individuals, and vice-versa for testing the significance of the discovered motif among individuals of African descent.)

Mitochondrial DNA haplogroups M and U

Extensive sequence data on the hypervariable segment 1 (HVS1) of the mitochondrial DNA (mtDNA) have been generated (Handt et al. 1998) and analyzed (Macaulay et al. 1999) in various global populations (http://www.hvrbase.org). Based on the presence or absence of specific restriction sites outside of the HVS1 in the mtDNA, two of the major haplogroups (HGs) identified are M and U (Wallace 1995). Within these haplogroups, specific motifs have been found in the HVS1, some of which are in contrast to those found in the CRS (Anderson et al. 1981). These motifs have been used to define haplogroups within the HGs (Kivisild et al. 1999). We have used data of 528 individuals from various ethnic populations of India (Basu et al. 2003). The total number of polymorphic sites in this data set was 153, and the numbers of individuals belonging to HGs M and U were, respectively, 338 and 115. We applied the motif-finding algorithm (with c = 100) separately on the HVS1 sequence data of HGs M and U. An objective function,G(S_p), that gives considerable weightage to the number of mismatches was used, that is, 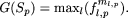For HG-M, G(S_p) attained a maximum value with m_l = 4, for all values of p ≥ 4. For m_l = 4, the sites at which nucleotides differed from the CRS were S = (16223, 16270, 16319, 16352). The frequency of this string, f_l, was 21 (= 6.21% of the total number of samples), and the nucleotides at the relevant positions were T, T, A, and C, respectively. The next most frequent string was (16223[T], 16274[A], 16319[A], and 16320[C]) with a frequency of 17 (5.03%). These two motifs belong to known subhaplogroups M^* (defined by C→T transition at the site 16223) and M2 (defined by C→T transition at the site 16223 and a G→T transition at the site 16319), which are prevalent in Indian populations (Bamshad et al. 2001).

For HG-U also, the objective function, coincidentally, attained a maximum at m_l = 4, and the motif identified was (16051[G], 16206[C], 16230[G], 16311[C]), with a frequency of 18 (=15.65% of the total number of samples). The vast majority of HG-U individuals in India belong to HG-U2i and U7. The U2i is the Indian-specific subcluster of U, as opposed to the Western-Eurasian subcluster U2e (Kivisild et al. 1999). Interestingly, the motif GCGC at nps 16051, 16206, 16230, and 16311, respectively, has been found on the U2i background, which is present in 18 of the 115 individuals. This motif is found almost exclusively among tribal, middle- and lower-caste populations, but not among the upper-caste populations or the Muslims (of Uttar Pradesh). This motif is also present in many of the Pakistani samples screened by Kivisild et al. (1999). Our bootstrap procedure for testing statistical significance of a motif indicated that in all of the above cases, the identified motifs were statistically significant at level <0.05.

These examples demonstrate that the proposed algorithm was able to identify previously discovered motifs, and therefore, can be profitably used in evolutionary studies to identify new motifs. The anthropological implications of our findings on HGs M and U presented above have already been described in Basu et al. (2003).

The !Kungs of Botswana, Africa

We have also applied our algorithm (with c = 100) on mtDNA HVS-1 data sets (Handt et al. 1998) of various African populations. The algorithm identified a motif of length 5 in the !Kung population of Botswana, which contrasts with the CRS. The motif is constituted by the sites 16129, 16223, 16230, 16294, and 16311. The nucleotides in the respective sites in the CRS are G, C, A, C, and T respectively, while in the !Kung population, the motif is ATGTC. The motif is present in 17 (68.0%) of 25 !Kung sequences. Using the procedure suggested earlier, with 10,000 replications, no variant motif of length 5 with a frequency higher than that of the identified motif was found, indicating that the statistical significance of the identified motif is very high. The uniqueness of the motif is not only characterized by its difference from that present in the CRS, but also because this motif is not present in any other African population (Table 4), and has probably risen to the present high frequency among the !Kungs by genetic drift.

Discussion

The problem of identifying motifs in genetic data arises commonly in human genetical research. Such data include DNA sequence data, haplotype data, and genotype data. Motif identification is necessary to draw inferences on evolutionary histories of populations or lineages, to examine associations in case-control studies, etc. More recently, with the initiation of the HapMap project (Couzin 2002), the problem of finding motifs within haplotype blocks, which probably occur because of variation in recombination rates across the human genome, arise naturally. In most of these applications, it is pertinent to identify motifs of nucleotides at a set of polymorphic sites, which may not be contiguous. For example, in research on complex diseases, often data are generated on multiple unlinked genes, and if, indeed, genotypes or haplotypes at a subset of these genes determine the susceptibility to the disease, then motifs will exist at a set of noncontiguous polymorphic sites. A search based on complete enumeration for such motifs can be computationally extremely time consuming and inefficient—it might not even be feasible in practice for large data sets. To the best of our knowledge, no computationally efficient algorithms exist for finding motifs at noncontiguous polymorphic sites. We have, therefore, devised a set of computationally fast and efficient algorithms based on probabilistic methods. We have first devised a search algorithm when the length of the motif is specified a priori, and have then extended it to take into account the possibility of the motif length not being known a priori. The specific functions (e.g., β_t, H(S)) used by us were chosen not only to satisfy the criteria required for convergence of this class of probabilistic search algorithms (Winkler and Lutz 2003), but also because of their simplicity and intuitive appeal. Our algorithms are not tied to these specific choices of functions; users may try other functions satisfying the general conditions required for convergence. For a given motif length, we have proposed a statistical criterion of assessing the significance of the motif discovery using a bootstrap procedure. When the motif length is not specified, we have devised a statistical criterion for determining the motif length from the data simultaneously with the search for a motif. We have proposed an alternative criterion of assessing statistical significance when the motif length is extended by sequential addition of sites and nucleotides. Finally, we have proposed methods for assessment of statistical significance of a discovered motif in a real data set, in relation to a random data set of similar structure. Using various synthetic data sets to mimic real-life applications, we have demonstrated that the proposed methods work well. We have also applied these methods to several real data sets—pertaining to case-control data on complex phenotypes and evolutionary data—and obtained many useful inferences.

Through our simulations, we have discovered some of limitations of our algorithm as well. In particular, when we assessed (Supplemental text 4) whether our algorithm converges correctly in a search space that contains exactly one global maximum, and also a large number of local maxima with values not very different from the global maximum, our algorithm failed to converge to the global maximum. This limitation is, of course, inherent to all numerical search procedures that do not use complete enumeration. Further, in simulated case-control data, our algorithm failed to identify the correct motif, especially when the relative risk attributable to a site included in the motif was small (Table 2). For a small relative risk, the identified motif was also statistically nonsignificant (Table 2). However, in most simulation runs, the identified motif shared several sites in common with the planted motif. The reason for nonconvergence to the correct motif was due to the fact that in realistic case-control data sets, there may be multiple motifs with high haplotype (motif) relative risks just by chance, especially when individual sites (SNPs) do not confer a large relative risk to the disease. This finding is consistent with published observations (e.g., Cardon and Bell 2001) that significant findings of haplotype associations from case-control studies are often not replicable. Our simulation results also underscore the need for replication of findings of case-control association studies.

We would finally like to emphasize that the convergence properties of the proposed algorithms are critically dependent on the control parameter, c. While from the user's point of view it is desirable to be able to prescribe some universal and objective guidelines for the choice of c, this is not possible. In specific applications like those presented here, one can identify a range of values of c that makes the algorithm computationally feasible, with a high probability of convergence to the true optimum. In practice, this range of c needs to be identified by trial and error. We first note that the speed of convergence is directly proportional to the value of c. Further, the probability of convergence to the true optimum for a specific choice of c is more dependent on the value of L than on N. Using these two facts, the user should make a judicious choice of c, but try with multiple values. We strongly recommend that some experimentation on the convergence behavior of the algorithm with respect to c in multiparameter settings be done to make a judicious choice of c. We have found that with N in the range of from 200 to 500 and L in the range of from 200 to 500, any value of c in the range of from 50 to 100 works very well.

Although we have formulated our algorithms keeping haplotype or haploid DNA sequence data in mind, there is no inherent limitation to use these methods on genotype data. Genotype data need only be recoded in order to apply these algorithms. For example, at a biallelic locus, with alleles A and a, the genotypes AA, Aa, and aa may be recoded as 1, 2, and 3. We finally note that there are other classes of probabilistic search algorithms—such as genetic algorithm (Goldberg 1989), Gibbsean annealing (Winkler and Lutz 2003), and evolutionary Monte Carlo (Liang and Wong 2001)—that may also be applicable to the problem considered in this study. We have not explored these classes of algorithms in any detail, and therefore, make no claim that the algorithms proposed by us will outperform other probabilistic search algorithms.

We have developed a computer program, MOTIFIND, implementing these algorithms. This program is written in C, and can be obtained by writing to the authors. This program can handle both haploid and diploid genotype data.