Systematic Analysis of DNA Microarray Data: Ordering and Interpreting Patterns of Gene Expression

From Gene Expression to Trees: The View From Systematics

Systematic methods have contributed greatly to the fields of comparative and evolutionary biology as tools for finding natural patterns in molecular and morphological data. Computational methods in systematic biology are designed to order data in terms of a hierarchy of relationships from which evolutionary history can be inferred (Miyamoto and Cracraft 1991). Gene expression profiles present a type of data that seems analogous to other types of data used in systematic analyses. Many recent attempts to organize the impressive amount of information in microarray studies have relied on techniques borrowed from systematic biology that offer quick computation and organization of the data (Eisen et al. 1998; Eisen and Brown 1999; Bassett et al. 1999). However, the goals of gene expression analyses differ significantly from the goals of reconstructing evolutionary history. Here, we review the systematic techniques currently applied to large gene expression data sets and discuss the ramifications of applying these and other systematic techniques to expression profiles. We suggest that the large body of work generated by phylogenetic systematists over the last few decades is relevant to understanding which techniques might be best applied to attain the specific goals of gene expression analysis. We believe these techniques could form a practical and theoretical framework for assessing the outcomes of DNA microarray studies.

The major goal of systematic analysis is to extract order from data that gives clues about biological reality. In phylogenetic systematics, the biological reality is the evolutionary relationships among taxa, and the biological order is the hierarchical pattern in the data that tracks the lineage splitting and divergence represented by a dendrogram or tree. In contrast, systematic treatment of microarray data assumes that order intrinsic to gene expression profiles will yield insights into molecular, cellular, and tissue level processes and functions. This approach, in turn, might allow for improved disease classification, diagnosis, prognosis, and drug design, among other pharmaceutical and medical goals.

The assumptions that are appropriate for any analytical method are determined by the type of biological order that the method seeks to recover. Although gene expression data are similar to other types of data collected for traditional systematic studies (e.g., DNA sequence data, morphological data), it is not immediately obvious how techniques initially designed to elucidate relationships between organisms should be applied to gene expression profiles. There is a longstanding philosophical debate contrasting similarity-based and character-based methods in the analysis of problems in evolutionary biology and organismal classification. Because the most widely used methods in microarray studies are based upon some measurement of overall similarity of genes or cells or tissue types, it may be informative to revisit this debate as it applies to microarray studies. Although both overall similarity and character-based techniques can produce trees, or branching diagrams, the fundamental assumptions and interpretations of the outcomes differ significantly. The choice between the two depends, therefore, on what the researcher is asking, the nature of the data being collected, and the biological context of the study.

Trees in Systematics: What Are at the Tips?

First, one must decide on the units for comparison and organization. In evolutionary systematic analyses, the units for comparison are called taxa. They can be species, individual organisms, genes, or other biological entities. The data collected for comparison are the attributes of the taxa. Through comparison of the attributes, taxa can then be grouped and categorized. For DNA microarray data, there are at least two basic types of taxa: genes, and biological samples (e.g., biopsies from individuals, cells, or tissue types). When genes are taxa, each gene's attributes are the expression levels in the different samples. This pattern is the basis for comparison among genes. Alternatively, each sample can be seen as a taxon, and the gene expression profile of all genes in the sample then becomes the basis for comparison. The two approaches to designating taxa permit two very different classes of questions. The first asks which genes group together because their expression levels are similar in the different samples. The second asks which samples (perhaps representing phenotypes, cell types, time points, environmental conditions) group together because the expression levels of their component genes are similar.

The choice between these two approaches to defining taxa depends on the goal of the study. Identifying genes that group with each other because of similar expression patterns might lead to the discovery of genes that interact, are coregulated, or are required in the same pathway, developmental stage or pathogenic process. Identifying samples that group together may be more helpful in the search for new isolates, more precise diagnoses, and more defined prognoses.

Chopping Down Phenetic Trees

Once the taxa have been chosen they can be grouped by several different systematic-based techniques. Only a small subset of these techniques have been used with microarray data. Examples range from simple visual inspection (Cho et al. 1998), to techniques that create unrelated clusters (Golub et al. 1999; Tamayo et al. 1999), to still other techniques that arrange clusters and taxa in a hierarchy that can be represented by either a tree diagram (Eisen et al. 1998; Spellman et al. 1998; Alon et al. 1999) or Venn diagrams (Holstege et al. 1998).

Microarray tree-building techniques, thus far, have relied on the process of grouping by overall similarity. The assumption is that the natural order of gene expression and cell phenotype is based on, or can be uncovered by, similarity in expression profiles. The explicit formulation of this idea is derived from the phenetics movement of the 1950s as codified by Sneath and Sokal (1973). Several of the techniques developed by pheneticists (e.g., the unweighted pair-group method using arithmetic averages (UPGMA) developed by Sokal and Michener (1958)) have been used as the clustering methods of choice in analyses of DNA microarray data (Eisen et al. 1998).

These techniques are used to construct phenetic trees (dendrograms). These trees are, strictly speaking, a visual representation of the overall degrees of similarity between samples based on the characters or attributes under consideration. Two samples that are most closely paired (sister taxa in the tree) are simply the two samples that most resemble one another based on the attributes being considered. They are not necessarily most closely related in terms of a recent common origin or common biological process, as discussed below.

To construct a similarity-based tree (dendrogram or phenogram), each taxon must be compared to every other taxon. The similarity between taxa can be estimated by multiple types of simple pairwise comparison or by vector/Euclidian techniques (Sneath and Sokal 1973). In all cases, the raw data are converted into a grid of pairwise similarities — the similarity matrix. This pairwise similarity matrix is then used as the basis for phenetic tree-building techniques.

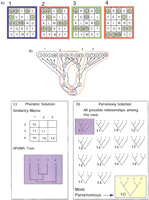
UPGMA clustering, or tree-building, finds the most similar pair of arrays or genes and groups them together. It then replaces these two taxa with the newly formed group as one new taxon. This “new” taxon is merely the arithmetic mean of the similarities of its members. With the new taxon in the similarity matrix, the technique finds the next pair of most similar taxa and repeats this process until all samples are included in the tree (Eisen et al. 1998). This is a tips-of-the-tree-down approach (see Fig.1C). Another technique recently used (Alon et al. 1999; Getz et al. 2000) is a bottom-up approach that starts with a pool of all the data. The pool is divided into two groups based on a normalized vector measure of similarity. Each respective group is then divided into two more groups, and this process continues iteratively to produce a tree.

Both of the above techniques of data analysis are similar in that they use criteria of overall similarity to organize the gene expression data. Is this the approach best suited to yielding insight into biological processes and further testable hypotheses? The answer lies in whether or not large-scale changes in gene expression are the primary determinant of biological function. If changes in a relatively small subset of genes can cause functional or phenotypic change, then overall similarity might not be the best way to evaluate gene expression profiles (Getz et al. 2000).

Phenetic trees have had only limited success in distinguishing between different types of leukemias and lymphomas (Wooster 2000). When applied to breast cancer, a clustering-based analysis could accurately identify tumors with BRCA1 mutations, but not BRCA2 mutations (Ingrid et al. 2001). One study using a phenetic approach found prognostically significant subgroups of diffuse large cell lymphoma. This model has yet to be verified as a clinically applicable predictor of tumor behavior.

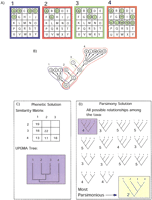
Furthermore, in examinations of evolutionary data, phenetics has several methodological shortcomings that have been addressed independently by several researchers (e.g., Farris 1982; Felsenstein 1988). These criticisms may be as appropriate for gene expression analyses as they are for evolutionary studies. First, for clustering methods such as UPGMA, clusters will reflect the underling hierarchy only when rates of change among the attributes are the same. Therefore, if we imagine that the mRNA expression profile of a cell is due to a set of interactions and reactions, then all of the changes between mRNA expression states would need to have occurred at a similar rate. The problem for gene expression analyses occurs when certain cascades of molecular events affect the expression of many more mRNA species compared to other cascades (Fig. 2). Alternatively, cellular events mediated by constitutively expressed genes or lingering protein products not recorded as changes in transcriptional expression may make certain expression profiles seem very similar when the taxa have actually experienced very different events.

Second, phenetics measures overall similarity and does not account for the presence of mRNA that has been retained from previous events. In evolutionary terms, phenetic approaches group taxa based on attributes that are shared, whether they be retained (i.e., ancestral or symplesiomorphic) or recently obtained (i.e., derived). Therefore, it may fail to group samples (taxa) that have very rapidly lost or gained expression of several genes with samples that are about to undergo this rapid change. For instance, consider a pathway that results in a general repression of several mRNA transcripts. If the cascade of events is sampled early, even though the cascade will eventually go to completion, not many genes are repressed yet. If a sample is taken toward the end of the cascade process, all genes will be repressed, making for a very different expression profile. The retention of regular mRNA expression through the first steps of a pathway for gene repression can be seen as retention of “ancestral” characters, whereas the first few genes expressed in the pathway represent shared derived characters between all cells that have entered the pathway. Because phenetics groups taxa based on both ancestral and derived states, it would group cells that had just begun the process with cells that are not undergoing the process, not with the more derived cells that are further along in the process. Therefore, no cluster in the phenogram would capture all of the cells in the repression process (including those in the early stages), and this natural biological order would be lost.

Phenetics might also not account for convergence in expression profiles. Similar patterns of gene expression may be due to different regulation events or pathways. Taxa that have arrived at similar states for different reasons will group together, and pathways that overlap by random chance or for some functional reason may be misclassified (Fig.1C, samples 2 and 3). In phylogenetic terms, this would represent homoplasy, or convergence.

Finally, phenetic methods lose information when the raw data are converted into a similarity matrix. For instance, two taxa can have exactly the same similarity score when each is compared to a third taxon without any overlap in the distribution of similar characters. If the goal of an analysis is to use the results of the clustering algorithm to identify biologically or clinically meaningful groups of cells or tissue types, then this loss of information has important consequences, especially if phenetic clustering techniques are used as a starting point for identifying diagnostic attributes.

The Other Forest of Trees

The other class of tree-building methods are character-based, meaning that taxa are grouped by discrete characters that they share with one another. The tree is built using some criterion that discovers the optimal distribution of discrete characters among the taxa. One major advantage of character-based tree building is that the raw data are conserved throughout the tree-building process. Currently, there are two widely used character-based methods in systematics that generate hierarchical relationships among taxa: parsimony and likelihood.

Likelihood methods use a specifiable model of how characters change from one form of the character (its state) to the next. Given this model, the method can then calculate which hierarchical pattern (represented by the likelihood tree) is the most probable explanation for the observed gene expression data. Likelihood methods appear at present to be inappropriate for gene expression data. While some systematists are developing maximum likelihood models to deal with discrete morphological data based on correlated changes (Lewis 2001), we suggest that we know so little about how expression patterns change that a generalized specifiable model of change is not forthcoming.

Parsimony analysis, also called cladistics or phylogenetic systematics, was developed by Willi Hennig at approximately the same time that phenetic techniques were first being formulated (Hennig 1966). As with phenetic techniques, parsimony analysis seeks to determine the hierarchical relationships among taxa, displayed in the form of a tree diagram referred to as a cladogram. Parsimony methods rely on the existence of a particular types of shared characters to distinguish groups of taxa from one another. These are referred to as shared derived characters, where derived means the state or version of the character that appeared more recently in evolutionary time than the alternative, ancestral version. This distinguishes parsimony methods from phenetic methods, which group taxa based on both shared derived and shared ancestral characters or attributes. In practical terms, trees are evaluated and the tree which requires the fewest number of changes among the characters is chosen as the preferred tree, or cladogram (see Fig. 1D). Thus, a cladogram represents the distribution of characters that requires the fewest number of character changes to explain the data. This can be thought of as a representation of the most plausible (the least ad hoc) series of events that created the observed states.

In gene expression data, the application of parsimony methods would produce a cladogram (tree) designed from the fewest number of molecular events that account for all of the variation in expression data. This explanation is the best estimation given the available data. This analysis would not rely on a calculation of overall similarity, would not require that the rate of molecular interaction or mRNA transcript change be constant, and should not be affected as much by the “noise” of convergent expression patterns.

Parsimony analysis of gene expression data also has several other advantages. First, because it would be based on a distribution of events that link groups of taxa (clades), these events can be reconstructed from the tree (cladogram) (Maddison and Maddison 1992). The cladogram can be used to determine genes that are associated with certain microarray conditions and microarray conditions that are associated with certain patterns of gene expression. This can lead to the formulation of hypotheses that such associations have functional or causal relationships, which can be tested in the biological systems. For instance, the functional role of genes that are associated with a clade of cancerous cell lines can be explored using molecular and genetic techniques at the bench. Similarly, microarray conditions may help identify conditions that trigger the expression of certain genes. In this way, examination of the endpoints from a cladistic perspective might help to direct research that aims to tease out cascades of functional interactions.

Another advantage of reconstructing attributes or events that correlate with certain groups in a parsimony analysis is that such events can be used as the basis for classification and diagnostic tests. If these attributes or events define members of a group to the exclusion of others, they can be seen as diagnostic features that can be used to place new taxa (e.g., samples or biopsies) in a group. The diagnosis of malignant transformed cell lines in cancer studies is a good example. Once a tree has been constructed for the cell lines and diagnostic gene expression events have been extracted from the tree, a sample from a patient suspected of having a malignant growth can be screened for the diagnostic expression patterns or events. Therefore, the number of diagnostic assays required by this approach would only be equal to the number of genes that show diagnostic expression patterns necessary to identify a type of cancer. This should be contrasted with phenetic techniques of classification that rely on estimates of overall similarity. Phenetic approaches to classification and diagnosis require expression profiles for all of the genes used in the study that lead to the identification of the groups in the first place. This process entails asking an experimental question about every gene in the microarray, which can lead to problems due to experimental variation, time, and money (Wooster 2000).

Interestingly, investigators have attempted to use parsimony techniques to map diagnostic events onto phenetic trees (Alizadeh et al. 2000). Because in phenetic trees the taxa are clustered using the assumption of overall similarity, and the raw data linking the individual gene expression patterns to the samples have been sacrificed, this approach may lead to incorrect interpretation of character mapping (i.e., character distribution) and diagnosibility. Even if a character seems to cleanly map onto a specific cluster in the phenetic tree, the groups defined by the phenetic clustering algorithm may not be the same groups supported by the distribution of a particular character. Discrepancies like this arise because the data responsible for the phenogram (i.e., the similarity matrix) are not the same as the character data considered on a gene-by-gene basis.

Gene Expression and Bins

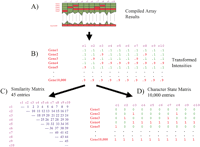
The data derived from a DNA microarray are the scaled and corrected intensities of hybridization at each gene locus. These intensities are shown in transformed matrices as numerical values that are continuous on predetermined and arbitrary scales (e.g., Alizadeh et al. 2000). In phenetic similarity analysis, a raw data matrix of 10,000 genes for 10 “taxa” (or 100,000 bits of information) would be reduced to a symmetrical matrix of 45 pairwise comparisons (Fig. 3).

Because microarray data exist on a continuous numerical scale (Fig.4), these data must be transformed if they are to be analyzed using a character-based approach. Although parsimony methods can use continuous data (Swofford 1987; Siddall 1998,2001), they are most efficient and valid with discrete characters. For instance, DNA sequences are particularly amenable to discrete character data; that is, they are a G, an A, a T, or a C. In some rare cases, natural breaks exist in seemingly continuous data (Fig. 4), and the continuous data can be broken easily into general discrete classes that have large gaps between the observed values. The biological meaning of natural breaks in the data set might be a threshold value in expression or a very tight kind of regulation. Microarray hybridization intensity data often lack these natural breaks.

To transform or convert continuous data to discrete data, one can erect boundaries (either arbitrary or logical in nature). Arbitrary artificial gaps can be imposed so that the continuous data are given discrete character states (Fig. 5). A simple approach would be to set some standard increment, such as whole number integers, and round all continuous values to the nearest increment. Another approach that we have developed is referred to as binning (Sarkar et al. 2001). In this approach, the matrix entries that coincide with certain ranges of continuous values (bins) are scored as predetermined character states (0, 1, 2, etc.). The entries that coincide with the values in regions between the bins are considered undetermined or missing, in the parlance of cladistics. The number and width of bins can be arbitrary, but the structure of the binning will determine the amount of missing data. Again, the choice of binning strategy depends on the goals of the study. If a study aims to determine which genes are highly expressed and which genes are extremely downregulated, a coding system in which a large gap exists between bins on the ends of the distribution of intensity values (see Fig. 5, binning 2) would be appropriate and defensible. If a study requires a finer scale of character states to detect subtle expression transcript changes, then the data can be coded with more bins (see Fig.5, binning 3). The binning approach may require empirical testing with any given data set, but also provides a more versatile way to analyze the data than simple rounding methods. Further, because there are so many entries in the original microarray matrix, coding some of them as undetermined may not be a severe detraction. Given that there can be a great deal of variance around each microarray measurement (Hughes et al. 2000) in a raw matrix, one might even extend the binning method to its limit in which it would be advantageous to use only the extreme values in the matrix and score all intermediate values as missing.

When Trees Rot

One very important issue relevant to systematic analysis that has been overlooked by most microarray studies is the question of robustness for the hierarchical inferences of classification or function. If the analysis is done several different times and in several different ways, does the tree look the same? Most analyses that use the criterion of overall similarity, by default give a single tree in each analysis because the algorithms can only pass through the data once. In contrast, cladistic methods often give multiple, equally parsimonious solutions to a data set as a result of lack of character support for those internal groupings that differ in the equally optimal trees. When multiple cladograms are obtained, a consensus tree is constructed and used to represent the set of equally parsimonious solutions. The consensus of equally parsimonious trees will never be fully resolved, meaning that some taxa or clades will not have a single closest relative; they will have a few or many in the tree. In this case the data are not able to assign taxa to specific groupings, which may mean that there are not enough data or that specific groupings are not supported by the data. The latter case may be very relevant to biological processes in which a single expressed gene can upregulate more than two possible expression pathways (i.e., there may be a common “origin” for several lineages). In addition, researchers may find it useful to test more than one hypothesis of biological classification or function. Generating multiple most-parsimonious (and even a range of slightly suboptimal) trees allows for this exercise.

To test the robustness of a given tree, there are several measures of support that are currently in use in systematics. All confidence tests give measures of robustness at branch points in the tree called nodes. Nodes represent the group composed of all taxa that branch from it. Resampling techniques such as the bootstrap (Felsenstein 1985) and the jackknife (Farris et al. 1996), where the resampling method gives a proportion (from 0% to 100%) of replicates that support particular groupings in the tree can be used as indicators of robustness for certain nodes. These algorithms ask how often trees built from subsampled portions of the data set reproduce the groupings seen in the tree built from the full data set. Both the jackknife and the bootstrap can be applied to similarity- and character-based data. A parsimony-based measure of robustness is the Bremer, or decay index (Bremer 1988, 1994), which measures the number of extra steps or changes in character states that are needed to refute a particular grouping in the most parsimonious tree. In other words, this test asks how many additional events and explanations need to be hypothesized to change the tree. Inferences made about trees without considering support are sometimes easily overturned by the addition of more data or by altering parameters in the analysis.

Clearing the Forest

One major question in considering systematic analyses of gene expression profiles is whether a tree is a good way to organize the data in the first place. Several phenetic algorithms that produce clusters with no relationship to one another are available (e.g., self-organizing maps [SOMs]; Kohonen 1997). Population aggregation analysis (PAA, Davis and Nixon 1992) is a character-based method that has been used in conservation biology to establish wildlife conservation units. This approach searches for fixed differences between and among predefined aggregates (groups) in analyses of character data. Because this technique relies on predefined groups, it requires some set of external criteria or preconceived notions to establish the groups, such as tissue types, cancer types, or developmental stage. One interesting result of this approach applied to conservation biology is that closely related aggregates are sometimes found to have no single diagnostic character. However, close examination of the data demonstrates the presence of attributes that are present in some, but not all, members of a group and are completely absent from the other group(s); these are “private” diagnostic characters. On their own, private diagnostics do not do much good; they simply define some members of a group. However, as long as every taxon in an aggregate has one private attribute for that group, then all members of the group can be identified. In gene expression data, a private character may represent a gene whose expression pattern contributes to a phenotype that is unique to that group and deserves further study. A cursory examination of several microarray data sets indicates that groups rarely have purely diagnostic characters, while private attributes are very common. Other types of character distributions may also be helpful in finding diagnostics for gene expression profiles (Sarkar et al. 2001).

It is also possible that tree types not discussed here may be needed to represent a biological process or function. The assumption in evolutionary biology is that the natural pattern of lineage divergence can be represented by a tree whose branches never rejoin. A similar assumption in expression profile data would be that gene expression is only ever regulated by (or observed as) the expression of one other gene. If this is not the case, then it may be necessary to develop techniques that can order microarray data as a network or reticulated tree.

Conclusion

The enormous amount of data in gene expression studies utilizing DNA microarray technology requires some method of analysis that efficiently organizes or “groups” the data. The analysis gains power when the specific traits or characters that diagnose a group can be identified. Character-based techniques such as those suggested here offer the ability to both determine groups and help recover the biological basis for the groups that they define. In general, much more work is necessary to clearly define assumptions and assess phylogenetic techniques as applied to gene expression data. As more DNA microarray studies are carried out, empirical testing and comparisons of methods will help evaluate the benefits and detractions of character-based and similarity-based approaches for answering specific questions using gene expression data sets.