Box 1.
Theory
| Notation and Assumptions |
| We now outline model specifications for the target size, clone size, clone library size, STC length, the rule for declaring a match of an STC and a region of a sequenced clone, the probability distribution for randomness of nucleotides, sequencing-error rates, frequencies of true and false overlap declaration, repeat families, problem clones, and economic cost considerations. |
| • Target and library specifications are denoted as follows: |
| • T is the length of the genomic target to be sequenced in base pairs. For simplicity, we will ignore edge effects at the ends of the target. |
| • C is the clone insert length in base pairs. This length can be varied to find the optimal clone size for a target of size T. |
| • N is the number of clones to be analyzed to form the library of STCs and from which selected clones are to be sequenced in their entirety. TheN clones of length C are assumed to be randomly and independently located along the target. Several tests (including FISH analyses of clones and the frequency of matches between the current set of STCs with known repeats and other sequences in the public databases) suggest that the clone inserts in the BAC libraries that are now in widespread use are fairly uniformly distributed across the genome (L. Hood, C. Venter, G. Mahairas, M.D. Adams, J. Young, and B.J. Trask, unpubl.). |
| • S =NC/T defines the coverage or redundancy as the total clone length divided by the target length, representing the expected number of clones covering each base of the target. |
| • STC length and decision rule are specified as follows: |
| • m is the number of bases that define an STC at each end of each clone. |
| • k specifies the rule used to decide overlap between an STC of one clone and a sequenced subregion of length m from another clone. If the STC sequence and the subregion sequence have k or more corresponding positions with the same base, they will be declared to overlap. This conservative rule was chosen for tractability; more complex rules might consider clustering of the matches and exclusion/adjustment for known frequent repeats, potentially improving performance by using additional information. |
| • Nucleotides are assumed to be drawn from the following probability distribution: |
| • αA, αC, αG, and αT specify the probabilities of choosing each base at random (so that αA + αC + αG + αT = 1). We assume that the target consists ofT independently selected random bases from this distribution. |
| • α = α2 A + α2 C + α2 G + α2 T is then the probability that two independently selected bases are identical by coincidence. |
| • Errors in sequencing STC ends and entire clones are modeled as follows: |
| • ɛSTCdenotes the STC sequencing problem rate (which will be used to define the observed sequencing error rate). We assume that bases are read independently. A base is read initially correctly with probability 1 − ɛSTC. With probability ɛSTC, the reading is instead an independently sampled random base (with distribution specified by αA, αC, αG, and αT) that may, by coincidence, be the correct base |
| • ɛ* STC denotes the STC sequencing error rate, that is, the probability that a given base in an STC sequence has been read incorrectly. Note that ɛ* STC = ɛSTC (1 − α), so the observed error rate is less than the problem rate ɛSTC. |
| • ɛclone denotes the clone sequencing problem rate, defined using the same process as for ɛSTC. We allow these problem rates to be different because the clone sequences are typically assembled as the consensus of many overlapping subclonal sequences [typically ≥7.5 (Rowen et al. 1997)], whereas the STC will result from a single end-sequence determination. |
| • ɛ* clonedenotes the clone sequencing error rate, that is the probability that a given base in a sequenced clone has been read incorrectly. We again have the relationship ɛ* clone = ɛclone (1 − α). |
| • Probabilities and frequencies of true and false matches are as follows: |
| • p true denotes the probability that a particular STC is (correctly) declared to match anm-base portion of a sequenced clone when, in fact, both sequences refer to the same m-base region of the target. A formula for p true is given in theorem 4 of Appendix . Whereas p true is expected to be close to 1, it may be beneficial to choose a high value for the decision rulek so that p true is slightly smaller to protect against the possibility of falsely matching a similar sequence from a repeat family. |
| • λtrue = (C − m + 1) [(N − 1)/(T− C + 1)] p true denotes the expected number of truly overlapping STCs detected within a particular sequenced clone that would extend that sequence in a particular direction (if the STC’s clone was selected and sequenced). This formula is justified in Appendix , following the proof of theorem 4. Locations of such STCs within the clone will be assumed to follow a Poisson process. Note that if m is small compared with C and if Cis small compared with T, then λtrue ≅Sp true. |
| • p falsedenotes the probability that a particular STC of one clone is (incorrectly) declared to match a particular m-base portion of a sequenced clone when, in fact, the two sequences represent distinct nonrepeat regions of the target (false matches owing to repeat regions are counted separately). A formula forp false is given in theorem 5 of Appendix. |
| • λfalse = 2(C −m + 1)(N − 1)p false denotes the expected number of nonoverlapping STCs declared (incorrectly, even in the absence of repeat homology) to overlap within a particular sequenced clone extending in a particular direction. This formula is justified in Appendix , following the proof of theorem 5. Locations of such STCs within the clone will be assumed to follow a Poisson process. |
| • Each repeat familywill be modeled, to ensure tractability, as a group of contiguous segments with similar sequences, and these segments will be conditionally independent given a family-prototype segment. This specification model expresses both similarity and randomness in a tractable manner. Placing the members of a repeat family in a contiguous group is intended to model a worst-case scenario. In reality, most repeated elements are separated by unique-sequence DNA. For the ith family (i = 1, …, φ) where φ denotes the number of families, we define: |
| • Li is the length, in bases, of each segment of the family. |
| • Ri is the number of repeating segments in the family. |
| • We assume that the family has a prototype segment (not necessarily present in the genome) consisting of Li bases selected independently at random from the αA, αC, αG, αT distribution. We recognize that the AT/GC content of some repeats deviates from the genomic average (e.g.,Alus are high in GC base pairs), but this assumption is made for tractability of the model. |
| • ɛi,family is the problem rate for the ith family (using the same terminology as earlier, even though these are not really “problems”). We assume that each segment’s bases are independently determined. A base is identical to the homologous prototype base with probability l − ɛi,family. With probability ɛi,family, the base is instead an independently sampled random base (with distribution specified by αA, αC, αG, and αT) that may, by coincidence, be the same base as in the prototype. |
| • ɛ* i,familyis the difference rate for the ith family, that is, the probability that a given base in one segment differs from the homologous base in another segment from the same family. Relationships are ɛ* i,family = [1 − (1 − ɛi,family)2](1 − α) and ɛi,family = 1 − √1̅ ̅−̅ ̅ɛ̅ ̅*̅ ̅ ̅ ̅i̅,̅f̅a̅m̅i̅l̅y̅/̅(̅1̅ ̅−̅ ̅α̅)̅, because differences can occur whenever either (or both) segments differ from the prototype. |
| • p i,repeatis the probability that a particular STC of one clone is (incorrectly) declared to match a particular homologous m-base portion of a sequenced clone (owing to repeat family homology) when, in fact, the two sequences refer to distinct, but homologous, regions of the target within the same repeat family. A formula forp i,repeat is given in theorem 6 of Appendix. |
| • λi,repeat = (C − m + 1)[Ri (N − 1)/(T −C + 1)]p i,repeat is the expected number of homologous STCs declared (incorrectly) to overlap within a particular sequenced clone (for a clone that is entirely within the repeat family) extending in a particular direction. This formula is justified in Appendix , following the proof of theorem 6. Locations of such STCs within the clone will be assumed to follow a Poisson process. |
| • Problems involving the selection of a clone to continue beyond a fully sequenced clone will be defined as follows: |
| • A problem I clone is one for which there is no clone in the library with a matching STC extending in a particular direction, either because this region is not represented in the library or because the STC match was not recognized owing to sequencing errors. Note that a problem I clone does not necessarily produce a gap, because the gap may be closed from the other direction, that is, the STC of the problem I clone may be declared to match the internal sequence of a clone being extended from another nucleation site. A general formula for the probability that a particular clone is a problem I clone is provided in theorem 7 of Appendix. |
| • A problem II clone is one for which at least one declared STC match extending in a particular direction exists in the library, but, of these declared matches, the one with minimum overlap is actually a false STC match. Note that some problem II clones will not actually pose a problem, because the clone with the STC match will be identified as false before being sequenced by using its fingerprint to establish consistency among overlapping clones, by using FISH to confirm its chromosomal location, or by identifying known repeats in the STC. In such a case, there may be a true declared STC match with larger overlap of the nucleation clone that could be chosen instead. A general formula for the probability that a particular clone is a problem II clone is provided in theorem 7 of Appendix. |
| • A problem clone is a clone that is either a problem I or a problem II clone extending in a particular direction. Note that a problem clone does not necessarily pose a problem in the sequencing effort because, in addition to the reasons cited in the two preceding paragraphs, a problem clone may never be selected for sequencing and extension (although it will be selected if it is identified as the minimally overlapping extension of a preceding clone that was sequenced). A general formula for the probability that a particular clone is a problem clone is provided in theorem 7 of Appendix . |
| • Costs are modeled as follows, with the basic unit being the sequencing cost per base of the STC resource and other costs expressed as ratios to this basic unit: |
| • Cost is measured in units of sequencing operations per base and is set here at 1 per base for STC sequencing and at 7.5 per base for sequencing an entire clone, although other values may be substituted. The costs per sequenced base pair are higher for the completely sequenced clone because a random shotgun strategy is assumed and multiple overlapping subclones need to be sequenced to assemble large contiguous sequences. Although each base in a clone assembled by shotgun is typically sequenced 8–10 times, we have used the more conservative value of 7.5, which is also intended to reflect the cost of isolating and handling each clone in the STC library. If, for example, m = 400 and C = 150,000, then the cost per clone is 800 to sequence both STC ends and 150,000 × 7.5 = 1.125 × 106 to sequence the entire clone. When converting to dollar values, these costs should include associated costs of clone isolation and storage. For example, if one cost unit is $0.03, then the cost per clone to sequence both STC ends would be $24, whereas the cost to sequence the entire clone would be $33,750. In the future, costs are expected to be lower. |
| • Cost per problem clone is set at twice the cost of sequencing an entire clone. This allows for the cost of sequencing an extra falsely matching clone, redundant sequencing of clones that have considerable overlap, and the cost of filling gaps in a directed fashion. Note that in practice the cost will often be much less, owing to rejection of the falsely matching clone before it is sequenced (e.g., based on fingerprinting and/or in situ hybridization). In addition, as previously noted, a problem clone may never even be selected for sequencing and extension. |
| The Expected Number of Problem Clones |
| An upper bound for the expected number of problem clones in the library, when extending in a particular direction, may be found by adding together the results of the following two theorems, which distinguish between clones that overlap a repeat region and those that do not. This result gives a conservative estimate of problem occurrences because a clone overlapping a repeat region is treated as though it is entirely contained within that region. |
| Theorem 1. The expected number of problem clones (for extension in a particular direction) that overlap repeat regions of the target is no larger than |
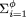
|
| Proof. This is the sum over repeat families of the expected number of clones that overlap that repeat region (first term within the summation) times the probability that a clone entirely within that repeat region is a problem (second term). A conservative bound results from applying the higher incidence of problems for clones entirely within the repeat family even to those that only partly overlap the repeat family. The probability has been obtained using theorem 7 in Appendix but recognizing that false STC matches may occur either at random or owing to homology within the repeat region; hence λf = λfalse + λl,repeat. |
| Theorem 2. The expected number of problem clones (for extension in a particular direction) that do not overlap any repeat region of the target is |
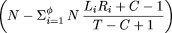
|
| Proof. This is the expected number of clones that do not overlap any repeat region (first term in parentheses) times the probability that such a clone is a problem (second term). The probability has been obtained using theorem 7 in Appendix , recognizing that false STC matches in this case may occur only at random. |
| The Expected Overlap for True STC Extensions |
| The overlap among clones selected for sequencing is costly because it increases the total number of clones that must be sequenced to cover the target. The size of this overlap is an indication of the amount of redundant effort because these bases in the target will have to be sequenced as part of the effort of sequencing both clones. When the minimally overlapping declared clone is selected for sequencing, it will overlap the clone being extended by at leastm base pairs. Overlap (in addition to this minimal amount) will decrease as the number of STCs in the library increases. |
| Theorem 3. Given a clone with at least one true declared STC match for extension in a particular direction, the expected size of the smallest overlap (in bases) among all true declared STC matches for extension in that direction is |

|
| If the entire target could be sequenced using clone extensions with this expected overlap size, then an estimate of the number of clones to be sequenced (ignoring problem clones for this calculation) is given by |
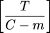
|
| Proof. In addition to the required m-base STC overlap, there will be an additional random overlap over the remaining C −m bases of the clone being extended. The probability distribution of the size of this random overlap is that of an exponential random variable (owing to the Poisson process) with mean (C − m)/λtrue, conditional on it being <C − m (i.e., there being a true STC event within this region). Adding the mean of this random variable to m, we have equation 3. The average extension is found by subtracting equation 3 from C. The estimated number of clones to sequence (equation 4) is then found by dividing the target length Tby this average extension. |
-
↵Although this model includes only substitution errors in the equations, our high chosen error rate is intended to account for both substitution and insertion/deletion errors, counting the insertion/deletion errors as substitutions.











