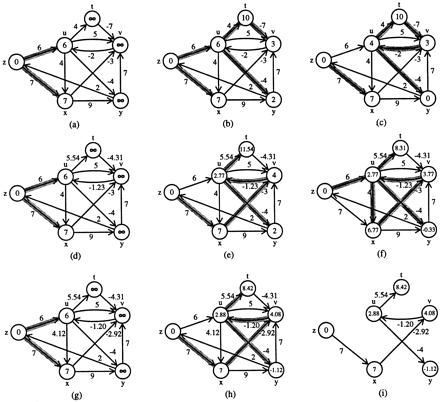
The individual steps of the modified Bellman–Ford algorithm are shown using the same graphical devices used in Figs. 5 and 6. a–ccorrespond to the first three relaxation passes of the Bellman–Ford algorithm. Once ATLAS detects the presence of the negative cycle <u, v, t> Bellman–Ford is halted, and the edge weights along the negative cycle are increased so as to eliminate the negative cycle. (d) The new edge weights.d–f represent the first three relaxation passes of Bellman–Ford on the modified constraint graph. Again, ATLAS detects the negative cycle <u, v, x> after three relaxation steps and Bellman–Ford is halted and the edge weights along the cycle are increased to eliminate the negative cycle. (g) The new constraint graph resulting from this modification. (h) The final solution given by Bellman–Ford for the constraint graph represented in g.











